Rev : 03 No : F.02.55

(1)

0

(2)

1

Rev : 03 No : F.02.55

BAB 1. LIMIT FUNGSI ALJABAR

3.30 Menentukan nilai limit aljabar

4.30 Menyelesaikan masalah yang berkaitan dengan limit fungsi aljabar KD/INDIKATOR SKKNI

-

KD/INDIKATOR IDUKA -

A. DEFINISI LIMIT

Pada dasarnya limit digunakan untuk menyatakan sesuatu yang nilainya mendekati nilai tertentu, seperti tak hingga yang pada dasarnya adalah angka yang sangat besar yang nilainya tidak dapat dipastikan. Limit menjelaskan suatu fungsi jika batas tertentu didekati. Jika suatu fungsi tidak terdefinisi untuk titik tertentu, tetapi kita masih bisa mencari nilai yang didekati oleh fungsi tersebut apabila titik tertentu makin didekati yaitu dengan limit.

Yuk, kita pelajari limit fungsi aljabar bersama, supaya pemahaman mengenai limit akan lebih mendalam.

Perhatikan fungsi f(x) = 2x + 1, dengan xR. Dalam hal ini, akan ditentukan f(x) dengan x bergerak mendekati 3. Hasilnya dapat dilihat pada tabel di bawah ini.

x … 2,98 2,99 3 3,01 3,02 3,03 …

f(x) = 2x + 1 … 6,96 6,98 … 7,02 7,04 7,06 …

Tabel 1.1 Limit Fungsi

Dari tabel 1.1 di atas, untuk x mendekati 3 dari arah kanan dan arah kiri, ternyata nilai f(x) semakin mendekati 7. Dalam notasi limit, ditulis sebagai berikut :

Limit kiri = Limit kanan KOMPETENSI DASAR :

MATERI PEMBELAJARAN

(3)

2

Rev : 03 No : F.02.55 Jika x mendekati c dari kiri dan kanan, maka nilai f(x) mendekati L dari kedua arah.

L merupakan limit fungsi f(x) untuk x mendekati c dan dirumuskan sebagai berikut :

Maksudnya adalah untuk nilai x yang mendekati c, maka f(x) akan mendekati L.

B. LIMIT FUNGSI ALJABAR 1. Limit Fungsi Berbentuk

Bentuk ini dapat diselesaikan dengan menggunakan Teorema Limit. Jika n adalah bilangan bulat positif, k suatu konstanta, serta f dan g adalah fungsi-fungsi yang memiliki limit di c, maka berlaku teorema limit berikut.

T – 1 T – 2 T – 3 T – 4 T – 5 T – 6

T – 7

T – 8

T – 9

dengan jika n genap atau jika n ganjil.

Contoh Soal

Hitunglah nilai limit berikut ini!

a. c.

Diingat ya !!!

(4)

3

Rev : 03 No : F.02.55 b. d.

Penyelesaian:

a. T – 1

b. T – 3

T – 8 T – 2

c. T – 5

T – 2

d. T – 7

T – 9

T – 4

T – 1 dan T – 2

(5)

4

Rev : 03 No : F.02.55 Berikut ini adalah contoh soal bentuk yang dapat diselesaikan dengan tidak menggunakan teorema limit.

a) Langsung disubstitusikan, jika hasilnya bukan bentuk tak tentu

Dalam menyelesaikan limit digunakan teorema substitusi, yaitu jika f(x) adalah suatu fungsi rasional, maka = f(c) asalkan dalam kasus fungsi rasional nilai penyebut di c tidak nol.

Contoh Soal

Hitunglah nilai dari limit berikut ini!

a. b.

Penyelesaian:

a.

b.

b) Jika setelah disubstitusikan menghasilkan bentuk tak tentu, maka langkah selanjutnya adalah difaktorkan, disederhanakan, kemudian disubstitusikan atau dengan menggunakan Teorema L’Hospital (turunan pertama fungsi)

TURUNAN PERTAMA FUNGSI

Contoh :



Informatif Bentuk tak tentu

(6)

5

Rev : 03 No : F.02.55

Contoh Soal

a. b.

Penyelesaian:

a.

Karena hasilnya tidak terdefinisi (tak tentu), maka harus diselesaikan dengan cara memfaktorkan, menyederhanakan, kemudian disubstitusikan.

Dengan cara Teorema L’Hospital:

b.

Karena hasilnya tidak terdefinisi (tak tentu), maka harus diselesaikan dengan cara memfaktorkan, menyederhanakan, kemudian disubstitusikan.

Dengan cara Teorema L’Hospital:

2. Limit Fungsi Berbentuk

Khusus untuk limit fungsi aljabar dengan x mendekati 0 berlaku :

Berlaku :

Untuk menyelesaikan limit fungsi aljabar yang mendekati 0 (nol), maka caranya adalah pembilang dan penyebut dibagi dengan variabel pangkat terendah.

Diingat ya !!!

(7)

6

Rev : 03 No : F.02.55 Nilai dari adalah :

 Jika pangkat terendah f(x) = pangkat terendah g(x), maka

 Jika pangkat terendah f(x) > pangkat terendah g(x), maka

 Jika pangkat terendah f(x) < pangkat terendah g(x), maka

Contoh Soal

a. b. c.

Penyelesaian:

a. (diambil variabel pangkat terendah)

b. (diambil variabel pangkat terendah)

c. (diambil variabel pangkat terendah)

3. Limit Fungsi Berbentuk

Khusus untuk limit fungsi aljabar dengan x mendekati berlaku :

Berlaku :

Untuk menyelesaikan limit fungsi aljabar yang mendekati ∞, maka caranya adalah pembilang dan penyebut dibagi dengan variabel pangkat tertinggi.

Diingat ya !!!

(8)

7

Rev : 03 No : F.02.55 Nilai dari adalah :

 Jika pangkat tertinggi f(x) = pangkat tertinggi g(x), maka

 Jika pangkat tertinggi f(x) > pangkat tertinggi g(x), maka

 Jika pangkat tertinggi f(x) < pangkat tertinggi g(x), maka

Contoh Soal

a. b. c.

Penyelesaian:

a. (diambil variabel pangkat tertinggi)

b. (diambil variabel pangkat tertinggi)

c. (diambil variabel pangkat tertinggi)

4. Limit Fungsi Berbentuk (Bentuk Akar)

Contoh Soal

a.

b.

Penyelesaian:

a. dari didapatkan nilai a = 1, b = 5 dan p = –4

(9)

8

Rev : 03 No : F.02.55 b. dari didapatkan nilai a = 4, b = –2 dan p = 4

C. APLIKASI LIMIT ALJABAR

Beberapa soal yang berkaitan dengan limit aljabar : 1.

2.

3.

Penyelesaian:

1.

2.

(10)

9

Rev : 03 No : F.02.55 3.

A. Penilaian Sikap

Penilaian dilakukan secara observasi untuk menumbuhkan budaya kerja (5R, PPK, 4C, Literasi dan lain sebagainya baik terintegrasi dalam KBM maupun observasi tidak langsung diluar KBM)

No Hari/Tanggal Nama Peserta Didik Nama

Kejadian/Perilaku Tindak Lanjut 1

2

B. Penilaian Pengetahuan LATIHAN 1

Pilihlah jawaban dengan memberi tanda silang (x) pada salah satu huruf A, B, C, D atau E yang dianggap paling benar!

Atau kerjakan melalui link https:/bit.ly/Latihanlimitaljabar dan ikuti petunjuk pengerjaan soal.

1. ...

3

3 27

lim

_3 ^x_x^_ ^ x

A. 3 1 B. 3 C. 9 D. 27 E. 81

2. ...

2 2 3

2 2

lim

_1 ^x_x ^__x^x_^ ^ x

A. 9 1

PENILAIAN HASIL BELAJAR

(11)

10

Rev : 03 No : F.02.55 B. 3

1

C. 0

D. 3

1

E. 9

1

3. ...

2

2 4

lim

_2 ^x_x_^ ^ x

A. –4 B. –2 C. 0 D. 2 E. 4

4. ...

2 2 3 2 ²

lim

_2 ^x _x^_^x^ ^ x

A. 0 B. 1 C. 3 D. 5 E. 7

5. ...

3 3 5 2 ²

lim

_3 ^x _x^_^x^ ^ x

A. 0 B. 4 C. 6 D. 7 E. 12

6. ...

3

2 9

lim

__3 ^x_x_^ ^ x

A. –6 B. –3 C. 3 D. 6 E. 9

7. ...

9 15 11 2

2 2

lim

_3 ^x _x^ _^x^ ^ x

A. 0 B. 6 1

C. 3 1

D. 6 5

E. 6 11

(12)

11

Rev : 03 No : F.02.55

8. ...

4 8 2

2 2

lim

2 ^ _ ^ ^

 x

x x

x

A. 4

 3

B. 2

 3

C. 0 D. 2

3

E. 4 3

No Soal PG Bobot Persoal PG Skor

Penilaian Nilai

1 13 100 Nilai Siswa

……….

Paraf Guru

……….

Dwi Yuni R., S.Pd

2 10

3 13

4 11

5 13

6 13

7 14

8 13

LATIHAN 2

Atau kerjakan melalui link https:/bit.ly/Latihanlimittakhingga dan ikuti petunjuk pengerjaan soal.

1. ₂ ...

2 4

lim

_0 ^x _x^^x ^ x

A. 1 B. 2 1

C. 0 D. 2

 1

E. –1

2. ...

1 4

5 2

3 2

lim

__ ^x _x^_^x^ ^

x

A. –1 B. 2

 1

C. 0 D. 2 1

(13)

12

Rev : 03 No : F.02.55 E. 1

3. ...

1 1

2 2

lim

__ _x^_^x^_x_^x ^

x

A. –1 B. 0 C. 1 D. 2 E. 3

4. ...

2 3

5 7 4

2 2

lim

__ ^x_^_x_^x^_x ^

x

A. ∞ B. 0 C. 3 4 D. 2 E. 4

5. 3 ² 4 ...

lim

_0 ^x _x^ ^x ^ x

A. –4 B. –1 C. 0 D. 3 4 E. ∞

6. ...

2 5

15 11 3

2 3 2

lim

__ ^x _x^_^x_x^ ^

x

A. 0 B. 5 3

C. 2 3

D. 5 7

E. ∞

7.

lim

__ ^x² ^2^x^ ^x² ^^x ^...

x

A. 2

 3

B. 2

 1

C. 2 1

D. 1 E. 2 3

(14)

13

Rev : 03 No : F.02.55 8.

lim

4 ² ^3 ^4^ 4 ²^5 ^4^...





x x x

x

A. –2 B. –1 C. 0 D. 1 E. 2

……….

Paraf Guru

……….

Dwi Yuni R., S.Pd

2 10

3 13

4 11

5 13

6 13

7 14

8 13

C. Penilaian Ketrampilan LATIHAN 3

Kerjakan soal-soal di bawah ini pada buku tulis kalian.

1. Diketahui fungsi Jika Nilai p = …

2. Sebuah mobil bergerak dengan kecepatan sesaat yang dirumuskan dengan

dengan dalam meter dan t dalam detik. Jika t mendekati 3 detik, maka kecepatan mobil tersebut adalah … m/detik.

3. Diketahui Nilai p yang memenuhi adalah …

4. Nilai dari adalah … 5. Nilai dari adalah …

Penskoran Penilaian Ketrampilan Proses

No Komponen/Sub Komponen Skor/Bobot

Penilaian

1 Proses 75

Uraian jawaban dengan rumus

1. Nilai variabel p 15

2. Kecepatan mobil 15

3. Nilai variabel p 15

4. Limit fungsi aljabar 15

5. Limit fungsi aljabar 15

2 Hasil 15

Hasil sesuai dengan rumus 15

3 Waktu 10

Ketepatan waktu kerja 10

(15)

16

Rev : 03 No : F.02.55 Hasil Penilaian Proses

SKOR/BOBOT Proses Hasil Waktu Nilai Siswa

Maks/Perolehan Paraf Guru

Skor Maksimal 75 15 10 100

…………..

Skor Perolehan ……. ……. ……. …………

Man Jadda Wajada

Barang Siapa Bersungguh-Sungguh Pasti Berhasil

(16)

17

Rev : 03 No : F.02.55

BAB 2. TURUNAN FUNGSI

3.31 Menentukan turunan fungsi aljabar menggunakan definisi limit fungsi atau sifat-sifat turunan fungsi serta penerapannya

3.32 Menganalisis keterkaitan turunan pertama fungsi dengan nilai maksimum, nilai minimum, dan selang kemonotonan fungsi serta kemiringan garis singgung kurva

4.31 Menyelesaikan masalah yang berkaitan dengan turunan fungsi aljabar

4.32 Menyelesaikan masalah kontekstual yang berkaitan dengan turunan pertama fungsi aljabar

KD/INDIKATOR SKKNI -

A. DEFINISI TURUNAN

Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel). Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

B. PENERAPAN TURUNAN

Berikut merupakan beberapa penerapan turunan.

 Turunan dapat diterapkan untuk menghitung gradien dari garis singgung suatu kurva.

 Turunan dapat digunakan untuk menentukan interval dimana suatu fungsi naik atau turun.

 Turunan dapat diterapkan untuk menentukan nilai stasioner suatu fungsi.

 Turunan dapat diterapkan dalam menyelesaikan permasalahan yang berkaitan dengan persamaaan gerak.

 Turunan dapat digunakan untuk menyelesaikan permasalahan maksimum-minimum.

KOMPETENSI DASAR :

MATERI PEMBELAJARAN

(17)

18

Rev : 03 No : F.02.55

C. RUMUS TURUNAN

Rumus Turunan adalah :

Berikut merupakan beberapa rumus dasar untuk menentukan turunan.

 f(x) = c; dengan c merupakan konstanta, maka f’(x) = 0

 f(x) = x, maka f’(x) = 1

 f(x) = U + V maka f’(x) = U’ + V’

 f(x) = U – V maka f’(x) = U’ – V’

 f(x) = U . V maka f’(x) = U’ . V + U . V’

 f(x) = V

U maka f’(x) = ' ₂ '

V UV V

U 

Contoh Soal

Tentukan turunan pertama dari :

a. f(x) = 8 d. f(x) = 5x³ +4x² – 3x + 2

b. f(x) = 3x⁴ e. f(x) = (x² – 3) (x² – 2x – 5)

c. f(x) = 2x³ + 2x f. f(x) =

5 2

2

2 3





 x

x x

Penyelesaian:

a. f(x) = 8 → f’(x) = 0

b. f(x) = 3x⁴ → f’(x) = 3.4x^4–1 = 12x³

c. f(x) = 2x³ + 2x → f’(x) = 2.3x^3–1 + 2 = 6x² + 2

d. f(x) = 5x³ +4x² – 3x + 2 → f’(x) = 5.3x^3–1 +4.2x^2–1 – 3 + 0 = 15x² + 8x – 3 e. f(x) = (x² – 3) (x² – 2x + 5)

Misalkan :

u(x) = x² – 3 → u’(x) = 2x

v(x) = x² – 2x + 5 → v’(x) = 2x – 2

f’(x) = u’(x) . v(x) + u(x) . v’(x)

= 2x . (x² – 2x + 5) + (x² – 3) . (2x – 2)

= 2x³ – 4x² + 10x + 2x³ – 2x² – 6x + 6

= 4x³ – 6x² + 4x + 6 Diingat ya !!!

(18)

19

Rev : 03 No : F.02.55 f.

5 2

2 ) 3

(

2





  x

x x x

f

Misalkan :

u(x) = x² – 3x + 2 → u’(x) = 2x – 3

v(x) = 2x – 5 → v’(x) = 2

2 2

2 2 2

) 5 2 (

11 10 2

) 5 2 (

4 6 2 15 6 10 4

) 5 2 (

) 2 ).(

2 3 ( ) 5 2 ).(

3 2 (

)) ( (

) ( ' ).

( ) ( ).

( ) '

( '





 











 







 

x x x

x

x x x

x x

x

x x x

x

x v

x v x u x v x x u

f

D. TURUNAN FUNGSI DENGAN BENTUK f(x) = {U}

ⁿ Jika f(x) = (U)ⁿ , maka untuk mencari turunan pertamanya

dapat menggunakan rumus :

Contoh Soal

1. Tentukan turunan pertama dari f(x) = (6x – 9)² ! Penyelesaian :

U = 6x – 9, → U’ = 6 ; n = 2 f(x) = (6x – 9)², maka didapatkan : f’(x) = n . (U)^n-1. U’

f’(x) = 2 . (6x – 9)^2–1. 6 f’(x) = 12 (6x – 9) f’(x) = 72x – 108

Didapatkan nilai f’(x) = 72x – 108

2. Tentukan turunan pertama dari f(x) = (5x + 1)³ ! Penyelesaian :

n = 3 ; U = 5x + 1 ; U’ = 5 f’(x) = n . (U)^n-1 . U’

f’(x) = 3 . (5x + 1)^3–1. 5 f’(x) = 15 (5x + 1)²

f’(x) = n . (U)

^n-1

. U’

Diingat ya !!!

(19)

20

Rev : 03 No : F.02.55 f’(x) = 15 {(5x + 1) (5x + 1)}

f’(x) = 15 {25x² +10x + 1}

f’(x) = 375x² + 150x + 15

Diapatkan nilai f’(x) = 375x² + 150x + 15

E. PERMASALAHAN YANG BERKAITAN DENGAN TURUNAN

Permasalahan 1 :

Keuntungan sebuah produsen ponsel tertentu dapat dirumuskan oleh fungsi berikut.

P(x) = –2.000x³ + 12.000x² + 126.000x

Dimana p adalah laba dalam dolar dan x adalah tingkat produksi dalam ribuan unit.

Berapa banyak unit yang harus diproduksi untuk memaksimalkan laba ? Penyelesaian :

P(x) = –2.000x³ + 12.000x² + 126.000x

Untuk memaksimalkan laba, maka nilai p’(x) = 0 P(x) = –2.000x³ + 12.000x² + 126.000x

P’(x) = –2000 . 3x² + 12000 . 2x + 126000 P’(x) = –6.000x² + 24.000x + 126.000 Maka –6.000x² + 24.000x + 126.000 = 0

↔ –6x² + 24x + 126 = 0 (sederhanakan bentuk dibagi 6) ↔ –x² + 4x + 21 = 0

↔ x² – 4x – 21 = 0 (Cari nilai x1 dan x² dengan cara pemfaktoran) (x – 7) (x + 3) = 0

x – 7 = 0 atau x + 3 = 0 x = 7 atau x = –3 Nilai yang memungkinkan adalah 7,

sehingga banyak unit dalam ribuan menjadi 7.000 unit Permasalahan 2 :

Sebuah peluru ditembakkan vertikal ke atas dengan kecepatan awal Vo m/detik. Tinggi peluru setelah t detik dinyatakan dengan fungsi h(t) = 100 + 40t − 4t². Tentukan tinggi masksimum yang dapat dicapai peluru tersebut ?

Penyelesaian : h(t) = 100 + 40t − 4t²

⇒ h'(t) = 40 − 8t

(20)

21

Rev : 03 No : F.02.55 Tinggi peluru akan maksimum, jika :

h'(t) = 0 40 − 8t = 0

⇒ −8t = −40 t = 5

h(t) = 100 + 40t − 4t² h(5) = 100 + 40(5) − 4(5)² h(5) = 100 + 200 – 100 h(5) = 200

Jadi, tinggi maksimum peluru dicapai pada saat t = 5, dengan tinggi maksimumnya adalah 200 meter.

F. FUNGSI NAIK DAN TURUN

Definisi Fungsi Naik dan Turun

 Suatu fungsi f dikatakan naik pada suatu selang jika untuk sembarang dua bilangan x1

dan x2 dalam selang tersebut x1 < x2 mengakibatkan f(x1) < f(x2).

 Suatu fungsi f dikatakan turun pada suatu selang jika untuk sembarang dua bilangan x1

dan x2 dalam selang tersebut x1 < x2 mengakibatkan f(x1) > f(x2).

Teorema Uji Fungsi Naik dan Turun

Misalkan f adalah fungsi yang kontinu pada selang tutup [a, b] dan terdiferensialkan pada selang buka (a, b).

1. Jika f ’(x) bertanda positif atau f ’(x) > 0 untuk semua x dalam (a, b), maka f naik pada [a, b].

2. Jika f ’(x) bertanda negative atau f ’(x) < 0 untuk semua x dalam (a, b), maka f turun pada [a, b].

3. Jika f ’(x) bertanda netral atau f ’(x) = 0 untuk semua x dalam (a, b), maka f konstan pada [a, b].

(21)

22

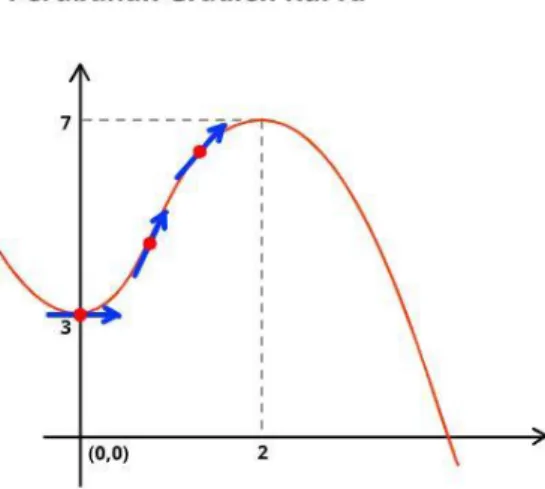
Rev : 03 No : F.02.55 Perhatikan sketsa grafik suatu fungsi f(x) berikut.

Perhatikan bahwa kurva yang ditandai dengan warna merah adalah ketika fungsi itu dikatakan naik, dan biru untuk fungsi turun. Titik a dan b disebut titik stasioner, yaitu titik di mana fungsi itu diam (tidak naik maupun tidak turun). Sehingga dapat disimpulkan:

 Fungsi f(x) naik saat x < a atau x > b

 Fungsi f(x) turun pada saat a < x < b

Contoh Soal

1. Diberikan fungsi f(x) = x³ + 3x² – 9x + 5. Tentukan interval x yang memenuhi kurva fungsi f(x) selalu naik !

Penyelesaian :

f(x) = x³ + 3x² – 9x + 5 f’(x) = 3x²+ 6x – 9

Syarat fungsi naik adalah f’(x) > 0 3x²+ 6x – 9 = 0 bagi 3

x²+ 2x – 3 = 0 (x + 3) (x – 1) = 0

x = –3 atau x = 1 (x1 bernilai lebih kecil dari x2), maka : Didapatkan x1 = –3 dan x2 = 1

f(x) naik pada interval x < x1 atau x > x2

x < –3 atau x > 1

Gambar 2.1 Grafik Fungsi Naik dan Turun

(22)

23

Rev : 03 No : F.02.55 2. Diberikan fungsi f(x) = 2x³ – 3x² – 12x + 7. Tentukan interval x yang

memenuhi kurva fungsi f(x) selalu turun ! Penyelesaian :

f(x) = 2x³ – 3x² – 12x + 7 f’(x) = 6x²– 6x – 12

Syarat fungsi turun adalah f’(x) < 0 6x²– 6x – 12 = 0 bagi 6

x²– x – 2 = 0 (x – 2) (x + 1) = 0

x = 2 atau x = –1 (x1 bernilai lebih kecil dari x2), maka : Didapatkan x1 = –1 dan x2 = 2

f(x) turun pada interval x1 < x < x2

–1 < x < 2

G. GARIS SINGGUNG DAN GARIS NORMAL

Pernahkah Kalian mengunjungi tempat wisata yang menyajikan permainan seperti roller coaster atau halilintar? Coba Kalian ingat, bentuk lintasan permainan itu seperti lengkungan atau kurva, bukan? Dalam kehidupan sehari-hari banyak kejadian suatu benda bergerak yang lintasannya berbentuk lengkungan atau kurva. Selain roller coaster, mungkin kalian pernah menyaksikan atraksi pesawat tempur yang meninggalkan bekas asap berbentuk lengkungan atau kurva. Perhatikan gambar lintasan pesawat yang berbentuk kurva berikut.

Gambar 2.2 Lintasan pesawat berbentuk kurva

(23)

24

Rev : 03 No : F.02.55 Jika lintasan pesawat tersebut digambarkan dalam bentuk kurva, kira-kira akan tampak seperti gambar di bawah ini.

Nah, kalau pada bagian sebelumnya Anda hanya mengenal gradien garis singgung untuk menentukan fungsi naik dan fungsi turun, pada kegiatan belajar kali ini Anda akan mempelajari persamaan garis tersebut.

GARIS SINGGUNG KURVA

Sebuah garis disebut sebagai garis singgung kurva jika garis tersebut hanya memiliki satu titik persekutuan (titik singgung) dengan kurva. Karena garis singgung hanya memiliki satu titik persekutuan dengan kurva, maka untuk mendapatkan nilai kemiringannya dapat kita dekati dengan garis lain (garis secan) yang gradiennya dapat ditentukan secara langsung.

GRADIEN GARIS SINGGUNG KURVA

\

Gambar 2.3 Perubahan gradien kurva

(24)

25

Rev : 03 No : F.02.55

Contoh Soal

Gradien garis singgung kurva y = x²+ 5x – 4 di titik (1, 3) adalah ...

Penyelesaian:

Dari f(x) = x² + 5x – 4, maka didapatkan turunan pertamanya : f’(x) = 2x + 5

x0 = 1, maka nilai gradiennya yaitu : m = f’(x0)

= 2x + 5 = 2(1) + 5 = 2(1) + 5 = 2 + 5

= 7 Jadi gradien garis singgung kurva adalah 7.

GARIS NORMAL KURVA

Setelah memahami definisi garis singgung dan gradien garis singgung, belum lengkap jika kalian belum mengetahui tentang garis normal. Karena pada setiap garis singgung suatu kurva, terdapat garis normal yang tegak lurus dengan garis singgung tersebut

Gambar 2.4 Garis singgung dan garis normal

(25)

26

Rev : 03 No : F.02.55

PERSAMAAN GARIS SINGGUNG KURVA

Garis singgung bergradien m, jika titik yang dilaluinya adalah titik singgung A(x1,y1) maka persamaan garis singgungnya adalah :

PERSAMAAN GARIS NORMAL KURVA

Persamaan garis normal bergradien m

1

dan melalui A(x1,y1) adalah :

Contoh Soal

Tentukan Persamaan garis singgung dan garis normal pada kurva y = x⁴ - 7x² + 20 di titik yang berabsis 2 !

Penyelesaian:

Persamaan Garis Singgung

x = 2, maka y = x⁴ - 7x² + 20 y = 2⁴ - 7.2² + 20

y = 16 - 28 + 20 = 8 Didapatkan, titik singgung A(2,8)

Gradien Garis singgung Dari y = x⁴ - 7x² + 20, maka : m = y' = 4x³ - 14 x

= 4.2³ - 14.2 = 32 - 28 = 4

Gradien = 4 melalui titik singgung A(2,8)

(26)

27

Rev : 03 No : F.02.55 Persamaan garis singgung dari gradien

m = 4 dan titik singgung A(2, 8) adalah : y – y1 = m(x – x1)

y – 8 = 4(x – 2) y – 8 = 4x – 8 y = 4x – 8 + 8 y = 4x

Jadi, persamaan garis singgungnya adalah y = 4x Persamaan Garis Normal

Gradien garis singgung m = 4, maka gradien garis normal

4 1

2

 m

Garis normal bergardien

4 1

2

 

m melalui titik singgung A(2,8),

yaitu x1 = 2 dan y1 = 8

Persamaan garis normalnya adalah : y – y1 = m2(x – x1)

y – 8 = 4

1

(x – 2)

y – 8 = x 4

1

+ 4 2

4y – 32 = –x + 2 x + 4y = 2 + 32 x + 4y = 34

Jadi, persamaan garis normalnya adalah x + 4y = 34

H. TITIK DAN NILAI STASIONER

Titik stasioner merupakan titik tempat fungsi berhenti naik atau turun untuk sementara, yaitu titi bergradien nol.

Perhatikan grafik fungsi di bawah ini !

Gambar 2.5 Titik stasioner Semua dikali 4

(27)

28

Rev : 03 No : F.02.55 Dari grafik diatas dapat dilihat bahwa f(a) adalah nilai stasioner di x = a dan f(b) adalah nilai stasioner di x = b, dimana turunan pertama di titik-titik tersebut bernilai nol.

Selanjutnya titik (a, f(a)) dan (b, f(b)) disebut titik stasioner dari fungsi f.

Contoh Soal 1:

Tentukan nilai stasioner dan titik stasioner dari fungsi f(x) = x² − 4x ! Penyelesaian:

(x) = x² − 4x f '(x) = 2x − 4

f(x) stasioner ⇒ f '(x) = 0

⇔ 2x − 4 = 0

⇔ 2x = 4

⇔ x = 2

Jadi, nilai stasioner dicapai pada saat x = 2

Contoh Soal 2:

Tentukan nilai stasioner dan titik stasioner dari fungsi f(x) = x³− 3x + 1 ! Penyelesaian:

f(x) = x³− 3x + 1 f '(x) = 3x² − 3

f(x) stasioner ⇒ f '(x) = 0

⇔ 3x² − 3 = 0

⇔ x² − 1 = 0

⇔ (x + 1)(x − 1 ) = 0

⇔ x = −1 atau x = 1

Nilai stasioner pada x = −1 : f(−1) = (−1)³ − 3(−1) + 1 = 3

Nilai stasioner pada x = 1 : f(1) = (1)³ − 3(1) + 1 = −1

Titik stasioner : (−1, 3) dan (1, −1)

Nilai stasioner sering juga disebut sebagai bakal calon nilai ekstrim.

Ada 2 jenis ekstrim fungsi, yaitu nilai balik maksimum dan nilai balik minimum. Nilai balik maksimum/minimum sering juga disebut dengan nilai maksimum/minimum relative atau maksimum/minimum lokal.

Nilai stasioner : f(2) = (2)² − 4(2) = −4 Titik stasioner : (2, −4)

(28)

29

Rev : 03 No : F.02.55 Untuk menentukan jenis ektrim suatu fungsi dapat dilakukan dengan uji turunan pertama dan uji turunan kedua.

Uji Turunan Pertama

Misalkan f(a) adalah nilai stasioner di x = a.

1. f(a) adalah nilai balik maksimum, jika : untuk x < a maka f '(x) > 0 (naik) untuk x > a maka f '(x) < 0 (turun) 2. f(a) adalah nilai balik minimum, jika : untuk x < a maka f '(x) < 0 (turun) untuk x > a maka f '(x) > 0 (naik)

Contoh Soal 3:

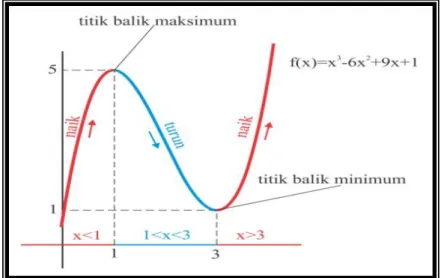
Dengan menggunakan uji turunan pertama, tentukan jenis ekstrim dari fungsi f(x) = x³ − 6x² + 9x + 1 !

Penyelesaian:

f(x) = x³ − 6x² + 9x + 1 f '(x) = 3x² − 12x + 9

f '(x) = 0

⇔ 3x² − 12x + 9 = 0

⇔ x² − 4x + 3 = 0

⇔ (x − 1) (x − 3) = 0

⇔ x = 1 atau x = 3

Nilai stasioner di x = 1 adalah f(1) = (1)³ − 6(1)² + 9(1) + 1 = 5

Nilai stasioner di x = 3 adalah f(3) = (3)³ − 6(3)² + 9(3) + 1 = 1

 Karena pada x = 1 terjadi perubahan dari naik menjadi turun, maka f(1) = 5 adalah nilai balik maksimum. Didapatkan pula titik balik maksimumnya (1, 5).

 Karena pada x = 3 terjadi perubahan dari turun menjadi naik, maka f(3) = 1 adalah nilai balik minimum. Didapatkan pula titik balik minimumnya (3, 1).

(29)

30

Rev : 03 No : F.02.55 Uji Turunan Kedua

Misalkan f(a) adalah nilai stasioner di x = a

 Jika f ''(a) < 0 maka f(a) adalah nilai balik maksimum.

 Jika f ''(a) > 0 maka f(a) adalah nilai balik minimum.

 Jika f ''(a) = 0 maka jenis ekstrim belum dapat ditetapkan (gunakan uji turunan pertama untuk menentukan jenis ekstrimnya)

Contoh Soal 4:

Dengan menggunakan uji turunan kedua, tentukan Titik balik maksimum dan minimum dari fungsi f(x) = x³− 6x²+ 9x + 1 !

Penyelesaian:

f(x) = x³− 6x²+ 9x + 1 f '(x) = 3x² − 12x + 9 f ''(x) = 6x – 12 f '(x) = 0

⇔ 3x² − 12x + 9 = 0

⇔ x² − 4x + 3 = 0

⇔ (x − 1) (x – 3) = 0

⇔ x = 1 atau x = 3

Nilai stasioner pada x = 1 : f(1) = (1)³ − 6(1)² + 9(1) + 1 = 5

Nilai stasioner pada x = 3 f(3) = (3)³ − 6(3)² + 9(3) + 1 = 1

Gambar 2.6 Titik stasioner contoh soal 3

(30)

31

Rev : 03 No : F.02.55 Uji Turunan Kedua

f ''(1) = 6(1) − 12 = −6 < 0

Karena f ''(1) < 0 maka f(1) = 5 adalah nilai balik maksimum. Titik balik maksimumnya (1, 5).

f ''(3) = 6(3) − 12 = 6 > 0

Karena f ''(3) > 0 maka f(3) = 1 adalah nilai balik minimum. Titik balik minimumnya (3, 1).

A. Penilaian Sikap

Penilaian dilakukan secara observasi untuk menumbuhkan budaya kerja (5R, PPK, 4C, Literasi dan lain sebagainya baik terintegrasi dalam KBM maupun observasi tidak langsung diluar KBM)

No Hari/Tanggal Nama Peserta Didik Nama

Kejadian/Perilaku Tindak Lanjut 1

2

B. Penilaian Pengetahuan LATIHAN 1

Atau kerjakan melalui link https:/bit.ly/Latihan1Turunan dan ikuti petunjuk pengerjaan soal.

1 Turunan pertama dari f(x) = 4x⁵ adalah … A. 4x⁶

B. 5x⁶ C. 4x⁴ D. 5x⁴ E. 20x⁴

2 Jika f(x) = , 4

8 2

5

3 



 x x

x , maka f’(x) = …

A. ₂

) 8 2 (

34

 x

PENILAIAN HASIL BELAJAR

(31)

32

Rev : 03 No : F.02.55

B. ₂

) 8 2 (

18

 x

C. ₂

) 8 2 (

1

 x

D. ₂

) 8 2 (

8



 x

E. ₂

) 8 2 (

34



 x

3 Turunan pertama dari fungsi f(x) = (2x² – 4)(3x + 3) adalah … A. 6x³ + 6x² – 12x – 12

B. 6x² + 12x – 12 C. 18x² + 12x – 12 D. 18x³ + 6x – 12 E. 18x³ + 6x – 8

4 Turunan pertama dari f(x) = 3x⁴ – 5x² + 2x + 7 adalah … A. f’(x) = 12x³ – 10x² + 2x + 2

B. f’(x) = 12x³ – 10x² + 2x + 7 C. f’(x) = 12x³ + x² – 10x + 2 D. f’(x) = 12x³ – 10x + 2 E. f’(x) = 12x³ – 10x + 9

5 Turunan pertama dari f(x) = (2x³ – 5x² – 3)(4x + 10) adalah … A. f’(x) = 32x³ + 40x² + 100x – 10

B. f’(x) = 32x³ – 40x² – 100x – 12 C. f’(x) = 32x³ – 100x – 12

D. f’(x) = 32x² – 100x + 12 E. f’(x) = 32x²– 100x – 12 6 Jika f(x) =

1 3 2



 x

x, maka f’(x) = …

A. ₂

) 1 (

6

 x

x

B. ₂

) 1 (

5 6



 x

x

(32)

33

Rev : 03 No : F.02.55

C. ₂

) 1 (

5 6





 x

x

D. ₂

) 1 (

5

 x

E. ₂

) 1 (

5



 x

……….

Paraf Guru

……….

Dwi Yuni R., S.Pd

2 20

3 15

4 15

5 15

6 15

LATIHAN 3

1 Interval x yang membuat kurva f(x) = x³ – 6x² + 9x + 2 selalu turun adalah …

A. –1 < x < 3 B. 0 < x < 3 C. 1 < x < 3 D. x < 1 atau x > 3 E. x < 0 atau x > 3

2 Diberikan fungsi g(x) = 2x³ – 9x² + 12x. Interval x yang memenuhi kurva fungsi g(x) selalu naik adalah …

A. x < –2 atau x > –1 B. x < –1 atau x > 2 C. x < 1 atau x > 2 D. 1 < x < 2

E. –1 < x < 2

(33)

34

Rev : 03 No : F.02.55 3 Grafik fungsi y = x³ – 3x² – 9x + 11 naik pada interval …

A. x < –1 atau x > 3 B. x < –3 atau x > 1 C. x < 1 atau x > 3 D. –1 < x < 3 E. –3 < x < 1

4 Grafik fungsi y = x³ – 6x² + 9x + 4 turun pada interval … A. x < 1 atau x > 3

B. x < –3 atau x > –1 C. x < –1 atau x > 3 D. 1 < x < 3

E. –3 < x < –1

5 Interval nilai x yang memenuhi agar grafik f(x) = x³ – 3x² + 5 turun adalah …

A. x < –2 atau x > 2 B. 0 < x < 2

C. –1 < x < 2 D. x > 2 E. x < 0

6 Diberikan fungsi f(x) = 2x³ – 3x² – 12x + 7. interval x yang memenuhi kurva fungsi f(x) selalu naik adalah …

A. x < –1 atau x > 2 B. x < 1 atau x > –2 C. –1 < x < 2 D. –2 < x < 1 E. 0 < x < 1

……….

Paraf Guru

……….

Dwi Yuni R., S.Pd

2 20

3 15

4 15

5 15

6 15

(34)

35

Rev : 03 No : F.02.55 LATIHAN 5

1 Nilai stasioner dari f(x) = x² +3x adalah ….

A. –9 B. –3 C. 0 D. 3 E. 9

2 Nilai balik maksimum dari fungsi f(x) = x³ – 3x² – 9x + 6 adalah … A. –11

B. –9 C. –6 D. 9 E. 11

3 Titik-titik stasioner dari grafik fungsi f(x) = x³ – 3x² – 9x + 10 adalah … A. (–1, –17) dan (3, 15)

B. (–1, 15) dan (3, –17) C. (–1, 16) dan (3, –15) D. (1, –5) dan (–3, –17) E. (1, –1) dan (–3, –17)

4 Titik stasioner pada fungsi f(x) = 7x² + 14x – 3 adalah … A. (–1, –10)

B. (–1, 10) C. (1, –10) D. (–2, –10) E. (2, –10)

5 Salah satu titik stasioner dari grafik fungsi f(x) = 2x³ + 4x² – 4x + 15 adalah … A. (–1, 29)

B. (–1, 31) C. (1, 5)

(35)

36

Rev : 03 No : F.02.55 D. (1, 7)

E. (1, 9)

6 Koordinat titik balik maksimum dari

3 7 1 3 4

) 1

(x  x³ x²  x

f adalah …

A. (–1, –3) B. (–1, 3) C. (1, 3) D. (7, 33) E. (7, –33)

……….

Paraf Guru

……….

Dwi Yuni R., S.Pd

2 15

3 20

4 15

5 15

6 20

C. Penilaian Ketrampilan LATIHAN 2

1. Tentukan turunan pertama dari bentuk : a. f(x) = (2x – 1)³

b. f(x) = (3x + 5)⁵

2. Sebuah peluru ditembakkan ke atas. Jika tinggi h meter setelah t detik dirumuskan dengan h(t) = 120t – 5t², tentukan tinggi maksimum yang dicapai peluru tersebut ! 3. Sebuah produksi rumahan memproduksi x buah barang. Setiap barang yang diproduksi

memberikan keuntungan (150x – x²) rupiah. Tentukan keuntungan maksimum yang diperoleh dari x buah barang tersebut !

Penskoran Penilaian Ketrampilan Proses

Penilaian

1 Proses 60

6. Turunan pertama 20

7. Tinggi maksimum peluru 20

8. Keuntungan maksimum 20

(36)

37

Rev : 03 No : F.02.55

2 Hasil 30

3 Waktu 10

Hasil Penilaian Proses

…………..

LATIHAN 4

6. Tentukan persamaan garis bergradien 2 melalui titik (1, 3) !

7. Tentukan persamaan garis singgung grafik y = x² – 5x + 6 di titik yang absisnya = 2 ! 8. Tentukan persamaan garis singgung y = x² + 2x + 4 di titik (1, 7) !

9. Tentukan persamaan garis normal y = x² + 2x + 4 di titik (1, 7) ! Penskoran Penilaian Ketrampilan Proses

Penilaian

1 Proses 70

9. Persamaan garis dengan gradien m 15

10. Persamaan garis singgung di titik yang absisnya = 2

15 11. Persamaan garis singgung di titik (1, 7) 20 12. Persamaan garis normal di titik (1, 7) 20

2 Hasil 20

3 Waktu 10

Hasil Penilaian Proses

…………..

Man Jadda Wajada

Barang Siapa Bersungguh-Sungguh Pasti Berhasil

(37)

37

Rev : 03 No : F.02.55

BAB 3. INTEGRAL

3.33 Menentukan nilai integral tak tentu dan tertentu fungsi aljabar

3.34 Menentukan luas permukaan dan volume benda putar dengan menggunakan integral tertentu

4.33 Menyelesaikan masalah yang berkaitan dengan integral tak tentu dan tertentu fungsi aljabar

4.34 Menyelesaikan masalah luas permukaan dan volume benda putar dengan menggunakan integral tertentu

KD/INDIKATOR SKKNI -

I. DEFINISI INTEGRAL TAK TENTU

Anda telah mengenal operasi yang saling invers (kebalikan), yaitu penjumlahan dan pengurangan, perkalian dan pembagian, serta kuadrat bilangan dan penarikan akar.

Pada bahasan kali ini, Anda akan mempelajari operasi invers untuk turunan atau diferensial, yaitu antiturunan (disebut juga antidiferensial atau integral).

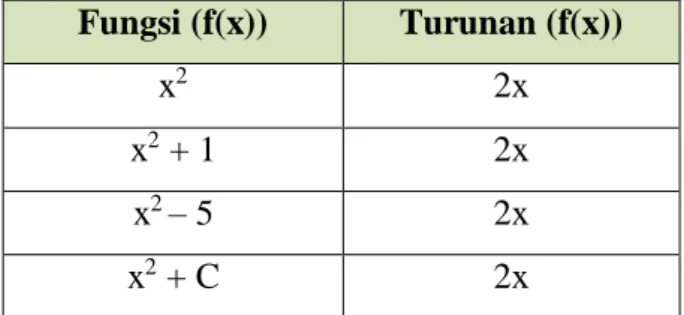
Untuk mengetahui hubungan antara fungsi turunan (diferensial) dan antiturunan (antidiferensial atau integral), perhatikan tabel berikut.

Fungsi (f(x)) Turunan (f(x))

x² 2x

x² + 1 2x

x²– 5 2x

x² + C 2x

MATERI PEMBELAJARAN KOMPETENSI DASAR :

Tabel 3.1 Hubungan antara fungsi dan turunan fungsinya

(38)

38

Rev : 03 No : F.02.55 Perhatikan bahwa beberapa fungsi yang berbeda memiliki turunan yang sama untuk semua x  R. Dapat dikatakan bahwa antiturunan dari f’(x) = 2x adalah f(x) = x2 + C dengan C adalah sembarang konstanta.

Pro ses untuk menentukan antiturunan dari suatu fungsi disebut pengintegralan.

Perhatikan kembali data pada Tabel 3.1. Antiturunan dari f’(x) = 2x adalah f(x) = x² + C dengan C sembarang konstanta, dapat juga dituliskan sebagai



²^x^^x² ^^C dengan C sembarang.

J. INTEGRAL TAK TENTU

Jika ingin mengetahui fungsi turunannya, fungsi awalnya dapat dicari dengan menggunakan integral.

Perhatikan tabel 3.2!

Fungsi Turunan Integral

f(x) = x² f’(x) = 2x



^f^'⁽^x⁾^dx^



²^xdx^₁_²₁^x¹^¹ ^^C^ ₂²^x² ^^C^^x² ^^C

f(x) = x³ f’(x) = 3x²



^f^'⁽^x⁾^dx^



³^x²^dx^₂³_₁^x²^¹ ^^C ^₃³^x³ ^^C^ ^x³ ^^C

f(x) = x⁴ f’(x) = 4x³



^f^'⁽^x⁾^dx^



⁴^x³^dx^₃_⁴₁^x³^¹^^C^ ₄⁴^x⁴ ^^C^^x⁴ ^^C

Dengan mengamati Tabel 3.2, diperoleh :

 ^ax

ⁿ

^dx ^ _n ^a _ ₁ ^x

ⁿ^¹

^ ^C

dengan n bilangan rasional dan n – 1.

Sifat-sifat Integral Tak Tentu:

1.



^dx^^x^^C

2.



^a ^dx^^ax^^C

3.

 

^f⁽^x⁾^^g⁽^x⁾



^dx^



^f⁽^x⁾^dx^



^g⁽^x⁾^dx

4.



^a ^f^(x⁾ ^dx ^^a



^f^(x⁾^dx

Tabel 3.2 Fungsi beserta turunan dari integralnya

Diingat ya !!!

(39)

39

Rev : 03 No : F.02.55

Contoh Soal

Tentukan integral dari :

1.



²^dx ^4.



⁽^x^⁵⁾⁽^x^⁸⁾^dx

2.



⁵^x²^dx ^5.

 ⁽ ⁹ ^x

³

^ ⁶ ^x

²

^ ⁷ ^x ^ ³ ⁾ ^dx

3.

 ⁽ ⁶ ^x

²

^ ⁴ ^x ^ ⁷ ⁾ ^dx

Penyelesaian:

1.



²^dx^²^x^^C

2.



⁵^x²^dx^ ₂⁵_₁^x²^¹^^C^⁵₃^x³ ^^C

3.

x x dx x x  x  C

 

 





^ ^

 ⁽ ⁶

²

⁴ ⁷ ⁾ ₂ ⁶ ₁

² ¹

₁ ⁴ ₁

¹ ¹

⁷

C x x

x

C x x

x













7 2

3 2 7 4 3

6

2 3

4.

 ⁽ ^x ^ ⁵ ⁾⁽ ^x ^ ⁸ ⁾ ^dx ^  ⁽ ^x

²

^ ³ ^x ^ ⁴⁰ ⁾ ^dx

C x x

x

C x x

x











 

 



^ ^

2 40 3 3

1 1 40 1

3 1

2 1

2 3

1 1 1

2

5.

 ⁽ ⁹ ^x

³

^ ⁶ ^x

²

^ ⁷ ^x ^ ³ ⁾ ^dx ^ ₃ ⁹ _ ₁ ^x

³^¹

^ ₂ ⁶ _ ₁ ^x

²^¹

^ ₁ _ ⁷ ₁ ^x

¹^¹

^ ³ ^x ^ ^C

C x x

x x

C x x

x x

















2 3 2 7

4 9

2 3 7 3

6 4

9

2 3

4

2 3

4

(40)

40

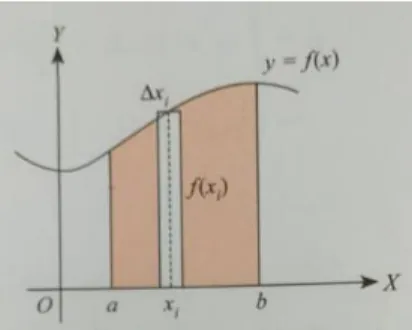
Rev : 03 No : F.02.55

K. INTEGRAL TERTENTU

Integral tertentu dipergunakan dalam melakukan pengintegralan pada interval- interval tertentu. Bentuk umum integral tertentu :



^b

a

x

f ( ) ^dx ^  ^F ⁽ ^x ⁾ 

^b_a

^ ^F ⁽ ^b ⁾ ^ ^F ⁽ ^a ⁾

Keterangan:

a disebut batas bawah b disebut batas atas

F(x)= fungsi hasil integral dari f(x) F(b) = nilai fungsi F(x) untuk x = b F(a) = nilai fungsi F(x) untuk x = a

Sifat-sifat Integral Tertentu:

1.



^b

a

x

f ( ) ^ ^ 

^a

b

x f

dx ( )

_dx

2.



^c

a

x

f ( )

_{dx =}



^b

a

x

f ( )

_{dx +}



^c

b

x

f ( )

dx ; a < b< c

3.



^a

a

x

f ( )

_{dx = 0}

4.



^b

a

k

f(x) dx = k



^b

a

x

f ( )

dx; k (konstanta)

Contoh Soal

Tentukan nilai integral dari :

1.



⁵

^ ^

2

6 1 )

3 ( x x dx

2.



³

^ ^

0

) 6 )(

3 ( x x dx

3.





3

1

)2

1 2

( x dx

Diingat ya !!!

(41)

41

Rev : 03 No : F.02.55 Penyelesaian:

1.



⁵

^ ^

2

6 1 )

3 ( x x dx

    

   

57 2 55

) 2 ( 55

2 12 8 5 75 125

2 ) 2 ( 3 ) 2 ( 5 ) 5 ( 3 ) 5 (

2 3

5 2

5

2

3 2 6 3

3 

































 





x x

x

x x

x

2.



³

^ ^

0

) 6 )(

3 ( x x dx

 

2 311 6

313 6 189

6

324 81

54

0 2 54

27 3

27

0 )

3 .(

18 )

3 2( ) 3 3 3( 1

2 3

) 18 3

(

2 3

3

0 3

0 2

2 18 3 3

1 2 18 3 3

1















 

 

 

  



 

 

  









 





 







x x

x

x x

x

dx x

x

(42)

42

Rev : 03 No : F.02.55

3.





3

1

)

2

1 2

( x dx  

 

3 251 3 41 21

3 21 13

3 3 6 3 4

18 36

1 3 2

3 4 3 18

108

) 1 ( ) 1 ( 2 ) 1 3( 3 4

) 3 ( 2 ) 3 3( 4

2 3

) 1 4 4

(

1 2 ) 1 2 (

2 3

3

1 3

1 2 3

1

3 2 4

2 4 3

4









 

 







  











  

 

 

  





     



 

  













 





 









x x

x

x x

x

dx x

x

dx x

x

L. APLIKASI INTEGRAL TAK TENTU DARI FUNGSI ALJABAR

Integral dapat diaplikasikan dalam berbagai bidang, misalnya dalam bidang ekonomi dan fisika. Dalam bidang ekonomi, dikenal fungsi marginal dan fungsi total.

Fungsi yang termasuk dalam fungsi marginal antara lain fungsi pendapatan marginal (MR) dan fungsi biaya marginal (MC). Fungsi yang termasuk fungsi total antara lain fungsi pendapatan total (TR) dan fungsi biaya total (TC). Hubungan antara fungsi total dan fungsi marginalnya adalah ^TR^



^MR^{dQ dan}^TC ^



^MC^dQ^.

Dalam bidang fisika, hubungan antara jarak (s), kecepatan (v), dan percepatan (a) adalah ^s^



^v^{dt dan}^v^



^adt dengan t = waktu.

Contoh Soal

1. Diketahui fungsi p[endapatan marginal (MR) suatu perusahaan adalah MR = 15Q² + 10Q – 5. Tentukan fungsi pendapatan totalnya (TR) jika pada Q = 2 unit,

nilai TR = 100 !