BAB 2
LANDASAN TEORI
Pada bab ini akan dibahas tentang teori-teori dan konsep dasar yang mendukung pembahasan dari sistem yang akan dibuat.
2.1. Katalog Perpustakaan
Katalog perpustakaan adalah suatu media yang dibutuhkan oleh perpustakaan agar dapat memudahkan pengunjung dalam memperoleh informasi mengenai koleksi apa saja yang dimiliki oleh perpustakaan.
Ada beberapa pengertian tentang katalog perpustakaan, antara lain yaitu :
a. Gates (1989) menyatakan bahwa katalog perpustakaan adalah suatu daftar yang sistematis dari buku dan bahan-bahan lain dalam suatu perpustakaan, dengan informasi deskriptif mengenai pengarang, judul, penerbit, tahun terbit, bentuk fisik, subjek, dan ciri khas bahan.
b. Sulistyo-Basuki (1991) menyatakan bahwa katalog perpustakaan adalah senarai dokumen yang dimiliki sebuah perpustakaan atau kelompok perpustakaan
2.2. Fitur atau Layanan Autocomplete
Autocomplete merupakan pola yang pertama kali muncul dalam bantuan fungsi aplikasi
dekstop, dimana pengguna mengentrikan teks ke dalam kotak kemudian saran pengetikan
akan muncul secara otomatis . Autocomplete memecahkan beberapa masalah umum pada pengetikan (Morville & Callender, 2010) yaitu :
a. Mengetik membutuhkan waktu.
b. Pengguna tidak dapat mengeja kata dengan baik.
c. Pengguna sering salah atau lupa ketika mengetikkan kata-kata, sulit mengingat istilah yang tepat.
Autocomplete bekerja ketika pengguna menulis huruf pertama atau beberapa huruf/karakter
dari sebuah kata, program yang melakukan prediksi akan mencari satu atau lebih kemungkinan kata sebagai pilihan. Jika kata yang dimaksud ada dalam pilihan kata prediksi maka kata yang dipilih tersebut akan disisipkan pada teks (Kusuma, 2012). Saat ini
autocomplete tidak hanya terdapat pada dekstop, tetapi terdapat juga pada web browser, email-programs, search engine interface, source code editors, database query tools, word processor, dan command line interpreters (Kusuma, 2012). Ilustrasi penggunaan layanan autocomplete dapat dilihat pada gambar 2.1.
Gambar 2.1. Ilustrasi Penggunaan Autocomplete
2.3. Fitur atau layanan Autocorrect
Auto Correct adalah fitur yang berguna untuk memberikan sugesti kata (suggestion). Dengan
mengetikkan beberapa huruf atau seluruh huruf maka sistem akan mencari kedalam database
apakah ada kata yang memenuhi kriteria dari huruf-huruf yang dimasukkan untuk mencari judul buku,penerbit bahkan pengarang dari buku tersebut. Ilustrasi penggunaan fitur autocorrect dapat dilihat pada gambar 2.2
Gambar 2.2. Ilustrasi Penggunaan Autocorrect
2.4. Approximate String Matching
Approximate string matching merupakan pencocokan string dengan dasar kemiripan dari segi
penulisannya (jumlah karakter dan susunan karakter), tingkat kemiripan ditentukan dengan jauh tidaknya beda penulisan dua buah string yang dibandingkan tersebut (Haryanto, 2011). Operasi mengubah string ini bisa berupa mengubah satu huruf ke huruf yang lain, menghapus satu huruf dari string, atau memasukkan satu huruf ke dalam string. Operasi-operasi ini digunakan untuk menghitung jumlah perbedaan yang diperlukan untuk pertimbangan kecocokan suatu string dengan string sumber, jumlah perbedaan tersebut diperoleh dari penjumlahan semua pengubahan yang terjadi dari masing-masing operasi. Penggunaan perbedaan tersebut diaplikasikan dalam berbagai macam algoritma, seperti Hamming, Levenshtein, Damerau-Levenshtein, Jaro-Winkler, Wagner-Fischer, dan lain-lain (Husain, 2013). Operasi penghitungan tersebut meliputi tiga operasi string seperti di bawah ini (Adiwidya, 2009).
2.4.1. Operasi penghapusan
Operasi penghapusan dilakukan dengan menghapus karakter pada indeks tertentu untuk menyamakan string sumber (S) dengan string target (T), misalnya S= matching dan T= match. Penghapusan dilakukan untuk karakter i pada lokasi ke-6, penghapusan karakter n
pada lokasi ke-7, penghapusan karakter g pada lokasi ke-8. Operasi penghapusan tersebut menunjukkan tranformasi S ke T, ilustrasinya adalah sebagai berikut :
1 2 3 4 5 6 7 8 T = m a t c h - - - S = m a t c h i n g 2.4.2. Operasi penyisipan
Operasi penyisipan dilakukan dengan menyisipkan karakter pada indeks tertentu untuk menyamakan string sumber (S) dengan string target (T), misalnya S= cerdas dan T= kecerdasan. Operasi penyisipan dapat dilakukan dengan menyisipkan e pada posisi 2, menyisipkan c pada posisi 3, menyisipkan a pada posisi 8 dan menyisipkan n pada posisi 9. Yang dapat diilustrasikan sebagai berikut:
K e c e r d a s a n K - - e r d a s - - 1 2 3 4 5 6 7 8 9 T = K e c e r d a s a n S = K - - e r d a s - - e c a n 2.4.3. Operasi penukaran
Operasi penukaran dilakukan dengan menukar karakter pada indeks tertentu untuk menyamakan string sumber (S) dengan string target (T), misalnya S= computer dan T= komputer. String S ditranformasikan menjadi T dengan melakukan penggantian (substitusi) pada posisi ke-1. Huruf C ditukar menjadi K. Prosesnya dapat diilustrasikan sebagai berikut:
1 2 3 4 5 6 7 8 T = k o m p u t e r S = c o m p u t e r k
2.5. Algoritma Levenshtein Distance
Algoritma Levenshtein Distance ditemukan oleh Vladimir Levenshtein, seorang ilmuan asal Rusia pada tahun 1965 (Janowski, 2010), algoritma ini sering juga disebut dengan Edit Distance (Husain,2013). Yang dimaksud dengan distance adalah jumlah modifikasi yang dibutuhkan untuk mengubah suatu bentuk string ke bentuk string yang lain, sebagai contoh hasil penggunaan algoritma ini, string “komputer” dan “computer” memiliki distance 1 karena hanya perlu dilakukan satu operasi saja untuk mengubah satu string ke string yang lain. Dalam kasus dua string di atas, string “computer” dapat menjadi “komputer” hanya dengan melakukan satu penukaran karakter „c‟ menjadi „k‟ (Andhika, 2010). Algoritma Levenshtein Distance digunakan secara luas dalam berbagai bidang, misalnya mesin pencari, pengecek ejaan (spell checking), pengenal pembicaraan (speech recognition), pengucapan dialek, analisis DNA, pendeteksi pemalsuan, dan lain-lain. Algoritma ini menghitung jumlah operasi string paling sedikit yang diperlukan untuk mentransformasikan suatu string menjadi string yang lain (Adiwidya, 2009). Algoritma Levenshtein Distance bekerja dengan menghitung jumlah minimum pentranformasian suatu string menjadi string lain yang meliputi penghapusan, penyisipan, dan penukaran (Husain, 2013). Selisih perbedaan antar string dapat diperoleh dengan memeriksa apakah suatu string sumber sesuai dengan string target. Nilai selisih perbedaan ini disebut juga Edit distance/ jarak Levenhstein. Jarak Levenshtein antar string s dan string t tersebut adalah fungsi D yang memetakan (s,t) ke suatu bilangan real nonnegatif, sebagai contoh diberikan dua buah string s = s(1)s(2)s(3)...s(m) dan t = t(1)t(2)t(3)...t(n) dengan | s | = m dan | t | = n sepanjang alfabet V berukuran r sehingga s dan t anggota dari V*. S(j) adalah karakter pada posisi ke-j pada string s dan t(i) adalah karakter pada posisi ke-i pada string t. Sehingga jarak Levenshtein dapat didefinisikan sebagai (Harahap, 2013).
D ( s, t) adalah banyaknya operasi minimum dari operasi penghapusan, penyisipan dan penukaran untuk menyamakan string s dan t. Pada implementasi pencocokan antar string, ketiga operasi tersebut dapat dilakukan sekaligus untuk menyamakan string sumber dengan string target seperti pada contoh berikut ini. Jika diberikan string sumber (S) = “pemrograman” dan T = “ algoritma” merupakan string target, dengan | s | = 11, | t | = 9, maka proses pencocokan string dapat diilustrasikan sebagai berikut :
1 2 3 4 5 6 7 8 9 10 11 T = a l g o r i t m a - - S = p e m p r o s e s a n a l g o i t m a
Pada contoh di atas terlihat bahwa proses penukaran karakter „p‟ pada indeks ke-1, „e‟ pada indeks ke-2,”m” pada indeks ke-3, ‟p‟ pada indeks ke-4, ‟o‟ pada indeks ke-6, ‟s‟ pada indeks ke-7, ‟e‟ pada indeks ke-8, penyisipan karakter „g‟ pada indeks ke-3 dan proses penghapusan karakter „a‟ pada indeks ke-9, dan „n‟ pada indeks ke-11. Maka jarak Levenshtein antara S dan T adalah sebagai berikut ini.
= d( s1, t1 ) + d( s2, t2 ) + d( s3, t3 ) + d( s4, t4 ) + d( s5, t5 ) + d( s6, t6 ) + d( s7, t7 ) + d( s8, t8 ) + d( s9, t9 ) + d( s10, t10 ) + d( s11, t11 ) + d( s12, t12 ) = d( a, p ) + d( l, e ) + d( g, - ) + d( o, m ) + d( r, r ) + d( i, o) + d( t, g ) + d( m, r) + d( a, a ) + d( -, m )+ d( -, a) + d(-, n) = 1 + 1 + 1 + 1 + 0 + 1 + 1 + 1 + 1 + 1 + 1 = 10
Sehingga jarak Levenshtein antara string T = “pemprosesan” dan T = “algoritma” adalah D(s, t) = 10.
2.6. Algoritma Boyer Moore
Algoritma Boyer Moore termasuk algoritma string matching yang paling efisien dibandingkan algoritma-algoritma string matching lainnya. Karena sifatnya yang efisien, banyak dikembangkan algoritma string matching dengan bertumpu pada konsep algoritma
Boyer Moore, beberapa di antaranya adalah algoritma Turbo BM dan algoritma Quick Search.( Chiquita. 2012).
Algoritma Boyer Moore menggunakan metode pencocokan string dari kanan ke kiri yaitu men-scan karakter pattern dari kanan ke kiri dimulai dari karakter paling kanan. Algoritma Boyer Moore menggunakan dua fungsi shift yaitu good-suffix shift dan
character shift untuk mengambil langkah berikutnya setelah terjadi ketidakcocokan antara
karakter pattern dan karakter teks yang dicocokkan ( Sagita Vina, 2012).
1. Deskripsi kerja algoritma Boyer Moore
Untuk menjelaskan konsep dari good-suffix shift dan bad-character shift diperlukan contoh kasus, seperti kasus ketidakcocokan ditengah pencocokan karakter pada teks dan
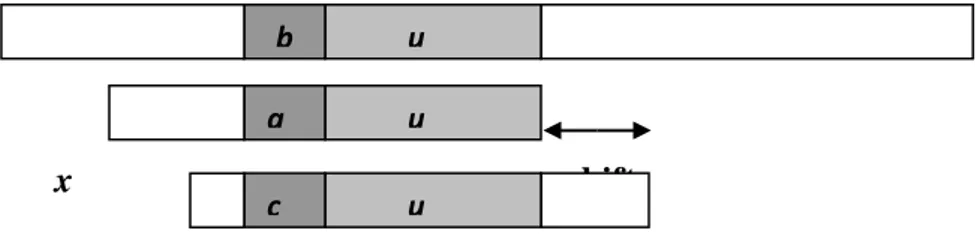
pattern. Karakter pattern x[i]=a tidak cocok dengan karakter teks y[i+j]=b saat pencocokan
pada posisi j. Maka x[i+l .. m-1]= y[i+j+1 .. j+m-1]=u dan x[i] ≠ y[i+j].
2. Good-suffix shift
Konsep dari fungsi good-suffix shift adalah sebagai berikut:
1. Good-suffix shift adalah pergeseran yang dibutuhkan dari x[i]=a ke karakter lain yang letaknya lebih kiri dari x[i] dan terletak di sebelah kiri segmen u. Kasus ini ditunjukkan pada Gambar 2.3.
y
x shift
x
Gambar 2.3 Good-suffix shift, uterjadi lagi didahului karakter c berbeda dari a
2. Jika tidak ada segmen yang sama dengan u, maka dicari u yang merupakan suffiks terpanjang u. Kasus ini ditunjukkan pada Gambar 2.4
u b u a u c u b u a v
y
x shift
x
Gambar 2.4 Good-suffix shift, hanya suffix dari u yang terjadi lagi di pattern x
3. Bad-character shift
Berdasarkan contoh kasus di atas, bad-character adalah karakter pada teks yaitu y [i+j] yang tidak cocok dengan karakter pada pattern.
Konsep dari fungsi bad-character shift adalah sebagai berikut:
1. Jika bad-character y[i+j] terdapat pada pattern di posisi terkanan k yang lebih kiri dari
x[i] maka pattern digeser ke kanan sejauh i-k. Kasus ini ditunjukkan pada Gambar 2.5.
y
x shift x
Gambar 2.5 Bad-character shift, b terdapat di pattern x
2. Jika bad-character y[i+j] tidak ada pada pattern sama sekali, maka pattern digeser ke kanan sejauh i. Kasus ini dit tunjukkan pada Gambar 2.6.
y u b u a Contains no b b u b u a Contains no b
x shift
x
Gambar 2.6 Bad-character shift, b tidak ada di pattern x
3. Jika bad-character y[i+j] terdapat pada pattern di posisi terkanan k yang lebih kanan dari x[i] maka pattern seharusnya digeser sejauh i-k yang hasilnya negatif (pattern digeser kembali ke kiri). Maka bila kasus ini terjadi. akan diabaikan.
Pada kasus ketidakcocokan di atas, algoritma akan membandingkan langkah yang diambil oleh fungsi good-suffix shift dan bad-character shift di mana langkah yang paling besar yang akan digunakan.
2.6.1 Cara kerja algoritma Boyer Moore
Cara kerja dari algoritma Boyer Moore adalah sebagai berikut:
1. Menjalankan prosedur preBmBc dan preBmGs untuk mendapatkan inisialisasi.
a. Menjalankan prosedur preBmBc. Fungsi dari prosedur ini adalah untuk menentukan berapa besar pergeseran yang dibutuhkan untuk mencapai karakter tertentu pada pattern dari karakter pattern terakhir/terkanan. Hasil dari prosedur preBmBc disimpan pada tabel BmBc.
b. Menjalankan prosedur preBmGs. Sebelum menjalankan isi prosedur ini, prosedur suffix dijalankan terlebih dulu pada pattern. Fungsi dari prosedur suffix adalah memeriksa kecocokan sejumlah karakter yang dimulai dari karakter terakhir/terkanan dengan sejumlah karakter yang dimulai dari setiap karakter
yang lebih kiri dari karakter terkanan tadi. Hasil dari prosedur suffix disimpan pada tabel suff. Jadi suff[i] mencatat panjang dari suffix yang cocok dengan segmen dari pattern yang diakhiri karakter ke-i.
c. Dengan prosedur preBmGs, dapat diketahui berapa banyak langkah pada pattern dari sebeuah segmen ke segmen lain yang sama yang letaknya lebih kiri dengan karakter di sebelah kiri segmen yang berbeda. Prosedur preBmGs menggunakan tabel suff untuk mengetahui semua pasangan segmen yang sama. Contoh pada Gambar 2.1, yaitu berapa langkah yang dibutuhkan dari au(u = segmen, a = karakter di sebelah kiri u) ke cu yang mempunyai segmen u pada pattern dengan karakter di sebelah kiri segmen yaitu c berbeda dari a dan terletak lebih kiri dari
au. Hasil dari prosedur preBmGs disimpan pada tabel BmGs.
2. Dilakukan proses pencarian string dengan menggunakan hasil dari prosedur preBmBc dan preBmGs yaitu tabel BmBc dan BmGs.
Berikut ini diberikan contoh untuk menjelaskan proses inisialisasi dari algoritma Boyer
Moore dengan pattern gcagagag yang akan dicari pada string gcatcgcagagagtatacagtacg.
1. Dengan prosedur preBmBc, didapatkan jumlah pergeseran pada pattern yang dibutuhkan untuk mencapai karakter a,c,g,t dari posisi terkanan. Berdasarkan contoh diketahui untuk mencapai masing-masing karakter tadi dibutuhkan pergeseran sebanyak 1, 6, 2 dan 8.
2. Dengan prosedur preBmGs, dijalankan prosedur suffix terlebih dulu. Dengan prosedur
suffix akan diketahui:
suff[0] = 1, 1 karakter g posisi 7 cocok dengan 1 karakter g posisi 0.
suff[1] = 0, karakter g posisi 7 tidak cocok dengan karakter c posisi 1.
suff[2] = 0, karakter g posisi 7 tidak cocok dengan karakter a posisi 2.
suff[3] = 2, 2 karakter dimulai dari karakter g posisi 7 cocok dengan 2 karakter dimulai dari karakter g posisi 3, yang artinya karakter a,g posisi 6,7 cocok dengan karakter a,g posisi 2,3.
suff[4] = 0, karakter g posisi 7 tidak cocok dengan karakter a posisi 4.
suff[5] = 4, 4 karakter dimulai dari karakter g posisi 7 cocok dengan 4 karakter dimulai dari karakter 5,artinya karakter a,g,a,g posisi 4,5,6,7 cocok dengan karakter a,g,a,g posisi 2,3,4,5.
suff[6] = 0,karakter g posisi 7 tidak cocok dengan karakter a posisi 6.
suff[7] = 8, 8 karakter g,c,a,g,a,g,a,g posisi 0,1,2,3,4,5,6,7 cocok dengan 8 karakter g,c,a,g,a,g,a,g posisi 0,1,2,3,4,5,6,7.
3. Dengan prosedur BmGs akan didapatkan: 0 1 2 3 4 5 6 7
g c a g a g a g
bmGs[0]= 7, karakter ke-0 g adalah karakter sebelah kiri segmen cagagag.Tidak ada segmen cagagag lain dengan karakter sebelah kiri bukan g maka digeser 7 langkah.
bmGs[1]= 7, karakter ke-1 c adalah karakter sebelah kiri segmen agagag. Tidak ada segmen agagag lain dengan karakter sebelah kiri bukan c maka digeser 7 langkah.
bmGs[2]= 7, karakter ke-2 a adalah karakter sebelah kiri segmen gagag. Tidak ada segmen gagag lain dengan karakter sebelah kiri bukan a maka digeser 7 langkah.
bmGs[3]= 2. karakter ke-3 g adalah karakter sebelah kiri segmen agag. Karena ada segmen agag posisi 2,3,4,5 dengan karakter sebelah kiri bukan g yaitu c posisi 1 maka digeser 2 langkah.
bmGs[4]= 7, karakter ke-4 a adalah karakter sebelah kiri segmen gag. Karena tidak ada seamen gag lain dengan karakter sebelah kiri bukan a maka digeser 7 langkah.
bmGs[5]= 4. karakter ke-5 g adalah karakter sebelah kiri seamen ag. Karena ada segmen ag posisi 2,3 dengan karakter sebelah kiri bukan g yaitu c posisi 1 maka digeser 4 langkah.
bmGs[6]= 7, karakter ke-6 a adalah karakter sebelah kiri segmen yaitu a posisi 7. Karena tidak ada segmen g dengan karakter sebelah kirinya bukan a maka digeser 7 langkah.
bmGs[7]= 1, karakter ke-7 g adalah karakter sebelah kiri segmen dan karena segmen tidak ada maka digeser 1 langkah
2.6.2 Prosedur Algoritma Boyer Moore
procedure preBmBc(in/out x: string, m: integer, output BmBc: array of integer) { ASIZE = ukuran ∑ }
i traversal [0..ASIZE - 1] BmBc[i] ← m
i traversal [0..m - 2]
BmBc[x[i] ] ← m - i - 1
Gambar 2.7 Prosedur preBmBc algoritma Boyer Moore
procedure suffix (in/out x: string, m: integer, output suff: array of integer)
suff [m – 1] ← m g ← m – 1
i traversal [m – 2..0]
if ( i > g and suff [i + m -1 – f] < i – g) then suff [i] ← suff [ i + m – 1 – f]
else if (i < g) then g ← i f ← i while (g ≥ 0 and x[g] ← x [ g + m - 1 - f ] ) do g ← g - 1 f ← i while ( g ≥ 0 and x [g] ← x [g] + m - 1 - f ] ) do g ← g - 1 suff [ i ] ← f - g
Gambar 2.7 Prosedur suffix algoritma Boyer Moore
procedure preBmGs(in/out x: string, m: integer, output BmGs: array of integer) suffix (x, m, suff)
i traversal [0..m - 1] BmGs[i] ← m
i traversal [m – 1 .. -1]
if (I = - 1 or suff [i] = i + 1 ) then
j traversal [ 0 .. m - 2 - i ) do
if (BmGs [j] = m) then BmGs [j] ← m - 1 - i
i traversal [0..m - 2]
BmGs [m - 1 - suff [i] ] ← m - 1 - i
Gambar 2.7 prosedur preBmGs algoritma Boyer Moore procedure BM(in/out x,y: string, m,n: integer)
{ Preprocessing } preBmGs(x, m, BmGs) preBmBc(x, m, BmBc) { Searching } j ← 0 while ( j ≤ n – m )do i traversal [m - 1..0] if (x[i] = y [ i + j ] ) then if ( i < 0 ) OUTPUT ( j ) j ← j + BmGs [ 0 ] else j ← j + MAX( BmGs [i] , BmBc [ y [ i + j ] ] - m + 1 + i )
2.7 Penelitian Terdahulu
Pada bagian ini akan dijelaskan beberapa penelitian terdahulu, layanan autocorrect dan
autocomplete telah banyak digunakan pada penelitian terdahulu. Seperti layanan autocomplete dan autocorrect pada teks editor (Chiquita, 2011), dengan menggunakan
algoritma Boyer-Moore dan Dynamic Programming. Kemudian layanan autocorrect juga pernah diterapkan pada Smart Phones (Pradhana, 2012), dengan menggunakan kombinasi algoritma Brute Force, Boyer-Moore dan Knuth-Morris Pratt. Untuk lebih jelasnya, pada tabel 2.1 berikut akan dijelaskan penelitian-penelitian yang telah dibuat sebelumnya.
Tabel 2.1 Penelitian sebelumnya
No. Judul Pengarang Tahun Kelebihan Kekurangan
1 Penerapan Algoritma Boyer-Moore-Dynamic Programming untuk Layanan Auto-Complete dan Auto-Correct Christabella Chiquita B 2011 Algoritma Boyer-Moore lebih mangkus dibandingkan dengan algoritma yang lain serta
sangat tepat digunakan sebagai layanan
auto-complete Tidak ada 2 Pencocokan string untuk fitur autocompletion pada text editor atau integrated development environment (IDE)
Muhammad Wachid
Kusuma 2012
Algoritma brute force dapat diterapkan untuk
membentuk fitur autocomplete pada text
editor dengan baik
Cara kerja algoritma brute force berjalan
lambat
3.
Penerapan String Matching pada Fitur Auto Correct dan Fitur Auto Text
di Smart Phones
Fandi Pradhana 2014
Penerapan algoritma string matching seperti Brute Force, Boyer-Moore dan
KMP pada fitur auto correct mampu memberikan hasil yang
benar-benar
Waktu pengecekan membuat sistem mejadi
lambat
4
Simulasi Algoritma Levenshtein Distance untuk fitur
Autocomplete pada aplikasi katalog
perpustakaan
Yuli Primadani 2014
Algoritma Levenshtein Distance dapat bekerja maksimal pada fitur
autocomplete
Tidak dilengkapi dengan fitur autocorrect