Dual Reciprocity Boundary Element Method untuk
menyelesaikan Masalah Infiltrasi Air pada Saluran Irigasi
Alur
Muhammad Manaqib
UIN Syarif Hidayatullah Jakarta muhammad.manaqib@uinjkt.ac,idAbstrak—Model matematika infiltrasi air pada saluran irigasi alur berberbentuk
Masalah Syarat Batas (MSB) dengan domain sebuah penampang melintang saluran irigai alur yang tertutup dan terbatas. Persamaan pengaturnya berbentuk Persamaan Helmholtz termodifikasi, sedangkan syarat batasnya berbentuk syarat batas campuran Neuman dan Robin. Penyelesaian analitik MSB Persamaan Helmhotlz sulit dilakukan, terlebih jika domain tidak beraturan dan melibatkan syarat batas campuran. Alternatif yang dapat dilakukan adalah dengan menggunakan pendekatan metode numerik. Dual Reciprocity Boundary Element Method (DRBEM) adalah metode numerik yang digunakan untuk menyelesaikan persamaan diferensial parsial yang ditemui pada fisika matematis dan teknik. Peneltian ini akan membahas bagaimana menyelesaikan model matematika infiltrasi air pada saluran irigasi alur menggunakan pendekatan numerik DRBEM. Hasilnya, DRBEM mampu memberikan solusi numerik yang cukup baik pada model matematika infiltrasi air saluran irigasi alur. Selain itu, juga diperoleh pengetahuan tentang persebaran kandungan air pada tanah di sekitar saluaran irigasi.
Kata kunci: DRBEM, irigasi alur, infiltrasi, Persamaan Helmholtz termodifikasi
I. PENDAHULUAN
Model matematika infiltrasi air pada saluran irigasi alur berupa Persamaan Helmhotz termodifikasi yang berbentuk persamaan diferensial parsial (PDP) dengan syarat batas atau dalam metematika disebut Masalah Syarat Batas (MSB). Domain dari model ini adalah potongan melintang suatu saluran irigasi alur dan syarat batasnya berupa syarat batas campuran. Penyelesaian analitik model ini masih memungkinkan dilakukan jika bentuk saluran irigasi sangat sederhana. Seperti yang dilakukan Batu [1], yaitu untuk saluran irigasi berbentuk datar/flat. Akan tetapi, dalam kenyataan saluran irigasi alur berbentuk flat jarang digunakan, yang umum digunakan berbentuk trapesium, setengah lingkaran ataupun persegi panjang. Penyelesaian analitik untuk alur berbentuk selain flat sangat sulit dilakukan. Salah salah satu pendekatan penyelesaian yang dapat digunakan adalah menggunakan metode numerik Dual Reciprocity Boundary Emement Method (DRBEM).
DRBEM adalah bagian atau pengembangan dari Boundary Elemen Method (BEM) atau dalam Bahasa Indonesia disebut Metode Elemen Batas (MEB). MEB adalah metode numerik yang digunakan untuk menyelesaikan persamaan diferensial parsial yang ditemui pada fisika matematis dan teknik. Seperti, Persamaan Laplace, Persamaan Helmholtz, Persamaan Konveksi Difusi, Persamaan Potensial dan Aliran Viskos, Persamaan Elektrostatik dan Elektromahnetik, serta Persamaan Linear Elastosatik dan Elestodynamik [2]. Ide utama Metode Elemen Batas adalah solusi dari PDP tersebut diekspresikan dalam persamaan integral batas yang menggandung solusi fundamental dari PDP tersebut [3].
Terdapat beberapa kelebihan MEB dibandingkan metode numerik yang lainnya, seperti Finite Element Method (FEM) dan Finite Difference Method (FDM). Berikut beberapa kelebihan tersebut [4].
1. Diskritisasi hanya dilakukan pada batas domain, sehingga membuat pemodelan numerik dengan MEB lebih sederhana dan mereduksi jumlah titik kolokasi yang diperlukan.
2. MEB yang dimodifikasi dapat menyelesaikan masalah dengan domain tak terbatas.
3. MEB terbukti efektif pada perhitungan turunan dari lapangan fungsi seperti flux, tegangan, tekanan, dan momen. MEB juga dapat menyelesaikan konsentrasi gaya dan momen pada interior domain dan batas domain.
4. Menggunakan satu himpunan titik kolokasi yang terletak pada batas-batas domain dapat digunakan untuk mencari solusi di semua titik pada domain. Berbeda dengan FEM dan FDM yang solusinya diperoleh hanya di titik kolokasi.
5. MEB juga dapat menyelesaikan masalalah dengan domain yang rumit, seperti sebuah retakan. Berdasarkan uraian diatas DRBEM sangat baik untuk menyelesaikan model matematika infiltrasi air pada saluran irigasi alur. Sehingga dalam penelitian ini akan dibahas bagaimana menyelesaikan MSB model matematika infiltrasi air pada saluran irigasi alur menggunakan DRBEM.
II. METODENUMERIK A. Boundary Element Method
Boundary Element Method (BEM) atau dalam Bahasa Indonesia disebut Metode Elemen Batas (MEB) adalah metode numerik yang digunakan untuk menyelesaikan persamaan diferensial parsial (PDP) yang ditemui pada fisika matematis dan teknik. Seperti Persamaan Laplace, Persamaan Helmholtz, Persamaan Konveksi Difusi, Persamaan Potensial dan Aliran Viskos, Persamaan Elektrostatik dan Elektromahnetik, serta Persamaan Linear Elastosatik dan Elestodynamik [5].
Ide utama metode elemen batas adalah solusi dari PDP tersebut diekspresikan dalam persamaan integral batas yang menggandung solusi fundamental dari PDP, oleh karena itu Teorema Gauss-Green dan Identitas Kedua Green berperan penting dalam metode ini. Metode ini dinamakan metode elemen batas kerena diskritisasi di lakukan pada batas domain dengan membagi menjadi ruas-ruas/segmen garis yang berhingga yang selanjutnya digunakan untuk mengevaluasi persamaan integral batasnya.
Metode Elemen Batas mulai berkembang pada abad ke-19, yang pada awalnya dikenal dengan istilah Boundary Integral Equation Method (BIEM), sebagai metode untuk menyelesaikan masalah fisika matematis. Pertamakali dikerjakan oleh G.Green pada tahun 1828 yaitu masalah syarat batas direclet dan neuman dari Persamaan Laplace dibentuk dalam integral solusinya, sehingga bentuk seperti ini disebut sebagai Fungsi Green [3]. Semenjak penemuan Fungi Green tersebutlah banyak para peneliti yang mengembangan Metode Elemen Batas.
Berdasarkan [6] secara garis besar prosedur penyelesaian persamaan deferensial parsial dengan syarat batas menggunakan MEB adalah sebagai berikut.
1. Tentukan solusi fundamental dari persamaan diferensial parsial tersebut.
2. Bentuk relasi reciprocal antara solusi yang akan dicari dengan solusi fundamental.
3. Bentuk persamaan integral batas, yang diperoleh dari relasi reciprocal dan modifikasi domain. 4. Selesaikan persamaan integral batas tersebut dengan mensubtitusikan titik-titik kolokasi ke
persamaan integral batas, sehingga diperoleh SPL.
5. Selesaikan SPL tersebut. Selanjutnya dengan mensubtitusikan solusi SPL ke persamaan integral batas, diperoleh suatu persamaan yang dapat digunakan untuk mengevalusi solusi persamaan diferensial parsial tersebut di semua titik pada domainnya.
B. Dual Reciprocity Boundary Element Method
Subbab ini akan membahas tentang bagaimana menyelesaikan Persamaan Helmhotz dua dimensi dengan syarat batas yang diketahui. Persamaan Helmhotz tersebut memiliki domain R, suatu daerah tertutup dan terbatas oleh kurva sederhana C. Berikut diberikan Persamaan Helmhotz dua dimensi dengan syarat batas campuran.
2 2 2 2 , , ( , ) , , , x y x y x y x y g x y x y
(1)dengan syarat batas
( , ) untuk(x, y) C , 1 1 ( , ) untuk(x, y) C , 2 2 f x y f x y n (2)
dimana 1C dan 2C adalah dua buah kurva yang tidak berpotongan sedemikian sehingga C1 C2 C. Menggunakan prosedur penyelesaian MSB dengan DRBEM yang telah diberikan [7], akan dicari solusi pendekatan di beberapa titik pada domainnya. Berikut prosedur penyelesaiannya.
1. Relasi reciprocal
Relasi reciprocal antara
x y, ; ,
solusi fundamental Persamaan Laplace dan
x y, solusi Persamaan Helmhothz (1) yang akan dicari pada domain R adalah sebagai berikut.
,
, ; ,
, ; , , ( , ) , ; , , , , , C x y x y x y x y ds x y x y g x y x y x y dxdy n n R (3) dengan
, x y, .2. Persamaan integral batas
Menggunakan relasi reciprocal (3) dan modifikasi domain diperoleh persamaan integral batas
, ; ,
,
, , x y, x y x y, ; , x y ds x y, ; , g x y, x y, x y dxdxy, , n n C R (4) dengan
0, jika , 1 , , jika , padabagian 2 1, jika , . R C smoothC R 3. Pendekatan integral domain
Menggunakan pendekaan fungsi basis radial, diperoleh pendekatan integral domain sebagai berikut.
( ) ( ) ( ) ( ) ( ) ( ) , ; , , , , , ; , , ; , 1 1 ( ), ( ) ( ), ( ) ( ), ( ) . M M R j j m m m m x y g x y x y x y dxdy a b a b a b j m j j j j j j g a b a b a b (5)4. Persamaan integral batas dalam bentuk integral garis.
Menggunakan persamaan integral batas dan pendekatan integral domain, diperoleh persamaan integral batas dalam bentuk integral garis sebagai berikut.
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 , , , ; , , ; , , , , , ; , , , , ; , untuk , R C. M M j j m m m m j j j j j j j m C a b a b a b g a b a b a b x y x y x y x y ds n n
(6)5. Penyelesaian persamaan integral batas
Dengan mensubtitusikan titik-titik kolokasi ke persamaan integral batas diperoleh SPL
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 1 , , , , , , , untukn=1, 2,..., N+L. N L n n n n nj j j j j j j j N k k n n k k n n k x y x y g x y x y x y f x y p f x y
(7)6. Persamaan untuk mengevaluasi solusi
Dengan mensubtitusikan solusi (7) diperoleh persamaan untuk mengevaluasi solusi Persamaan (1) sebagai berikut.
( )
( ) ( )
( ) ( ) ( ) ( )
( ) ( )
2 1 1 1 , , , , , N L N j j j j j k k k k j k a b a b g x y f a b p f a b
(8) dengan
a b C R, III. HASIL DAN PEMBAHASAN A. Model Matematika Infiltrasi pada Saluran Irigasi Alur
Bentuk saluran irigasi alur yang diteliti adalah trapesium, karena bentuk ini lazim digunakan oleh para petani. Asumsi-asumsi yang digunakan pada saluran adalah [8]
1. Lebar saluran irigasi memiliki lebar yang sama dan memiliki panjang yang cukup panjang, sehingga dalam model ini panjang saluran irigasi diabaikan.
2. Saluran irigasi berbentuk trapesium dengan panjang penampang permukaan saluran sebesar 2L. 3. Jarak antar titik tengah dua buah saluran yang berdekatan adalah 2(L+D).
4. Saluran selalu penuh dengan air.
5. Pengaruh dari saluran irigasi lain diabaikan.
6. Laju infiltrasi air/besar flux masuk pada permukaan saluran irigasi adalah konstan, yakni sebesar
v
0. 7. Tidak ada aliran air yang masuk kecuali dari saluran.Berdasarkan asumsi-asumsi model yang digunakan maka dapat dibentuk model matematika infiltrasi air dalam saluran irigasi alur dengan domain R yang tertutup dan terbatas oleh kurva
C
(CC1C2C3C4C5) berbentuk MSB sebagai berikut. Secara sistematis MSB tersebut dapat digambarkan sebagai berikut [9].GAMBAR1.MSB DENGAN DOMAIN R YANG TERTUTUP DAN TERBATAS OLEH KURVA C
B. Penyelesaian Model Matematika Infiltrasi Air pada Saluran Irigasi Alur dengan DRBEM
Langkah utama penyelesaian menggunakan DRBEM adalah membentuk SPL, tetapi sebelumnya perlu dibentuk persamaan integral batasnya. Subtitusikan syarat batas model matematika infiltrasi air [ada saluran irigasi alur ke persamaan integral batas Persamaan Helmhotz, yang telah diberikan pada (4). Diperoleh
1 2 5 1 3 4 ( ) 2 2 , , , ; , , , , ; , , , ; , , , ; , , , , ; , , , z k C C C C C C R x z e n x z ds x z L x z x z x z ds x z n x z x z ds x z x z x z dxdz n
(9)dengan
x z, ; ,
adalah solusi fundamental Persamaan Laplace dimensi dua.Setelah persamaan integral batas diperoleh dapat dibentuk SPL dengan mendiskritisasi batas domain kedalam sejumlah ruas garis berhingga dan memilih sejumlah titik interior. Misalkan jumlah ruas garis dan titik-titik interior tersebut berturut-turut N dan L. Namakan ruas-ruas garis tersebut (1) (2) ( )
, ,..., N
diambil titik tengah ruas garis tersebut, namakan
( ) ( )
, ,
i i
a b untuk i1,2,...,N Selanjutnya untuk titik interior namakan
( ) ( )
,
N i N i
a b untuk i1,2,...,L. Kesejumlah N L titik-titik tersebutlah yang diambil sebagai titik-titik kolokasi yang akan digunakan untuk mencari solusi pendekatan numerik dari
x z, pada domain R C .Selanjutnya, persamaan integral batas (9) dapat diubah menjadi SPL berikut,
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 , , , , , ; , untukn=1, 2,..., N+L N n n n k k n n k k n n k N N L k z k n n n n j j j k j a b f a b f a b f l e f a b a b a b
(10) dengan ( ) ( ) ( ) 2 5 ( ) ( ) 2 5 , , , k k k k k n C C n C C ( )n adalah nilai
yang dievalusi pada
( ) ( )
,
n n
a b ,
fl
( )k adalah flux di titik kolokasi
a( )k,b( )k
dan 2( )k
n adalah komponen vektor normal pada sumbu-Z di titik kolokasi
( ) ( )
,
k k
a b yang berarah keluar domain R. Selanjutnya SPL (10) akan diubah dalam bentuk persamaan matrik
Ax b (11)
dengan
x
adalah vektor kolom yang memuat variabel yang belum diketahui
( )k,
k
1, 2,3,...,
N
L
.
Lebih lanjut, matrikA
dan vektorb
dapat dikonstruksikan dari (10), diperoleh
( ) ( ) ( ) ( ) 1 1 , ,untukn=1, 2, 3,..., N+L. N k z k n n n k b fl e f a b
(12) serta
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 ( ) ( ) ( ) ( ) ( ) 1 , , , ; , , untukk=1, 2,..., N. 2 , ; , untukk=N+1, N+2,..., N+L. k n n k k n n n n k k nk nk n n k k nk nk A f a b f a b a b a b A a b a b
(13) dengan ( ) 0, jikak n 1, jikak=n. nk
Diasumsikan bahwa matrik
A
nonsingular, sehingga nilai
( ) ( )
,k k
a b
k
1, 2,...,
N
L
dapatdiperoleh. Menggunakan nilai
( ) ( )
,k k
a b
yang telah diperoleh tersebut, dapat digunakan untuk mencari nilai
a b
,
, dengan
a b
,
adalah sebarang titik padaR
C
, menggunakan rumus
( ) ( )
( ) ( )
( ) ( )
( ) 2 1 1 1 , , , , , ; , . N N L k k k k j j j k j a b a b f a b p f a b a b a b
(14) C. Simulasi NumerikPenelitian ini menggunakan DRBEM untuk menyelesaikan masalah infiltrasi air dalam irigasi alur pada jenis tanah Plainfield Sand. Jenis tanah Plainfield Sand memiliki nilai 2
2, 62 10 , 0 0, 03 K ,
0, 045
r
, s 0, 43 dan n2, 68. Nilai dari L dan D dipilih 50 cm, m 1 1/n [10] dan nilaiv
04, karena berdasarkan penelitian sebelumnya dengan nilai c=4 memberikan pendekatan numerik yang baik serta tidak memberikan efek siknifikan dari nilai
. Selanjutnya metode DRBEM akan diimplementasikan dalam program Matlab.Implementasi Matlab dalam kasus ini dibagi menjadi tiga tahap, yaitu yang diberi nama Pre-processing, Processing, dan Post-processing. Setiap tahap memerlukan input dan menghasilkan output. Beberapa tahap juga memerlukan output tahap sebelumnya untuk dijadikan input pada tahap tersebut. Setelah implementasi program Matlab selesai dibuat, selanjutnya digunakan untuk menyelesaikan masalah infiltrasi pada jenis tanah Plainfield Sand. Dipilih N=200 dan M=612, yaitu banyaknya segmen garis untuk diskritisasi batas domain dan titik kolokasi pada interior domain. Dipilih jumlah tersebut karena berdasarkan [12] akurasi dari pendekatan numerik yang dihasilkan cukup baik. Selanjutnya, akan dievaluasi nilai
dan
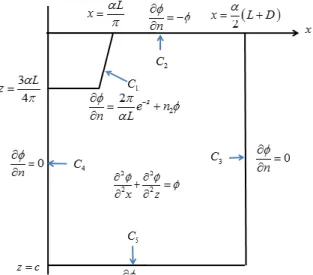
di beberapa titik sepanjang garis X=10 cm, X=30 cm, X=50 cm, X=70 cm, dan X=90 cm, untuk 0 Z 200 cm.A. SUCTION POTENTIAL B. WATER CONTENT GAMBAR2.SUCTION POTENTIAL DAN WATER CONTENT UNTUK X=10
A. SUCTION POTENTIAL B. WATER CONTENT GAMBAR3.SUCTION POTENTIAL DAN WATER CONTENT UNTUK X=30
A. SUCTION POTENTIAL B. WATER CONTENT GAMBAR4.SUCTION POTENTIAL DAN WATER CONTENT UNTUK X=50
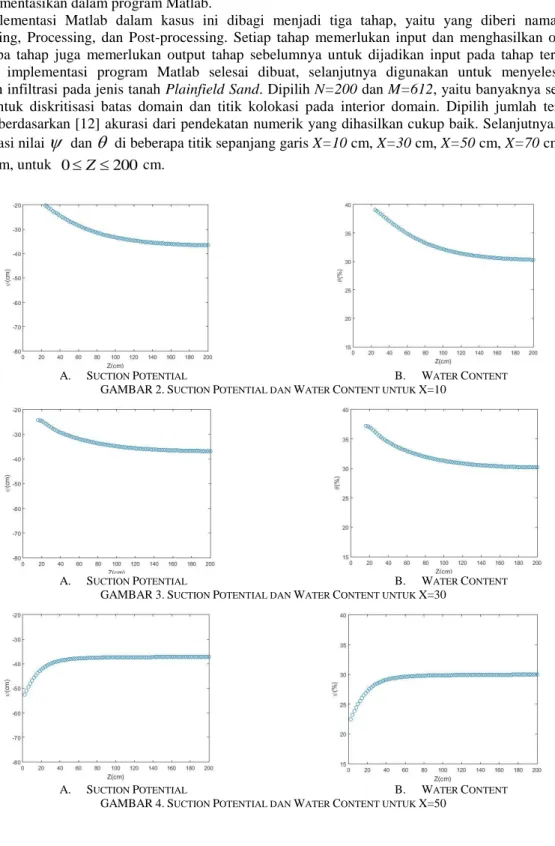
A. SUCTION POTENTIAL B. WATER CONTENT GAMBAR5.SUCTION POTENTIAL DAN WATER CONTENT UNTUK X=70
A. SUCTION POTENTIAL B. WATER CONTENT GAMBAR6.SUCTION POTENTIAL DAN WATER CONTENT UNTUK X=90
Diperhatikan bahwa Gambar 2 dan 3 merupakan grafik nilai
dan
sepanjang garis X=10 cm dan X=30 cm, untuk0
Z
200
cm. Jelas bahwa nilai
dan
sepanjang garis-garis tersebut merupakan nilai
dan
dibawah saluran air. Berdasarkan Gambar 2 dan 3 diketahui bahwa nilai
dan
turun seiring dengan kedalaman yang bertambah dan menuju titik kekonvergenannya. Hal ini mengindikasikan bahwa nilai suction potential berbading lurus dengan kandungan air. Selain itu dapat disimpulkan bahwa kandungan air di posisi yang dangkal lebih besar dari pada posisi yang dalam untuk tanah yang berada dibawah saluran. Hal ini sesuai dengan asumsi bahwa air masuk dari saluran, yang selanjutnya air merembes ke dalam tanah yang lebih dalam dibawah saluran.Selanjutnya Gambar 4-6 merupakan grafik nilai
dan
sepanjang garis X=50 cm, X=70 cm, dan X=90 cm, untuk 0 Z 200 cm. Jelas bahwa nilai
dan
sepanjang garis-garis tersebut merupakan nilai
dan
untuk tanah yang tidak di bawah saluran air irigasi. Berdasarkan Gambar 7-9 diketahui bahwa nilai
dan
naik seiring dengan kedalaman yang bertambah dan menuju titik kekonvergenannya. Hal ini menguatkan kesimpulan sebelumnya bahwa nilai suction potential berbading lurus dengan kandungan air. Nilai
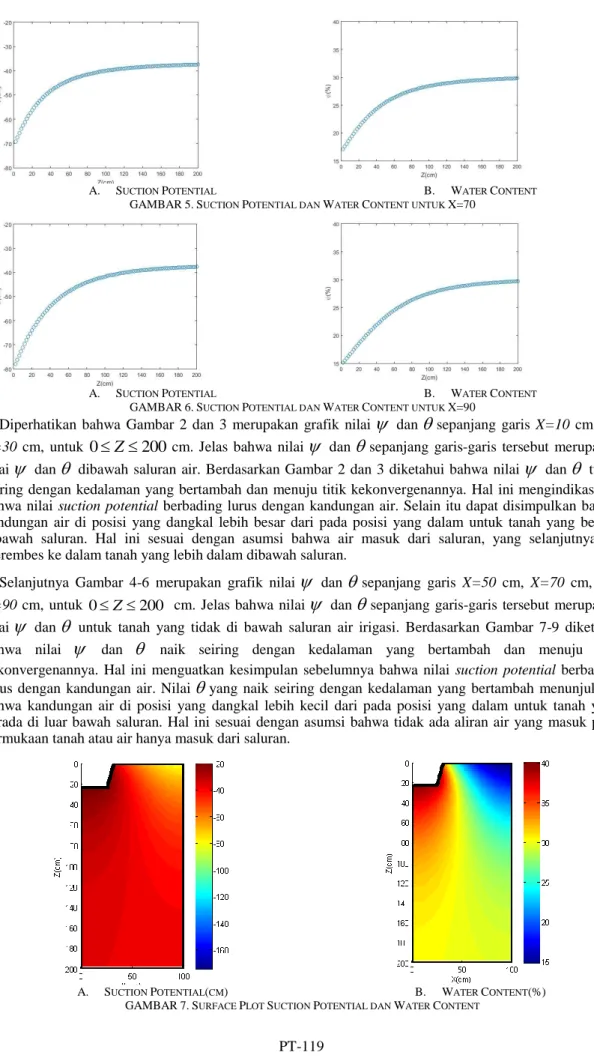
yang naik seiring dengan kedalaman yang bertambah menunjukkan bahwa kandungan air di posisi yang dangkal lebih kecil dari pada posisi yang dalam untuk tanah yang berada di luar bawah saluran. Hal ini sesuai dengan asumsi bahwa tidak ada aliran air yang masuk pada permukaan tanah atau air hanya masuk dari saluran.A. SUCTION POTENTIAL(CM) B. WATER CONTENT(%) GAMBAR7.SURFACE PLOT SUCTION POTENTIAL DAN WATER CONTENT
Selanjutnya untuk melihat variasi atau pola persebaran nilai suction potential dan water content pada domain dibuatlah surface plot nilai suction potential dan water content pada domain. Berdasarkan Gambar 7 terlihat bahwa nilai suction potential paling besar terletak di bawah saluran, sedangkan yang paling kecil di permukaan tanah pada luar saluran yang berjarak paling jauh dari pusat saluran. Selain itu dapat terlihat bahwa pada lapisan tanah bagian atas semakin jauh jarak dari saluran maka suction potential-nya semakin kecil, berbeda dengan lapisan tanah bagian bawah nilai suction potential-nya hampir sama. Dapat terlihat pula bahwa kandungan air paling besar terletak di bawah saluran, sedangkan yang paling kecil di permukaan tanah pada luar saluran yang berjarak paling jauh dari pusat saluran. Selain itu dapat terlihat bahwa pada lapisan tanah bagian atas semakin jauh jarak dari saluran maka kandungan airnya semakin kecil, berbeda pada lapisan tanah bagian bawah kandungan airnya cinderung sama dan tidak bergantung jarak dari saluran.
IV. SIMPULAN DAN SARAN
Berdasarkan pembahasan pada bab sebelumnya, maka dapat disimpulakan sebagai berikut. DRBEM dapat menyelesaikan model matematika masalah infiltrasi saluran irigasi alur di dalam tanah homogen yang berbentuk MSB dengan persamaan pengaturnya adalah Persamaan Helmholtz termodifikasi dan syarat batasnya adalah syarat batas campuran. Nilai Kandungan air yang terbesar terletak di bawah saluran dan kandungan air terkecil di permukaan tanah pada luar saluran yang berjarak paling jauh dari pusat saluran. Pada lapisan tanah bagian atas semakin jauh jarak dari saluran maka kandungan airnya semakin kecil, berbeda pada lapisan tanah bagian bawah kandungan airnya cinderung sama dan tidak bergantung pada jarak dari saluran.
Masalah infiltrasi dalam penelitian ini pada kasus keadaan tanah jenuh, artinya untuk perubahan waktu yang ada infiltrasinya tetap. Penelitian selanjutnya dapat menggunakan DRBEM untuk masalah infiltrasi yang bergantung pada waktu, karena DRBEM juga dapat menyelesaikan Masalah Nilai Awal dan Syarat Batas (MNASB).
DAFTAR PUSTAKA
[1] V. Batu, “Steady Ilfiltration from Single and Periodik Strip Source”, Soil Sci.Soc. Am. J, Amerika, vol.42, pp. 544-549, 1978. [2] H. Mayer dan M. William, Boundary Value Problems and Partial Differential Equation, Boston: PWS-KENT, 1992.
[3] M. Lobo, Dual Reciprocity Boundary Element Methods for the Solution of a Class of Ilfiltration Problems, Faculty of Engineering, Coputer and Mathematical Sciences, University of Adelaide, Doctor Disertation, 2008.
[4] J. Katsikadelis, Boundary Element : Theory and Applications, Oxford: Elsevier Science, 2002.
[5] C. Pozrikidis, A Practical Guide to Boundary Element Methods with The Software Library BEMLIB, Florida: Chapman & Hall/CRR , 2002.
[6] M. Manaqib, Dual Reciprocity Boundary Element Methods untuk Menyelesaikan Masalah Infiltrasi Saluran Irigasi Alur di dalam Beberapa Jenis Tanah Homogen, Universitas Gadjah Mada, Master Tesis, 2015.
[7] W. T. Ang, A Beginners Course in Boundary Element Methods, Florida: Universal Publishers, 2007.
[8] I. Solekhudin, Dual Reciprocity Boundary Element Methods for Water Ilfiltration Problems in Irrigation, National Institude of Education, Nangyang Technological University, Doctor Dissertation, 2013.
[9] M. Manaqib, “Pemodelan Matematika Infiltrasi Air pada Saluran Irigasi Alur”, Jurnal Matematika Mantik, Surabaya, vol. 03 No.1, pp 25-31, 2017.
[10] A.W. Warrick, Soil Physics Companion, Washington D.C: CRC Press, 2002.
[11] H.A. Basha, ”Multidimensional Linearized Nonstedy Infiltration with Prescribed Boundary Conditions at the Soil Surface”, Water Resources Research, Amerika, vol. 35(1), pp 75-83, 1999.
[12] I. Solekhudin dan K.C. Ang, ”Suction Potential and Water Absorption from Periodic Chanel in Different Types of Homogeneous Soil“, Electronic Jurnal of Boundary Element, Singapura, vol.10, pp. 42-55, 2012.