BAB 2
LANDASAN TEORI
2.1 Vehicle Routing Problem
Vehicle routing problem memiliki peranan pokok dalam manajemen logistik.
Vehicle routing problem berperan dalam merancang rute yang optimal yang digunakan oleh sejumlah kendaraan yang ditempatkan pada depot untuk melayani sejumlah pelanggan dengan permintaan yang diketahui (Toth dan Vigo, 2002). Laporan ilmiah dari Dantzig dan Ramser (1959) secara luas dianggap sebagai laporan ilmiah pertama tentang vehicle routing. Yang menguraikan tentang rute armada truk pengiriman bensin antara terminal curah dan sejumlah besar stasiun layanan yang dipasok dari terminal.
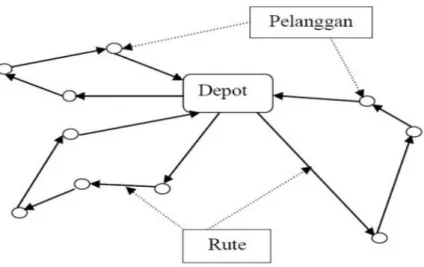
Toth dan Vigo menggambarkan vehicle routing problem sebagai suatu graf lengkap 𝐺 = (𝑉,𝐴), di mana 𝑉 = {0, . . . ,𝑛} adalah himpunan titik dan 𝐴 himpunan busur. Node𝑖 = 1, … ,𝑛, menunjukkan pelanggan, sedangkan node 0
menunjukkan depot. Terkadang depot digambarkan juga dengan 𝑛 + 1. Biaya
non negative/jarak tempuh (𝑐𝑖𝑗𝑘), terkait dengan setiap busur (𝑖,𝑗)∈ 𝐴 dan merupakan biaya travel yang dikeluarkan dalam perjalanan dari titik𝑖 ke titik𝑗. Tujuan vehicle routing problem adalah untuk mengatur rute biaya terendah kendaraan sedemikian hingga:
• Setiap rute dimulai dan diakhiri di depot.
• Setiap pelanggan dikunjungi tepatnya sekali dengan satu kendaraan.
• Jumlah permintaan dari rute kendaraan yang ada tidak melebihi kapasitas kendaraan.
Gambar 2.1 Visualisasi Vehicle Routing Problem
Kallehauge dkk. (2001) mendefinisikan pemasalahan 𝑚-TSP (Traveling Salesman Problem) sebagai salah satu variasi dari TSP (Traveling Salesman Problem), di mana terdapat 𝑚 salesman yang mengunjungi sejumlah kota dan tiap kota hanya dikunjungi oleh tepat satu salesman saja. Tiap salesman berawal dari suatu depot dan pada akhir perjalanannya juga harus kembali ke depot tersebut. Permasalahan 𝑚-TSP (Traveling Salesman Problem) ini dikenal sebagai Vehicle Routing Problem (VRP). Kallehauge dkk. juga memformulasikan sebuah model dari vehicle routing problem sebagai berikut:
Fungsi tujuan: Min 𝐶 = � � � 𝑐𝑖𝑗𝑘 𝑁+1 𝑗=0 𝑁+1 𝑖=0 𝐾 𝑘=1 𝑥𝑖𝑗𝑘 2.1 Kendala: � � 𝑥𝑖𝑗𝑘 = 1; 𝑖= 1, 2, … ,𝑁 2.2 𝑁+1 𝑗=0 𝐾 𝑘=1 � 𝑑𝑖 𝑁 𝑖=1 � 𝑥𝑖𝑗𝑘 ≤ 𝑣𝑘; 𝑘 = 1, 2, … ,𝐾 2.3 𝑁+1 𝑗=0
� 𝑥0𝑗𝑘 = 1; 𝑘= 1, 2, … ,𝐾 𝑁+1 𝑗=0 2.4 � 𝑥𝑖ℎ𝑘− � 𝑥ℎ𝑗𝑘 = 0; ℎ= 1, 2, … ,𝑁;𝑘= 1, 2, … . ,𝐾 𝑁+1 𝑗=0 𝑁+1 𝑖=0 2.5 � 𝑥𝑖,𝑁+1,𝑘 = 1; 𝑘 = 1, 2, … . ,𝐾 𝑁+1 𝑖=0 2.6 𝑥𝑖𝑗𝑘 ∈ {0, 1}; 𝑖= 0, 2, … ,𝑁+ 1;𝑘= 1, 2, … . ,𝐾 2.7 dengan:
𝑐𝑖𝑗𝑘 = biaya travel antara konsumen 𝑖dan 𝑗.
𝐾 = nomor kendaraan.
𝑑𝑖 = total permintaan kendaraan 𝑘sampai konsumen 𝑖.
𝑁 = nomor pelanggan (0menunjukkan depot).
𝑣𝑘 = kapasitas maksimum kendaraan 𝑘.
Persamaan (2.1) menunjukkan fungsi tujuan dari permasalahan ini, yaitu untuk meminimalkan total biaya travel. Persamaan (2.2) menunjukkan bahwa tiap konsumen hanya dapat dilayani oleh satu kendaraan saja. Persamaan (2.3) digunakan untuk membatasi total jumlah permintaanyang dibawa oleh kendaraan
𝑘, tidak boleh melebihi kapasitas dari kendaraan tersebut. Persamaan (2.4)-(2.6) digunakan untuk memastikan bahwa tiap kendaraan berangkat dari depot 0, dan setelah selesai melayani seorang konsumen, kendaraan tersebut akan pergi, serta pada akhirnya, kendaraan tersebut akan kembali ke depot𝑁+ 1.
Vehicle routing problem mungkin dapat memiliki kendala tambahan yang akan mengarah pada varian yang berbeda. Varian tersebut pada dasarnya dibentuk dengan modifikasi pada satu atau lebih elemen dalam vehicle routing problem.
Terdapat empat elemen yang membentuk model dari varian tersebut, yaitu: jaringan jalan, kendaraan, pelanggan, dan ketidakpastian pada model. Elemen-elemen ini dapat diatur dengan cara yang berbeda. Seperti misalnya, pertimbangan
dalam jaringan jalan, perbedaan kendaraan, time windows, dan perbedaan tipe dari permintaan pelanggan (pick-up atau delivery). Selain itu, beberapa ketidakpastian juga dapat dipertimbangkan, seperti ketidakpastian dalam permintaan dan waktu perjalanan. Beberapa contoh varian dari vehicle routing problem adalah vehicle routing problem with time windows, vehicle routing problem with backhaul,
vehicle routing problem with pick-up and delivery, dan stochastic vehicle routing problem.
2.2 Teori Himpunan Fuzzy
Dalam mengatasi permasalahan himpunan dengan batas yang tidak tegas, Zadeh mengaitkan himpunan semacam itu dengan suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan konsep yang merupakan syarat keanggotaan himpunan tersebut. Fungsi tersebut dapat dikatakan sebagai fungsi keanggotaan dan fungsi tersebut juga dapat dikatakan sebagai derajat keanggotaan suatu unsur dalam himpunan. Hal ini untuk selanjutnya disebut sebagai himpunan
fuzzy. Maka dapat dikatakan setiap unsur dalam semesta memiliki derajat keanggotaan tertentu dalam himpunan tersebut.
Derajat keanggotaan dinyatakan dengan suatu bilangan real dalam selang tertutup [0,1]. Dengan perkataan lain, fungsi keanggotaan dari suatu himpunan
fuzzy A� dalam 𝑋 adalah pemetaan 𝜇Ã(𝑥) dari 𝑋 ke selang [0,1], yaitu 𝜇Ã : 𝑋 →
[0,1]. Nilai fungsi 𝜇Ã(𝑥) menyatakan derajat keanggotaan unsur 𝑥 Є 𝑋 dalam himpunan fuzzy A�. Nilai fungsi sama dengan 1 menyatakan keanggotaan penuh, dan nilai fungsi sama dengan 0 menyatakan sama sekali bukan anggota himpunan
fuzzy tersebut. Maka himpunan tegas juga dapat dikatakan sebagai kejadian khusus dari himpunan fuzzy, yaitu himpunan fuzzy yang fungsi keanggotaannya hanya bernilai 0 atau 1 saja. Jadi fungsi keanggotaan dari suatu himpunan tegas 𝐴 dalam semesta 𝑋adalah pemetaan dari 𝑋ke himpunan {0,1}.
2.2.1 Fungsi Keanggotaan
Secara matematis suatu himpunan fuzzy A� dalam semesta 𝑋 dapat dinyatakan sebagai himpunan pasangan berurut:
𝐴̃= ��𝑥,𝜇A�(𝑥)�|𝑥 ∈ 𝑋� 2.8
di mana 𝜇A� adalah fungsi keanggotaan dari himpunan fuzzy 𝐴̃, yang merupakan suatu pemetaan dari himpunan semesta 𝑋 ke selang tertutup [0,1]. Apabila semesta 𝑋 adalah himpunan yang kontinu, maka himpunan fuzzy 𝐴̃ dinyatakan dengan:
𝐴̃= �𝜇𝐴�𝑥(𝑥)
𝑥∈𝑋
2.9
di mana lambang ʃ di sini bukan lambang integral seperti dalam kalkulus, tetapi melambangkan keseluruhan unsur-unsur 𝑥 ∈ 𝑋 bersama dengan derajat keanggotaannya dalam himpunan fuzzy 𝐴̃. Apabila semesta 𝑋 adalah himpunan yang diskrit, maka himpunan fuzzy 𝐴̃dinyatakan dengan:
𝐴̃= �𝜇𝐴�𝑥(𝑥)
𝑥∈𝑋
2.10
di mana lambang ∑ di sini tidak melambangkan operasi jumlahan seperti dalam aritmatika, tetapi melambangkan keseluruhan unsur-unsur 𝑥 ∈ 𝑋 bersama dengan derajat keanggotaannya dalam himpunan fuzzy 𝐴̃.
Pendukung (support) dari suatu himpunan fuzzy 𝐴̃, yang dilambangkan dengan 𝑃𝑒𝑛𝑑(𝐴̃), adalah himpunan tegas yang memuat semua unsur dari semesta yang mempunyai derajat keanggotaan tidak nol dalam (𝐴̃), yaitu:
𝑃𝑒𝑛𝑑�𝐴̃�= {𝑥 ∈ 𝑋 | 𝜇𝐴�(𝑥) > 0} 2.11 Tinggi (height) dari suatu himpunan fuzzy (𝐴̃), yang dilambangkan dengan
𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃), didefinisikan sebagai:
𝑇𝑖𝑛𝑔𝑔𝑖�𝐴̃�= sup
Teras (core) dari suatu himpunan fuzzy (𝐴̃), yang dilambangkan dengan
𝑇𝑒𝑟𝑎𝑠(𝐴̃), adalah himpunan semua unsur dari semestanya yang mempunyai derajat keanggotaannya sama dengan 1, yaitu:
𝑇𝑒𝑟𝑎𝑠�𝐴̃�= {𝑥 ∈ 𝑋 | 𝜇𝐴�(𝑥) = 1} 2.13 Pusat dari suatu himpunan fuzzy didefinisikan sebagai berikut: jika nilai purata dari semua titik di mana fungsi keanggotaan himpunan fuzzy itu mencapai nilai maksimum adalah berhingga, maka pusat himpunan fuzzy itu adalah nilai purata tersebut. Jika nilai purata itu tak hingga positif, maka pusat himpunan fuzzy
itu adalah yang terkecil di antara semua titik yang mencapai nilai fungsi keanggotaan maksimum. Dan begitu pun sebaliknya jika nilai purata itu tak hingga negatif, maka pusat himpunan fuzzy itu adalah yang terbesar di antara semua titik yang mencapai nilai fungsi keanggotaan maksimum.
Dua buah himpunan fuzzy 𝐴̃ dan 𝐵� dalam semesta 𝑋dikatakan sama
�𝐴̃= 𝐵��, jika dan hanya jika
𝜇𝐴�(𝑥) =𝜇𝐵�(𝑥) 2.14 untuk setiap 𝑥 ∈ 𝑋. Himpunan fuzzy 𝐴̃ dikatakan merupakan himpunan bagian dari himpunan fuzzy 𝐵��𝐴̃ ⊆ 𝐵��, jika dan hanya jika
𝜇𝐴�(𝑥)≤ 𝜇𝐵�(𝑥) 2.15 untuk setiap 𝑥 ∈ 𝑋. Jadi 𝐴̃ = 𝐵� jika dan hanya jika 𝐴̃ ⊆ 𝐵� dan 𝐵� ⊆ 𝐴̃.
Fungsi keanggotaan trapesium/trapezoidal merupakan salah satu fungsi keanggotaan himpunan fuzzy yang mempunyai empat buah parameter, yaitu a, b,
c, d ∈ ℝ dengan a < b < c < d, dan dinyatakan dengan trapesium (x; a, b, c, d) dengan aturan: 𝜇(𝑥) = ⎩ ⎪ ⎨ ⎪ ⎧𝑥 − 𝑎𝑏 − 𝑎 untuk 𝑎 ≤ 𝑥 ≤ 𝑏 1 untuk 𝑏 ≤ 𝑥 ≤ 𝑐 𝑑 − 𝑥 𝑑 − 𝑐 untuk 𝑐 ≤ 𝑥 ≤ 𝑑 0 untuk lainnya
Fungsi keanggotaan tersebut dapat diformulasikan sebagai berikut:
Trapesium(𝑥;𝑎,𝑏,𝑐,𝑑) =𝑚𝑎𝑥 �𝑚𝑖𝑛 �𝑥 − 𝑎𝑏 − 𝑎, 1,𝑑 − 𝑥𝑑 − 𝑐�, 0� 2.16
Berikut gambar yang memperlihatkan fungsi keanggotaan trapesium (x; a, b, c, d).
𝜇(𝑥) 1
0 𝑎 𝑏 𝑐 𝑑 𝑥 Gambar 2.2 Fungsi Keanggotaan Bilangan Fuzzy Trapezoidal
2.2.2 Penegasan (Defuzzifikasi)
Input dari proses defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari suatu komposisi aturan-aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu bilangan pada himpunan fuzzy tersebut. Sehingga jika diberikan suatu himpunan fuzzy dalam range tertentu, maka harus dapat diambil suatu nilai
crisp tertentu sebagai output. Menurut Kusumadewi (2004), ada beberapa metode defuzzifikasi pada komposisi aturan Mamdani. Salah satunya adalah metode
centroid (Composite Moment). Pada metode ini, solusi crisp diperoleh dengan cara mengambil titik pusat daerah fuzzy. Secara umum dirumuskan sebagai berikut:
Untuk domain kontinu:
𝑍0 =∫ 𝑍 𝑏
𝑎 𝜇(𝑍)𝑑𝑧
∫ 𝜇𝑎𝑏 (𝑍)𝑑𝑧
di mana:
𝑍 = nilai domain ke−𝑖
𝜇(𝑍) =derajat keanggotaan titik tersebut
𝑍0 = nilai hasil penegasan Untuk domain diskrit:
𝑍=∑𝑛𝑖=1𝑑𝑖.𝑈𝐴𝑖(𝑑𝑖)
∑ 𝑈𝑛𝑖=𝑗 𝐴𝑖(𝑑𝑖)
2.18
di mana:
𝑍 = nilai hasil penegasan (defuzzyfikasi)
𝑑𝑖 = nilai keluaran pada aturan ke−𝑖
𝑈𝐴𝑖(𝑑𝑖)= derajat keanggotaan nilai keluaran pada aturan ke –𝑖
𝑛 = banyaknya aturan yang digunakan
2.2.3 Distribusi Possibility
Misalkan 𝑋 menjadi variabel yang mengambil nilai-nilai dalam semesta wacana
𝑈, dengan unsur umum 𝑈 dinotasikan dengan 𝑢. Maka:
𝑋=𝑢 2.19
menandakan bahwa 𝑋diberi nilai 𝑢, 𝑢 ∈ 𝑈.
Misalkan 𝐹 menjadi subset fuzzy dari 𝑈 yang ditandai dengan fungsi keanggotaan 𝜇𝐹. Kemudian 𝐹 adalah batasan fuzzy pada 𝑋 (atau berhubungan dengan 𝑋) jika𝐹 bertindak sebagai kendala elastis pada nilai-nilai yang dapat ditugaskan untuk 𝑋 dalam arti bahwa penugasan nilai 𝑢untuk 𝑋 memiliki bentuk:
𝑋=𝑢:𝜇𝐹(𝑢) 2.20 di mana 𝜇𝐹diartikan sebagai derajat yang kendalanya diwakili oleh 𝐹, di mana 𝐹 memenuhi bila 𝑢 ditugaskan untuk 𝑋. Sama seperti, (2.20) menunjukkan bahwa
1− 𝜇𝐹(𝑢) adalah derajat yang mana kendalanya harus dilebarkan untuk memenuhi tugas 𝑢 untuk 𝑋.
Misalkan 𝑅(𝑋) menunjukkan batasan fuzzy yang berhubungan dengan 𝑋. Kemudian, untuk menyatakan bahwa 𝐹 memainkan peran dari batasan fuzzy
dalam hubungannya dengan 𝑋, maka dapat ditulis:
𝑅(𝑋) =𝐹 2.21
Persamaan bentuk ini disebut persamaan tugas rasional karena hal tersebut menggambarkan penugasan dari himpunan fuzzy (atau relasi fuzzy) dengan batasan yang berhubungan dengan 𝑋.
Definisi 1
Misalkan 𝐹 himpunan bagian kabur dari semesta 𝑈 yang ditandai dengan fungsi keanggotaan 𝜇𝐹, dengan tingkat keanggotaan, 𝜇𝐹(𝑢), diartikan sebagai kecocokan dari 𝑢 dengan konsep yang bertanda 𝐹.
Misalkan 𝑋 menjadi variabel yang nilainya diambil dalam 𝑈, dan misalkan
𝐹 bertindak sebagai batasan fuzzy, 𝑅(𝑋), yang berhubungan dengan 𝑋. Kemudian permasalahan "𝑋 adalah𝐹", yang diterjemahkan menjadi:
𝑅(𝑋) =𝐹 2.22
menghubungkan distribusi possibility, Π𝑥, dengan 𝑋 yang didalilkan sama dengan
𝑅 (𝑋), yaitu:
Π𝑥= 𝑅(𝑋) 2.23 Sejalan dengan itu, fungsi distribusi possibility berhubungan dengan 𝑋 (atau fungsi distribusi possibility dari Π𝑥) dinotasikan dengan 𝜋𝑥 dan didefinisikan sebagai numerik yang sama dengan fungsi keanggotaan 𝐹, yaitu:
dengan demikian 𝜋𝑥(𝑢), di mana kemungkinan bahwa 𝑋=𝑢, adalah untuk mendalilkan menjadi sama dengan 𝜇𝐹(𝑢).
Dalam gambaran (2.23), persamaan tugas relasional (2.22) dapat dinyatakan setara dalam bentuk:
Π𝑥= 𝐹 2.25 menempatkan bukti bahwa dalil 𝑝 ≜ 𝑋 adalah 𝐹, yang memiliki efek untuk menghubungkan 𝑋 dengan distribusi possibility Π𝑥, di mana (2.23) adalah sama dengan 𝐹. Ketika dinyatakan dalam bentuk (2.25), persamaan tugas relasional akan disebut persamaan tugas possibility, dengan pengertian bahwa Π𝑥 diinduksi oleh 𝑝.
a. Ukuran possibility
Misalkan 𝐴 himpunan bagian nonfuzzy dari 𝑈 dan misalkan Π𝑥 menjadi distribusi
possibility yang terhubung dengan variabel 𝑋 yang mengambil nilai dalam 𝑈. Kemudian, ukuran possibility 𝜋(𝐴) dari 𝐴 didefinisikan sebagai bilangan dalam
[0, 1] yang diberikan oleh:
𝜋(𝐴)≜ 𝑆𝑢𝑝𝑢∈𝐴𝜋𝑥(𝑢) 2.26 di mana 𝜋𝑥(𝑢) adalah fungsi distribusi possibility Π𝑥. Jumlah ini kemudian mungkin diartikan sebagai possibility bahwa nilai 𝑋 milik 𝐴, yaitu:
𝑃𝑜𝑠𝑠{𝑋 ∈ 𝐴}≜ 𝜋(𝐴)≜ 𝑆𝑢𝑝𝑢∈𝐴𝜋𝑋(𝑢) 2.27 Ketika 𝐴 adalah himpunan fuzzy, yang termasuk nilai dari 𝑋 ke 𝐴 adalah tidak berarti.
Definisi 2
Misalkan 𝐴 himpunan bagian fuzzy dari 𝑈 dan misalkan Π𝑥 menjadi distribusi
possibility yang berhubungan dengan variabel 𝑋 yang mengambil nilai dalam 𝑈. Ukuran possibility𝜋(𝐴) dari 𝐴 didefinisikan dengan:
𝑃𝑜𝑠𝑠{𝑋𝑎𝑑𝑎𝑙𝑎ℎ𝐴}≜ 𝜋(𝐴)≜ 𝑆𝑢𝑝𝑢∈𝑈𝜇𝐴(𝑢)⋀𝜋𝑋(𝑢) 2.28 di mana "𝑋 adalah 𝐴" diganti "𝑋 ∈ 𝐴" dalam (2.27), 𝜇𝐴 adalah fungsi keanggotaan dari 𝐴, dan ⋀ berdiri, seperti biasa, untuk minimal.
Perlu dicatat bahwa, dalam hal height dari suatu set fuzzy, yang didefinisikan sebagai supremum dari fungsi keanggotaan, (2.27) dapat dinyatakan dengan jelas dengan persamaan:
𝜋(𝐴)≜ 𝐻𝑒𝑖𝑔ℎ𝑡(𝐴⋂Π𝑋) 2.29 b. Possibility dan informasi
Jika 𝑝 adalah sebuah dalil dari bentuk 𝑝 ≜ 𝑋 adalah 𝐹 yang diterjemahkan ke dalam persamaan tugas possibility:
Π𝐴(𝑋) =𝐹 2.30 di mana𝐹 adalah himpunan bagian fuzzy dari 𝑈 dan 𝐴 (𝑋) adalah sifat tersirat dari 𝑋 yang mengambil nilai dalam 𝑈, maka informasi yang disampaikan oleh 𝑝,
𝐼(𝑝), dapat diidentifikasi dengan distribusi possibility, Π𝐴(𝑋), dari variabel fuzzy
𝐴(𝑋). Dengan demikian, hubungan antara 𝐼(𝑝),Π𝐴(𝑋), R(A(X)) dan 𝐹 dinyatakan oleh:
𝐼(𝑝)≜ Π𝐴(𝑋) 2.31 di mana:
Π𝐴(𝑋) =𝑅�𝐴(𝑋)�=𝐹 2.32
2.3 Program Possibilistic
Berikut merupakan formulasi program possibilistic. Pertimbangkan masalah program linear berikut:
Fungsi tujuan:
Kendala:
𝐴𝑥 ≤ 𝑏
𝑥 ≥0, 2.33
Di mana 𝑐 = (𝑐1, … ,𝑐𝑛) merupakan vektor baris 𝑛-dimensi, 𝑥= (𝑥1, … ,𝑥𝑛)𝑡 merupakan vektor kolom 𝑛-dimensi, 𝑏= (𝑏1, … ,𝑏𝑚)𝑡 merupakan vektor kolom
𝑚-dimensi dan 𝐴 =�𝑎𝑖,𝑗� merupakan matriks 𝑚 x 𝑛. Bilangan fuzzy L-R 𝐴𝑖,𝑗 dapat ditentukan dengan sebuah pusat 𝑎𝑖𝑗𝑐 dengan penyebaran kiri 𝑤𝑎𝑖𝑗𝑙 dan penyebaran kanan 𝑤𝑎𝑖𝑗𝑟 , dan dapat direpresentasikan sebagai 𝐴𝑖,𝑗 =<
𝑎𝑖𝑗𝑐, 𝑤𝑎𝑖𝑗𝑙 , 𝑤𝑎𝑖𝑗𝑟 >. 𝑐𝑗 diperkirakan sebagai bilangan fuzzy L-R 𝑐𝑗 =<
𝑐𝑗𝑐,𝑤
𝑐𝑗𝑙 ,𝑤𝑐𝑗𝑟 >.
Bilangan fuzzy yang membatasi nilai fungsi possibilistic linear didefinisikan oleh prinsip perluasan. Menerapkan prinsip perluasan, misalnya, untuk fungsi tujuan dari permasalahan (2.33), 𝑓0(𝑥1, … ,𝑥𝑛) =∑𝑛𝑗=1𝑐𝑗𝑥𝑗, bilangan
fuzzy 𝐹0(𝑥1, … ,𝑥𝑛) dengan batasan 𝑓0(𝑥1, … ,𝑥𝑛) didefinisikan oleh fungsi keanggotaan berikut:
𝜇𝐹0(𝑥1,…,𝑥𝑛)(𝑟) = Sup𝑝 1,…,𝑝𝑛
min�𝜇𝑐1(𝑝1), … ,𝜇𝑐𝑛(𝑝𝑛)� 2.34 Di mana 𝑟= 𝑝1𝑥1+⋯+𝑝𝑛𝑥𝑛. Mempertimbangkan fakta bahwa 𝑐𝑗 adalah bilangan fuzzy L-R < 𝑐𝑗𝑐,𝑤𝑐𝑗𝑙 ,𝑤𝑐𝑗𝑟 >, bilangan fuzzy 𝐹0(𝑥1, … ,𝑥𝑛) juga menjadi bilangan fuzzy L-R, yaitu:
𝐹0(𝑥1, … ,𝑥𝑛) =<� 𝑐𝑗𝑐𝑥𝑗, 𝑛 𝑗=1 � 𝑤𝑐𝑗𝑙 𝑥𝑗, 𝑛 𝑗=1 � 𝑤𝑐𝑗𝑟𝑥𝑗 𝑛 𝑗=1 > 2.35
Persamaan kedua adalah dari non-negatif dalam 𝑥𝑗 dari permasalahan (2.33). misalkan 𝐹𝑖(𝑥1, … ,𝑥𝑛) menjadi bilangan fuzzy yang membatasi nilai sisi kiri dari kendala ke-𝑖 dari (2.33), oleh karena itu untuk 𝑖= 1, … ,𝑚,
𝐹𝑖(𝑥1, … ,𝑥𝑛) =< � 𝑎𝑖𝑗𝑐𝑥𝑗, 𝑛 𝑗=1 � 𝑤𝑎𝑖𝑗𝑙 𝑥𝑗,� 𝑤𝑎𝑖𝑗𝑟 𝑥𝑗 > 2.36 𝑛 𝑗=1 𝑛 𝑗=1 Catatan 1
Asumsikan 𝐴𝑖𝑗 dan 𝑐𝑗 adalah bilangan fuzzy triangular simmetris sebagai berikut:
𝐴𝑖𝑗 =<𝑎𝑖𝑗𝑐,𝑤𝑎𝑖𝑗𝑐 >,𝑐𝑗 =<𝑐𝑗𝑐,𝑤𝑐𝑗𝑐 >
Jika ditetapkan 𝐿(𝑥) =𝑅(𝑥) = 1− 𝑥, kemudian permasalahan (2.33) dirumuskan sebagai permasalahan program linear berikut:
Fungsi tujuan: 𝑚𝑎𝑥 � 𝑐𝑗𝑐𝑥 𝑗 − 𝑎 � 𝑤𝑐𝑗𝑥𝑗 𝑛 𝑗=1 𝑛 𝑗=1 Kendala: � 𝑎𝑖𝑗𝑐𝑥𝑗+𝑎 � 𝑤𝑎𝑖𝑗𝑐 𝑥𝑗 ≤ 𝑏𝑖,𝑖 = 1, … ,𝑚 𝑛 𝑗=1 𝑛 𝑗=1 𝑥𝑗 ≥0,𝑗 = 1, … ,𝑛 2.37
2.4 Metode Saving Matriks
Metode saving matriks pada hakikatnya adalah metode untuk meminimumkan jarak atau waktu dan ongkos dengan mempertimbangkan kendala-kendala yang ada. Berikut ini langkah-langkah pembentukan rute distribusi dengan menggunakan metode saving matriks, yaitu:
1. Identifikasi Matriks Jarak
Pada langkah ini, diperlukan jarak antara gudang dan ke masing-masing toko dan jarak antar toko. Untuk menyederhanakan permasalahan, lintasan terpendek digunakan sebagai jarak antar lokasi. Jadi, dengan mengetahui koordinat masing-masing lokasi maka jarak antar dua lokasi bisa dihitung dengan menggunakan rumus jarak standar. Apabila jarak riil antar lokasi diketahui, maka jarak tersebut lebih baik digunakan dibanding dengan jarak teoritis dengan menggunakan rumus. Jarak dari gudang ke masing-masing
toko dan jarak antar toko akan digunakan untuk menentukan matriks penghematan (saving matriks) yang akan dikerjakan pada langkah berikutnya.
2. Mengidentifikasi matriks penghematan ( saving matriks)
Pada langkah ini, diasumsikan bahwa setiap toko akan dikunjungi oleh satu armada secara eksklusif. Saving matriks merepresentasikan penghematan yang bisa direalisasikan dengan menggabungkan dua pelanggan ke dalam satu rute. Untuk perhitungan penghematan jarak dapat mengunakan persamaan:
𝑆(𝑥,𝑦) = 𝐽 (𝐺,𝑥) + 𝐽(𝐺,𝑦) – 𝐽(𝑥,𝑦)
di mana:
𝑆(𝑥,𝑦) = Penghematan Jarak
𝐽 (𝐺,𝑥) = Jarak gudang ke toko 𝑥
𝐽 (𝐺,𝑦) = Jarak gudang ke toko 𝑦
𝐽 (𝑥,𝑦) = Jarak toko 𝑥 ke toko 𝑦 3. Mengalokasikan Distributor ke rute
Dengan menggunakan tabel penghematan jarak, dapat dilakukan pengalokasian toko ke kendaraan atau rute. Pada tahap awal, tiap toko alokasikan ke rute yang berbeda, namun toko-toko tersebut bisa digabungkan sampai pada batas kapasitas truk yang ada. Penggabungan akan dimulai dari nilai penghematan terbesar karena diupayakan memaksimumkan penghematan.