BAB I
GAMBARAN UMUM GEOMETRI FRAKTAL
1. Latar Belakang Adanya Geometri Fraktal
Setelah membuat definisi tentang 4 unsur primitif dan 5 postulat, Euclidus menurunkan berbagai dalil tentang geometri bidang datar. Tetapi ternyata geometri ini hanya bisa digunakan untuk menerangkan secara konsepsional objekobjek linear atau objek-objek buatan manusia, bukan objek-objek alam. Sebenarnya sejak lama para ahli matematika telah berupaya untuk merumuskan objek-objeknon linear seperti yang dilakukan oleh Bolyai, Lobachevski, maupun Riemann. Pada dasarnya mereka ingin mengubah postulat ke 5 (postulat kesejajaran) dari Euclidus agar dapat keluar dari paradigma linearitas.
Bolyai menunjukkan bahwa dari 29 dalil ternyata 28 dalil pertama dari Euclidus dapat dibuktikan tanpa menggunakan postulat yang ke 5. Dengan menggunakan 4 yang pertama dari 5 postulat Euclidus, Bolyai mampu membuktikan bahwa melalui suatu titik B di luar garis lurus bdapat dilukis paling sedikit 1 garis lurus yang sejajar dengan garis b. Kemudian lebih jauh Lobachevski juga menggantikan postulat ke 5 dari Euclidus dengan postulat: melalui 1 titik di luar suatu garis lurus paling sedikit dapat dilukis 2 buah garis lurus yang sejajar. Dengan postulat pengganti ini, Lobachevski ingin membuktikan bahwa postulat ke 5 dari Euclidus itu hanya merupakan akibat dari 4 postulat lainnya. Walaupun Lobachevski tidak berhasil membuktikan itu, tetapi dengan postulat pengganti yang tampaknya tidak masuk akal itu (beserta4 postulat pertama dari Euclidus) Lobachevski malah berhasil membangun suatu geometri lain yang juga konsisten. Geometri Lobachevski tidak menggunakan bidang datar melainkan bentuk terompet.
Selain itu Riemann membuat postulat: tidak ada 2 buah garis lurus yang sejajar. Postulat ini sejalan dengan fenomena dalam membatasi bidang permukaan yang berbentuk bola. Geometri Riemann yang semula dipandang aneh ini ternyata kemudian melandasi lahirnya Teori Relativitas Einstein.
melinearkan setiap objek (baik itu buatan manusia ataupun objek alam) melalui pembuatan fungsi-fungsi kurva dan menggunakan operasi yang sangat terkenal dengan istilah diferensialintegral. Memang dengan kemajuan seperti yang dicapai dalam Persamaan Diferensial maupun Teori Fuzzy dalam memformulasikan sistem dinamis, kalkulus juga mencapai kemajuan yang sangat mengesankan yang pada puncaknya dapat mendeskrispsikan Teori Kekacauan (Chaos Theory). Tetapi, kedua teori ini tidak mempunyai basis yang konsepsional melainkan dengan menggunakan aproksimasi numerik.
Suatu ironis bahwa Geometri Euclidus merupakan geometri yang paling banyak digunakan tetapi paling jarang dijumpai di alam. Penemuan Himpunan Debu Cantor, Kurva Koch, Media Berpori seperti Spon, Karpet dan GasketSierpinski (Gambar 2 - 6) merupakan teka-teki (puzzles)bagi kalkulus yang merupakan anak kandung (offspring) dari Geometri Euclidus. Semua objek tersebut adalah objek-objek kontinyu tetapi tidak diferensialble. Artinya objek-objek selalu dikeluarkan dari pembahasan kalkulus. Himpunan Debu Cantor (Cantor Set) tidak bisa dikatakan sebagai objek berdimensi 1 (garis lurus) ataupun 0 (titik). Kurva Koch, Gasket dan Karpet Sierpinski tidak bisa dikatakan sebagai objek berdimensi 1 ataupun 2 (bidang datar). Sedangkan media berpori spon (Menger Sponge) bukanlah objek berdimensi 2 ataupun 3.
dapat dipecahkan dengan Gasket Sirpinskie. Begitu pula model pertumbuhan populasi.
2. Pengertian dengan Geometri Fraktal
Bahasa Inggris dari fraktal adalah fractal. Istilah fractal dibuat oleh Benoît Mandelbrot pada tahun 1975 dari kata Latin fractus yang artinya "patah", "rusak", atau "tidak teratur". Sebelum Mandelbrot memperkenalkan istilah tersebut, nama umum untuk struktur semacamnya adalah kurva monster.
Menurut Mandelbrot, setiap objek alam berperilaku sebagai fraktal dalam hal ini merupakan hasil kerja gaya yang sama yang bekerja pada berbagai tingkatan skala pada suatu objek sehingga mengakibatkan iterasi atau pengulangan bentuk dasar (fractal seed atau fractal generator) yang hasilnya menyatu dalam satu objek yang bersangkutan. Proses itu dikenal sebagai proses self similiarity yang bersifat scale invariant: artinya diamati dengan skala berapapun bentuk geometrinya maupun dimensinya tetap sama dengan benih fraktalnya.
3. Kegunaan Geometri Fraktal dalam Kehidupan
Geometri Fraktal ini telah dipergunakan hampir di semua bidang bahkan untuk ilmu social, ekonomi maupun bidang seni Dalam ilmu tanah penggunaan Geometri Fraktal masih terbatas pada bidang fisika tanah. Dalam hal ini pertama kali dipelopori oleh Tyler dan Wheatcraft untuk menentukan parameter percabangan pori-pori tanah dalam usaha untuk meniadakan pekerjaan fitting parameter dan untuk mereduksi pekerjaan empiris di laboratorium ataupun di lapangan sehingga pemodelan retensi ataupun pergerakan air tanah beserta bahan-bahan polutan yang terlarut di dalamnya dapat dikerjakan secara konsepsional, dalam arti secara matematika absah dan mempunyai landasan hukum-hukum fisika yang telah diterima secara universal serta cepat, murah dan tidak banyak memakan waktu.
4. Pengelompokan Fraktal
Fraktal dibedakan menjadi dua, yaitu:
yang lebih kecil. Tetapi benda-benda alam tidak pernah betul-betul simetris sehingga fraktal deterministik kurang realistis.
2. Fraktal random. Fraktal random dihasilkan oleh kombinasi aturan-aturan yang dipilih secara random pada skala yang berbeda. Contoh: sebuah garis pantai. Dari pesawat terbang, garis pantai terlihat seperti garis tak teratur yang mulus. Makin rendah pesawat terbang, makin bergerigi garis pantai itu, sampai pada jarak dekat setiap batas terlihat. Semakin dekat, semakin jelas terlihat detail garis pantai tersebut. Harga saham mirip dengan garis pantai tersebut. Makin dekat kita melihat (makin kecil unit waktunya), makin banyak detail yang terlihat.
Fraktal bisa juga dikelompokkan menjadi tiga kategori luas. Pengelompokan berikut didasarkan pada cara pendefinisian atau pembuatannya.
1. Iterated Function System - memiliki aturan geometris tetap. Misalnya himpunan debu Cantor , karpet Sierpinski, gasket Sierpinski, kurva Peano, bunga salju Koch, kurva naga Harter-Highway, T-Square , spons Menger
2. Escape-time fractals - ditentukan dengan formula atau relasi rekursi di setiap titik. Contoh himpunan Mandelbrot, himpunan Julia , fraktal Burning Ship, fraktal Nova dan fraktal Lyapunov
3. Random fractals - dibentuk oleh proses stokastik bukan dari proses deterministik.Contoh lintasan gerak Brown , penerbangan Levy , fraktal lanskap fraktal dan pohon Brownian .
Fraktal juga bisa dikelompokkan berdasarkan keserupa diriannya. Ada tiga tingkat keperupadirian pada fraktal:
Serupa diri secara persis — Ini adalah keserupa dirian yang paling kuat. Fraktalnya terlihat sama persis pada berbagai skala. Fraktal yang didefinisikan oleh sistem fungsi teriterasi biasanya bersifat serupa diri secara persis.
Serupa diri secara lemah — Ini adalah keserupa dirian yang tidak terlalu ketat. Fraktalnya terlihat mirip (tapi tidak persis sama) pada skala yang berbeda. Fraktal jenis ini memuat salinan dirinya sendiri dalam bentuk yang terdistorsi maupun rusak.
BAB II
MACAM-MACAM GEOMETRI FRAKTAL
1. Himpunan Mandelbrot
Mandelbrot, Benoit B. (20 November 1924 – 14 October 2010) adalah seorang matematikawan Perancis kelahiran Polandia, yang mengembangkan geometri fraktal sebagai salah satu cabang baru matematika.Mandelbrot dilahirkan di Warsawa dan mengenyam pendidikan sekolah di Perancis dan USA, meraih gelar doktor dalam bidang matematika dari Universitas Paris pada tahun 1952.Ia mengajar ekonomi di Universitas Harvard, teknik di Universitas Yale, psikologi di Albert Einstein College of Medicine, matematika di Paris dan Genewa. Sejak 1958 ia berkerja sebagai anggota IBM di Pusat Riset Thomas B. Watson di New York.
Pada tahun 1960-an Benoît Mandelbrot mulai menyelidiki keserupa dirian dalam berbagai tulisannya seperti How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension.Penyelidikannya merupakan pengembangan dari penelitian Lewis Fry Richardson.Dengan pendekatan yang sangat visual, Mandelbrot mendapatkan hubungan dari berbagai topik matematika yang sebelumnya tidak berkaitan.Di tahun 1975, Mandelbrot menggunakan kata fractal untuk mendeskripsikan benda-benda serupa diri yang tidak memiliki dimensi yang jelas. Dia menurunkan kata fractal dari kata Latin fractus yang artinya "patah", "rusak", atau "tidak teratur". Kata fractal bukan diturunkan dari katafractional (pecahan), seperti yang dipercaya banyak orang.Katafractional sendiri juga diturunkan dari fractus.
yang berdimensi pecahan.Sebagai contoh, kurva fraktal snowflake Koch memiliki dimensi 1.2618.
Himpunan Mandelbrotadalahhimpunan titik-titikpada
bidangkompleks.Untuk membangunhimpunanMandelbrot, kita
menggunakanalgoritmaberdasarkanrumusrekursif:
memisahkanpoindaribidang kompleksmenjadi dua kategori: •titik di dalamhimpunanMandelbrot,
•titik di luar himpunanMandelbrot.
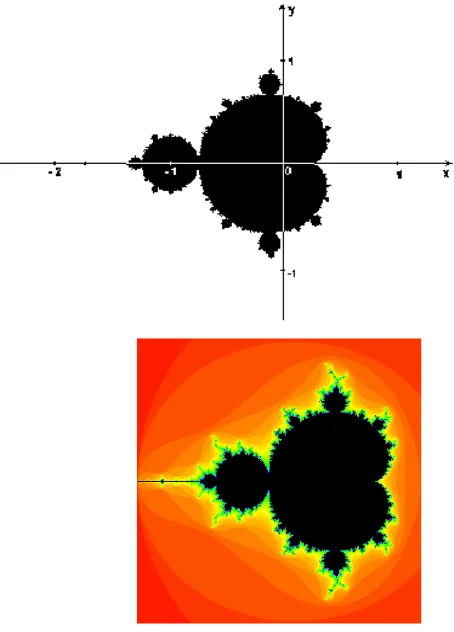
Gambar di bawah menunjukkansebagian daribidang kompleks.Titik-titikdari himpunanMandelbrottelahberwarnahitam.
Untuk membuathimpunanMandelbrotkita harusmemilih titik(C) padabidang kompleks.Bilangan kompleks yang berkorespondensi dengantitik inimemilikibentuk:
Setelahmenghitungnilai dari ekspresisebelumnya:
Kita misalkan Z0=0 , lalu kita tentukan nilai C sebagai hasilnya. Langkah selanjutnyaadalahmenetapkanhasil dari Z1 , dan ulangi perhitungan hingga didapat hasil C2+C . Setelah itu kita harus menentukan nilai untuk Z2 dan ulangi prosesnya lagi.
Proses ini dapat direpresentasikan sebagai"migrasi" darititik awalC pada bidang.
Apa yang terjadi padatitik ketikakitaberulang kali melakukan iterasi pada fungsi tersebut? Apakah akantetapdekatke asalatauakanpergijauh dari itu, bertambahnya jarakdari titik asaltanpabatas? Dalamkasus pertama, kita mengatakan bahwaCtermasuk himpunanMandelbrot(itu adalah salah satutitik hitampada gambar); sebaliknya,kita mengatakan bahwa titikini menuju tak hinggadan kitamenentukanwarnauntukCtergantung padakecepatan di manatitik tersebut"pergi"/ “menjauh” dari titik asal.
Kita bisa melihat pada algoritma dari sudut pandang yang berbeda . Mari kita bayangkan bahwa semua titik bidang ditarik pada : tak hingga dan himpunan Mandelbrot. Membuat ini mudah untuk memahaminya:
Titik-titik yang jauh dari himpunan Mandelbrot bergerak dengan
cepat bergerak menuju tak hingga.
Titik-titik yang dekat dengan himpunan Mandelbrot secara perlahan bergerak menuju tak hingga.
2. Segitiga Sierpinski
Sierpinski Triangle dinamai oleh matematikawan Polandia, Waclaw Sierpinski tahun 1916. Cara Membuat Segitiga Sierpinski :
1. Buat segitiga sama sisi
2. Hubungkan masing-masing titik tengah sisi segitiga
3. Hilangkan segitiga yang di tengah
4. Ulangi langkah 1,2,3 untuk 3 buah segitiga yang ada
Cara menghitung luas segitiga sierpinski adalah sebagai berikut. Setelah iterasi/pengulangan ke-n,
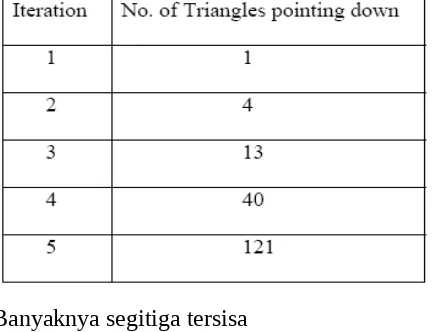
Luas segitiga sierpinski = (0,75)n x luas segitiga sama sisi awal Cara menghitung banyaknya segitiga yang masih ada setelah iterasi ke-n?:
Tabel 1. Daftar Jumlah Segitiga Pada Interasi ke-n
Banyaknya segitiga tersisa
2. Kurva Von Koch
Kurva Von Koch dihasilkan oleh prosedur geometris sederhana yang dapat diiterasikan tak terbatas dengan membagi segmen garis lurus menjadi tiga bagian yang sama dan mengganti bagian tengah dengan dua segmen yang sama panjang. Von Koch The Curve adalah contoh yang sangat dasar dari fraktal, karena mengikuti aturan sederhana konstruksi.
a) Melukis Edge Koch
2. Garis lurus dibagi menjadi 3 bagian yang sama, dan bagian tengah digantikan oleh dua segmen linier pada sudut 60o dan 120o .
3. Ulangi langkah 1 dan 2 untuk empat segmen garis.
4. Iterasi selanjutnya akan menghasilkan kurva berikut.
b) Sifat-sifat Edge Koch
Kurva Von Koch jelas menunjukkan kesamaan-diri fraktal. Pola yang sama selalu muncul sepanjang kurva dalam skala yang berbeda, dari yang dapat terlihat sampai yang sangat kecil.
Idealnya proses iterasi (pengulangan) tanpa batas dan iterasi juga dapat dihentikan.
Total Panjang Edge Koch
Untuk mempertahankan perpindahan di antara dua titik konstan, ukuran
panjang dikalikan dengan 4
3 di setiap iterasinya.
Dari aturan sederhana iterasi, kita dapat menggunakan rumus panjang total dari Edge Koch pada iterasi ke-n.
Di ulang 3 ×
L=
(
4 3)
n
Untuk menghitung dimensi Kurva Koch, kita melihat citra fraktal dan mengetahui bahwa Kurva Koch memiliki faktor pembesaran tiga dan setiap iterasi dibagi menjadi empat bagian yang lebih kecil. Sehingga didapatkan:
D=ln 4 ln3=
1,3863
1,0986=1,2619
Jadi, Kurva Koch memiliki dimensi 1,2619.
Jumlah Edge Koch
Setelah iterasi, setiap sisi tunggal berubah menjadi empat segmen berukuran
sama dengan panjang 1
3 dari panjang aslinya.
Dengan demikian, setelah iterasi n, jumlah Edge Koch adalah 4n .
c) Contoh Lain Kurva Koch Koch Snowflake
Jika kita menerapkan proses di atas pada dua sisi suatu segitiga sama sisi (tidak termasuk bagian dalam), kita akan memiliki pola sebagai berikut.
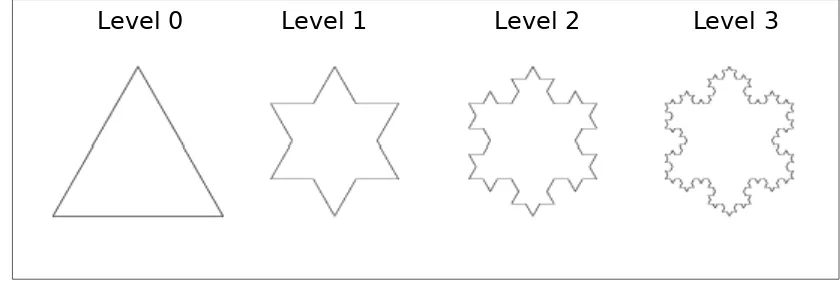
Pada tingkat yang sangat tinggi, kita akan memiliki gambar di bawah ini:
Level 0 Level 1 Level 2 Level 3
Kurva Koch ini disebut kurva snowflake.
Koch Star
Selain segitiga sama sisi, proses yang sama dapat diterapkan pada sisi sembarang polygon.
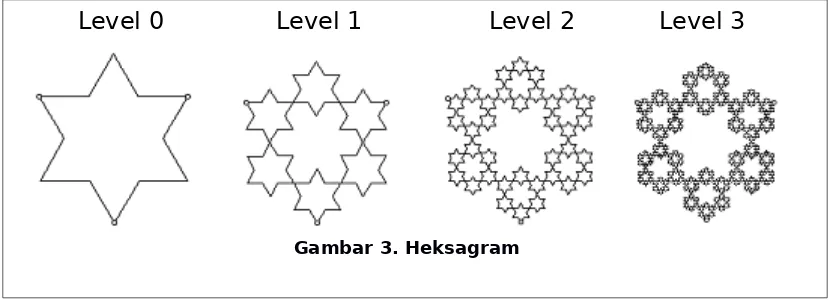
Salah satu contohnya adalah heksagram. Pada setiap tingkat, heksagram baru yang lebih kecil dihasilkan di enam simpul dari heksagram asli. Hasil dari heksagram yang baru mirip dengan heksagram yang asli.
3. Kurva Hilbert
Kurva Hilbert pertama kali diperkenalkan oleh David Hilbert (1862-1943). Kurva ini disebut kurva pengisi ruang, karena pada akhirnya akan menutupi seluruh bidang setelah beberapa iterasi.
a) Melukis Kurva Hibert
Mulailah dengan bentuk dasar seperti berikut.
Level 0 Level 1 Level 2 Level 3
Gambar 2. Kurva Snowflake
Perkecil kurva sebelumnya menjadi setengah ukurannya. Secara bersamaan, perkecil ukuran grid oleh dua faktor. Tempatkan empat salinan dari kurva tersebut pada grid. Dua salinan kurva yang berada di bawah tetap seperti sebelumnya, dan dua salinan kurva yang di atas harus diputar sebuah , satu ke kiri dan yang lainnya ke kanan. Terakhir, menghubungkan empat potong pendek segmen untuk mendapatkan kurva langkah berikutnya, dapat dihubungkan segmen horizontal maupun vertikal.
Semua sisa kurva dibuat secara berurutan satu dari yang lain dengan menggunakan algoritma yang sama.
b) Sistem-L
Berbeda dengan segitiga Sierpinski dan kurva Von Koch, dalam proses melukis kurva Hilbert, bentuk pokok yang sama akan menyusut dan berubah di tempat lain dan beberapa dari kurva diputar 90o . Algoritma ini disebut Lindenmayer
System (L-sistem). Ini adalah langkah-langkah menulis ulang sistem yang terutama digunakan untuk menghasilkan fraktal dengan dimensi antara 1 dan 2. Setelah transformasi, kurva harus dihubungkan dengan memperkenalkan beberapa baris segmen. Itulah sebabnya, setelah beberapa iterasi (sekitar ke-7 sampai ke-9), kurva akan menutupi seluruh bidang.
c) Panjang Kurva
BAB III
APLIKASI FRAKTAL
1. Aplikasi Fraktal dalam Kehidupan Sehari-Hari
Dalam kehidupan sehari-hari, ada banyak sekali aplikasi fraktal dari banyak aspek. Seperti membuat komputer dengan bantuan mammograpy, membuat gambar nyata, membuat musik fraktal dan sebagainya. Pada makalah ini akan dibahas beberapa aplikasi dari fraktal.
A. Pengubinan
Karena keindahan gambar dari fraktal, maka fraktal-fraktal sering digunakan untuk mengisi suatu bidang. Gambar fraktal terkadang ditemukan di lantai, jendela yang antik, atau pada karpet.
Pengisian dengan Von Koch Curves
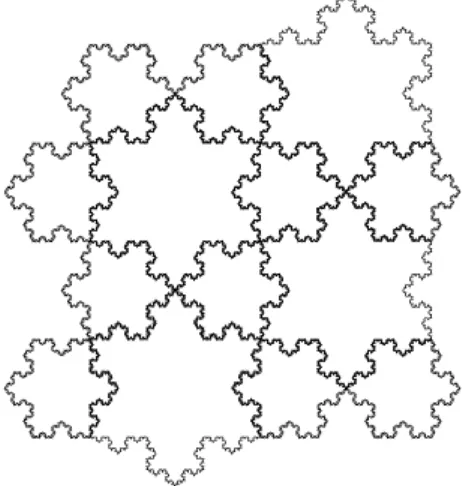
The Koch Snowflake yang kita diskusikan sebelumnya ternyata sangat bagus untuk dijadikan sebagai pengubinan. Dibawah ini merupakan gambar dari Koch Snowflakes dengan perbandingan 1:3 pada sebuah bidang.
Gambar 5. Von Koch Curves
pengubinan hexagon memiliki banyak jalan. Disini ada beberapa contoh dari pengubinan dengan menggunakan Koch Snowflakes.
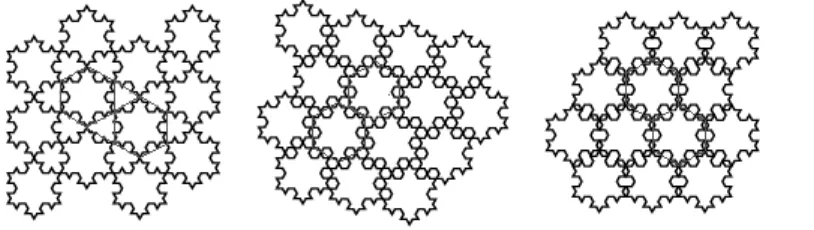
Gambar 6. Pengubinan Koch Snowflakes
Diatas adalah gambar dengan ukuran yang sama pada The Koch Star. Kemudian pengubinan dengan semua hexagon pada bidang akan diperoleh
Gambar 7. Hexagon The Koch Star
Gambar 8. Pengubinan Jendela Kuno di China
Pengisian Ruang Fraktal
Terdapat tipe fraktal yang berfungsi untuk membuat gambar yang berwarna penuh tanpa ada lubang dengan interasi yang terus menerus. Kita menyebutnya pengisian ruang fraktal. The Hibert Curve yang kita bahas sebelumnya merupakan contoh yang bagus dalam pengisian ruang fraktal. Jenis lain yang menarik dari pengisian ruang fraktal adalah The Peano Curve. Tidak seperti The Hibert Curveyang dibentuk dari persegi. The Peano Curve dibentuk dengan persegi panjang.
Pengisian ruang fraktal lainnya seperti Peano-Gosper Curve,Dragon Curve terdapat pada gambar dibawah ini.
B. Gambar Yang Nyata
Aplikasi yang sangat penting adalah membuta gambar nyata seperti awan, pohon, gunung, dan sebagainya. Ini dikarenakan banyak benda-benda alam seperti tumbuhan sangat kompleks dan beberapa bagian mirip dengan aslinya. Kompleksnya fraktal dan kelengkapan fraktal dalam mengulang-ulang bentuknya ternyata berperan besar dalam membuat gambar nyata.
The Koch Snowflake yang telah kita bahas sebelumnya ternyata dapat digunakan untuk mendesain gambar alami yang lengkap. The Koch Snowflakes itu sendiri sangat umum sebagai Snowflakes di gambar alami.
The Koch Snowflakesyang didiskusikan sebelumnya ternyata adalah awal yang bagus untuk memulai titik dalam mendesain kurva alami yang kompleks. The Koch Snowflake itu sendiri sudah sangat umum di dunia alami.
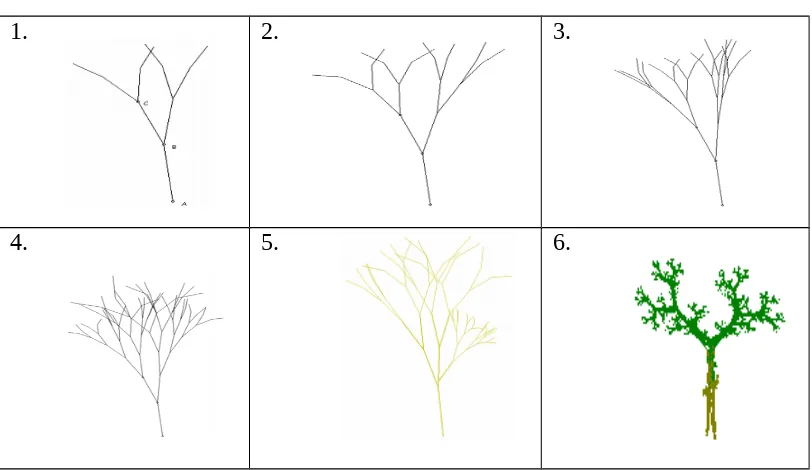
Gambar dibawah ini akan menunjukkan pembuatan pohon dengan fraktal.
Tabel 2. Alur Pembentukan Pohon dengan Fraktal
1. 2. 3.
4. 5. 6.
BAB IV
FRAKTAL KOMPRESI DAN BATIK FRAKTAL
1. Fraktal Kompresi
We've already known that fractals can be used to resemble real-life object, andKita sudah mengetahui bahwa fraktal dapat digunakan untuk membuat gambar yang menyerupai objek dalam kehidupan nyata, danwe've discussed how it works as well. kita telah membahas cara kerjanya juga. However, as researchers proceeded on thisUntuk mengubah sebuah image into a fractal by approximation. gambar ke dalam fraktal diperlukan suatu pendekatan.DWith the faster computer nowadays, they actually achieve the goal of compressingDengan komputer yang lebih cepat saat ini, kita dapat memampatkan real images into fractal images.gambar nyata ke dalam gambar fraktal.The advantage of using fractal compression isFraktal biasanya digambar oleh komputer dengan perangkat lunak fraktal. Fraktal acak memiliki kegunaan praktis yang terbesar sebab dapat digunakan untuk mendeskripsikan banyak benda di alam. Teknik-teknik fraktal juga telah digunakan pada kompresi gambar fraktal dan berbagai disiplin sains.
Keuntungan menggunakan kompresi fraktal adalah being able to enlarge the fractal without getting a blocky picture. bisa untuk memperbesar fraktal tanpa mendapatkan gambar gumpal. We could say the Kita bisa mengatakan fractal "smoothes out the details," making it much better for pictures required fraktal "menghaluskan detil," sehingga jauh lebih baik untuk gambar yang diperlukan some sort of zoom. semacam zoom. That is because fractals are infinitely detailed and so Itu karena fraktal sangat jauh lebih rinci dan begitu enlargement causes it is "smooth" the rough spots. memperhatikan pembesaran yang disebabkan oleh kehalusan dari bintik-bintik kasar. Compare the two pictures of
Gambar 12. Kompresi Daun
If you compare the two closely, you will find that the one on the right has more Jika Anda membandingkan dua dekat, Anda akan menemukan bahwa satu di sebelah kanan memiliki lebih banyakdetails. detail. The one on the left is just an enlargement of a bitmap. Yang satu di sebelah kiri hanya sebuah pembesaran bitmap. The compressed Yang merupakan gambar kompresiimage (on the right), however, has much more detail. (di sebelah kanan) adalah yang lebih detail.
2. Kegagalan Euclidean
Perkembangan geometri fraktal berbeda dengan pandangan geometri Euclid yang selama ini dikenal. Euclid menyederhanakan alam menjadi objek-objek yang simetris dan murni: titik, garis satu dimensi, ruang dua dimensi, dan bangun ruang tiga dimensi. Objek tersebut tidak ada yang memiliki lubang di dalamnya dan tidak ada yang kasar. Semuanya adalah bentuk yang mulus dan murni. Mungkin kegagalan geometri euclidean untuk menggambarkan bentuk alam karena tidak dapat menunjukkan bentuk selanjutnya. Dalam geometri euclidean, semakin dekat seseorang melihat pada objek, semakin sederhana objek tersebut. Bentuk tiga dimensi menjadi bentuk datar dua dimensi menjadi satu dimensi sampai akhirnya kelihatan menjadi titik. Sedangkan objek alam, memperlihatkan semakin detail seseorang melihatnya, seluruhnya terlihat sampai level subatomik. Ternyata fraktal memiliki sifat ini. Semakin dekat diuji, semakin detail terlihat.
karena memiliki lubang dan lipatan. Dimensinya antara 2 dan 3. Makin padat bola diremas, makin dekat ke 3 dimensi, atau benda padat. Bola yang diremas memiliki dimensi berupa bilangan pecahan atau dimensi fraktal. tidak berupa bilangan bulat. Geometri euclidean, atas kemurnian, bentuk halus tidak dapat menggambarkan bola kertas diremas tersebut. Bola kertas tidak dapat ditiru menggunakan geometri euclidean, kecuali melalui sejumlah besar interpolasi linear.
3. Karakteristik Fraktal
Salah satu karakteristik fraktal ialah kesamaan diri, artinya masing-masing bagian berkaitan dengan keseluruhannya. Sebagai contoh, pohon bercabang memiliki ranting-ranting kecilnya, mirip dengan bentuk keseluruhan pohon, tetapi tiap-tiap cabang itu unik. Bentuk fraktal menunjukkan kesamaan diri dalam ruang.
Secara umum fraktal bentuknya tidak teratur (tidak halus), jadi bukan termasuk benda yang terdefinisikan oleh geometri tradisional. Ini berarti bahwa fraktal cenderung memiliki detil yang signifikan, terlihat dalam skala berapapun, saat ada keserupa dirian, ini bisa terjadi karena memperbesar fraktal tersebut akan menunjukkan gambar yang mirip. Himpunan-himpunan tersebut biasanya didefinisikan dengan rekursi. Pohon dan pakis adalah contoh fraktal di alam dan dapat dimodel pada komputer menggunakan algoritma rekursif. Sifat rekursifnya bisa dilihat dengan mudah misalkan dengan mengambil satu cabang dari suatu pohon dan akan terlihat bahwa cabang tersebut adalah miniatur dari pohonnya secara keseluruhan (tidak sama persis, tapi mirip).
Sebagai perbandingan, ambil benda Euclid biasa, misalnya lingkaran. Lengkung pada lingkaran akan terlihat semakin datar jika diperbesar. Pada perbesaran tak terhingga tidak mungkin lagi terlihat perbedaan antara lengkung lingkaran dengan garis lurus. Fraktal tidak seperti ini. Ide konvensional kurvatur, yang merupakan
resiprokal dari jari-jari lingkaran aproksimasi, tidak bisa digunakan. Pada fraktal, meningkatkan perbesaran akan menunjukkan detil yang tidak terlihat sebelumnya.
Beberapa contoh fraktal yang umum adalah himpunan Mandelbrot, fraktal Lyapunov, himpunan Cantor, segitiga Sierpinski, karpet Sierpinski, spons Menger,
Contoh yang relatif sederhana adalah himpunan Cantor, di mana selang terbuka yang pendek dan semakin pendek tersebar pada selang dasar [0, 1], menyisakan himpunan yang mungkin serupa diri, dan mungkin memiliki dimensi d yang memenuhi 0 <d< 1. Suatu resep sederhana, yaitu menghilangkan digit 7 dari
ekspansi desimal, menghasilkan himpunan Cantor yang serupa diri pada perbesaran
lipat 10.
Gambar 13. Himpunan Mandelbrot Gambar 14. Menger Sponge
Gambar 15. Dragon Curve Gambar 16. Fraktal Lyapunov
Benda-benda yang mendekati fraktal bisa ditemukan dengan mudah di alam. Benda-benda tesebut menunjukkan struktur frakral yang kompleks pada skala tertentu. Contohnya adalah gunung, jaringan sungai, sistem pembuluh darah, awan, turbulensi, kilatan petir, salju (snow flake), kristal, ngarai (Grand Canyon), gunung, fosil, lidah api, dedaunan, brokoli, kulit salak dan bonggol nanas. Ron Eglash mengungkapkan bahwa karya budaya bangsa Afrika juga banyak yang berbau fraktal. Fraktal afrika dapat ditemukan pada rumah, patung, tekstil hingga cornrow yaitu tatanan rambut tradisional mereka.
Suatu himpunan Julia, fraktal yang berhubungan dengan himpunan Mandelbrot. Brokoli yang
merupakan fraktal alami.
Fraktal yang mirip bunga.
Lahir dari matematika, saat ini geometri fraktal geometri fraktal dapat diterapkan di banyak bidang sains. Fraktal banyak diaplikasikan pada bidang:
Klasifikasi histopatologi di ilmu kedokteran
Pembuatan musik jenis baru
Pembuatan berbagai bentuk karya seni baru Kompresi data dan sinyal
Seismologi
Kosmologi
Metode pemampatan gambar digital Industri kimia
Metreologi Fisika
4. Batik Fraktal
Batik fraktal adalah batik yang sentuhan desainnya (corak dan ragam hiasnya) dibuat dengan rumus-rumus matematika yang dikerjakan dengan teknologi komputer. Secara proses pembuatan batik fraktal dibagi menjadi 2 tahap, tahap pertama adalah pembuatan desain yang dilakukan oleh tim desain fraktal, dan tahap kedua dilakukan oleh tim pembuat batik. Pengembangan sofware Batik Fraktal dilakukan di Bandung oleh Tim Pixel People dan Bandung Fe Institute, sedangkan produksi batiknya dilakukan oleh Batik Komar di Bandung pula. Pada tahap pertama hanya menghasilkan sampai batas pola gambar (warna) yang dicetak pada selembar kertas dengan ukuran Folio. Tahap berikutnya akan dilanjutkan pada proses batik yang dikerjakan oleh tim produksi batik.
Sebelum membuat batik, hal pertama yang harus dilakukan adalah mengukur DNA batik tersebut. Mengukur keteraturan motif dan ciri khas batik dengan menggunakan alat yang disebut Dimensi Fraktal. Hasil pengukuran tersebut selanjutnya disebut DNA batik. Sebagai contoh motif parang rusak dari Yogyakarta. Pertama-tama, motif batik tersebut ditransformasikan dalam rumus matematika fraktal dengan bahasa L-System. Rumus tersebut kemudian dimodifikasi dengan mengubah parameter-parameternya sehingga menghasilkan rumus yang lebih kompleks dan rumit.
Selanjutnya, rumus tersebut diolah dengan program JBatik, sebuah aplikasi yang dibangun dengan basis open source software. Rumus ini akan menghasilkan gambar motif batik yang berbeda dari motif asli. Desainer dapat terus mengubah parameter rumusnya sehingga gambar yang dihasilkan sesuai dengan estetika desainer. Setelah desainer mendapatkan motif yang diharapkan, motif tersebut kemudian diberikan kepada pembatik tradisional untuk dicanting di atas kain.
yang mampu mengakomodasi konsep tentang kesamaan diri (Geometri Fraktal, Mendelbrot 1967).
Contoh penggalan rumus desain fraktal dengan tema “Patran Kangkung motif batik Tradisional Cirebonan” yang pernah dicoba dibuat sebagai berikut: “E=[A][B][C][D],A=C+FAE,B=C-FBE,C=C?FCE, D=C&FDE” artinya lambang [ ] menandakan percabangan, ‘+’, ‘-‘, ‘&’, ?, menandakan sudut dalam 3 dimensi.
Kelebihan dari sofware Jbatik ini yang kami rasakan adalah jika kita telah mendapatkan beberapa modul gambar (rumus), maka pengolahan dan pengembangan desain selanjutnya akan lebih mudah dan lebih banyak mendapatkan variasi desain yang berbeda dan sangat cepat sekali bila dibandingkan dengan langkah mendesain secara manual. Kita bisa membuat simulasi desain dengan komposisi layout motif, detail motif (lengkap dengan variasi isen-isen), visualisasi desain dengan tiga dimensi, memperbesar dan memperkecil gambar, simulasi warna yang sangat cepat dan indah sesuai dengan yang kita inginkan.
Gambar 21. Gambar dibuat dengan Komputer
3. Pencetakan Desain pada Kertas
Gambar atau desain yang telah dibuat oleh desainer batik fraktal kemudian dicetak pada selembar kertas ukuran Folio. Langkah selanjutnya gambar atau desain tersebut harus kita perbesar dengan menggunakan mesin fotokopi terlebih dahulu untuk mendapat ukuran yang semestinya dengan lebar kain yang digunakan. Kain yang digunakan umumnya berukuran lebar 110 cm hingga 120 cm sedangkan panjang kain tergantung dari jenis batik yang akan diproduksi, misalnya untuk bahan kemeja maka perlu panjang kain 270 cm. Khusus untuk desain fraktal yang akan dikerjakan dengan proses batik cap, maka desainnya tidak perlu dilakukan pembesaran terlebih dahulu, desain fraktal cukup di cetak dengan ukuran maksimal 20 cm x 20 cm.
4. Penyalinan Desain Fraktal
Desain fraktal yang telah diperbesar dengan mesin fotokopi, kemudian harus disalin ke kertas transparan ukuran A0 dengan menggunakan spidol gambar atau pena rapido. Pekerja yang menyalin (penterjemah) gambar asli fraktal harus memiliki kemampuan proses membatik tradisional dan mengerti membuat desain-desain batik. Desain fraktal bentukan software Jbatik harus sedikit direduksi dan disesuaikan dengan pola-pola kerja proses perajin batik dalam menggunakan canting batik. Jika orang yang menyalin gambar desain fraktal belum mengerti proses mencanting dengan mengggunakan lilin batik maka desain fraktal akan sulit dikerjakan oleh perajin batik tradisional.
5. Penulisan Desain Fraktal pada Kain
Proses selanjutnya, kain putih yang telah ada gambarnya kemudian dikerjakan dengan menggunakan canting batik. Canting yang digunakan biasanya akan disesuaikan dengan besar kecilnya garis-garis gambar. Ukuran lubang ujung canting sangat bervariasi, dan goresan canting akan mengikuti dengan bentuk detil gambar, baik berupa pengerjaan isen-isen atau penutupan (nembok).
7. Pewarnaan
Setelah proses pelilinan selesai dikerjakan, kemudian kain diberi warna dengan teknik rintang celup sesuai dengan yang kita inginkan. Setelah kain dijemur hingga kering, kemudian kita tutupi lagi pada bagian detil gambar dengan menggunakan canting yang diisi lilin, setelah selesai penutupan lilin kemudian dilakukan pewarnaan kembali dengan unsur warna yang berbeda. Langkah selanjutnya bisa dilakukan berulang-ulang sesuai dengan proses pewarnaan yang kita perlukan hingga diakhiri dengan proses pelorodan lilin (menghilangkan lilin dengan cara direbus dengan air yang mendidih).
Gambar 24.Produk Batik
Proses pengerjaan batik fraktal tidak semudah mengerjakan batik-batik tradisional pada umumnya dan membutuhkan biaya produksi yang cukup besar, namun hasilnya pun tidak kalah menariknya dengan desain-desain batik tradisional. Batik fraktal merupakan pelengkap ragam hias motif-motif batik tradisional dan memberikan pilihan baru bagi pecinta batik Indonesia. Waktu yang dibutuhkan untuk mengerjakan satu desain batik fraktal hampir sama dengan pengerjaan batik tulis motif tradisional, ada yang memerlukan waktu 2 hingga 6 bulan untuk menghasilkan kualitas batik yang baik.
DAFTAR PUSTAKA
Fraktal. http://id.wikipedia.org/wiki/Perangkat_lunak_aplikasi. (Diakses 14 Mei 2014).
http://translate.google.co.id/translate?hl=id&langpair=en|
id&u=http://www.fractal.org/Bewustzijns-Besturings-Model/Fractals-Useful-Beauty.htm. (Diakses 14Mei)
http://www.amazon.com/Fractal-Geometry-Nature-Benoit-Mandelbrot/dp/0716711869.
(Diakses 14Mei 2014).
http://en.wikipedia.org/wiki/Fractal. (Diakses 14Mei 2014).
http://www.scientificamerican.com/blog/post.cfm?id=benoit-mandelbrot-dead-at-85-2010-10-18. (Diakses Mei 2014)
http://sains-anak.blogspot.com/2010/07/kupu-kupu-fraktal.html
http://www.metasains.com/fraktal-di-batik-jawa-ketika-sains-dan-tradisi-saling-menginspirasi.html
http://www.cs.queensu.ca/home/xiao/doc/coding.pdf
http://translate.google.co.id/translate?hl=id&langpair=en|