Directory UMM :Data Elmu:jurnal:A:Agricultural & Forest Meterology:Vol104Issue3Sept2000:

(1)

Agricultural and Forest Meteorology 104 (2000) 215–231

Statistical treatment of sunfleck length inside willow coppice

J. Ross

∗

, M. Mõttus

Tartu Observatory, 61602 Tõravere, Tartumaa, Estonia

Received 4 January 2000; received in revised form 11 April 2000; accepted 12 April 2000

Abstract

Different sunfleck characteristics, length and number of sunflecks per metre and sunfleck fractional area, were measured at different depths inside willow (Salix viminalis) canopy. All these characteristics depend on the pathlength of the direct solar radiation beam into the canopy,τ=L/sin h, where L is the downward cumulative leaf area index and h is the solar elevation. The mean sunfleck lengthhlSidecreases exponentially withτ. The maximum length of short sunflecks (length

<6 cm) decreases linearly withτ, but not exponentially. Like the number of short sunflecks, the total number of sunflecks increases withτ, reaches a maximum value of 10–12 sunflecks m−1 _at_τ₌_{2.5 and then decreases slowly to zero at}_τ₌_6.

The vertical profiles of the sunfleck fractional area are different for long (length >6 cm) and short sunflecks. The fractional area of long sunflecks decreases withτexponentially; the fractional area of short sunflecks, kSS, can be approximated by the

formula kSS=0.19τexp(−0.15τ2), and the fractional area of all sunflecks kS, by the formula kS=exp(−0.18τ2). Within the

canopy, direct solar radiation is present in two areas — in sunflecks and in penumbra. The total flux of direct solar radiation in penumbra is smaller than it is in sunflecks and reaches its maximum value of 50% at the pathlengthτ=2. There exists a good correlation with R2=0.94 between the fractional area of umbra, kU, and the fractional area of sunflecks, kS, which can

Keywords: Sunflecks; Willow coppice; Radiation statistics in plant canopy

1. Introduction

If the solar discs were a source of point radiation, as it has been assumed in many earlier models of ra-diation transfer in a plant canopy, two types of areas would form inside the canopy:

1. sunflecks, where the area is illuminated by a parallel beam of direct solar radiation with the irradiance S0(W m−2), and

2. umbra (shade), where the area is shaded by

over-∗_{Corresponding author. Tel.:}₊_{372-7-410-278;} fax:+372-7-410-205.

E-mail address: ross@aai.ee (J. Ross).

lying leaves or other phytoelements and where the irradiance of direct solar irradiation S=0.

In fact, the solar disc has a finite angular diameter, and hence a third type of area, penumbra, is formed inside the canopy. In penumbra, the solar disc is partly covered by leaves and S may vary from 0 to S0.

Exis-tence of penumbra complicates greatly the treatment of radiation transfer in canopies. Due to the extremely complicated geometrical aspect of the problem, its comprehensive theoretical treatment is impossible. In our earlier work (Ross and Mõttus, 2000), we presented an overview of the relevant literature.

As a first attempt, our statistical treatment of sun-flecks, umbra and penumbra may suggest some new clues to a solution of the problem. Statistical treatment

(2)

216 J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231

of sunflecks, umbra and penumbra is closely related to the progress of new comprehensive computer mod-els of canopy photosynthesis and evapotranspiration, which require detailed 3D characteristics of different radiation types for input. As the interrelationship be-tween PAR and photosynthesis is nonlinear, the mean values of radiation do not yield correct results. In our opinion, for further calculation of canopy photosyn-thesis, leaves in plant canopies should be divided into three groups according to the type of direct sunlight they receive: sunflecks, umbra and penumbra; and photosynthesis should be calculated separately for each group. Therefore, it is necessary to know the area of sunflecks, its vertical distribution and tempo-ral dynamics in order that different data for umbra, penumbra and sunflecks could be used in modern radiation transfer models.

Ross et al. (1998) proposed a statistical treatment of PAR variability and its application to willow cop-pice. In this treatment, statistical distribution of PAR global irradiance, obtained with a LI-COR quantum sensor, was approximated by a normal distribution in sunfleck and umbra areas, and the fractional area of penumbra was approximated by the Beta-distribution and considered to be function of pathlength τ and solar elevation h.

This paper is a continuation of the previous work by Ross and Mõttus (2000) on a statistical treatment of umbra length and is focused on the statistical treatment of sunfleck length inside a willow coppice. Experi-mental data were obtained with a new instrument — the sunfleck sensor constructed by Sulev; the method-ology of statistical data processing is analogous to that used in our previous paper (Ross and Mõttus, 2000).

Sunfleck’s different statistical characteristics, such as sunfleck length distribution, sunfleck fractional area, number of sunflecks, mean sunfleck length, etc. in different canopy layers will be studied as the func-tions of the pathlength of the direct solar radiation1

τ=L/sin h, where L(z) = RzU

z uL(z)dz is the

down-ward cumulative leaf area index and uL(z) is the leaf

area density.

1_{In our previous paper (Ross and Mõttus, 2000), we used the}

term ‘optical pathlength’ for this quantity. However, to avoid any confusion that might arise from this general term, we use a more comprehensive term, ‘pathlength of the direct solar radiation beam’, in this paper.

2. Materials and methods

Radiation and phytometrical measurements were carried out during the foliated periods during 1995–1998 in a willow coppice of Salix viminalis, clone 78 021, located at Tartu Observatory, Tõravere (latitude 58◦16′N, longitude 26◦28′E, altitude 70 m above sea level), Estonia. More details of the research area, measuring system and data processing methods are given in Ross and Mõttus (2000).

Phytometrical data on leaf, shoot, stem and coppice characteristics used in this paper were published in Ross and Ross (1998), Ross and Mõttus (2000) and Ross et al. (2000). The measurements were carried out on different cloudless days during the whole growth period from June until October for solar elevation of 20–55◦during the years 1995–1999. The data used in this paper were obtained with the sunfleck sensor. The sunfleck sensor (Fig. 1) is, in principle, a miniature actinometer with an angle of view of 10◦in the verti-cal direction and 15◦in the horizontal direction. Such an angle of view guarantees that the sun will remain completely in the field of view for 6 min. A silicon photodiode was used as a sensor, and the instrument was calibrated on the pyrheliometric scale using a ref-erence actinometer. Due to the different spectral sen-sitivities of receivers and the special configuration of the field of view, this calibration is less accurate than the calibration of standard actinometric instruments.

The sunfleck sensor has a polar mounting and must be directed manually towards the sun before each scan.

(3)

J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231 217

The accuracy of determination of the linear dimen-sions of sunflecks and umbrae is±5 mm. The height of the horizontal bar inside coppice on which the sen-sor is mounted, can be changed from 0.4 to 6 m. One measurement scan consisted of a transit of the carriage perpendicular to willow rows from one end of the bar to the other and back with a total scan length of about 12 m. Because of leaf flutter caused by the wind, the data obtained from the two transits were not identi-cal; to increase the statistical reliability of the sample, the data from the two transits were considered as one measurement. The passage took about 400 s, and dur-ing each scan 2400 readdur-ings were recorded.

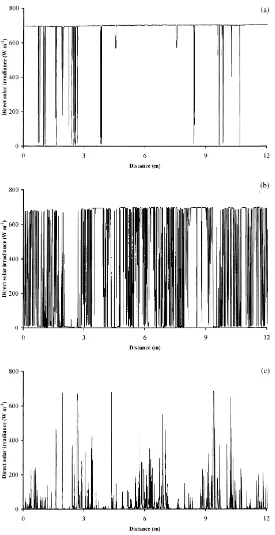
As an example, Fig. 2 shows the recordings of the sunfleck sensor on a cloudless day, 14 September 1998, at three heights (relative heights z/zU 0.85 (a),

0.65 (b) and 0.36 (c)), with the coppice height zU=

3.1 m. Fig. 2 shows how the large variation in the recordings of the sunfleck sensor depend on measur-ing height within the coppice.

3. Coppice architecture

As mentioned above, measurements with the sun-fleck sensor were performed during 1995–1998. The years 1995, 1996, 1997 were the third, fourth and fifth growing years, respectively. At the end of 1997, the plants were cut and 1998 was the first growing year after cutting.

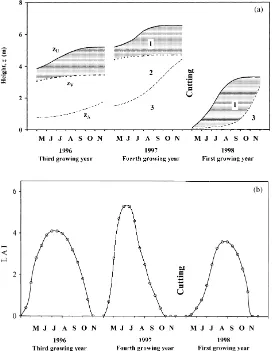
Some phytometrical characteristics of the planta-tion (Fig. 3) show the growth dynamics of coppice architecture. The architecture of willow coppice is de-scribed in more detail in Ross and Ross (1998), Ross and Mõttus (2000) and Ross et al. (2000), where it was demonstrated that it would be reasonable to di-vide willow coppice into three layers.

The upper foliage layer zU−zVconsists of

current-year stems and branches modelled as differently ori-ented foliage cylinders with leaves distributed along their axes; we assume random spatial distribution of cylinders. Cylinders start growing from the apices of previous-year stems and branches. In the first year, this layer consists of nearly vertical foliage cylinders, in the following years, of shoot and branch foliage cylin-ders of the current year. So, starting from the second growing year, the character and structure of the upper foliage cylinder layer does not change considerably.

The lower foliage layer zU−zA consists of branch

and shoot foliage cylinders with greatly varied orien-tations and dimensions. This layer is almost homo-geneous, and for its architecture, the turbid medium model (Ross, 1981) will be used. The architecture of this layer is characterised by the vertical distribution of the leaf area density uL(z) and probability

distribu-tion funcdistribu-tion of the leaf area orientadistribu-tion gL(rrrL)/2π.

The spatial distribution of leaves is assumed to be ran-dom. Since in both foliage layers the share of stems, branches and twigs is less than 10% of that of leaves, their area will be neglected.

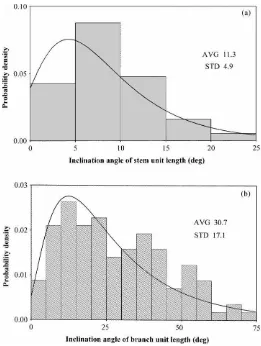
The lowest leafless coppice layer consists of nearly vertical stems (Fig. 4a). Orientation of cylindrical branches (Fig. 4b) varies over a wide range, the domi-nant inclination anglesϑSbeing between 10◦and 30◦.

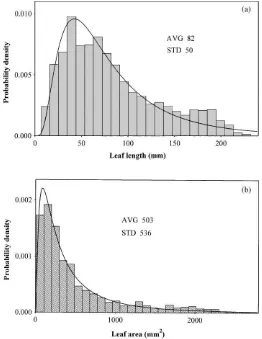
In accordance with the measurements performed by Ross in 1997 and 1998, an S. viminalis plantation is characterised by a large number of leaves per stem and a great variability of leaf length (Fig. 5a) and leaf area

SL(Fig. 5b). In midsummer, an S. viminalis stem with

a height of 500 cm has about 7000 leaves, the area of the smallest leaves being 0.3 cm2and the area of the largest ones, 27 cm2. The size of a leaf depends on its age: the smallest leaves are the youngest, located at the top of the shoot, and the largest ones are about 50 cm lower down the stem.

4. Statistical treatment

Let NS(L, h) be the number of sunflecks per metre

of scan at the depth L, where L is the downward cumu-lative leaf area index and h is the solar elevation; these sunflecks have different lengths varying from zero to

lSmax, and their lengths are statistically distributed in

the interval [0,lSmax]. Let nS(lS) be the sunfleck length

distribution function, i.e. the number of sunflecks with a length between lSand lS+1lSper metre of scan and

l_Smax

X

lS=0

nS(lS)=NS. (1)

In our case, the distance between two consecutive mea-surements,1lS=0.7 cm. Mean sunfleck length is

hlSi = PlSmax

lS=0lSnS(lS)

NS

(4)

Fig. 2. Examples of the sunfleck sensor’s recordings at different heights inside the willow coppice on a cloudless day, 14 September 1998, at coppice height zU=310 cm: (a) h=35◦, z=2.60, z/zU=0.84, τ=0.1; (b) h=35◦, z=2.00, z/zU=0.65,τ=2.1; and (c) h=32◦, z=1.10,

z/zU=0.36,τ=5.5. h, solar elevation; z, measurement height; z/zU, relative height;τ, pathlength of the direct solar radiation beam through

(5)

Fig. 3. (a) Development of three vegetation layers of a willow coppice during the growing seasons of 1996–1998. zU — coppice height,

zV— height of the surface located between the upper foliage cylinder layer (1) and the lower foliage turbid medium layer (2), z — height

of the lowest leafless stem layer (3). (b) Variation in the leaf area index (LAI) during the same periods.

and the fractional area of sunflecks inside the coppice equals sunfleck length per metre of scan:

kS=

l_Smax

X

lS=0

lSnS(lS). (3)

From (2) and (3) it follows that

kS= hlSiNS. (4)

For analysis of sunfleck length variability, the sun-fleck length distribution function nS(lS) and the

cumu-lative sunfleck fractional area FS(lS) are used. FS(lS)

denotes the fraction of the transect occupied by

sun-flecks larger than lS, or the fractional area of sunflecks

with length from lS tolSmax:

FS(lS)=

lmax

X

l=lS

lnS(l),

or in the integral form

FS(lS)= Z lSmax

lS

lnS∗(l)dl, (5)

where

nS∗(lS)= lim

1lS→0

nS(l) 1lS

(6)

Fig. 4. Probability histogram of stem (a) and branch (b) inclination angle, fitted by a lognormal distribution, measured in 1997 and 1998.

From (3) and (4) it follows that

FS(0)=kS, FS(lSmax)=0. (6)

Analysis of FSand nSshows that for upper layers it is

reasonable to divide the interval between 0 andlSmax

into two parts (Fig. 6a and b):

1. ASS, interval of short sunflecks [0, lSS], kSS(L, h)=FS(0)−FS(lSS);

2. ASL, interval of long sunflecks [lSS,lSmax], kSL(L,

h)=FS(lSS).

The fractional sunfleck area for the intervals kSSand kSLis defined so that

kS=kSS+kSL. (7)

It should be noted that the location of point lSS

sep-arating the intervals and, consequently, the fractional areas kSSand kSLis somewhat arbitrary and subjective.

It is appropriate to assume that short sunflecks are caused by the gaps between individual leaves at least in upper canopy layers and are hence determined by the effective diameter of a leaf, while the length of long sunflecks is determined by the distance between shoot cylinders. Large sunflecks occur only in upper canopy layers, where the distance between neighbour-ing shoots is large.

(7)

characteris-J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231 221

Fig. 5. Probability histogram of leaf length (a) and leaf area (b), fitted by a lognormal distribution, measured by Ross in 1997 and 1998.

tics of leaf, shoot, plant and canopy architecture. The first two factors determine the pathlength of the direct solar radiation beam in the plant canopy,τ=L/sin h.

Hereafter, sunfleck length characteristics will be con-sidered as functions of pathlengthτ, assuming that it is the key factor determining the absorption pattern of direct sunlight.

5. Results and discussion

5.1. Sunfleck length distribution function

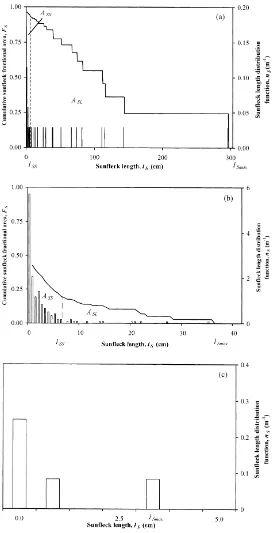
As an example, Fig. 6 expresses three sunfleck length distribution functions nS(lS) and cumulative

sunfleck fractional area functions FS(lS) for 14

September 1998 at different relative heights z/zU0.85

(a), 0.65 (b) and 0.36 (c), when coppice height was

zU=310 cm, and nS(l) and FS(lS) are calculated using

the recordings in Fig. 2. From Figs. 2 and 6, we can draw the following conclusions:

1. The averaging length 6+6 m corresponding to the track length of the sunfleck sensor seems to be too short to obtain the sunfleck distribution function, especially at large lS. As the distribution function nS(lS) is not continuous, we will use it together

with the cumulative fractional area function FS(lS).

2. The character of sunfleck distribution statistics de-pends strongly on the pathlengthτ.

It is practically impossible to fit the distribution function nS(lS) by some theoretical distribution given

(8)

sun-222 J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231

Fig. 6. Sunfleck length distribution function nS(lS) and sunfleck fractional area function FS(lS) calculated using data in Fig. 2a–c for

(9)

fleck length distribution nS(lS) by means of different

numerical parameters. Since the character of nS(lS)

depends mostly on the pathlength of the solar radia-tion beam in coppice,τ, we will treat these numerical parameters as functions ofτ.

In dense lower layers, the number of sunflecks per scan may be so small that determination of nS(lS) and FS(lS) proves impossible (Fig. 6c); below a canopy

with L>4, direct solar radiation penetrates only in penumbra, but no sunflecks exist.

5.2. Vertical distribution of sunfleck length

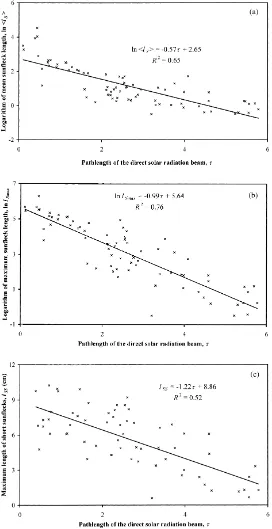
Fig. 7a–c expresses three sunfleck length character-istics: mean sunfleck length hlSi (a), maximum

sun-fleck lengthlSmax(b) and the maximum length of short

sunflecks lSS(c) as the functions of the pathlengthτ.

The data are collected from measurements during the growth period of 1996–1998.

Values ofhlSiandlSmax decrease with τ

exponen-tially. The maximum length of short sunflecks (Fig. 7c) decreases withτ linearly but not exponentially, with a small correlation coefficient (R2=0.52).

In the S. viminalis coppice, the maximum length of sunflecks in the upper cylindrical layer take the values of 2.0–3.0 m, the length of short sunflecks in lower lay-ers, only 0.01–0.03 m. The maximum sunfleck length

lSmax and the mean sunfleck lengthhlSiare statistically

interdependent (Fig. 7a and b): the mean length hlSi

increases logarithmically with increasinglSmax.

Theo-retically, ifτ→0,hlSi→∞; ifτ→∞,hlSi→0.

5.3. Vertical distribution of the number of sunflecks NS

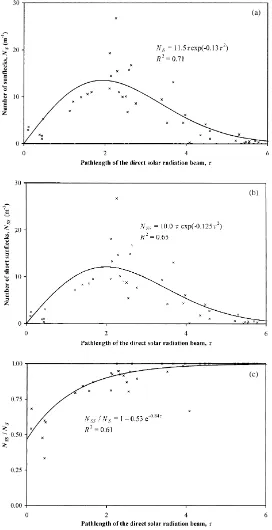
Fig. 8 shows the number of sunflecks, NS per unit

scan length (a), number of short sunflecks NSS(b) and

the share of short sunflecks in the total number of sunflecks NSS/NS(c) versus the pathlengthτ.

The total number of sunflecks as well as the number of short sunflecks increases with τ, reaches a maxi-mum value of 10–12 sunflecks m−1atτ=2.5 and then decreases slowly to zero atτ=6. As the function ofτ,

NS has been fitted by the formula NS=11.5τexp(−0.13τ2), R2=0.71

and NSSby the formula

NS=10.0τexp(−0.13τ2), R2=0.65.

Fig. 8c demonstrates that the number of short sun-flecks dominates in all layers, while in lower layers, starting from τ=2.5, practically all sunflecks are ‘short’ (lS.6 cm).

The function NS(τ) is different for the 1-year-old

(1998) and for the several-years-old coppice (1995– 1996). The number of sunflecks is greater in the for-mer, which is evidently due to its better expressed cylindrical vertical structure that enhances penetration of direct solar radiation.

Large deviations from the mean value indicate the existence of specific random configurations in willow coppice where the number of sunflecks is extremely large.

5.4. Vertical distribution of the sunfleck fractional areakS

From Eq. (4), kS=NShlSi, it follows that mean

sun-fleck length and the number of sunsun-flecks determine the fractional area of sunflecks, kS, which is an

im-portant radiation characteristic. In Ross and Mõttus (2000), it was taken that the sunfleck sensor’s reading

SF (W m−2) corresponds to sunfleck when it is larger

than 0.95S0(S0is the sunfleck sensor’s reading above

the canopy), and the sunfleck sensor’s reading corre-sponds to umbra when it is smaller than 0.007S0. In

accordance with this definition, the irradiance of di-rect solar radiation in sunflecks equals almost exactly the irradiance above the canopy, S0(h).

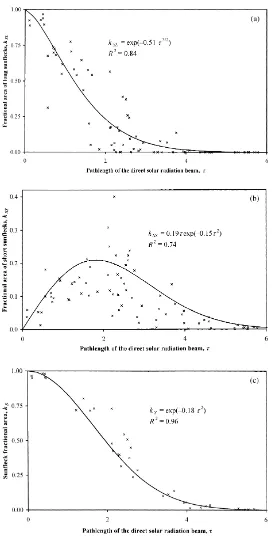
Fig. 9 expresses the vertical distribution of the frac-tional area of (a) long sunflecks, kSL(τ) and (b) short

sunflecks, kSS(τ), and shows that the distribution is

different for each group. The decrease of fractional area kSL (Fig. 9a) is nearly exponential and can be

fitted by the formula

kSL=exp(−0.51τ3/2), R2=0.84.

Unlike the fractional area of long sunflecks, the frac-tional area of short sunflecks increases almost linearly when the pathlength τ increases (Fig. 9b), reaches a maximum at τ=1.5 and decreases then to zero at

(10)

Fig. 7. Logarithm of mean sunfleck length hlSi (a), logarithm of maximum sunfleck length

lSmax

(11)

Fig. 8. Vertical distribution of the number of sunflecks per unit scan length NS(τ) (a), number of short sunflecks NSS(τ) (b) and fraction

(12)

Fig. 9. Fractional area of long sunflecks kSL(a), short sunflecks kSS(b) and sunfleck fractional area kS in 1998 (c) as the function of the

(13)

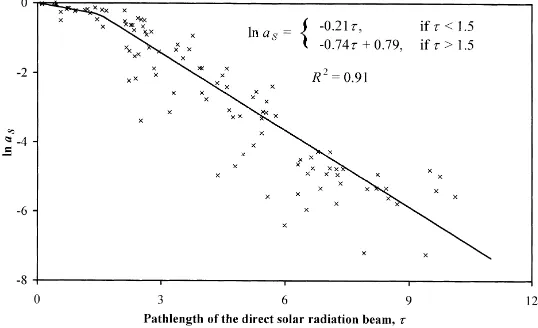
Fig. 10. The mean value of the penetration function of the direct solar radiation aS(τ) versus pathlength of the direct solar radiation beam

in coppiceτ.

As we can see in Fig. 9c, sunfleck fractional area kS(τ)

decreases withτ nearly exponentially, the argument beingτ2but notτ, and for the year 1998 data can be fitted by the formula

kS(τ )=exp(−0.18τ2), R2=0.96.

5.5. Penetration function of direct solar radiation

The mean value of one scan of the sunfleck sensor’s readings,hSFi, at the pathlengthτ, divided by the

ir-radiance above the canopy, S0, is equal to the mean

value of the penetration function, i.e. aS(τ)=hSFi/S0.

Fig. 10 expresses the logarithm of aSas the function of

the pathlengthτ and shows that aS(τ) is not a simple

exponential function ofτ. It appears that the canopy can be divided into two layers: the upper canopy layer, where 0<τ <1.5, and the lower layer, where τ>1.5. For these two layers, as a first approximation, aS(τ)

can be expressed by the formula

aS(τ )=

exp(−0.21τ ), 0< τ <1.5, R2=0.91,

2.2 exp(−0.74τ ),1.5< τ, R2=0.91.

(8)

As the transition between a clumped and a semireg-ular leaf distribution is continuous and measurements were carried out during several growth periods and at different solar elevations, the location of the surface separating these layers cannot be determined exactly.

However, the division of aS(τ) is justifiable by

vi-sual observation. The uppermost layer of the coppice (Ross and Ross, 1998) contains only nearly vertical foliage cylinders, inside of which the leaf area density

uLis high. The lower coppice layer consists of shorter

shoots and branches with approximately random shoot orientation and semiregular orientation. The small ex-tinction coefficient of the upper layer, 0.21<0.5, in-dicates clumping, whereas in the lower layer, where extinction coefficient 0.74 >0.5, leaf distribution must be semiregular.

5.6. Interrelationship between sunfleck area and penumbra area

The mean value of one scan of the sunfleck sensor is

hSFi =S0kS+ hSFUikU+ hSFPikP, (9)

wherehSFUiandhSFPiare the mean values of direct

solar irradiance, measured in shade and penumbra, re-spectively, kS, kU and kP are the fractional areas of

sunflecks, shade and penumbra, respectively, with the condition

kS+kU+kP =1. (10)

The irradiance in umbra area is practically zero,hSFUi <0.007S0. So, neglecting the umbral irradiance, the

(14)

hSFPi =

hSFi −kSS0 kP

(11)

and the penetration function of direct solar radiation in penumbra area,aSP(τ )= hSFPi/S0, in accordance

with (11), is

aSP(τ )=

aS(τ )−kS(τ ) kP(τ )

. (12)

Thus, the total mean penetration of direct solar radia-tion in the canopy at the pathlengthτ consists of two parts

aS(τ )=kS(τ )+kP(τ )aSP(τ ). (13)

The first term determines the mean penetration in sunflecks and the latter, penetration in penumbra.

Fig. 11. (a) Penumbra fractional area kP as the function of the pathlength of the direct solar radiation beam in coppiceτ; (b) penetration

function for direct solar radiation in penumbra aSP as the function of the pathlength of the direct solar radiation beam in coppiceτ.

Measurements with the sunfleck sensor allow calcu-lation of all terms in formula (13).

The fractional area of penumbra, kP(τ), as the

func-tion of pathlength (Fig. 11a) shows that the role of penumbra is the greatest in the medium layer where

τ is between 2 and 4. The maximum values of kPare

about 0.35. The function kP(τ) was approximated by

the formula

kP(τ )=0.32τ2exp(−0.69τ ), R2=0.60. (14)

Fig. 11b expresses the penetration function aSP(τ) in

penumbra area as the function of the pathlengthτ and shows that aSP(τ) decreases exponentially not withτ,

(15)

J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231 229 Table 1

Penetration function of direct solar radiation in sunfleck (kS) and

penumbra (kPaSP) areas as the function of pathlength of the direct

solar radiation beam in coppice (τ)

τ 0 0.5 1 2 3 4 6 8

kS 1.00 0.98 0.71 0.22 0.07 0.02 0 0

kPaSP 0 0.02 0.06 0.11 0.08 0.05 0.01 0

the penumbral area may increase total penetration by about 0.3–0.6. Penetration in penumbral area reaches the deeper layers (untilτ=8–9) while penetration in sunfleck reaches the depthτ=4 only.

The irradiance of the direct solar radiation in the sunfleck area (in units of S0) is kS(τ), and the

ir-radiance of direct solar radiation in penumbra is

kP(τ)aSP(τ).

The difference kS(τ)−aSP(τ)kP(τ) shows how much

irradiance is smaller in penumbra (in units of S0) than

in sunflecks. Table 1 shows the energetical contribu-tions of sunflecks (kS(τ)) and penumbra (aSP(τ)kP(τ))

to total penetrated direct solar radiation as the function of the pathlengthτ. In upper layers, the role of penum-bra is rather small but it increases rapidly between

τ=1 and 3 to dominate in lower layers whereτ>3.

5.7. Correlation between sunfleck and umbra characteristics

Calculation shows that there is no correlation be-tween sunfleck length and umbra length, and bebe-tween

Fig. 12. Interrelationship between umbra fractional area kU and sunfleck fractional area kS.

the number of sunflecks and umbrae. However, there exists a quite good correlation with R2=0.94 between their products — sunfleck fractional areas kS=NShlSi

and umbra fractional area kU=NUhlUi, respectively

(Fig. 12). This correlation was fitted by the exponen-tial formula

kU=0.63 exp(−2.30kS), R2=0.94, (15)

which shows that sunfleck fractional area increa-ses exponentially with decreasing umbra fractional area.

There exists a specific layer inside willow coppice (betweenτ=2 and 4), where the total number of short sunflecks, umbra fractional area as well as the num-ber of umbrae (Fig. 7, Ross and Mõttus, 2000) reach their maxima. In this layer, the maximum number of sunflecks reaches 17, while the maximum number of umbrae is 18, i.e. in this layer, the number of umbrae and sunflecks are equal. Penumbrae (Fig. 11a) too ex-ert a maximum effect in this layer. While sunflecks dominate above this layer, then umbrae together with penumbrae dominate below it.

6. Concluding remarks

(16)

fractional area are highly variable and require statisti-cal treatment. Variability of sunflecks is mainly caused by architectural coppice characteristics at leaf, shoot, stem and coppice levels. In willow coppice, the prob-lem is more complicated because of the great, about 100-fold, variability of the area of a single leaf.

Besides structural parameters, there are two other factors which determine the mean values of sunfleck characteristics. One is solar elevation — different in-clinations of solar rays correspond to different path-lengths through the plant canopies, which causes dif-ferences in the distribution of sunflecks. The other factor is depth inside canopy, which is characterised by the downward cumulative leaf area index L. It is expedient to merge these two factors into one factor

τ=L/sin h, i.e. pathlength of the direct solar radiation

beam in the canopy. Introduction ofτ facilitates anal-ysis of the problem.

An important methodological problem is how to perform the statistical data processing. Our measure-ment system enables us to use a maximum averaging length of 12 m. However, Fig. 6a–c shows that the obtained sample size is too small for sufficiently exact determination of probability density distribution char-acteristics. Calculations (not given here) show that for willow coppice, an averaging length of about 50–70 m would be required. Since this is impossible to realise technically, only mean values and standard deviations can be used in data processing, which, however, does not allow us to study distribution functions in great detail.

Existence of long sunflecks in the uppermost cop-pice layers and their rapid exponential decrease to zero nearτ=4 is typical of the S. viminalis coppice. The bulk of registered sunflecks have a length of 1–2 cm. The longest sunflecks measured within our willow coppice had a length of 300 cm, but their number decreases exponentially with depth.

The number of sunflecks, NS, changes with depth

(Fig. 8a). NSincreases with depth up to a maximum at τ=1–2 and then decreases slowly with further increase inτ.

It should be noted that the sunfleck length lS and

number NS are very variable characteristics and do

not characterise separately the regime of direct solar radiation effectively. A more appropriate characteristic is their product kS=hlSiNS, i.e. the fractional area. As

is evident from Fig. 9a–c, vertical change is different

for short, long and total sunflecks: the fractional area of long sunflecks, kSL, decreases most rapidly.

Experimental data have been fitted with the for-mula k(τ)=Aτ2exp(−Bτb). At small values of τ, exp(−Bτb)≈1 and k(τ)∼τ2; in lower canopy layers whereτ>2–3, the term exp(−Bτb) is more important. Thus, in upper canopy layers, k(τ) decreases propor-tionally withτ2, at longer pathlengths, k(τ) decreases exponentially, which may be the result of manifold shading in lower layers.

We have also studied the interrelationship between sunflecks and penumbra. When the vertical profile (de-pendence on z) of sunflecks is exponential, the frac-tional area of penumbra kP(τ) is similar to that of short

sunflecks kSS(τ): the existence of short sunflecks

in-creases the fractional area of penumbra.

7. Nomenclature

aS(τ)

=hS(τ )i/S0 penetration function for direct solar

radiation within canopy (–)

aSP(τ)

=hSP(τ )i/S0 penetration function for direct solar

radiation in penumbra (–)

ASL interval of long sunflecks [lSS, lSmax] (–)

ASS interval of short sunflecks

[0, lSS] (–)

FS(lS) cumulative sunfleck fractional

area (–)

gL(rL)/2π PDF of leaf area orientation (–) h solar elevation (◦)

kP penumbra fractional area (–) kS=kSS+kSL sunfleck fractional area (–) kS+kP+kU=1

kSL fractional area of long sunflecksb (–) kSS fractional area of short sunflecks (–) kU umbra fractional area (–)

L(z) downward cumulative leaf area index (–)

lS sunfleck length (cm)

hlSi mean sunfleck length (cm) lSmax maximum sunfleck length (cm)

lSS maximum length of short

sunflecks (cm)

(17)

J. Ross, M. Mõttus / Agricultural and Forest Meteorology 104 (2000) 215–231 231 NS number of sunflecks per metre (m−1)

NSS number of short sunflecks per

metre (m−1)

NU number of umbrae per metre (m−1) nS(lS) sunfleck length distribution

function (m−1₎ rrrL leaf normal (–)

hSi mean value of direct solar irradiance within canopy (W m−2)

SF sunfleck sensor’s reading (W m−2)

hSFPi mean value of direct solar irradiance

measured in penumbra (W m−2)

hSFUi mean value of direct solar irradiance

measured in shade (W m−2)

SL leaf area (cm2)

S0 direct solar irradiance in sunfleck

and above coppice (W m−2)

uL(z) leaf area density (m2m−3)

zA height of the lowest leafless coppice

layer (m)

zU coppice height (m)

zV height of the boundary surface

located between the upper foliage cylinder layer and the lower foliage turbid medium layer (m)

ϑL inclination angle of the branch

cylinder axis (◦)

ϑS inclination angle of the stem

cylinder axis (◦)

τ=L/sin h pathlength of the direct solar radiation beam in coppice (–)

Acknowledgements

This research was supported by ETF grant No. 2668. The authors thank Madis Sulev, Vello Ross, Peeter Saarelaid and Enn-Märt Maasik for assistance in field measurements and Mr. Ester Jaigma and Mrs. Viivi Randmets for preparing the manuscript. For valuable comments and critical remarks, the authors express their deep gratitude to the anonymous reviewers and to Dr. J.B. Stewart.

References

Ross, J., 1981. The Radiation Regime and Architecture of Pant Stands. W. Junk Publishers, The Hague, 391 pp.

Ross, J., Mõttus, M., 2000. Statistical treatment of umbra length inside willow coppice. Agric. For. Meteorol. 100, 89– 102.

Ross, J., Ross, V., 1998. Statistical description of the architecture of the fast growing willow coppice. Agric. For. Meteorol. 91, 23–37.

Ross, J., Sulev, M., Saarelaid, P., 1998. Statistical treatment of the PAR variability and its application to willow coppice. Agric. For. Meteorol. 91, 1–21.