BAB III PERSAMAAN PANAS DIMENSI SATU

BAB III

PERSAMAAN PANAS DIMENSI SATU

Pada bagian sebelumnya, kita telah membahas penerapan metoda Runge-Kutta orde 4 untuk menyelesaikan masalah nilai awal dari persamaan diferensial biasa orde 1. Pada bab ini, kita akan melakukan pengujian terhadap metode Runge-Kutta orde 4 yang diterapkan untuk mencari solusi numerik dari suatu persamaan diferensial parsial linier. Pengujian tersebut dapat dilakukan dengan cara membandingkan solusi numerik yang diperoleh dengan solusi analitiknya.

Persamaan diferensial parsial linier yang akan kita tinjau di sini yaitu persamaan panas dimensi 1. Contoh masalah berikut diambil dari Nakamura [2] untuk solusi analitik.

Misalkan suatu kawat besi tipis dengan panjang 10 cm yang permukaan lateralnya diberi isolator, mula-mula suhunya 0 . Suhu pada ujung kiri kawat dibuat tetap dan pada ujung kanan kawat 100 . Untuk lebih jelasnya, gambar 3.1 berikut ini merupakan sketsa dari kondisi tersebut.

o C 0oC oC 0 10

( )

0, 0o T t = C T

(

10,t

)

=100oC x

Gambar 3.1 Sketsa kondisi perambatan panas.

Model perambatan panas, untuk setiap waktu, suhu di setiap titik pada kawat memenuhi

( )

, 10 22

( )

, T x t T x t t x ∂ ₌ ∂ ∂ ∂ , 0<x<10, t>0 (6)

dengan kondisi awal dan kondisi batas ,

( )

0, 0 T t = T

(

10,t

)

=100 (kondisi batas) (7) . (kondisi awal)

( )

, 0 0 T x =

3.1 Solusi Analitik

Pada bagian ini, solusi analitik dari model perambatan panas akan ditentukan dengan menggunakan metoda pemisahan variabel, sebagai pembanding terhadap solusi numeriknya. Langkah-langkah dalam mencari solusi analitik dari persamaan diferensial parsial di atas yaitu sebagai berikut:

1. Mencari solusi steady state

Telah diketahui bahwa dari pengamatan secara empirik, solusi dari persamaan (6) untuk t menuju tak hingga, T x t

( )

, mendekati temperatur steady state yang bersesuaian dengan menetapkan

( )

ss

T x

0 t

T = pada masalah nilai batas di atas. Oleh karena

itu, T_ss

( )

x adalah solusi masalah nilai batas 2

2Tss 0,

x

∂ ₌

∂ Tss

( )

0 =0, Tss

( )

10 =100. (8) Dengan mengintegralkan persamaan (8) sebanyak dua kali terhadap x, kita dapatkan

persamaan

( )

ss

T x =Ax+B. (9)

A dan B adalah konstanta sebarang yang ditentukan dari kondisi batas. Kedua kondisi

batas dari persamaan (8) disubtitusikan ke persamaan (9), maka temperatur steady

state dari persamaan (6) adalah

( )

10

ss

T x = x (10)

2. Mencari solusi transien

Temperatur transien T_tr

(

x t,

)

dinyatakan sebagai

( )

,

( )

,

( )

tr ss

T x t =T x t −T x . (11)

Akan dibuktikan bahwa, T_tr

(

x t,

)

memenuhi 2 2 10 , tr tr T t x ∂ ∂ = ∂ ∂ T (12)

( )

0,

(

10,

)

0, tr tr T t =T t =

( )

, 0

( )

, 0

( )

0 10 10 tr ss T x =T x −T x = − x= − x.

Bukti: Karena t ∂ ∂ , 2 2 x ∂

∂ adalah operator linear, maka persamaan (6) menjadi 2 2 10 T T t x ∂ ₌ ∂ ∂ ∂

(

Ttr Tss

)

10 22

(

Ttr Tss

)

t x ∂ ∂ ⇔ + = + ∂ ∂ 2 2 2 2 10 tr ss tr ss T T T T t t x x ⎛ ⎞ ∂ ∂ ∂ ∂ ⇔ + = _⎜ + _⎟ ∂ ∂ _⎝∂ ∂ _⎠. (13)

Karena T_ss = x10 , maka persamaan (13) menjadi 2 2 0 10 0 tr tr T T t x ⎛ ⎞ ∂ _{+ =} ∂ ₊ ⎜ ⎟ ∂ _⎝∂ _⎠ 2 2 10 tr tr T T t x ∂ ∂ ⇔ = ∂ ∂ .

Selanjutnya, kondisi batasnya menjadi, Batas kiri:

( )

0, 0 T t =

( )

0,

( )

0 0 tr ss T t T ⇔ + = = =

( )

0, 0 0 tr T t ⇔ +

( )

0, 0 tr T t ⇔ = Batas kanan:

(

10,

)

100 T t =

(

10,

)

( )

10 100 tr ss T t T ⇔ + = Karena Tss

( )

10 =100, maka

( )

0, 0 tr T t = Kondisi awal:

( )

, 0 0 T x =

( )

, 0

( )

0 tr ss T x T x ⇔ +

( )

, 0 10 0 tr T x x ⇔ + =

( )

, 0 10 tr T x x ⇔ = − .

Jadi, T_tr memenuhi persamaan (12) beserta kondisi awal dan batasnya.

Selanjutnya, kita akan mencari solusi transien T_tr

( )

x t, yang memenuhi persamaan (12) dan kondisi yang diberikan. Misalkan Ttr

( )

x t, =u x v t

( ) (

)

, maka

persamaan (12) menjadi

( ) ( )

/ //

( ) ( )

10

u x v t = u x v t . (14)

dengan membagi kedua ruas persamaan (14) dengan 10 , maka diperoleh persamaan uv // / 10 u v u = v (15)

Ruas kiri persamaan (15) adalah fungsi terhadap x saja sedangkan ruas kanan adalah fungsi terhadap t saja. Jika t dibuat tetap maka ruas kanan

//

u

u haruslah tetap untuk

setiap nilai x. Begitu juga sebaliknya, jika x dibuat tetap maka ruas kanan /

10

v v

haruslah tetap untuk setiap nilai t. Akibatnya, kesamaan akan tercapai jika setiap ruas persamaan (15) sama-sama konstan. Maka, persamaan (15) menjadi

// /

10

u v

u = v= − (16) λ

dengan λ adalah konstanta positif.

Persamaan (16) terdiri dari dua buah persamaan

( )

( )

// 0 u x +λu x = (17)

( )

( )

/ 10 0 v t + λv t = (18)

sedangkan, kondisi batasnya menjadi

( )

0,

( ) ( )

0 0

tr

T t =u v t = , T_tr

(

10,t

)

=u

( ) ( )

10 v t =0. (19) Jika adalah fungsi tak trivial, maka persamaan (19) dapat dipenuhi hanya jika

. Oleh karena itu,

( )

tr

T t

( )

0

( )

10

// 0 u +λu= (20)

( )

0 0 u = , u

( )

10 =0

Misalkan λ β= 2 >0. Solusi umum dari persamaan (20) adalah

( )

cos sin

u x = A βx+B βx. Kondisi u

( )

0 =0 mengakibatkan A=0, sehingga

( )

sin

u x =B βx. Kondis u

( )

10 =0 mengakibatkan

( )

10 sin10 0

u =B β = . (21)

Karena kita ingin mencari yang tak trivial, maka haruslah . Persamaan (21) dapat terpenuhi, jika 10

( )

u x B≠0

β merupakan kelipatan dari π . Akibatnya, kita mempunyai barisan untuk nilai β

10β_n =nπ 10 n n π β ⇔ = , untuk n=1, 2, 3,... dan 2 2 100 n n π λ = , untuk n=1, 2, 3,... Sehingga, diperoleh barisan fungsi eigen

( )

sin 10 n

n

u x =B π x

yang berkorespondensi dengan nilai eigen

2 2

100 n

n π

λ = , untuk n=1, 2, 3,... Selanjutnya, persamaan (18) menjadi

( )

( )

/

10 0

n n n

v t + λv t = . (22)

Sehingga, solusi umum dari persamaan (22) adalah

( )

10 _nt

n n

v t =C e− λ . (23)

Karena Ttr

( )

x t, =u x v t

( ) (

)

, maka kita peroleh barisan solusi transien

( )

2 2 10 , sin 10 n n t tr n n T x t C e x π _π − = , dengan Cn =C Bn . (24)

Persamaan (12) merupakan persamaan linier. Dengan menggunakan sifat kelinieran, setiap kombinasi linier dari solusi juga merupakan solusi, maka solusi umum dari persamaan (12) adalah

( )

102 2 1 , 10 n t tr n n n T x t C e π sin π ∞ ₋ = =

∑

(25)

Subtitusikan kondisi awal ke persamaan (25), sehingga persamaan (25) menjadi

( )

, 0 10 tr T x = − x

( )

1 , 0 sin 10 tr n n n T x C π x ∞ = =

∑

. (26)

Persamaan (26) merupakan deret Fourier sinus. Dimana, konstanta deret Fourier sinus di atas adalah 10 0 2 10 sin 10 10 n n x C = −

∫

x π dx

( )

200 1 n n C nπ ⇔ = −

Sehingga, kita dapatkan solusi transien

( )

( )

2102 1 200 1 , 1 s 10 n t n tr n n T x t e x n π in π π ∞ ₋ = =

∑

− . 3. Menentukan solusi T x t

( )

,

Dari definisi temperatur transien, solusi persamaan panas semula adalah

( )

, _ss

( )

, _tr

( )

T x t =T x t +T x t,

( )

( )

2 2 10 1 200 1 , 10 1 sin 10 n t n n n T x t x e x n π _π π ∞ ₋ = = +

∑

− . (27)

3.2 Solusi Numerik Persamaan Panas Dengan Menggunakan Metoda

Runge-Kutta Orde 4

Pada bagian ini, solusi numerik dari persamaan (6) beserta kondisi yang diberikan akan ditentukan. Solusi numerik ini merupakan hampiran terhadap solusi analitik yang telah diperoleh pada sub bab sebelumnya.

Panjang dari besi penghantar 10 cm. Kita bagi domain pengamatan tersebut menjadi M + buah titik diskrit dengan ukuran langkah 1 Δx dan interval waktu pengamatan dibagi menjadi N+1 buah titik diskrit dengan ukuran langkah . Selanjutnya, kita nyatakan temperatur di titik

t Δ

(

x t sebagai j, i

)

, dengan dan

(

, i j j T ≡T x ti

)

t 0 i t = + Δt i x_j =x₀+ Δx , untuk j i=0, 1, 2,..., N dan j=0, 1, 2,..., M . Sehingga, kondisi batas dan kondisi awal dapat dituliskan berturut-turut sebagai

, , dan . 0 0 i T = T_Mi =100 0 0 j T =

Turunan parsial terhadap variabel x dihampiri dengan menggunakan metoda beda pusat. Hampiran beda pusat untuk

(

2 2 j, i T

₎

x t x ∂ ∂ adalah

(

)

2 1 1 2 2 2 , i i j j j i T T T T x t x x i j − − + + ∂ _≅ ∂ Δ .

Maka, persamaan (6) menjadi

(

)

1 2 2 , 10 i i j j j j i T T T T x t t x 1 i − − + + ∂ = ∂ Δ . (28)

Untuk kemudahan, kita misalkan T f_ji f T

( )

_ji t ∂ _{≡ =} ∂ . Maka persamaan (28) mempunyai bentuk 1 2 2 10 i i j j i j T T T f x 1 i j − − + + = Δ . (29)

Selanjutnya, turunan parsial terhadap variabel t pada persamaan (6) dihampiri dengan menggunakan metoda Runge-Kutta orde 4. Maka, nilai , untuk

dan , ditentukan dengan menggunakan formula 1 i j T + 0, 1, 2,..., 1 i= N− j=1, 2,..., M −1

(

1 1 2 3 1 2 2 6 i i j j T + =T + K + K + K +K₄

)

. (30)

dengan , 1 i j K = Δt f 1 2 2 i j K K = Δt f T⎛_⎜ + ⎞_⎟ ⎝ ⎠, 2 3 2 i j K K = Δt f T⎛_⎜ + ⎞_⎟ ⎝ ⎠,

(

)

4 3 i j K = Δt f T +K .

Di sini, kita akan melakukan contoh perhitungan untuk menentukan nilai K₁ danK₂.

1 1 1 2 2 10 i i i j j j i j T T T K t f t x − + ⎛ − + ⎞ = Δ = Δ ⎜_⎜ ⎟_⎟ Δ ⎝ ⎠. 1 2 2 i j K K = Δt f T⎛_⎜ + ⎞_⎟ ⎝ ⎠

karena f linier, maka

( )

1 2 2 i j K K = Δt ⎛_⎜ f T + ⎜ ⎟f ⎛ ⎞⎞_⎟ ⎝ ⎠ ⎝ ⎠ dimana

( )

1 1 1 2 2 K f ⎛_⎜ ⎞ =_⎟ f K ⎝ ⎠ 1 1 2 2 1 10 2 i i i j j j T T T f t x − + ⎛ ⎛ − + ⎞⎞ = ⎜_⎜ Δ ⎜_⎜ ⎟_⎟⎟_⎟ Δ ⎝ ⎠ ⎝ ⎠

(

1 1

)

2 5 2 i i i j j j t f T T T x − + Δ = − + Δ

( )

( ) ( )

(

1 1

)

2 5 2 i i j j t f T f T f T x − + Δ = − + Δ i j

(

1 1

)

2 5 2 i i i j j j t f f f x − + Δ = − + Δ Jadi,

(

)

2 2 1 5 2 i i i j j j j t K t f f f f x − + Δ ⎛ ⎞ = Δ _⎜ + − + _⎟ Δ ⎝ 1 ⎠ i

(

)

3 2 1 1 2 2 1 1 5 5 2 4 6 4 i i i i i i i i i j j j j j j j j j t t K t f f f f f f f f f x − + x − − + + ⎛ Δ ⎛ Δ ⎞ = Δ _⎜ + _⎜ − + + − + − + _⎟⎟ Δ ⎝ Δ ⎠ ⎝ 2 ⎠ ⎞

(

4 2 1 1 2 2 1 10 5 2 4 6 4 i i i i i i i i j j j j j j j j t t K t f f f f f f f f f x − + x − − + ⎛ Δ ⎛ Δ = Δ _⎜ + _⎜ − + + − + − + Δ ⎝ Δ ⎝ 1 2 i j+ 5 ₂

(

i₃ 6 i₂ 15 i₁ 20 i 15 i₁ 6 i₂ i ₃

)

j j j j j j j t f f f f f f f x − − − + + + ⎞ Δ ⎞⎞ + − + − + − + _⎟⎟⎟ Δ _⎠⎠⎠.

Jika kita perhatikan formulasi di atas, nilai T_ji+1, untuk i=0, 1, 2,..., N-1 dan , melibatkan nilai-nilai T 1, 2,..., 1 j= M − 4 i j− , T 3 i j− , T 2 i j− , T 1 i j− , T , T , T , T , dan T . Sehingga, stensil dari persamaan (30) adalah seperti pada gambar 3.2 berikut. i j 1 i j+ + + + 2 i j 3 i j 4 i j 1 i j T + 3 i j T₋ i T 2 i j T₋ 1 i j T₋ Tji 1 i j T₊ 2 i j T₊ 3 i j T₊ 4 i j T₊ j−4

Gambar 3.2 Stensil dari skema Runge-Kutta orde 4 untuk persamaan panas.

Dari stencil di atas, untuk menghitung i 1 j

T + diperlukan sebanyak 9 nilai T , yaitu sampai dengan T . Kesulitan muncul ketika kita akan menghitung T

i 1 4 i j T₋+ 14 i j + + 2 1 i+ , , , , , dan T karena akan melibatkan nilai-nilai di luar domain pengamatan. untuk mengatasi kesulitan tersebut, nilai-nilai di luar domain pengamtan dihampiri dengan cara ekstrapolasi linier. nilai-nilai di sebelah kiri luar domain pengamatan salah satunya dihampiri dengan menggunakan metoda beda maju

1 3 i T + T₄i+1 T_mi+₋1₃ T_mi+₋1_{2 m}i+₋1₁

(

)

1 1 1 1 i i j j i i j j j j T T T x x x x + − − + − = − − j +Tj, untuk j=1, 0, dan 1−

dan untuk nilai-nilai di sebelah kanan luar domain pengamatan dihampiri dengan menggunakan metoda beda mundur

(

)

1 1 1 1 1 i i j j i i j j j j j T T T x x x x − + + − − − = − − +Tj−1, untuk j=M M, 1, + dan 2M + .

Jadi, skema numerik dari masalah panas di atas adalah

(

)

1 1 2 3 1 2 2 6 i i j j T + =T + K + K + K +K₄ , untuk i=0, 1, 2,..., N−1 dan j=1, 2,..., M − 1 terhadap 0 0 j T = untuk j=1, 2,..., M −1

(

)

1 1 1 1 i i j j i i j j j j j j T T T x x T x x + − − + − = − + − , untuk i=0, 1,..., N− , 1 j=1, 0, dan 1− 0 0 i T = , untuk i=0, 1,..., N

(

)

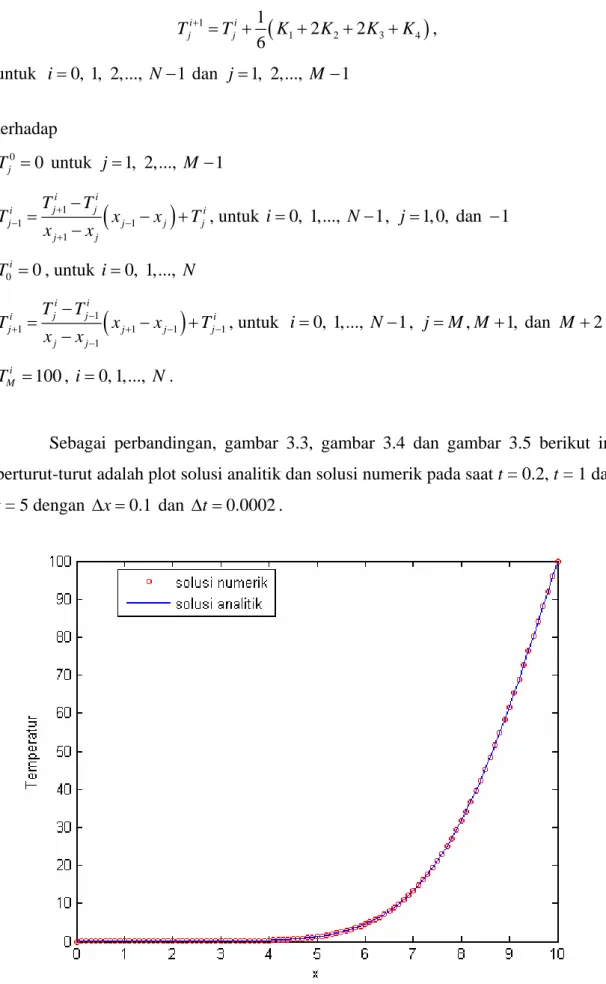
1 1 1 1 1 i i j j i 1 j j j j j j T T T x x T x x − + + − − − − = − + − 0, 1,..., 1 i , untuk i= N− , j=M M, +1, dan M + 2 100 i M T = , i=0, 1,..., N.

Sebagai perbandingan, gambar 3.3, gambar 3.4 dan gambar 3.5 berikut ini berturut-turut adalah plot solusi analitik dan solusi numerik pada saat t = 0.2, t = 1 dan

t = 5 dengan Δ =x 0.1 dan Δ =t 0.0002.

Gambar 3.4 Plot temperatur di setiap titik pada saat t=1

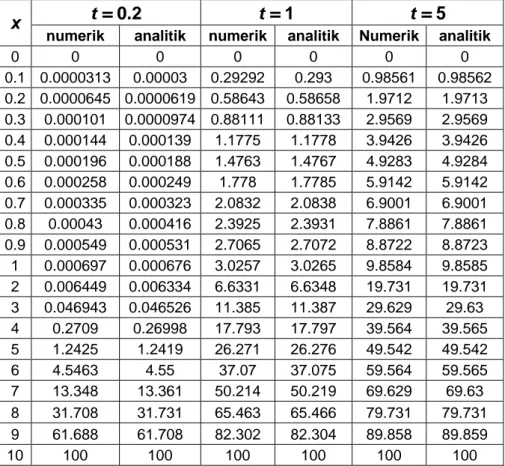
Tabel 3.1 berikut ini merupakan perbandingan antara solusi numerik dengan solusi analitik pada saat t = 0.2, t = 1 dan t =5.

t = 0.2 t = 1 t = 5

x

numerik analitik numerik analitik Numerik analitik

0 0 0 0 0 0 0 0.1 0.0000313 0.00003 0.29292 0.293 0.98561 0.98562 0.2 0.0000645 0.0000619 0.58643 0.58658 1.9712 1.9713 0.3 0.000101 0.0000974 0.88111 0.88133 2.9569 2.9569 0.4 0.000144 0.000139 1.1775 1.1778 3.9426 3.9426 0.5 0.000196 0.000188 1.4763 1.4767 4.9283 4.9284 0.6 0.000258 0.000249 1.778 1.7785 5.9142 5.9142 0.7 0.000335 0.000323 2.0832 2.0838 6.9001 6.9001 0.8 0.00043 0.000416 2.3925 2.3931 7.8861 7.8861 0.9 0.000549 0.000531 2.7065 2.7072 8.8722 8.8723 1 0.000697 0.000676 3.0257 3.0265 9.8584 9.8585 2 0.006449 0.006334 6.6331 6.6348 19.731 19.731 3 0.046943 0.046526 11.385 11.387 29.629 29.63 4 0.2709 0.26998 17.793 17.797 39.564 39.565 5 1.2425 1.2419 26.271 26.276 49.542 49.542 6 4.5463 4.55 37.07 37.075 59.564 59.565 7 13.348 13.361 50.214 50.219 69.629 69.63 8 31.708 31.731 65.463 65.466 79.731 79.731 9 61.688 61.708 82.302 82.304 89.858 89.859 10 100 100 100 100 100 100

Tabel 3.1 Perbandingan solusi numerik dengan solusi analitik pada saat t = 0.2, 1, dan 5.

Dari plot dan tabel solusi di atas, dapat kita lihat, solusi analitik dari persamaan panas dimensi satu dapat dihampiri oleh solusi numerik dengan menggunakan metode Runge-Kutta orde 4. Semakin besar nilai t, kurva solusi analitik dan solusi numerik akan semakin mendekati kurva linier yang merupakan solusi steady state.

( )

10

ss

T x = x

Berdasarkan pada pembahasan di atas, pada bab selanjutnya, kita akan menggunakan metode Rungge-Kutta orde 4 untuk mencari solusi numerik dari suatu sistem persamaan diferensial parsial linier yang merupakan model dari masalah aliran fluida yang terganggu oleh adanya gundukan yang berada pada dasar saluran.