Koleksi Soal UKD3UP

INTERAKTIF

INTERAKTIF

UJI KEMAMPUAN DIRI 3

GURU PEMBIMBING :

SULIS RIYANTO, S.PD

NEXT

NEXT

Saran & Kritik : sulisr_xxx@yahoo.co.id

KUNCI

KUNCI

X

1. Jika p*q artinya “kalikan bilangan pertama dengan bilangan kedua, kemudian hasilnya dikurangkan dari bilangan kedua”. Hasil dari 8*(-2) adalah ….

a. -18 c. 14 b. -14 d. 18 Jawab :

8*(-2) = 8 x (-2) = -16

(-2) – (-16) = (-2) + 16

= 14

2. Dalam kejuaraan sepakbola, setiap kesebelasan jika menang mendapat skor 3, jika kalah -1, dan jika seri skornya 1. Dalam 12 kali pertandingan, sebuah kesebelasan menang 7 kali, seri 2 kali, dan sisanya kalah. Skor yang diperoleh kesebelasan tersebut adalah ….

a. 19 c. 22 b. 20 d. 23 Jawab :

Main 12 kali = 7M + 2S + 3K = 7(3) + 2(1)+ 3(-1) = 21 + 2 + (-3)

3. Urutan naik dari pecahan 15%, 0,3, dan adalah …. a. 0,3 ; 15% ; c. 0,3 ; ; 15%

b. ; 15% ; 0,3 d. 15% ; ; 0,3 4 1 4

1 4

1 4 1

4 1 Jawab :

Mendesimalkan : 15% =

100 15

= 0,15 0,3

4 1

= 0,25

Urutan naik : 15% ; 4 1

; 0,3

4. Suatu pekerjaan jika dikerjakan jika dikerjakan oleh Ady akan selesai selama 6 hari, sedangkan oleh Wira selama 12 hari. Jika Ady dan Wira bekerja bersama-sama, pekerjaan tersebut akan selesai selama ….

a. 18 hari c. 6 hari b. 9 hari d. 4 hari Jawab :

Ady 6 hari

Wira 12 hari Ady =

12

6 = 2 Wira Ady + Wira t

2Wira + Wira t 3Wira t

Wira 12 hari 3Wira t

t = 12 3

5. Pada gambar dengan skala 1 : 400, kolam berbentuk persegi panjang mempunyai ukuran panjang 24 cm dan lebar 6 cm. Luas sebenarnya kolam tersebut adalah …. a. 2.304 m2 c. 240 m2

b. 2.284 m2 d. 120 m2

Jawab :

Skala = 1 : 400 1 cm mewakili 400 cm = 4 m 24 cm 24 x 4 m = 96 m

6 cm _{6 x 4 m = 24 m} Luas kolam = 96 x 24

= 2.304 m²

6. Perbandingan uang Tono dan Tini adalah 8 : 7. Jika jumlah uang mereka Rp 750.000,00, uang Tini adalah ….

a. Rp 50.000,00 c. Rp 350.000,00 b. Rp 200.000,00 d. Rp 400.000,00 Jawab :

Jumlah uang mereka = Rp 750.000,00 Sehingga :

Uang Tini = 7

15 x Rp 750.000,00 = Rp 350.000,00

7. Jarak dua kota dapat ditempuh selama 1,5 jam oleh sebuah kendaraan dengan kecepatan rata-rata 60 km/jam. Dengan kecepatan rata-rata 40 km/jam, jarak tersebut dapat ditempuh selama ….

a. 2 jam 30 menit c. 1 jam 45 menit b. 2 jam 15 menit d. 1 jam 30 menit Jawab :

1,5 jam 60 km/ jam

t 40 km/ jam t =

1,5 x 60 40

= 2,25 jam

= 2 jam 15 menit

8. Seorang pedagang membeli 2 lusin sarung dengan harga Rp 1.200.000,00. Jika harga penjualannya Rp 60.000,00/buah, yang dialami pedagang adalah ….

a. Untung Rp 1.440.000,00 c. Rugi Rp 1.440.000,00 b. Untung Rp 240.000,00 d. Rugi Rp 240.000,00 Jawab :

Harga beli = Rp 1.200.000,00

Total penjualan = 24 x Rp 60.000,00 = Rp 1.440.000,00

Jual > Beli

UNTUNG

Keuntungan = Rp 1.440.000,00 – Rp 1.200.000,00 = Rp 240.000,00

9. Dengan harga jual Rp 2.300.000,00 seorang pedagang untung 15%. Harga pembeliannya adalah ….

a. Rp 345.000,00 c. Rp 2.000.000,00 b. Rp 1.955.000,00 d. Rp 2.645.000,00 Jawab :

Harga jual = Rp 2.300.000,00 115% Harga pembelian = 100

115 x Rp 2.300.000,00 = Rp 2.000.000,00

10. Budi menabung sebesar Rp 1.000.000,00 dengan bunga 8% setahun. Setelah 9 bulan, besar bunga yang diperoleh Budi adalah ….

a. Rp 60.000,00 c. Rp 1.060.000,00 b. Rp 80.000,00 d. Rp 1.080.000,00 Jawab :

Besar bunga = 8

100 x 9

12 x Rp 1.000.000,00 = Rp 60.000,00

11. Setelah 8 bulan menabung, saldo tabungan Ali di Bank sebesar Rp 3.120.000,00. Jika Bank memberi bunga 6% setahun, besar uang yang ditabung Ali adalah ….

a. Rp 3.307.200,00 c. Rp 2.932.800,00 b. Rp 3.000.000,00 d. Rp 187.200,00

Jawab :

Bunga 8 bulan = 6% x 8

12 = 4%

Sehingga : Rp 3.120.000,00 104% Yang ditabung Ali =100

104 x Rp 3.120.000,00 = Rp 3.000.000,00

12. Rumus suku ke-n suatu barisan bilangan adalah Un = 7 – 3n. Selisih antara suku ke-8 dan suku ke-9 adalah ….

a. -37 c. 3 b. -3 d. 37 Jawab :

Un = 7 – 3n U₈ = 7 – 3(8)

= 7 – 24 U_{8 = -17}

U₉ = 7 – 3(9) = 7 – 27 U_{9 = -20}

Selisih suku ke-8 dan suku ke-9 = U₉ – U₈

= -20 – (-17)

13. Empat suku pertama barisan bilangan dengan Un = 5n – 12 adalah ….

a. -7, -2, 3, 8 c. 7, 2, -3, -8 b. -7, -5, -4, -3 d. 7, 12, 17, 22 Jawab :

Un = 5n – 12 U₁ = 5(1) – 12

= 5 – 12 = -7

U₂ = 5(2) – 12 = 10 – 12 = -2

U₃ = 5(3) – 12 = 15 – 12 = 3

U₄ = 5(4) – 12 = 20 – 12 = 8

Empat suku pertama : -7, -2, 3, 8

14. Suatu jenis bakteri setiap menit berkembang biak sebanyak 2 kali lipat. Jika pada menit ke-4 jumlah bakteri ada 3, banyak bakteri pada menit ke-9 adalah ….

a. 18 c. 48 b. 24 d. 96 Jawab :

M ₄ 3

M ₅ 6

M ₆ 12

M ₇ 24

M ₈ 48

M ₉ 96

15. Hasil dari 2a2c4 x 52a5b3 adalah ….

a. 50a10b3c4 c. 52a10b3c4

b. 50a7b3c4 d. 140a7b3c4

Jawab :

2a2c4 x 52a5b3 = 2a2c4 x 25 a5b3

= 50 a2+5 b3c4

= 50 a7b3_c4

16. Diketahui P = x2 + 8x dan Q = 3x² – 15x.

Hasil P – Q adalah ….

a. 4x2 – 23x c. -2x2 – 23x

b. 4x2 + 23x d. -2x2 + 23x

Jawab :

P – Q = x² + 8x – (3x² – 15x) = x² + 8x – 3x² ++ 15x = x² – 3x² + 8x + 15x = -2x² + 23x

17. Hasil dari (5x2 – 4y)2 adalah ….

a. 25x4 – 40xy + 16y2

b. 25x4 – 20xy – 16y2

c. 25x4 – 40xy + 16y2

d. 25x4 – 20xy + 16y2

Jawab :

(a + b)² = a² + 2ab + b²

(5x² – 4y)² = (5x²)² + 2.(5x²).(-4y) + (-4y)² = 25x4 – 40x²y + 16y²

18. Bentuk sederhana adalah …. 21 10x x 15 x 2x 2 2     a. 7) (x 5) (2x  

b. (2x_{(x 7)}5)

  c. 7) (x 5) (2x  

d. (2x_{(x }₇₎5) Jawab : 21 10x x 15 x 2x 2 2     =

2x² + x – 15 =

pq = -30 p + q = 1

p = 6 q = -5

(2x + 6)(2x – 5) 2

= (x + 3)(2x – 5) (x + 3)(2x – 5)

(x + 3)(x + 7) =

(2x – 5) (x + 7)

19.Hasil dari – adalah …. a. 2) 4)(x 6)(x (x 10 4x     b. c. d. Jawab : 24 -2x x 3 2

 x 4x -12

1 2  2) 4)(x 6)(x (x 2 4x     2) 4)(x 6)(x (x 2 2x     2) 4)(x 6)(x (x 2 2x     24 -2x x 3

2 _ – _{x 4x -12}

1

2 _ = _{(x 6)(x 4)}

3



 – (x 6)(x-2)

1



=

(x+6)(x-4)(x-2) (x+6)(x-4)(x-2) 3 (x-2) 1 (x-4)

=

(x+6)(x-4)(x-2) (x+6)(x-4)(x-2) 3x – 6 x – 4 = 3x – 6 – x + 4

(x+6)(x-4)(x-2) =

2x – 2

20. Penyelesaian 3(2a – 5) = -2a + 25 adalah …. a. 10 c. -5

b. 5 d. -10 Jawab :

3(2a – 5) = -2a + 25 6a – 15 = -2a + 25 6a + 2a = 25 + 15

8a = 40 a = 40

8 a = 5

21. Jumlah tiga bilangan ganjil yang berurutan adalah 69. Bilangan terkecilnya adalah ….

a. 33 c. 25 b. 29 d. 21 Jawab :

Misal bilangan I = x

bilangan II = x + 2

bilangan III = x + 4, Sehingga : x + (x + 2) + (x + 4) = 69

3x + 6 = 69

3x = 69 – 6 3x = 63

x = 63

3 = 21

Bilangan terkecil = x = 21

22. Perhatikan diagram Venn ! K L adalah ….

a. {a, d, e} c. {a, d} b. {b, e, f} d. { e }



Jawab :

Dari diagram Venn, maka : A



K = { e }

23. Suatu kompleks perumahan yang terdiri dari 60 orang, ternyata 20 orang berlangganan majalah, 35 orang berlangganan Koran, dan 10 orang tidak berlangganan majalah maupun koran. Yang berlangganan majalah dan koran adalah ….

a. 20 orang c. 12 orang b. 15 orang d. 5 orang Jawab :

Cara diagram Venn : S _{M K}

20 35

10 x

20 – x 35 – x

Sehingga :

20 – x + x + 35 – x + 10 = 60 65 – x = 60

-x = 60 – 65 -x = -5

x = 5

Yang berlangganan koran dan majalah ada 5 orang

24.Perhatikan diagram panah !

Yang merupakan kodomain adalah …. a. {2, 3, 5} c. {4, 6}

b. {4, 6, 8} d. { 8 } Jawab :

Kodomain = kaerah kawan Kodomain = {4, 6, 8}

25. Diketahui M = {1, 2, 3, 4}, dan N = {0, 2, 4, 6, 8, 10}. Relasi dari himpunan M ke N adalah “setengah dari”. Himpunan pasangan berurutan dari relasi tersebut adalah ….

a. {(1, 0), (2, 4), (3, 6), (4, 8)} b. {(1, 2), (2, 4), (3, 6), (4, 8)} c. {(2, 4), (3, 6), (3, 8), (4, 8)} d. {(2, 4), (3, 6), (4, 8), (4, 0)} Jawab :

Analisa jawaban :

Relasi : “Setengah dari”

X

X X

26. Diketahui f(x) = 2x – 9. Jika f(c) = -1, nilai c adalah …. a. -11 c. 4

b. -10 d. 8 Jawab :

f(x) = 2x – 9

f(c) = -1 f(c) = 2c – 9 = -1 2c = -1 + 9 2c = 8

c = 4

27. Diketahui fungsi h(x) = px + q. Jika h(4) = -28 dan h(-5) = 26, nilai h(-12) adalah ….

a. 68 c. 12 b. 40 d. -16 Jawab :

h(x) = px + q

h(4) = -28 4p + q = -28 h(-5) = 26 _{-5p+q = 26}

9p = -54 p = -54

9 p = -6

p = -6 4p + q = -28 4(-6) + q = -28 -24 + q = -28

q = -28 + 24 q = -4

Sehingga :

h(x) = -6x – 4

h(x) = -6x – 4

h(-12) = -6(-12) – 4 = 72 – 4

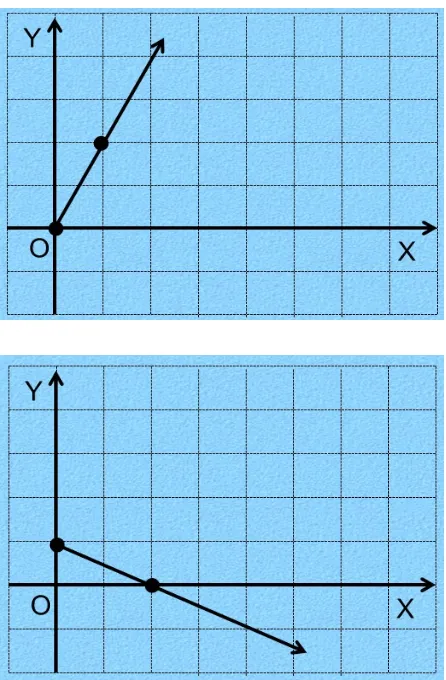
28. Diketahui f : x + 1.

Grafik fungsi f untuk daerah asal bilangan nol dan bilangan positif adalah ....

2 1

28. Diketahui f : x + 1.

Grafik fungsi f untuk daerah asal bilangan nol dan bilangan positif adalah ....

2 1

Jawab :

f : x + 1 ₂1 Notasi

Daerah asal = {0, bilangan positif} x = 0 _{f : 2}1 (0) + 1

= 0 + 1 = 1

Titik : (0, 1)

x = 2 _{f : 2}1 (2) + 1 = 1 + 1 = 2

Titik : (2, 2)

29. Gradien garis yang melalui titik A(1, 4) dan B(0, 2) adalah ….

a. 2 c. -2 b. d. - Jawab :

2 1

2 1 Gradien titik A(1, 4) dan B(0, 2)

m = y2 – y1 x₂ – x₁ = 2 – 4

0 – 1 = -2

-1

30. Persamaan garis yang melalui titik (-6, 2) dan tegak lurus garis dengan persamaan x – 3y = 8 adalah ….

a. y = 3x – 20 c. y = -3x – 20 b. y = 3x – 16 d. y = -3x – 16 Jawab :

Gradien garis x – 3y = 8 a = 1, b = -3 Gradien (m1) = - a

b = - 1-3 = 3 1 Karena tegak lurus, maka m2 = -3

y – y ₁ = m (x – x ₁ ) y – 2 = -3 (x – (-6 )) y – 2 = -3 (x + 6 ) y – 2 = -3x – 18

y = -3x – 18 + 2 y = -3x – 16

31. Diketahui tiga buah titik yaitu P(-3, 0), Q(x, 3), dan R(2, 5). Jika ketiga titik itu terletak pada satu garis, maka nilai x adalah ….

a. -2 c. 1 b. 0 d. 3 Jawab :

Gradien titik P(-3, 0) dan R(2, 5) : m = y2 – y1

x₂ – x₁ = 5 – 0

2 – (-3) = 5

5 = 1

y – y ₁ = m (x – x ₁ ) y – 0 = 1 (x – (-3))

y = x + 3

(x, 3) y = x + 3 3 == x + 3 x = 3 – 3 x = 0

32. Persamaan grafik berikut !

Persamaan garis g adalah …. a. 2y + x = 8

b. 4y + 2x = 8 c. 2y – x = -8

d. 4y – 2x = 8 O 2

4

x y

Jawab :

Punyaku,…. Punyamu,…. Sehingga :

2x + 4y = 8 atau 4y + 2x = 8

33. a dan b merupakan penyelesaian sistem persamaan linear a + b = 6 dan 2a – b = 0.

Nilai 3a – b adalah …. a. 4 c. -2 b. 2 d. -4 Jawab :

a + b = 6

2a – b = 0 + 3a = 6

a = 2

a = 2 a + b = 6 2 + b = 6

b = 6 – 2 b = 4

Nilai 3a – b = 3(2) – 4 = 6 – 4

34. Harga 2 buku dan 3 pensil Rp 85.000,00. Sedangkan harga 3 buku dan 1 pensil yang sejenis Rp 75.000,00. Jika Budi membeli satu buku dan satu pensil, jumlah yang harus dibayar adalah ….

a. Rp 15.000,00 c. Rp 35.000,00 b. Rp 20.000,00 d. Rp 50.000,00 Jawab :

Misal : buku = a, pensil = b Persamaan :

2a + 3b = 85.000 3a + b = 75.000

x1 x3

2a + 3b = 85.000 9a + 3b = 225.000 -7a = -140.000

a = 20.0000

3a + b = 75.000

3(20.000) + b = 75.000 60.000 + b = 75.000

b = 75.000 – 60.000 b = 15.000

Yang dibayar Budi = a + b

= 20.000 + 15.000 = Rp 35.000,00

35. Luas lingkaran dengan diameter 20 cm adalah ….(π = 3,14)

a. 1.256 cm2 c. 314 cm2

b. 628 cm2 d. 154 cm2

Jawab :

d = 20 cm r = 10 cm L = πr²

= 3,14 x 10 x 10 = 314 cm²

36. Di antara pasangan sisi-sisi segitiga berikut !

(i) 13 cm, 5 cm, 12 cm (iii) 7 cm, 15 cm, 17 cm (ii) 8 cm, 10 cm, 6 cm (iv) 12 cm, 16 cm, 20 cm Yang bukan ukuran sisi segitiga siku-siku adalah …. a. (iv) c. (ii)

b. (iii) d. (i) Jawab :

Siku-siku jika membentuk tripel Pythagoras. Syarat tripel Pythagoras : a² + b² = c², c > a, b Analisa jawaban :

5² + 12² = 13² 25 + 144 = 169 8² + 6² = 10² 64 + 36 = 100

7² + 15² = 17² 49 + 225 = 289

X

12² + 16² = 20² 144 + 256 = 400

37. Dari rumah Deni berjalan menuju ke sekolah. Mula-mula ia berjalan sejauh 600 meter ke arah timur, kemudian dilanjutkan 800 meter ke arah utara. Jarak terdekat dari rumah Deni ke sekolah adalah ….

a. 1.400 meter c. 500 meter b. 1.000 meter d. 200 meter Jawab :

Sketsa : U

600 m

800 m A B

C ?

AC² = AB² + BC² 600² + 800² =

= 360.000 + 640.000 AC² = 1.000.000

AC = 1.000.000 AC = 1.000 m

38. Perhatikan gambar !

Luas taman yang ditanami rumput adalah …. a. 280 m2 c. 178 m2

b. 203 m2 d. 126 m2

20 m

14 m

Kolam ikan

Taman Ditanami rumput

Jawab : Luas persegipanjang = p x l

= 20 x 14 = 280 m²

L. ½ lingk = ½ π r² = ½ x

7 22

x 7 x 7 = 77 m²

Yang ditanami rumput = 280 – 77

39. Median data : 31, 24, 30, 35, 25, 28, 35, 30, 24, 26 adalah ….

a. 35 c. 29 b. 30 d. 24 Jawab :

Median = Nilai tengah data terurut

Data terurut : 24, 24, 25, 26, 28, 30, 30, 31, 35, 35 Median = 28 + 30

2 = 29

40. Rata-rata berat badan 12 orang siswa 46 kg. Setelah bertambah 3 orang, rata-rata berat badannya menjadi 46,4 kg. Rata-rata berat badan 3 orang yang baru masuk adalah ….

a. 48 kg c. 45 kg

b. 46,2 kg d. 44,8 kg Jawab :

15 x 46,4 = 696 12 x 46 = 552 Berat 3 orang = 144 Rata-rata =

3 144 = 48 kg

HOME HOME KUNCI JAWABAN KUNCI JAWABAN 11

CC

22

BB

33

D

D

44

D

D

55

AA

66

CC

77

BB

88

BB

99

CC

10 10

AA

11 11

BB

12 12

BB

13 13

AA

14

14

D

D

15

15

BB

16

16

D

D

17 17

EE

18 18

AA

19 19

EE

20 20

BB

21

21

D

D

22

22

D

D

23

23

D

D

24 24

BB

25 25

BB

26 26

CC

27 27

AA

28 28

AA

29 29

AA

30

30

D

D

31 31

BB

32 32

BB

33 33

BB

34 34

CC

35 35

CC

36 36

BB

37 37

BB

38 38

BB

39 39

CC

40 40

AA

→ Melihat kunci, klik nomor soal → Melihat cara, klik kunci jawaban

X