Penyelesaian masalah pemotongan rol kertas dengan metode penghasil kolom.

(1)

Industri kertas memproduksi rol kertas pada mesin kertas. Rol kertas kemudian dipotong menjadi beberapa rol dengan lebar yang berbeda. Lebar rol ditentukan oleh permintaan pelanggan dan jumlah rol yang dipesan berbeda-beda. Oleh karena itu dibutuhkan penyusunan pola pemotongan dari sebuah rol jumbo menjadi rol-rol kecil. Penyusunan pola pemotongan ini bertujuan untuk meminimumkan jumlah rol jumbo yang digunakan.

Penelitian ini mengimplementasikan metode penghasil kolom untuk menyelesaikan masalah tersebut. Metode Penghasil Kolom merupakan salah satu teknik program linear untuk masalah pemotongan persediaan. Iterasi metode penghasil kolom menggunakan Metode Simpleks direvisi dan masalah Knapsack dengan penyelesaian metode cabang-batas. Jika solusi bukan bilangan bulat, maka diperlukan metode first-fit decreasing. Kemudian dibuat suatu program tampilan dengan MATLAB berdasarkan algoritma penghasil kolom tersebut. Pada program ini, solusi yang dihasilkan berupa banyaknya rol atau berat rol. Selanjutnya, solusi dapat dipindahkan ke File Excel.

Contoh numerik diberikan untuk menunjukkan efektivitas metode. Berdasarkan hasil penelitian ini diperoleh solusi optimal yaitu jumlah rol minimum. Dibandingkan dengan perhitungan manual yang biasa dilakukan oleh industri kertas, hasilnya sesuai. Namun untuk masalah yang besar, pendekatan ini lebih baik karena perhitungan manual hampir tidak mungkin dilakukan.

(2)

rolls are then cut into smaller rolls with different widths. The widths of rolls are determined by the customers’ demands and the different number of ordered rolls so that it is necessary to have an organization of cutting pattern from a jumbo into small rolls. The organization of cutting pattern aims to minimize the number of jumbo rolls used.

This research implements a column generation method to solve the problem. The column generation method is one of the linear programming techniques for the problem of cutting stock. The iteration of column generation method uses revised simplex and Knapsack problem with the completion of branch-and-bound method. If a solution is not an integer, the solution is converted into the integer using the first-fit decreasing method. Then, a display program with MATLAB is made based on the column generation algorithm. In this program, the solution may be in form of the number of rolls or the weight of rolls. Moreover, the solution can be transferred to Excel File.

Numerical examples are then carried out to show the effectiveness of the method. Based on the result of this research, the optimal solution is obtained, namely the minimum number of jumbo rolls. In comparison to the manual calculation commonly practiced by paper industry, the results are well fitted. However, for big problems our approach is better because manual calculation is almost impossible done due to the expanding number of possible cutting pattern combinations.

(3)

PENYELESAIAN MASALAH PEMOTONGAN ROL KERTAS DENGAN

METODE PENGHASIL KOLOM

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Rosa Ajeng Mahadika

NIM: 123114003

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(4)

i

PENYELESAIAN MASALAH PEMOTONGAN ROL KERTAS DENGAN

METODE PENGHASIL KOLOM

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Rosa Ajeng Mahadika

NIM: 123114003

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(5)

ii

PAPER ROLL CUTTING PROBLEM SOLUTION WITH THE COLUMN

GENERATION METHOD

A THESIS

Presented as Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains

Mathematics Study Program

Written by: Rosa Ajeng Mahadika Student ID: 123114003

MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

(6)

(7)

(8)

v

HALAMAN PERSEMBAHAN

Skripsi ini saya persembahkan untuk

Tuhan Yesus dan Bunda Maria,

orang tua saya tercinta, Barnabas Bambang Pitoyohadi dan Anastasia Sumarni,

(9)

(10)

vii

ABSTRAK

Industri kertas memproduksi rol kertas pada mesin kertas. Rol kertas kemudian dipotong menjadi beberapa rol dengan lebar yang berbeda. Lebar rol ditentukan oleh permintaan pelanggan dan jumlah rol yang dipesan berbeda-beda. Oleh karena itu dibutuhkan penyusunan pola pemotongan dari sebuah rol jumbo menjadi rol-rol kecil. Penyusunan pola pemotongan ini bertujuan untuk meminimumkan jumlah rol jumbo yang digunakan.

Penelitian ini mengimplementasikan metode penghasil kolom untuk menyelesaikan masalah tersebut. Metode Penghasil Kolom merupakan salah satu teknik program linear untuk masalah pemotongan persediaan. Iterasi metode penghasil kolom menggunakan Metode Simpleks direvisi dan masalah Knapsack dengan penyelesaian metode cabang-batas. Jika solusi bukan bilangan bulat, maka diperlukan metode first-fit decreasing. Kemudian dibuat suatu program tampilan dengan MATLAB berdasarkan algoritma penghasil kolom tersebut. Pada program ini, solusi yang dihasilkan berupa banyaknya rol atau berat rol. Selanjutnya, solusi dapat dipindahkan ke File Excel.

Contoh numerik diberikan untuk menunjukkan efektivitas metode. Berdasarkan hasil penelitian ini diperoleh solusi optimal yaitu jumlah rol minimum. Dibandingkan dengan perhitungan manual yang biasa dilakukan oleh industri kertas, hasilnya sesuai. Namun untuk masalah yang besar, pendekatan ini lebih baik karena perhitungan manual hampir tidak mungkin dilakukan.

(11)

viii

ABSTRACT

Paper industry produces jumbo paper rolls by using a paper machine. The jumbo paper rolls are then cut into smaller rolls with different widths. The widths

of rolls are determined by the customers’ demands and the different number of

ordered rolls so that it is necessary to have an organization of cutting pattern from a jumbo into small rolls. The organization of cutting pattern aims to minimize the number of jumbo rolls used.

This research implements a column generation method to solve the problem. The column generation method is one of the linear programming techniques for the problem of cutting stock. The iteration of column generation method uses revised simplex and Knapsack problem with the completion of branch-and-bound method. If a solution is not an integer, the solution is converted into the integer using the first-fit decreasing method. Then, a display program with MATLAB is made based on the column generation algorithm. In this program, the solution may be in form of the number of rolls or the weight of rolls. Moreover, the solution can be transferred to Excel File.

Numerical examples are then carried out to show the effectiveness of the method. Based on the result of this research, the optimal solution is obtained, namely the minimum number of jumbo rolls. In comparison to the manual calculation commonly practiced by paper industry, the results are well fitted. However, for big problems our approach is better because manual calculation is almost impossible done due to the expanding number of possible cutting pattern combinations.

(12)

(13)

x

KATA PENGANTAR

Puji dan syukur kepada Tuhan Yesus dan Bunda Maria atas berkat yang selalu menyertai penulis dalam menyelesaikan skripsi ini tepat waktu. Skripsi ini dibuat sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Universitas Sanata Dharma. Banyak tantangan dalam proses penulisan skripsi ini, namun dengan penyertaan Tuhan serta dukungan dari berbagai pihak akhirnya skripsi ini dapat diselesaikan. Untuk itu penulis ingin mengucapkan terima kasih kepada:

1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D. selaku Dekan Fakultas Sains dan Teknologi.

2. Bapak Hartono, Ph.D. selaku Kepala Program Studi Matematika dan dosen pembimbing yang dengan sabar dan penuh antusias dalam membimbing selama proses penulisan skripsi ini.

3. Seluruh Dosen Program Studi Matematika serta karyawan Fakultas Sains dan Teknologi. Terimakasih atas bimbingan, pelajaran, dan masukan yang diberikan selama berkuliah di Universitas Sanata Dharma.

4. Bapak Tjoeng Chayahin selaku mentor di divisi PPIC PT. Indah Kiat Tangerang yang dengan sabar membimbing selama penelitian dan proses penulisan skripsi ini.

(14)

xi

6. Ibu Theresia Titirani selaku HRD PT Indah Kiat yang sudah memberikan kesempatan untuk melaksanakan penelitian dan mengambil data di PT Indah Kiat.

7. Kedua orang tuaku, Barnabas Bambang Pitoyohadi dan Anastasia Sumarni, serta adikku Agata Woro Mahastuti yang selalu mendoakan dan mendukungku dengan penuh kasih dan memberikan masukan positif kepadaku.

8. Sahabat dan teman-teman angkatan 2012 (Arum, Happy, Ilga, Auxi, Boby, Rian, Budi, Ega, Lia, Putri, Noni, Dewi, Sila, Ferni, Risma, Anggun, Manda, Juli, dan Tika), Stanislaus Yhanna Pradita, Vianita, Maya, Clement yang sudah memberikan dukungan serta semangat kepadaku.

Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu dalam penyusunan skripsi ini. Semoga segala doa, perhatian, dukungan, bantuan, dan cinta yang telah diberikan mendapatkan balasan dari Tuhan Yesus. Penulis menyadari bahwa masih banyak kekurangan dalam penulisan skripsi ini. Oleh karena itu, penulis mengharapkan kritik dan saran demi penyempurnaan skripsi ini. Harapan penulis, semoga skripsi ini bermanfaat bagi pembaca dan menjadi referensi belajar yang baik.

Yogyakarta, Agustus 2016 Penulis,

(15)

xii

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTRACT ... viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... ix

KATA PENGANTAR ... x

DAFTAR ISI ... xii

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah... 1

B. Rumusan Masalah ... 9

C. Pembatasan Masalah ... 9

D. Tujuan Penulisan ... 10

E. Manfaat Penulisan ... 10

F. Metode Penulisan ... 10

(16)

xiii

BAB II PROGRAM LINEAR ... 13

A. Program Linear ... 13

B. Metode Simpleks Direvisi ... 24

C. Program Linear Bilangan Bulat ... 34

D. Masalah Knapsack ... 43

BAB III MASALAH PEMOTONGAN PERSEDIAAN ... 61

A. Masalah Pemotongan Persediaan (Cutting Stock Problem) ... 61

B. Metode Penghasil Kolom ... 64

BAB IV PENERAPAN METODE PENGHASIL KOLOM UNTUK MASALAH PEMOTONGAN ROL KERTAS ... 84

BAB V PENUTUP ... 91

A. Kesimpulan ... 91

B. Saran ... 92

DAFTAR PUSTAKA ... 93

LAMPIRAN A ... 95

(17)

1

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Masalah pemotongan persediaan (cutting stock) sering terjadi pada proses produksi. Masalah pemotongan persediaan biasanya berkaitan dengan pemakaian bahan baku yang optimal yaitu yang meminimumkan biaya produksi bahan baku. Pada industri kertas, untuk dapat meminimumkan biaya produksi salah satu cara yang ditempuh adalah dengan memproduksi jumlah rol yang optimal dalam arti yang sesuai dengan kebutuhan/pesanan dan juga harus memperhatikan pola pemotongan. Semakin sedikit jumlah rol yang digunakan untuk memenuhi pesanan maka efisiensi akan meningkat.

(18)

Proses pemotongan rol kertas pada mesin penggulung yang menghasilkan rol-rol kecil dapat dilihat pada gambar 1.1.

Gambar 1.1: Proses yang terjadi pada mesin penggulung

Berikut gambar produk kertas yang dapat dipesan dan siap untuk dikirim yaitu rol kertas, lembar kertas besar, dan potongan kertas kecil.

Gambar 1.2: Produk kertas: (a) rol kertas, (b) large sheet, dan (c) cut size

(a) (b)

(19)

Jika rol kertas masuk ke pisau pemotong rangkap dan pisau pemotong tunggal maka produk berupa lembar kertas besar. Perbedaan pisau pemotong rangkap dan pisau pemotong tunggal terdapat pada cara pemotongannya. Pada pisau pemotong rangkap terdapat 2 pisau pemotong dimana hasil dari setiap potongan memiliki ukuran yang sama, sedangkan pisau pemotong tunggal memiliki 1 pisau pemotong dimana hasil dari setiap potongan ada salah satu yang berbeda ukuran.

Proses pemotongan rol kertas pada pisau pemotong rangkap ditunjukkan pada gambar 1.3.

Gambar 1.3: Proses yang terjadi pada pisau pemotong rangkap

Kemudian dari pisau pemotong (rangkap atau tunggal), kertas dipotong sesuai ukuran yang diminta lalu dikemas atau dapat juga langsung dikemas dengan ukuran potongan kertas dalam bentuk besar (large size). Terdapat juga pisau pemotong kecil (mini cutter) yang digunakan memotong rol kertas yang sudah dipotong menjadi beberapa rol kecil menjadi ukuran yang diminta.

2 Cutter Knives

Reel Produce by Paper Machine (Input)

(20)

Berikut skema proses produksi kertas.

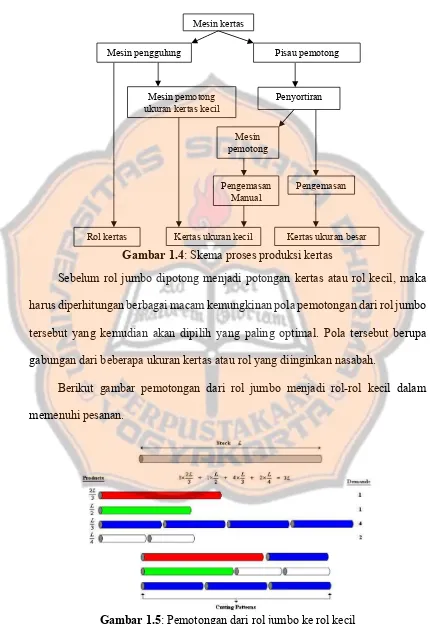
Gambar 1.4: Skema proses produksi kertas

Sebelum rol jumbo dipotong menjadi potongan kertas atau rol kecil, maka harus diperhitungan berbagai macam kemungkinan pola pemotongan dari rol jumbo tersebut yang kemudian akan dipilih yang paling optimal. Pola tersebut berupa gabungan dari beberapa ukuran kertas atau rol yang diinginkan nasabah.

Berikut gambar pemotongan dari rol jumbo menjadi rol-rol kecil dalam memenuhi pesanan.

Gambar 1.5: Pemotongan dari rol jumbo ke rol kecil Mesin kertas

Mesin penggulung Pisau pemotong

Rol kertas

Mesin pemotong ukuran kertas kecil

Kertas ukuran kecil

Penyortiran

Mesin pemotong

Pengemasan Manual

Pengemasan

(21)

Pembentukan pola tersebut juga harus memperhatikan beberapa kendala berikut agar didapat hasil yang optimal. Berikut kendala yang perlu diperhatikan: 1. Lebar kertas maksimal (deckle) 276 cm untuk 70 gsm (grams per square meter)

ke atas dan 272 untuk 70 gsm ke bawah.

2. Dalam 1 rol jumbo yang akan dipotong menjadi rol-rol kecil haruslah memuat pesanan dengan diameter rol, panjang rol, jenis kertas, warna kertas, dan gsm yang sama.

Terdapat banyak metode untuk menyelesaikan masalah tersebut salah satunya dengan program linear. Banyak persoalan yang dapat diselesaikan menggunakan metode program linear diantaranya persoalan transportasi, program penugasan, program dinamis, dan program bilangan bulat. Secara umum, masalah program linear dapat dirumuskan sebagai berikut:

Maksimumkan atau minimumkan

=

Dengan kendala

=

dengan = , , … , � , = , , … , , = [

,

⋱

,

], dan =

[ ].

Contoh 1.1

(22)

ini dapat dipotong menjadi 2 rol dengan lebar 93 cm,1 rol dengan lebar 108 cm, dan menyisakan rol dengan lebar 6 cm.

Misalkan pesanan yang diterima adalah sebagai berikut.

Tabel 1.1 Pesanan yang diterima untuk contoh 1.1 Banyak rol Lebar rol (cm)

97 135

610 108

395 93

211 42

Permasalahannya menjadi bagaimana menentukan pola pemotongan rol jumbo agar pesanan dapat dipenuhi dengan banyaknya rol jumbo yang harus dipotong sesedikit mungkin.

Ada 12 kemungkinan/cara memotong rol jumbo ke dalam rol kecil sesuai pesanan (dengan sisa pemotongan kurang dari 42 cm) yaitu:

Kemungkinan

�

Lebar rol

Sisa

135 108 93 42

1 2 0 0 0 30

2 1 1 0 1 15

3 1 0 1 1 30

4 1 0 0 3 39

(23)

6 0 1 2 0 6

7 0 1 1 2 15

8 0 1 0 4 24

9 0 0 3 0 21

10 0 0 2 2 30

11 0 0 1 4 39

12 0 0 0 7 6

Pola 1 dari tabel di atas berarti 1 rol jumbo dengan lebar 3 meter akan dipotong menjadi 2 rol kecil dengan lebar 135 cm dengan sisa kemungkinan 30 cm. Pola 2 berarti 1 rol jumbo akan dipotong menjadi 1 rol kecil dengan lebar 135, 1 rol kecil dengan lebar 108 dan 1 rol kecil dengan lebar 42 cm dengan sisa kemungkinan 15 cm. Demikian seterusnya berlaku cara membaca data yang sama untuk pola-pola pemotongan yang lain.

Untuk setiap kemungkinan pola � di atas, kita memperkenalkan variabel

yang menunjukkan banyaknya rol jumbo yang harus dipotong menurut pola

�. Dengan demikian, fungsi tujuan adalah meminimumkan jumlah rol jumbo yang

dipotong yaitu ∑ ₌ . Agar pesanan terpenuhi maka untuk setiap ukuran lebar

yang dipesan ditambahkan 1 kendala. Sebagai contoh, untuk pesanan 395 rol dengan lebar 93 cm, maka fungsi kendala dapat dituliskan

(24)

yang berarti jumlah rol kecil dengan lebar 93 cm yang dihasilkan dengan memotong rol jumbo menurut berbagai pola pemotongan tidak boleh kurang dari 395 rol (jumlah rol pesanan). Demikian seterusnya sehingga diperoleh masalah program linear berikut.

Minimumkan

∑

=

Dengan kendala

+ + + + +

+ + +

+ + + +

+ + + + + + + +

Dalam menyelesaikan masalah program linear, metode yang sering digunakan adalah metode simpleks. Selain metode simpleks, metode yang lebih cocok digunakan untuk menyelesaikan masalah pemotongan yaitu metode penghasil kolom.

(25)

menjadi rol-rol kecil dan dengan pola pemotongan satu dimensi (lihat gambar 1.1 dan 1.5). Yang dimaksud dengan pola pemotongan satu dimensi adalah memotong rol kertas dengan mempertimbangkan satu ukuran saja yaitu lebar rol sehingga untuk ukuran panjang dan tebal/diameter rol adalah sama untuk setiap potongan. Sedangkan untuk pola pemotongan dua dimensi yaitu memotong rol kertas dengan mempertimbangkan dua ukuran yaitu lebar dan panjang kertas (lihat gambar 1.3).

B. Rumusan Masalah

Berdasarkan latar belakang tersebut, secara garis besar uraian rumusan masalah yang dibahas dalam tugas akhir ini adalah:

1. Bagaimana memodelkan masalah pemotongan kertas agar didapat solusi yang optimal?

2. Bagaimana menyelesaikan masalah pemotongan kertas dengan menggunakan metode penghasil kolom?

3. Bagaimana menyelesaikan masalah pemotongan kertas dengan menggunakan MATLAB?

C. Pembatasan Masalah

(26)

D. Tujuan Penulisan

Tujuan yang ingin dicapai penulis dalam penulisan tugas akhir ini selain untuk memenuhi syarat tugas akhir dalam Program Studi Matematika Universitas Sanata Dharma, yaitu sebagai berikut.

1. Memodelkan masalah pemotongan kertas.

2. Menyelesaikan masalah pemotongan kertas dengan metode penghasil kolom. 3. Menyelesaikan masalah pemotongan kertas dengan program MATLAB.

E. Manfaat Penulisan

Manfaat penulisan dari tugas akhir ini adalah:

1. Dapat memodelkan dan mengaplikasikan program linear dalam masalah pemotongan kertas.

2. Dapat membantu berbagai pihak untuk menentukan pola pemotongan kertas yang optimal.

F. Metode Penulisan

(27)

G. Sistematika Penulisan

BAB I. PENDAHULUAN A. Latar Belakang Masalah B. Perumusan Masalah C. Pembatasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan

BAB II. PROGRAM LINEAR A. Program Linear

B. Metode Simpleks Direvisi C. Program Linear Bilangan Bulat

D. Masalah Knapsack (Knapsack Problem)

BAB III. MASALAH PEMOTONGAN PERSEDIAAN

A. Masalah Pemotongan Persediaan (Cutting Stock Problem) B. Metode Penghasil Kolom

(28)

BAB V. PENUTUP A. Kesimpulan B. Saran

DAFTAR PUSTAKA

LAMPIRAN A

(29)

13

BAB II

PROGRAM LINEAR

A. Program Linear

Program Linear muncul pada tahun 1939 di Departemen Pertahanan Inggris dan Amerika untuk menjawab masalah optimisasi perencanaan operasi perang melawan Jerman dalam Perang Dunia ke-II. Pada tahun 1947 teori dan teknik simpleks dikembangkan oleh Dantzig dan para pakar lainnya. Masalah dalam program linear adalah mengoptimumkan suatu fungsi linear yang terbatas oleh kendala-kendala berupa persamaan dan pertidaksamaan linear. Program linear termasuk model yang relatif sederhana di antara model-model riset operasi. Beberapa contoh penggunaan program linear ialah penjadwalan produksi, penjadwalan penerbangan, siasat perang, analisis sosial, dan lain-lain.

Model program linear memiliki tiga komponen dasar yaitu:

1. Variabel keputusan adalah variabel yang menguraikan secara lengkap keputusan-keputusan yang akan dibuat, yang merupakan formulasi dari apa yang dicari dalam persoalan tersebut. Variabel keputusan ini dituliskan dengan

, = , , … , .

2. Fungsi tujuan merupakan fungsi dari variabel keputusan yang harus dicapai agar solusi optimal dapat ditentukan dari semua nilai-nilai yang layak.

3. Fungsi kendala merupakan formulasi dari kendala-kendala yang dihadapi dalam menentukan nilai variabel-variabel keputusan.

(30)

1. Linearitas

Fungsi tujuan dan kendala haruslah fungsi linear. 2. Proporsionalitas

Nilai variabel dari semua fungsi kendala dan fungsi tujuan yang linear haruslah proporsional atau sebanding. Sebagai contoh, satu potong roti menghasilkan 77,5 kalori maka untuk 2 potong roti menghasilkan 155 kalori.

3. Aditivitas

Fungsi tujuan adalah jumlahan langsung dari kontribusi individual dari variabel-variabel yang berbeda. Sebagai contoh, 2 potong roti menghasilkan 155 kalori dan 1 butir telur menghasilkan 80 kalori maka dihasilkan 235 kalori dengan mengkonsumsi 2 potong roti dan 1 butir telur.

4. Kepastian

Setiap parameter (koefisien fungsi tujuan, koefisien kendala, dan nilai di sisi kanan) diketahui dengan pasti dan tidak berubah selama periode analisis.

Secara umum, masalah umum program linear bisa dinyatakan sebagai berikut:

(31)

Memaksimumkan atau meminimumkan

= ∑

=

2.3

Dengan kendala

∑

=

= , = , … , 2.4

, = , … , 2.5

dimana setiap pertidaksamaan (2.4) memiliki simbol, , , =, yang hanya dipilih salah satu yang disebut kendala utama, sedangkan pertidaksamaan (2.5) disebut kendala tak negatif. Kendala tak negatif mengasumsikan nilai variabel harus

bernilai tak negatif. Fungsi linear (2.3) disebut fungsi tujuan. Dengan disebut

koefisien teknis, disebut koefisien ongkos, dan disebut suku tetap di ruas kanan

disingkat “suku tetap” atau “ruas kanan”. Jika , = , … , memenuhi semua

kendala maka disebut solusi layak. Solusi layak yang juga mengoptimumkan disebut solusi optimum.

Untuk menyelesaikan masalah minimum maka bentuk minimum dapat diubah menjadi bentuk maksimum dengan cara mengalikan fungsi tujuan dengan

− . Selanjutnya, diselesaikan seperti masalah maksimum. Solusi yang diperoleh

(32)

Metode yang sering digunakan untuk menyelesaikan masalah program linear adalah metode grafik dan metode simpleks. Metode grafik digunakan untuk memecahkan persoalan model program linear dua variabel. Lalu pada tahun 1947, Dantzig mengembangkan metode yang dapat memecahkan persoalan model program linear dengan lebih dari dua variabel yang disebut metode simpleks.

Metode Simpleks

Metode simpleks yang dikenalkan oleh George B. Dantzig telah dikembang-kan dan diterapdikembang-kannya ke persoalan bisnis. Metode simpleks adalah metode siste-matis dari suatu solusi layak ke solusi layak lainnya dan dilakukan berulang-ulang sehingga tercapai suatu solusi layak yang optimum.

Definisi 2.1

Variabel pengetat (slack variable) merupakan variabel tambahan yang mengubah suatu pertidaksamaan menjadi persamaan, dengan cara menambahkan variabel pengetat pada ruas kiri suatu pertidaksamaan. Variabel pengetat ini digunakan pada kendala pertidaksamaan yang berbentuk lebih kecil sama dengan (≤).

Misalkan diberikan masalah program linear bentuk standar sebagai berikut. Memaksimumkan

= ∑

(33)

Dengan kendala

∑

=

, = , … , 2.6

, = , … ,

Maka dapat didefinisikan variabel pengetat ₊ , ₊ , … , ₊ dan fungsi tujuan sebagai berikut.

+ = − ∑

=

, = , … , 2.7

= ∑

=

2.8

Dengan notasi ini, masalah ini dapat diuraikan kembali menjadi

Memaksimumkan dengan kendala , , … , ₊ 2.9

Setiap solusi layak , , … , dari (2.6) ditunjukkan oleh + bilangan bulat tak negatif , , … , ₊ dengan ₊ , ₊ , … , ₊ yang didefinisikan pada (2.7). Hal ini dapat dikatakan bahwa (2.7) menunjukkan kesamaan/ekuivalensi antara (2.6) dan (2.9). Untuk lebih jelasnya yaitu sebagai berikut.

1. Setiap solusi layak , , … , dari (2.6) dapat diperluas, dengan cara yang

ditunjukkan oleh (2.7), menjadi , , … , ₊ dari (2.9).

(34)

Di setiap iterasi, metode simpleks mengganti solusi layak , , … , ₊ menjadi solusi layak lain ̅ , ̅ , … , ̅ ₊ yang lebih baik dari sebelumnya sehingga

∑ ̅

=

> ∑

=

Sistem linear untuk menemukan solusi layak dengan menyatakan nilai-nilai variabel sisi kanan menjadi nilai-nilai yang sesuai dari variabel sisi kiri dan fungsi tujuan disebut kamus (dictionaries). Dengan demikian, setiap kamus dari (2.6) akan menjadi suatu sistem persamaan linear dalam variabel , , … , ₊ dan .

Pertama definisikan ₊ , ₊ , … , ₊ dan , serta + + variabel yang saling bergantung. Saling ketergantungan ini harus didasarkan oleh setiap kamus terkait (2.6) dimana terjemahan harus tepat. Lebih tepatnya, kamus-kamus harus memenuhi syarat-syarat berikut.

1. Setiap solusi dari himpunan persamaan yang memuat kamus harus juga solusi dari (2.7), begitu sebaliknya.

2. Persamaan setiap kamus harus memperlihatkan variabel dari , , … , ₊ dan fungsi tujuan dalam variabel tersisa.

3. Menetapkan variabel sisi kanan nol dan mengevaluasi variabel sisi kiri sampai pada solusi layak.

(35)

Definisi 2.2

Variabel dasar (basic) adalah variabel yang diperoleh dari banyaknya persamaan pada masalah program linear. Sedangkan variabel lainnya adalah variabel tidak dasar (nonbasic). Variabel ini adalah variabel yang dihasilkan dari selisih banyaknya variabel dengan banyaknya persamaan pada masalah program linear dan merupakan variabel yang bernilai nol.

Variabel yang muncul pada sisi kiri kamus disebut dasar dan variabel

yang muncul pada sisi kanan disebut tidak dasar. Variabel dasar merupakan basis. Basis berubah pada setiap iterasi. Pada setiap iterasi, dipilih variabel tidak dasar untuk masuk basis lalu mengeluarkan variabel dasar dari basis. Pemilihan variabel masuk disebabkan oleh keinginan untuk meningkatkan nilai dan penentuan variabel keluar didasarkan pada persyaratan bahwa semua variabel harus diasumsikan bernilai tak negatif. Variabel keluar adalah variabel dasar tak negatif yang menyebabkan batas atas terketat pada kenaikan variabel masuk. Rumus untuk variabel keluar muncul di baris sumbu (pivot row) kamus. Proses perhitungan dari pembuatan kamus baru disebut berputar (pivoting).

Contoh 2.1

Maksimumkan

+ +

Dengan kendala

(36)

− +

+ −

, ,

Pada contoh ini, kamus layak awal dapat dituliskan sebagai berikut.

= − − −

= + −

= − + −

= − − +

= + +

2.10

Kamus layak ini menunjukkan variabel keputusan , , merupakan variabel tidak dasar (diberi nilai nol) dan variabel pengetat , , , merupakan variabel dasar. Jadi solusi layak yang bersesuaian adalah = , = , = , =

, = , = , = , dan = . Sehingga memenuhi syarat kedua dan ketiga

dalam kamus.

Pada iterasi pertama, kita mencoba meningkatkan nilai dengan membuat

(37)

nilai , , , dan tidak satupun diizinkan menjadi negatif, maka diberikan batas pada tiap variabel yaitu

= − − −

= − + −

= − − +

Dimana nilai meningkat sehingga tidak menjadi batas atas kenaikan dan = . Sehingga kendala adalah batas atas terketat dan mengimplikasikan . Dalam meningkatkan solusi layak diperoleh = dan = . Variabel masuk menjadi basis dan variabel keluar menjadi variabel tidak dasar (diberi nilai nol). Persamaan keempat (2.10) dapat dituliskan sebagai berikut.

= − + − 2.11

Substitusikan (2.11) ke dalam persamaan yang tersisa dari (2.10).

= − + −

= − − +

= − − −

= + − +

= − + −

2.12

Kamus (2.12) menyelesaikan iterasi pertama metode simpleks. Kamus layak ini menunjukkan variabel tidak dasar , , (diberi nilai nol) dan variabel dasar

(38)

, = , = , = , = , dan = . Sehingga memenuhi syarat kedua

dan ketiga dalam kamus.

Pada iterasi kedua, untuk meningkatkan nilai dipilih positif. Hal ini karena

adalah satu-satunya variabel tidak dasar yang memiliki koefisien positif pada di (2.12). Karena nilai meningkat, maka begitu juga nilai = / . Namun, nilai , , dan menurun, dan tidak satu pun diizinkan menjadi negatif. Ketiga kendala , , memberikan batas atas pada kenaikan , diberikan batas tiap variabel yaitu = , = / , = sehingga kendala adalah

batas atas terketat dan mengimplikasikan / . Dalam meningkatkan solusi layak diperoleh = / dan = . Variabel masuk menjadi basis dan variabel keluar menjadi variabel tidak dasar (diberi nilai nol). Dengan cara substitusi seperti iterasi pertama, maka dapat dituliskan kamus ketiga sebagai berikut.

= + + −

= − − −

= − +

= − − +

= + − −

(39)

Kamus (2.13) menyelesaikan iterasi kedua metode simpleks. Kamus layak ini menunjukkan variabel tidak dasar , , (diberi nilai nol) dan variabel dasar

, , , . Jadi solusi layak yang bersesuaian adalah = / , = , =

/ , = , = / , = , = , dan = / . Sehingga memenuhi syarat

kedua dan ketiga dalam kamus.

Pada iterasi ketiga, untuk meningkatkan nilai dipilih positif. Hal ini karena adalah satu-satunya variabel tidak dasar yang memiliki koefisien positif pada

di (2.13). Karena nilai meningkat, maka nilai , , , dan menurun, dan tidak satu pun diizinkan menjadi negatif. Keempat kendala , ,

, memberikan batas atas pada kenaikan , diberikan batas tiap variabel

yaitu = / , = / , = / , = sehingga kendala

adalah batas atas terketat dan mengimplikasikan / . Dalam meningkatkan solusi layak diperoleh = / dan = . Variabel masuk menjadi basis dan variabel keluar menjadi variabel tidak dasar (diberi nilai nol). Dengan cara substitusi seperti iterasi pertama, maka kamus yang dihasilkan.

= − + −

= − − −

= − − +

= + − +

(40)

= − − −

Kamus layak ini menunjukkan variabel tidak dasar , , (diberi nilai nol) dan

variabel dasar , , , . Jadi solusi layak yang bersesuaian adalah =

/ , = / , = / , = / , = , = , = , dan = .

Sehingga memenuhi syarat kedua dan ketiga dalam kamus.

Pada kamus (2.14) tidak terdapat variabel tidak dasar yang dapat dimasukkan basis. Sedemikian hingga kamus terakhir (2.14) menunjukkan solusi optimal, yaitu =

, = , = dan menghasilkan = . Hal ini memenuhi syarat kedua dan

ketiga dalam kamus.

Untuk setiap pilihan bilangan , , , , , , dan , berikut pernyataan ekuivalen yang memenuhi syarat pertama dalam kamus:

1. , , , , , , dan merupakan solusi (2.10)

B. Metode Simpleks Direvisi

(41)

metode simpleks direvisi kurang dari sama dengan iterasi dari metode simpeks. Kita dapat menuliskan masalah program linear bentuk standar sebagai berikut.

Maksimumkan

=

Dengan kendala

Dimana = , , … , �, = , , … , , = [

,

⋱

,

],

dan = [ ].

Setelah ditambahkan dengan variabel pengetat ₊ , ₊ , … , ₊ maka masalah ini menjadi sebagai berikut.

Maksimumkan

= (2.15)

Dengan kendala

= (2.16)

Dimana = , , … , ₊ �, = , , … , ₊ , =

[ ⋱ , +

, +

(42)

Pendekatan umum dari metode simpleks dan metode simpleks direvisi adalah memperoleh suatu urutan solusi-solusi layak yang semakin baik sampai tercapai suatu solusi optimal. Salah satu ciri pokok dari metode simpleks direvisi mencakup dengan cara mana setiap solusi layak akan diselesaikan, yaitu setelah variabel-variabel dasar dan tidak dasar diketahui.

Untuk setiap solusi layak ∗ yaitu , , … , ₊ dibagi ke dalam variabel

dasar dan variabel tidak dasar. Contohnya, membagi vektor menjadi dan _� sehinggamatriks terbagi menjadi dan _�, dan menjadi dan _�. Dengan demikian kita dapat menuliskan = menjadi

[ �] [ _�] =

= − � �

(2.17)

Dengan

= = [ �] [

�] = + � �

Dimana matriks adalah nonsingular.

Teorema 2.1

Matriks adalah nonsingular.

Bukti:

Kita tunjukkan bahwa matriks adalah nonsingular dengan menunjukkan

= tepat memiliki satu solusi. Karena solusi layak ∗ memenuhi persamaan

∗ ₌ _dan �

(43)

∗₋

� �∗ = . Untuk memeriksa bahwa tidak ada solusi lain, dimisalkan

terdapat sebarang solusi layak ̃ sedemikian hingga ̃ = dan ̃_�= . Dengan demikian vektor ̃ memenuhi ̃ = ̃ + _�̃_� = , itu harus memenuhi persamaan di kamus yang bersesuaian dengan ∗. Tetapikarena ̃_�=

maka ̃ = ∗. Jadi, terbukti matriks adalah nonsingular.█

Matriks disebut juga matriks basis atau basis. Matriks basis dapat kita

notasikan menjadi matriks . Karena adalah matriks nonsingular maka − akan selalu ada. Sehingga kita dapat menuliskan persamaan dan menjadi =

− ₋ −

� � dan = − + �− − � �. Tentunya − tak

lain adalah vektor ∗ yang menentukan nilai dari variabel dasar dan haruslah

− _.

Pada metode simpleks direvisi akan dilakukan dengan iterasi yang terus berulang sampai diperoleh solusi yang optimal. Di setiap iterasi metode simpleks direvisi, pertama-tama kita memilih variabel masuk lalu mencari variabel keluar dan akhirnya memperbaharui solusi layak.

Untuk memilih variabel masuk dengan koefisien positif, maka perhatikan vektor baris _�− − _� . Dalam metode simpleks direvisi, vektor ini dihitung

melalui dua langkah. Pertama, menemukan = − dengan menyelesaikan sistem = . Kedua, menghitung _�− _� kemudian dipilih elemen dari

(44)

Untuk menentukan variabel keluar, maka variabel masuk dinaikan sebesar � dari nol sampai suatu nilai positif. Nilai variabel dasar berubah sampai nilai variabel

turun ke nol meninggalkan basis. Pada persamaan = ∗ − − _{� �},

berubah dari ∗ menjadi ∗ − � dengan merupakan kolom − _� yang

bersesuaian dengan variabel masuk atau dapat dituliskan = − . Jika terdapat elemen yang memenuhi ∗ − � = maka variabel tersebut menjadi variabel keluar.

Berikut iterasi dari metode simpleks direvisi yaitu sebagai berikut.

1. Selesaikan sistem = dimana adalah matriks basis awal, sehingga ditemukan vektor .

2. Tentukan kolom yang masuk, yaitu jika variabel tidak dasar berhubungan

dengan elemen dari _� dan kolom dari _�, maka _�− _� = − .

Untuk masalah maksimum (minimum), kolom dipilih yang memiliki −

paling positif (negatif). Untuk masalah maksimum (minimum) jika semua elemen − < ( − > ), maka tidak terdapat kolom masuk dan

iterasi berhenti sehingga didapatkan solusi optimal. Jika tidak, maka lanjut ke langkah 3.

3. Selesaikan sistem = , sehingga didapat vektor .

4. Tentukan kenaikan nilai � terbesar dari nol sampai suatu nilai positif dengan

cara mencari nilai paling minimum dari ∗ sedemikian hingga ∗ − � .

(45)

tak terbatas atau tidak memiliki penyelesaian. Jika terdapat elemen yang memenuhi ∗ − � = maka kolom tersebut menjadi kolom keluar.

(46)

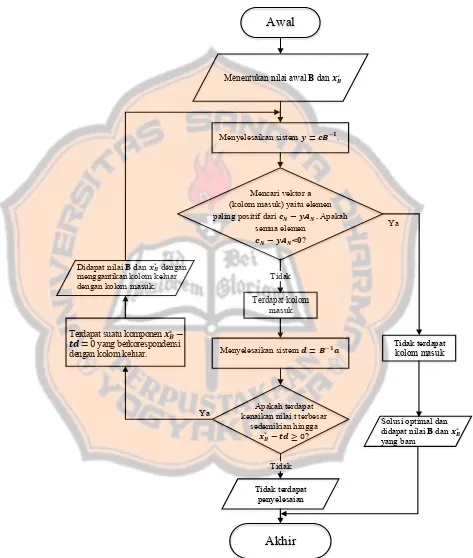
Berikut diagram alir metode simpleks direvisi.

Menyelesaikan sistem = −

Apakah terdapat kenaikan nilai t terbesar

sedemikian hingga

∗_{− �} ₀_? Terdapat suatu komponen ∗−

� = 0 yang berkorespondensi

dengan kolom keluar. (kolom masuk) yaitu elemen paling positif dari _�− _�. Apakah

semua elemen

�− �<0?

(47)

Contoh 2.2

Misalkan diberikan masalah program linear berikut. Maksimumkan

= + + +

Dengan kendala

+ + +

, , ,

Ketiga kendala tersebut kemudian diubah ke dalam bentuk persamaan.

+ + + + =

Dimana , dan adalah variabel pengetat. Sehingga persamaan di atas dapat dituliskan dalam bentuk matriks = dengan

= [ ], = [ ], dan =

[ ]

(48)

Setelah iterasi kedua dengan metode simpleks didapatkan kamus berikut.

= − , − , − , + ,

= − , − , + , − ,

= + , − , + , + ,

= − , + , − , − ,

Untuk menekankan fakta bahwa hanya variabel dasar , dan yang tidak diketahui, maka dapat ditulis seperti persamaan (2.17) dimana

= [ ], _� = [ ], = [ ], _�= [ ], = [ ], _�=

[ ], dan = [ ].

Dengan menggunakan metode simpleks direvisi, penyelesaian dari masalah program linear tersebut yaitu:

Pertama, menentukan matriks awal yaitu matriks dan vektor ∗ = [

∗

� ∗

�

∗] =

[ ], kemudian mulai iterasi.

Iterasi 1:

1. Menyelesaikan sistem = sehingga diperoleh vektor = [

(49)

2. Tentukan kolom yang masuk dengan menyelesaikan _�− _�= −

yaitu sebagai berikut

[ ] − [ ,, ] [ ] = [ − ,

, − , − ,

]

Dari hasil tersebut terlihat bahwa terdapat satu elemen yang memenuhi −

> yaitu elemen kedua yang berkaitan dengan variabel . Jadi, variabel

adalah variabel masuk dan vektor kolom dari variabel yang terkait merupakan kolom masuk.

3. Selesaikan sistem = , sehingga didapat vektor = [

, , , ].

4. Didapatkan nilai � = sedemikian hingga ∗ − � dan terdapat 1

komponen dari ∗ − � = yaitu variabel yang menjadi variabel keluar. 5. Didapat matriks awal yang baru dengan menukar kolom masuk dengan

kolom keluar yaitu

= [ ] dan vektor ∗ = [ ].

Iterasi 2:

1. Menyelesaikan sistem = sehingga diperoleh vektor = [ ].

2. Tentukan kolom yang masuk dengan menyelesaikan _�− _�= −

(50)

[ ] − [ ] [ ] = [ − − − −

]

Dari hasil tersebut terlihat bahwa semua elemen memenuhi − < . Jadi,

tidak terdapat kolom masuk dan iterasi berhenti sehingga didapatkan solusi optimal yaitu

= [ ] dan ∗ = [ ].

C. Program Linear Bilangan Bulat

Pada program linear, solusi dapat berupa pecahan dan bilangan bulat. Namun untuk kasus tertentu solusi mengharuskan untuk berupa bilangan bulat. Contohnya pada masalah transportasi, masalah Knapsack, masalah penjadwalan, masalah pengiriman barang, dan masalah pemotongan persediaan. Program linear dengan solusi bilangan bulat inilah yang disebut sebagai program linear bilangan bulat. Program linear bilangan bulat terdiri dari dua macam yaitu program linear bilangan bulat murni dan program linear bilangan bulat campuran. Program linear bilangan bulat dikatakan program bilangan bulat murni jika semua variabel adalah bilangan bulat. Sedangkan jika sebagian variabelnya bukan bilangan bulat atau sebagian bilangan real maka dapat dikatakan program linear bilangan bulat campuran.

(51)

Metode Pencabangan dan Pembatasan (Branch and Bound Method)

Metode pencabangan dan pembatasan adalah suatu metode untuk menyelesaikan persoalan program linear bilangan bulat murni dan persoalan program linear bilangan bulat campuran. Metode ini diusulkan pertama kali oleh A. H. Land dan A. G. Doig pada tahun 1960.

Metode ini dilakukan dengan melakukan perhitungan satu persatu atau mengenumerasi semua nilai variabelnya melalui pencabangan. Dengan mengenumerasi semua variabel tersebut, maka diperoleh suatu solusi optimal, yaitu solusi yang meminimumkan atau memaksimumkan fungsi tujuannya.

Metode pencabangan dan pembatasan merupakan suatu pendekatan untuk menyelesaikan persoalan yang didasarkan pada pembagian semua solusi layak terhadap sebuah masalah ke dalam masalah yang lebih kecil. Selanjutnya, sub-masalah ini dapat diselesaikan secara sistematis sampai diperoleh solusi optimal. Cara inilah yang kemudian menjadi dasar metode pencabangan dan pembatasan.

Dalam menyelesaikan program linear bilangan bulat menggunakan pencabangan dan pembatasan terdapat 3 langkah utama, yaitu:

1. Pencabangan

Pencabangan dilakukan ketika solusi belum berbentuk bilangan bulat yaitu dengan memecah masalah program linear awal � menjadi dua bagian yaitu

� dan � dengan menambahkan kendala baru. Dalam pencabangan, kendala

(52)

a. � = � + , dimana adalah pembulatan ke bawah dari solusi program linear berbentuk pecahan.

b. � = � + , dimana adalah pembulatan ke atas dari solusi

program linear berbentuk pecahan.

Proses ini terus berlangsung sampai diperoleh solusi bilangan bulat untuk pertama kalinya.

2. Pembatasan

Pembatasan dilakukan setelah proses pencabangan. Langkah ini untuk membatasi solusi agar didapatkan solusi optimal. Terdapat dua batas pada metode ini yaitu batas bawah dan batas atas. Batas bawah digunakan untuk menyelesaikan masalah maksimum. Jika � menghasilkan solusi bilangan bulat yang lebih baik atau lebih besar dari batas bawah, maka perbarui batas bawah dengan solusi tersebut. Jika tidak, maka solusi diabaikan dan memilih sub-masalah baru lalu mengulangi terus sampai semua sub-masalah diteliti dan diperoleh solusi optimal yaitu batas bawah terakhir. Sedangkan untuk batas atas digunakan untuk menyelesaikan masalah minimum. Jika � menghasilkan solusi bilangan bulat yang lebih baik atau lebih kecil dari batas atas, maka perbarui batas atas dengan solusi tersebut. Jika tidak, maka solusi diabaikan dan memilih sub-masalah baru lalu mengulangi terus sampai semua sub-masalah diteliti dan diperoleh solusi optimal yaitu batas atas terakhir. 3. Penghentian cabang

Penghentian cabang dilakukan jika:

(53)

b. Sub-masalah menghasilkan semua variabel keputusan bernilai bulat, dan c. Pada masalah maksimasi, fungsi tujuan tidak lebih besar atau sama dengan

nilai batas bawah. Sebaliknya, pada masalah minimisasi, fungsi tujuan tidak lebih kecil atau sama dengan nilai batas atas.

Berikut langkah-langkah metode pencabangan dan pembatasan untuk menyelesaikan program linear dengan solusi bilangan bulat:

1. Menyelesaikan masalah program linear sampai menghasilkan solusi optimum. Apabila solusi berbentuk bilangan bulat, maka perhitungan dihentikan. Sebaliknya, jika solusi berbentuk bilangan pecahan maka perhitungan dilanjutkan.

2. Kemudian menambah kendala baru yang membatasi nilai salah satu variabel yang tidak bulat.

3. Penambahan ini akan berakibat terbelahnya daerah layak menjadi 2 bagian sehingga terbentuklah 2 sub-masalah baru yang kemudian harus diselesaikan. Dengan kata lain, terjadi pencabangan dari masalah aslinya menjadi 2 sub-masalah baru.

4. Batas untuk nilai fungsi tujuan kemudian dapat ditentukan. Batas ini dapat digunakan untuk mengeliminasi sub-masalah yang tidak diperlukan dan menentukan apakah solusi optimalnya sudah tercapai.

(54)

Contoh 2.3

Misalkan diberikan masalah program linear awal � sebagai berikut.

Minimumkan = +

Dengan kendala

{ ++

, dan bilan�an bulat

Jawab:

1. Menyelesaikan masalah program linear tersebut sehingga mendapatkan solusi optimal = , , = , dan = , . Solusi yang diperoleh tidak berbentuk bilangan bulat maka lanjut ke langkah 2.

2. Selanjutnya, masalah program linear bulat di atas dicabangkan menjadi dua

masalah program linear bulat baru dengan menambahkan kendala



dan



.

3. Sehingga didapatkan dua sub-masalah baru yang harus diselesaikan sebagai berikut.

Sub-masalah 1: � = � + , , Minimumkan = +

Dengan kendala

{

+ +



,

(55)

Sub-masalah 2: � = � + , ,

4. Batas untuk nilai tujuan belum dapat ditentukan karena belum mendapatkan solusi bilangan bulat.

5. Dari sub-masalah 1 diperoleh = , = , , dan = , . Solusi yang diperoleh tidak berbentuk bilangan bulat maka kembali ke langkah 2.

Langkah 2: Sub-masalah program linear dicabangkan menjadi dua masalah

(56)

Dengan kendala mendapatkan solusi bilangan bulat.

Langkah 5: Dari sub-masalah 3 cabang dihentikan karena sub-masalah tidak memiliki daerah layak.

Dari sub-masalah 4 diperoleh = , , = , dan = , . Solusi tidak berbentuk bilangan bulat maka kembali ke langkah 2.

(57)

Minimumkan = + mendapatkan solusi bilangan bulat.

Langkah 5: Dari sub-masalah 5 diperoleh = , = , , dan = , . Solusi yang diperoleh tidak berbentuk bilangan bulat maka kembali ke langkah 2.

(58)

dan

Sub-masalah 8: � = � + , , Minimumkan = +

Dengan kendala

{

+ +





,

Langkah 4: Batas untuk nilai tujuan belum dapat ditentukan karena belum mendapatkan solusi bilangan bulat.

Langkah 5: Dari sub-masalah 7 cabang dihentikan karena sub-masalah tidak memiliki daerah layak.

Dari sub-masalah 8 diperoleh = , = , dan = . Solusi berbentuk bilangan bulat maka = dijadikan sebagai batas atas.

Dari sub-masalah 6 diperoleh = , = , dan = . Solusi berbentuk

bilangan bulat dan = lebih kecil dari batas atas sebelumnya maka = dijadikan sebagai batas atas yang baru.

Dari sub-masalah 2 diperoleh = , = , dan = . Solusi berbentuk bilangan bulat dan = lebih kecil dari batas atas sebelumnya maka = dijadikan sebagai batas atas yang baru.

(59)

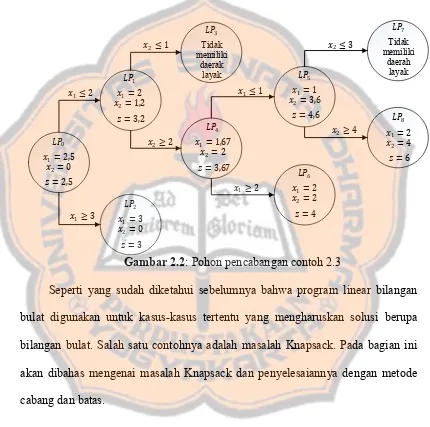
Berikut gambar pohon pecabangan dari contoh 2.3.

Gambar 2.2: Pohon pencabangan contoh 2.3

Seperti yang sudah diketahui sebelumnya bahwa program linear bilangan bulat digunakan untuk kasus-kasus tertentu yang mengharuskan solusi berupa bilangan bulat. Salah satu contohnya adalah masalah Knapsack. Pada bagian ini akan dibahas mengenai masalah Knapsack dan penyelesaiannya dengan metode cabang dan batas.

D. Masalah Knapsack

(60)

biasanya digunakan untuk menyusun barang ke dalam karung besar yang tidak dapat memuat semua barang. Permasalahan Knapsack ini mencari solusi terbaik dari semua kemungkinan susunan barang yang akan dimasukkan ke dalam karung.

Masalah Knapsack dapat dituliskan sebagai berikut. Maksimumkan = ∑₌

Dengan kendala

∑

=

� (2.18)

Dimana adalah bilangan bulat tak negatif = , , . . . , dan merupakan banyaknya barang ke- yang dimasukan ke dalam karung, adalah ukuran barang

ke-i yang bernilai positif dan � adalah ukuran karung yang bernilai positif.

Kita asumsikan adalah nilai barang ke-i yang bernilai positif (variabel dengan dapat segera dihapus). Perbandingan ⁄ merupakan nilai per satuan ukuran dari barang ke- atau sebagai efisiensi variabel . Kita asumsikan lagi efisiensi variabel diurutkan secara menurun:

⁄ ⁄ ⁄ (2.19)

Untuk setiap solusi optimal dari masalah Knapsack memenuhi:

� − ∑

=

< (2.20)

(61)

masalah Knapsack dapat dibuat menjadi pohon enumerasi yang memuat cabang-cabang yang merupakan solusi-solusi layak itu sendiri.

Untuk membuat suatu cabang, pada setiap cabang dibuat nilai sebesar

mungkin lalu dilanjutkan pada cabang berikutnya dengan nilai ₊ sebesar

mungkin begitu seterusnya. Secara resmi, adalah bilangan bulat yang diperoleh dengan membulatkan nilai ke bawah, solusi ini didefinisikan dengan rekursi (perulangan)

= � − ∑

−

=

⁄

(2.21)

Dengan = , , . . . , dan biasanya, = �⁄ . Sekarang mencari solusi terbaik dan mengganti solusi lain dengan yang lebih baik. Karena sudah didapatkan solusi layak , , … , , maka solusi layak diperbaharui dengan solusi layak yang lebih baik. Misalkan solusi terbaik yang didapatkan ∗, ∗, … , ∗ menghasilkan

∑ ∗

=

Jika ∑₌ > , maka mengganti dengan ∑₌ dan mengganti

∗_, ∗_{, … ,} ∗ _dengan _{, , … ,} _.

Selanjutnya menemukan cabang yang baru dari solusi layak ( , , … , ) dengan = − dan tetap mereduksi sampai > ditemukan. Jika

(62)

Berdasarkan (2.19), setiap variabel ₊ , ₊ , … , ₊ memiliki efisiensi

Oleh karena itu asumsi

∑

Kecuali kalau sisi kanan dari persamaan di atas melebihi , maka tidak ada solusi

̅ , ̅ , … , ̅ yang memiliki kesempatan untuk meningkatkan nilai ∗, ∗, … , ∗ .

dibuatkan cabang lagi (atau cabang dipotong) dimana koefisien adalah bilangan bulat positif. Sehingga harus dibuatkan cabang lagi yaitu dengan menemukan terbesar sedemikian hingga − dan > dan ditunjukkan bahwa ̅ = untuk = , , . . . , − dan ̅ = − .

(63)

dapat dibuat yaitu ketika = dan = . Pertidaksamaan (2.22) dapat diganti ketika koefisien bukan bilangan bulat positif menjadi

∑ ̅

=

+ +

+ (� − ∑ ̅₌ ) +

Metode ini disebut dengan metode cabang dan batas yang akan ditunjukkan dengan ringkas pada langkah-langkah di bawah.

1. Menentukan nilai awal yaitu = dan = .

4. Menemukan cabang selanjutnya.

Menemukan terbesar sedemikian hingga − dimana > . Kita dapat tuliskan ̅ = untuk = , , . . . , − .

a. Jika = maka berhenti; selain itu ganti dengan − .

b. Jika = , maka kembali ke 4a, selain itu ganti dengan = − . 5. Pencarian cabang yang lebih baik.

Jika ∑₌ ̅ +��+1

��+1(� − ∑= ̅ ) (untuk koefisien bukan

bilangan bulat positif) atau ∑₌ ̅ + ��+1

��+1(� − ∑= ̅ ) + (untuk

(64)

(65)

Awal

Mereduksi k sampai diperoleh

> 0 lalu mengganti dengan ̅ = −1, dimana ̅= untuk = 1, 2, . . . , −1.

Tidak Apakah koefisien

bilangan bulat positif? Menentukan perpanjangan cabang.

Untuk = + 1, + 2, . . . , maka

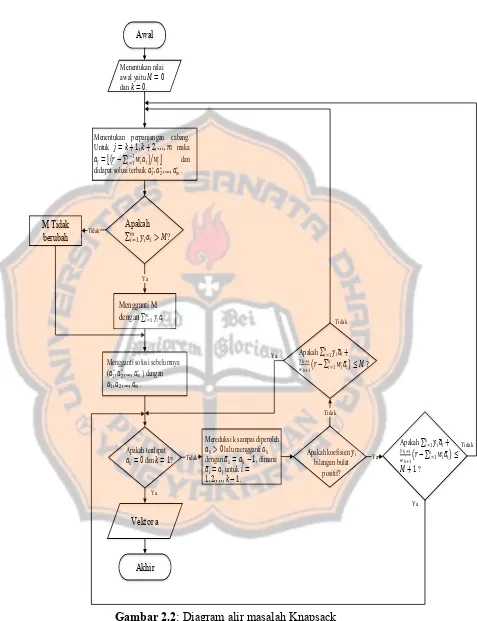
Gambar 2.2: Diagram alir masalah Knapsack

(66)

Maksimumkan 3. Menentukan apakah solusi yang diperoleh meningkat?

Karena ∑₌ = > = , maka = dan ∗ = , ∗ = ∗ = ∗ = diganti menjadi = , = = = .

4. Didapatkan k=3 = lalu dikurangkan sampai diperoleh k=1 dimana >

, maka kita ganti = menjadi ̅ = .

5. Apakah cabang layak untuk dibuatkan cabang lagi?

Karena koefisien bukan bilangan bulat positif, maka kita uji pertidaksamaan

(67)

∑ ̅

Karena pertidaksamaan tersebut tidak terpenuhi maka cabang layak untuk dibuatkan cabang lagi. Kembali ke langkah 2

2. Diketahui k=1 dan = ̅ = , maka diperoleh

4. Didapatkan k=3 = lalu dikurangkan sampai diperoleh k=2 dimana > diperoleh. Maka kita ganti = dengan ̅ = .

(68)

Karena pertidaksamaan tersebut terpenuhi maka cabang tidak layak untuk dibuatkan cabang lagi. Kembali ke langkah 4

4. Didapatkan k=2 = lalu dikurangkan sampai diperoleh k=1 dengan diperoleh > . Maka kita ganti = dengan ̅ = .

(69)

Karena pertidaksamaan tersebut terpenuhi maka cabang tidak layak untuk dibuatkan cabang lagi. Kembali ke langkah 4.

4. Kita peroleh k=1 dimana > , maka kita ganti = dengan ̅ = . 5. Apakah cabang layak untuk dibuatkan cabang lagi?

Karena koefisien bukan bilangan bulat positif, maka kita uji pertidaksamaan berikut dengan k=1 dan ̅ = .

∑ ̅

=

+ +

+ (� − ∑ ̅₌ )

∑ ̅

=

+ +

+ (� − ∑ ̅₌ ) ,

( . ) + /_{, ( −} , . ) ,

= , ,

Karena pertidaksamaan tersebut terpenuhi maka cabang tidak layak untuk dibuatkan cabang lagi.

4. Kita peroleh k=1 dan = , maka iterasi berhenti.

Jadi didapatkan solusi optimal yaitu ∗ = , ∗ = , ∗ = , ∗ = dan =

, .

(70)

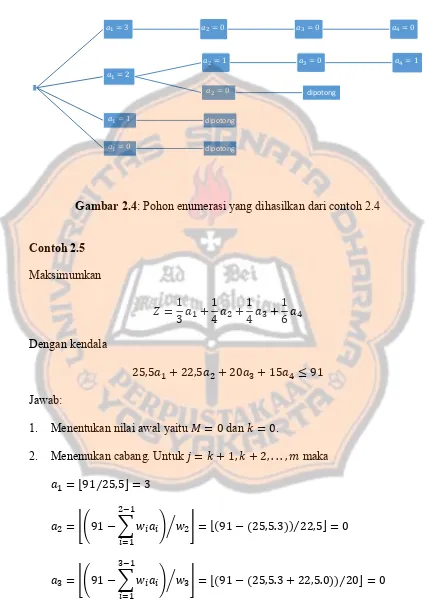
Gambar 2.4: Pohon enumerasi yang dihasilkan dari contoh 2.4

Contoh 2.5

Maksimumkan

= + + +

Dengan kendala

, + , + +

Jawab:

1. Menentukan nilai awal yaitu = dan = .

2. Menemukan cabang. Untuk = + , + , . . . , maka

= ⁄ , =

= ⌊( − ∑

−

=

)⁄ ⌋ = − , . ⁄ , =

= ⌊( − ∑

−

=

)⁄ ⌋ = − , . + , . ⁄ =

= = = =

=

= = =

= dipotong

(71)

= ⌊( − ∑

−

=

)⁄ ⌋ = − , . + , . + . ⁄ =

Maka didapat solusi terbaik ∗ = , ∗ = ∗ = ∗ = . 3. Menentukan apakah solusi yang diperoleh meningkat?

Karena ∑₌ = > = , maka = dan ∗ = , ∗ = ∗ = ∗ = diganti menjadi = , = = = .

, maka kita ganti = menjadi = .

2. Diketahui k=1 dan = ̅ = , maka diperoleh

= ⌊( − ∑ ̅

−

=

(72)

= ⌊( − ∑ ̅

. Maka kita ganti = dengan ̅ = .

Karena koefisien bukan bilangan bulat positif, maka kita uji pertidaksamaan berikut dengan k=2 dan ̅ = , ̅ = .

2. Diketahui k=2, = ̅ = dan = ̅ = , maka diperoleh

= ⌊( − ∑ ̅

−

=

(73)

= ⌊( − ∑ ̅ 5. Apakah cabang layak untuk dibuatkan cabang lagi?

berikut dengan k=3 dan ̅ = , ̅ = , ̅ = .

4. Didapatkan k=3 dan > , maka kita ganti = menjadi ̅ = . 5. Apakah cabang layak untuk dibuatkan cabang lagi?

berikut dengan k=3 dan ̅ = , ̅ = , ̅ = .

∑ ̅

=

+ +

(74)

∑ ̅

4. Didapatkan k=3 = lalu dikurangkan sampai diperoleh k=1 dimana > dan kita ganti = dengan ̅ = .

(75)

∑ ̅

=

+ +

+ (� − ∑ ̅₌ )

∑ ̅

=

+ +

+ (� − ∑ ̅₌ ) ,

( . ) + /_{, ( −} , . ) ,

= , ,

4. Kita peroleh k=1 dengan = maka iterasi berhenti.

Jadi didapatkan solusi optimal yaitu ∗ = , ∗ = , ∗ = , ∗ = dan =

(76)

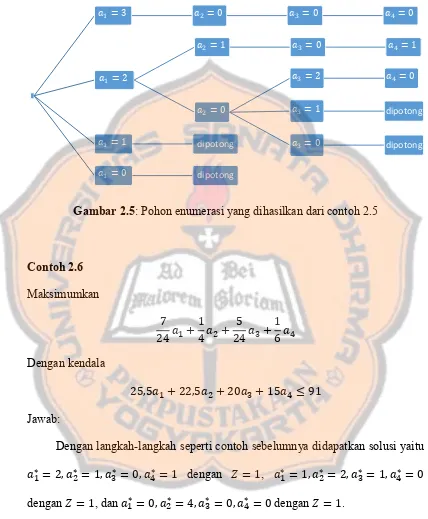
Berikut pohon enumerasi dari solusi-solusi yang sudah didapat diatas.

Contoh 2.6

Maksimumkan

+ + +

Dengan kendala

, + , + +

Jawab:

Dengan langkah-langkah seperti contoh sebelumnya didapatkan solusi yaitu

∗ _{= ,} ∗ _{= ,} ∗ _{= ,} ∗ ₌ _dengan ₌ _, ∗ _{= ,} ∗ _{= ,} ∗ _{= ,} ∗ ₌

dengan = , dan ∗ = , ∗ = , ∗ = , ∗ = dengan = .

= = = =

=

= = =

=

= =

= dipotong

(77)

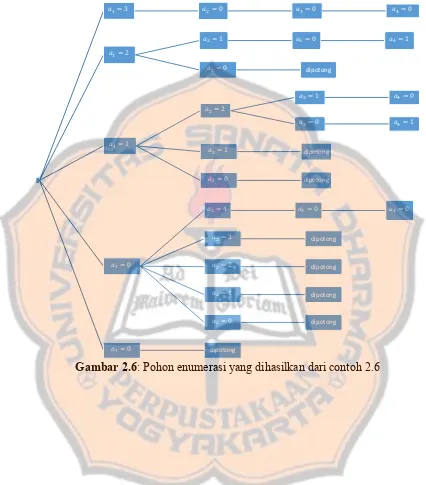
Berikut pohon enumerasi dari solusi-solusi yang sudah didapat diatas.

= = = =

=

= = =

= dipotong

=

= =

= dipotong

=

= = =

= dipotong

(78)

61

BAB III

MASALAH PEMOTONGAN PERSEDIAAN

A. Masalah Pemotongan Persediaan (Cutting Stock Problem)

Dalam suatu industri kertas, mesin kertas (paper machine) memproduksi rol kertas jumbo, dengan lebar maksimum yang sudah ditetapkan yang disebut dengan

deckle. Kemudian rol jumbo melewati beberapa proses produksi dalam memenuhi pesanan. Salah satu proses produksi yang paling penting adalah pemotongan rol kertas jumbo menjadi rol yang lebih kecil atau potongan kertas persegi panjang. Proses pemotongan tersebut harus dapat meminimumkan jumlah rol jumbo yang akan dipotong. Sebelum proses pemotongan berlangsung, hal yang dilakukan adalah membuat pola pemotongan pada rol jumbo. Pada masalah nyata, untuk menemukan pola pemotongan yang optimal biasanya dilakukan secara manual yaitu dengan membuat semua kemungkinan pola pemotongan lalu menentukan jumlah rol yang akan dipotong pada masing-masing pola sampai semua pesanan terpenuhi. Pola pemotongan pada rol jumbo dapat berupa pola pemotongan untuk rol ke rol (satu dimensi) atau rol ke potongan kertas (dua dimensi). Proses pemotongan satu dimensi dan dua dimensi dapat dilihat pada gambar 1.1 dan 1.3. Pada tulisan ini akan dibahas tentang pemotongan rol jumbo menjadi potongan rol kecil dengan ukuran yang bervariasi (pola pemotongan satu dimensi).

Misalkan terdapat kemungkinan pola pemotongan untuk rol jumbo dengan

(79)

kecil dengan lebar (� bilangan bulat tak negatif) sehingga ∑₌ � �. Maka masalah pemotongan ini dapat diselesaikan dalam program linear sebagai berikut. Minimumkan

= ∑

=

(3.1)

Dengan kendala

∑ �

=

(3.2)

dan � adalah banyaknya rol kecil dengan lebar dalam pola pemotongan ke-j,

adalah banyaknya permintaan rol kecil dengan lebar , variabel menunjukkan

banyaknya rol jumbo yang dipotong pada pemotongan ke- .

Berikut gambar pemotongan satu dimensi dari rol jumbo menjadi rol kecil.

Gambar 3.1:Pemotongan rol jumbo menjadi beberapa bagian (rol kecil).

(80)

dengan program QM for Windows yang merupakan perangkat lunak digunakan untuk membantu proses perhitungan secara teknis pengambilan keputusan secara kuantitatif. Program ini menyediakan modul-modul dalam area pengambilan keputusan bisnis seperti assignment, forecasting, integer programming, linear programming, quality control, inventory, dan lain-lain.

Berikut adalah hasil yang didapat menggunakan QM.

Gambar 3.2: Hasil QM pada contoh 1.1

Dari gambar di atas, didapatkan solusi optimal yaitu = , , = , ,

= , , dan selainnya bernilai 0. Itu berarti untuk memenuhi pesanan

diperlukan rol sebanyak 48,5 untuk pola pemotongan pertama, 206,25 rol untuk pola pemotongan kelima, dan 197,5 rol untuk pola pemotongan keenam. Dengan demikian, banyaknya rol jumbo yang digunakan sebanyak 452,25 rol.

(81)

manual (menyusun tabel kemungkinan pemotongan kemudian diselesaikan dengan program linear). Masalah lain yang mungkin muncul dan tidak mudah diselesaikan adalah solusi yang didapatkan belum tentu merupakan bilangan bulat sehingga diperlukan cara tertentu untuk mengubah solusi tersebut menjadi bilangan bulat. Dalam kasus rol kecil yang dipesan dengan jumlah yang tidak banyak, maka pola yang digunakan pada solusi optimal bilangan bulat mungkin berbeda dengan solusi optimal aslinya (dalam pecahan). Oleh karena itu, skripsi ini menggunakan metode penghasil kolom (column generation) yang dapat menyelesaikan masalah pemotongan secara lebih efisien.

B. Metode Penghasil Kolom

Metode penghasil kolom adalah suatu metode untuk menemukan himpunan dari pola pemotongan optimum pada masalah pemotongan persediaan. Dalam metode ini, pada dasarnya, setiap pola merupakan suatu kolom dari masalah program linearnya. Pada masalah nyata, banyaknya pola pemotongan dapat menjadi sangat banyak. Daripada mempertimbangkan banyaknya kemungkinan pola pemotongan, metode penghasil kolom bekerja dengan membangun suatu model bagian dari masalah pemotongan persediaan yang secara sistematis menghasilkan pola baru sehingga solusi optimum dapat dicapai. Pola baru ini ditambahkan ke model bagian dengan program bantuan bilangan bulat.

(82)

Diasumsikan terdapat beberapa pola pemotongan _� yang bukan bagian dari

model bagian pemotongan persediaan. Misalkan komponen dari vektor _�.

Setiap komponen berkorespondensi dengan banyaknya rol ukuran yang digunakan pada pola pemotongan. Misalkan adalah koefisien pada fungsi tujuan yang berhubungan dengan setiap keperluan permintaan pada model bagian pemotongan

persediaan. Maka pola pemotongan _� yang harus ditambahkan ke model bagian

sewaktu-waktu adalah

− ∑

�

=

<

Kondisi ini adalah syarat optimal pada metode simpleks direvisi ketika diaplikasikan ke model pola pemotongan persediaan.

Perhatikan masalah pemotongan persediaan dimana rol jumbo berukuran � dan banyaknya pesanan tiap rol kecil dengan lebar = , , … , . Maka masalah pemotongan persediaan dengan metode penghasil kolom dapat dimodelkan sebagai berikut.

Minimumkan

Dengan kendala = ,

Dimana adalah vektor kolom dengan komponen , , … , dan adalah

vektor baris dengan komponen , , . . . , . Setiap kolom _�=[ , , … , ]� dari

menunjukkan pola pemotongan rol jumbo menjadi rol kecil dengan lebar

= , , … , . Jadi _� adalah kolom dari jika hanya jika , , … ,

(83)

simpleks yang direvisi ditunjukkan adanya kolom tidak dasar dari di langkah 2

dari setiap iterasi, yaitu ketika kolom baru _� (kolom masuk) ditemukan. Setelah

menghitung vektor baris (harus berupa bilangan bulat tak negatif), kita mencari

, , … , bilangan bulat tak negatif sedemikian hingga

, untuk setiap bilangan bulat

∑

Ketika ∑�₌ > , maka pertidaksamaan (3.5) terpenuhi. Pertidaksamaan ini dapat ditulis sebagai fungsi tujuan dengan kendala pertama dan kedua dari formulasi model (3.3) dan (3.4) di atas. Ketika nilai optimal dari program matematika lebih besar dari satu, maka pola pemotongan ditemukan. Ketika nilai optimal kurang dari atau sama dengan satu, maka tidak terdapat pola pemotongan yang dapat meningkatkan nilai tujuan dari masalah pemotongan persediaan. Sehingga model penghasil pola pemotongan dapat dituliskan sebagai berikut. Maksimumkan = ∑₌

Dengan kendala

∑

=

�

, untuk setiap bilangan bulat

(84)

Dalam menyelesaikan masalah pemotongan persediaan dengan metode simpleks direvisi yang menggunakan metode penghasil kolom, perlu diawali dengan solusi layak terdekat: jika nilai awal dari fungsi tujuan dekat dengan nilai optimum, maka banyaknya iterasi simpleks yang diperlukan untuk mencapai optimum sedikit.

Mencari Nilai Awal

Misalkan rol jumbo dengan lebar � dan banyaknya pesanan rol kecil dengan lebar adalah . Diasumsikan lebar rol kecil diurutkan dari terbesar sampai terkecil:

> > >

Akan dibentuk nilai awal dan ∗ dengan iterasi. Dimulai iterasi , diketahui � terdiri − + dari subscript , , . . . , . Untuk setiap subscript di

�, terdapat ′ yang menunjukkan sisa permintaan rol kecil dengan lebar (untuk

nilai awal kita tentukan ′= untuk setiap i). Pada iterasi ke-j, kita definisikan

kolom ke-j dengan = [ , , … , ]� yang akan membentuk .

= {

, jika �

� − ∑

−

=

⁄ , jika �

Solusi awal ∗ akan menggunakan pola ini sampai sisa permintaan ′