Genel Fizik 1- Prof. Dr. Mustafa POLAT Ders Notları

GENEL FİZİK I

DERS NOTLARI

Haz

ı

rlayanlar:

Prof. Dr. Mustafa POLAT

Prof Dr Leyla TATAR YILDIRIM

Prof. Dr. Leyla TATAR YILDIRIM

2012

2012

BÖLÜM-1

Ölçme

Bu bölüm kapsam

ı

nda a

ş

a

ğı

daki ba

ş

l

ı

klar üzerinde durulacakt

ı

r:



Bir fiziksel niceli

ğ

ğ

in ölçülmesi

ç



Birimler, birim sistemleri



Mekanikte temel birimler



Birim dönü

ş

ümleri



Ölçümlerdeki duyarl

ı

l

ı

k

(1-1)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Fizikte nicelikleri ölçmek için birtak

ı

m deneyler yapar ve ölçülen

Ölçme:

miktar belirleme i

ş

lemidir.

Fizikte, nicelikleri ölçmek için birtak

ı

m deneyler yapar ve ölçülen

nicelikler aras

ı

nda bir ba

ğ

kurmaya çal

ışı

r

ı

z. Bu ba

ğ

lar genellikle

matematiksel e

ş

itlikler yoluyla ifade edilir

matematiksel e

ş

itlikler yoluyla ifade edilir.

Buna en iyi örnek Ohm Yasas

ı

’ d

ı

r Bu yasan

ı

n özü bir iletkenin iki

Buna en iyi örnek Ohm Yasas

ı

d

ı

r. Bu yasan

ı

n özü, bir iletkenin iki

ucu aras

ı

na uygulanan potansiyel fark ile iletken üzerinden akan

elektrik ak

ı

m

ı

n

ı

n ölçülmesi esas

ı

na dayan

ı

r.

elektrik ak

ı

m

ı

n

ı

n ölçülmesi esas

ı

na dayan

ı

r.

Uygulanan potansiyel fark (

V

) ile elektrik ak

ı

m

ı

(

I

) aras

ı

ndaki ili

ş

ki

çizgiseldir ve a

ş

a

ğı

daki matematiksel form ile verilir

Constant

V

R

I





_sabit

I

Bu e

ş

itlik “Ohm Yasas

ı

” olarak bilinir

(1-2)

Bu e

ş

itlik

Ohm Yasas

ı

olarak bilinir.

E

ş

itlikteki

R

, iletkenin “direnci” dir.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Birimler: Fiziksel bir büyüklüğü tam olarak tanımlayabilmek için o büyüklüğün nasıl ölçüleceğini bir kurala bağlamak ve bir birim ile ifade etmek gerekir. Böylece büyüklükleri bir standarda bağlamış oluruz.

Temel Büyüklükler: Büyüklüklerin tümü birbirinden bağımsız değildir. Bazı büyüklükler temel büyüklük diğerleri ise bu temel büyüklüklerden Bazı büyüklükler temel büyüklük, diğerleri ise bu temel büyüklüklerden

türetilmiş büyüklüklerdir.

Temel büyüklükler için bir standart saptanır ve diğer büyüklükler temel büyüklükler cinsinden birimlendirilir.

Temel büyüklüklerin belirlenmesi amacı ile, 1875 yılında kurulan ve halen Paris’te bulunan Uluslararası Ağırlık ve Ölçmeler Bürosu (IBWM = International Bureau of Weights and Measurements) 1971 (IBWM International Bureau of Weights and Measurements) 1971 yılında bir toplantı yapmış ve Tablo 1’de verilmiş olan 7 büyüklüğü temel bü üklük l k i ti

büyüklük olarak seçmiştir.

(1-3)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

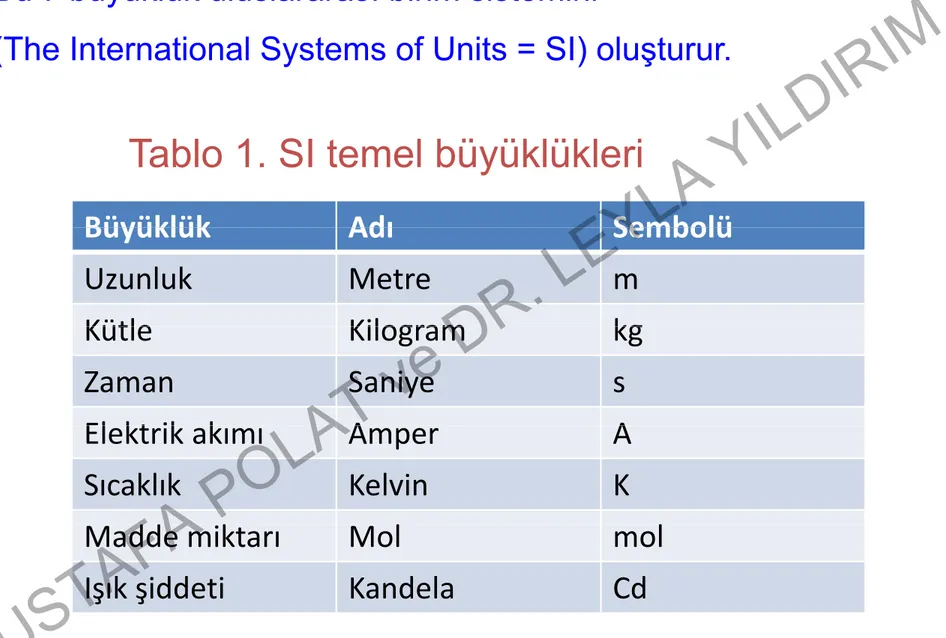
Bu 7 büyüklük uluslararası birim sistemini

(The International Systems of Units = SI) oluşturur.

Büyüklük Adı Sembolü

Tablo 1. SI temel büyüklükleri

Büyüklük Adı Sembolü Uzunluk Metre m Kütle Kilogram kg Kütle Kilogram kg Zaman Saniye s El kt ik k A A Elektrik akımı Amper A Sıcaklık Kelvin K dd k l l

Madde miktarı Mol mol

Işık şiddeti Kandela Cd

Mekanikte sadece üç tane niceli

ğ

e ihtiyaç duyulur.

Bunlar

uzunluk, zaman ve kütledir

.

(1-4)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Metre:

Başlangıçta metre, kuzey kutbu ile ekvator arasındaki

mesafenin on-milyonda biri olarak tanımlanmıştır (1792) mesafenin on milyonda biri olarak tanımlanmıştır (1792).

;

(

1 m



AB

₇

; (

R



6370 km)

1 m

1

0

R

Dünya



6370 k

m)



P tik d l d ötü ü d h t Pratik nedenlerden ötürü daha sonra metre,

platin-iridyumdan yapılmış standart bir ölçüm çubuğu üzerindeki iki çizgi arasındaki mesafe olarak üzerindeki iki çizgi arasındaki mesafe olarak tanımlanmıştır.

1983’ ten beri metre, 1/299792458 s’ lik zaman aralığında ışığın boşlukta aldığı yol olarak tanımlanmıştır. Bu yeni tanımın sebebi, ışık hızının çok hassas bir şekilde ölçülebiliyor olmasıdır

(1-5)

hassas bir şekilde ölçülebiliyor olmasıdır.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Saniye:

Başlangıçta saniye, Dünya’nın kendi ekseni etrafındaki tam bir dönüş süresinin (24x60x60)’ ta biri olarak aşağıdaki gibi tanımlanmıştır.

1

1 saniye

24 60 60



 

B t d ki bl kild Bu tanımdaki problem, şekilde gösterildiği gibi, bir günlük sürenin sabit olmayışıdır

sürenin sabit olmayışıdır.

Bu nedenle 1967’ den beri saniye, Cessium-133 elementinin yaydığı b lli bi d l b d ki ğ 9192631770 tit i i i i ü

(1-6) belli bir dalga-boyundaki ışığın 9192631770 titreşimi için geçen süre

olarak tanımlanmaktadır.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Kilogram:

SI birim sisteminde kütle standardı olan bir platin-iridyum silindir ap y şş ğağıda verilmiştir.

B ili di i kü l i 1 kil l k k b l dil i P i ’ ki Bu silindirin kütlesi 1 kilogram olarak kabul edilmiş ve Paris’ teki Uluslararası Kütle Ölçüm Bürosu’ nda tutulmaktadır. Hassas kopyaları

da başka ülkelere gönderilmiştir

(1-7)

da başka ülkelere gönderilmiştir.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Birimdönü

ş

türme:

Ço

ğ

u zaman fiziksel niceliklerin birimlerini de

ğ

i

ş

tirmeye ihtiyaç duyar

ı

z Bunu

Birim dönü

ş

türme:

Ço

ğ

u zaman fiziksel niceliklerin birimlerini de

ğ

i

ş

tirmeye ihtiyaç duyar

ı

z. Bunu

yapmak için, iki birim aras

ı

ndaki dönü

ş

üm faktörünü bilmemiz gerekir.

karayolu hız limiti olan 65 mil/saat' i m/s cinsinden ifade ediniz.

Örnek: y 1 mil = 1609 m ve 1 saat = 3600 s Bu durumda, mil 1609 m m 65 65x 29 saat 3600 s s    _{ }    saat _ 3600 s _ s (1-8)

bulunur. _{Bu hız limitini km/sa cinsinden bulunuz.}

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Ölçümlerdeki Duyarl

ı

l

ı

k :

Belli bir nicelik, örneğin bir cismin uzunluğu , L değişik duyarlılıklarda belirlenebilir. Duyarlılık ölçüm yöntemine ve ölçüm aletine bağlıdır.

En küçük ölçeği 1 mm olan bir cetvel ile ölçüm yapıyorsak uzunluL ğunu

= 1.234

En küçük ölçeği 1 mm olan bir cetvel ile ölçüm yapıyorsak uzunluğunu, m şeklinde vermek gerekir.

Yani nl ğ dört anlamlı sa ı ile erilmelid ri

L

L

L

Yani L uzunluğu dört anlamlı sayı ile verilmelid r i .

Cetvel üzerindeki en küçük ölçek 1 mm oldu

ğ

undan

Cetvel üzerindeki en küçük ölçek 1 mm oldu

ğ

undan,

' yi

L

= 1.2

34

6

m biçiminde vermek anlams

ı

z o

lacakt

ı

r

.

L

= 1.234

Diğer taraftan, duyarlılığı 0.1 mm olan verniyeli kumpas kullanıyorsak,

m şeklinde verilebilir ve bu durumda beş anlamlı sayı ile ifade edi r

6 li .

L

Hesaplanan nicelikteki anlamlı sayı, hesaplamalarda kullanılan niceliklerin anlamlı

ş ş y

(1-9) sayılarından fazla olamaz.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Sabit h

ı

z

ı

yla hareket eden bir araç

= 123 m' lik yolu = 7 89 s' de al

ı

yor

Örnek:

v

d

= 123 m' lik yolu = 7.89 s' de al

t

ı

yor.

Arac

ı

n h

ı

z

ı

n

ı

bulunuz.

d

t

123 m

Arac

ı

n h

ı

z

ı

: = =

=

15.5

8

m/

s

7 89

93536

d

v

t

i if d

k i i d k

k

k ll

k

l

l d ildi

7.89 s

t

' yi ifade etmek için dokuz rakam kullanmak anlaml

ı

de

ğ

ildir.

Çünkü, ' nin hesaplanmas

ı

nda kullan

ı

lan ve

nicelikleri

v

v

d

t

sadece üç anlaml

ı

say

ı

ile verilmi

ş

tir.

Dolay

ı

s

ı

yla ' de üç anlaml

v

ı

say

ı

içerecek

ş

ekilde verilmelidir:

=

15.6

m/

s.

v

(1-10)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Birimlerin alt ve üst katları: Bazı büyüklükler aynı birim ile ifade edildiği halde sayısal değerleri birbirinden çok farklı olabilir. Örneğin, bir atomun yarıçapı ile Dü ’ t l k if d dili k l d ğ l i k f kl d

Faktör İsim Sembol Günlük dildeki adı

Dünya’ nın yarıçapı metre olarak ifade edilir, ancak sayısal değerleri çok farklıdır. Bu nedenle SI birimlerin alt ve üst katlarını gösteren işaretler kullanılır.

Faktör İsim Sembol Günlük dildeki adı

1024 _{Yotta Y 1 septilyon} 1021 _{Zetta Z 1 sekstilyon} 1018 _{Exa E 1 kentilyon} 1018 _{Exa E 1 kentilyon} 1015 _{Peta P 1 katrilyon} 1012 _{Tera T 1 trilyon} 109 _{Giga G 1 milyar} 109 _{Giga G 1 milyar} 106 _{Mega M 1 milyon} 103 _{Kilo k bin} 102 _{H t h ü} 102 _{Hecto h yüz} 101 _{Deka da on}

10-1 _{Deci d onda bir}

10 2 _{C ti ü d bi}

10-2 _{Centi c yüzde bir}

10-3 _{Milli m binde bir}

10-6 _{Micro m milyonda bir}

10 9 _{N il d bi}

10-9 _{Nano n milyarda bir}

10-12 _{Pico p trilyonda bir}

10-15 _{Femto f katrilyonda bir}

10 18 _{Att k til d bi}

10-18 _{Atto a kentilyonda bir}

10-21 _{Zepto z sekstilyonda bir}

10-24 _{Yocto y septilyonda bir} (1-11)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Baz

ı

Ölçme Aletleri

Baz

ı

Ölçme Aletleri

(1-12)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Cetvel

Cetvel

(1-13)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Verniyeli Kumpas

y

p

(1-14)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Mikrometre (1-15)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

BÖLÜM-2

V ktö l

Vektörler

Fizikte sadece büyüklükleri ile tanımlanan niceliklere “skaler”

Büyüklük yanında ayrıca yön bilgisi içeren veya gerektiren diğer fiziksel y

nicelikler diyoruz. Sıcaklık, kütle, enerji bunlardan bazılarıdır.

Büyüklük yanında ayrıca yön bilgisi içeren veya gerektiren diğer fiziksel niceliklere ise “vektörel” nicelikler diyoruz. Yer-değiştirme, hız, ivme, kuvvet bunlardan bazılarıdır.

Bu bölüm kapsamında, aşağıdaki konulara değineceğiz:

Vektörleri geometrik toplama ve çıkarma işlemi

Vektörleri bileşenlerine ayırma

Birim vektör notasyonu

Bileşenler yardımıyla toplama ve çıkarma

Bir vektörün bir skaler ile çarpılması

İki vektörün skaler (dot veya nokta) çarpımı

(2-1)

İki vektörün vektörel (cross) çarpımı

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Bir vektörün üç eleman

ı

vard

ı

r.

Uygulama Noktası (başlangıç noktası): Vektörel büyüklüğün uygulandığı noktaya uygulama ya da başlangıç noktası denir.

k d ki k l k k d

Yukarıdaki vektörün uygulama noktası O noktasıdır.

Vektörün say

ı

sal de

ğ

erine o vektörün büyüklü

ğ

ü denir.

Büyüklü

ğ

ü:

y

ğ

y

ğ

Ş

ekilde verilen vektörünün büy

y

üklü

ğ

ğ

ü '

dir.

a



a



AB

Vektörel büyüklüğün yönü, doğru parçasının ucuna konulan

okun yönündedir. Şekildeki vekötürnün yönü O' dan ' ya yöneliktir Yönü:

a A

okun yönündedir. Şekildeki vekötürnün yönü O dan ya yöneliktir veya doğu yönündedir. a A (2-2)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

A noktasından B noktasına hareket eden bir cismin yer-değiştirme

A noktasından B noktasına hareket eden bir cismin yer değiştirme vektörü A noktasından B noktasına çizilen bir okla gösterilir.

Ok n nl ğ er değiştirmenin bü üklüğü ile orantılıdır Okun uzunluğu yer-değiştirmenin büyüklüğü ile orantılıdır. Okun yönü ise yer-değiştirmenin yönü ile ilgilidir.

Şekilde A dan B ye, A' den B' ne ve A'' nden B'' ne çizilen vektörlerin büyüklükleri ve yönleri aynıdır.

Vektörler, büyüklükleri ve doğrultuları değiştirilmeden istenildiği gibi kaydırılabilir.

Kitaplarda vektörler sembolik olarak iki şekilde gösterilir:

a



a

(niceliğin üzerine bir ok çizilir) ( i lik k l )

a

(nicelik koyu yazılır)

(2-3)

a



a

Vektörün büyüklüğü de veya biçiminde sembolize edilir.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Vektör i

ş

lemleri

• Vektörlerin E

ş

itli

ğ

i

• Vektörlerin E

ş

itli

ğ

i

• Bir Vektörün Negatifi

• Vektörün Ta

ş

ı

nmas

ı

• Vektörlerin Toplanmas

ı

• Vektörlerin Ç

Vektörlerin Ç

ı

ı

kar

kar

ı

ı

lmas

lmas

ı

ı

• Vektörün Bile

ş

enlerine Ayr

ı

lmas

ı

• Vektörün Büyüklü

ğ

ünün Bulunmas

ı

V ktö ü bi k

l

t

ğ

b l

• Vektörün bir eksenle yapt

ı

ğ

ı

aç

ı

n

ı

n bulunmas

ı

• Vektörlerin bile

ş

ş

enleri cinsinden toplanmas

p

ı

devam  (2-4)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektör i

ş

lemleri

•

Vektörlerin Çarp

ı

lmas

ı

:

1. Bir Vektörün Bir Skaler ile Çarp

ı

lmas

ı

2.

İ

ki Vektörün Skaler (dot veya nokta çarp

ı

m) Çarp

ı

lmas

ı

3

İ

ki Vektörün Vektörel Çarp

ı

lmas

ı

3.

İ

ki Vektörün Vektörel Çarp

ı

lmas

ı

•

Vektörlerin Skalere Bölünmesi

VEKTÖR VEKTÖRE BÖLÜNMEZ !!!

•

VEKTÖR VEKTÖRE BÖLÜNMEZ !!!

(2-5)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektörlerde Geometrik Toplama :

s a b

 

 



ktö ü ü b l

kt

ktö ü ü

b



vektörünün ba

ş

lang

ı

ç noktas

ı



vektörünün

ucuna gelecek

ş

ekilde

vektörü

kayd

ı

r

ı

l

ı

r.

b

a

b



vektörünün ba

ş

lang

ı

ç noktas

ı

ndan

vektörünün

k

i il

k

k

d

a



b





İ

uç noktas

ı

na çizilen vektör vektörüdür.

s



2 2 2

İ

ki vektör aras

ı

ndaki aç

ı

olmak üzere, vektörünün büyüklü

ğ

ü,

= + +2 cos

a b

s

s

ab







(2-6)

ile verilir (kosinüs teoremi).

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Vektörlerde Geometrik Toplama :

A B A R=A+B=? A R=A+B R=A+B=? B A C C D R=A+B+C+D A _B C D R=A+B+C+D=? B R A+B+C+D A (2-7)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektörel toplama i

ş

leminin

"değişme öze

Vektörel top

lliği"

lama i

ş

leminin

vard

ı

r:

a b b a



  







vektörünün negatifi (- ),

b



b



vektörü ile ayn

ı

büyüklükte

fakat ters yöndedir.

b



fakat ters yöndedir.

(2-8)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

o

Kuzeye do

ğ

ru yönelmi

ş

20 km' lik bir vektör ile 60

Örnek :

y

ğ

y

ş

kuzey-bat

ı

ya do

ğ

ru yönelmi

ş

35 km' lik vektörün bile

ş

kesini bulunuz.

o

İ

ki vektör aras

ı

ndaki aç

ı

60 ' dir.

Kosinüs teoremine göre bile

ş

ke vektörün büyüklü

ğ

ü,

2 2 2 2

+ +2 cos

s



a

b

ab



   

2 2

  

 

_o

20 + 35 +2 20 35 cos 60

= 48 2 km



= 48.2 km

i



i



b

35

sin

sin

35

sin

sin

sin(120 ) 0.629

48.2

b

b

s

s



_



_

_

_

_

_



_

(2-9) o





38.9

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektörlerde Geometrik Ç

ı

karma:

d



 

a b





 

biçiminde yazılabilir

d



    

a b a







 

b



biçiminde yazılabilir.

d



a b a

 

b

vektörü bulunur ve vektörü ile toplanır.

vektöründen

b





b



a



p

N

V k ö l i bil

l i

l

l

k

k

k

Not:

Vektörleri bile

ş

enleri vas

ı

tas

ı

yla toplamak veya ç

ı

karmak

mümkündür. Uygulamada bu yöntem çok daha kullan

ı

ş

l

ı

ve kolayd

ı

r.

(2-10)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektörlerde Geometrik Ç

ı

karma:

A -B B A R=A-B=? R=A-B A B B B A _B C R=A-B+C=? _A R=A-B+C B A _B R A B C ? _A C -B (2-11)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

i

k

bi k

d ki bil

i

k

k

Vektörün bile

ş

enleri ve bir eksenle yapt

ı

ğ

ı

aç

ı

:

Bir vektörün bir eksen yönündeki bile

ş

eni, vektörün o eksen

üzerindeki izdü

ş

ümüdür. Örne

ğ

ğ

in ,

a a

_x



vektörünün

x -

ekseni

üzerindeki izdü

ş

ümüdür. Vektörün bile

ş

eni, ba

ş

lang

ı

ç ve uç

noktalar

ı

ndan

ekseni

x

x

a

x

ne çizilen dikmeler aras

ı

mesafedir

noktalar

ı

ndan ekseni

x -

ne çizilen dikmeler aras

ı

mesafedir.

vektörünün - ve -bile

ş

enleri

a



x

y

eşitlikleri ile verilir.

cos

ve

sin .

x y

a



a



a



a



eşitlikleri ile verilir.

ve bileşenleri biliniyorsa, vektörün büyüklüğü

x y

a a

ve sırasıyla ve ekseni ile yaptx y ığı açı bulunabilir.

dik üçgeninden: ABC 2 2 _ta di n t k üçgeninden: an ;

ve

y _x x y x y ABC a _a a  a  a     (2-12) olarak bulunur. y y x y a a

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Herhangi bir doğrultuda büyüklüğü "1" olan vektöre "birim vektör" denir

Birim vektörler :

Herhangi bir doğrultuda, büyüklüğü 1 olan vektöre birim vektör denir.

Birimsizdir ve sadece sadece yön göstermek amacıyla kullanılır.

ve

eksenleri yönündeki birim vektörler

x y

, ve eksenleri yönündeki birim vektörler,

z

-s

ı

ras

ı

yla, , ve ile gösterilirler

ˆ ˆ

i j

k

ˆ

.

x y

z

Tüm vektörler birim vektörler cinsinden yazılabilir. Şekildeki vektörler: a  a_xˆi  a _yˆj ; b  b_xiˆ  b_yˆj



ve yönündeki birim vektörler: ; ile verilir ˆ a ˆ b a b a = b =     ; ile verilir. Bu durumda ve vektörleri,a b a = b = a b   ,

; biçiminde ˆ de yazılabili

ˆ r. a aa b bb     (2-13)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Bile

ş

enleri Yard

ı

m

ı

yla Vektörlerin Toplanmas

ı

:

ˆ

_i

ˆ

_j

a a



i



a

j



?

ˆ

_i

ˆ

_j

x y

a a

a

r

a b

b

b

b





 

 



















i

j

x y

b



b



b

_





ˆ

_i





ˆ

_j

x x y y

r





a



b



a



b

Bile

ş

enleri Yard

ı

m

ı

yla Vektörlerin Ç

ı

kar

ı

lmas

ı

:



_{x x}





_{y y}



j

Bile

ş

enleri Yard

ı

m

ı

yla Vektörlerin Ç

ı

kar

ı

lmas

ı

:

ˆ

_i

ˆ

_j

x y

a a





a







_

_

j

?

ˆ

ˆ

i

j

x y x y

d

a b

b b



b

 

 

















ˆ

ˆ



x y







ˆ

_i





ˆ

_j

x x y y

d





a



b



a



b

(2-14)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Bir cisim üç ard

ı

ş

ı

k yer-de

ğ

i

ş

tirme yap

ı

yor. Bunlar s

ı

ras

ı

yla,

Örnek :

1

15i 30j 12k cm,

ˆ

ˆ

ˆ

2

23i

ˆ

ˆ

j 5k cm ve

ˆ

3

13i 15j cm

ˆ

ˆ

ld

ğ

ö

t l

d

ğ

i ti

ktö ü ü bil

l i i

14

d =



+

+

d =







d =





+

oldu

ğ

una göre, toplam yer-de

ğ

i

ş

tirme vektörünün bile

ş

enlerini ve

büyüklü

ğ

ünü bulunuz.



 

 



1 2 3

15 23 13 i

ˆ

30 14 15 j 12 5 k

ˆ

ˆ

R d









d





d









+



+

+



ˆ

ˆ

ˆ

= 25i 31j 7k cm

+

+

x

25 cm ; 31

y

cm

; 7

z

cm

R

_x



;

R

_y



;

R

_z



     

2 2 2 2 2 2 x

+

y

+

z

25

31

7

40.4 cm

R



R

R

R









(2-15)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Örnek: A şehri B şehrinin 46 km batı ve 35 km güneyinde yer almaktadır Bu iki şehir arasındaki en kısa mesafenin büyüklüğünü almaktadır. Bu iki şehir arasındaki en kısa mesafenin büyüklüğünü ve yönünü bulunuz.

ˆ

ˆ



46 km

ˆ

ˆ

46 –

35

R

 

i

j

B B 2 2

(46 km)

(35 km)

R





35



R

= 57.8 km

km

R = ? R = ?

35 km



_{35 km}

AA

tan

46 km









= 37.3

0 (2-16)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Örnek: Bir erkek çocuğu bir kıza, şekildeki gibi, 240 N’ luk bir kuvvet uygulamaktadır. Kızın kolu yatayla 28 açı yaptığına göre bu kuvvetin bileşenlerini bulunuz.

F

F

= 240 N

= 240 N

280

F

F

_FF y y

F

F

_yy F F_xx

F_xx = -|(240 N) cos 28|( ) 0| = - 240*0.88=| -212 N Birim vektörler cinsinden F_y = +|(240 N) sin 280| =240*0.47= +113 N F   212



N i

 

ˆ 113 N j



ˆ  y |( ) | (2-17)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Örnek: Bir kaplumbağa aşağıda verilen ardışık üç yerdeğiştirme ve bu yer dey ğğ şiştirmelerin yatayla yapty y y p ığğı aççı verilmişştir. Kaplumbap ğğanın toplam yer değiştirme vektörü R’ nin büyüklüğünü ve yönünü bulunuz. C 0 5 B = 2 1 m C = 0.5 m

R

A = 5 m, 00

A 5

B = 2.1 m 200



B = 2.1 m, 200 C = 0 5 m 900

A = 5 m

C 0.5 m, 90 cos 200_{= 0 94 sin 20}0_{= 0 34}

Vektör

f

X-bile

ş

eni (

i

)

Y-bile

ş

eni (

j

)

cos 200_{= 0.94 sin 20}0_{= 0.34}

ş

( )

ş

(

j

)

A=5 m

0

0

_{+ 5 m}

₀

B 2 1

20

0

_{(2 1 )}

₂₀

0

_{(2 1 ) i 20}

0

B=2.1m 20

0

_{+(2.1 m) cos 20}

0

_{+(2.1 m) sin 20}

0

C=0.5 m 90

0

₀

_{+ 0.5 m}

R

_x

= A

_x

+B

_x

+C

_x

R

_y

= A

_y

+B

_y

+C

_y (2-18)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Örnek devam:

Verilen üç vektörün toplam

ç

p

ı

n

ı

bulunuz.

A = 5 m,0

0

_{; B = 2.1 m, 20}

0

_{; C = 0.5 m, 90}

0

_.

x-bile

ş

eni (

i

)

y-bile

ş

eni (

j

)

A

+ 5 00 m

A

0

A

_x

= + 5.00 m

A

_y

= 0

B

_xx

= +1.97 m

9

B

_yy

= +0.718 m

0

8

C

_x

= 0

C

_y

= + 0.50 m

A A = 5.00 = 5.00 i i + 0 + 0 jj B B = 1.97 = 1.97 ii + 0.718 + 0.718 jj C C 00 ii + 0 50+ 0 50 jj C C = 0 = 0 i i + 0.50+ 0.50 jj R R 6 976 97 ii + 1 22+ 1 22 jj R R == 6.97 6.97 ii + 1.22 + 1.22 jj (2-19)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Bi V k ö ü Bi Sk l l Ç

Bir Vektörün Bir Skalerle Çarpımı

:

bir skaler nicelik ve ' da bir vektör olmak üzere,

bunlar

ı

n çarp

ı

m

ı

ile verilen yeni bir vektördür

s

a

b



sa





_

bunlar

ı

n çarp

ı

m

ı

b



sa

ile verilen yeni bir vektördür.

B i k ö ü bü üklüğü b | | il ili

Bu yeni vektörün büyüklüğü ile verilir. 0 ise, vektörü ile aynı yöndedir.

= | |

s b a

b s a

  

0 ise, vektörü ile ters yöndedi .r

s  b a

:

F

ma

Örnek







(2-20)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

İ

ki Vektörün Skaler Çarpımı

:

İ

ki

ktö ü

k l

"d t

kt "

l

k d bili i

Ç p

İ

ki vektörün skaler ça

rp

ı

m

ı

, çarp

"dot vey

a no a

kt "

ı

m olarak da bilin

ir.

ve vektörlerinin skaler çarpımı = cos ifadesi ile verilir

a ve vektörlerinin skaler çarpb ımı a b   abcos



ifadesi ile verilir.

a b a b ab



Örnek: İş

W

 

F x

 

(2-21)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Bile

ş

enleri Cinsinden Skaler Çarp

ı

m :



 



Bile

ş

enleri Cinsinden Skaler Çarp

ı

m :



ˆ

ˆ

ˆ

 

ˆ

ˆ

ˆ



=

_x

i

_y

j

_z

k

_x

i

_y

j

_z

k

a b







a



a



a



b



b



b

ˆ ˆ

_i

_{ }

_{j k}

ˆ

_oldu

_ğ

_undan,

ˆ ˆ ˆ ˆ ˆ ˆ

i i

     

j j k k 1





i i

j j k k 1

ˆ ˆ ˆ ˆ

_{i j j i 0}

bulunur

a b a b

a b

a b





   



 













ˆ ˆ

_{i k k i 0}

ˆ ˆ

ˆ ˆ

ˆ

bulunur.

ˆ

j k k j

x x y y z z

a b a b

 



a b



a b



   

_







j k k j 0

   



_

(2-22)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

ˆ

ˆ ˆ

ˆ

ˆ ˆ

2i 3j k ve

4i 2j k vektörleri aras

ı

ndaki

A =

+ +

B =



+



Örnek :



j



j

aç

ı

y

ı

bulunuz.

Bu soruda, iki vektör arasındaki açıyı bulmak için vektörlerin iki farklı yolla skaler çarpım işleminden yararlanacağız. İki sonucu birleştirerek açıya geçeceğiz

birleştirerek açıya geçeceğiz.

2 2 2 2 2 2

cos = (2)

(3)

(1)

( 4)

(2)

( 1) cos

= 14

21 cos

A B

AB

θ

θ

θ

I. Yol :

 

 

















= 14



21 cos



θ

(2)( 4) (3)(2) (1)( 1)

3

A B A B

A B

A B

II Y l

A B A B

 

_{x x}



A B

_{y y}



A B

_{z z}

(2)( 4) (3)(2) (1)( 1)





3

II. Yol :

 







 



  

o

3

3

cos =

0.175

= 100

14 21

294

A B

θ

θ

AB



 

 

 





 

(2-23)

14 21

294

AB

_

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

ve vektörlerinin büyüklükleri ayn

A

B

ı

ve 5 birimdir.

Örnek :





ˆ

6 oldu

ğ

una göre, bu iki vektör aras

ı

ndaki aç

ı

y

ı

bulunuz.

A+ B = i





2 2

 

_{2 2}

2 2 2

Kosinüs teoremine göre: +

2

cos

'

d

ı

r.

6

5

5

2 5 5 cos

A B

A + B +

A B

+ +







  

  



6



5

+ +

5

2 5 5 cos

  



2 2 2

Buna göre,

(6 0)



(5)



(5)

14

_o

(6.0)

(5)

(5)

14

cos

0.28

106.3 bulunur.

2(5)(5)

50





 

 







ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

6i 8j ;

8i 3j ve

26i 19j vektörleri veriliyor.

A

 

B

 

+

C



+

Örnek :







0 e

ş

itli

ğ

ini sa

ğ

layan

ve

say

ı

lar

ı

n

ı

hesaplay

ı

n

ı

z.

aA+bB+C =







a

b

ˆ

ˆ

(6

8

26)i ( 8

3

19)j 0

A+bB+C







(6

8

b+

26)i ( 8

+



3

b



19)j 0

aA+bB+C



a



b+

+



a



b





6

8

26

5

7 b l

a

b

b



 

_



(2-24)

5 ve

7 bulunur.

8

a

3

b

19

a

b











 

_{  }

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Vektörel Çarpma:

ve vektörleri aras

ı

ndaki vektörel çarpma i

ş

lemi,

a

b

c a b

 

Vektörel Çarpma:







 

ile verilen yeni bir vektör olu

ş

turur.

vektörünün

büyüklü

ğ

ü

ile verilir v

si

n

e ile vektörlerinin olu

ş

tur u

d u

ğ

c

c a



b



a

b







ş

ğ



sa

ğ

-el-ku

düzleme diktir. Yönü "

ral

ı

" ile belirle

nir:

Vektörel çarp

ı

m,

"cross"

çarp

ı

m olarak da bi

linir.

.

ve

vektörlerinin ba

ş

lang

ı

ç noktalar

ı

n

ı

birle

ş

tiriniz.

i a



b



Sa

ğ

el kural

ı

:

. ve vektörlerinin ba

ş

lang

ı

ç noktalar

ı

n

ı

birle

ş

tiriniz.

. vektörünü parmak uçlar

ı

n

ı

z onun yönünü gösterecek

kild

ğ

i i

t

i a

b

ii a



ş

ekilde sa

ğ

avuç içine yat

ı

r

ı

n

ı

z.

. vektörünü küçük aç

ı

yönünde '

iii a



b



nin üzerine süpürünüz.

(2-25)

. Ba

ş

parma

ğ

ı

n

ı

z vektörünün yönünü verir.

iv

c



DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Sa

ğ

el kural

ı

:

(2-26)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

x

1

i

Vektörel çarp

ı

m

ı

n özellikleri: c a b

b











1.

sin

2. ve birbirine paralel veya antiparalel ise

0'd

ı

r.

c ab

a

b

c











p

y

p

3.

vektörü

ve 'nin

bulundu

ğ

u düzleme diktir.

c

a

c

a

b

 



















ğ

4.

5.

c

b

c



 







(

b

x ) vektörel çarp

a

ı

mda de

ğ

i

ş

me özelli

ğ

i yoktur.







(2-27)

5.

c

( x ) vektörel çarp

b

a

ı

mda de

ğ

i

ş

me özelli

ğ

i yoktur.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Bile

ş

enleri Cinsinden Vektörel Çarpma :



ˆ

_i

ˆ

_j

_k

ˆ

 

ˆ

_i

ˆ

_j

_k

ˆ



x y z x y z

a b



 





a



a



a

 



b



b



b



ˆ ˆ_{i i} ˆ ˆ_{j j k k}ˆ ˆ ₀ ˆ ˆ_{i j k j i}ˆ ˆ ˆ _kˆ      





i j k ; j i k ˆ ˆ ˆ ˆ ˆ ˆ k i j ; i k j

oldu

ğ

undan

         







ˆ ˆ_{j k } ˆ ˆ ˆ_{i ; k j  }ˆ_i



_





ˆ

_i





ˆ

_j





ˆk

y z z y z x x z x y y x

a b



 



a b



a b



a b



a b



a b



a b

i j k

, aşağıdaki determinant yolu ile de belirlenebilir.

a b Not :     

 

i j k ; a_x a_y a_z b_x b_y b_z a b   Not :a b    b a  (2-28) b_x b_y b_z

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ

2i 3j k, 4i 2j k ve 5i 2j vektörleri verilsin.

A = + + B =



+



C 



Örnek :   

) ? , ) ( + ) olduğunu gösteriniz.

a A B =   b C  A B   C A+C B     ˆ ˆ ˆ i j k ˆ ˆ ˆ ) 2 3 1 = 5i 2j +16k a  A B     4 2 1   ˆ ˆ ˆ i j k ˆ ) ( ) 5 2 0 = 21k b) C (A+ B )  5 2 0 21k 2 5 0 ˆ ˆ ˆ ˆ ˆ ˆ b C  A+ B  i j k i j k ˆ ˆ ˆ ˆ ˆ ˆ 5 2 0 = 2i 5j +19k ve 5 2 0 = 2i + 5j + 2k C A      C B    2 3 1 4 2 1 (2-29)



ˆ ˆ ˆ

 

ˆ ˆ ˆ



ˆ = 2i 5j +19k 2i + 5j + 2k 21k ( + ) C A C B          C A B 

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

(2-30)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

(2-31)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

(2-32)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

 0 (2-33)  cos = 0

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

BÖLÜM-3

Bir Do

ğ

ru Boyunca Hareket

B bölü d

i i l i bi d

ğ

b

h

k ti i i

l

ğ

i

Bu bölümde, cisimlerin bir do

ğ

ru boyunca hareketini inceleyece

ğ

iz.

A

ş

a

ğ

ı

daki fiziksel nicelikleri ayr

ı

nt

ı

l

ı

bir

ş

ekilde tan

ı

mlayaca

ğ

ı

z.



Konum ve Yer-de

ğ

i

ş

tirme



Ortalama H

ı

z



Ortalama Sürat



Anl

ı

k H

ı

z



O

A

İ

Sabit ivmeli hareket için herhangi bir andaki h

ı

z

ı

ve konumu



Ortalama ve Anl

ı

k

İ

vme

Sabit ivmeli hareket için, herhangi bir andaki h

ı

z

ı

ve konumu

veren ba

ğ

ı

nt

ı

lar

ı

türetece

ğ

iz.

Ayrıca, yer yüzeyine yakın noktalarda yerçekimi etkisi altında cisimlerin hareketini inceleyeceğiz.

(3-1) Son olarak da, ivmenin sabit olmadığı durumlarda, cismin hareketini eğri

alt

DR.

ındaki alanın hesaplanması yöntemiyle inceleyeceğiz.

MUSTAFA

POLAT

ve

DR.

LEYLA

Ki tik i i l i h k ti i i l k iği bi lt d l d

Kinematik, cisimlerin hareketini inceleyen mekaniğin bir alt dalıdır. Bir cismin konumu zamanla değişiyorsa o cisim hareketlidir deriz.

Hareketli cisimlerin noktasal parçacıklardan oluştuğunu ve hepsinin de ayny ı şşekilde hareket ettiğğini kabul edeceğğiz.

Bu bölümde, harekete neyin sebep oldu

ğ

uyla ilgilenmeyece

ğ

iz.

x-ekseni boyunca hareket eden bir cisim düşünelim. Herhangi bir t anında, orijine göre cismin konumu x(t) ile tanımlanır. x-ekseninin hangi tarafında bulunduğuna göre, cismin koordinatı negatif veya pozitif olabilir.

KONUM: Bir cismin yerinin bir referansa göre belirlenmesidir.

Bir cismin “konum vektörü”, bulunduğu koordinat sisteminin orijininden cismin bulunduğu noktaya çizilen

ktö dü (3-2) vektördür.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Not:

Yer-de

ğ

i

ş

tirme ile gidilen toplam yol ayn

ı

ş

ey de

ğ

ildir !!

B

A

(3-3)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

B _{Yol=100 m}

50 m

Yer değiştirme

A

Ö

Örnek: x₁  5 m konumundan pozitif yönde x₂  200 m konumuna

giden ve oradan tekrar başlangıçtaki konumuna dönen bir cisim dü ü li

düşünelim.

Cisim toplam olarak 390 m yol aldığı halde, yer-değiştirmesi Δx  0’ dır. y ğ ş (3-4)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Yer-de

ğ

i

ş

tirme Vektörü:

Bir cisim x₁ konumundan x₂ konumuna

hareket etmişse, konumundaki değişim yer-değiştirme ile tanımlanır. hareket etmişse, konumundaki değişim yer değiştirme ile tanımlanır.

x

x

x



_





_





_



yer değiştirme _{son konum ilk kon}

1 um 2

x

x

x





Ö ği ilk k 5 k 12 l bi i i SI sisteminde birimi (m)

Örneğin, ilk konumu x₁  5 m ve son konumu x₂  12 m olan bir cismin yer-değiştirmesi Δx  12–5  7 m olacaktır. Δx’ in pozitif olması, yer-değğ şiştirmenin +x yönünde olduy ğğunu gösterir.g

Cisim x₁  5 m konumundan x₂  1 m konumuna hareket etseydi, yer-d ği ti Δ 1 5 4 l d Δ ’ i tif l

değiştirme Δx  1–5  – 4 m olurdu. Δx’ in negatif olması, yer-değiştirmenin –x yönünde olduğunu gösterir.

Yer-değiştirme, hem büyüklüğü hem de yönü olan vektörel bir niceliktir. T k b tt ki h k ti i l diği i b bölü d d ği ti ö ü

(3-5) Tek boyuttaki hareketi incelediğimiz bu bölümde, yer-değiştirme yönü

olarak Δx’ in işaretini kullanacağız.

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

Konum-zaman Grafi

ğ

i ve Ortalama H

ı

z:

Bir cismin hareketini tanımlamanın bir yolu, cismin konumunu zamana bağğlı olarak çizmektir.ç

Herhangi bir t₁ anı ile t₂anı arasında, canlının x₁ konumundan x₂ konumuna ne k d h l ittiği k d “ t l h ” bi bi fiki kti

Konum-zaman grafiğinde (t₁, x₁) noktasından (t₂, x₂) noktasına çizilen doğrunun kadar hızlı gittiği konusunda “ortalama hız” bize bir fikir verecektir.

g ğ ( ₁, ₁) ( ₂, ₂) ç ğ

eğimi, cismin t₁ ve t₂ aralığındaki v_ort hızına eşittir.

2 1 ort 2 1

x

x

x

v

t

t

t





















ortalama hız 2 1

t

t



t

(3-6)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Hareket ve konum zaman grafi

ğ

i

Hareket ve konum-zaman grafi

ğ

i

x

t

Cismin hareketini tanımlayınız. Ci i d

Duran bir cismin konum-zamana grafiği. Cisim duruyor. (3-7)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Hareket ve konum zaman grafi

ğ

i

Hareket ve konum-zaman grafi

ğ

i

x

tt

Ci i h k ti i t l

Cismin hareketini tanımlayınız.

Cisim +x yönünde sabit hızla gidiyor.

Değişen bir hızla hareket eden bir canlının konum-zaman

grafiği grafiği (3-8)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Hareket ve konum zaman grafi

ğ

i

x (m)

Hareket ve konum zaman grafi

ğ

i

x (m)

x

B

t



x



A

t



t

Bir cismin konum-zaman grafiği grafikte verilmiştir. Bu cismin

/

ort

v

  

x

t

g e ve ş . u c s ortalama hızı hesaplayınız. v =  x/ t=2 0/6 0=1/3 m/s v_ort =  x/ t=2.0/6.0=1/3 m/s (3-9)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Örnek: Şekilde bir cismin t = 1 s ve t = 4 s anlarındaki konumları

Örnek: Şekilde bir cismin t₁ = 1 s ve t₂ = 4 s anlarındaki konumları x₁ =  4 m ve x₂= 2 m’dir.

Cismin ortalama hızını bulalım Cismin ortalama hızını bulalım.

2 1 ort 2 ( 4) 6 m 2 m/s 4 1 3 s x x v t t          2 1 4 1 3 s t t (3-10)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Ortalama Sürat (

v

_{sürat_ort}

):

v_{sürat_ort} toplam yol t





Ortalama sürat, Δt zaman aralığında alınan “toplam yol” cinsinden tarif edilir.

Ortalam sürat ortalama hızın büyüklüğü değildir. t



Şekildeki otomobilin A ve F

Örnek :

Ortalam sürat ortalama hızın büyüklüğü değildir. Şekildeki otomobilin, ve

noktaları arasındaki, ortalama hızını

ve süratini hesaplayınız ( = 0 ve_A A F t Örnek : ve süratini hesaplayınız ( 0 ve = 30 m ; = 50 s ve = 53 m). A A F F t x t x  53 30 ort 53 30 50 0 F A F A x x v t t        83 1.66 m/s 50     sürat_ort 22+52+53 50 50 AB BD DF x x x v     (3-11) 127 2.54 m/s 50  

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

-ekseni boyunca hareket eden bir cismin

x

Örnek :

konum-zaman grafiği yanda verilmiştir. Cismin 0 2 s ; 0 4 s ; 0 7 s ; 0 8 s    aralıklarında ortalama hızını bulunuz.

0 8 s aral ığında cismin hız-zaman grafiğini çiziniz.

Konum-zaman grafiğinden;

ğ g ğ ç ort(0-2) ort(0-4) 10 0 5 0 5 m/s ; 1.25 m/s 2 0 4 0 v    v      ort(0-7) ort(0-8) 5 0 0 0 0.714 m/s ; 0 7 0 8 0 v      v      (0-2) (2-4) 10 0 5 10 5 m/s ; 2.5 m/s 2 0 4 2 dx v v v dt            (4-5) (5-7) 2 0 4 2 5 5 5 5 0 ; 5 m/s 5 4 7 5 dt v v             (3-12) (7-8) 0 ( 5) 5 m/s 8 7 v     

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Anl

ı

k H

ı

z:

O t l h bi i i l ğ d Ortalama hız, bir cismin t₁ ve t₂ zaman aralığında

ne kadar hızlı olduğu bilgisini içerir. Herhangi bir

t anında cismin ne kadar hızlı olduğu bilgisi “anlık t anında cismin ne kadar hızlı olduğu bilgisi anlık

hız” tanımıyla verilir.

Anlık hız, ortalama hızın Δt →0 durumundaki limitidir.

lim

0

x

dx

v

t

dt

t











_t

0



t

dt

 

B d l k h i i k

Bu tanımdan anlık hız, cismin x konumunun

zamana göre birinci türevidir.

Yani, konum-zaman grafiğinin herhangi bir andaki eğimidir.

(3-13)

Anl

DR.

ı

k sürat anl

ı

k h

ı

z

ı

n büyüklü

ğ

üdür.

MUSTAFA

POLAT

ve

DR.

LEYLA

-ekseni boyunca hareket eden bir cismin konumu x

Örnek :

2

( ) 4 +2

ifadesine göre değişmektedir ( saniye, metre cinsindendir).

x t t t

t x

 

ifadesine göre değişmektedir ( saniye, metre cinsindendir).

) 0 1 s ve 1 3 s aralıklarında cismin ortalama

t x

a ) 0 1 s ve 1 3 s aralıklarında cismin ortalama hızını bulunuz a   hızını bulunuz. ) 2 5 d ki h b l b ) 2.5 s anındaki hızını bulunuz. b t



  

ort(0-1) 4 2 0 ) 2 m/s 1 0 a v        ) ( ) 4 4 m/s dx b v t + t dt    



 12 18

 

  4 2



(2.5)v  4 4(2.5) 6 m/s+ 



 



ort(1-3) 12 18 4 2 4 m/s 3 1 v      ( ) ( ) (3-14)

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM

Ortalama

İ

vme:

t t l d ki t l i

t₁ ve t₂ anları arasındaki ortalama ivme:

2 2 1

_/

v

₂



v

₁



v

₂ ort 2 1

m/ s

a

t

t

t









Anlık İvme:

Anlık ivme, ortalama ivmenin Δt→0 durumundaki limitidir ve herhangi bir t anında hızın ne kadar hızlı değiştiğini gösterir

2

lim v dv ; dv d dx d x

a    a   _ _  hızın ne kadar hızlı değiştiğini gösterir.

2 0 lim ; t a a t dt dt dt dt dt       _{ }   _{ } B t d l k i i i h

Bu tanımdan anlık ivme, cismin hızının zamana göre birinci türevidir. Yani, hız-zaman grafiğinin herhangi bir andaki eğimidir.

(3-15) g ğ

DR.

MUSTAFA

POLAT

ve

DR.

LEYLA

YILDIRIM