www.elsevier.com/locate/dsw
A Sokhotski–Plemelj problem related to a robot-safety
device system
E.J. Vanderperre
∗Department of Quantitative Management, University of South Africa
Received 1 November 1999; received in revised form 1 January 2000
Abstract
We introduce a robot-safety device system attended by two dierent repairmen. The twin system is characterized by the nat-ural feature of cold standby and by an admissible “risky” state. In order to analyse the random behaviour of the entire system (robot, safety device, repair facility), we employ a stochastic process endowed with probability measures satisfying general steady-state dierential equations. The solution procedure is based on the theory of sectionally holomorphic functions. An application of the Sokhotski–Plemelj formulae determines the long-run availability of the robot-safety device. Finally, we con-sider the particular but important case of deterministic repair. c2000 Published by Elsevier Science B.V. All rights reserved.
Keywords:Robot; Safety device; Invariant measure; Availability; Risk-criterion
1. Introduction
Innovations in the eld of microelectronics and micromechanics have enhanced the involvement of “smart” robots in all kind of advanced technical systems [2].
Unfortunately, no robot is completely reliable. Therefore, up-to-date robots are often connected with a safety device [3–5]. Such a device prevents possi-ble damage, caused by a robot failure, in the robot’s neighbouring environment. However, the random be-haviour of the entire system (robot, safety device, repair facility) could jeopardize some prescribed
∗Correspondence address: Ruzettelaan 183, Bus 158, B-8370 Blankenberge, Belgium.
E-mail address:[email protected] (E.J. Vanderperre).
safety requirements. For instance, if we allow the robot to operate during the repair time of the failed safety device. Such a “risky” state is called admissi-ble, if the associate event: “The robot is operative but the safety device is under repair”, constitutes arare
event. Therefore, an appropriate statistical analysis of robot-safety device systems is quite indispensable to support the system designer in problems of risk acceptance and safety assessments.
In order to avoid undesirable delays in repairing failed units, we introduce a robot-safety device at-tended bytwo dierent repairmen (henceforth called aT-system). TheT-system satises the usual
condi-tions, i.e. independent identically distributed random variables and perfect repair [6].
Each repairman has his own particular task. Repair-manSis skilled in repairing the safety unit, whereas
repairman R is an expert in repairing robots. Both
repairmen are jointly busy if, and only if, both units (robot + safety device) are down. In the other case, at least one repairman is idle. In any case, the safety de-vice always waits (in cold standby [1]) until the repair of the robot has been completed.
In order to analyse the random behaviour of the
T-system, we introduce a stochastic process
en-dowed with probability measures satisfying general steady-state dierential equations. The solution pro-cedure is based on the theory of sectionally holomor-phic functions [7]. An application of the Sokhotski– Plemelj formulae determines the long-run availability of the robot-safety device.
Finally, we consider the particular but important case of deterministic repair.
2. Formulation
Consider a T-system satisfying the usual condi-tions.
The robot has a constant failure rate ¿0 and a general repair time distribution R(•); R(0) = 0 with meanand variance2.
The operativesafety device has a constant failure rate s¿0 but a zero failure rate in standby (the
so-called cold standby state) and a general repair time distributionRs(•); Rs(0) = 0 with mean s and
vari-ance2
s. The corresponding repair times are denoted
byrandrs.
Characteristic functions (and their duals) are for-mulated in terms of a complex transform variable. For instance,
Eei!r= Z ∞
0
ei!xdR(x); Im!¿0:
Note that
Ee−i!r= Z ∞
0
e−i!xdR(x)
=
Z 0
−∞
ei!xd(1−R((−x)−)); Im!60:
The corresponding Fourier–Stieltjes transforms are calleddualtransforms.
Without loss of generality (see our forthcoming re-marks), we may assume that both repair time
distribu-tions have bounded densities (in the Radon–Nikodym sense) dened on [0;∞).
In order to analyse the random behaviour of the T-system, we introduce a stochastic
pro-cess {Nt; t¿0} with arbitrary discrete state space
{A; B; C; D} ⊂[0;∞), characterized by the following events:
{Nt=A}: “Both units are operating in parallel at
timet”.
{Nt =B}: “The robot is operative but the safety
device is under repair at time t”. State B is the so-called risky state.
{Nt=C}: “The safety device is in cold standby and
the robot is under repair at timet”.
{Nt=D}: “Both units are simultaneously down at
timet”.
A Markov characterization of the process {Nt} is
piecewise and conditionally dened by:
{Nt}, ifNt=A(i.e. if the event{Nt=A}occurs).
{Nt; Xt}, ifNt=B, whereXtdenotes theremaining
repair time of the safety device in progressive repair at timet.
{Nt; Yt}, if Nt=C, whereYt denotes the
remain-ingrepair time of the robot in progressive repair at timet.
{(Nt; Xt; Yt)}, ifNt=D.
The state space of the underlying Markov process is given by
{A} ∪ {(B; x);x¿0} ∪ {(C; y);y¿0}
∪{(D; x; y);x¿0; y¿0}:
Next, we consider theT-system in stationary state
(the so-called ergodic state) with invariant measure
{pK;K=A; B; C; D},PKpK= 1, where
pK:=P{N=K}:= lim
t→∞P{Nt=K|N0=A}:
Finally, we introduce the measures
’B(x) dx:=P{N=B; X ∈dx}
:= lim
t→∞
P{Nt=B; Xt∈dx|N0=A};
’C(y) dy:=P{N=C; Y ∈dy}
:= lim
’D(x; y) dxdy:=P{N=D; X ∈dx; Y ∈dy}
:= lim
t→∞
P{Nt=D; Xt∈dx; Yt∈dy|N0=A}:
Notations. The indicator of an eventEis denoted by
5(E) := (
1 if Eoccurs;
0 otherwise:
Note that, for instance,
E{ei!XeiY5(N=D)}
The real line and the complex plane are denoted by
RandC with obvious superscript notationsC+,C−, C+ ∪R, C− ∪R. For instance, C+:={! ∈ C :
Im ! ¿0}.
The robot and the safety device are only jointly available (operative) in state A.
Therefore, the long-run availability of the robot-safety device, denoted byA, is given bypA.
Finally, we propose the following risk-criterion: State B is admissible if pB satises the relation
pB¡ ≪1 for some ¿0, called the security level.
3. Dierential equations
In order to determine the’-functions, we rst con-struct a system of steady-state dierential equations based on a time independent version of Hokstad’s supplementary variable technique (see e.g. Ref. [8, p. 526]). Forx ¿0; y ¿0, we obtain
Note that our equations are well adapted to an integral transformation. The integrability of the
’-functions and their corresponding derivatives im-plies that each ’-function vanishes at innity irre-spectiveof the asymptotic behaviour of the underly-ing repair time densities! Applyunderly-ing a routine Fourier transform technique to the equations and invoking the boundary condition (s+)pA=’B(0) +’C(0),
Eq. (2) constitutes a boundary value problem on the real line which can be solved by the theory of sectionally holomorphic functions. An application of Rouche’s (see the appendix) theorem reveals that the function 1 +’−(!), Im !60, has no
Im !60, is analytic inC−, bounded and
continu-Moreover, ’ is (uniformly) Lipschitz continuous on R. (Indeed, |’′(t)| is bounded on R. Therefore,
our assertion follows from the mean value theorem). Finally,’is Holder continuous at innity, i.e.|’(t)|= O(|t|−1), if|t| → ∞.
Consequently, the Cauchy-type integral
1 2i
Z
’() d
−!;
(see the appendix) exists forall!∈C (real or
com-plex) and denes a sectionally holomorphic function vanishing at innity. A straightforward application of the Cauchy formulae for the regionsC+andC−,
en-Note that by the Sokhotski–Plemelj formulae,
+(0) =1
Applying the limit procedure to Eq. (1) and invok-ing the conditionpA+pB+pC+pD= 1, yields the
we have completely determined the invariant measure simply and solely depending upon +(0). We state
the following
all the relevant properties to ensure the existence of the Cauchy integral forarbitraryrepair time distribu-tions with nite mean and variance. First of all, the order relation|’(t)|= O(|t|−1),|t| → ∞, also holds
for arbitrary characteristic functions. Moreover, the H-continuity of’onRdoes not depend on the
canoni-cal structure (decomposition) ofRorRs. For instance,
the Holder inequality
|Eeit2r−Eeit1r|6|t
2−t1|; (t1; t2∈R);
always holds foranyrwith mean.
The requirement of nite variances is extremely mild since the current probability distributions em-ployed to model repair times [1] even have moments of all orders!
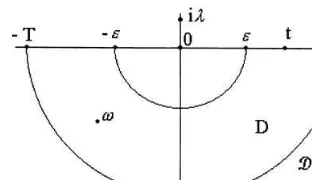
Fig. 1. Region D with boundaryD.
From the identity
1 2i
Z
’(t) dt
t−!
=
is(e−t0−ei!t0)
!−i if Im! ¿0; !6= i;
st0e−t0 if != i;
we obtain +(0) =−1
s(1−e−t0). Hence,
A= 1
(1 +−1
s(1−e−t0))(1 +t0):
Appendix
Denition. Letf(t),t∈Rbe a bounded and
contin-uous function.fis called -integrable, if
lim
T→∞ ↓0
Z
LT;
f(t) dt
t−u; u∈R;
exists, whereLT; := (−T; u−]∪[u+; T). The
cor-responding integral, denoted by 1
2i
Z
f(t) dt
t−u;
is called a Cauchy principal value in double sense.
Lemma. The function1+’−(!);Im!60;has no zeros inC−∪R.
Proof. Clearly, 1 +’−(0) = 1 + ¿0. Hence,
!= 0 is not a zero. Consider region D with boundary
Das depicted in Fig. 1.
For!6= 0 we have
1 +’−(!) =+ i! i! (1−L
−
(!));
where
L−(!) :=
+ i!Ee
−i!r; Im!60:
Note thatL−(t) is the characteristic function of a non-lattice random variable. Consequently, L−(t) 6= 1 on (−T;−]∪[; T). Therefore, 1 +’−(t) has no zeros in R. Furthermore,|L−(!)|¡1, ∀! ∈ D.
Moreover,L−(!) is analytic in D and continuous on
D∪D. Applying Rouche’s theorem to the functions 1
and−L−(!) reveals that 1 +’−(!) has no zeros
inC−∪R. In addition, note that
lim
|!|→∞
6arg!62
(1 +’−(!)) = 1:
References
[1] A. Birolini, Quality and Reliability of Technical Systems, Springer, Berlin, 1994.
[2] B.A. Brandin, The real-time supervisory control of an experimental manufacturing cell, IEEE Trans. Robotics Automation 12 (1996) 1–13.
[3] B.S. Dhillon, A.R.M. Fashandi, Robotic systems probability analysis, Microelectron. Reliab. 37 (1997) 187–209. [4] B.S. Dhillon, N. Yang, Availability analysis of a robot with
safety system, Microelectron. Reliab. 36 (1996) 169–177. [5] B.S. Dhillon, N. Yang, Formulae for analyzing a
redundant robot conguration with a built-in safety system, Microelectron. Reliab. 37 (1997) 557–563.
[6] I.B. Gertsbakh, Statistical Reliability Theory, Marcel Dekker, New York, 1989.
[7] N.I. Muskhelishvili, Singular Integral Equations, Noordho, Leiden, 1997.