BAB II
TINJAUAN PUSTAKA
2.1. Logika Fuzzy
Sebelum munculnya teori logika fuzzy (Fuzzy Logic), dikenal sebuah logika tegas (Crisp Logic) yang memiliki nilai benar atau salah secara tegas. Prinsip ini
dikemukakan oleh Aristoteles sekitar 2000 tahun yang lalu sebagai hukum Excluded Middle dan hukum ini telah mendominasi pemikiran logika sampai saat ini. Namun, pemikiran mengenai logika konvensional dengan nilai kebenaran yang pasti yaitu benar atau salah dalam kehidupan nyata sangatlah tidak cocok. Fuzzy logic (logika samar) merupakan suatu logika yang dapat merepresentasikan keadaan yang ada di dunia nyata. Logika fuzzy merupakan sebuah logika yang memiliki nilai kekaburan atau kesamaran (fuzzy) antara benar dan salah.
Teori tentang himpunan logika fuzzy pertama kali dikemukakan oleh Prof. Lofti Zadeh sekitar tahun 1965 pada sebuah makalah yang berjudul ‘Fuzzy Sets’. Ia berpendapat bahwa logika benar dan salah dari logika boolean/konvensional tidak dapat mengatasi masalah yang ada pada dunia nyata. Tidak seperti logika boolean, logika samar mempunyai nilai yang kontinu. Samar dinyatakan dalam derajat dari suatu keanggotaan dan derajat dari kebenaran. Oleh sebab itu sesuatu dapat dikatakan sebagian benar dan sebagian salah pada waktu yang bersamaan. Teori himpunan individu dapat memiliki derajat keanggotaan dengan nilai yang kontinu, bukan hanya 0 dan 1 (Zadeh, 1965).
Dengan teori himpunan logika samar, kita dapat merepresentasikan dan menangani masalah ketidakpastian yang dalam hal ini bisa berarti keraguan, ketidaktepatan, kurang lengkapnya suatu informasi, dan kebenaran yang bersifat sebagian (Altrock, 1997). Di dunia nyata, seringkali kita menghadapi suatu masalah yang informasinya sangat sulit untuk diterjemahkan ke dalam suatu rumus atau
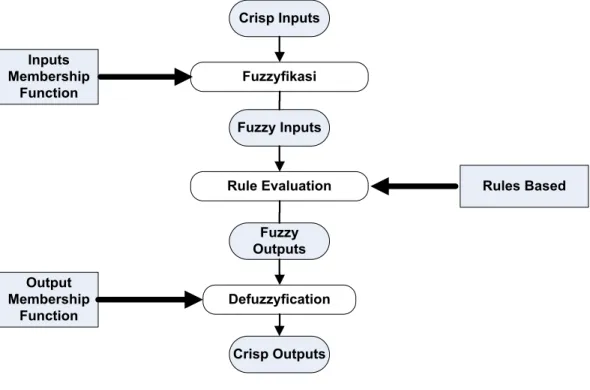
angka yang tepat karena informasi tersebut bersifat kualitatif (tidak bisa diukur secara kuantitatif). Pada Gambar 2.1 diperlihatkan diagram blok pengendali logika fuzzy. Crisp Inputs Fuzzyfikasi Fuzzy Inputs Rule Evaluation Fuzzy Outputs Defuzzyfication Crisp Outputs Inputs Membership Function Output Membership Function Rules Based
Gambar 2.1 Diagram blok pengendali logika fuzzy. Sumber : Jang et al. (1997)
Himpunan samar (fuzzy sets) adalah sekumpulan objek X di mana masing-masing objek memiliki nilai keanggotaan (membership function), M atau yang disebut juga dengan nilai kebenaran dan nilai ini dipetakan ke dalam daerah hasil range (0,1). Jika X merupakan sekumpulan objek dengan anggotanya dinyatakan dengan X maka himpunan samar dari A di dalam X adalah himpunan dengan sepasang anggota (Zadeh, 1968).
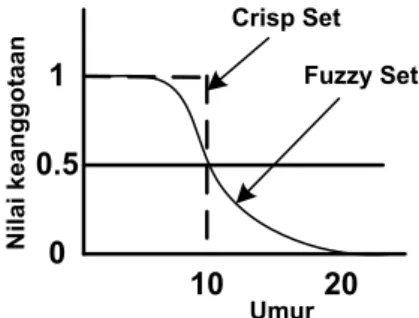
Teori himpunan samar merupakan suatu teori tentang konsep penilaian dan segala sesuatu merupakan persoalan derajat atau diibaratkan bahwa segala sesuatu memiliki elastisitas. Pada Gambar 2.2 diperlihatkan ilustrasi fuzzy dan crisp set himpunan umur.
Nilai keanggotaan Crisp Set Fuzzy Set Umur 1 0 10 0.5 20
Gambar 2.2: Ilustrasi fuzzy dan crisp set. Sumber : Hagan (1996)
Pada Gambar 2.2 diilustrasikan representasi dengan crisp set yang
menyatakan bahwa jika seseorang berumur dibawah 10 tahun maka ia merupakan himpunan orang muda, jika tidak maka ia tergolong tua. Sebaliknya dengan menggunakan fuzzy set, himpunan orang muda ditentukan oleh derajat keanggotaannya. Secara khusus kurva semacam ini disebut sebagai fungsi keanggotaan (membership function).
2.2 Fuzzyfikasi (Fuzzyfication)
Fuzzyfikasi adalah suatu proses pengubahan nilai tegas/real yang ada kedalam fungsi keanggotaan (Hagan, 1996). Pada gambar 2.3 diperlihatkan contoh fungsi keanggotaan suhu. Dari Gambar 2.3 akan dihitung fuzzyfikasi dari suhu 35o C.
Gambar 2.3 : Fungsi keanggotaan suhu Sumber : Hagan (1996)
Dengan menggunakan fungsi keanggotaan segitiga, maka crisp input suhu 35o
15 30 45 60 Panas Dingin A2 A1
µ
µ
Suhu (oC) C dikonversi ke nilai fuzzy dengan cara :Suhu 35o C berada pada nilai linguistik dingin dan panas. Semantik atau derajat keanggotaan untuk dingin dihitung dengan menggunakan rumus:
(2.1)
Dimana b=30 dan c=45, sehingga derajat keanggotaan dingin adalah :
Sedangkan semantik atau derajat keanggotaan untuk panas dihitung dengan menggunakan rumus:
(2.2)
Dimana a=30 dan b=45, sehingga derajat keanggotaan panas adalah :
Dari hasil perhitungan diatas, maka, proses fuzzyfikasi menghasilkan 2 fuzzy input, yaitu suhu dingin (2/3) dan suhu panas (1/3)
2.2.1 Linguistic Variable
Dalam teori logika fuzzy dikenal himpunan fuzzy (fuzzy set) yang merupakan pengelompokan sesuatu berdasarkan variabel bahasa (variabel linguistic) yang dinyatakan dalam fungsi keanggotaan. Variabel linguistik adalah variabel yang berupa kata/kalimat, bukan berupa angka. Sebagai alasan menggunakan kata/kalimat dari pada angka karena peranan linguistik kurang spesifik
dibandingkan angka, namun informasi yang disampaikan lebih informatif. Variabel linguistik ini merupakan konsep penting dalam logika samar dan memegang peranan penting dalam beberapa aplikasi (Zadeh, 1968).
Konsep tentang variabel linguistik ini diperkenalkan oleh Lofti Zadeh. Menurut Zadeh variabel linguistik ini dikarakteristikkan dengan (X, T(x), U, G, M), dimana: (Zadeh, 1968)
X = nama variabel (variabel linguistik)
T(x) = semesta pembicaraan untuk x atau disebut juga nilai linguistik dari x
U = jangkauan dari setiap nilai samar untuk x yang dihubungkan dengan variabel dasar U
G = aturan sintaksis untuk memberikan nama (x) pada setiap nilai X M = aturan semantik yang menghubungkan setiap X dengan artinya.
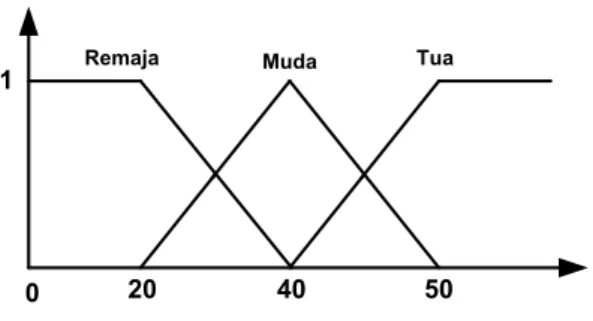
Sebagai contoh, jika :
X = ”umur” dengan U [10,80] dan T (umur) = {remaja, muda, tua}
Maka M untuk setiap X, M (x) adalah M (remaja), M (muda), M (tua), dimana : M (remaja) = himpunan samarnya ”umur dibawah 20 tahun” dengan
fungsi keanggotaan m remaja.
M (muda) = himpunan samarnya ”umur mendekati 40 tahun” dengan fungsi keanggotaan m muda
M (tua) = himpunan samarnya ”umur diatas 50 tahun” dengan fungsi keanggotaan m tua.
Maka nilai dari M dapat dilihat dari Gambar 2.4 berikut ini :
Degree of
Membeship Remaja Muda Tua
1
0 20 40 50
Gambar 2.4 : Fungsi keanggotaan kelompok umur Sumber : Russel (2002)
2.2.2 Membership Function
Di dalam fuzzy systems, fungsi keanggotaan memainkan peranan yang sangat penting untuk merepresentasikan masalah dan menghasilkan keputusan yang akurat. Menurut Jang et al. (1997), Membership Function (MF) adalah kurva yang memetakan setiap titik pada input-an (universe of discourse) ke sebuah nilai keanggotaan (derajat keanggotaan) yang memiliki nilai antara 0 dan 1 yang didefinisikan secara matematis oleh persamaan:
μA(x) : X → [0, 1] (2.3) Setiap elemen x dipetakan pada sebuah nilai keanggotaan oleh MF. Nilai ini merupakan derajat keanggotaan dari x pada himpunan fuzzy A.
μA(x) = Degree (x ∈ A) (2.4)
Dimana nilai keangotaan dari x dibatasi oleh:
0 ≤ μA(x) ≤ 1 (2.5)
Fungsi keanggotaan yang umum digunakan adalah: fungsi segitiga, fungsi trapesium, fungsi gaussian, fungsi bell dan fungsi sigmoid. Bentuk dari masing-masing fungsi keanggotaan adalah sebagai berikut (Jang et al. 1997) :
1. Fungsi linear
Pada representasi linear, pemetaan input ke dejarat keanggotaannya digambarkan sebagai suatu garis lurus. Ada dua keadaan himpunan fuzzy linear, yaitu :
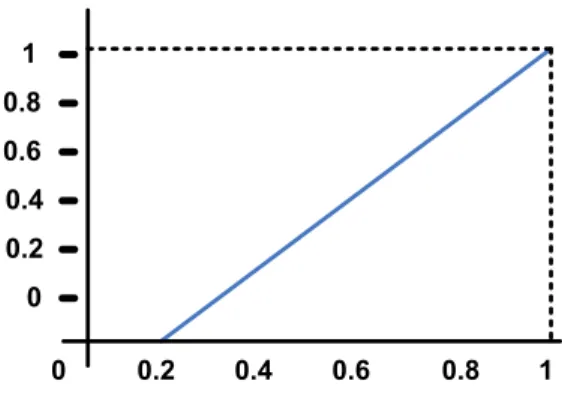
a. Kenaikan himpunan dimulai pada nilai domain yang memiliki derajat keanggotaan nol (0) bergerak ke kanan menuju ke nilai domain yang memiliki derajat keanggotaan lebih tinggi, seperti pada Gambar 2.5 :
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 Derajat Keanggotaan
Gambar 2.5 : Fungsi keanggotaan linear naik Sumber : Jang et al. (1997)
Fungsi keanggotaan :
(2.6)
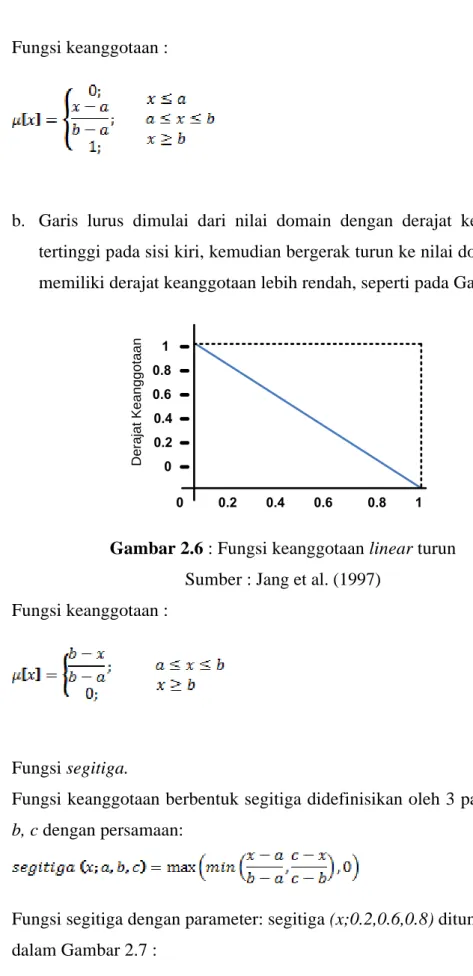
b. Garis lurus dimulai dari nilai domain dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak turun ke nilai domain yang memiliki derajat keanggotaan lebih rendah, seperti pada Gambar 2.6 :
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 Derajat Keanggotaan
Gambar 2.6 : Fungsi keanggotaan linear turun Sumber : Jang et al. (1997)
Fungsi keanggotaan :
(2.7)
2. Fungsi segitiga.
Fungsi keanggotaan berbentuk segitiga didefinisikan oleh 3 parameter a, b, c dengan persamaan:
(2.8)
Fungsi segitiga dengan parameter: segitiga (x;0.2,0.6,0.8) ditunjukkan dalam Gambar 2.7 :
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 mf1 Derajat Keanggotaan
Gambar 2.7 : Fungsi keanggotaan segitiga (triangle). Sumber : Yan et al. (1994)
3. Fungsi Trapesium.
Fungsi keanggotaan berbentuk trapesium didefinisikan oleh 4 parameter a, b, c, d dengan persamaan :
(2.9) Fungsi Trapesium dengan parameter: trapesium (x;0.1,0.2,0.6,0.95) ditunjukkan dalam Gambar 2.8:
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 mf1 Derajat Keanggotaan X
Gambar 2.8 : Fungsi keanggotaan trapesium (trapezoidal). Sumber : Yan et al. (1994)
4. Fungsi Gaussian.
Fungsi keanggotaan berbentuk Gaussian didefinisikan oleh 2 parameter σ, dan c dengan persamaan:
Fungsi Gaussian dengan parameter: Gaussian (x;0.15,0.5) ditunjukkan dalam Gambar 2.9 berikut ini:
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 mf1 Derajat Keanggotaan X
Gambar 2.9 : Fungsi keanggotaan gaussian. σ = standar deviasi, c = pusat.
Sumber : Jang et al. (1997)
5. Fungsi Bell.
Fungsi keanggotaan berbentuk bell didefinisikan oleh 3 parameter a, b dan c dengan persamaan:
(2.11)
Fungsi Bell dengan parameter: bell (x;0.25,2.5,0.5) ditunjukkan dalam Gambar 2.10: 1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 mf1 Derajat Keanggotaan X
Gambar 2.10 : Fungsi keanggotaan Bell. Sumber : Yan et al. (1994)
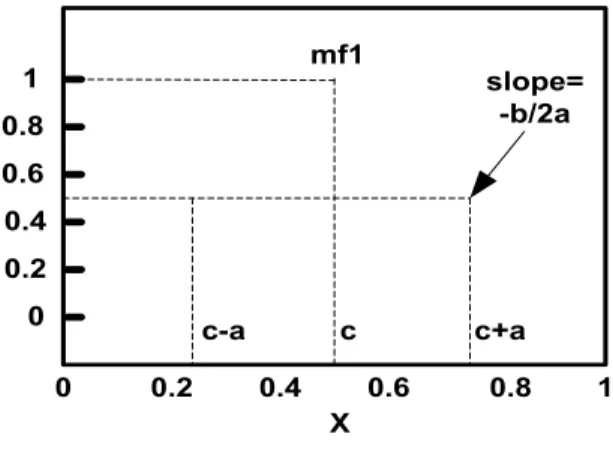
Parameter a, b dan c yang menspesifikasikan fungsi Bell ditunjukkan dalam Gambar 2.11 berikut ini:
1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0.4 0.2 0 mf1 Derajat Keanggotaan X c-a c c+a slope= -b/2a
Gambar 2.11 : Letak parameter a,b dan c pada fungsi keanggotaan bell. Sumber : Yan et al. (1994)
6. Fungsi Sigmoid.
Fungsi keanggotaan Sigmoid didefinisikan oleh 2 parameter a dan c dengan persamaan:
(2.12)
Jika nilai a > 0, maka fungsi sigmoid akan membuka ke kanan, sedang jika a < 0 maka fungsi sigmoid akan membuka ke kiri. Fungsi Sigmoid membuka ke kanan dengan parameter: sigmoid (x;12,0.25) ditunjukkan dalam Gambar 2.12:
Sumber : Yan et al. (1994)
Sedangkan fungsi Sigmoid membuka ke kiri dengan parameter: sigmoid (x;-12,0.75) ditunjukkan dalam Gambar 2.13 berikut ini:
Gambar 2.13 : Fungsi keanggotaan sigmoid membuka ke kiri. Sumber : Jang et al. (1997)
2.2.3 Aturan Dasar
Aturan dasar pada kontrol logika fuzzy merupakan suatu bentuk aturan relasi/implikasi “Jika-maka” atau “If-Then” seperti pada pernyataan berikut (Haykin, 1999):
“Jika” X=A dan “jika” Y=B “Maka” Z=C
Jadi aturan dasar pada control logika fuzzy (fuzzy logic control)
ditentukan dengan bantuan seorang pakar yang mengetahui karakteristik objek yang akan dikendalikan. Aturan dasar tersebut dapat dinyatakan dalam bentuk matriks aturan dasar kontrol logika fuzzy. Contoh aturan dasar dari rancangan pengaturan suhu ruangan dapat dilihat pada tabel 2.1.
Tabel 2.1 Contoh matriks aturan dasar perancangan kontrol logika fuzzy
Y X B S K B K K B Z S K S K K B K B Dimana :
B : Besar, S : Sedang, K : kecil
2.2.4 Defuzzyfication
Defuzzyfication merupakan proses pemetaan himpunan fuzzy kehimpunan tegas (crisp) (Haykin, 1999). Proses ini merupakan kebalikan dari proses fuzzyfikasi. Proses defuzzyfikasi diekspresikan sebagai berikut :
Z* = defuzzifier (Z) (2.13)
Dimana :
Z = Hasil penalaran fuzzy
Z* = Keluaran kontrol fuzzy logic Defuzzifier = Operasi defuzzier
Metode dalam melakukan defuzzifikasi antara lain : 1. Metode Max (Maximum)
Metode ini juga dikenal dengan metode puncak dimana nilai keluaran dibatasi oleh fungsi :
(2.14)
2. Metode Titik Tengah (Center of Area)
Metode ini juga disebut pusat area. Metode ini lazim dipakai dalam proses defuzzyfikasi. Metode ini diekspresikan dengan persamaan :
(2.15)
3. Metode Rata-Rata (Average)
Metode ini digunakan untuk fungsi keanggotaan keluaran yang simetris. Persamaan dari metode ini adalah :
(2.16)
4. Metode penjumlahan Titik Tengah (Summing of center area) Metode ini dinyatakan dengan persamaan :
(2.17)
5. Metode Titik Tengah Area Terbesar.
Dalam metode ini keluaran dipilih berdasarkan titik pusat area terbesar yang ada. Metode ini dinyatakan dalam bentuk :
(2.18)
Selanjutnya keluaran dari defuzzyfikasi tersebut akan digunakan sebagai keluaran kontrol logika fuzzy.
2.3 Neural Networks
Neural Networks (NN) atau Jaringan Syaraf Tiruan (JST) adalah prosesor yang terdistribusi paralel, terbuat dari unit-unit yang sederhana, dan memiliki kemampuan untuk menyimpan pengetahuan yang diperoleh secara eksperimental dan siap pakai untuk berbagai tujuan (Rajasekaran, 2005). JST merupakan sistem adaptif yang dapat mengubah strukturnya untuk memecahkan masalah berdasarkan informasi eksternal maupun internal yang mengalir melalui jaringan tersebut. Secara sederhana, JST adalah sebuah alat pemodelan data statistik non-linier. JST dapat digunakan untuk memodelkan hubungan yang kompleks antara input dan output untuk menemukan pola-pola pada data.
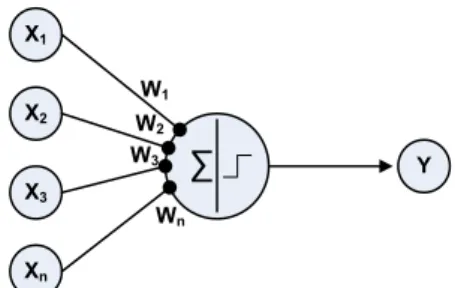
Jaringan syaraf tiruan merupakan algoritma pembelajaran yang meniru cara kerja sel syaraf. Selama proses pembelajaran, bobot-bobot dan bias selalu diperbaharui menggunakan algoritma belajar, jika ada error pada keluaran. Untuk proses identifikasi, bobot-bobot yang secara langsung memboboti masukan inilah yang dinamakan sebagai parameter yang dicari, seperti terlihat pada Gambar 2.14, parameter yang dicari adalah harga W1, W2, W3 dan Wn. Dalam identifikasi secara
on-line, neuron ataupun jaringan neuron akan selalu ‘belajar’ setiap ada data masukan dan keluaran.
X1 Xn X3 X2 ∑ Y W1 W2 W3 Wn
Gambar 2.14: Proses komunikasi antar neuron Sumber : Rajasekaran (2005)
Gambar 2.14 memperlihatkan bahwa NN terdiri atas satuan-satuan pemroses berupa neuron. Y sebagai output menerima input dari neuron X1, X2, X3,
…, Xn dengan bobot W1, W2, W3, …, Wn
Konsep jaringan saraf tiruan bermula pada makalah
. Hasil penjumlahan seluruh impuls neuron dibandingkan dengan nilai ambang tertentu melalui fungsi aktivasi f setiap neuron. Fungsi aktivasi digunakan sebagai penentu keluaran suatu neuron.
Waffen McCulloch dan Walter Pitts pada tahun 1943. Dalam makalah tersebut mereka mencoba untuk memformulasikan model matematis sel-sel otak. Metode yang dikembangkan berdasarkan sistem saraf biologi ini, merupakan suatu langkah maju dalam industri komputer.
Suatu jaringan saraf tiruan memproses sejumlah besar informasi secara paralel dan terdistribusi, hal ini terinspirasi oleh model kerja otak biologis. Zurada (1992) mendefinisikan jaringan syaraf tiruan sebagai berikut: “Sistem saraf tiruan atau jaringan saraf tiruan adalah sistem selular fisik yang dapat memperoleh, menyimpan dan menggunakan pengetahuan yang didapatkan dari pengalaman”. Haykin (1994) mendefinisikan jaringan saraf sebagai berikut: “Sebuah jaringan saraf adalah sebuah prosesor yang terdistribusi paralel dan mempunyai kecenderungan untuk menyimpan pengetahuan yang didapatkannya dari pengalaman dan membuatnya tetap tersedia untuk digunakan”. Hal ini menyerupai kerja otak dalam dua hal yaitu:
1. Pengetahuan diperoleh oleh jaringan melalui suatu proses belajar;
2. Kekuatan hubungan antar sel saraf yang dikenal dengan bobot sinapsis digunakan untuk menyimpan pengetahuan.
2.3.1 Backpropagation Neural Network (BPNN)
Salah satu metode pelatihan dalam NN adalah pelatihan terbimbing (supervised learning). BPNN merupakan salah satu metode yang menggunakan supervised learning. Pada pelatihan terbimbing diperlukan sejumlah masukan dan target yang berfungsi untuk melatih jaringan hingga diperoleh bobot yang diinginkan. Pada setiap kali pelatihan, suatu input diberikan ke jaringan, kemudian jaringan akan memproses dan mengeluarkan keluaran. Selisih antara keluaran jaringan dengan target merupakan kesalahan yang terjadi, dimana jaringan akan memodifikasi bobot sesuai dengan kesalahan tersebut.
Algoritma pelatihan Backpropagation Neural Network (BPNN) pertama kali dirumuskan oleh Werbos dan dipopulerkan oleh Rumelhart dan Mc.Clelland (Hagan, 1996). Pada supervised learning terdapat pasangan data input dan output yang dipakai untuk melatih JST hingga diperoleh bobot penimbang (weight) yang diinginkan. Penimbang itu sendiri adalah sambungan antar lapis dalam JST. Algoritma ini memiliki proses pelatihan yang didasarkan pada interkoneksi yang sederhana, yaitu apabila keluaran memberikan hasil yang salah, maka penimbang dikoreksi agar galat dapat diperkecil dan tanggapan JST selanjutnya diharapkan dapat mendekati nilai yang benar. BPNN juga berkemampuan untuk memperbaiki penimbang pada lapis tersembunyi (hidden layer).
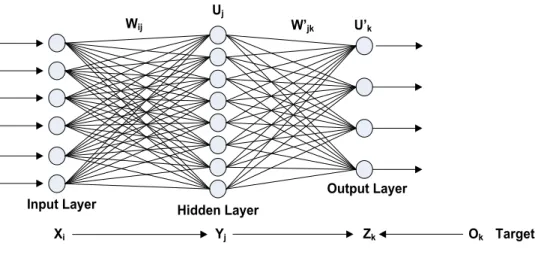
Wij W’jk U’k
Uj
Input Layer Hidden Layer Output Layer
Xi Yj Zk Ok Target
Gambar 2.15 : Lapis dan aliran sinyal dalam algoritma BPNN Sumber : Fausset (1994)
Secara garis besar BPNN terdiri atas tiga lapis (layer) yaitu lapis masukan (input layer) xi, lapis tersembunyi (hidden layer) yj, dan lapis keluaran (output
layer) zk. Lapis masukan dan lapis tersembunyi dihubungkan dengan penimbang wij
dan antara lapis tersembunyi dan lapis keluaran dihubungkan oleh penimbang w’jk
Pada dasarnya, metode pelatihan backpropagation terdiri dari tiga langkah, yaitu : .
1) Data dimasukkan kedalam input node atau jaringan (feedforward); 2) Perhitungan dan propagasi balik dari error yang bersangkutan; 3) Pembaharuan (adjustment) bobot dan bias.
Pada pelatihan BPNN, ketika JST diberi pola masukan sebagai pola pelatihan maka pola tersebut akan menuju ke unit pada lapis tersembunyi untuk diteruskan pada unit yang berada pada lapis keluaran. Keluaran sementara pada lapis tersembunyi uj akan diteruskan pada lapis keluaran dan lapis keluaran akan
memberikan tanggapan yang disebut sebagai keluaran sementara u’k. Ketika u’k ≠
ok dimana ok adalah target yang diharapkan, maka selisih (error) keluaran
sementara u’k
Untuk mempercepat proses pelatihan digunakan parameter laju pelatihan (learning rate) yang nilainya berada pada kisaran 0-1. Selain parameter laju pelatihan, untuk mempercepat proses pelatihan dapat digunakan parameter tambahan berupa momentum yang nilainya dijaga antara 0.5 - 0.9. Ketika proses pelatihan selesai dan JST dapat digunakan untuk menyelesaikan masalah, tahap tersebut disebut sebagai tahap penggunaan yang disebut mapping atau pemetaan.
akan disebarkan mundur (backward) pada lapis tersembunyi dan diteruskan ke unit pada lapis masukan. Oleh karena itu proses tersebut disebut propagasi balik (backpropagation) dimana tahap pelatihan dilakukan dengan merubah penimbang yang menghubungkan unit dalam lapis JST ketika diberi umpan maju dan umpan balik.
Algoritma pelatihan BPNN terdiri dari dua tahap, yaitu feedforward propagation dan feed backward propagation. Untuk selengkapnya, notasi-notasi yang akan digunakan pada algoritma BPNN adalah :
x Data trainning untuk input x = ( x1,…,xi,…,xn
t
)
Data trainning untuk output (target/desired output) t = ( t1,…,tk,…,tm )
α
Learning rate, yaitu parameter yang mengontrol perubahan bobot selama pelatihan. Jika learning rate besar, jaringan semakin cepat belajar, tetapi hasilnya kurang akurat. Learning rate biasanya dipilih antara 0 dan 1 Unit input ke-i. untuk unit input, sinyal yang masuk dan keluar pada suatu unit dilambangkan dengan variabel yang sama, yaitu
Hidden unit ke-j. sinyal input pada dilambangkan dengan
.
Sinyal output (aktivasi) untuk dilambangkan denganBias untuk hidden unit ke-j
Bobot antara unit input ke-i dan hidden unit ke-j
Unit output ke-k. sinyal input ke dilambangkan
.
Sinyal output (aktivasi) untuk dilambangkan denganBias untuk unit output ke-k
Bobot antara hidden unit ke-j dan unit output ke-k Faktor koreksi error untuk bobot
Faktor koreksi error untuk bobot
Langkah-langkah Algoritma Backpropagation Neural Network (BPNN). a. Algoritma Pelatihan
Pelatihan suatu jaringan dengan algoritma backpropagation meliputi dua tahap : 1. Feedforward propagation.
2. Feed backward propagation.
Selama proses feedforward propagation, tiap unit masukan (xi) menerima
sebuah masukan sinyal ini ke tiap-tiap lapisan tersembunyi z1,…..,zp. Tiap unit
ke tiap unit keluaran. Tiap unit keluaran menghitung aktivasinya untuk membentuk respon pada jaringan untuk memberikan pola masukan. Selama pelatihan, tiap unit keluaran membandingkan perhitungan aktivasinya dengan nilai targetnya untuk menentukan kesalahan pola tersebut dengan unit itu.
Berdasarkan kesalahan ini, faktor (k = 1,..,m) dihitung. digunakan untuk menyebarkan kesalahan pada unit keluaran yk kembali ke semua unit pada
lapisan sebelumnya (unit-unit tersembunyi yang dihubungkan ke ), selain itu juga digunakan (nantinya) untuk meng-update bobot-bobot antara keluaran dan lapisan tersembunyi. Dengan cara yang sama, faktor (j = 1,…,p) dihitung untuk tiap unit tersembunyi , tanpa perlu untuk menyebarkan kesalahan kembali ke lapisan masukan, tetapi δj
Setelah seluruh faktor δ ditentukan, bobot untuk semua lapisan diatur secara serentak. Pengaturan bobot w
digunakan untuk meng-update bobot-bobot antara lapisan tersembunyi dan lapisan masukan.
jk (dari unit tersembunyi ke unit keluaran
) didasarkan pada faktor dan aktivasi dari unit tersembunyi didasarkan pada faktor dan aktivasi unit masukan. Untuk langkah selengkapnya adalah (Laurence, 1994) :
b. Prosedur Pelatihan
Berikut adalah langkah-langkah pelatihan backpropagation secara lebih detail. Langkah 0 : Inisialisasi bobot dan bias. (sebaiknya diatur pada nilai acak
yang kecil, disekitar 0 dan 1 atau -1 (bias positif atau negatif));
Langkah 1 : Jika kondisi berhenti belum tercapai, lakukan langkah 2-9; Langkah 2 : Untuk setiap data trainning, lakukan langkah 3-8.
Umpan Maju (Feedforward Propagation):
Langkah 3 : Tiap unit input (xi, i = 1,…, n) menerima sinyal xi dan
menyebarkan sinyal ini ke seluruh unit lapisan di atasnya (hidden unit). Input xi yang dipakai adalah input trainning
data yang sudah diskalakan. Pertama, input yang mungkin dipakai dalam sistem dicari nilai terendah dan tertingginya, kemudian, skala yang digunakan tergantung dari fungsi aktivasinya;
Langkah 4 : Setiap hidden unit ( , j = 1,…, p) akan menjumlahkan bobot sinyal masukannya, termasuk biasnya;
(2.19)
Dimana voj = bias pada unit tersembunyi j, kemudian
aplikasikan fungsi aktivasi yang telah ditentukan untuk menghitung sinyal output dari hidden unit yang bersangkutan;
= f ( ) (2.20)
lalu kirimkan sinyal output ini keseluruh unit pada lapisan diatasnya (output unit).
Langkah 5 : Tiap unit ouput ( , k = 1,…, m) akan menjumlahkan bobot sinyal masukannya, termasuk biasnya;
(2.21)
Dimana wok = bias pada unit keluaran k, kemudian
aplikasikan fungsi aktivasi yang telah ditentukan untuk menghitung sinyal output dari unit output yang bersangkutan;
= f ( ) (2.22)
lalu kirimkan sinyal output ini keseluruh unit pada lapisan diatasnya (output unit).
Propagasi error (Feed backward propagation).
Langkah 6 : Tiap unit ouput ( , k = 1,…, m) menerima pola target (desired output) yang sesuai dengan pola input (input trainning pattern) untuk menghitung kesalahan (error) antara target dengan output yang dihasilkan jaringan;
(2.23) Dimana : δk = error pada node ke-k
= target ke-k f’(x) = f(x) [1-f(x)]
Output trainning data tk
Gunakan faktor
telah diskalakan menurut fungsi aktivasi yang dipakai.
untuk menghitung koreksi bobotnya (digunakan untuk memperbaharui wjk nantinya);
(2.24)
Hitung koreksi biasnya (digunakan untuk memperbaharui wok
nantinya)
(2.25)
Kirimkan faktor δk ini ke unit-unit pada lapisan dibawahnya
(layer pada langkah 7);
Langkah 7 : Setiap hidden unit ( , j = 1,…, p) menjumlahkan input delta dari unit-unit lapisan diatasnya (yang dikirim dari layer pada langkah 6) yang sudah berbobot;
(2.26)
digunakan untuk menghasilkan faktor koreksi error dimana :
(2.27)
Faktor ini digunakan untuk menghitung koreksi error ( ) (digunakan untuk memperbaharui vij nanti), dimana;
(2.28)
Selain itu juga dihitung koreksi bias (digunakan untuk memperbaharui voj nanti), dimana;
(2.29)
Pembaharuan bobot (adjustment) dan bias.
Langkah 8 : Tiap unit output ( , k = 1,…, m) akan mengupdate bias dan bobotnya dari setiap hidden unit (j = 0,…, p) ;
(baru) = (lama) + Δ
(2.30)
Tiap unit hidden unit ( , j = 1,…, p) akan mengupdate bias dan bobotnya dari setiap unit input (i = 0,…,n) :
(baru) = (lama) + Δ (2.31)
Langkah 9 : Test kondisi berhenti.
Jika stop condition (kondisi berhenti) telah terpenuhi, maka proses pelatihan dapat dihentikan. Ada dua cara yang dapat dilakukan untuk menentukan stopping condition (test kondisi berhenti), yaitu :
Cara 1 : Membatasi jumlah iterasi yang ingin dilakukan (satu iterasi merupakan perulangan langkah 3
sampai dengan langkah 8 untuk semua trainning data yang ada). Jika jumlah iterasi telah terpenuhi, maka proses pelatihan akan berhenti.
Cara 2 : Membatasi error. Untuk metode BPNN, metode yang digunakan adalah Mean Square Error, untuk menghitung rata-rata error antara output yang dikehendaki pada trainning data dengan output yang dihasilkan oleh jaringan. Besarnya persen error ini tergantung kepresisian yang dibutuhkan oleh sistem yang bersangkutan.
c. Prosedur Pengujian :
Setelah pelatihan, jaringan saraf backpropagation diaplikasikan dengan hanya menggunakan tahap perambatan maju dari algoritma pelatihan. Prosedur aplikasinya adalah sebagai berikut :
Langkah 0 : Inisialisasi bobot (dari algoritma pelatihan).
Langkah 1 : Untuk tiap vektor masukan, lakukan langkah 2 - langkah 4. Langkah 2 : for i = 1,…, n : atur aktivasi unit masukan xi
Langkah 3 . : for j = 1,…, p : (2.32) zj = f ( ) (2.33) for k = 1,…, m : Langkah 4 : (2.34) yk = f ( ) (2.35)
Langkah 5 : Jika yk≥ 0,5 maka yk = 1, else yk
2.3.2 Algoritma Kohonen Map
Kohonen Map atau bisa disebut Self Organizing Map diperkenalkan pertama kali oleh Prof. Teuvo Kohonen dari Finlandia pada tahun 1982 (Kohonen, 1982). Kohonen map merupakan salah satu algoritma jaringan syaraf tiruan yang cukup unik karena membangun sebuah topology preserving map dari ruang berdimensi tinggi ke dalam neuron-neuron sebagai representasi dari datapoint yang ada.
Kohonen map merupakan salah satu metode jaringan syaraf tiruan unsupervised learning (tidak terawasi). Jaringan ini tidak mendapatkan target, sehingga JST mengatur bobot interkoneksi sendiri. Belajar tanpa pengawasan (Self Organizing Learning) adalah belajar mengklasifikasikan tanpa dilatih. Pada proses belajar tanpa pengawasan, JST akan mengklasifikasikan contoh pola-pola masukan yang tersedia ke dalam kelompok yang berbeda-beda. Ketika data diberikan ke dalam jaringan syaraf, data akan mengatur struktur dirinya sendiri untuk merefleksikan dari pola yang diberikan. Pada kebanyakan model ini, batasan mengacu pada determinasi kekuatan antar neuron.
Pada jaringan kohonen, suatu lapisan yang berisi neuron-neuron akan menyusun dirinya sendiri berdasarkan input nilai tertentu dalam suatu kelompok yang dikenal dengan istilah cluster. Selama proses penyusunan diri, cluster yang memiliki vektor bobot paling cocok dengan pola input (memiliki jarak yang paling dekat) akan terpilih sebagai pemenang. Neuron yang menjadi pemenang beserta neuron-neuron tetangganya akan memperbaiki bobot-bobotnya.
Langkah-langkah Algoritma Kohonen
Berikut merupakan langkah-langkah algoritma kohonen : Langkah 0 : Inisialisasi bobot :
Set parameter-parameter tetangga Set parameter learning rate
Langkah 1 : Kerjakan jika kondisi berhenti bernilai FALSE a. Untuk setiap vektor input x, kerjakan :
• Untuk setiap j, hitung :
boboti =
• Bandingkan boboti
• Untuk bobot
untuk mencari bobot terkecil
i terkecil, ambil (lama)
untuk mendapatkan :
(baru)= (lama) + α (xi – (lama))
(2.36)
(2.37)
b. Perbaiki learning rate
α (baru) =0,5 * α (2.38)
c. Kurangi radius ketetanggaan pada waktu-waktu tertentu, dengan cara meng-update nilai boboti
d. Tes kondisi berhenti (min error atau maxepoch terpenuhi)
2.4 Normalisasi Data
Dalam proses pembelajaran (trainning), jaringan membutuhkan data trainning yaitu data yang di-input-kan. Pada proses yang menggunakan derajat keanggotaan yang berada pada interval 0 dan 1 maka transformasi data hendaknya dilakukan pada interval yang lebih kecil yaitu [0.1 , 0.9], untuk itu perlu dilakukan normalisasi data, agar terbentuk data yang berada diantara 0 dan 1. Salah satu rumus yang dapat digunakan dalam proses normalisasi data tersebut adalah persamaan berikut :
(2.39) Dimana :
: data actual yang telah dinormalisasi : nilai maksimum data actual
: nilai minimum data actual a : data terkecil
b : data terbesar
2.5 Smoothing Grafik
Proses smoothing grafik dilakukan untuk mendapatkan hasil grafik yang lebih baik. Proses ini dilakukan dengan mengambil titik puncak dari grafik hasil trainning yang telah terbentuk dari titik puncak grafik tersebut, kemudian akan ditarik garis linear dari titik awal dan titik akhir sehingga dapat menghasilkan grafik yang lebih baik.
2.6 Riset Terkait
Dalam melakukan penelitian, penulis menggunakan beberapa riset terakait yang dijadikan acuan yang membuat penelitian berjalan lancar. Adapun riset-riset terkait tersebut adalah :
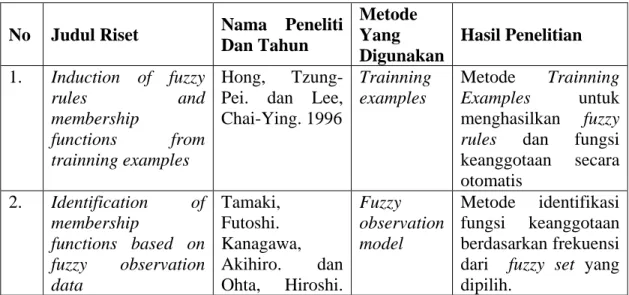
Tabel 2.2. Riset terkait No Judul Riset Nama Peneliti
Dan Tahun Metode Yang Digunakan Hasil Penelitian 1. Induction of fuzzy rules and membership functions from trainning examples Hong, Tzung-Pei. dan Lee, Chai-Ying. 1996 Trainning examples Metode Trainning Examples untuk menghasilkan fuzzy rules dan fungsi keanggotaan secara otomatis 2. Identification of membership functions based on fuzzy observation data Tamaki, Futoshi. Kanagawa, Akihiro. dan Ohta, Hiroshi. Fuzzy observation model Metode identifikasi fungsi keanggotaan berdasarkan frekuensi dari fuzzy set yang dipilih.
1998
Tabel 2.2. Riset terkait (Lanjutan) 3. Neural Networks in Materials Science. Bagis, Aytekin. 2003. Tabu search. Optimasi membership functions untuk kontroler logika fuzzy menggunakan
algoritma tabu search. 4. Fuzzy Membership
Function Elicitation using Plausible Neural Network.
Li, Kuo-chen Li. dan Chang, Dar-jen. 2005 Plausible Neural Network. Pembangkit fungsi keanggotaan otomatis dengan atau tanpa
label class berdasarkan similarity dan pengukuran likelihood sampel data. 5. Generating fuzzy membership function with self-organizing feature map Yang, Chih-Chung. dan Bose, N.K. 2006 Self-organizing feature map Pembangkit fungsi keanggotaan fuzzy otomatis menggunakan self-organizing feature map
2.7 Perbedaan Dengan Riset Yang Lain
Berdasarkan riset yang telah dilakukan, peneliti membuat beberapa perbedaan dalam penelitian ini, yaitu;
1) Algoritma yang digunakan adalah Neural Network;
2) Metode yang digunakan pada pembentukan membership function adalah metode Backpropagation Neural Network;
3) Jumlah variabel input awal adalah satu variabel, yang dibangkitkan secara random sesuai dengan dataset yang digunakan;
4) Dataset yang digunakan dalam penelitian ini terbagi dua, yaitu dataset yang digunakan untuk setiap proses trainning yang terdiri dari dataset umur dan suhu, serta dataset untuk proses testing yaitu dataset data nilai siswa dan berat;
5) Algoritma yang digunakan untuk penentuan target awal pada proses trainning adalah algoritma kohonen;
yang terdiri dari Sangat Rendah (SR), Rendah (R), Sedang (S), Tinggi (T) dan Sangat Tinggi (ST).
2.8 Kontribusi Riset
Dalam penelitian ini, algoritma yang akan digunakan dalam membangkitkan membership function adalah metode Backpropagation Neural Network, diharapkan dari penelitian ini akan didapatkan metode yang lebih efektif dalam menentukan nilai membership function secara otomatis.