BAB 2 TINJAUAN PUSTAKA
2.1. Teori Relativitas Umum
Teori Relativitas Umum adalah salah satu teori fisika modern yang cukup besar
peranannya dalam menerangkan struktur ruang-waktu dan jagad raya. Teori ini adalah
teori yang indah, memiliki daya pikat ramalan terhadap gejala alam yang cukup
menarik, namun memiliki persyaratan matematik berupa analisis tensor.
Pada tahun 1915 sebelum teori Relativitas Umum (TRU) diperkenalkan oleh
Einstein, orang mengenal sedikitnya tiga hukum gerak yaitu mekanika Newton,
relativitas khusus dan gravitasi newton. Mekanika Newton sangat berhasil di dalam
menerangkan sifat gerak benda berkelajuan rendah. Namun mekanika ini gagal untuk
benda yang kelanjuannya mendekati laju cahaya. Di samping itu,transformasi Galilei
gagal apabila diterapkan pada hukum-hukum seperti persamaan Maxwell yang
sifatnya menjadi tidak kovarian di dalam kerangka inersial.
Kekurangan ini ditutupi oleh Einstein dengan mengemukakan Teori Relativitas
Khusus (TRK). Teori ini dibangun di atas dua asas, yaitu :
1. Semua hukum fisika memiliki bentuk yang tetap (kovarian) di dalam sembarang
kerangka inersial.
2. Kelajuan cahaya di dalam ruang hampa bernilai tetap (invarian) dan tidak
bergantung pada gerak sumber maupun pengamat.
Asas kedua di atas merupakan tulang punggung TRK Einstein. Tanpa adanya
pernyataan kedua tersebut, tidak ada TRK Einstein, yang ada hanyalah teori relativitas
klasik (Newton-Galilei).
Teori Relativitas Khusus Einstein berhasil menerangkan fenomena benda saat
melaju mendekati laju cahaya. Di samping itu TRK berhasil merumuskan
kekovarianan persamaan Maxwell di sembarang kerangka inersial dengan
menggunakan transformasi Lorentz sebagai pengganti transformasi Galilei. Teori ini
juga lebih lengkap daripada mekanika Newton, karena untuk gerak dengan kelajuan
rendah, mekanika relativistik tereduksi menjadi mekanika Newton. Salah satu implikasi teori ini adalah ungkapan tidak ada benda atau sinyal yang dapat bergerak
2.2. Teori Medan Gravitasi Einstein
Hingga saat ini pekerjaan kita seluruhnya adalah matematika murni (terpisah dari asumsi fisis bahwasannya lintasan partikel adalah geodesik). Pekerjaan ini telah dilakukan sejak satu abad yang lalu dan diterapkan ke ruang lengkung dalam
sembarang jumlah dimensi. Tempat dimana jumlah dimensi akan muncul dalam
formalisme adalah dalam persamaan :
�µµ = jumlah dimensi. Einstein membuat asumsi, dalam ruang kosong :
�µ = (2.1)
Relasi ini memenuhi hukum gravitasinya. ”Kosong” disini berarti tak ada materi yang hadir dan tak ada medan fisis kecuali medan gravitasi. Medan gravitasi tidak mengganggu kekosongan. Medan yang lain mengganggu kekosongan. Syarat
ruang kosong berlaku dalam aproksimasi yang baik untuk ruang antar planet dalam
sistem matahari dan persamaan (2.1) berlaku di sana.
Ruang datar dengan nyata memenuhi persamaan (2.1). Bila geodesik adalah
garis lurus, maka partikel akan bergerak sepanjang garis lurus. Namun ruang tidaklah
datar, hukum Einstein mengajukan pembatasan pada kelengkungan. Dikombinasikan
dengan asumsi planet-planet bergerak sepanjang geodesik memberikan informasi
tentang gerak benda-benda luar angkasa.
Pada pandangan pertama hukum gravitasi Einstein tidak nampak seperti
hukum gravitasi Newton. Untuk melihat keserupaannya, kita harus melihat gµν sebagai potensial yang menggambarkan medan gravitasi. Terdapat sepuluh yang
menggambarkan medan gravitasi, sebagai ganti hanya satu potensial dari teori
Newton. Hal ini menggambarkan tak hanya medan gravitasi, tetapi juga sistem
koordinat. Medan gravitasi dan sistem koordinat tercampur padu dalam teori Einstein, dan kita tak dapat mendeskripsikan salah satu tanpa yang lain. (Dirac PAM, 2005)
2.3. Latar Belakang Schwarzschild
Schwarzschild (shvarts-shilt atau shwortschIld) merupakan anak laki-laki dari
seorang pebisnis Yahudi yang sukses di Frankfurt am Main, Jerman. Beliau memiliki
dua jurnal tentang orbit biner ketika beliau baru berumur 16 tahun. Dua tahun setelah
berkuliah di Universitas Strasbourg, ia melanjutkan studinya di Universitas Munich
pada tahun 1893, serta mendapatkan gelar PhD pada tahun 1896. Beliau bekerja di
Observator Kuffner di Vienna mulai tahun 1896 sampai 1899 dan setelah beberapa
periode menjadi dosen dan banyak menulis maka pada tahun 1901 beliau mendapatkan
gelar Profesor Asosiasi, serta Guru Besar di Universitas Göttingen dan menjadi
direktur di Observator di Universitas tersebut. Pada tahun 1909 Beliau diangkat
menjadi direktur Observator Astrofisika di Potsdam. Beliau juga menjadi relawan
dinas militer pada tahun 1914 ketika permulaan perang dunia I, dan beliau dipulangkan
karena sakit pada tahun 1916. Beliau menderita penyakit kulit aneh dan dari penyakit
inilah beliau kemudian meninggal dunia.
Keterampilan praktis Schwarzschild telah ditunjukkan oleh
instrumen-instrumen yang dirancangnya, teknik pengukuran telah ia lakukan, dan pengamatan
yang ia perbuat. Pada tahun 1890, ketika penggunaan fotografi untuk tujuan ilmiah
masih dalam masa pertumbuhan, ia telah mengembangkan metode-metode untuk
mengukur magnitudo tampak, yaitu mengamati kecerahan dari bintang-bintang yang
bisa diukur secara akurat dari pelat fotografi. Pada waktu itu, magnitudo bintang
biasanya ditentukan hanya dengan mata. Ia kemudian mampu membuat fotografi
magnitudo dari 3.500 bintang yang magnitudonya lebih besar dari 7,5 dan terletak di
antara 0 ° sampai 20 ° di atas equator. Ia juga telah menentukan magnitudo pada
bintang yang sama secara visual, mendemonstrasikan bahwa kedua metode tidak
menghasilkan hasil yang identik. Perbedaan antara magnitudo visual dan magnitudo
fotografi dari suatu bintang, diukur pada panjang gelombang tertentu, sekarang dikenal
sebagai indeks warna.
Schwarzschild juga telah membuat kontribusi-kontribusi besar terhadap
astronomi teoritis, subjek-subjeknya meliputi ilmu mekanika orbit, kurva ruang, dan
struktur permukaan matahari. Pada tahun 1906 beliau mempublikasikan sebuah
naskah jurnal yang menjelaskan bahwa bintang tidak hanya terdiri dari gas yang
tertahan secara bersamaan oleh gravitasi milik bintang tersebut.
Pertanyaan-pertanyaan tentang termodinamika kemudian bermunculan, dengan memperhatikan
perpindahan panas dalam bintang secara radiasi dan konveksi, yang membutuhkan
dipublikasikan pada tahun 1916. Ketika sedang berdinas di Russia, Schwarzschild
menuliskan dua naskah jurnal tentang teori Einstein tersebut, yang juga dipublikasikan
pada tahun 1916.
Beliau memberikan solusi “ – the first to be found – of the complex partial equation” (- penemuan pertama – dari persamaan parsial kompleks), teori ini
dinyatakan secara matematis dan memperkenalkan gagasan yang mana sekarang
dikenal sebagai Radius Schwarzschild. Ketika sebuah bintang, sedang berkontraksi di
bawah pengaruh gravitasi, jika mencapai radius tertentu maka potensial gravitasi akan
bernilai tak hingga. Sebuah Objek harus melakukan perjalanan dengan kecepatan
cahaya untuk melarikan diri dari medan gravitasi bintang. Nilai dari radius ini, Radius
Schwarzschild (Schwarzschild Radius, SR) , tergantung pada massa objek. Jika sebuah
objek mencapai radius kurang dari radius Schwarzschild, termasuk cahaya, akan dapat
melepaskan diri dari potensial gravitasi ini dan potensial gravitasi inilah yang akan
menjadi apa yang sekarang dikenal sebagai "lubang hitam." SR untuk matahari adalah
3 kilometer sedangkan radius sebenarnya adalah 700.000 kilometers. Studi teoritis tentang lubang hitam dan keberlanjutan penelitian tentangnya telah menjadi bidang
penting dalam astronomi modern. Anak dari Schwarzschild bernama Martin yang juga
tercatat sebagai seorang astronom. (Dantith J, 2009)
2.4. Ruang Waktu Minkowski
Setiap teori fisika dibuat berdasarkan “gambar-gambar” pengamatan -pengamatan dari fenomena fisis dalam ruang geometrikyang disebut teori tentang “ruang”. Dalam fisika Newtonian ruang ini merupakan ruang euclidean E3. Dalam teori relativitas khusus ruang ini disebut dengan ruang-waktu dan hal ini merupakan
perbedaan yang sangat fundamental terhadap ruang E3 dari fisika Newtonian.
Untuk pertama kali, konsep tentang ruang-waktu diperkenalkan oleh H.
Minkowski dalam pidatonya pada seminar Kongres ke-80 Saintis Jerman pada seminar
Sains Fisika, yang mana bertempat di Cologne pada tanggal 21 September 1908, tiga
tahun setelah merayakan pekerjaan Einstein tentang Teori Relativitas Khusus.
Kata-kata dari H. Minkowski pada kongres yang menjadi pertimbangan untuk menjadi hal klasik berdasarkan : Pandangan-pandngan mengenai ruang dan waktu yang mana ingin
dan bahwa hal tersebut bebohong tentang kekuatannya. Hal ini sangat radikal. Oleh
karenanya ruang dengan dirinya sendiri, dan waktu pula dengan dirinya sendiri, adalah
hal terbodoh yang harus dibuang jauh kedalam bayang-bayang, dan hanya beberapa kesatuan dari yang “dua” akan memberikan sebuah kenyataan yang hakiki. (Tsamparlis M, 2010)
Ruang-waktu Minkowski adalah gagasan matematika Minkowski dengan
menggunakan vektor yang memungkinkan orang mengukur jarak dalam ruang-waktu,
dua hal yang sudah mengkristal menjadi satu kesatuan. Tahun 1907, Minkowski
mengungkapkan bahwa karya Lorenz dan Einstein akan lebih mudah dipahami lewat
konsep ruang non-Euclidian. Menggagas ruang dan waktu, yang awalnya disangka dapat dipisahkan, ternyata menjadi “pasangan abadi” dalam dimensi keempat dari ‘kontinuum ruang-waktu’. Temuan ini digunakan sebagai kerangka acuan dalam elektrodinamika. Karya-karya ini dituang dalam Raum und Zeit (1907) dan Zwei
Abhandlungen uber die grundgleichungen der Elektrodynamik (1909).
Ruang waktu dapat dianggap sebagai sistem koordinat empat dimensi di mana
sumbu diberikan oleh (x, y, z, ct). Sumbu tersebut dapat dinotasikan ulang sebagai (x1,
x2, x3, x4). Dimana x4 mewakili ct. Alasan untuk mengukur waktu dalam satuan
kecepatan cahaya pada koordinat waktu adalah agar satuan waktu sama dengan satuan
ruang. Ruang waktu memiliki perbedaan panjang busur yang diberikan oleh
= − + + + (2.2)
Ini berarti ruangwaktu memiliki tensor metrik yang diberikan oleh
� = [ −
]
Hermann Minkowski memperkenalkan metode tertentu untuk sistem koordinat
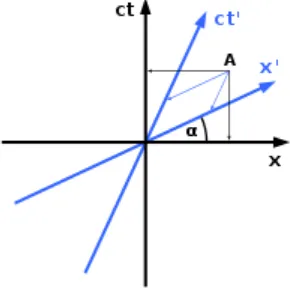
grafik di ruang minkowski. Seperti yang terlihat pada gambar, sistem koordinat yang
berbeda tidak dapat dipergunakan pada orientasi dan posisi spasial suatu objek pada
waktunya. Seperti yang dapat dilihat dari diagram, hanya ada satu sumbu spasial
(sumbu x) dan satu sumbu waktu (sumbu ct). Jika perlu, seseorang dapat
memperkenalkan dimensi ruang ekstra, (sumbu y); Sayangnya, ini adalah batas jumlah
dimensi: grafik dalam empat dimensi tidaklah memungkinkan. Aturan untuk grafik di
1. Sudut antara sumbu x dan x’ adalah � � = dimana v adalah kelajuan objek
2. Kecepatan cahaya melalui ruangwaktu selalu membuat sudut 45 derajat dengan
kedua sumbu.
Gambar 2.1. Grafik ruang-waktu Minkowski 4 dimensi
Pada umumnya ruang-waktu Minkowski dianggap sebagai tempat yang tepat
untuk merumuskan hukum fisika yang tidak merujuk secara khusus pada fenomena
gravitasi. Kita akan meluangkan waktu sejenak sebagai permulaan untuk memeriksa
beberapa keadaan yang menimbulkan kepercayaan ini.
Kita akan mengadopsi sudut pandang bahwa masalah dasar sains pada umumnya adalah deskripsi suatu “peristiwa” yang terjadi secara fisis di alam semesta dan analisis hubungan antar peristiwa tersebut. Dalam hal ini kita menggunakan istilah “peristiwa”, namun dalam pengertian ideal lain “pokok-peristiwa” adalah suatu kejadian fisis yang tidak memiliki perluasan ruang dan tidak berada dalam durasi atau
perubahan waktu. Kita dapat membayangkan sebuah tabrakan seketika atau sebuah ledakan atau kejadian “seketika” yang terjadi pada beberapa partikel atau foton (dianggap sebagai “partikel cahaya”). Dengan cara ini, keberadaan partikel atau foton dapat direpresentasikan oleh rangkaian kejadian yang berkelanjutan yang disebut kejadian “duniawi”. Kemudian kita akan mulai dengan himpunan abstrak M yang elemennya kita sebut “peristiwa.” Kita akan mengasumsikan M sebagai struktur matematis yang mencerminkan fakta-fakta sederhana tentang pengalaman manusia
sebagai hasil eksperimental fisika yang agak sepele.
peristiwa bekerja pada alam sebagai alat untuk melakukan persepsi bahwa kita mengidentifikasi kejadian dengan “lokasi dalam ruang dan waktu”, kita harus menentukan cara pengamat untuk menyelesaikannya agar dianggap “dapat diterima”. (Naber G L, 2010)
Menjelang musim gugur tahun 1908, Minkowski telah berbicara secara terbuka
tentang pandangannya mengenai relativitas pada beberapa kesempatan, namun tidak
pernah berada di luar Gottingen. Pertemuan tahunan Asosiasi Jerman merupakan
kesempatan pertama Minkowski untuk berbicara tentang relativitas sebelum
pertemuan internasional elit fisikawan, matematikawan, astronom, ahli kimia dan
insinyur. Tidak ada pertemuan lain yang bisa dilakukan ilmuwan di Jerman untuk
berinteraksi dengan ilmuan lain yang bekerja pada disiplin ilmu di luar negerinya
sendiri.
Organisasi dari berbagai bagian disiplin dalam pertemuan tahunan Asosiasi
Jerman dikelola oleh perhimpunan ilmuan yang sesuai. Sebagai contoh, Perhimpunan
Fisikawan Jerman mengatur bagian fisika dan Perhimpunan Matematikawan Jerman
mengelola bagian matematika. Untuk bagian yang terakhir yaitu tentang tema diskusi
diumumkan pada akhir April oleh presiden perhimpunan yang bernama Felix Klein.
Dalam sebuah panggilan untuk makalah, Klein mendorong penulis untuk
menyerahkan karya terutama di bidang mekanika. Namun, sebelum pengumuman
tersebut, Klein pasti sudah mengatur setidaknya satu kontribusi mengenai mekanika,
karena dia menambahkan sebuah penggoda, menjanjikan "aspek ahli" dari
penyelidikan baru-baru ini di bidang mekanika. Dorongan ini sangat menggoda
Minkowski untuk memberikan ceramah, draf yang dikirimkan sebelumnya kepada
Klein menjadi referensi awal untuk mengawali pertemuan ini. Ceramahnya adalah
ceramah pertama dari tujuh di bagian matematika pada pertemuan Perhimpunan
Matematikawan Jerman. (Walter S, 1999)
2.5. Solusi Schwarzschild
Persamaan Medan sendiri mungkin diturunkan dengan melihat kembali pada
analogi dan mencatat cara pada persamaan Laplace yang terkait pada medan tersebut
� = � = (2.3) yang merupakan persamaan medan, sehingga berdasarkan persamaan tersebut dapat
ditemukan di sini. Dalam kasus ini, bagaimanapun, tensor Riemann-Christoffel
memiliki sifat simetri tertentu, dan sebagai hasil persamaan ini mewakili sepuluh
persamaan skalar. Hal tersebut merupakan jumlah yang tepat untuk menentukan
sepuluh koefisien metrik. Solusi yang paling terkenal dari persamaan ini dan solusi
pertama yang ditemukan adalah berdasarkan simetri bola. Bentuk simetris pada solusi
simetris statis berbentuk bulat / bola tidak bisa lebih umum daripada :
= − − � + � � � (2.4)
di mana , , adalah fungsi dari r. Namun, kita harus ingat bahwa kita diperbolehkan
melakukan berbagai transformasi koordinat, dan oleh karena itu mungkin untuk
menggantikan vektor radius oleh r yang lain sedemikian rupa untuk memastikan v = 0
(setidaknya ini adalah apa yang diasumsikan pada awal teori, meskipun sekarang
menyadari bahwa ada satu kasus yang luar biasa di mana hal ini tidak mungkin, yaitu
ketika v = - log r). Oleh karena itu koefisien bukan nol dari metrik adalah
� = , � = − , � = − , � = − � � (2.5)
dan sesuai simbol dengan akhiran yang diangkat
� = − , � = − − , � = − 2, � = − 2 2
� (2.6) di mana bilangan prima menunjukkan diferensiasi terhadap r, dan melihat rumus untuk
koefisien persamaan koneksi menunjukkan bahwa hanya yang bukan nol yang dapat
{ } = ′ 2 − ,
{ } = ′,
{ } = ′,
{ } = − − ,
{ } = ,
{ } = − � �,
{ } = ,
{ } = − sin � cos � ,
{ } = cot �.
Langkah selanjutnya adalah menghitung kelengkungan tensor yang
terkontraksi atau tensor Ricci seperti yang telah dikenal. Rumus untuk ini dapat ditulis
sedikit berbeda dalam bentuk
� = �, − Γ , + Γ�Γ� − Γ��,� , (2.7)
Dimana � = �√ −� . Hal ini juga demikian, dengan
Γ� = � [ , ] = � ��, − �� , + � ,� (2.8)
Dalam ungkapan ini dua suku pertama adalah anti-simetris di k dan l dan tidak
memberikan apa-apa ketika dijumlahkan dengan gkl. Hubungan yang tersisa adalah
� � ,�= ��,� ,
dimana g sekarang ditulis untuk penentu gij}. Karena, dengan nilai g negatif (dalam
sistem lokal Cartesian itu - 1) ini adalah yang terbaik yang ditulis dalam bentuk ф,p.
Sekarang masalah sedikit membosankan, tetapi langsung untuk menghitung semua
komponen yang mungkin bukan nol:
� = ′′− ′ ′+ ′ − ′,
� = − ( + ′− ′ ) − ,
� = − − ′′+ ′ ′− ′ − ′ ,
Dan � yang secara fakta kemudian menjadi bernilai nol.
Persamaan medan yang sekarang adalah � = . Di dapat dari :
� + − � = − ( ′+ ′), (2.9)
Hal ini berdasarkan bahwa
′+ ′=
Pada titik ini dalam teori tersebut mulai terbukti sangat tidak tepat untuk menampilkan kecepatan cahaya с pada setiap kali terjadi. Oleh karena itu lebih tepat untuk mengadopsi sebuah unit tertentu dari panjang bahwa unit waktu adalah satu detik, dan с = 1. (Artinya, kita mengadopsi sebagai satuan panjang jarak tempuh cahaya dalam satu detik.) metrik relativitas khusus akan memiliki bentuk :
= − + + (2.10)
kita kemudian akan memiliki alasan untuk memperbaiki unit massa juga, sehingga
Situasi akhir hanya akan ada satu standar waktu yang diperlukan. Jika kita mengambil
ruang datar di tak terhingga sebagai syarat batas, sehingga kita dapat memperbaiki
sistem koordinat dengan kebutuhan
→ , → (2.11)
Pada r ∞, hal ini memberikan + = . Disubtitusikan pada � = sehingga memberikan
+ ′ = (2.12)
Yaitu :
( ) = (2.13)
Sehingga :
≈ − , (2.14)
dimana konstan integral tertentu telah disebut -2m, untuk alasan yang akan menjadi
jelas segera. Solusi yang kita temukan merupakan penemuan Schwarzschild (1916),
maka memiliki bentuk
= − − 2
Kita dapat langsung menggunakan solusi ini tanpa perhitungan lebih lanjut jika
kita mempertimbangkan bidang statis lemah, gerakan lambat, dengan melakukan
pendekatan teori.(Kilmister CW, 1973)
2.6. Radius Schwarzschild
Akhirnya bentuk metrik isotropik statik untuk ruang−waktu 4 dimensi berkoordinat bola adalah
= − ( − �) + ( − �)− + � + � � �
(2.16)
Bentuk metrik ini pertama kali diturunkan oleh Karl Schwarzschild pada tahun
1916. Karena itu, metrik ini sering disebut metrik Schwarzschild. Bentuk metrik
tersebut masih mengisikan nilai c = 1. Apabila nilai c diisikan, bentuk metrik
Schwarzschild menjadi
= − ( − �) + ( − �)− + � + � � �
(2.17)
Bentuk 2GM/c2 sering disingkat menjadi m (bersatuan panjang), sehingga
metrik di atas menjadi
= − ( − ) + ( − )− + � + � � �
(2.18)
Metrik Schwarzschild ini bersifat simetri bola dan merepresentasikan medan
gravitasi di luar suatu partikel bersimetri bola dengan pusat partikel terletak pada pusat
koordinat bola ( , �, �) .
Dari pers. (2.17) tampak bahwa metrik tersebut tidak valid untuk
= = ��2 (2.19)
Jarak tersebut dinamakan radius Schwarzschild. Dalam satuan SI nilai c = 3 ×
108 dan untuk bumi, GM = 3,991 × 1014, sehingga radius Schwarzschild untuk partikel
bumi adalah sekitar 9 mm, karena itu tidak ada persoalan jika metrik ini diterapkan untuk bumi. Namun ada keadaan tertentu jika radius Schwarzschild cukup besar, hal
ini terjadi jika M bernilai cukup besar, sementara radius objek tersebut cukup kecil,
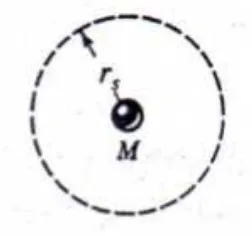
Penggambaran radius Schwarzschild dalam lubang hitam dapat dilihat pada
Gambar 2.1.
Gambar 2.2. Lubang Hitam Schwarzschild bermassa M beradius rs
2.7. Lubang Hitam Schwarzschild
Pada tahun 1930-an, beberapa ilmuwan (tidak termasuk Einstein) percaya
bahwa lubang hitam mungkin ada, tapi tidak ada yang tahu bagaimana mereka dapat
dibuat karena tekanan yang sangat tinggi sangat yang diperlukan. Salah satu caranya
harus memeras matahari dari radius saat ini dari sekitar 435.000 mil (700.000 km) ke 1,9 mil (3 km). Untuk membuat lubang hitam dari Bumi ukuran bumi harus dikompresi
hingga ukuran kacang polong. Pertanyaan yang dihadapi fisikawan diantaranya adalah
dapatkah sesuatu menghasilkan tekanan tinggi seperti itu? Selanjutnya, jika demikian,
apa yang membuatnya demikian? Jawaban - ya dan gravitasi - yang ditemukan pada
bintang-bintang.
Bintang adalah bentuk keseimbangan antara tarikan ke dalam gravitasi dan
tekanan luar yang diberikan oleh gas panas pada inti bintang. Energi yang
memanaskan gas berasal dari fusi nuklir. Namun, bahan bakar untuk fusi itu, terutama
hidrogen dan helium, akhirnya akan habis, dan ketika hal itu terjadi, gravitasi sedang
menunggu. Di bawah kekuatan tanpa henti, bintang kemudian akan runtuh.
Titik akhir keruntuhan sebuah bintang tergantung pada ukurannya. Bintang
dengan massa hampir sama dengan Matahari melalui beberapa tahapan untuk mati,
seperti meluas dan berkontraksi dan meniup lapisan luar gas karena hal ini menguras
bahan bakar nuklirnya. Apa yang akhirnya ditinggalkan adalah inti membara dari
gravitasi bintang yang dikompresi, sisa padat karbon dan oksigen ion dan elektron.
dari gas panas seperti pada sebuah bintang bersinar. Hal itu berasal dari prinsip
pengecualian Pauli.
Meningkatnya tekanan gravitasi di inti sisa akan meremas elektron secara
bersama-sama, membentuk gas elektron yang merosot. Karena, sebagai salah satu
prinsip terkenal Pauli, tidak ada dua elektron yang dapat dipisahkan oleh posisi yang
menempati keadaan kuantum yang sama, kompresi lebih lanjut mendorong
elektron-elektron tersebut ke tingkat energi yang lebih tinggi dan lebih tinggi lagi. Energi
tingkat tinggi ini, elektron berkecepatan tinggi sangat menolak kompresi. Resistensi
terhadap kompresi ini disebut tekanan degenerasi elektron. Hal ini terjadi dalam segala
materil, tapi hal ini dapat diabaikan pada kepadatan yang biasa.
Ketika bintang-bintang berukuran matahari runtuh, tekanan degenerasi
mengimbangi gaya gravitasi. Hasilnya adalah sebuah objek padat yang disebut bintang
katai putih. Sisa-sisa bintang ini adalah konsekuensi dari gravitasi ekstrim, yang telah
meninggalkan mereka dengan sifat yang luar biasa.
Sebuah Bintang yang berukuran seperti matahasi akan berakhir sebagai bintang
katai putih seukuran Bumi. Kepadatan bintang katai putih yang khas adalah 109
kilogram per meter kubik, satu juta kali kepadatan air. Satu sendok teh bintang katai
putih adalah sebesar dari 5 ton (4.536 kg). Sifat lain dari degenerasi materi adalah
hubungan antara ukuran dan massa. Massa yang berukuran dua kali dari bintang
normal atau gas biasa (atau cair atau padat) pada tekanan tetap dan suhu dan
volumenya akan berlipat ganda. Dua kali lipat massa bintang katai putih dan
volumenya akan berkurang. Ini berarti bahwa bintang yang lebih besar akan
membentuk bintang katai putih yang lebih kecil. Penyebab di balik sifat mengejutkan
ini adalah gravitasi: Semakin besar massa berarti gravitasi yang lebih tinggi. gravitasi
yang lebih tinggi menghasilkan kepadatan yang lebih tinggi pula dan dengan ukuran
yang lebih kecil. (Manning, Philip, 2012)
2.8. Graphic User Interface
Dalam teknologi komputasi, antarmuka pengguna grafis atau APG (Inggris:
Graphical User Interface atau GUI) adalah jenis antarmuka pengguna yang
penggunaan komputer, peranti bergerak seperti pemutar MP3, pemutar media portabel
atau piranti permainan, peralatan rumah tangga, dan peralatan kantor. GUI
menggambarkan informasi dan perintah yang tersedia untuk pengguna menggunakan
ikon grafis. Contoh: Microsoft Windows, MacOS dan Xwin menggunakan jenis GUI
yang berbeda. (https://id.wikipedia.org/wiki/Antarmuka_pengguna_grafis)
Dewasa ini hampir semua software berlomba untuk membuat GUI-nya
menjadi lebih menarik sehingga pengguna juga akan tertarik untuk menggunakan
software tersebut. Hal yang dituntut dari GUI sudah bukan lagi user
friendly melainkan usability, yaitu: a measure of the ease with which a system can be
learned or used, its safety, effectiveness and efficiency, and attitude of its users towards
it. Usablity memiliki 3 aspek yaitu learnability (kemudahan bagi pengguna baru untuk
dapat menggunakan sistem secara efektif dan mencapai kinerja yang paling
optimal), flexibility (variasi cara/model bagi pengguna dan sistem dalam bertukar
informasi), dan effectiveness/robustness (tingkat dukungan yang disediakan bagi
pengguna untuk mencapai tujuannya dengan sukses dan memberikan penilaian tingkah
laku yang diarahkan oleh suatu tujuan). Ketiga aspek ini jika tercapai maka akan
memberikan nilai attitude (kenyamanan bagi pengguna). Evaluasi GUI dilihat dari
prinsip user friendly maupun usability dapat dilakukan dengan melihat bagaimana
perkembangan GUI dari masa ke masa. Kadang kita sangat sulit untuk mendapatkan
informasi perkembangan GUI tersebut karena mungkin kita belum pernah
menggunakannya. Tetapi hal ini sudah tidak menjadi masalah lagi karena di era
Internet ini ada situs-situs yang telah menyediakan fungsi sebagai ‘museum’ GUI,
yaitu GUIdebook dan Graphical User Interface Gallery.Berdasarkan data-data dari
situs-situs ini, misalnya screenshot, maka kita dapat melakukan evaluasi mengenai
GUI tersebut.
(https://blogs.uajy.ac.id/sigitpurnomo/2006/06/13/graphical-user-interface-gui-dari-masa-ke-masa/)
2.9. Fisika Komputasi
Secara garis besar, ilmu fisika dapat dipelajari dengan tiga cara, yaitu
1. Menggunakan konsep atau teori fisika yang akhirnya melahirkan fisika teori.
2. Eksperimen yang menghasilkan aliran fisika eksperimental
Untuk dapat lebih memahami suatu gejala fisis dan untuk pengembangan ilmu
fisika, perlu dilakukan sesuatu eksperimen. Eksperimen adalah suatu hal yang mutlak
harus dilakukan dalam bidang fisika, karena eksperimen adalah hakim kebenaran
dalam fisika. Eksperimen selalu diperlukan untuk pengujian teori dan pengembangan
teori-teori baru, di samping itu dalam proses belajar mengajar eksperimen juga dapat
membantu untuk lebih memahami hukum-hukum fisika.
Namun demikian, dalam melakukan suatu eksperimen selalu ditemukan
kendala-kendala, antara lain disebabkan oleh beberapa faktor, yaitu:
1. Gejala fisika yang diteliti prosesnya relatif cepat sehingga sukar diukur dan diamati
visualisasinya.
2. Ukuran benda yang akan diteliti relatif kecil (mikro) sehingga sukar diukur.
3. Gejala yang diteliti cenderung berbahaya.
4. Peralatan yang diperlukan untuk analisis suatu gejala relatif mahal atau sukar
dioperasikan.
5. Data hasil eksperimen yang diperoleh cukup besar dan tidak linear sehingga sukar
dianalisis.
Kendala-kendala tersebut menyebabkan karakteristik suatu gejala fisis tidak
dapat terungkap secara tuntas, hal ini menyebabkan ketidaklengkapan informasi dan
akan mengganggu perkembangan ilmu fisika itu sendiri.Dalam hal lain pada
pembahasan fisika teoretis hukum-hukum fisika diformulasikan dalam bentuk bahasa
matematis. Hubungan suatu besaran fisis lainnya dalam suatu sistem pada umumnya
dapat dinyatakan dalam bentuk model matematis. Model matematis tersebut disusun
secara deduktif berdasarkan hukum-hukum alam yang telah teruji kebenarannya.
Berdasarkan model matematis suatu sistem fisis, dapat diketahui karakteristik sistem
fisis tersebut, dan melalui karakteristik sistem fisis dapat diramalkan hal-hal yang akan
terjadi bila sistem diberi suatu perlakuan tertentu. Dalam fisika teori, hukum-hukum
fisika akan diformulasikan dalam bentuk model matematis, dengan prinsip analogi,
linearisasi, simetri dan pendekatan sehingga model matematis tersebut dapat dengan
mudah diselesaikan secara analitis. Akan tetapi, dalam banyak hal model matematis
yang membangun suatu sistem fisis bentuknya sangat kompleks dan rumit sehingga
tidak dapat diselesaikan secara analitis. Bila model matematis suatu sistem fisis tidak
dalam model matematis tersebut tidak menggambarkan keadaan yang sesungguhnya
dengan kata lain karakteristik gejala fisis tidak dapat terungkap secara tuntas.
Model-model matematis yang tidak dapat atau relatif sulit diselesaikan secara
analitis, dapat diselesaikan dengan metode numerik. Metode numerik merupakan salah
satu penyelesaian matematis dengan proses secara bertahap dengan melakukan
perulangan sampai ditemukan kondisi yang diinginkan. Sesuai dengan perkembangan
teknik komputasi maka untuk memilih metode numerik yang sesuai, dipakai kriteria
berikut:
1. Galat numerik global metode yang dipilih kecil.
2. Mudah menukar ukuran langkah yang dipakai.
3. Mudah disusun programnya.
4. Langkah-langkah untuk mencapai konvergensi atau untuk mencapai nilai yang
diinginkan sederhana.
Langkah-langkah untuk melakukan analisis suatu sistem fisis dengan
pendekatan fisika komputasi adalah sebagai berikut:
1. Menyusun model matematis.
2. Melakukan modifikasi model matematis sehingga dapat diselesaikan dengan
pendekatan numerik.
3. Memilih model metode numerik yang sesuai.
4. Melakukan pendekatan sedemikian rupa, sehingga dapat diselesaikan secara
analitis. Nilai pendekatan analitis ini diperlukan untuk validasi atau testing program
apakah telah berjalan dengan baik.
5. Meneliti program-program paket yang tersedia.
6. Merancang program komputer bila tidak tersedia program paket (Zarlis M, 1994).
Dalam fisika komputasi data-data eksperimen yang besar dan tidak linear
dapat diolah dengan bantuan perangkat lunak komputer demikian juga kendala yang
lain dapat diatasi dengan eksperimen simulasi dengan komputer, model matematis
yang non-linear dan non-simetri dapat diselesaikan dengan bantuan metode numerik
dalam bentuk program komputer. Dengan demikian keberadaan fisika eksperimen,
fisika teori, dan fisika komputasi adalah saling mendukung dalam penelitian dan
Fisika komputasi adalah satu bagian integral dari perkembangan masalah atau
gejala-gejala fisika dan berkemampuan untuk mengantisipasinya dengan
menggunakan perangkat komputer. Pembuatan simulasi gejala-gejala fisika ini dapat
dilakukan dengan algoritma dan program komputer. Penerapan komputer dalam ilmu
fisika banyak terlihat pada pemecahan masalah-masalah analitik yang kompleks dan
pekerjaan-pekerjaan numerikal untuk penyelesaian secara interaktif. Oleh karena itu,
fisika komputasi menawarkan penggabungan tiga disiplin dan ilmu, yakni ilmu fisika,
analisis numerik, dan pemrograman komputer.
2.10. Wolfram Mathematica 10.2
Mathematica terdiri dari dua bagian: kernel dan antar muka. kernel melakukan
yang perhitungan, dan antar muka menyediakan penghubung antara pengguna dan
kernel. Sedangkan kernel tetap sama, antar muka dioptimalkan untuk setiap jenis
sistem komputer. (Patrick T T, 1997)
Wolfram Mathematica atau yang sering disebut dengan Mathematica
merupakan suatu sistem aljabar komputer (CAS, Computer Algebra System) yang
mengintegrasikan kemampuan komputasi (simbolik, numerik), visualisasi (grafik), bahasa pemprograman, dan pengolahan kata (word processing) ke dalam suatu
lingkungan yang sudah di gunakan.
Mathematica merupakan software aplikasi buatan Wolfram Research yang
handal dengan fasilitas terintegrasi lengkap untuk menyelesaikan beragam masalah
matematika. Dengan Mathematica kita akan merasakan sebuah revolusi pada peran
dan praktik matematika yang dengannya beragam kasus matematika, dari masalah
yang paling sederhana hingga perhitungan yang paling rumit, dapat diselesaikan
dengan mudah, ringkas, cepat dan tepat. Mathematica memiliki fasilitas fungsi
matematika terpasang (built-in mathematics function) lebih dari 750 buah yang
menjadikan sintak programnya dapat dinyatakan dalam satu atau beberapa baris
sederhana saja. Kesederhanaan bahasa program inilah yang menjadikan Mathematica
dapat digunakan siapapun tanpa harus terlebih dahulu menguasai suatu bahasa
pemprograman tertentu.
Mathematica menyediakan fasilitas lengkap untuk melaksanakan semua komputasi
matematika tersebut dalam suatu lingkungan kerja yang terintegrasi. Dalam
lingkungan kerja yang demikian maka kita dapat melaksanakan beragam perhitungan
matematika, seperti perhitungan aritmatika, perhitungan aljabar, perhitungan dan
operasi simbolik dalam aljabar matriks, aljabar linear, linear programing, metode
numerik, teori bilangan, matematika diskrit, kalkulus, transformasi laplace,
transformasi fourier, transformasi-z, statistika, geometri, pemodelan matematika dan
simulasi, dan lain-lain.
Mathematica juga memiliki fasilitas lengkap untuk membuat beragam grafik.
Kita dapat membuat grafik fungsi al jabar, fungsi transenden, fungsi parametrik dan
fungsi implisit, fungsi polar, kurva kontur, skaterplot, beragam grafik permukaan
dimensi tiga, grafik medan vektor dimensi dua dan dimensi tiga, grafik animasi,
diagram batang, diagram lingkaran dan lain-lain.Kini Mathematica merupakan salah
satu piranti lunak pilihan dalam pendidikan, penelitian, bisnis dan sebagainya,
khususnya untuk melakukan:
1. Komputasi matematika, baik untuk perhitungan numerik maupun simbolik.
2. Visualisasi grafik fungsi dimensi-dua dan dimensi-tiga.
3. Pemprograman, pemodelan matematika dan simulasi.
4. Analisis statistik dan visualisasi data dalam bentuk tabel dan grafik.
Untuk pengoperasiannya, aplikasi ini mempunyai tampilan yang interaktif
dengan tiga sistem pengoperasian yang mudah. Pertama, pengguna bisa langsung
mengetikkan pertanyaan matematika dalam bahasa Inggris dan Mathematica akan
memberikan jawabannya berdasarkan data statistik dari berbagai organisasi
internasional melalui koneksi internet. Sistem yang kedua disebut palletes, pengguna
memilih daftar fungsi yang ingin digunakan pada menu yang telah disediakan.
Terakhir, pengguna bisa mengetikkan sendiri pertanyaannya sesuai dengan bahasa
matematika yang benar berdasarkan ketentuan - ketentuan penulisan yang ada.
Mathematica dapat melakukan berbagai macam perhitungan mulai dari
perhitungan fungsi - fungsi sederhana hingga algoritma pemrograman yang kompleks
dengan pemodelan 2D, proyeksi 3D, hingga image recognition bisa dihasilkan dengan
aplikasi ini. Tidak hanya hasil akhir, dengan fitur "step-by-step solution" juga dapat
perhitungan yang sudah dibuat sedemikian mudah inilah, aplikasi ini memfasilitasi
pengajar maupun peneliti mana pun untuk mengembangkan berbagai kemungkinan
yang bisa dihasilkan tanpa terlalu memusingkan kerumitan perhitungan yang ada di
dalamnya.
Mathematica adalah, aplikasi serbaguna, paket handal untuk melakukan
perhitungan matematika dan penerbitan hasil matematika. Ini berjalan pada sistem
operasi workstation yang paling populer, termasuk Microsoft Windows, Apple
Macintosh OS, Linux, dan sistem berbasis Unix lainnya. Mathematica digunakan oleh
para ilmuwan dan insinyur dalam disiplin ilmu mulai dari astronomi hingga zoologi;
aplikasi khas termasuk teori bilangan komputasi, pemodelan ekosistem, keuangan
harga derivatif, perhitungan kuantum, analisis statistik, dan ratusan lebih.
Cara terbaik untuk memahami Mathematica adalah dengan melihatnya dalam tindakan. Bagian di bawah ini menjelaskan tiga kategori utama penggunaan:
Sebagai alat pengguna akhir: Mathematica dapat digunakan untuk melakukan
perhitungan, baik secara numerik atau simbolik. Hasil dapat dilihat dengan
menggunakan 2-D dan grafis 3-D. (http://coretan-nafis.blogspot.co.id/2014/11/meng