Jika ketaksamaan<berlaku, maka kita katakan bahwaf naik sejatipadaH. Definisi serupa dapat dirumuskan untuk fungsiturundanturun sejatipadaH. Fungsi naik atau turun disebut fungsimonoton. Fungsi yang naik dan turun sekaligus padaH mestilah konstan padaH.
Contoh 1. (i) Fungsi f : R→ Ryang didefinisikan sebagai f(x) = x3 merupakan fungsi naik sejati padaR.
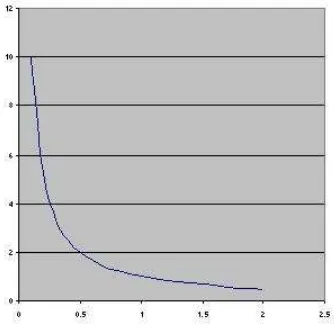
(ii) Fungsi g : (0,∞) → R yang didefinisikan sebagai g(x) = 1
x merupakan fungsi turun sejati pada (0,∞).
Proposisi 2. Jikaf naik pada[a, b], makaf mencapai nilai minimum diadan nilai maksimum di b.
Bukti. Misalkana < x < b. Maka menurut definisi kita mempunyai
f(a)≤f(x)≤f(b).
Jadif mencapai nilai minimum diadan nilai maksimum di b.
Sekarang kita akan membahas limit fungsi monoton. Untuk itu, kita perke-nalkan notasi
f(c−) = lim x→c−
f(x)
Gambar 11.1(i)Grafik fungsif(x) =x3
Gambar 11.1(ii)Grafik fungsig(x) = 1 x
dan
f(c+) = lim x→c+f(x),
asalkan kedua limit ini ada.
Contoh 3. Misalkanf :R→Rdidefinisikan sebagai
f(x) =
x, x≤1;
3
x∈(a,b)
suatu δ > 0 sedemikian sehingga jika b−δ < x < b, maka |f(x)−M| < ǫ atau M −ǫ < f(x)< M+ǫ.
Ketaksamaanf(x)< M +ǫselalu terpenuhi karenaM merupakan batas atas untuk f pada (a, b). Selanjutnya, karenaM −ǫbukan merupakan batas atas untuk f pada (a, b), maka terdapat suatu y ∈ (a, b) sedemikian sehingga M −ǫ < f(y). Namunf naik pada (a, b), sehingga untuk setiapxyang memenuhiy < x < bberlaku
M−ǫ < f(y)≤f(x).
Jadi, pilihlahδ=b−y. (ii) Serupa dengan (i).
Akibat 5. Misalkan f naik pada(a, b). Jikac∈(a, b), maka f(c−)danf(c+)ada, dan
f(x)≤f(c−)≤f(c)≤f(c+)≤f(y)
untuk a < x < c < y < b.
Soal Latihan
1. Buktikan Teorema 4 bagian (ii). Mulai dengan memisalkan m= inf x∈(a,b)f(x).
2. Buktikan jikaf turun dan terbatas di bawah pada (a, b), maka
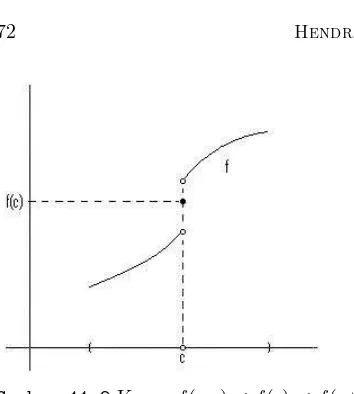
Gambar 11.2Kasus f(c−)< f(c)< f(c+)
3. Buktikan jikaf dang naik (sejati) padaH, makaf+gnaik (sejati) padaH.
4. Diketahui f(x) > 0 untuk setiap x ∈ H, dan g := 1f. Buktikan jika f naik (sejati) padaH, makag turun (sejati) padaH.
5. Diketahui f naik sejati pada A. Buktikan bahwaf merupakan korespondensi 1-1 antaraAdanB :=f(A), sehinggaf−1ada. Buktikan bahwaf−1naik sejati
padaB.
11.2 Fungsi Monoton yang Mempunyai Turunan
Pada bagian ini kita akan membahas bagaimana kita dapat menyelidiki kemono-tonan suatu fungsi melalui turunannya, bila fungsi tersebut mempunyai turunan. Persisnya, kita mempunyai teorema berikut.
Teorema 6. Misalkan f kontinu pada[a, b] dan mempunyai turunan pada(a, b).
(i)Jikaf′(x)≥0untuk tiapx∈(a, b), makaf naik pada [a, b]. Jikaf′(x)>0 untuk
tiapx∈(a, b), makaf naik sejati pada[a, b].
(ii) Jika f′
(x) ≤0 untuk tiap x∈ (a, b), makaf turun pada [a, b]. Jika f′
(x) <0
Contoh 7. Misalkanf :R→Rdidefinisikan sebagaif(x) =x(1−x). Turunannya adalah
f′
(x) = 1−2x. Jadi f′(x)≥0 untuk
x≤ 1 2 dan f
′(x) ≤0 untuk x≥ 1
2. Dengan demikianf naik
pada (−∞,12] dan turun pada [12,∞).
Soal Latihan
1. Misalkan n ∈ N. Buktikan bahwa fungsi f : [0,∞) → R yang didefinisikan sebagai
f(x) = (x+ 1)1/n−x1/n merupakan fungsi turun pada [0,∞).
2. Misalkan f mempunyai turunan dan naik pada suatu interval terbukaI. Buk-tikan bahwa f′(x) ≥ 0 untuk tiap
x ∈ I. Jika f naik sejati pada I, apakah dapat disimpulkan bahwaf′(x)>0 untuk tiapx∈I? Jelaskan.
11.3 Invers Fungsi Monoton
I, maka daerah nilainya juga merupakan suatu interval, sebutlahJ =f(I) (Teorema 10 pada Bab 8). Lebih jauh, kita mempunyai teorema berikut.
Teorema 8. Misalkan f :I→J denganI interval dan J =f(I). Jika f naik sejati dan kontinu pada I, maka f−1:J →I kontinu pada J.
Bukti. Andaikanf−1tidak kontinu di suatu titikd∈J. Asumsikan bahwadbukan
titik ujungJ. Maka, mengingatf−1 naik sejati pada J, f−1(d−) danf−1(d+) ada,
danf−1(d−)< f−1(d+). Sekarang misalkanc∈I sedemikian sehingga
f−1(d−)
< c < f−1(d+) dan
c6=f−1(d).
Karena ituf(c) tidak terdefinisi (buatlah ilustrasinya!), dan ini bertentangan dengan hipotesis bahwaf terdefinisi padaI.
Teorema 9. MisalkanI danJ interval,I◦dan
J◦interval terbuka yang mempunyai
titik ujung sama dengan titik ujung I dan J. Misalkan f : I → J kontinu dan
J =f(I). Jikaf mempunyai turunan padaI◦dan
Catatan. Bukti Teorema 9 dapat dilihat di [2].
Soal Latihan
1. Misalkan f :R→Rdidefinisikan sebagaif(x) = 1 +x+x3. Tunjukkan bahwa f mempunyai invers dan hitunglah nilai (f−1)′(−1).
2. Berikan sebuah contoh fungsi f :A→Ryang naik sejati dan kontinu padaA, tetapi f−1 tidak kontinu pada B = f(A). (Petunjuk. Himpunan A tentunya
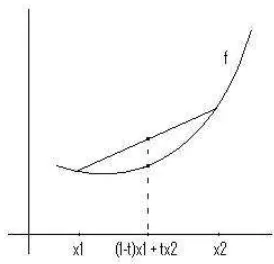
Gambar 11.3Grafik fungsi konveks
Sebuah fungsi konveks tidak harus mempunyai turunan di setiap titik. Sebagai contoh, f(x) = |x| merupakan fungsi konveks pada R tetapi tidak mempunyai tu-runan di 0. Namun, dapat ditunjukkan jikaf konveks pada interval terbukaI, maka f mempunyai ‘turunan kiri’ dan ‘turunan kanan’ di setiap titik dalam I. Sebagai akibatnya, setiap fungsi konveks pada interval terbuka merupakan fungsi kontinu.
Teorema berikut memperlihatkan kaitan antara fungsi konveks dan turunan keduanya, bila fungsi tersebut mempunyai turunan kedua. Istilah konveks dalam hal ini setara dengan istilah ‘cekung ke atas’ yang telah kita bahas pada Bab 9.
f′′
Sebaliknya, misalkanf′′(x)≥0 untuk tiap
x∈I. Untuk membuktikan bahwa f konveks padaI, ambilx1, x2∈I dan 0< t <1, dan misalkanx0= (1−t)x1+tx2.
Berdasarkan Teorema Taylor, terdapatξ1 di antarax0 danx1 sedemikian sehingga
f(x1) =f(x0) + (x1−x0)f′(x0) +
(x1−x0)2
2 f
′′ (ξ1)
dan juga terdapatξ2 di antarax0dan x2 sedemikian sehingga
f(x2) =f(x0) + (x2−x0)f′(x0) +
ada untuk setiapc∈I, dan sebagai akibatnyaf kontinu padaI.
4. Misalkan f mempunyai turunan pada interval terbuka I. Buktikan f konveks jika dan hanya jikaf′ naik padaI.
5. Misalkan I interval terbuka, f : I → Rnaik sejati, konveks, dan mempunyai turunan pada I. Misalkan c ∈ I sedemikian sehingga f(c) = 0. Konstruksi barisanhxnidengan x1> cdan
xn+1=xn−
f(xn)
f′(xn), n= 1,2,3, . . . .
Buktikan bahwa xn → c untuk n → ∞. (Metode penghampiran ‘akar’ f ini dikenal sebagai Metode Newton-Raphson. Untuk f(x) = x2−a, metode ini