TEOREMA GOURSAT Konstruksi subgrup dari grup darab langsung

(1)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 12

A‐2 TEOREMA GOURSAT

Konstruksi subgrup dari grup darab langsung

M.V.Any Herawati,S.Si.,M.Si.

Program Studi Matematika

Universitas Sanata Dharma

Abstrak

Darab langsung G×H dari grup G dan H adalah grup terhadap perkalian per komponen. Selain itu bila A adalah subgrup dari G dan C adalah subgrup dari H, maka A×C adalah subgrup dari G×H. Sedangkan bila S×T adalah subgrup dari G×H, belum tentu S merupakan subgrup dari G dan T merupakan subgrup dari H. Teorema Goursat memberikan prosedur yang sistematis untuk mencari semua subgrup dari suatu grup darab langsung.

Kata kunci : darab langsung, grup, subgrup.

1.Pendahuluan

1,1 Latar Belakang Masalah

Dalam perkuliahan tentang teori grup, mahasiswa diperkenalkan dengan

bermacam‐macam metode untuk mengkonstruksi contoh‐contoh yang merupakan

grup atau bukan grup. Apa yang kelihatannya luput dalam silabus perkuliahan teori

grup adalah sebuah teorema, yang pertama kali dibuktikan oleh Edouard

Jean_Baptiste Goursat (1858‐1936) pada tahun 1889, yang menunjukkan hubungan

yang ‘indah’ antara beberapa topik elementer dari teori grup. Pembahasan tentang

subgrup dari suatu darab langsung, bila ada, biasanya singkat dan tidak lengkap.

Goursat dikenal di kalangan matematikawan karena bukunya Cours d’analyse mathematique ( A Course in Mathematical Analysis ), yang dalam buku tersebut

Goursat memperbaiki teorema integral Cauchy, yang kemudian dikenal secara luas

sebagai Teorema Cauchy‐Goursat. Teorema tersebut menyatakan bahwa integral dari

(2)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Tulisan ini akan membahas teorema Goursat yang lain, yang secara lengkap

menjelaskan tentang subgrup dari suatu darab langsung. Selanjutnya teorema tersebut

akan disebut sebagai Teorema Goursat. Adapun bukti dari Teorema Goursat cukup

didasarkan pada beberapa topik dasar dari teori grup: subgrup, subgrup normal, koset,

grup kuosien, indeks, order,darab langsung, bijeksi, dan isomorfisma. Dengan demikian

mudah diterima oleh mahasiswa yang mengikuti perkuliahan aljabar abstrak,

khususnya teori grup. Di samping itu penulis akan mencoba menyusun kembali bukti

Teorema Goursat tersebut dan Corollarynya ke dalam barisan teorema‐teorema — yang dalam perkuliahan bisa dijadikan sebagai kumpulan soal‐soal latihan — dengan

maksud agar pada akhir semester, teorema tersebut dapat dipahami dan dibuktikan

tanpa banyak kesulitan.

Digunakan notasi A_<B untuk menyatakan A adalah subgrup normal dari B ,

notasi eG untuk menyatakan elemen identitas dari grup G (atau dengan e bila

konteksnya jelas), dan notasi 1 untuk menyatakan subgrup trivial dari G. Notasi teori

grup yang lainnya adalah standar. Dalam tulisan ini untuk menyingkat penulisan, bukti

teorema tidak disertakan.

1.2. Rumusan Masalah

Berdasar uraian dalam latar belakang masalah di atas, dapat dituliskan rumusan

masalah sebagai berikut :

1.Bagaimana bunyi Teorema Goursat yang mengenai konstruksi subgrup dari

grup darab langsung?

2. Bagaimana langkah‐langkah pembuktian teorema tersebut?

1.3. Tujuan dan Manfaat

Tujuan penulisan makalah ini adalah untuk memberikan kontribusi

terhadap pengembangan matematika khususnya bidang aljabar abstrak dan

pengajarannya.

(3)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 14 2. Pembahasan

2.1.Subgrup dari suatu darab langsung

Teorema 1. Bila A adalah subgrup dari G dan C adalah subgrup dari H, maka A×C

adalah subgrup dari G×H.

Teorema 2. Diagonal dari G×G, yang didefinisikan dengan D = {(g,g)|g∈D},

adalah subgrup dari G×G.

Untuk melihat bahwa Teorema 1 dan 2 belum memberikan daftar yang lengkap

dari subgrup‐subgrup, misalkan Z₃ = x = { , , 2}

x x

e , dan perhatikan darab langsung 3

3 Z

Z × . Mudah diperiksa bahwa himpunan {( , ),( , 2),( 2, )}

x x x x e e adalah subgrup

yang bukan merupakan darab langsung dari subgrup‐subgrup, bukan pula subgrup

diagonal. Seperti yang dikatakan di depan bahwa Teorema Goursat akan

memperlihatkan prosedur yang sistematis untuk memeriksa setiap subgrup dari darab

langsung.

2.2.Teorema Goursat

Kita akan menggunakan istilah grup kuosien atau disingkat kuosien, untuk bentuk

B

A/ , di mana A adalah grup dan B<A. Bila A = B, maka A/B disebut kuosien trivial

karena isomorfis dengan grup trivial berorde 1.

Teorema Goursat. Misal G dan H adalah grup. Maka terdapat bijeksi antara himpunan S yang terdiri dari subgrup dari G×H dan himpunan T yang terdiri dari semua tripel

) , / , /

(A B C D ϕ di mana A/B adalah kuosien dalam G, C/D adalah kuosien dalam H,

dan ϕ:A/B→C/D adalah isomorfisma.

Atau secara sederhana, Teorema Goursat mengatakan bahwa struktur subgrup

(4)

PROSIDING ISBN : 978‐979‐16353‐3‐2

bahwa, di samping isomorfisma identitas, isomorfisma yang lain mungkin ada antara

kuosien‐kuosien tak trivial yang isomorfis, masing‐masing berkorespondensi dengan

subgrup tunggal dalam darab langsung. Alasan mengapa Z₃×Z₃ memuat subgrup

yang tidak dapat diperoleh dari Teorema 1 dan 2 (lihat paragraf di bawah Teorema 2)

adalah bahwa kedua teorema tersebut hanya meneliti subgrup‐subgrup yang

berkorespondensi dengan isomorfisma trivial atau identitas.

Alat yang dipakai untuk membantu menggambarkan struktur subgrup dari

suatu grup adalah diagram Hasse. Dalam diagram Hasse, subgrup dinyatakan dengan

titik, dan relasi termuat dinyatakan dengan garis yang menghubungkan subgrup‐

subgrup. Dengan ketentuan bahwa subgrup yang memuat subgrup yang lain digambar

lebih tinggi. Diagram Hasse dalam Gambar 1 menunjukkan subgrup‐subgrup yang

relevan dengan subgrup U dari G×H. Subgrup‐subgrup antara dua subgrup di sana

tidak digambar.

Gambar 1. Visualisasi subgrup U dari G×H.

(5)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 16 2.2.Pembuktian Teorema Goursat

Misal G dan H adalah grup, misal S adalah himpunan semua subgrup dari G×H, dan

misal T adalah himpunan semua tripel (A/B,C/D,ϕ) di mana B_<A≤ G , D_<C≤ H,

dan ϕ:A/B→C/D adalah isomorfisma grup.

Teorema 3. Misal (A/B,C/D,ϕ) adalah tripel dalam T, dan didefinisikan

} ) ( | ) , {(g h A C gB hD Uϕ = ∈ × ϕ = .

Maka Uϕadalah subgrup dari G×H.

Teorema 4. Untuk subgrup U dalam S, misalkan

U h g G g A_U ={ ∈ |( , )∈ untuk suatu h∈H}, B_U ={g∈G|(g,1)∈U},

C_U ={h∈H |(g,h)∈U untuk suatu g∈G}, dan D_U ={h∈H |(1,h)∈U},

dan didefinisikan pemetaan ϕU :AU /BU →CU /DU dengan U

U

U(gB )=hD

ϕ bila (g,h)∈U.

Maka

(a). AU adalah subgrup dari G dan CU adalah subgrup dari H. (Subgrup ini

kadang disebut proyeksi dari U pada grup faktor .)

(b). BU adalah subgrup normal dari DU adalah subgrup normal dari CU.

(c). ϕUadalah isomorfisma grup.

Teorema 5. Didefinisikan pemetaan α:S →T dan β :T →S dengan

= ) (U α (AU /BU,CU /DU,ϕU ) dan ϕ ϕ β(A/B,C/D, )=U .

(6)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Teorema 3 dan 4 menunjukkan bagaimana membentuk subgrup dalam S bila

diberikan suatu tripel dalam T, dan sebaliknya.Yaitu, bila diberikan tripel

) , / , /

(A B C D ϕ dalam T, kita tentukan bayangan dari koset gB terhadap ϕ. Maka Uϕ

tidak lain adalah himpunan semua pasangan terurut elemen‐elemen dari gB dan hD .

Sebaliknya, bila diberikan subgrup U, himpunan koordinat pertamanya membentuk A,

dan himpunan koordinat pertamanya yang dipasangkan dengan elemen identitas

membentuk B; subgrup C dan D dibentuk dengan cara sama. Isomorfisma ϕ kemudian

dapat ditentukan. Contoh‐contoh di bawah ini menunjukkan langkah‐langkah tersebut.

2.3.Contoh‐contoh

Contoh 1. Misal G = Z₃= x ,dan misal H =Z₉= y . Dalam G×H, enam subgrup

1

1× , 1× y3 , 1×Z₉, Z₃×1, Z₃× y3 , dan Z₃×Z₉ diperoleh dari kuosien trivial.

Satu‐satunya kuosien tak trivial dari Z₃ adalah Z₃/1, yang isomorfis dengan kedua

kuosien Z₉ / y3 dan y3 /1 dalam Z9. Masing‐masing pasangan ini berkorespondensi dengan dua subgrup, yaitu yang diperoleh dari dua isomorfisma

yang berbeda dari grup siklik berorde 3 ke dirinya sendiri. Diagram Hasse untuk 9

3 Z

Z × lengkapnya ditunjukkan dalam Gambar 2.

Gambar 2. Diagram Hasse dari Z3×Z9

(7)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 18 Contoh 2. Misal G =

3 6

Z = x , dan misal H adalah grup yang terdiri dari enam simetri

dari segitiga samasisi di mana dua rotasi berorde 3 dinyatakan dengan r dan r2, dan

pencerminan berdorde 2 dengan s1, s2, dan s31. Tabel 1 mendaftar kuosien‐kuosien

yang dipakai.

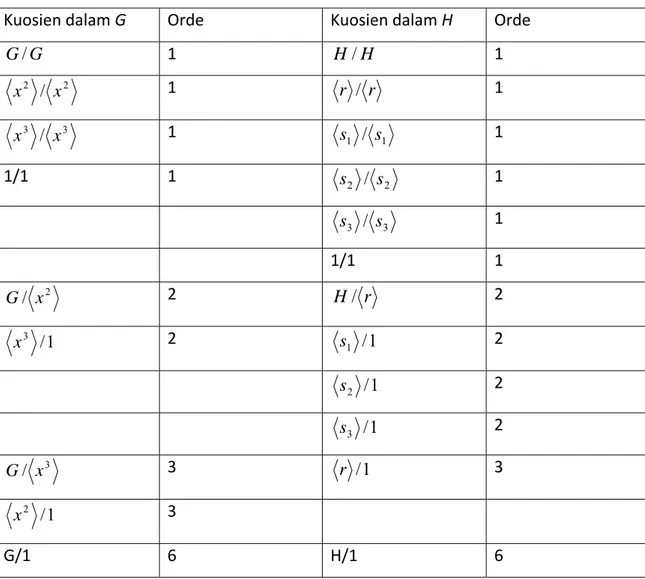
Tabel 1. Kuosien‐kuosien untuk Contoh 2

Kuosien dalam G Orde Kuosien dalam H Orde

G G/ 1 H/H 1 2 2 _/ x x 1 r / r 1 3 3 _/ x x 1 s1 / s1 1 1/1 1 s₂ / s₂ 1 s₃ / s₃ 1 1/1 1 2 / x G 2 H/ r 2 1 / 3 x 2 s1 /1 2 s₂ /1 2 s₃ /1 2 3 / x G 3 r /1 3 1 / 2 x 3 G/1 6 H/1 6

Misalkan kita akan mencari subgrup U yang berkorespondensi dengan tripel

(G/ x3 , r /1,ϕ), di mana ϕ: G/ x3 → r /1 didefinisikan dengan ( 3 ) 21 r x x = ϕ . Karena } { }) , ({ 3 H G x e e = ϕ ,

(8)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 19 } { }) , ({ 4 2 r x x = ϕ , } { }) , ({ 2 5 r x x = ϕ , maka {( , ),( 3, ),( , 2),( 4, 2),( 2, ),( 5, )} r x r x r x r x e x e e U = G H H .

Sebaliknya, misal diberikan subgrup V, akan dicari tripel yang berkorespondensi

dengan subgrup tersebut. Sebagai contoh, bila ) , {(eG eH V = , (eG,r), (eG, 2 r ), (x,s1), (x,s2), (x,s3), ( 2 x ,eH), ( 2 x ,r), (x2,r2), (x3,s1), ( 3 x ,s2), ( 3 x ,s₃), (x4,e_H), (x4,r), (x4,r2), (x5,s1), ( 5 x ,s₃), (x5,s₃)},

maka A adalah himpunan semua koordinat pertama, B adalah himpunan semua

koordinat petama yang dipasangkan dengan e_H, C adalah himpunan semua koordinat

kedua, dan D adalah himpunan semua koordinat kedua yang dipasangkan dengan eG.

Dngan demikian A = {eG, x, 2 x , x3, x4, x5} = G B = {eG, 2 x , x4} = x2 C = {e_H, r, r2, s1, s2, s3} = H D = {eH, r, 2 r }.

Karena A/B dan C/D berorde 2, isomorfisma ϕ harus isomorfisma identitas. Maka,

subgrup V berkorespondensi dengan tripel (G / x2 , H / r , ϕ) , di mana ϕ: G / x2 → H / r didefinisikan dengan ϕ(x x2 )=s₁ r .

Perhatikan bahwa kuosien yang berorde 6 hanyalah G/1 dan H/1, yang tidak

isomorfis, sehingga G×H tidak mempunyai subgrup yang berkorespondensi dengan

kuosien‐kuosien ini.

2.4.Aplikasi Teorema Goursat

Kita dapat membentuk subgrup dari suatu darab langsung bila diberikan dua

kuosien yang isomorfis yaitu dengan mencari semua pasangan terurut yang mungkin

yang koordinat pertamanya diambil dari A dan koordinat keduanya diambil dari

(9)

PROSIDING ISBN : 978‐979‐16353‐3‐2

orde dan indeks subgrup dari suatu darab langsung berhingga, seperti yang dinyatakan

dalam Teorema 6 berikut, yang diambil dari buku [ 1 ].

Teorema 6. Misal G dan H adalah grup berhingga, dan misal U adalah subgrup dari

H

G× . Maka :

(a). |AU |.|DU | = | U | = |BU |.|CU |.

(b). [G:AU].[H :DU] = [G×H:U] = [G:BU].[G:CU].

Teorema 7. Misal G=H1×...×Hn adalah grup berhingga di mana orde subgrup Hi

dan

i j

H adalah relatif prima bila i≠ j. Bila U adalah subgrup dari G, maka

n H U H U U = _I ₁×...× _I .

3.Kesimpulan dan Saran

Bila A adalah subgrup dari G dan C adalah subgrup dari H, maka A×C adalah

subgrup dari G×H. Selain itu diagonal dari G×G, yang didefinisikan dengan D =

} |

) ,

{(g g g∈D , juga merupakan subgrup dari G×G. Akan tetapi subgrup dari suatu

darab langsung belum tentu merupakan darab langsung dari subgrup‐subgrup.

Teorema Goursat yang intinya mengatakan bahwa struktur subgrup dari suatu darab

langsung bergantung pada struktur kuosien dari grup faktor, memberikan prosedur

yang sistematis untuk mencari semua subgrup dari suatu darab langsung. Dan secara

persisnya diperoleh bahwa bila G=H1×...×Hn adalah grup berhingga di mana orde

subgrup Hi dan i j

H adalah relatif prima bila i≠ j. Bila U adalah subgrup dari G, maka

n H U H U U = _I ₁×...× _I .

Disarankan mengingat keterbatasan waktu dalam perkuliahan, materi tersebut

dibahas dalam bentuk kumpulan soal‐soal latihan dan dijadikan tugas kelompok —

dengan maksud agar pada akhir semester, teorema tersebut dapat dipahami dan

dibuktikan tanpa banyak kesulitan.

(10)

PROSIDING ISBN : 978‐979‐16353‐3‐2

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009 21 Daftar Pustaka

Crawford, R.R. and Wallace, K.D., On the number of subgrup of index two—an application of Goursat’s theorem, Math.Mag.48 (1975) 172‐174.

Gallian, J.A., Contemporary Abstract Algebra, 4th ed., Houghton Mifflin, Boston, 1998.

Hungerford, T.W., Abstract Algebra: An Introduction, 2nd ed., Brooks/Cole, Pacific

Grove CA, 1997.

Petrillo, J., Goursat’s Other Theorem, The College Mathematics Journal, Vol.40, No.2

(2009) 119‐124