BAB I SINYAL DAN SISTEM. Input Output Sistem Environment

BAB I SINYAL DAN SISTEM

1.1. Definisi

Sistem dapat didefinisikan sebagai sekumpulan objek yang disusun membentuk proses dengan tujuan tertentu. Sebagai model matematis yang menghubungkan antara input dan output, umumnya disebut IO Sistem, seperti tampak dalam gambar 1 dibawah ini :

gambar 1 Model matematik IO Sistem

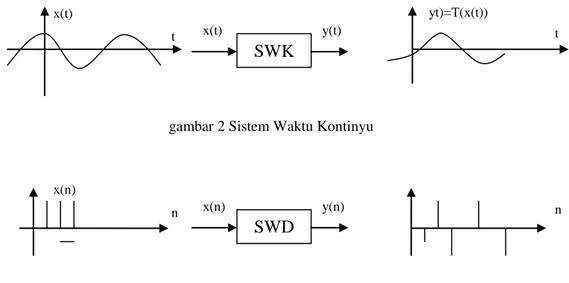
Masukan dari lingkungan (environment) ke sistem dan keluaran dari sistem ke environment disebut sinyal. Sistem yang menghubungkan sinyal input kontinu dengan sinyal output kontinyu disebut Sistem Waktu Kontinyu dan yang menghubungkan deretan sinyal input (diskrit) dengan deretan sinyal output disebut Sistem Waktu Diskrit (SWD), seperti tampak pada gambar 2 dan gambar 3

gambar 2Sistem Waktu Kontinyu

gambar 3 Sistem Waktu Diskrit

Analisis sistem, periksa apakah sistem tersebut :

x(n) n SWD x(n) y(n) _n x(t) t SWK x(t) y(t) _t Input – Output Sistem Sinyal Output Sinyal Input Environment yt)=T(x(t))

 Stabil/tidak stabil  Kausal/tidak kausal

 Tak ubah waktu/berubah waktu  Linier/non linier

 Statis/dinamis

 Deterministik/stokastik

Tools Analisis = model matematis  Persamaan linier

 Transformasi = jembatan=memindahkan satu kawasan ke kawasan yang lain, dengan : 1. transformasi fourier

2. transformasi laplace 3. transformasi z

4. transformasi Fourier Diskrit

Bedakan antara waktu kontinyu dengan waktu diskrit dan kawasan frekuensi kontinyu dengan kawasan frekuensi diskrit

1.1. Sifat dan Klasifikasi sistem

Sistem statis jika keluaran sistem hanya tergantung pada masukan pada saat itu (memoryless), sedangkan sistem dinamis jika keluaran sistem mengingat masa lalu (with memory)

b. Linier

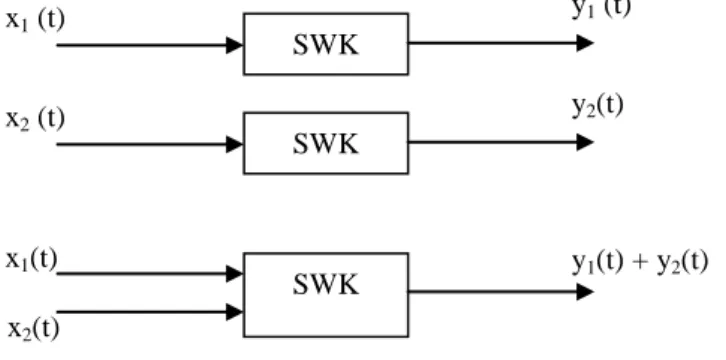
Sistem linier jika memenuhi prinsip superposisi, seperti tampak pada gambar 4 dibawah ini :

gambar 4 Prinsip superposisi

Dan homogenitas :

x1 (t) + x2(t) = y1(t) + y2(t)

c. Pergeseran waktu

Sistem tak ubah waktu (invariant) jika output sistem tidak berubah betuk walaupun outputnya akan bergeser sejauh pergeseran input.

gambar 5. Sistem tak ubah waktu

Jika y1(t) adalah output dari x1 (t) dan y2 (t) adalah output dari x2 (t) dan x1 (t) =

x1(t-t0) maka y1 (t) = y1 (t-t0) Sistem disebut LTW atau LTI (Linier Time

Invariant) jika linier tak ubah waktu SWK y1 (t) x1 (t) SWK y2(t) x2 (t) y1(t) + y2(t) x1(t) SWK x2(t) x (t) SWK SWK x (t-2) y (t-2) 2 1 y (t) 2 1 2 3

d. Kausalitas

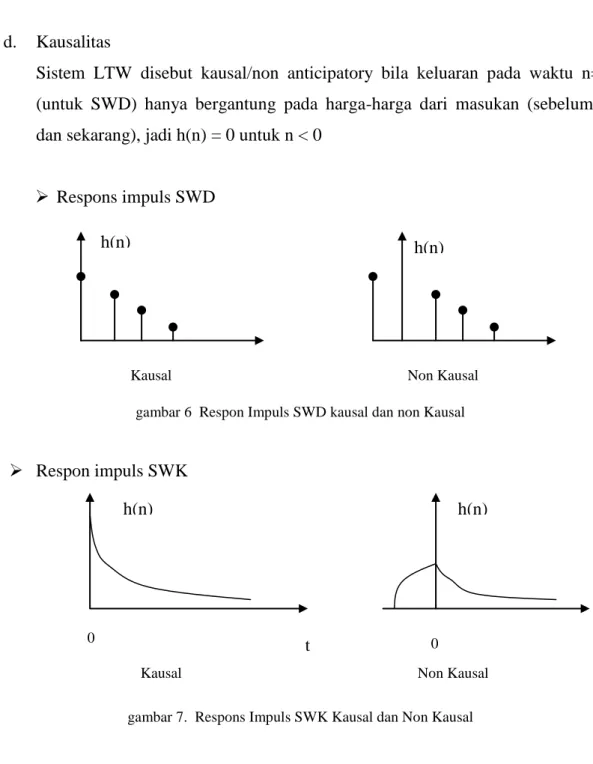
Sistem LTW disebut kausal/non anticipatory bila keluaran pada waktu n=n0 (untuk SWD) hanya bergantung pada harga-harga dari masukan (sebelumnya dan sekarang), jadi h(n) = 0 untuk n < 0

 Respons impuls SWD

gambar 6 Respon Impuls SWD kausal dan non Kausal

 Respon impuls SWK

gambar 7. Respons Impuls SWK Kausal dan Non Kausal

Catatan : sistem yang dapat direalisasi harus kausal

e. Stabilitas

Sistem LTW disebut stabil bla setiap masukan terbatas menghasilkan keluaran terbatas”BIBO” = Bounded Input Bounded Output

h(n) _h(n) Non Kausal Kausal Non Kausal Kausal h(n) h(n) t 0 t 0

...

n

...

n

stabil Tidak stabil



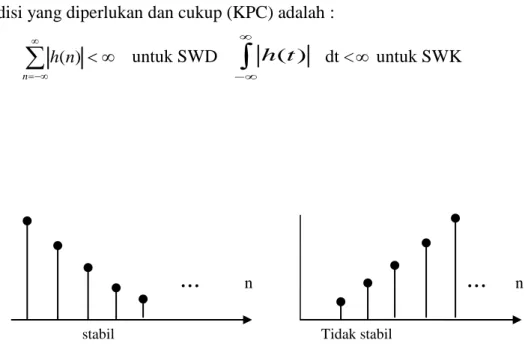
   ) (t h

Kondisi yang diperlukan dan cukup (KPC) adalah :



     n n h( ) untuk SWD dt < untuk SWK

gambar 8 Respon Impuls LTW suatu SWD, Stabil dan tidak stabil

 Stabilitas sistem dapat juga dilihat dari letak pole dari fungsi transfer sistem

 Untuk SWK letak pole di sebelah kiri sumbu imaginer

 Untuk SWD letak pole di dalam lingkaran satuan

Jadi untuk kuliah ASL ini sistem yang perlu adalah LTW/LTI (Linier tak ubah Waktu/Linier Time Invariant), dengan menentukan apakah sistem tersebut kausal dan stabil.

Contoh :

Diketahui suatu SWD yang merupakan transformasi deretan masukan x(n) dengan keluaran y(n) dengan hubungan :

a. y(n) = ax 2 (n-1)

b. y(n) = ax(n-2) + bx(n+2) Periksa sistem di atas. Jawab.

a. y(n) = ax 2 (n-1)  Linieritas

Jika input x1 (n) maka output y1 (n) = ax12 (n-1)

Jika input x2 (n) maka output y2 (n) = ax22 (n-1)

Ambil X(n) = x3 (n) = x1 (n) + x2(n) Maka : Y(n) = y3 (n) = a[x(n-1)]2 b. y(n) = ax(n-2) + bx(n+2) 1.2.Operator p dan q Suatu operator L ≡ input output

= Fungsi Transfer sistem Untuk SWK L(p) = ) ( ) ( p D p N

Persamaan 1 Fungsi Transfer

N = numerator D = denominator

Dimana p = operator maju

p = operator integral c dt Untuk SWD L(q) = ) ( ) ( q D q N

Dimana q = operator maju q = operator tunda q x(n) = x (n-1)

q x(n) = x (n+1)

Untuk menganalisis suatu sistem maka buat dulu model matematis input-outputnya Contoh 1.2.1

Model matematis sistem :

L dt t di( ) +



  t t i C ( ) 1 d t = v (t) 1 dt i(t) v(t) C R dt d L      _{ }



1 p i(t) v(t) C R Lp      _{ } L(p) = C C x p p x C p R Lp t v t i input output / 1 ) ( ) (     = 1  RCp LCp pC Persamaan 2 Model Matematika Sistem

1.3.Diference Equation Model

a. SWK persamaan Diferensial

 

 

_{ }

_{ }

 

_{ }

n t x b dt t x d b t y a t y dt d a dt t y d a dt t y d a _{m a} m m n n n n n n n           1 ... 1 1 ... 1 1 L R C i(t) v(t) + -

Output sistem = i(t) Input sistem = v(t)

Persamaan 3 Model Persamaan diferensial n = orde persamaan diferensial



 n t a 0

1 = koefisien penyebut = koefisien D(p)



 m t b 0

1 = koefisien pembilang = koefisien N(p)

Umumnya n > m. Ambil p = d/dt maka :





 





 

   

_{ }

_{ }

 

n n n n n n m m m m n m m n n n n n a p a p a p a b p b p b p b p D p N t x t y p L t x b p b t y a p a p a p a                      1 1 1 1 1 1 1 1 ... ... ... ... Dimana :

 

 

 

p sistemoperator L a p b p b p b p N a p a p a p a p D n m m m m n n n n n               1 1 1 1 1 1 1 ... ... Jadi : D(p) y(t)=N(p) x(t)

Solusi ada dua, yaitu komplementer dan partikuler 1. Solusi komplementer (yc(t)) jika input x(t) = 0,

Jadi :

   

p y t 0a p a _1p 1...a₁pa₀ 0 D _{c n} n _n n Didapat :

 



 

 

 

 

      n i n n i i c t Ay t Ay t A y t A y t y 1 2 2 1 1 ... Dimana : y1(t) = en(t) Yi = akar-akar polynomial D(p)

Ai = konstanta yang dihitung dari kondisi awal

Kemungkinan akar D(p) adalah riil atau kompleks dan simpel atau jamak. Maka :

i. y1(t) = erit untuk semua akar riil yang berbeda

iii. y1(t) = eαt cos βt ; eαt sin βt untuk akar komplek yang berbeda ini

dari

eαt = α + jβ

iv. y1(t) = eαt cos βt ; eαt sin βt  (1)

= teαt cos βt ; teαt sin βt  (2)

2. Solusi khusus (particular) jika input sistem ada , x(t) ≠ 0

   

   

 

_{       }

 

xt L p xt p D p N t y t x p N t y p D p p   

Kasus khusus jika input eksponensial maka output juga eksponensial. Ambil

x(t) = Aest Maka

yp(t) = L(p) x (t) , p = s

jika input sinudoida maka buat menjadi eksponensial. Ingat : ejt cost jsint

Jika x(t) = A cos (t) = Re ( Aejt) Maka y(t) = ( L(p) x(t)),p = j

Jika x(t) = A sin (t) = Im ( Aejt) Maka y(t) = ( L(p) x(t)),p = j

Didapat :

Solusi persamaan : solusi komplemeter + solusi particular y(t) = yc(t) + yp(t)

1.4.Realisasi Sistem Waktu Kontinyu dan Sistem Waktu Diskret

Syarat sistem dapat direalisasi jika kausal. Dapat direalisasi dalam bentuk : a. Struktur langsung type I

b. Struktur langsung type II

a. Realisasi untuk Sistem Waktu Diskrit

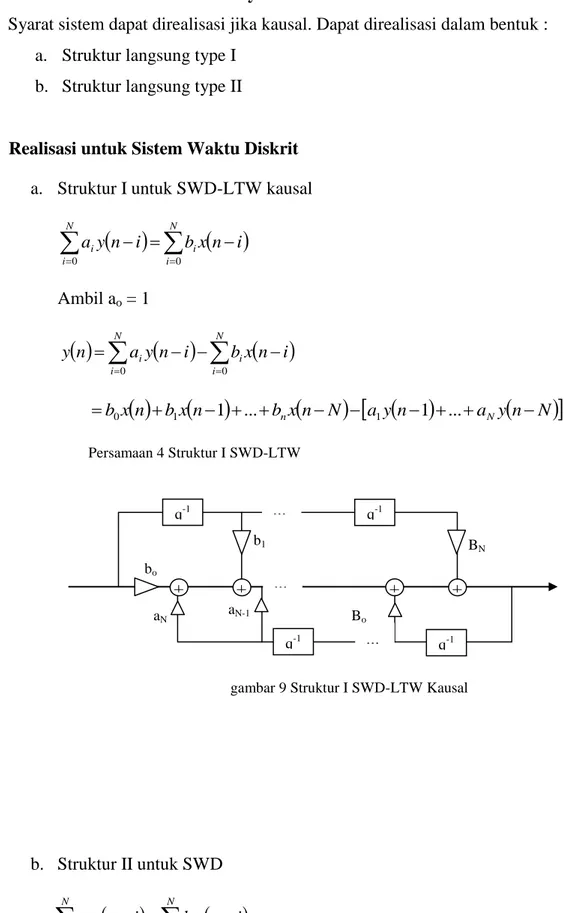
a. Struktur I untuk SWD-LTW kausal













     N i N i i iy n i bx n i a 0 0 Ambil ao = 1

 

_





_





      N i N i i iy n i bx n i a n y 0 0

 

n bx



n



b x



n N





a y



n



a y



n N





x b     n      N   0 1 1 ... 1 1 ... Persamaan 4 Struktur I SWD-LTW

gambar 9 Struktur I SWD-LTW Kausal

b. Struktur II untuk SWD













     N o i N i i iy n i bx n i a 0 + + + + q-1 q-1 q-1 ... ... ... ... q-1 ... ... aN-1 aN bo b1 _BN Bo

a₀y

 

n a₁y



n1



...a_ny



nN



b₀y

 

n b₁y



n1



...b_ny



nN



y

 

n



a

_o



a

₁

q

1



...



a

_N

q

N





x

 

n



b

_o



b

₁

q

1



...



b

_N

q

N



   

 

 

 

_



      























N o i N o i N N o N N o

q

b

q

a

q

a

q

a

a

q

b

q

b

b

q

X

q

y

q

D

q

N

q

L

₁ 1 1 1 1 1 1 1

1

...

...

Persamaan 5 Struktur II SWD

 

 

 

 



 



   









N o i N o i

n

x

q

a

n

n

x

n

q

a

q

L

₁ 1 1 1 1

1



_

gambar 10 Struktur II SWD

   

 



   





 

    

_

_

_

_





N o i N o i N o i i

i

n

b

q

b

n

n

y

q

b

n

n

y

q

L







1 1 1 1 2 gambar 11 Struktur II SWD Rangkaian total digabung

L2(q) = L1(q).L2(q)

 

 

x

   

   

n n n y n n x n y    + q-1 q-1 q-1 y(n) x(n) y(n) x(n) ₊ q-1 q-1 q-1

gambar 12 Rangkaian total

Contoh 1.3.1

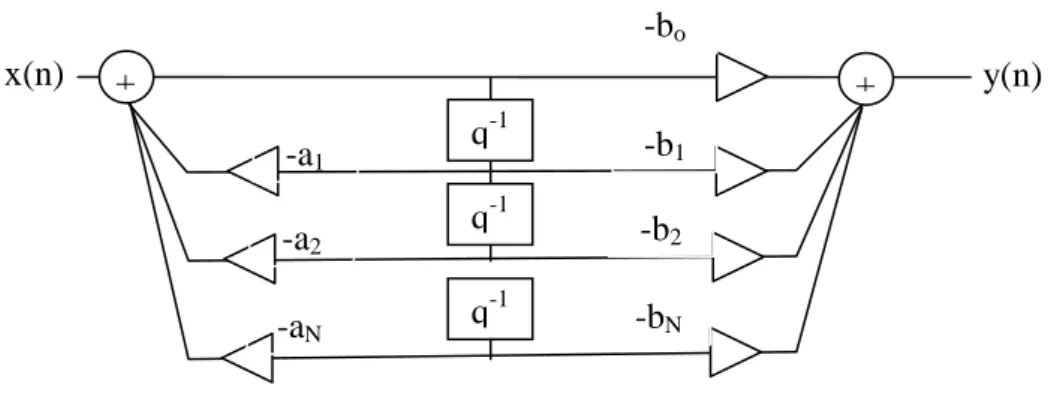
SWD dengan y(n)+y(n-1)+5y(n-2)+7y(n-3)=6x(n)+4x(n-1) Buat realisasi type I dan type II sistem diatas Jawab :

y(n) x(n) ₊ q-1 q-1 q-1 + -bo -b1 -b2 -bN -a1 -a2 -aN

1.5.Stabilisasi Sistem Linier

SWK stabil jika bagian riil akar persamaan D(p) adalah negatif. Pada sistem di atas pole p = -6 dan p = -4 adalah negatif, maka sistem stabil  sistem stabil.

Jika Y =  + j stabil jika  < 0 Bidang p :

gambar 13 Bagian negatif D (p)

1.5.1. Persamaan Diference (untuk SWD)

Bentuk umum sistem LTW













     N i M i i iy n i bx n i a 0 0

Persamaan 6 Bentuk umum LTW

Ambil ao = 1

 

n a y



n



a y



n N





b x

 

n b x



n M





y  1 1 ... N   0 ... M  Dengan operator q : Dimana : q-1 x(n) = x(n-1) dan q x(n) = x (n+1) maka : y(n) (1 + a1 q-1 + …+ aN q-N) = x (n) (b0 + b1 q-1+…..+ bM q-M L(q) =

_{ }

 



 

_{ }

 q D q N n x n y Daerah stabil Im(p) riil(p)

         N) -q aN 1 -q a1 (1 -q bM .. 1 -q b1 (b0 Jadi : D (q)y(n) = N (q) x(n) Solusi : y (n) = yc(n) + yp(n)

1.5.2. Solusi komplementer  jika deretan masukan = 0

D(q) yc(n) = N (q).0 = 0 , maka D (q) = 0 dengan solusi, yc(n) = rk riil dan

tunggal, dimana rk = akar polynomial D (q) dengan solusi :

1. rk riil dan tunggal  yk (n) = rk

2. rk riil dan jamak sejumlah m buah

3. rk kompleks tapi tunggal

4. rk kompleks dan jamak sejumlah m buah

1.5.3. Solusi partikuler  jika deretan masukan ada

D(q) y p (n) = N (q) x (n) y p (n) = ) ( ) ( q D q N x(n) = L(q) x (n)

kasus khusus jika input eksponensial, ambil x(n) = A (s) n Didapatkan : y p (n) =

[L(q) x(n)]q Stabilitas sistem SWD, stabil jika amplitudo akar polinomial D(q) <1 atau

di dalam lingkaran satuan.

Contoh :

1. Suatu persamaan

Y(n+3) – 8 y(n+2) + 37 y(n+1) – 50 y(n) = 8 (0.5) n Dengan

Y(0) = 2 , y (1) = 3, y(2) = 5

1.6.Klasifikasi Sinyal

Sinyal adalah sebuah fungsi yang dapat direpresentasikan secara fisik maupun variable yang mengandung informasi. Sinyal dapat diklasifikasikan dalam : (scaum series)

a. Continous Time dan Diskrit Time Signals b. Analog dan Digital Signals

c. Real dan Kompleks Signals

d. Deterministic dan Random Signals e. Even dan Odd Signals

f. Periodik dan Non periodik Signals g. Energy dan Power Signals

Adapun Macam-macam sinyal-sinyal Dasar adalah 1. Unit Step Kontinyu u (t)

 

      0 , 0 0 , 1 t t t u

gambar 14 Unit step kontinu u (t)

2. Unit step diskrit u(n)

        0 , 0 0 , 1 n n n u

gambar 15 Unit step diskrit u (n)

3. Fungsi segiempat  (t)

 

         lainnya t t t , 0 5 . 0 5 . 0 , 1 u(t) 1 0 t u(n) 0 1 2 3 n Π(t) -0.5 0 0.5 t

gambar 16 Unit fungsi segi empat  (t)

4. Fungsi segitiga

 

t  t

 1

1t1 gambar 17 Unit fungsi segi tiga

5. Fungsi sinc

 

 t t t t c   sin sin

gambar 18 Unit fungsi sinc

6. Fungsi impuls delta kontinyu

 

      lainnya t t t , 0 0 , 1 

gambar 19 impuls delta kontinyu

7. Fungsi impuls diskrit δ (t)

 

      lainnya n n n , 0 0 , 1



Ʌ(t) -t 1 t δ (t) 1 0 t δ (n) 1 0 n = 0 untuk t = ± 1, ± 1, ... = 1 untuk t = 0 -3 -2 -1 0 1 2 3 t Sinc(t)

Operasi Pencerminan, Penskalaan waktu dan pergeseran 1. Sinyal kontinyu f (t)





_                 a b t a f b at f 2. sinyal diskrit





_                 a b n a f b ax f Contoh :

1. Diketahui sinyal kontinyu f(t)

               lainnya t t t t t f , 0 2 0 , 5 . 0 1 0 1 , 1 f(t) 1 1-0.5t

+ geser kiri, - geser kanan a = kompressi ax, a ≥ 1 1/a = ekspansi ax pencerminan

 

             lainnya t t t t t f , 0 1 0 , 1 0 5 . 0 , 1 2

 

                 1 0.5(2 ),0 2 2 0 2 1 , 1 2 t t t t f 2.        3 1 f f(2t)  ekspansi 3x       t f 3 1 f(2t) 1 1-t 0.5 0 1 t a. f(2t)  kompressi 2x ,-0.5 ≤ t ≤ 0 1-t ,0 ≤ 1 ≤ 1 = 0 , t lainnya -3 -2 -1 0 1 2 3 4 5 6 t 1 t 6 1 1







 















t

t

f

6

1

1

3

1

3. f(t-3)  geser kanan 3 step





         3 t f \ 4. f(-t)

 

         t f 5. f(-0.5t) 1 , -1 ≤ t-3 ≤ 0 , -2 ≤ t ≤ 3 1 – 0.5(t-3) , 0 ≤ t-3 ≤ 2 2.5 – 0.5 t , -3 ≤ t ≤ 5 0 , t lainnya 1 2 3 4 5 t 2.5 – 0.5t 1 f(t-3) 1 , -1 ≤ t ≤ 0 , 0 ≤ t ≤ 1 1 – 0.5(-t) , 0 ≤ -t ≤ 2 1+0.25t , -2 ≤ t ≤ 0 0 , t lainnya -2 0 1 t 1- 0.5t f(-t) f(-0.5t) 0 , t lainnya





          t f 0.5

6. f(3-t) = f-(t-3) = f(-t+3_ balik, geser kanan 3





          t f 0.5

1.7.Konversi Sinyal Waktu Kontinyu ke Sinyal Waktu Diskrit Sinyal

Konversi sinyal kontinyu ke diskrit dapat digambarkan seperti gambar 21 sebagai berikut :

1.8.Respon Impuls

Respons impuls adalah respons atau output sistem jika masukannya diberi fungsi impuls/ delta. Waktu kontinyu t Waktu diskrit n Frekuensi diskrit  Frekuensi kontinyu Ω sampling rekonstruksi sampling rekonstruksi Pasangan diskrit Pasangan kontinyu -1 _{ }-1  1 , -1 ≤ -0.5t ≤ 0 , 0 ≤ t ≤ 2 1 – 0.5(-0.5t) , 0 ≤ -0.5t ≤ 2 1+0.25t , -4 ≤ t ≤ 0 0 , t lainnya -1 0 2 t 1- 0.25t 1 1 , -1 ≤ 3-t≤ 0 , 3 ≤ t ≤ 4 1 – 0.5(3-t) , 0 ≤ 3-t ≤ 2 -0.5+0.5t , 1 ≤ t ≤ 3 0 , t lainnya 0 1 3 4 t f(3-t)=f-(t-3) -0.5+0.5t 1

gambar 20 Hubungan Pasangan Kontinyu dan Pasangan Diskrit

δ(n)

h(n) SWD

gambar 21 Respon Impulse

Sistem sering digambarkan dengan respons impulsnya karena dengan respons impulsnya dapat dilihat apakah sistem tersebut kausal dan stabil

gambar 22 Respon Impulse (2)

1. Respons Impuls SWD

Contoh :

Diketahui SWD-LTW

y(n) + a1y(n-1) + a2 y(n-2) + ...+ aN y (n-N) = x(n)

Respon impuls sistem jika x(n) = (n) Maka y(n) = h(n)

Jadi

h(n) + a1h(n-1) + a2h(n-2) + ...+ a N h(n-N) =  (n)

Karena kausal maka h(n) = 0 untuk n < 0 Maka

N = 0 h (0) =  (0) = 1 ; h(n-1) =0, h (n-2) = 0 dst N = 1 h (1) = h (1) + a1 h(0) + 0 + ...+ 0 =  (1) = 0 N = 2 h(2) + a1 h(1) + a2 h (0) + ...=  (2) = 0

Dst

Ingat solusi perbedaan y(n) = yc (n) + yp(n)

D(q) y(n) = N(q) x (n)

SWD x(n) h(n) y(n)

yc(n)  D(q) yc (n) = 0 maka D (q) = 0 maka yc (n) =



 m k n k kr A 1

yp(n)  yp(n) = L (q) x (n) dimana q = s untuk x (n) =  (s)n tetapi input di sini

bukan eksponensial maka yp(n) = 0

contoh : y(n)-0,8y(n-1) + 0,15y(n-2) = x(n) respons impuls h(n) – 0,8h(n-1) + 0,15h(n-2) = δ(n) n=0  h(0) – 0,8h(-1) + 0,15h(-2) = δ (0) = 1  h(0) = 1 n=1  h(1) – 0,8h(0) + 0,15h(-1) = δ (1) = 0  h(1) = 0,8 n=2  h(2) – 0,8h(1) + 0,15h(0) = δ (2) = 0  h(2) = 0,8 . 0,8 – 0,15 = 0,49 Solusi

 



 

 

    m k n n n k k c n A r A r A r y 1 2 2 1 1 Dimana y

 

n



10,8q1 0,15q2



 x

 

n

 

_

_

_

3 , 0 5 , 0 15 , 0 8 , 0 15 , 0 8 , 0 1 2 2 2 2 2 2 1          _{ } q q q q q q q q q q q q L Jadi y_c

 

n  A

 

0,5 n B

 

0,3 n n = 0  yc(n) = A + B = 1 n = 1  yc(n) = 0,5A + 0,3B = 0,8 A + 0,6B = 1,6 A + B = 1 - 0,9B = 0,6  B = -1,5 dan A = 2,5 Maka

y

 

n



h

 

n





2

,

5

 

0

,

5

n



1

,

5

 

0

,

3

n



u

 

n

Bagaimana jika inputnya superposisi ?

Karena sistem linier maka outputnya juga superposisi

2. Respons Impuls SWK

Dari pers Diferensial

 



_

 





 



 



 

a

y

t

dt

t

dy

a

dt

t

y

d

a

dt

t

y

d

a

_n n n n n n 1 1 0 1 1

...

 

 

 

b

x

 

t

dt

t

dx

b

dt

t

x

d

b

dt

t

x

d

b

_m m n m m n 1 1 0 1 1



...







_  _

Persamaan 7 Respon impulse SWK Dalam operator p

 

 

_{ }

_{ }

 

D

   

p

y

t

N

   

p

x

t

t

x

t

y

p

D

p

N

p

L









Respon impuls y(t) = h(t) jika input x(t) = δ (t) Dimana y(t) = h(t) = yk(p) + yp(t)  yp(t) = 0

 

 

 









n i t r i c

t

A

e

y

t

h

0 1

r = akar dari polinomial D(p)

jika input superposisi maka output superposisi  prinsip linieritas dengan mencari terlebih dahulu h(t) untuk satu harga δ(t)

jadi

 

 

 

_{   }

t

t

y

a

dt

t

dy

a

dt

t

y

d

a

dt

t

y

d

a

_n n n n n n



 1





1



0





1 1

...

dengan kondisi awal (0) = 0, kalikan kedua sisi dengan dt kemudian diintegrasikan dari 0- hingga 0+ didapat

 



 

 





   0 0 1 1 1

1

0

dt

t

dt

y

d

n n



Contoh : x

 

t dt dx y dt dy dt y d 3 2 3 4 2 2     y

 

p



p2 4p3







2p3



x

 

t

 

_

_

_

1 3 3 2 3 4 2 3 2         p p p p p p p L

 

t t c t Ae Be y  3   t = 0  yc(t) = A + B = 0

  

t  3A B 1 dt t dy_c -2A = 1  A = - ½ dan B = ½

y

c

 

t

e

e

t 3 1

2

1

2

1



_





Input x

 

t h₁

 

t e t e 3t 2 3 2 3 3 1      Input

 

 

e t e t dt t dy t h dt dx _{  }  _   3 2 2 3 2 2 Jadi

h

 

t



h

₁

 

t



h

₂

 

t

h

 

t





1

,

5

e

3t



0

,

5

e



u

 

t

1.9.Konvolusi

Konvolusi adalah suatu operasi perkalian sekaligus penjumlahan. Dalam kawasan waktu dapat digunakan untuk mendapatkan respon sistem terhadap masukan bebas. Jadi merupakan transformasi dari masukan ke keluaran.

1.9.1. Penjumlahan Konvolusi

Teorema

Jika x(n) adalah input suatu SWD-LTW dan y(n) output sistem tsb dimana y(n) = T [x(n)] maka :

 



  







  

          k k k h k n x k n h k x n y Persamaan 8 Konvolusi

Dimana semua operasi di atas didefinisikan sebagai operator konvolusi ” *” sehingga

     



  







  

     











k k

k

h

k

n

x

k

n

h

k

x

n

h

n

x

n

y

*

h(n) = respon impuls x(n) h(n) y(n) y(n) = x(n) * h(n) Sifat : 1. Commutative x(n) * h(n) = h (n) * x(n)

2. Assosiative x(n) * [y(n) * z(n) ] = [ x(n) * y(n)] * z (n) 3. Distributive untuk operasi penjumlahan

x(n) * [y(n) * z(n) ] = x(n) * y(n) * z(n) 4. Memiliki elemen identity

x(n) *  (n)=  (n) * x (n) = x(n)

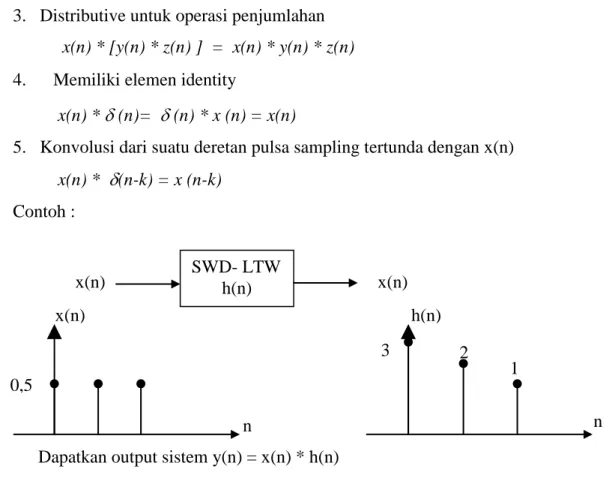
5. Konvolusi dari suatu deretan pulsa sampling tertunda dengan x(n) x(n) * (n-k) = x (n-k)

Contoh :

gambar 23 Konvolusi x(n) dan h(n)

1.9.2. Integral Konvolusi

Prinsip dan sifatnya sama dengan SWD dimana  diganti dengan 

 

t x

   

t *h t x

  





  

y x -



 



     



h t



dt x t



h



d



x

Persamaan 9 Konvolusi Integral

x(n) SWD- LTW _h(n) x(n) n n h(n) x(n) 0,5 3 ₂ 1

Dapatkan output sistem y(n) = x(n) * h(n)

secara grafis :

 Gambarkan x() dan h (t0 - ) dimana h (t0 - ) = h- ( - t0 ) yaitu h() yang

dicerminkan kemudian digeser sejauh t0 kemudian di integralkan

 Disini  merupakan variabel integrasi, jadi set satu harga t kemudian lakukan operasi di atas dimana hasil integrasi merupakan luas bawah kurva

Contoh : Hitung y(t) Jawab

 

   



  



      x t h t x h t  d t y * Set 0 < t < 1 R=1Ω y(t) L=1H x(t) x(t) t 1 1 x(t) h(t) y(t) x(t) h1(t) = e-tu(t) h(-t) 1 t t t 1 1 x(τ) τ 0 t 1

 

 

 



  



  







x

t

h

t

x



h

t



d



t

y

*





   t r t

d

e

0

1







t t t

e

d

e

e

0



1

1

0 1





e

e

e

e

e t t



1

.

e

1

BAB II ANALISIS FOURIER PADA SINYAL WAKTU KONTINYU

2.1.Pendahuluan

Analisis Fourier, diambil setelah ilmuwan fisika Prancis Jean Baptise Fourier (1768-1830), memecahkan bahwa hampir seluruh fungsi periodik dapat direpresentasikan sebagai sinusoidal pada seluruh frekuensi yang terkait. Kerja Fourier telah membawa dampak yang nyata dalam teori sistem linier khususnya dalam teori komunikasi. Bukan hanya membuat kita untuk dapat mengerti sinyal periodik melalui

spektrum frekuensinya tetapi juga dapat mengembangkan pengetahuan dasar pada sejumlah sinyal periodik melalui transformasi Fourier.

Kontribusi Fourier dapat disimpulkan oleh pernyataan bahwa sinyal yang digunakan dalam engineering dapat direpresentasikan dalam domain waktu dan

domain frekuensi, lebih dari itu representasinya mempunyai hubungan secara unik sehingga pengubahan representasi sinyal tersebut dalam satu domain akan mengubah representasinya dalam domain yang lain.

2.2.Deret Fourier Untuk Sinyal Perodik

Sinyal x(t) dikatakan periodik jika memenuhi persamaan dibawah ini untuk sejumlah nilai T,

x(t + T)=x(t)

Persamaan 10 Deret fourier untuk sinyal periodik

nilai terkecil T yang memenuhi Persamaan 10 diatas disebut sebagai periode sinyal. Besaran fo=1/T dikatakan frekuensi dasar sinyal (Hertz) dan Ωo=2foadalah frekuensi

dasar dalam radian perdetik.

Sinusoidal dengan frekuensi nfo, dimana n adalah integer, dikatakan sebagai

harmonik ke n.

2.2.1. Bentuk Trigonometri pada Deret Fourier

Jika x(t) adalah fungsi periodik dengan periode T, hampir dalam setiap kasus dapat diekspresikan dengan teorema Fourier seperti Persamaan 11 dibawah ini :

 

_







      1 sin cos n o n o n o a n t b n t a t x

Persamaan 11 Teorema fourier

Persamaan 11 tersebut disebut sebagai deret fourier untuk x(t) konstanta ai dan b1

gambar 24 Beberapa sinyal periodik yang sering digunakan

x(t) dapat didekati dengan penjumlahan sejumlah sinyal sinusoidal dengan periode T=2Ωo.

Analisis Fourier pada sinyal waktu kontinyu bertujuan untuk memindahkan sinyal dari kawasan tertentu ke kawasan frekuensi, yaitu dengan menggunakan Deret Fourier Waktu Kontinyu (DFWK) untuk sinyal periodik, dan dengan Transformasi Fourier Waktu Kontinyu (TFWK) untuk sinyal tidak periodik (aperiodik). Deret x(t) sebagaimana Persamaan 12 dapat juga dinyatakan dalam bentuk sebagai berikut :

 

_







      1 cos n o o n o d n t a t x Persamaan 12 Deret x (t)

Hubungan koefisien andan bn terhadap dn dan φn dapat ditunjukkan sebagai berikut :

an = dn cos υn

bn = dn sin υn

Persamaan 13 koefisien andan bn

Untuk keperluan perhitungan koefisien fourier digunakan sifat dasar ortogonalitas sinusoidal. Beberapa integral penting yang dapat secara mudah dihasilkan untuk to dan

bilangan bulat n dan m maka :



T   o n t t ot dt n 0 sin (2.5)

Persamaan 14 koefisien fourier 1



T   o n t t ot dt n 0 cos (2.6)

Persamaan 15 koefisien fourier 1I

X(t ) X(t ) X(t )



T    o n t t o ot m t dt n cos 0 sin (2.7)

Persamaan 16 koefisien fourier 1II



 _      T o n t t o o m n jika T m n jika dt t m t n 2 / 0 sin sin (2.8)

Persamaan 17 koefisien fourier 1V



 _      T o n t t o o m n jika T m n jika dt t m t n 2 / 0 sin sin (2.9) Persamaan 18 koefisien V

Kita dapat menggunakan identitas diatas untk mengevaluasi koefisien fourier. Pertama, kita kalikan kedua sisi dari Persamaan 11 dengan dt dan mengintegralkan sepanjang satu perioda, misal t0 sampai t0 + t. Dengan menggunakan Persamaan 14 dan

Persamaan 15 maka sisi kanan akan hilang, kecuali a0. Sehingga kita peroleh :

 



  t T t x t dt T a 0 0 1 0 (2.10) Persamaan 19 koefisien V

Begitu pula pengalian kedua sisi Persamaan 11 dengan cos nΩ0t dan mengintegralkan

sepanjang satu perioda, akan kita peroleh harmonisa ke-n :

 



   t T t n x t n t dt T a 0 0 0 cos 2 (2.11)

Persamaan 20 Harmonisa an dan bn

 



   t T t n xt n t dt T b 0 0 0 sin 2 (2.12)

Persamaan 21 armonisa an dan bn (2)

Bentuk eksponensial dari deret Fourier didasarkan pada identitas Euler,yang dapat ditulis sebagai berikut :

2 cos 0 0 0 t jn t jn e e t n    _   (2.13)

Persamaan 22 Identitas euler

j e e t n t jn t jn 2 sin 0 0 0    _   (2.14)

Persamaan 23 Identitas euler (2)

Persamaan diatas kita substitusikan ke dalam Persamaan 11, kita peroleh :

 

_







      1 0 0 0 cos sin n n n n t b n t a a t x



                   1 0 2 2 0 0 0 0 n t jn t jn n t jn t jn n j e e b e e a a



            _    1 0 0 0 2 2 n t jn n n t jn n n e jb a e jb a a (2.15)

Persamaan 24 Identitas euler (3)

Selanjutnya dapat lebih disederhanakan dengan substitusi dibawah ini :

c₀ a₀





2 n n n jb a c  





2 n n n jb a c_   Sehingga :

 



       n t jn ne c a t x 0 0 (2.16)

Demikian juga, dengan mensubtitusi integral an dan bn dari Persamaan 20 dan

Persamaan 21, kita peroleh :





tT

 

  t t jn n x t e dt T c 0 0 0 1 (2.17) Persamaan 26 Transformasi fourier

Persamaan 25 dan Persamaan 26 diatas mendifinisikan deret fourier bentuk eksponensial yang mana Persamaan 26 merupakan persamaan analisis untuk menganalisa persamaan bentuk periodik ke dalam komponen fourier. Sedangkan Persamaan 25 dikatakan sebagai persamaan sintesis yang dapat digunakan mensintesa bentuk gelombang dari komponen Fourier.

Hubugan antara koefisien fourier bentuk trigonometri dengan bentuk eksponensial ditunjukkan sebagai berikut :

j _n

n n

n jb d e c

a   n _{2 (2.18)}

Persamaan 27 Koefisien fourier

Contoh 2.2

Kita perhatikan gelombang bentuk persegi seperti pada contoh 3-1, misalnya lebar pulsa ∆1 tinggi A1 dan periode T, maka :

 











                      t T t T T t jn T T t jn T T t jn t jn n Ae dt e dt e dt T dt e t x T c 0 0 0 0 0 0 2 2 2 2 . 0 . 0 1 1



    2 2 0 1 A A t jn dt Ae T

 

_                 j e j e T n A e T jn A A jn t jn t A t jn 2 2 2 0 0 0 0 2 2 0





                2 sin 2 sin ₀ 0 0 n c T A n n T A

Untuk n=0 dengan L1 Hopital diperoleh

T A c₀  , sehingga :

 

_

              z n t jn e n c T A T A t x 1 0 0 2 sin (2.19)

Persamaan 28 Fungsi L Hospital

2.2.3. Pengaruh Simetri

Sebuah sinyal periodik dikatakan fungsi genap jika memenuhi persamaan :

x(t) = x(-t) (2.20)

Persamaan 29 Fungsi genap dan dikatakan fungsi ganjil jika :

x(t) = -x(-t) (2.21)

Persamaan 30 Fungsi ganjil

Persamaan 29 dan Persamaan 30 diatas menunjukkan bahwa fungsi genap adalah simetri pada sumbu vertikal pada t=0, dan fungsi ganjil adalah antisimetri terhadap sumbu vertikal. Beberapa contoh fungsi genap dan ganjil ditunjukkan pada gambar 25

Dengan demikian bahwa sin nΩ0t adalah ganjil dan cos nΩ0t adalah genap untuk

seluruh nilai n. Hasil dari penjumlahan dari beberapa fungsi ganjil adalah fungsi ganjil, dan hasil dari penjumlahan sejumlah fungsi genap adalah fungsi genap. Sehingga Deret Fourier untuk fungsi periodik ganjil dapat berisi hanya sinus dan konstanta. Sama halnya, deret fourier untuk fungsi periodik genap dapat berisi hanya cosinus dan konstanta. Konstanta akan bernilai nol jika daerah dibawah setengah siklus positif sama dengan daerah dibawahsetengah siklus negatif. Jika kita menggunakan bentuk eksponensial, koefisien yang muncul adalah majiner untuk fungsi ganjil dan real untuk fungsi genap.

gambar 25 Contoh fungsi genap dan ganjil (a) fungsi genap (b) fungsi ganjil (c) fungsi genap

Dari keterangan diatas dapat kita pahami bahwa, jika sebuah sinyal periodik mempunyai simetri ganjil atau genap, maka pengintegralan dapat dilakukan hanya setengah periode, oleh karena setengah periode yang lainnya identik. Dengan mengalikan hasil integral setengah periode tersebut dengan 2, akan diperoleh hasil akhir integral lengkap.

Sebuah fungsi periodik dikatakan mempunyai simetri setengah gelombang jika :

 

t x T t x        2

Persamaan 31 Simetri setengah gelombang

Jenis simetri ini dapat divisualisasikan dengan catatan bahwa, jika bagian setengah gelombang negatif dari gelombang digeser sepanjang setengah periode maka akan merupakan cermin (bayangan) dari bagian setengah-gelombang positif terhadap sumbu waktu t.

Beberapa bentuk gelombang yang mempunyai simetri setengah gelombang ditunjukkan dengan gambar 26

gambar 26 Contoh bentuk gelombang dengan setengah-gelombang

2.2.4. Sifat-sifat Deret Fourier Waktu Kontinyu

x(t)

t

x(t)

Dengan memahami sifat-sifat deret fourier, maka akan mempermudah dalam menentukan deret fourier dari beberapa fungsi periodik. Untuk itu kita akan memulai dengan operasi penurunan (deferensial) dan pengintegralan.

2.2.4.1. Diferensial dan Integrasi Sinyal Periodik

Jika deret fourier untuk sinyal periodik diketahui, maka deferensial atau integral sinyal tersebut dapat diketahui jika penurunan atau mengintegralkan tiap-tiap bagian dari deret tersebut. Lebih jelasnya, jika penurunan deret kedua sisi deret fourier komplek yang diberikan persamaan 2.16 akan diperoleh :





      _{ }  n t t jn n t jn ne jn tc e c dt d dt dx _{0 0} . . 0 (2.23)

Persamaan 32 Differensial dan integrasi sinyal periodik

Dari Persamaan 32 dapat kita lihat bahwa pengaruh diferensial adalah pengalian koefisien fourier dengan jnΩ0. Dengan kata lain, jika koefisien deret fourier komplek

diberikan oleh jnΩ0 cn. Ini menunjukkan bahwa pengaruh penurunan akan menaikkan

magnituda ke harmoni yang lebih tinggi.

Demikian halnya integrasi adalah kebalikan turunan. Pengaruh integrasi akan membagi koefisien bentuk komplek pada deret fourier oleh jnΩ0. Sehingga, integrasi

mempunyai pengaruh pengurangan magnituda pada harmonik yang lebih tinggi dari sinyal tersebut. Dalam integrasi ini harus dihitung juga konstanta integrasi. Hal ini dapat diperoleh secara sederhana, komponen dc dari integrasi diperoleh dari daerah dibawah satu putaran penuh fungsi itu.

2.2.4.2. Pengaruh Pergeseran waktu pada bentuk gelombang

Diberikan sebuah sinyal x(t) dengan deret Fouriernya adalah :

 



      n t jn n e c t x _. 0 _(2.24)

Misalkan kita definisikan sinyal lainnya y(t), yang mempunyai korelasi dengan x(t) sebagai berikut :

y(t) = x(t-τ) (2.25)

Persamaan 34 Deret fourier (2)

Sinyal x(t) dan y(t) ditunjukan dalam gambar 2-6. Menunjukkan bahwa keterlambatan tersebut dapat diperoleh dari transformasi sederhana dengan mengubah variable t menjadi (t-τ). Konskuensinya, deret fourier untu y(t) akan diperoleh dengan penggantian t menjadi (t-τ) kedalam persamaan 2.24, sehingga diperoleh :

 

_

         n t jn ne c t x _. 0  _(2.26)

Persamaan 35 Deret fourier (3)

Koefisien Fourier untuk fungsi yang telah digeser, Ĉn diperoleh :

Ĉn = c.e-jnΩ0τ (2.27)

Persamaan 36 Koefisien fourier

Ini menunjukkan bahwa dua koefisien Fourier tersebut adalah bilangan kompplek dengan amplituda sama, akan tetapi argumen berbeda :

gambar 27. Pergeseran sepanjang sumbu waktu

Didepan telah kita singgung bahwa hampir setiap kasus sebuah fungsi periodik dapat diekspresikan dalam bentuk deret fourier. Hal ini benar untuk hampir seluruh

x(t)

t

t τ

sinyal yang digunakan dalam masalah engineering, tetapi perlu sekali mengetahui kondisi yang diperlukan agar deret konvergen untuk fungsi yang diberikan. Kondisi ini dikatakan Dirichlet Condition. Jika sebuah fungsi memenuhi kondisi ini maka

deret fourier dengan nilai tak terhingga (infinite), dijamin konvergen untuk seluruh nilai t, dengan pengecualian pada titik diskontinyu sinyal. Kondisi tersebut adalah seperti dibawah ini :

1. Fungsi tersebut dapat diintegralkan secara mutlak (absolutly integrable) sepanjang beberapa periode, sehingga :

 





t T t x t dt 0 0 (2.28)

Persamaan 37 absolutly integrable

2. Fungsi harus mempunyai nilai maksima dam minima terbatas (finite) sepanjang perioda penuh.

3. Fungsi harus mempunyai jumlah diskontinuitas terbatas sepanjang perioda penuh.

Dalam kenyataannya, dapat dibuktikan bahwa jika suatu fungsi memenuhi ketiga kondisi tersebut, maka deret Fourier Truncuted akan merupakan pendekatan terbaik untuk sinyal aslinya, dibandingkan dengan beberapa fungsi harmonik lainnya.

2.3.Sistem Dengan Input Periodik

2.3.1. Respon Steady-State Terhadap Input Sinusoidal

Dalam Bab I kita telah membahas solusi particular persamaan diferensial linier untuk fungsi sinusoidal yang mana telah diperoleh sangat sesuai menggunakan aljabar komplek. Sebagaimana hal ini, dasar pendekatan adalah identik dan didasarkan pada penggantian operator p dengan jΩ, dimana Ω adalah frekuensi sinusoidal dalam radian perdetik.

Diberikan sebuah sistem linier yang dijelaskan oleh persamaan diferensial dibawah ini, ditulis dalam notasi operator :

   

p y t N

   

p u t

D  (2.29)

Dimana D(p) dan N(p) adalah polinomial adalah operator diferensial p. Kita akan meninjau kasus khusus dimana fungsi input u(t) adalah sinusoidal, diberikan oleh :

 

t A



t



u cos (2.30)

Persamaan 39 Fungsi input sinusiodal

Misalkan dengan identitas Euler kita tulis sebagai berikut :

 





j t j t e U e U t A t u  cos         (2.31)

Persamaan 40 Identias euler

Dimana :



j

Ae

U0.5 (2.32)

Persamaan 41 Identitas euler Dan



 j

Ae

U 0.5  (2.33)

Persamaan 42 Identitas euler

Catatan bahwa secara umum U dan U adalah bilangan komplek dan konjugatnya U dikatakan sebagai phasor yang merepresentasikan sinusoidal, yang mana berisi informasi mengenai magnituda dan phase sinusoidal tersebut.

Dalam bab terdahulu, komponen steady-state akan diperoleh dengan menggunakan superposisi :

 

 

_{ }

_{ }

 

j t j p t j j p Ue p D p N Ue p D p N t y          (2.34)

Persamaan 43 Komponen steady state

 

 

_{ }

j j p Me p D p N t y  _ (2.35)

Persamaan 44 Komponen steady state (2)

Dimana M adalah modulus pada bilangan komplek dan  adalah argument, kita dapat menuliskan persamaan diatas :

 

j t j t e Y e Y t y      (2.36)

Persamaan 45 Komponen steady state (2)

Dimana bilangan komplek

 

_ j _ j MAe U Me t Y (2.37)

Persamaan 46 Komponen steady state (2)

Dan Y konjugat komplek

Dengan mensubtitusikan Y dan Y kedalam persamaan (2.36) diatas, kita peroleh solusi steady-state :

 

t  MA



t



y_ss 2 cos (2.38)

Persamaan 47 Komponen steady state (3)

Contoh 2-3 :

Rangkaian listrik seperti gambar dibawah dengan masukan sistem sebagai berikut :

 

              3 6 cos 8 4 3 cos 20 10 t  t  t x (2.39)

Persamaan 48 Komponen steady state (4) Kita akan menghitung keluaran sistem stedy-state yss

gambar 28 Rangkaian RLC 2 Loop

Rangkaian tersebut jika nyatakan dalam operator p : 1 Mohm 1 Mohm

1 µF 1 µF



P33P1



y

   

t xt , maka

   

_{ }

1 3 1 3    P P t x t y p L

Dalam kasus ini, input terdiri atas tiga komponen, dengan frekuensi0, 3, dan 6 radian. Oleh karena itu kita akan mengevaluasi sistem dalam frekuensi tersebut dan kemudian mengalikan nilainya secara berurutan dengan phasor input untuk memperoleh phasor output yang sesuai.

1 1 3 1 0 3  Pj  P P 22974 3 3 0.8305 1 3 1 j j P e P P     266658 6 3 0.0254 1 3 1 j j P e P P    

Akhirnya tegangan keluaran steady-state diberikan oleh :

      _{ }        _{ }   2.66658 3 6 cos 0203 . 0 2974 . 2 4 3 cos 609 . 16 10 2   t t v (2.40)

Persamaan 49 Tegangan keluaran steady state

2.4.Spektrum Sinyal Periodik

Pada umumnya, fungsi periodik terdiri fungsi sinusoidal dasar dan sejumlah harmoniknya (secara teori tak terhingga). Jenis fungsi bergantung pada perubahan nilai pada tiap-tiap harmonik. Jika kita menggunakan bentuk eksponensial untuk deret Fourier, maka cnt yang secara umum adalah bilangan komplek,mengandung informasi

tentang magnituda dan phase tiap-tiap komponen gelombang. Jika cnt magnituda cn

diplot terhadap nΩ0t kita akan memperoleh spektrum frekuensi magnituda fungsi

periodik tersebut. Dengan jalan yang sama kita dapat memplot spektrum frekuensi dari phase cn. Dalam penggunaan yang umum, spektrum dari magnituda dikatakan sebagai

spektrum frekuensi, mungkin karena tidak berubah terhadap pergeseran waktu, dimana spektrum dari phasa berubah terhadap pergeseran sepanjang sumbu waktu.

2.5.Daya Rata-Rata Sinyal Periodik

t jn n ne c t x     



  ) ( 



tT

 

t x t dt T P 0 0 2 1 (2.41) Persamaan 50 Daya rata-rata sinyal periodik

Dimana T adalah perioda sinyal. Dapat ditunjukkan bahwa kuantitas P akan merepresentasikan daya rata-rata sebenarnya yang dikirim kedalam resistor 1 ohm jika x(t) adalah arus yang mengalirinya atau tegangannya.

Sifat ortogonalitas antar harmonik dalam deret Fourier, sebagaimana ditunjukkan dalam bantuan Persamaan 10 dan Persamaan 11, bahwa : memungkinkan utuk menghitung daya rata-rata dalam komponen koefisien Fourier tanpa harus mengerjakan integrasi seperti yang diberikan dalam persamaan (2.41).

Hal ini dapat ditunjukkan dengan mudah, melalui bantuan Persamaan 10 dan Persamaan 11, bahwa :

 



 



__  t T t n n c dt t x T P 0 0 2 2 1 (2.42)

Persamaan 51 Daya rata-rata sinyal periodik (2)

Dimana cn adalah koefisien deret Fourier komplek. Persamaan diatas juga mungkin

diekspresikan dalam bentuk koefisien deret Fourier trigonometri, sehingga :







      n n n b a a P ₀2 2 2 2 1 (2.43) Persamaan 52 Koefisien deret fourier trigonometri

2.6.Transformasi Fourier

Pada bahasan 2.4 telah dijelaskan bahwa spectrum frekuensi pada sinyal periodik adalah diskret dan dapat diperoleh dengan deret Fourier. Dengan pendekatan bentuk eksponensial, dimana nilai spektralnya adalah diskret terhadap frekuensi, cn = f() dengan n nilai integer.



     t t t t jn n x t e T c 0 0 ) ( 1

Sekarang kita akan membahas konsep spektrum frekuensi dari sinyal aperiodik. Hal ini sangat penting karena hamper setiap saat kita dihadapkan pada sinyal yang tidak periodik. Untuk keperluan ini digunakan Transformasi Fourier. Untuk mempelajari masalah ini kita gunakan pendekatan pengaruh kenaikan periode pada sinyal. Dalam batas tertentu, ketika periode mendekati tak terhingga, kita akan memperole sinyal aperiodik.

Dengan kata lain sebuah sinyal aperodik dapat dianggap sebagai sinyal periodik dengan perode tak terhingga.

0=

T 2

 0 untuk T  

Sehingga d untuk sinyal periodik sangat kecil.

Konsekuensinya, spectrum diskret untuk fungsi perodk akan digantikan dengan spectrum kontinyu untuk fungsi aperiodik.





       d e x t x ( ) j t 2 1 ) (  (2.47)

Persamaan 53 Integral spectrum discret

x



x t e jn tdt       ) ( ) ( (2.48)

Persamaan 54 Integral spectrum kontinou

Dimana spectrum frekuensi x() adalah transformasi Fourier dari x(t) dan x(t) adalah invers transformasi Fourier dan x().

Sebagaimana pada deret Fourier, fungsi x(t) harus memenuhi Diriclet Condition agar transformasi Fourier ada. Kondisi ini menjamin bahwa integral yang didefinisikan dalam persamaan 2.38 akan konvergen. Kondisi tersebut adalah

(2.49)

Persamaan 55 absolutely integrable

2. X(t) harus mempunyai jumlah maxima dan minima terhingga dalam interval waktu terbatas

3. x(t) harus mempunyai jumlah diskontinyu terhinga dalam sejumlah interval dan tiap-tiap diskontinyu terhingga

2.6.1. Beberapa Pasangan Transformasi Fourier

Dalam bahasan ini kita akan memberikan contoh mencarimencari tranformasi Fourier untuk beberapa fungsi aperiodik, kemudian diikuti pencarian invers transformasi Fouriernya.

2.6.2. Sifat-Sifat Transformasi Fourier

Dengan mengenal sifat-sifat transformasi Fourier akan mebuat kita mengerti hubungan representasi sinyal pada kawasan waktu dan kawasan frekuensi. Selain itu juga akan membantu kita memperoleh transformasi Fourier dengan lebih mudah.

Dalam hal ini kita sepkati bahwa :

X() = F [x(t)] menunjukkkan bahwa X() adalah transformasi Fourier dari x(t) X(t) = F -1 [X()] x(t) adalah transformasi Fourier dari X ()

2.6.2.1. Linieritas

Sifat linieritas ditunjukkan : X1 () = F [x1(t)] dan X2 () = F [x2(t)]

Maka

Persamaan 56 Sifat linieritas

2.6.2.2. Dualitas

Dalam bahasan terdahulu, bahwa transformasi Fourier dari pulsa segiempat dalah fungsi sinc , dan transformasi fungsi sinc adalah pulsa segiempat. Demikian juga transformasi suatu konstanta adalah impuls dan impuls adalah suatu konstanta.

Hubungan dualitas transformasi Fourier ditunjukan sbb : Jika

X () = F [x(t)] maka F [X(t)] = 2 x (-) Persamaan 57 Prinsip dualitas

2.6.2.3. Turunan Dan Integral Dalam Kawasan Waktu

Seringali kita perlu menentukan transformasi Fourier untuk fungsi waktu dengan memperolehnya dari fungsi waktu yang lain yang telah diketahui transformasi Fouriernya. Persamaan berikut dapat membantu kita untuk keperluan ini.

Jika X () = F [x(t)] maka F [px(t)] = j x () Dan ) ( ) 0 ( ) ( 1 ) ( 1            _{ } X j X j t x p F

Persamaan 58 Turunan dan itegral dalam kawasan waktu

2.6.2.4. Penskalaan Waktu Dan Frekuensi

 

 __   a X a at makaFx t x F JikaX( ) ( ) ( ) 1

Persamaan 59 Penskalaan waktu dan frekuensi Dimana a adalah konstanta real

2.6.2.5. Pergeseran Waktu Theorema :

 

( )



( 0)



( ) ( ) ) ( F x t makaF tt at e 0X  JikaX  jt

2.6.2.6. Pergeseran Frekuensi Theorema :

 

( )





( ) ( ) ) ( F x t makaX o at Fe x t JikaX     jot

Persamaan 61 Pergeseran frekuensi

2.6.2.7. Turunan Dan Integral Dalam Kawasan Frekuensi

Theorema :

 

( ) : ( )



( )



) ( F jtx t d dX maka t x F JikaX      

Persamaan 62 Turunaan dan integral dalam kawasan frekuensi

2.6.3. Konvolusi

2.6.3.1. Konvolusi Dalam Kawasan Waktu

Teorema : Misalkan:

X () = F [x(t)] , H()= F[h(t), dan jika Y () = F [y(t)]

dimana x(t), h(t), dan y(t) dihubungkan oleh integral konvolusi sbb :



     x h t  d t y( ) ( ) ( ) Y() H()X()

Persamaan 63 Konvolusi dalam kawasan waktu

2.6.3.2. Konvolusi Dalam Kawasan Frekuensi

Teorema: Misalkan :

X () = F [x(t)] dan Y () = F [y(t)] maka : F



x t y t



X(u)y( u)du 2 1 ) ( ) ( 



    

Persamaan 64 Konvolusi dalam kawasan frekuensi

2.6.4.1. Transformasi Fourier Pada Suatu Konstanta

Pada contoh 2.8 telah ditunjukkan bahwa invers transformasi Fourier untuk fungsi impuls unit () adalah satu konstanta 1/2 leh karena itu, transformsi Fourier suatu konstanta adalah 2 A ()

2.6.4.2. Transformasi Fourier Pada Sinusoidal

Transformasi Fourier untuk sinusoidal dapat ditentukan dari pernyataan bentuk eksponensial kompleks sebagai berikut:

2 cos ot jn ot jn e e ot n    _   j e e ot ot jn ot jn 2 sin    _  

Persamaan 65 Eksponensial kompleks

Konsekuensinya, untuk mengevaluasi transformasi fungsi tersebut, pertama kali kita harus memperolehtransformsi fourier pada fungsi eksponensial. Kita dapat mengerjakannya dengan mencari invers transformasi fourier untuk fungsi impuls (- 0). _



_ jt _ jot e d e o t x    2 1 ) ( 2 1 ) ( F

 

ejot 2o Fcost 



(o)



(o)]



( ) ( )



sin t j o o F       

Hasil ini membrkan kita suatu pendekatan lain untuk menjelaskna modulasi. Perkalian sinyal pemodulasi dengan pembawa sinusoidal sama dengan konvolusi dalam kawasan frekuensi.

Tabel 1 Pasangan Transformasi Fourier

X(t) X() Keterangan

1. A(t-to) j to

Ae  Impuls pada t=to

2. A 2A() Fungsi step 3. A(t)         ( ) 1 _  j

A Hanya benar untuk a>0

4. A e –at (t)

  j a

A

Hanya benar untuk a>0

5. A e –at 2 ) ( 2 2   j a Aa

Hanya benar untuk a>0

6. A e –at cos o t (t) 2 ) ( ) (       j a j a A

Hanya benar untuk a>0 7. A e –at sin o t (t) 2 ) (     j a o A

Hanya benar untuk a>0 8. A t e –at (t) 2

) (a j

A

Hanya benar untuk a>0 9. A e –jt 2A(o)

10. A cos o t A



(o)(o)



11. A sin o t jA



(o)(o)

