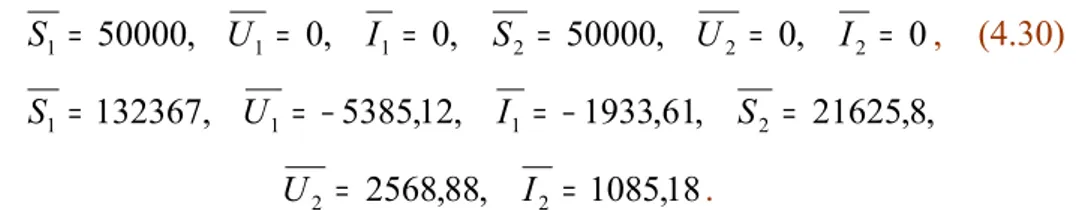ANALISIS KESTABILAN MODEL PENYEBARAN HIV PADA POPULASI HOMOSEKSUAL

ANALISIS KESTABILAN MODEL PENYEBARAN HIV PADA POPULASI HOMOSEKSUAL

oleh

LISDA PUJI SRI HASTUTI M0102030

SKRIPSI

ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika.

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET

SURAKARTA 2006

ABSTRAK

Lisda Puji Sri Hastuti, 2006. ANALISIS KESTABILAN MODEL PENYEBARAN HIV PADA POPULASI HOMOSEKSUAL. Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret.

HIV (Human Immunodeficiency Virus) merupakan jenis virus obligat yang menyerang sistem kekebalan tubuh manusia dan kemudian menimbulkan AIDS. Virus ini menyebar secara cepat dan memiliki angka kematian yang cukup tinggi. Oleh karena itu dipandang perlu untuk mempelajari model penyebaran HIV, terutama pada populasi homoseksual karena penyebaran HIV berawal dari populasi tersebut. Tujuan dari skripsi ini adalah menganalisis kestabilan di titik kesetimbangan bebas penyakit dan memberikan interpretasi terhadap hasil yang diperoleh.

Metode penelitian yang digunakan adalah studi literatur. Adapun langkah-langkahnya yaitu menentukan titik kesetimbangan, menganalisis kesetimbangan dan menganalisis kestabilan pada titik-titik kesetimbangan. Untuk menganalisis kestabilan digunakan kriteria kestabilan Routh-Hurwitz.

Dapat disimpulkan bahwa model penyebaran HIV pada populasi homoseksual dapat dibedakan menjadi dua, yaitu model penyebaran HIV tanpa adanya tes darah dan model penyebaran HIV dengan adanya tes darah. Masing-masing model memiliki dua titik kesetimbangan bebas penyakit. Titik kesetimbangan stabil jika rasio reproduksi R₀ < 1. Jika titik kesetimbangan stabil, hal ini menunjukkan bahwa HIV tidak akan berkembang menjadi endemis.

ABSTRACT

Lisda Puji Sri Hastuti, 2006. STABILITY ANALYSIS OF THE SPREADING OF HIV MODEL IN HOMOSEXUAL POPULATION. Faculty of Mathematics and Natural Sciences Sebelas Maret University.

Human Immunodeficiency Virus (HIV) is one of the virus which attacks human immunity and causes AIDS. This virus spreads quickly and has a great mortality rate. Therefore, it is important to study the spreading of the HIV, especially in homosexual populations because the spreading of the HIV started in it. The purposes of this research are to analyze the stability of the equilibrium point and to give the interpretation of the result in the example.

The research uses literary study. The steps to find the goal are determining the equilibrium point, analizing the equilibrium and the stability of the model. The stability is analyzed by Routh-Hurwitz Criterion.

As the conclusion, the spreading of HIV model can be divided into model without blood screening and model with blood screening. Each model has two free equilibrium points. Those equilibrium points will be stable if the reproduction ratio R₀ < 1. If the equilibrium points are stable, then the virus will not go into the endemic situation.

MOTO

Allah kelak akan memberikan kelapangan sesudah kesempitan.

(Q. S. Ath Thalaq : 7)

Kesukaran yang kita jumpai dalam menempuh tujuan merupakan jalan terdekat ke arah

tujuan itu.

(Kahlil Gibran)

Segala kesulitan dan ujian hidup, akan membuat kita menjadi manusia yang lebih kuat

dan lebih baik.

PERSEMBAHAN

Skripsi ini penulis persembahkan untuk : ♥ Almarhum Bapak tercinta,

salah satu anugerah terbesar dalam hidupku adalah terlahir sebagai putrimu. Aku tidak tahu bagaimana harus mengungkapkan betapa aku merindukanmu, I love you Dad...

♥ Ibu, Azis dan seluruh keluarga besarku,

kalian adalah api semangat dalam hidupku, yang selamanya akan terus menyala dan memberiku kekuatan untuk terus berdiri tegar.

♥ My lovely one....

terima kasih karena selalu berada di sisiku di saat senang maupun di saat-saat tersulit dalam hidupku. Semoga kamu bisa menjadi Imamku di dunia maupun di akhirat nanti.

KATA PENGANTAR

Puji syukur alhamdulillah penulis panjatkan kehadirat Allah SWT yang senantiasa memberikan rahmat serta hidayah-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi ini.

Penulis menyadari bahwa skripsi ini dapat terselesaikan dengan baik karena adanya bantuan dari berbagai pihak. Untuk itu dengan segala kerendahan hati penulis mengucapkan terima kasih kepada semua pihak yang telah membantu dalam penulisan skripsi ini, terutama penulis tujukan kepada :

1. Bapak Drs. Sutrima, M. Si. selaku Dosen Pembimbing I, yang telah meluangkan waktu untuk membimbing dan mengarahkan penulis dalam menyelesaikan penulisan skripsi ini.

2. Bapak Irwan Susanto, S. Si., DEA selaku Dosen Pembimbing II, yang telah memberi masukan bagi penulis.

3. Ibu, Azis dan Yusuf yang telah banyak memberikan dorongan semangat dan doa selama penyusunan skripsi ini.

4. Mas Win, Mas Bayu, Mbak Ari, Mbak Surati, Lisna dan Astrid yang selalu meluangkan waktu untuk membantu penulis.

5. Teman-teman angkatan 2002 yang telah memberikan bantuan dan motivasi. 6. Semua pihak yang telah membantu penulis dalam menyusun skripsi ini.

Semoga Allah SWT membalas segala bantuan yang telah diberikan kepada penulis. Penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak yang membutuhkan.

Surakarta, Oktober 2006

DAFTAR ISI JUDUL... i PENGESAHAN... ii ABSTRAK... ... iii ABSTRACT... ... iv MOTO... v PERSEMBAHAN... ... vi KATA PENGANTAR... ... vii DAFTAR ISI... ... viii DAFTAR TABEL... x DAFTAR GAMBAR... ... xi DAFTAR NOTASI... ... xii BAB I PENDAHULUAN

1.1.Latar Belakang Masalah... 1 1.2.Perumusan Masalah... 3 1.3.Batasan Masalah... 3

1.4.Tujuan Penulisan... 3

1.5.Manfaat Penulisan... 3

BAB II LANDASAN TEORI 2.1.Tinjauan Pustaka... 4

2.1.1Teori HIV/AIDS... 4

2.1.2Model Matematika... 5

2.1.3Persamaan Diferensial... 5

2.1.4Matriks... 7

2.1.5Kestabilan Sistem Persamaan Diferensial... 8 2.1.6Kriteria Kestabilan Routh-Hurwitz...

... 11

2.2.Kerangka Pemikiran... ... 12

BAB III METODE PENULISAN... ... 13

BAB IV PEMBAHASAN

4.1.Model Penyebaran Virus HIV Tanpa Adanya Tes Darah... ... 16 4.1.1Titik Kesetimbangan... ... 17... 4.1.2Analisis Kestabilan... ... 18

4.2.Model Penyebaran Virus HIV Dengan Adanya Tes Darah... ... 21 4.2.1Titik Kesetimbangan... ... 22 4.2.2Analisis Kestabilan... ... 23 4.3.Simulasi... ... 26 4.3.1Simulasi Pertama... ... 26 4.3.2Simulasi Kedua... ... 31 4.3.3Simulasi Ketiga... ... 34 BAB V PENUTUP 5.1.Kesimpulan... ... 37 5.2.Saran... ... 37 DAFTAR PUSTAKA... ... 38

DAFTAR TABEL

Tabel 4.1 Tabel Nilai Parameter untuk Simulasi Pertama... 26 Tabel 4.2 Tabel Nilai Parameter untuk Simulasi Kedua... 31 Tabel 4.3 Tabel Nilai Parameter untuk Simulasi Ketiga... 34

DAFTAR GAMBAR

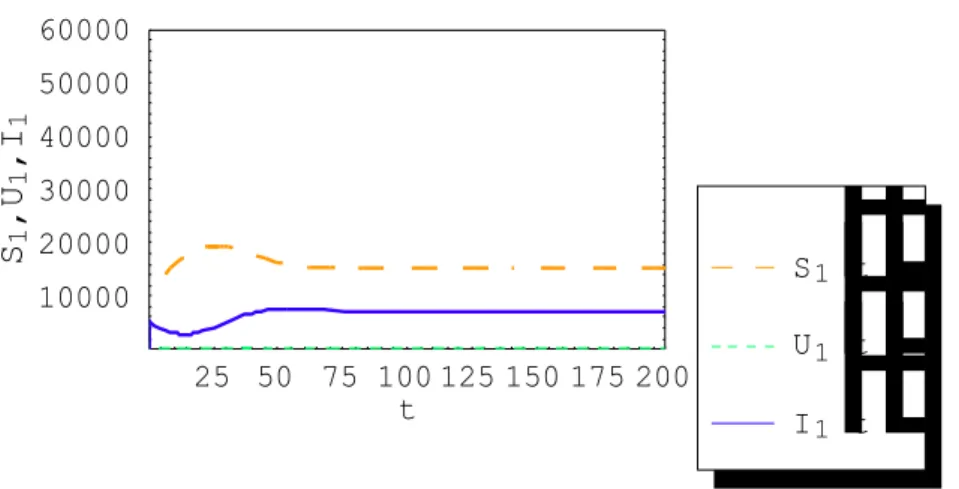
Gambar 2.1 Trayektori pada Bidang Fase... 10 Gambar 4.1 Grafik S₁

( )

t , U₁

( )

t dan I₁

( )

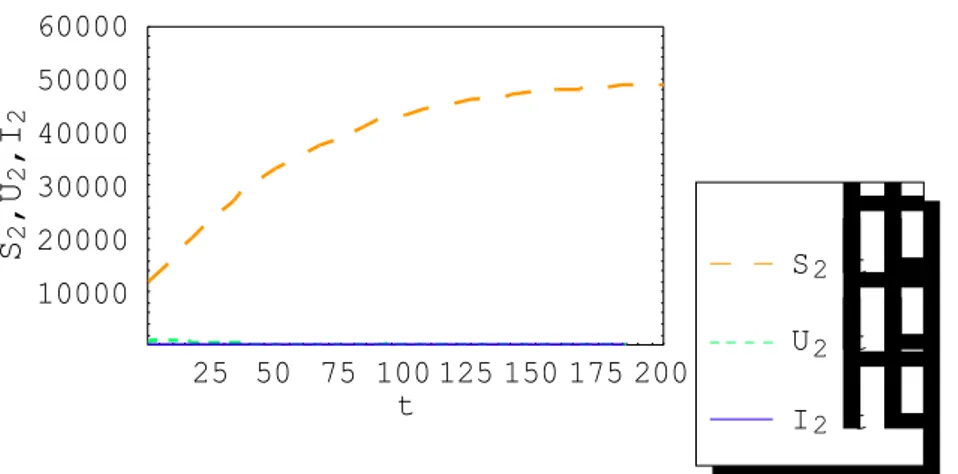
t terhadap t untuk

σ ₁ = σ ₂ = 5000... 28 Gambar 4.2 Grafik S₂

( )

t , U₂

( )

t dan I₂

( )

t terhadap t untuk

σ ₁ = σ ₂ = 5000... 29 Gambar 4.3 Grafik S₁

( )

t , U₁

( )

t dan I₁

( )

t terhadap t untuk

σ ₁ = σ ₂ = 33000... 30 Gambar 4.4 Grafik S₂

( )

t , U₂

( )

t dan I₂

( )

t terhadap t untuk

σ ₁ = σ ₂ = 33000... 30 Gambar 4.5 Grafik S₁

( )

t , U₁

( )

t dan I₁

( )

t terhadap t untuk

Gambar 4.6 Grafik S₂

( )

t , U₂

( )

t dan I₂

( )

t terhadap t untuk

Simulasi Kedua... 33 Gambar 4.7 Grafik S₁

( )

t , U₁

( )

t dan I₁

( )

t terhadap t untuk

Simulasi Ketiga... 35 Gambar 4.8 Grafik S₂

( )

t , U₂

( )

t dan I₂

( )

t terhadap t untuk

Simulasi Ketiga... 36

DAFTAR NOTASI

i

S : kompartemen manusia rawan terinfeksi

j

U _{: kompartemen manusia tidak sadar terinfeksi}

k

I : kompartemen manusia sadar terinfeksi

l

β : probabilitas transmisi virus dari manusia terinfeksi ke manusia rawan terinfeksi

m

σ : banyaknya tes darah yang dilakukan µ _{: angka kematian}

p

N _{: laju pertambahan manusia rawan terinfeksi}

q

η : rata-rata periode aktifitas seksual manusia terinfeksi T : populasi total manusia

r

i

S : titik kesetimbangan manusia rawan terinfeksi

j

U : titik kesetimbangan manusia tidak sadar terinfeksi

k

I : titik kesetimbangan manusia sadar terinfeksi

0 R : rasio reproduksi J : matriks Jacobian I : matriks identitas λ : nilai eigen v : vektor eigen z : perturbasi BAB I PENDAHULUAN

1.1 Latar Belakang Masalah

Penemuan kasus HIV (Human Immunodeficiency Virus) pertama kali terjadi sekitar tahun 1981 pada populasi homoseksual oleh ahli kesehatan di kota Los Angeles, Amerika Serikat. Di dalam tubuh seorang gay ditemukan penyakit pneumonia (Pneumonic Carinii) yang disertai dengan penurunan kekebalan tubuh (imunitas). Kemudian pada tahun 1982, para ilmuwan menemukan sindrom yang dikenal sebagai Gay Related Immune Deficiency (GRID), yaitu penurunan kekebalan tubuh yang terjadi pada populasi homoseksual. HIV sendiri baru diketahui sekitar tahun 1983 oleh Lug Montaigneur, seorang ahli mikrobiologi Perancis. Pada awalnya, penyebaran HIV hanya ditemukan pada populasi homoseksual saja. Tetapi karena pada populasi homoseksual juga terdapat biseksual, maka pada akhirnya penyebaran HIV semakin meluas dan tidak hanya terbatas pada populasi homoseksual saja (Silalahi, 2004).

Menurut UNAIDS (Badan PBB untuk penanggulangan AIDS) sampai dengan akhir tahun 1995, jumlah orang yang terinfeksi HIV di dunia telah mencapai 28 juta dengan 2,4 juta diantaranya adalah kasus bayi dan anak. Setiap hari terjadi infeksi baru sebanyak 8500 orang. Sedangkan pada saat ini di beberapa negara, terutama negara di benua Afrika, lebih dari 35% populasi penduduk yang berumur antara 15 sampai 50 tahun terinfeksi HIV, dan secara global telah menyebabkan kematian hingga 16 juta manusia (Tuckwell, 2001).

Virus ini menyebar secara cepat dan memiliki angka kematian yang cukup tinggi. Oleh karena itu diperlukan suatu model matematika yang dapat menyatakan realitas penyebaran HIV, terutama pada populasi homoseksual karena penyebaran HIV berawal dari populasi tersebut. Piqueira, Castano dan Monteiro (2004) telah menyusun model penyebaran HIV pada populasi homoseksual yang didefinisikan sebagai sistem persamaan diferensial nonlinear berikut

1 1 1 1 1 2 1 2 3 1 1 4 1 2 S1 T I S T I S T U S T U S N dt dS µ β β β β _{− − − −} − = , 1 1 1 1 2 1 2 3 1 1 4 1 2 1 1

(

₁

)

_U1 T U T I S T I S T U S T U S dt dU η µ σ β β β β _{+ + + − − +} = ,

(

2

)

1 1 1 1 _I T U dt dI η µ σ + − = , 2 2 5 2 1 6 2 2 7 2 1 8 2 2 S2 T I S T I S T U S T U S N dt dS µ β β β β _{− − − −} − = , 2 5 2 1 6 2 2 7 2 1 8 2 2 2 2

(

₃

)

_U2 T U T I S T I S T U S T U S dt dU η µ σ β β β β _{+ + + − − +} = , 2 2 2

(

4

)

I2 T U dt dI η µ σ _{− +} = , dengan

Si : kompartemen manusia rawan terinfeksi kelompok ke i, i= 1,2 j

U _{: kompartemen manusia tidak sadar terinfeksi kelompok ke j,} j = 1,2 k

l

β : probabilitas transmisi virus dari manusia terinfeksi ke manusia rawan

terinfeksi, l = 1,2,,8 m

σ : banyaknya tes darah pada manusia terinfeksi kelompok ke m, m= 1,2

µ : angka kematian,

p

N _{: laju pertambahan manusia rawan terinfeksi kelompok ke p,} p= 1,2 q

η : rata-rata periode aktifitas seksual manusia terinfeksi ke q, q= 1,2,3,4

T : populasi total manusia

Tr : populasi total manusia pada kelompok ke r, r = 1,2 2

1 T

T

T = + , T1 = S1+ U1 + I1 dan T2 = S2 + U2 + I2

Untuk menentukan apakah virus akan punah atau menjadi endemis, maka perlu dilakukan analisis kestabilan terhadap model penyebaran HIV ini. Analisis kestabilan dilakukan di sekitar titik kesetimbangan.

1.2Perumusan Masalah

Berdasarkan latar belakang masalah di atas, permasalahan yang akan dikaji dalam penulisan skripsi ini adalah

1. Bagaimana menganalisis kestabilan di sekitar titik kesetimbangan? 2. Bagaimana interpretasi model?

1.3 Batasan Masalah

Adapun pembatasan masalah di sini adalah

1. Model mengabaikan adanya transmisi HIV melalui alat suntik, transfusi darah dan infeksi pada anak yang ibunya pengidap HIV. Pembahasan dalam skripsi ini dibatasi dengan asumsi bahwa transmisi virus hanya terjadi melalui hubungan seksual.

2. Titik kesetimbangan yang dibahas dalam skripsi ini dibatasi hanya pada titik kesetimbangan bebas penyakit.

1.4 Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah dapat menganalisis kestabilan model di sekitar titik kesetimbangan dan dapat memberikan interpretasi. Analisis kestabilan dilakukan dengan kriteria kestabilan Routh-Hurwitz.

1.5 Manfaat Penulisan

Manfaat dari penulisan skripsi ini diharapkan dapat meningkatkan pemahaman tentang model matematika khususnya di bidang biologi dan kedokteran.

BAB II

LANDASAN TEORI

2.1 Tinjauan Pustaka

Untuk dapat menyelesaikan masalah yang dirumuskan, maka diperlukan teori-teori yang mendasari pembahasan. Pada bagian pertama bab ini, diberikan tinjauan pustaka yang terdiri atas beberapa definisi dan teorema sebagai dasar pengertian untuk mempermudah pembahasan selanjutnya. Sedangkan pada bagian kedua, disusun suatu kerangka pemikiran berdasarkan definisi dan teorema pada tinjauan pustaka.

2.1.1 Teori HIV/AIDS

HIV atau Human Immunodeficiency Virus adalah virus yang menyerang

sistem kekebalan tubuh manusia dan kemudian menimbulkan AIDS. Sedangkan

AIDS (Acquired Immuno Deficiency Syndrome) adalah kumpulan gejala penyakit

jenis virus obligat yaitu virus yang hanya dapat hidup dalam sel atau media hidup. Virus ini hidup dan berkembang biak pada sel darah putih manusia. HIV menyerang salah satu jenis dari sel-sel darah putih yang bertugas menangkal infeksi. Sel darah putih tersebut termasuk limfosit yang disebut "sel T-4" atau disebut juga "sel CD-4" (Sasongko, 2004).

Virus dapat ditemukan pada cairan tubuh yang mengandung sel darah putih seperti darah, cairan plasenta, air mani atau cairan sperma, cairan sumsum tulang, cairan vagina, air susu ibu dan cairan otak. Transmisi HIV terjadi kalau ada pencampuran cairan tubuh yang mengandung HIV, seperti hubungan seksual dengan pasangan yang mengidap HIV, jarum suntik dan alat-alat penusuk (tato, tindik dan cukur) yang tercemar HIV, transfusi darah atau produk darah yang mengandung HIV dan ibu hamil yang mengidap HIV kepada janin atau bayinya.

2.1.2 Model Matematika

Sebelumnya akan diberikan beberapa definisi tentang model matematika yang mendasari penulisan skripsi ini.

Definisi 2.1 [Meyer, 1984] Model adalah konsep yang digunakan untuk mempresentasikan sesuatu dan mengubahnya ke dalam bentuk yang dapat dipahami.

Definisi 2.2 [Meyer, 1984] Model matematika adalah model yang merupakan bagian dari konsep matematika yang didesain untuk mempelajari sistem yang timbul dalam masalah nyata.

2.1.3 Persamaan Diferensial

Menurut Kreiszig (1991), persamaan diferensial merupakan persamaan yang melibatkan turunan pertama atau lebih dari fungsi yang tidak diketahui terhadap variabel bebasnya. Sedangkan persamaan yang hanya melibatkan turunan pertama disebut persamaan diferensial orde satu.

Definisi 2.3 [Braun, 1978]Persamaan diferensial linear orde satu secara umum berbentuk ) ( ) (t y b t a dt dy _{+ =} .

Fungsi a(t) dan b(t) merupakan fungsi kontinu terhadap waktu t. Jika b(t) identik dengan nol maka disebut persamaan diferensial linear homogen orde satu, jika b(t) tidak identik nol maka disebut persamaan diferensial linear nonhomogen orde satu.

Sistem persamaan diferensial linear orde satu dari n fungsi yang tidak diketahui berbentuk ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 2 1 1 2 2 2 22 1 21 2 1 1 2 12 1 11 1 t f x t a x t a x t a dt dx t f x t a x t a x t a dt dx t f x t a x t a x t a dt dx n n nn n n n n n n n + + + + = + + + + = + + + + =    

dengan fi dan aij

(

i = 1,2,...,n; j = 1,2,...,n

)

adalah fungsi kontinu. Jika setiap

fungsi f₁(t),f₂(t),,f_n(t) identik dengan nol, sehingga

, ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 2 2 1 1 2 2 22 1 21 2 1 2 12 1 11 1 n nn n n n n n n n x t a x t a x t a dt dx x t a x t a x t a dt dx x t a x t a x t a dt dx + + + = + + + = + + + =     (2.1)

maka dikatakan sistem persamaan diferensial linear homogen orde satu. Jika ) ( , ), ( ), ( ₂ 1 t f t f t

f  _{n tidak identik dengan nol maka disebut sistem persamaan}

diferensial linear nonhomogen orde satu.

Sistem persamaan diferensial nonlinear orde satu dengan n fungsi tidak diketahui berbentuk ), , , , , ( ) , , , , ( ) , , , , ( 2 1 2 1 2 2 2 1 1 1 n n n n n x x x t f dt dx x x x t f dt dx x x x t f dt dx     = = = (2.2)

dengan fi adalah fungsi nonlinear, untuk i= 1,2,,n. Agar sistem persamaan (2.2) memiliki penyelesaian, maka fi harus merupakan fungsi kontinu.

2.1.4 Matriks

Menurut Kreiszig (1991), matriks merupakan suatu susunan bilangan

(

i m j n

)

a_ij = 1,2,..., ; = 1,2,..., _{dalam empat persegi panjang, dilambangkan dengan}

huruf besar dicetak tebal yang berbentuk

11 12 1 21 22 2 1 2 3 ... ... ... ... ... ... n n m m m mn a a a a a a a a a a       =         A . (2.3)

Bilangan aij disebut sebagai unsur matriks A atau elemen matriks A. Garis

horizontal disebut sebagai baris atau vektor baris, dan garis vertikal disebut sebagai kolom atau vektor kolom. Matriks dengan m baris dan n kolom, seperti pada (2.3), disebut sebagai matriks m×n. Jika suatu matriks hanya terdiri dari satu baris, disebut matriks baris atau vektor baris dan dilambangkan dengan huruf kecil tebal. Demikian pula, matriks kolom atau vektor kolom adalah matriks yang hanya terdiri dari satu kolom, dan juga dilambangkan dengan huruf kecil tebal.

Mariks bujur sangkar (square matrix) n × n adalah matriks yang mempunyai jumlah baris dan kolom sama.

Definisi 2.4 [Braun, 1978] Misal A adalah matriks berukuran nx n dengan elemen aij dan x vektor komponen dengan komponen x1,...,xn. Didefinisikan perkalian A dengan x, dinyatakan dengan Ax, yang merupakan vektor dengan komponennya vektor ke-i adalah

ai1x1+ ai2x2 + ...+ ainxn i= 1,2,...,n.

Dari definisi tersebut maka sistem persamaan (2.1) dapat dinyatakan dalam bentuk vektor yaitu

x = Ax dt d , (2.4) dengan 11 12 1 21 22 2 1 2 3 ... ... ... ... ... ... n n m m m mn a a a a a a a a a a       =         A dan

[

1 2 ...

]

t n x x x = x .

Persamaan diferensial linear homogen orde satu mempunyai penyelesaian berupa fungsi eksponensial, yaitu _{x(t)= ve}λt_{, dengan v merupakan vektor kolom} konstan. Persamaan _{x(t)= ve}λt _{merupakan penyelesaian dari persamaan (2.4) jika} dan hanya jika λ dan v memenuhi

(A− λI)v= 0. (2.5) Menurut Braun (1978), vektor tak nol v yang memenuhi persamaan (2.5) disebut vektor eigen dari A dengan nilai eigen λ .

2.1.5 Kestabilan Sistem Persamaan Diferensial Persamaan (2.2) dapat dituliskan dalam bentuk

x f (t,x) dt

d i

Sistem persamaan diferensial (2.6) dimana variabel bebas tidak muncul secara

eksplisit dinamakan sistem autonomous. Dalam sistem ini, pasangan

(

x1,x2,,xn

)

disebut fase, sedang bidang x1,x2,,xn disebut bidang fase. Bila

penyelesaian dari sistem persamaan (2.6) disajikan dalam bidang fase dengan variabel bebas t berubah, maka terbentuk kurva penyelesaian di bidang fase yang disebut trayektori.

Definisi 2.5 [Bellomo and Preziosi, 1995] Titik xe sedemikian sehingga

( )

_e = 0

f x disebut titik kesetimbangan sistem autonomous x f(x) dt

d ₌

.

Persamaan diferensial pada umumnya merupakan deskripsi dari sistem-sistem fisik, maka beberapa nilai variabel tak bebas sering sudah diketahui sebelumnya, misalkan untuk t = t₀ (biasanya t₀ = 0). Nilai ini disebut syarat/kondisi awal. Jika suatu sistem persamaan diferensial ditambahkan dengan suatu syarat awal maka sistem persamaan diferensial tersebut dinamakan masalah nilai awal (MNA). Syarat/nilai awal digunakan untuk menentukan nilai-nilai konstanta.

Titik kesetimbangan dikatakan stabil jika untuk sembarang syarat awal yang cukup dekat dengan titik kesetimbangan, trayektori dari penyelesaian tetap dekat dengan titik kesetimbangan. Titik kesetimbangan dikatakan stabil asimtotik jika titik kesetimbangan tersebut stabil dan trayektori dari penyelesaiannya menuju titik

kesetimbangan untuk t menuju tak hingga.

Menurut Bellomo dan Preziosi (1995), sistem persamaan (2.6) dapat didekati dengan bentuk linear

z x J z ) ( _e dt d ₌ , dengan J adalah matriks Jacobian yang berbentuk

                    ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = n n n n n n x f x f x f x f x f x f x f x f x f        2 1 2 2 2 1 2 1 2 1 1 1 J .

Teorema 2.1 [Bellomo dan Preziosi, 1995]Misalkan fi diferensiabel

dievaluasi pada titik kesetimbangan, dan Re

( )

λi bagian real dari λi, n

i= 1,,

(1) jika untuk setiap i, Re

( )

λi < 0, maka xe disebut stabil asimtotik,

(2) jika terdapat i sedemikian sehingga Re

( )

λi > 0, maka xe disebut tidak stabil.

Nilai eigen matriks Jacobian dapat bernilai real atau kompleks. Misal λ1 dan 2

λ adalah nilai eigen matriks Jacobian 2×2, maka trayektori untuk masing-masing nilai eigen adalah sebagai berikut

1. λ1 dan λ2 real

i. Jika keduanya negatif maka trayektori berbentuk stable nodal point. ii. Jika salah satunya positif maka trayektori berbentuk unstable nodal point. iii. Jika keduanya positif maka trayektori berbentuk saddle point.

2. λ1 = λ + iω dan λ2 = λ − iω kompleks

iv. Jika Re

( )

λ₁ = Re

( )

λ₂ < 0 maka trayektori berbentuk stable focal point. v. Jika Re

( )

λ₁ = Re

( )

λ₂ > 0 maka trayektori berbentuk unstable focal point. vi. Jika Re

( )

λ₁ = Re

( )

λ₂ = 0 maka trayektori berbentuk vortexpoint.

Gambar 2.1 Trayektori pada Bidang Fase(Bellomo dan Preziosi, 1995)

2.1.6 Kriteria Kestabilan Routh Hurwitz

Jika A adalah matriks m× m, λ adalah nilai eigen dan I adalah matriks identitas, maka persamaan |A− λI| 0= dapat diturunkan menjadi persamaan polinomial orde ke-m. Persamaan polinomial ini biasa disebut persamaan karakteristik yaitu 1 1 2 2 ... 0 m m m m a a a λ ₊ λ − ₊ λ − _{+ + = . (2.7)}

Persamaan (2.7) dapat dibawa ke bentuk matriks sebagai berikut

            = ... ... ... ... ... ... ... ... 1 ... 0 0 1 ... 0 0 0 0 1 1 2 3 4 5 1 2 3 1 a a a a a a a a a H , (2.8)

dengan chief minor

1 a1 ∆ = , 2 1 3 2 1 a a a ∆ = , 1 3 3 2 1 5 4 3 1 0 a a a a a a a ∆ = , …, ... ... ... ... ... ... ... ... 1 ... 0 0 1 ... 0 0 0 0 1 1 2 3 4 5 1 2 3 1 1 a a a a a a a a a m = ∆ ₋ , ∆ =m am∆m−1, m> 2.

Teorema 2.2 [ Schröer, 2002]Jika H adalah matriks (2.8) maka bagian real λi akan bernilai negatif jika hanya jika setiap determinan chief minor dari matriks Hpositif untuk i=1,2,…m.

Karena bagian real λ1bernilai negatif maka menurut Teorema 2.1 dapat dikatakan

bahwa titik kesetimbangan sistem persamaan diferensial stabil asimtotik. Hal ini selanjutnya disebut kriteria kestabilan Routh-Hurwitz.

2.2 Kerangka Pemikiran

Dengan mengacu pada teori dan pengertian pada Tinjauan Pustaka, dapat disusun kerangka pemikiran dari skripsi ini. HIV (Human Immunodeficiency Virus) adalah virus yang menyerang sistem kekebalan tubuh manusia dan kemudian menimbulkan AIDS. Penyebaran HIV pada populasi homoseksual dapat dibawa ke model matematis dan didefinisikan sebagai enam persamaan diferensial nonlinier. Selanjutnya, digunakan Definisi 2.5 untuk mencari titik kesetimbangan model dan menganalisis kesetimbangannya dengan membawa ke bentuk nyata. Model yang diperoleh merupakan bentuk nonlinear sehingga didekati dengan bentuk linearnya menggunakan matriks Jacobian. Untuk menentukan perilaku model di sekitar titik kesetimbangan, maka dilakukan analisis kestabilan dengan menggunakan kriteria Routh-Hurwitz. Analisis kestabilan dilakukan dengan menggunakan Teorema 2.1 dan Teorema 2.2.

BAB III

METODOLOGI PENELITIAN

Metodologi yang digunakan dalam penulisan skripsi ini adalah studi literatur yang mengacu pada buku-buku pemodelan matematika dan jurnal yang terkait dengan model penyebaran virus HIV. Adapun langkah-langkah yang ditempuh adalah

1. Digunakan Definisi 2.6 untuk menentukan titik kesetimbangan model penyebaran HIV pada populasi homoseksual.

2. Titik kesetimbangan yang telah diperoleh pada langkah pertama dibawa ke bentuk nyata untuk menganalisis kesetimbangan model penyebaran HIV pada populasi homoseksual.

3. Model yang diperoleh merupakan bentuk nonlinear, maka didekati dengan

bentuk linearnya dengan menggunakan matriks Jacobian.

4. Digunakan kriteria kestabilan Routh-Hurwitz untuk menganalisis kestabilan model penyebaran HIV pada populasi homoseksual.

BAB IV

PEMBAHASAN

Pada bab ini diberikan pembahasan tentang analisis kestabilan model penyebaran HIV pada populasi homoseksual. Dalam analisis kestabilan digunakan kriteria kestabilan Routh-Hurwitz. Bab ini terdiri dari tiga bagian yaitu analisis kestabilan model tanpa adanya tes darah, model dengan adanya tes darah dan simulasi.

Piqueira, Castano dan Monteiro (2004) telah menyusun model penyebaran HIV pada populasi homoseksual. Pada model tersebut dipelajari pengaruh perbedaan sikap pencegahan terhadap penyebaran virus. Oleh karena itu, berdasarkan sikap pencegahannya model dibagi menjadi dua kelompok yaitu kelompok pertama yang dinotasikan dengan indeks 1 dan kelompok kedua yang dinotasikan dengan indeks 2. Perbedaan sikap pencegahan antara dua kelompok

terletak pada perbedaan probabilitas transmisi virus (β ) untuk tiap kelompok.

yang positif, dan sebaliknya jika nilai β relatif besar maka kelompok tersebut memiliki sikap pencegahan yang negatif. Model penyebaran HIV pada populasi homoseksual didefinisikan sebagai sistem persamaan diferensial nonlinier berikut:

1 2 1 4 1 1 3 2 1 2 1 1 1 1 1 _S T I S T I S T U S T U S N dt dS µ β β β β _{− − − −} − = , 1 1 1 1 2 1 2 3 1 1 4 1 2 1 1

(

1

)

U1 T U T I S T I S T U S T U S dt dU η µ σ β β β β _{+ + + − − +} = , 1 1 1

(

₂

)

_I1 T U dt dI η µ σ _{− +} = , (4.1) 5 2 1 6 2 2 7 2 1 8 2 2 ₂ 2 2 _S T I S T I S T U S T U S N dt dS µ β β β β _{− − − −} − = , 2 5 2 1 6 2 2 7 2 1 8 2 2 2 2

(

3

)

U2 T U T I S T I S T U S T U S dt dU η µ σ β β β β _{+ + + − − +} = , 2 2 2

(

4

)

I2 T U dt dI η µ σ _{− +} = , dengan

Si : kompartemen manusia rawan terinfeksi kelompok ke i, i= 1,2 j

U : kompartemen manusia tidak sadar terinfeksi kelompok ke j, j = 1,2 k

I : kompartemen manusia sadar terinfeksi kelompok ke k, k = 1,2 l

β : probabilitas transmisi virus dari manusia terinfeksi ke manusia rawan

terinfeksi, l = 1,2,,8 m

σ : banyaknya tes darah pada manusia terinfeksi kelompok ke m, m= 1,2

µ : angka kematian,

p

N : laju pertambahan manusia rawan terinfeksi kelompok ke p, p= 1,2 q

η : rata-rata periode aktifitas seksual manusia terinfeksi ke q, q= 1,2,3,4

T : populasi total manusia

Tr : populasi total manusia pada kelompok ke r, r = 1,2 2

1 T

T

Dalam skripsi ini, laju pertambahan manusia rawan terinfeksi

( )

N

yang digunakan ada dua yaitu konstan dan tidak konstan. Untuk N tidak konstan diperoleh dengan asumsi-asumsi sebagai berikut, pada awalnya tidak ada manusia rawan terinfeksi maupun manusia tidak sadar terinfeksi dan hanya ada manusia sadar terinfeksi, sehingga pada awalnya N bernilai nol. Ketika ada manusia dari luar populasi yang mulai memiliki kebiasaan

homoseksual, maka manusia tersebut akan mulai menjadi bagian dari manusia rawan terinfeksi. Apabila jumlah manusia rawan terinfeksi semakin bertambah

maka N juga akan semakin bertambah. Pada saat jumlah manusia rawan

terinfeksi cukup besar, ada kecenderungan bahwa manusia rawan terinfeksi akan lebih suka melakukan hubungan seksual dengan manusia dari dalam populasinya sendiri. Hal ini berarti bahwa pada saat jumlah manusia rawan

terinfeksi menuju ke tak hingga, maka N akan menuju ke nol. Fungsi yang

dapat digunakan untuk menggambarkan kondisi tersebut adalah _{k Se} k2S

1 − untuk N1 dan 3 2 4 2 S k e S

k − untuk N2, dengan k1, k2, k3 dan k4 sembarang

konstanta.

Tes darah merupakan salah satu faktor penting dalam upaya

pencegahan penyebaran HIV. Dengan adanya tes darah, diharapkan manusia yang terinfeksi HIV sadar akan kondisi dirinya dan berhenti melakukan hubungan seksual agar virus tidak menyebar ke manusia lain. Sebaliknya, ketiadaan tes darah dimungkinkan dapat meningkatkan laju penyebaran HIV. Hal ini disebabkan manusia yang terinfeksi HIV tidak sadar akan kondisinya

sehingga tetap melakukan aktifitas seksual dan mentransmisikan virus ke pasangannya. Sebagai contoh, dalam penelitian organisasi kesehatan dunia WHO dilaporkan bahwa pertambahan populasi manusia berpendapatan rendah dapat meningkatkan resiko terinfeksi HIV. Hal ini disebabkan pada populasi tersebut jumlah manusia yang mendapatkan informasi tentang HIV tidak signifikan. Bahkan beberapa informasi dasar seperti mekanisme transmisi atau metode pencegahan belum banyak diketahui. Hal ini berakibat populasi tersebut tidak melakukan tes darah secara periodik maupun memiliki sikap pencegahan yang positif, sehingga HIV dapat menyebar secara cepat. Oleh karena itu, dalam skripsi ini dibahas dua model, yaitu model penyebaran HIV tanpa tes darah dan dengan tes darah.

4.1.Model Penyebaran HIV tanpa Adanya Tes Darah

Ketiadaan tes darah berakibat banyaknya tes darah yang dilakukan bernilai nol

(

σ = 0

)

. Selain itu, banyaknya manusia sadar terinfeksi juga akan menjadi nol karena tidak ada manusia yang sadar akan kondisinya yang telah terinfeksi HIV. Oleh karena itu, model hanya akan terdiri dari manusia rawan terinfeksi dan tidak sadar terinfeksi, sehingga diperoleh model penyebaran HIV tanpa tes darah sebagai berikut 1 1 1 2 1 2 ₁ 1 1 _S T U S T U S N dt dS µ β β _{− −} − = , 1 1 1 1 2 1 2

(

₁

)

_U1 T U S T U S dt dU η µ β β _{+ − +} = , (4.2) 2 2 5 2 1 6 2 2 S2 T U S T U S N dt dS µ β β _{− −} − = , 2 5 2 1 6 2 2

(

3

)

U2 T U S T U S dt dU η µ β β _{+ − +} = ,

dengan T = T1+ T2, T1 = S1+ U1 dan T2 = S2 + U2.

4.1.1 Titik Kesetimbangan

Dari model (4.2) dapat dicari titik kesetimbangan dengan dua laju pertambahan manusia rawan terinfeksi yang berbeda yaitu N1 dan N2 konstan

atau 21 1 1 1 S k e S k N = − dan 4 2 2 3 2 k S e kS

N = − . Dalam skripsi ini, titik kesetimbangan

manusia rawan terinfeksi dan tidak sadar terinfeksi untuk masing-masing kelompok dinotasikan dengan S₁ , U₁, S₂ dan U₂ . Titik kesetimbangan diperoleh jika persamaan (4.2) bernilai nol. Dengan software Mathematica 5

diperoleh titik-titik kesetimbangan sebagai berikut

(

, , ,

)

= _ 1,0, 2 ,0_ 2 2 1 1 µ µ N N U S U S , (4.3)

(

)

            = ,0 ln , 0 , ln , , , 4 3 2 1 2 2 1 1 k k k k U S U S µ µ , (4.4)

(

)

    + − + − = 3 2 2 2 1 1 1 1 2 2 1 1, , , , , , _{µ η} µ η µ µ N S S S N S U S U S , (4.5)

(

)

(

)

(

)

_       + − + − = − − 3 2 3 2 1 1 1 1 2 2 1 1 2 4 1 2 , , , , , , η µ µ η µ µ k e S S S e k S U S U S S k S k , (4.6) dengan

(

)

1 1 1 _β η µ + = T S _dan

(

)

6 3 2 _β η µ + = T S _.

Titik (4.3) dan (4.4) berturut-turut diperoleh dengan asumsi N1 dan N2

konstan atau 2 1 1 1 1 S k e S k N = − dan 4 2 2 3 2 S k e S k

N = − . Kedua titik ini disebut titik

kesetimbangan bebas penyakit karena menggambarkan situasi dimana HIV tidak muncul dan banyaknya manusia yang terinfeksi adalah nol. Di pihak lain, dimungkinkan untuk mendapatkan titik kesetimbangan endemis yang menggambarkan situasi dimana penyakit berada dalam populasi. Titik ini

ditunjukkan oleh (4.5) untuk N1 dan N2 konstan, dan (4.6) untuk 1 1 1 21 S k e S k N = − dan 4 2 2 3 2 k S e kS

N = − . Tetapi titik kesetimbangan ini tidak akan dibahas,

pembahasan dalam skripsi ini hanya dibatasi untuk titik kesetimbangan bebas penyakit saja.

Rasio reproduksi R0 dapat diartikan sebagai rata-rata jumlah manusia

terinfeksi baru yang disebabkan oleh satu orang manusia terinfeksi. Menurut Hethcote (2000), banyaknya manusia terinfeksi baru dipengaruhi oleh β₁S₁/T,

T S₁/

2

β , β₅S₂ /T dan β₆S₁/T . Sedangkan probabilitas seorang manusia mencapai tahap terinfeksi aktif untuk setiap kelompok adalah 1/

(

β1S1− T

(

µ + η1

)

)

dan 1/

(

β6S2 − T

(

µ +η3

)

)

. Rata-rata periode infeksi adalah sebesar

(

2 1 2

)

/

1 µ +η +η . Dari uraian tersebut, maka rasio repoduksi dapat dirumuskan

(

)

(

1 3

)

(

1 1

(

1

)

)

(

6 2

(

3

)

)

2 6 1 1 2 1 5 2 0 _{2µ η η β µ η β µ η} β β β β + − + − + + + = T S T S T S S S S R _.

Jika R₀ < 1 maka virus akan musnah dan jika R₀ > 1 maka virus akan berkembang menjadi suatu endemis.

4.1.2 Analisis Kestabilan

Kestabilan titik kesetimbangan bebas penyakit menentukan kemungkinan perkembangan HIV di persekitaran titik kesetimbangan. Analisis kestabilan dilakukan pada titik-titik kesetimbangan dengan menggunakan kriteria kestabilan Routh-Hurwitz. 1. Titik kesetimbangan

(

, , ,

)

= _ 1,0, 2 ,0_ 2 2 1 1 _{µ µ} N N U S U S

Karena sistem persamaan diferensial (4.2) nonlinear, maka didekati dengan bentuk linearnya menggunakan matriks Jacobian. Diperoleh matriks Jacobian

(

)

(

)

                   + − + − − − − − + − + − − − − − = 3 2 6 2 6 1 5 2 5 2 6 2 6 1 5 2 5 1 2 1 1 1 2 2 1 1 1 2 1 1 2 2 1 1 0 0 0 0 η µ β β β β β µ β β β β η µ β β β β β µ β β T S T U T U T S T S T U T U T S T S T U T U T U T S T S T U T U J _.(4.7)

Selanjutnya disubstitusikan titik kesetimbangan (4.3) ke matriks (4.7), sehingga

(

)

(

)

_                    + − − − − + − − − − = 3 2 6 2 5 2 6 2 5 1 2 1 1 1 1 2 1 1 0 0 0 0 0 0 η µ µ β µ β µ β µ µ β µ β η µ µ β µ β µ β µ T N T N T N T N T N T N T N T N J .

Dari matrik Jacobian di atas diperoleh persamaan karakteristik

(

_{λ + µ}

)

2

(

_λ2 ₋

(

_{α + ρ}

)

_{λ + α ρ − γ δ}

)

₌ 0_, dengan

(

1

)

2 1 1 1 _{µ η} β α − + + = N N N ,

(

3

)

2 1 2 6 _{µ η} β ρ − + + = N N N , 2 1 1 2 N N N + = β γ dan 2 1 2 5 N N N + = β

δ . Untuk menyederhanakan perhitungan, digunakan asumsi bahwa

laju pertambahan manusia rawan terinfeksi pada setiap kelompok memiliki nilai yang sama atau N1 = N2 = N.

Persamaan karakteristik di atas mempunyai empat nilai eigen. Dari

(

_{λ + µ}

)

2 _{diperoleh dua nilai eigen yaitu} λ = −µ 2 ,

1 . Nilai eigen tersebut akan

selalu real dan negatif, karena parameter µ positif. Dua nilai eigen tersisa ditentukan dari

_λ2 _{+ a1λ + a2 =} 0_{, (4.8)}

dengan a1 = −

(

α + ρ

)

dan a2 = α ρ − γ δ .

Menurut Teorema 2.1 titik kesetimbangan akan stabil asimtotik jika semua nilai eigennya negatif. Oleh karena itu matriks J akan stabil jika dan hanya jika

semua nilai eigennya negatif. Persamaan (4.8) akan memiliki nilai eigen yang negatif jika memenuhi kriteria Routh-Hurwitz yaitu, ∆₁ > 0 dan ∆ ₂ > 0. Dari syarat ∆ =1 a1> 0, akan dipenuhi apabila

₍

₎

1 2 2 _{1 3} 6 1 _< + + + η η µ β β . (4.9) Sedangkan dari ∆ ₂ = a₂.∆₁ > 0 dipenuhi apabila ∆₁ > 0 dan

₍

₍

₎

₎

₍

₍

₎

₎

1 2 2 _{1 6 3} 1 5 2 _< + − + − µ η β µ η β β β . (4.10) Persamaan (4.9) dan (4.10) dapat disajikan sebagai berikut

(

)

(

2

)

(

2

(

)

)

(

2

(

)

)

1 2 _{1 2 1 1 6 3} 6 1 5 2 _< + − + − + + + η µ β η µ β η η µ β β β β ,

dimana ruas kiri merupakan persamaan R0. Hal ini menunjukkan bahwa R0 < 1

yang artinya kestabilan terjadi jika rasio reproduksi kurang dari satu. Karena kriteria Routh-Hurwitz dipenuhi, maka model penyebaran HIV (4.2) stabil di titik kesetimbangan (4.3) untuk R₀ < 1. 2. Titik kesetimbangan

(

)

            = ,0 ln , 0 , ln , , , 4 3 2 1 2 2 1 1 k k k k U S U S µ µ

Dengan cara yang serupa pada titik kesetimbangan (4.3), analisis dilakukan dengan mensubstitusikan titik kesetimbangan (4.4) ke matriks Jacobian (4.7). Diperoleh persamaan karakteristik

(

₊

)

2

(

2 ₋

(

₊

)

_{+ −}

)

₌ 0 γ δ α ρ λ ρ α λ µ λ , dengan

(

1

)

2 1 1 1 _{µ η} β α − + + = S S S ,

(

3

)

2 1 2 6 _{µ η} β ρ − + + = S S S , 2 1 1 2 S S S + = β γ dan 2 1 2 5 S S S + = β

dua diantaranya adalah λ1,2 = −µ . Dua nilai eigen yang lain ditentukan dari

persamaan

_λ2 _{+ a1λ + a2 =} 0_{, (4.11)}

dengan a1 = −

(

α + ρ

)

dan a2 = α ρ − γ δ .

Persamaan (4.11) akan memiliki nilai eigen yang negatif jika ∆₁ > 0 dan

0

2 >

∆ . Akan berlaku ∆ =1 a1 > 0 apabila

₍

₎

1 2 _{1 3} 2 6 1 1 _< + + + η η µ β β T S S . (4.12) Akan berlaku ∆ ₂ = a₂.∆₁ > 0 apabila ∆₁ > 0 dan

(

)

(

1 1 1

)

(

6 2

(

3

)

)

1 2 1 5 2 _< + − + − µ η β µ η β β β T S T S S S . (4.13)

Persamaan (4.12) dan (4.13) dapat disajikan sebagai berikut

(

)

(

2 _{1 3}

)

(

_{1 1}

(

₁

)

)

(

_{6 2}

(

₃

)

)

1 2 6 1 1 2 1 5 2 _< + − + − + + + η µ β η µ β η η µ β β β β T S T S T S S S S ,

dimana ruas kiri merupakan persamaan R0. Hal ini menunjukkan bahwa R0 < 1

yang artinya kestabilan terjadi jika rasio reproduksi kurang dari satu. Karena kriteria Routh-Hurwitz dipenuhi, maka model penyebaran HIV (4.2) stabil di titik kesetimbangan (4.4) untuk R₀ < 1.

4.2.Model Penyebaran HIV dengan adanya Tes Darah

Pada sub bab sebelumnya telah dikemukakan bahwa tes darah merupakan salah satu faktor penting dalam upaya pencegahan virus HIV. Oleh karena itu, pada sub bab ini dibahas pengaruh adanya tes darah terhadap penyebaran HIV. Model penyebaran HIV dengan adanya tes darah didefinisikan pada persamaan (4.1). Tes darah mampu mendeteksi adanya HIV pada tubuh manusia, sehingga manusia tersebut sadar akan kondisinya. Manusia yang sadar telah terinfeksi diharapkan dapat melakukan upaya pencegahan yang positif atau berhenti melakukan hubungan seksual agar HIV tidak menyebar. Diasumsikan manusia

yang telah sadar terinfeksi akan berhenti melakukan hubungan seksual, sehingga berakibat β₃ = β₄ = β₇ = β₈ = 0. Sehingga diperoleh model penyebaran HIV dengan adanya tes darah

1 2 1 2 1 1 1 1 1 _S T U S T U S N dt dS µ β β _{− −} − = , 1 1 1 1 2 1 2 1 1

(

₁

)

_U1 T U T U S T U S dt dU η µ σ β β _{+ − − +} = , 1 1 1

(

₂

)

_I1 T U dt dI η µ σ _{− +} = , (4.14) 5 2 1 6 2 2 ₂ 2 2 _S T U S T U S N dt dS µ β β _{− −} − = , 2 5 2 1 6 2 2 2 2

(

3

)

U2 T U T U S T U S dt dU η µ σ β β _{+ − − +} = , 2 2 2

(

₄

)

_I2 T U dt dI η µ σ _{− +} = , dengan T = T1+ T2, T1 = S1+ U1+ I1 dan T2 = S2 + U2 + I2. 4.2.1 Titik Kesetimbangan

Dari model (4.14) diperoleh titik kesetimbangan bebas penyakit dengan

1

N dan N2 konstan atau 1 1 1 21

S k e S k N = − dan 4 2 2 3 2 k S e kS N = − . Diperoleh

titik-titik kesetimbangan bebas penyakit sebagai berikut

(

, , , , ,

)

= _ 1,0,0, 2 ,0,0_ 2 2 2 1 1 1 µ µ N N I U S I U S , (4.15)

(

)

            = ,0,0 ln , 0 , 0 , ln , , , , , 4 3 2 1 2 2 2 1 1 1 k k k k I U S I U S µ µ . (4.16)

Sedangkan untuk titik kesetimbangan endemis diasumsikan populasi terinfeksi dan tidak sadar terinfeksi mencapai nilai setimbang S₁, U₁, S₂ dan U₂ .

Sehingga diperoleh titik kesetimbangan endemis dengan N1dan N2 konstan atau 1 2 1 1 1 S k e S k N = − dan 4 2 2 3 2 S k e S k N = − adalah

(

S1,U1,I1,S2,U2,I2

)

dengan

(

)

2 1 1 1 1 1 η µ µ η µ + − + − = N U S I dan

(

)

4 2 2 3 2 2 η µ µ η µ + − + − = N U S I untuk laju

pertambahan manusia rawan terinfeksi konstan. Sedangkan untuk laju

pertambahan manusia 2 1 1 1 1 S k e S k N = − dan 4 2 2 3 2 k S e kS N = − diperoleh

(

)

(

)

2 1 1 1 1 1 1 2 η µ η µ µ + + − − = k e− S U I S k dan

(

)

(

)

4 2 3 2 3 2 2 4 η µ η µ µ + + − − = k e− S U I S k . Tetapi titik kesetimbangan ini tidak akan dibahas, pembahasan dalam skripsi ini hanya dibatasi untuk titik kesetimbangan bebas penyakit saja.

Rasio reproduksi R0 dapat diartikan sebagai rata-rata jumlah manusia

terinfeksi baru yang disebabkan oleh satu orang manusia terinfeksi. Menurut Hethcote (2000), banyaknya manusia terinfeksi baru dipengaruhi oleh β₁S₁/T,

T S₁/

2

β , β₅S₂ /T dan β₆S₁/T . Sedangkan probabilitas seorang manusia mencapai tahap terinfeksi aktif untuk masing-masing kelompok adalah

(

)

(

1 1 1 1

)

/

1 β S − σ − T µ + η dan 1/

(

β6S2 − σ 2 − T

(

µ + η3

)

)

. Rata-rata periode infeksi

adalah sebesar 1/

(

σ1 + σ 2 + T

(

2µ + η1+ η2

)

)

. Dari uraian tersebut, maka rasio

repoduksi dapat dirumuskan

(

)

(

)

(

1 2 1 3

)

(

1 1 1

(

1

)

)

(

6 2 2

(

3

)

)

2 6 1 1 2 1 5 2 0 2µ η η β σ µ η β σ µ η σ σ β β β β + − − + − − + + + + + = T S T S T S S S S R _.

Jika R₀ < 1 maka virus akan musnah dan jika R₀ > 1 maka virus akan berkembang menjadi suatu endemis.

Analisis kestabilan dilakukan pada titik-titik kesetimbangan (4.15) dan (4.16). Analisis dilakukan dengan menggunakan kriteria kestabilan Routh-Hurwitz. 1. Titik kesetimbangan

(

, , , , ,

)

= _ 1,0,0, 2 ,0,0_ 2 2 2 1 1 1 _{µ µ} N N I U S I U S

Karena sistem persamaan diferensial (4.14) nonlinear, maka didekati dengan bentuk linearnya menggunakan matriks Jacobian. Diperoleh matriks

Jacobian sebagai berikut

(

)

(

)

(

)

(

)

                             + − + − − − − − + − + − − − − − = 4 2 3 2 2 6 2 5 2 6 2 5 2 1 1 2 1 1 1 1 1 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 η µ σ η µ σ β β β µ β η µ σ β η µ σ β β β µ T T T U T S T S T S T T S T T S T S T S J _.

Dari matrik Jacobian di atas diperoleh persamaan karakteristik

(

λ + µ

) (

2 λ + A

)(

λ + B

) (

(

λ − C

)(

λ − D

)

− EF

)

= 0, dengan

(

3

)

2 1 2 2 1 2 6 σ µ _{µ η} β _{− +} + − + = N N N N N D _,

(

₁

)

2 1 1 2 1 1 1 σ µ _{µ η} β _{− +} + − + = N N N N N C _,

(

µ + η4

)

= A , B=

(

µ +η 2

)

, 2 1 1 2 N N N E + = β dan 2 1 2 5 N N N F + = β .

Persamaan karakteristik di atas mempunyai enam nilai eigen. Dari

(

λ + µ

) (

2 λ + A

)(

λ + B

)

diperoleh empat nilai eigen yaitu λ1,2 = −µ ,

(

2

)

3 µ η

kriteria Routh-Hurwitz yaitu, ∆₁ > 0 dan ∆ ₂ > 0. Dari syarat ∆ =1 a1 > 0, akan dipenuhi apabila

₍

₍

₎

(

₍

)

₎

₎

1 2 2 1 3 2 1 6 1 _< + + + + + η η µ µ σ σ β β N N . (4.17) Sedangkan dari ∆ ₂ = a₂.∆₁ > 0 dipenuhi apabila ∆₁ > 0 dan

₍

₍

₎

₎

₍

₍

₎

₎

1 3 2 6 1 1 1 5 2 2 < + − − + − − σ µ µ η β σ µ µ η β β β N N N N N . (4.18)

Persamaan (4.17) dan (4.18) dapat disajikan sebagai berikut

(

)

(

)

(

)

(

_{1 2} 2 2 _{1 3}

)

(

_{1 1}

(

₁

)

)

(

_{6 2}

(

₃

)

)

1 6 1 5 2 3 < + − − + − − + + + + + η µ µ σ β η µ µ σ β η η µ µ σ σ β β β β N N N N N N , dimana ruas kiri merupakan persamaan R0. Hal ini menunjukkan bahwa R0 < 1

yang artinya kestabilan terjadi jika rasio reproduksi kurang dari satu. Karena kriteria Routh-Hurwitz dipenuhi, maka model penyebaran HIV (4.14) stabil di titik kesetimbangan (4.15) untuk R₀ < 1.

2. Titik kesetimbangan

(

)

            = ,0,0 ln , 0 , 0 , ln , , , , , 4 3 2 1 2 2 2 1 1 1 k k k k I U S I U S µ µ

Dengan cara yang serupa pada titik kesetimbangan (4.15), analisis dilakukan dengan mensubstitusikan titik kesetimbangan (4.16) ke matriks

Jacobian. Diperoleh persamaan karakteristik

(

λ + µ

) (

2 λ + A

)(

λ + B

) (

(

λ − C

)(

λ − D

)

− EF

)

= 0, dengan

(

3

)

2 1 2 2 1 2 6 σ µ _{µ η} β _{− +} + − + = S S S S S D _,

(

₁

)

2 1 1 2 1 1 1 σ µ _{µ η} β _{− +} + − + = S S S S S C _,

(

µ + η4

)

= A , B=

(

µ +η 2

)

, 2 1 1 2 S S S E + = β , dan 2 1 2 5 S S S F + = β .

Dari persamaan karakteristik di atas terdapat enam nilai eigen, empat diantaranya adalah λ1,2 = µ , λ3 = −

(

µ +η 2

)

dan λ4 = −

(

µ + η4

)

. Dua nilai eigen yang lain

ditentukan dengan syarat ∆₁ > 0 dan ∆ ₂ > 0. Akan berlaku ∆ =1 a1 > 0 apabila

₍

₍

₎

₎

1 2 _{1 3} 2 1 2 6 1 1 _< + + + + + η η µ σ σ β β T S S . (4.19) Akan berlaku ∆ ₂ = a₂.∆₁ > 0 apabila ∆₁ > 0 dan

₍

₍

₎

₎

₍

₍

₎₍

₎

₎

1 3 2 1 2 2 6 1 1 1 1 2 1 5 2 _< + + − − + − − σ µ η β σ µ η β β β S S T S T S S S . (4.20)

Persamaan (4.19) dan (4.20) dapat disajikan sebagai berikut

(

)

(

)

(

_{1 2} 2 _{1 3}

)

(

_{1 1 1}

(

₁

)

)

(

_{6 2 2}

(

₃

)

)

1 2 6 1 1 2 1 5 2 _< + − − + − − + + + + + η µ σ β η µ σ β η η µ σ σ β β β β T S T S T S S S S . Hal ini menunjukkan bahwa R₀ < 1 yang artinya kestabilan terjadi jika rasio reproduksi kurang dari satu. Karena kriteria Routh-Hurwitz dipenuhi, maka model penyebaran HIV (4.14) stabil di titik kesetimbangan (4.16) untuk R₀ < 1.

4.3 Simulasi

Pada sub bab ini dilakukan beberapa simulasi dengan nilai parameter yang berbeda. Simulasi pada skripsi ini diambil dari Piqueira, Castano dan Monteiro (2004). Untuk semua simulasi ditentukan waktunya selama 200 tahun (t= 200).

4.3.1 Simulasi Pertama

Pada simulasi pertama ini diperlihatkan pengaruh adanya tes darah yang dilakukan pada manusia terinfeksi, sehingga simulasi dapat dibagi menjadi dua kasus dengan banyaknya tes darah yang berbeda. Untuk kasus yang pertama diketahui banyaknya tes darah adalah 5000

(

σ ₁ = σ ₂ = 5000

)

dan untuk kasus kedua banyaknya tes darah adalah 33000

(

σ₁ = σ ₂ = 33000

)

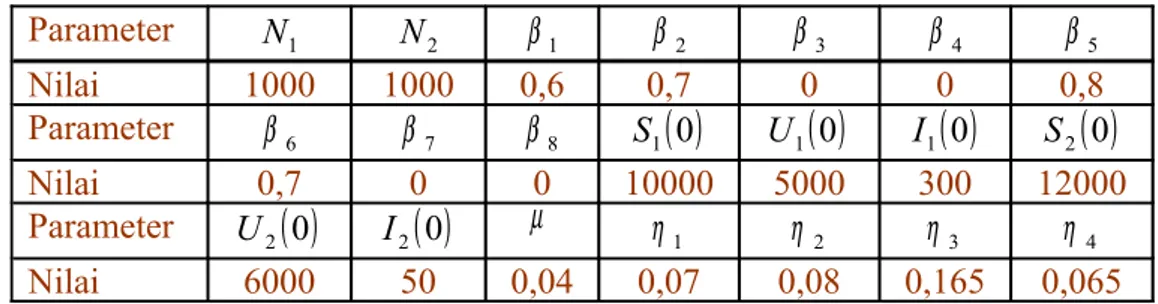
. Sedangkan nilai parameter yang lain diberikan pada Tabel 4.1.

Tabel 4.1 Tabel Nilai Parameter untuk Simulasi Pertama Parameter N₁ N₂ β₁ β 2 β 3 β 4 β5 Nilai 1000 1000 0,6 0,7 0 0 0,8 Parameter _{β 6 β7 β8} S₁

( )

0 U₁

( )

0 I₁

( )

0 S₂

( )

0 Nilai 0,7 0 0 10000 5000 300 12000 Parameter U₂

( )

0 I₂

( )

0 µ η₁ η ₂ η₃ η ₄ Nilai 6000 50 0,04 0,07 0,08 0,165 0,065

Berdasarkan nilai parameter pada Tabel 4.1, diperoleh sistem persamaan diferensial 1 1 1 1 2 0,04 1 33350 7 , 0 33350 6 , 0 1000 SU SU S dt dS − − − = , 1 1 1 1 2 1 1 _{0,11 1} 33350 33350 7 , 0 33350 6 , 0 U U U S U S dt dU _{= + −} σ ₋ , 1 1 _{0,12 1} 33350 5000 I U dt dI − = , (4.21) 2 2 1 2 2 0,04 2 33350 7 , 0 33350 8 , 0 1000 S U S U S dt dS − − − = , 2 2 1 2 2 2 2 0,205 2 33350 33350 7 , 0 33350 8 , 0 U U U S U S dt dU − − + = σ , 2 2 _{0,105 2} 33350 5000 I U dt dI _{= −} . 1. Tes Darah σ₁ = σ ₂ = 5000

Analisis dimulai dengan menentukan titik kesetimbangan model dengan

banyaknya tes darah σ ₁ = σ ₂ = 5000. Dengan menggunakan software

Mathematica 5 diperoleh dua titik kesetimbangan yaitu,

S₁ = 25000, U₁ = 0, I₁ = 0, S₂ = 25000, U₂ = 0, I₂ = 0, (4.22) S₁ = 14447,5, U₁ = 1623,93, I₁ = 2028,9, S₂ = 16909,6,

Pada titik kesetimbangan (4.22), nilai U₁ = 0, I₁ = 0, U₂ = 0, I₂ = 0

menunjukkan bahwa tidak ada manusia yang terinfeksi HIV dan disebut dengan titik kesetimbangan bebas penyakit. Sedangkan titik kesetimbangan (4.23) menunjukkan adanya manusia yang terinfeksi dan disebut dengan titik kesetimbangan endemis. Tetapi titik kesetimbangan yang dibahas dalam skripsi ini hanya titik kesetimbangan bebas penyakit.

Selanjutnya pada titik kesetimbangan yang diperoleh, dianalisis kestabilannya. Analisis dilakukan dengan mensubstitusikan titik kesetimbangan (4.22) ke matriks Jacobian                     − − − − − − − − = 105 , 0 1 , 0 0 0 0 0 0 045 , 0 0 0 4 , 0 0 0 35 , 0 04 , 0 0 4 , 0 0 0 0 0 12 , 0 1 , 0 0 0 35 , 0 0 0 09 , 0 0 0 35 , 0 0 0 3 , 0 04 , 0 J .

Dari matriks Jacobian di atas diperoleh persamaan karakteristik

(

λ + 0,04

) (

2 λ + 0,12

)(

λ + 0,105

) (

(

λ − 0,09

)(

λ − 0,045

)

− 0,14

)

= 0.

Persamaan karakteristik di atas mempunyai enam nilai eigen. Dari

(

λ + 0,04

) (

2 λ + 0,12

)(

λ + 0,105

)

diperoleh empat nilai eigen yaitu λ1,2 = −0,04,

12 , 0

3 = −

λ dan λ₄ = −0,105. Dua nilai eigen tersisa ditentukan dari

_λ2 ₋ 0,135_{λ −} 0,144₌ 0_{. (4.24)}

Dari persamaan (4.24) diketahui ∆₁ = −0,135< 0dan ∆ ₂ = 0,019> 0, sehingga berdasarkan Teorema 2.2 dapat dikatakan bahwa sistem persamaan (4.21) tidak stabil untuk jumlah tes darah σ₁ = σ ₂ = 5000. Hal ini juga dapat diperlihatkan pada Gambar 4.1 dan 4.2.

25 50 75 100 125 150 175 200 t 5000 10000 15000 20000 25000 30000 S1 , U1 , I1 I1

H

t

L

U₁

H

t

L

S1

H

t

L

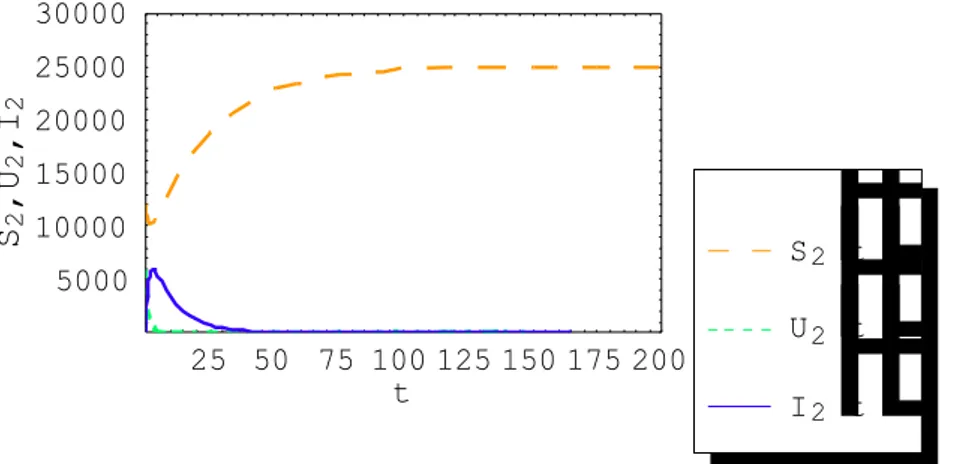
Gambar 4.1 Grafik S₁

( )

t , U₁

( )

t dan I₁

( )

t terhadap t untuk σ₁ = σ ₂ = 5000

25 50 75 100 125 150 175 200 t 5000 10000 15000 20000 25000 30000 S1 , U1 , I1 I1

H

t

L

U₁

H

t

L

S1

H

t

L

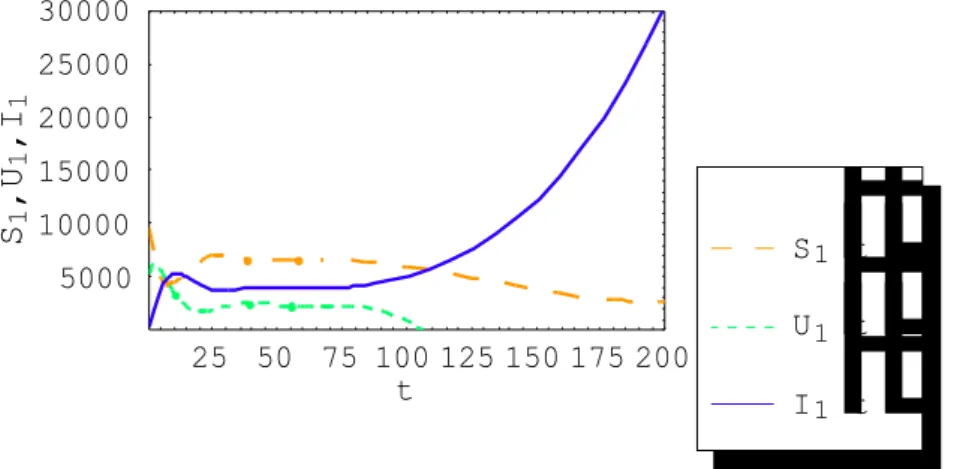
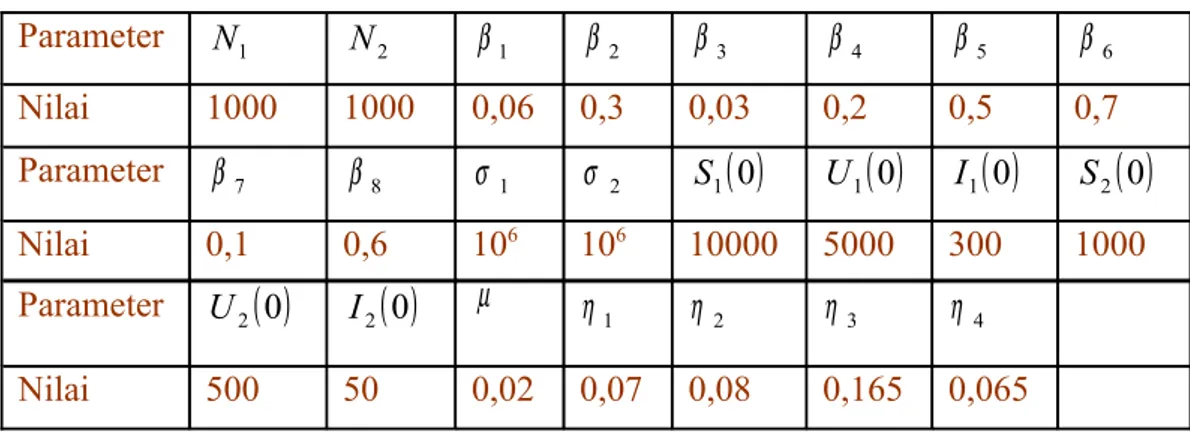
Gambar 4.2 Grafik S₂

( )

t , U₂

( )

t dan I₂

( )

t terhadap t untuk σ₁ = σ ₂ = 5000

Dari Gambar 4.1 dan Gambar 4.2 terlihat bahwa setelah 85 tahun banyaknya manusia rawan terinfeksi dan tidak sadar terinfeksi semakin sedikit. Sedangkan banyaknya manusia sadar terinfeksi terus bertambah setelah 25 tahun. Hal ini menunjukkan bahwa sistem persamaan (4.23) tidak stabil, sehingga HIV akan berkembang menjadi suatu endemis pada populasi tersebut. Dapat disimpulkan bahwa tes darah sebesar 5000 atau 15% dari total populasi awal, tidak cukup untuk menekan penyebaran HIV.