PROPERTY DAN PERDAGANGAN SEBAGAI SEKTOR DOMINAN PADA DATA BURSA SAHAM DENGAN PRINCIPAL COMPONENT ANALYSIS (PCA)

666

PROPERTY

DAN

PERDAGANGAN

SEBAGAI

SEKTOR

DOMINAN

PADA

DATA

BURSA

SAHAM

DENGAN

PRINCIPAL COMPONENT ANALYSIS

(PCA)

Hanna A Parhusip, Deva Widyananto1 ,dan Bernadeta Desinova Kr2

Center of Applied Mathematics (CAM), Program Studi Matematika Fakultas Sains dan Matematika (FSM)

Universitas Kristen Satya Wacana (UKSW) (www.uksw.edu)

1

mahasiswa S1, mate mat ika – FSM – UKSW 2

mahasiswa S1, mate mat ika – FSM – UKSW

ABSTRAK

Pada ma ka lah ini d ibahas tentang analisa beberapa sektor saham yang ada di Indonesia. Data dia mbil dari Bursa Efe k Ja karta ( BEJ ) dan menggunakan data pada bulan Januari 2008 sampa i dengan Januari 2010. Analisa menggunakan PCA (Principal Component Analysis). Metode ini dila kukan dengan cara menyusun matriks kovariansi dari data.Va riabe l mula -mula X d itransformasi menjadi variabel baru Y dengan P=XY dan

P adalah matriks yang vektor-vektor kolo mnya adalah vektor eigen dari matriks kovariansi. Ve ktor eigen dari

nila i e igen terbesar disebut komponen prinsip dan me rupakan bobot penyusun variabel baru sebagai ko mbinasi linear dari variabe l yang la ma .

Data menunjukkan bahwa ada 8 variabel sebagai sektor – sektor yang me miliki nilai sahan cukup tinggi. Variabel tersebut adalah pertanian, industri dasar, aneka industri, barang konsumsi, keuangan, pertambangan, properti, dan perdagangan. Seluruh variabel diu ji untuk mendapatkan variabel yang dominan. Dipe roleh bahwa properti dan perdagangan adalah variabel yang dominan yang ditunjukkan dengan variansi terbesar me la lui Principal Component Analysis. Jika variabel distandarisasi maka tidak dapat ditunjukkan variabel yang dominan.

Kata Kunci : k omponen prinsip, nilai eigen, vek tor eigen.

PENDAHULUAN

Saham merupakan bagian terpenting didalam dunia bisnis dan cukup menjanjikan. Keuntungan yang didapat dari menanamkan uang dalam bentuk uang cukup besar, begitu pula kerugian yang dapat diterima. Oleh karena itu banyak orang berlomba – lomba untuk menanamkan sebagian kekayaan yang dimiliki dalam bentuk saham. Saham sendiri terbagi kedalam beberapa se ktor / bidang seperti pertanian, industri, pertambangan, keuangan, konsumsi / bahan pangan, property dan perdagangan. Penulis melakukan observasi data di website bursa efek untuk mengetahui variabel yang dapat memberikan keuntungan cukup besar dan meminimalkan kerugian yang didapat.

Agar semua variabel yang ada pada data saham tersebut dapat diketahui mana yang berpengaruh terhadap untung rugi yang didapat maka penulis mencari variabel – variabel yang dominan terhadap saham tersebut. Semua variabel dominan yang mempengaruhi nilai saham tersebut dipilih menggunakan metode Principal Component Analisys ( PCA ).

667

Pada makalah ini teori yang digunakan ditunjukkan pada bagian PCA sedangkan penjelasan metode yang digunakan ditunjukkan pada Bab 3. Hasil analisa dijelaskan pada Bab 4 dan kesimpulan dituliskan pada bagian akhir makalah ini.

PCA (PRINCIPAL COMPONENT ANALYSIS)

PCA telah digunakan oleh berbagai peneliti untuk memilih variabel yang dominan agar variabel yang banyak dapat tereduksi. Sebagai salah satu contoh adalah mencari variabel dominan pada berbagai jenis variabel pakan yang diberikan pada sapi untuk mengenali variabel yang dominan yang berpengaruh terhadap berat sapi optimum untuk memproduksi susu sapi (

Parhusip dan

Siska. 2009). Teori yang telah diulas pada literatur tersebut ditulis kembali pada makalah

ini. Akan tetapi pada makalah ini ditambahk an penyusunan komponen prinsip dengan PCA

untuk variabel yang telah distandarisasi.

Secara aljabar PCA merupakan suatu kombinasi linear khusus untuk p variabel random X1, . . . , Xp.

Secara geometri, kombinasi linear menyatakan pemilihan sistem koordinat baru yang diperoleh dari merotasi sistem mula-mula X1, . . . , Xp sebagai sumbu-sumbu koordinat. Sumbu koordinat yang

baru sangat tergantung dari matriks kovariansi (atau matrik korelasi). Matriks kovariansi pada makalah ini disimbolkan



dan haruslah positif tegas (positive definite). Istilah ini dijelaskan pada Definisi 1.

Definisi 1: (Peressini,1988)

Misalkan 

 

a_ij sebuah matriks simetri

n







n

maka matriks 

 

a_ij positif (negatif) tegas (definite positive (negative)) jika dan hanya jika semua nilai eigennya positif (negatif) . Sedangkan mattriks yang semipositif (seminegatif) tegas jika dan hanya jika semua nilai eigennya taknegatif (takpositif) .

Teorema 2. (Johnson , and Wichern, 2002)

Sebutlah matriks X = [X1, . . . , Xp] adalah matriks yang vektor-vektor kolomnya adalah vektor

random (dianggap berdistribusi normal) yang mempunyai matriks kovariansi



(simetris dan positif tegas (positive definite)) dengan nilai eigen



1 



2 ...



p 0 dan sebutlah vektor eigen

yang bersesuaian untuk setiap 12...p 0 adalah e ep  

,...,

1 yang saling ortogonal. Komponen prinsip ke-i adalah

, ... 2 21 1 1i pi p T i i e X e X e X e X Y       i= 1,2,...,p . (1.a)

Dengan pemilihan ini

Var i i T i i e e Y)   



( , i =1,2,...,p , (1.b) Cov(

Y ,

i

Y

k)=  k 0 T i e e  ,

i



k

. (1.c) Perlunya e ep   ,...,

1 yang saling ortogonal adalah bahwa kita dapat menyusun kombinasi linear

Y

i

dengan basis {e ep  

,...,

1 }. Jika beberapa



i ada yang sama maka pemilihan vektor eigen ada yang

sama. Sebenarnya dapat dipilih vektor eigen yang berbeda dengan menggunakan generalisasi vektor eigen (generalized eigenvector) tetapi tidak dibahas pada makalah ini. Oleh karena itu

Y

_i tidak tunggal.

Bukti : (Johnson and Wichern, 2002, hal.358) .

668

Akibat 3.

Sebutlah matriks X = [X1, . . . , Xp] adalah matriks yang vektor-vektor kolomnya adalah vektor

random yang mempunyai matriks kovariansi



dengan nilai eigen



₁ 



₂ ...



_p 0 dan sebutlah vektor eigen yang bersesuaian untuk setiap



₁ 



₂ ...



_p 0 adalah e₁,...,e_p dan komponen-komponen prinsip ditentukan oleh persamaan (1.a). Maka

)

(

...

)

(

...

1 1 1 22 11





 

















p i i p p i i pp

Var

X





Var

Y







(1.d) ii



menyatakan variansi populasi yang ke-ii.

Bukti :

Diketahui dari aljabar linear bahwa jumlahan elemen diagonal dari suatu matriks disebut sebagai

trace (tr) matriks tersebut (Lay,2003). Dalam hal ini berarti ) ( ...

11 



pp tr 



.

Kita dapat menuliskan





PDP

T dengan D adalah matriks diagonal yang elemen diagonal adalah



_i dan P = [e1 ep]

  

adalah matriks yang vektor-vektor kolomnya merupakan vektor eigen dan saling ortogonal sehingga

PP

T



P

T

P



I

(matriks identitas). Dari sifat tr bahwa tr dari perkalian matriks A dan B berlaku tr(AB) = tr(BA). Sehingga berlaku

. ... ) ( ) ( ) ( )) ( ( ) ( 1 p T T D tr DI tr P DP tr DP P tr tr





        Jadi

)

(

)

(

)

(

)

(

1 1





 









p i i p i i

tr

tr

D

Var

Y

X

Var

.

Akibat 1 menyatakan bahwa total variansi populasi =



₁₁...



_pp 



₁...



_p.

Akibat 4. Proporsi variansi komponen prinsip ke-i didefinisikan sebagai

p k















₂

...

1 , k =1,..., p.

Nilai e_ki menyatakan ukuran pentingnya variabel ke-k terhadap komponen prinsip ke-i. Secara khusus, e_kimenyatakan korelasi antara komponen-komponen

Y

_i dan variabel-variabel X_k. Hal ini ditunjukkan pada Teorema 5.

Teorema 5.

Jika

Y

₁



e



₁TX,

Y

₂



e



₂TX,...,

Y

_p



e



_pTX adalah komponen prinsip yang diperoleh dari matriks

kovariansi



maka kk i ki X Y e k i







,  , i,k =1,2,...,p (2a)

adalah koefisien korelasi antara komponen-komponen

Y

i dan variabel-variabel Xk.

669

Kita telah mempunyai informasi bahwa korelasi antara variabel mula-mula yang tidak memuat dimensi sehingga variansi data bebas dari variansi yang memuat dimensi yaitu dengan koefisien korelasi populasi



_ik yang didefinisikan sebagai

kk ii ik ik









 . (2b)

Koefisien korelasi ini mengukur hubungan linear antara variabel random

X

_i dan X_k. Matriks korelasi merupakan matriks simetri p x p yaitu

                       pp pp pp pp p pp p pp p pp p                                    22 2 11 1 22 2 22 22 22 22 11 12 11 1 22 11 12 11 11 11 =





























1

1

1

2 1 2 12 1 12















p p p p













. (2c)

Komponen prinsip secara geometri memenuhi persamaan ellipsoida 2 2 2 2 2 1 1 2

1

...

1

1

p p

y

y

y

c















, c : konstan . (3)

Karena



1 



2 ...



p 0, persamaan (3) menyatakan sistem koordinat dengan sumbu-sumbu p

y

y ,...,₁ pada arah berturut-turut diberikan oleh e₁,...,e_p(yang telah saling ortonormal).

Untuk selanjutnya akan ditentukan variabel dominan yang mempengaruhi nilai saham di berbagai sektor maka dapat digunakan PCA dengan menyusun matriks kovariansi terlebih dahulu dengan mengasumsikan bahwa data disimpan dalam sebuah vektor random X dimana elemen baris menyatakan N observasi X= [X1...Xp] dan banyaknya kolom menyatakan p variabel X1, . . . , Xp

pada matriks p x N. Rata-rata untuk vektor X didefinisikan sebagai



X

X

p



p

M



1

₁



...



. (4.a)

Akan dicari

Xˆ

_k untuk k=1....p, dimana:

X

ˆ

_k



X

_k



M

. (4.b) Sehingga kolom matriks N x p dapat ditulis sebagai:

B = [Xˆ₁ Xˆ₂ ...

Xˆ

_p] (4.c) dimana B merupakan bentuk deviasi rata-rata untuk setiap X yang diperoleh dari persamaan (4.b). Sedangkan matriks kovariansi matriks adalah p x p matriks S yang didefinisikan sebagai:

T

BB

p

S

1

1





(4.d) T

BB

merupakan matriks positive definite (nilai eigen matriks tersebut semua positif) sesuai dengan Teorema 1.

Total variansi didefinisikan sebagai jumlahan semua variansi sebagaimana ditunjukkan pada persamaan (1.d). Hal ini diperoleh dengan cara jumlahan dari elemen diagonal matriks S. Jumlahan dari semua diagonal matriks S yang dikuadratkan merupakan trace dari matriks S ( tr(S) ) .

Nilai eigen dari S harus diurutkan dari besar ke kecil agar diketahui variabel apa yang paling dominan yang mempengaruhi nilai saham.

670

Untuk selanjutnya perlu disusun matriks P = X Y dengan P adalah matriks yang terdiri dari vektor-vektor kolom dari setiap vektor-vektor eigen yang diperoleh. Vektor eigen ini diperoleh dengan menyelesaikan



S





_i

I



e



_i



0



, i = 1,...,p (5a)

dengan n banyaknya sampel saham. Sedangkan nilai eigen



perlu diperoleh terlebih dahulu dengan menyelesaikan persamaan karakteristik yaitu det(S-



I)= 0 yang diperoleh dari

e

e

S









. (5b)

PCA dengan standardisasi Variabel

Variabel random dapat distandarisasi dengan cara





, 11 1 1 1





  X Z





, 22 2 2 2     X Z ... ,





. pp p p p X Z     (5c)

Dengan notasi matriks vektor persamaan (5c) ditulis sebagai

Z = (V1/2)-1 (X -



) (5d)

dengan (V1/2)-1 merupakan matriks diagonal yaitu

(V1/2)-1 =                   pp   1 0 0 0 0 . 0 0 0 0 . 0 0 0 0 1 11 . (5e).

Dengan menggunakan persamaan (2c) dan (5e) dapat diperoleh



= (V1/2)-1



(V1/2)-1 . (5f)

Dengan variabel random yang sudah distandarisasi kita dapat menyusun komponen prinsip berdasarkan Teorema 6 .

Teorema 6.

Komponen prinsip ke-i dari variabel standard ZT = [Z1, Z2,...,Zp], dengan Cov(Z) =



diberikan oleh T i i e Y   Z = e_iT (V1/2)-1 (X -



) , i =1,2,..., p . (5g) Selain itu p Z Var Y Var p i i p i i 







  ) ( ) ( 1 1 dan _{Y Z}

e

_{ki i} k i





_,



, i,k = 1,2, ... , p. (5h)

Pada Teorema ini nilai eigen dan vektor eigen diperoleh dari matriks korelasi (5f).

Agar PCA dapat diperkenalkan dengan jelas berikut ini diberikan contoh penggunaaannya dengan menggunakan bantuan MATLAB.

Contoh : Misal data yang diperoleh saham dari sektor Pertanian, Industri Dasar, Aneka Industri

671

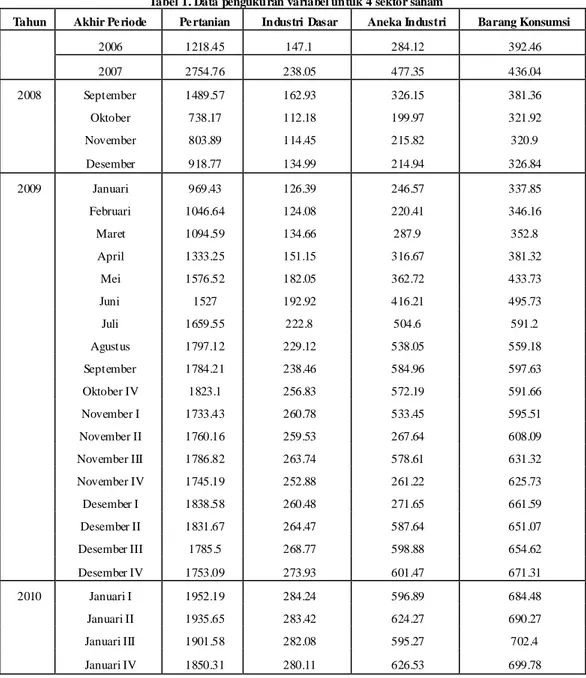
Tabel 1. Data pengukuran variabel untuk 4 sektor saham

Tahun Akhir Pe riode Pe rtanian Industri Dasar Aneka Industri Barang Konsumsi

2006 1218.45 147.1 284.12 392.46 2007 2754.76 238.05 477.35 436.04 2008 September 1489.57 162.93 326.15 381.36 Oktober 738.17 112.18 199.97 321.92 November 803.89 114.45 215.82 320.9 Desember 918.77 134.99 214.94 326.84 2009 Januari 969.43 126.39 246.57 337.85 Februari 1046.64 124.08 220.41 346.16 Maret 1094.59 134.66 287.9 352.8 April 1333.25 151.15 316.67 381.32 Mei 1576.52 182.05 362.72 433.73 Juni 1527 192.92 416.21 495.73 Juli 1659.55 222.8 504.6 591.2 Agustus 1797.12 229.12 538.05 559.18 September 1784.21 238.46 584.96 597.63 Oktober IV 1823.1 256.83 572.19 591.66 November I 1733.43 260.78 533.45 595.51 November II 1760.16 259.53 267.64 608.09 November III 1786.82 263.74 578.61 631.32 November IV 1745.19 252.88 261.22 625.73 Desember I 1838.58 260.48 271.65 661.59 Desember II 1831.67 264.47 587.64 651.07 Desember III 1785.5 268.77 598.88 654.62 Desember IV 1753.09 273.93 601.47 671.31 2010 Januari I 1952.19 284.24 596.89 684.48 Januari II 1935.65 283.42 624.27 690.27 Januari III 1901.58 282.08 595.27 702.4 Januari IV 1850.31 280.11 626.53 699.78

672

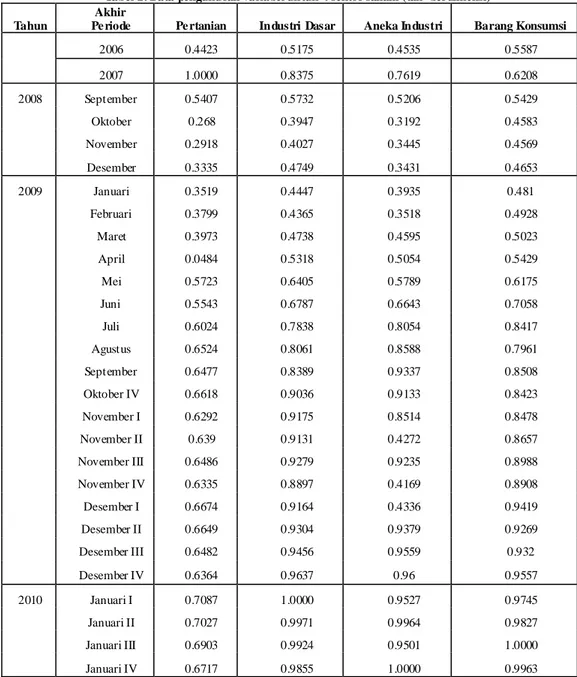
Tabel 2. Data pengukuran variabel untuk 4 sektor saham (tak berdimensi) Tahun

Akhir

Pe riode Pe rtanian Industri Dasar Aneka Industri Barang Konsumsi

2006 0.4423 0.5175 0.4535 0.5587 2007 1.0000 0.8375 0.7619 0.6208 2008 September 0.5407 0.5732 0.5206 0.5429 Oktober 0.268 0.3947 0.3192 0.4583 November 0.2918 0.4027 0.3445 0.4569 Desember 0.3335 0.4749 0.3431 0.4653 2009 Januari 0.3519 0.4447 0.3935 0.481 Februari 0.3799 0.4365 0.3518 0.4928 Maret 0.3973 0.4738 0.4595 0.5023 April 0.0484 0.5318 0.5054 0.5429 Mei 0.5723 0.6405 0.5789 0.6175 Juni 0.5543 0.6787 0.6643 0.7058 Juli 0.6024 0.7838 0.8054 0.8417 Agustus 0.6524 0.8061 0.8588 0.7961 September 0.6477 0.8389 0.9337 0.8508 Oktober IV 0.6618 0.9036 0.9133 0.8423 November I 0.6292 0.9175 0.8514 0.8478 November II 0.639 0.9131 0.4272 0.8657 November III 0.6486 0.9279 0.9235 0.8988 November IV 0.6335 0.8897 0.4169 0.8908 Desember I 0.6674 0.9164 0.4336 0.9419 Desember II 0.6649 0.9304 0.9379 0.9269 Desember III 0.6482 0.9456 0.9559 0.932 Desember IV 0.6364 0.9637 0.96 0.9557 2010 Januari I 0.7087 1.0000 0.9527 0.9745 Januari II 0.7027 0.9971 0.9964 0.9827 Januari III 0.6903 0.9924 0.9501 1.0000 Januari IV 0.6717 0.9855 1.0000 0.9963

Data pada Tabel 1 perlu dinyatakan dalam bentuk tak berdimensi. Hal ini dilakukan dengan cara membagi data tiap baris dengan maksimum per baris yang ditunjukkan pada Tabel 2.

Matriks kovariansi dari Tabel 2 dapat dicari dengan menghitung rata-rata data tiap baris yang disebut dalam vektor M dan dicari matriks deviasi B menggunakan bantuan MATLAB. Sehingga matriks kovariansinya adalah

673 S =             0398 . 0 0397 . 0 0420 . 0 0229 . 0 0397 . 0 0644 . 0 0445 . 0 0285 . 0 0420 . 0 0445 . 0 0471 . 0 0292 . 0 0229 . 0 0285 . 0 0292 . 0 0251 . 0 .

Setelah matriks kovariansi(S) diperoleh, maka dapat dicari nilai eigennya. yaitu



harus memenuhi

x

x

S









(persamaan 5b) dengan x[x₁ x₂ x₃ x₄]T bukan vektor nol (dan disebut sebagai vektor eigen) yang harus dicari. Untuk itu berarti (S



I)x0, agar x[x1 x2 x3 x4]T



bukan vektor nol maka disyaratkan det(S



I)=0 (Lay,2003).

Dengan menggunakan bantuan MATLAB maka dapat diperoleh 4 nilai eigen

004 . 0 , 0085 . 0 0149 . 0 , 1526 . 0 _{2 3 4} 1 















dan diperoleh nilai

vektor eigen , 6032 . 0 0032 . 0 7341 . 0 3117 . 0 1                e , 5174 . 0 0175 . 0 0627 . 0 8533 . 0 2              e , 3695 . 0 8002 . 0 4081 . 0 2377 . 0 3                e _. 4815 . 0 5994 . 0 5390 . 0 3439 . 0 4              e

Dapat ditunjukkan bahwa

e



_i

,

e



_j = 0 dan dengan

i



j

dimana

i

,

j



1

,

2

,

3

,

4

. Hal ini berarti masing – masing vektor saling tegak lurus dan mempunyai nilai 1, sehingga dapat digunakan sebagai basis untuk Y_i.Oleh karena itu komponen prinsip adalah

, 6032 . 0 0032 . 0 7341 . 0 3117 . 0 1 2 3 4 1 X X X X Y     , 5174 . 0 0175 . 0 0627 . 0 8533 . 0 1 2 3 4 2 X X X X Y     , 3695 . 0 8002 . 0 4081 . 0 2377 . 0 1 2 3 4 3 X X X X Y     . 4815 . 0 5994 . 0 5390 . 0 3439 . 0 _{1 2 3 4} 4 X X X X Y    

Untuk selanjutnya korelasi antara

Y

₁ dan

X

_i, i =1,…,4 dapat ditunjukkan dengan mengikuti formula (2) yaitu berturut-turut

11 1 11 , 1 1 s e X Y    =-0.0383; 22 1 21 , ₂ 1 s e X Y





 =0.0267; 33 1 31 , 3 1 s e X Y





 =0.3852; 44 1 41 , 4 1 s e X Y





 = 0.9425.

Karena nilai korelasi

X

₄(barang konsumsi) dekat dengan 1 (

4 1, X Y



= 0.9425), maka variabel

X

₄ mempengaruhi nilai sahan Indonesia periode Januari 2008 – Januari 2010.

METODE PENELITIAN

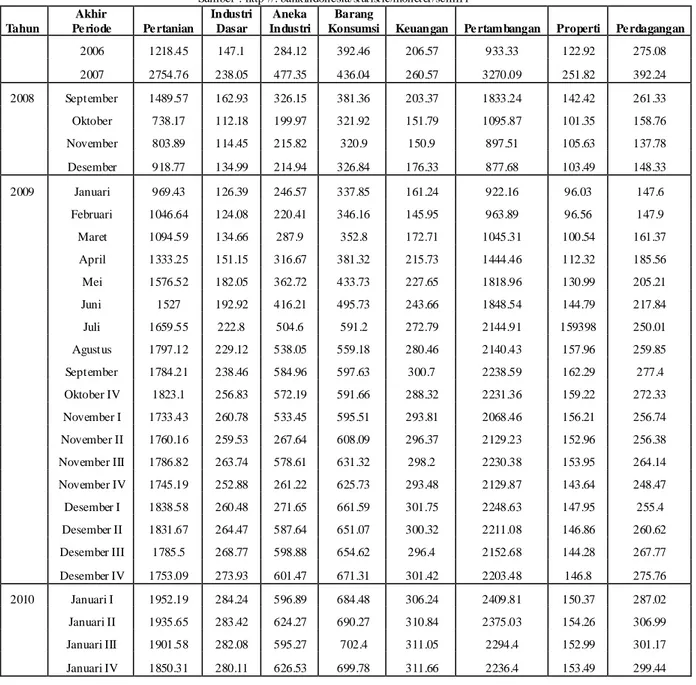
1. Pengumpulan Data : data yang digunakan adalah data saham Januari 2008 – 2010 yang ditunjukkan pada Tabel 3. Data setiap vektor-vektor kolom dianggap sebagai variabel random yang berdistribusi normal. Dapat pula dilakukan pengujian normalitas data.

674

3. Menghitung nilai eigen dan vektor eigen yang bersesuaian dengan nilai eigennya

menurut persamaan (5a)-(5b). Vektor eigen sebagai penyusun koefisien pada

komponen prinsip.

4. Menyatakan variabel prinsip sebagai kombinasi linear dari variabel mula- mula

menggunakan persamaan (1a).

5. Menentukan koefisisen korelasi antara komponen prinsip dan variabel mula mula

dengan persamaan (2).

Tabel 3. Data Saham Januari 2008 – Januari 2010 Sumber : http //: bankindonesia/statistic/moneter/semi11 Tahun Akhir Pe riode Pe rtanian Industri Dasar Aneka Industri Barang

Konsumsi Keuangan Pe rtambangan Properti Pe rdagangan

2006 1218.45 147.1 284.12 392.46 206.57 933.33 122.92 275.08 2007 2754.76 238.05 477.35 436.04 260.57 3270.09 251.82 392.24 2008 September 1489.57 162.93 326.15 381.36 203.37 1833.24 142.42 261.33 Oktober 738.17 112.18 199.97 321.92 151.79 1095.87 101.35 158.76 November 803.89 114.45 215.82 320.9 150.9 897.51 105.63 137.78 Desember 918.77 134.99 214.94 326.84 176.33 877.68 103.49 148.33 2009 Januari 969.43 126.39 246.57 337.85 161.24 922.16 96.03 147.6 Februari 1046.64 124.08 220.41 346.16 145.95 963.89 96.56 147.9 Maret 1094.59 134.66 287.9 352.8 172.71 1045.31 100.54 161.37 April 1333.25 151.15 316.67 381.32 215.73 1444.46 112.32 185.56 Mei 1576.52 182.05 362.72 433.73 227.65 1818.96 130.99 205.21 Juni 1527 192.92 416.21 495.73 243.66 1848.54 144.79 217.84 Juli 1659.55 222.8 504.6 591.2 272.79 2144.91 159398 250.01 Agustus 1797.12 229.12 538.05 559.18 280.46 2140.43 157.96 259.85 September 1784.21 238.46 584.96 597.63 300.7 2238.59 162.29 277.4 Oktober IV 1823.1 256.83 572.19 591.66 288.32 2231.36 159.22 272.33 November I 1733.43 260.78 533.45 595.51 293.81 2068.46 156.21 256.74 November II 1760.16 259.53 267.64 608.09 296.37 2129.23 152.96 256.38 November III 1786.82 263.74 578.61 631.32 298.2 2230.38 153.95 264.14 November IV 1745.19 252.88 261.22 625.73 293.48 2129.87 143.64 248.47 Desember I 1838.58 260.48 271.65 661.59 301.75 2248.63 147.95 255.4 Desember II 1831.67 264.47 587.64 651.07 300.32 2211.08 146.86 260.62 Desember III 1785.5 268.77 598.88 654.62 296.4 2152.68 144.28 267.77 Desember IV 1753.09 273.93 601.47 671.31 301.42 2203.48 146.8 275.76 2010 Januari I 1952.19 284.24 596.89 684.48 306.24 2409.81 150.37 287.02 Januari II 1935.65 283.42 624.27 690.27 310.84 2375.03 154.26 306.99 Januari III 1901.58 282.08 595.27 702.4 311.05 2294.4 152.99 301.17 Januari IV 1850.31 280.11 626.53 699.78 311.66 2236.4 153.49 299.44

675

ANALISA DAN PEMBAHASAN

Dengan mengikuti Bab 2, berikut ini akan dianalisa data Tabel 3 untuk mencari variabel yang dominan pada nilai saham tiap sektor. Langkah pertama yang dilakukan adalah menghitung rata-rata data tiap kolom, dan ditunjukkan dalam vektorx yaitu



0.5757 0.7542 0.6790 0.7496 0.8114 0.5722 0.0366 0.6172





T

x

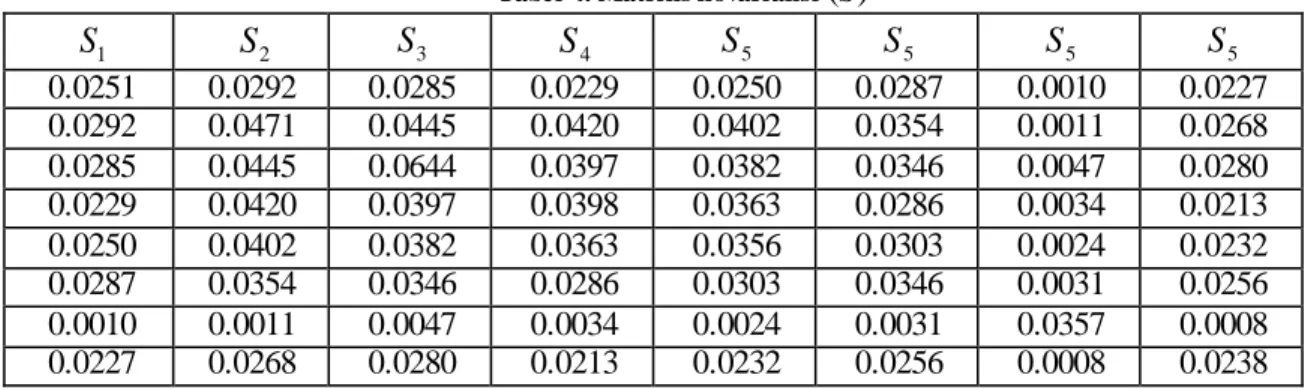
Dengan menggunakan persamaan (4.d) matriks kovariansi S dapat diperoleh dan ditunjukkan pada Tabel 4.

Tabel 4. Matriks kovariansi (S) 1

S

S

₂

S

3

S

4

S

5

S

5

S

5

S

5 0.0251 0.0292 0.0285 0.0229 0.0250 0.0287 0.0010 0.0227 0.0292 0.0471 0.0445 0.0420 0.0402 0.0354 0.0011 0.0268 0.0285 0.0445 0.0644 0.0397 0.0382 0.0346 0.0047 0.0280 0.0229 0.0420 0.0397 0.0398 0.0363 0.0286 0.0034 0.0213 0.0250 0.0402 0.0382 0.0363 0.0356 0.0303 0.0024 0.0232 0.0287 0.0354 0.0346 0.0286 0.0303 0.0346 0.0031 0.0256 0.0010 0.0011 0.0047 0.0034 0.0024 0.0031 0.0357 0.0008 0.0227 0.0268 0.0280 0.0213 0.0232 0.0256 0.0008 0.0238

Tampak bahwa matriks kovariansi S adalah matriks simetris. Kita dapat mencari nilai eigen sebagaimana ditunjukkan pada Teori Ujinormalitas dan dengan menggunakan bantuan MATLAB maka nilai eigen adalah







0

.

2312

0

.

0358

0

.

0191

0

.

0154

0

.

0029

0

.

0008

0

.

0006

0

.

0003



.

8 7 6 5 4 3 2 1























T

Sedangkan vektor eigen untuk tiap nilai eigen diperoleh berturut-turut ditunjukkan pada tiap kolom pada Tabel 5 dan dapat ditunjukkan bahwa vektor eigen tersebut saling ortonormal.

Tabel 5. Nilai Vektor eigen untuk data Ta bel 3.

1

u



u



₂

u

3



4

u



u

5



6

u



u



₇

u



₈ 0.4043 0.6699 0.1841 -0.1714 -0.2206 0.4298 -0.0566 0.2965 -0.6881 0.3835 -0.2473 -0.0466 0.3426 -0.0002 -0.0703 0.4402 0.0070 0.0086 0.0249 -0.0667 -0.5731 -0.6643 0.0763 0.4683 0.5947 -0.0871 -0.3955 0.1113 0.5286 -0.2029 0.0152 0.3861 -0.0354 -0.2525 0.8242 0.0760 0.3240 0.0055 -0.0212 0.3800 -0.0487 -0.5485 -0.2184 -0.5459 -0.1750 0.4399 -0.0096 0.3562 -0.0402 0.0456 0.0044 0.0324 0.0360 0.1035 0.9910 0.0336 -0.0635 -0.1726 -0.1445 0.8043 -0.2987 0.3585 -0.0563 0.2785

Menurut Bab 2, maka perlu didefinisikan variabel random yang disusun berdasarkan vektor-vektor kolom dari matriks kovariansi S, yaitu

                                                                                                                                                                                                                                                     2785 . 0 0336 . 0 3562 . 0 3800 . 0 3861 . 0 4683 . 0 4402 . 0 2965 . 0 , 0563 . 0 9910 . 0 0096 . 0 0212 . 0 0152 . 0 0763 . 0 0703 . 0 0566 . 0 , 3585 . 0 1035 . 0 4399 . 0 0055 . 0 2029 . 0 6643 . 0 0002 . 0 4298 . 0 , 2987 . 0 0360 . 0 1750 . 0 3240 . 0 5286 . 0 5731 . 0 3426 . 0 2206 . 0 , 8043 . 0 0324 . 0 5459 . 0 0760 . 0 1113 . 0 0667 . 0 0466 . 0 1714 . 0 , 1445 . 0 0044 . 0 2184 . 0 8242 . 0 3955 . 0 0249 . 0 2473 . 0 1841 . 0 , 1726 . 0 0456 . 0 5485 . 0 2525 . 0 0871 . 0 0086 . 0 3835 . 0 6699 . 0 , 0635 . 0 0402 . 0 0487 . 0 0354 . 0 5947 . 0 0070 . 0 6881 . 0 4043 . 0 8 7 6 5 4 3 2 1 X X X X X X X X

676

Karena komponen prinsip yang terpenting adalah yang pertama maka komponen prinsip pertama adalah . 0635 . 0 0402 . 0 0487 . 0 0354 . 0 5947 . 0 0070 . 0 6881 . 0 4043 . 0 1 2 3 4 5 6 7 8 1 X X X X X X X X Y        

Dapat ditunjukkan bahwa

Y

_i dan Y_j saling bebas linear , i,j =1,..,8. yaitu bahwa Cov(

Y

_i,Y_j) = 0. Untuk selanjutnya korelasi antara

Y

₁ dan

X

_i, i =1,…,8 dapat ditunjukkan dengan mengikuti formula (2) yaitu berturut-turut

11 1 11 , 1 1 s e X Y    = 0.0442; 22 1 21 , 2 1 s e X Y    = 0.0419; 33 1 31 , 3 1 s e X Y    = 0.0027 44 1 41 , 4 1 s e X Y    = 0.0301; 55 1 51 , 5 1 s e X Y    = 0.2132; 66 1 21 , 6 1 s e X Y    = 0.3266. 77 1 21 , 7 1

s

e

X Y







= 0.9931; 88 1 21 , 8 1 s e X Y    = 0.8682.

Karena nilai korelasi variabelX₇( properti ) dan

X

₈ ( perdagangan ) dekat dengan 1, maka variabel X₇dan

X

₈ sebagai variabel yang paling berpengaruh terhadap nilai saham.

Hasil PCA dengan standardisasi variabel

Hasil PCA dengan standardisasi variabel diharapkan memberikan kesimpulan yang sama tentang variabel yang dianggap dominan. Dengan menggunakan persamaan (5c) data distandardisasi. Diperoleh nilai eigen







6

.

0037

1

.

0036

0

.

5486

0

.

2895

0

.

1072

0

.

0222

0

.

0179

0

.

0072



.

8 7 6 5 4 3 2 1























T

Sehingga vektor eigen untuk nilai eigen terbesar adalah



0.3793 0.3964 0.3482 0.3727 0.3854 0.0324 0.3664



1        

T

e .

Komponen prinsip dengan variabel standard untuk nilai eigen terbesar adalah

.

3664

.

0

0324

.

0

3854

.

0

3937

.

0

3727

.

0

3482

.

0

3964

.

0

3793

.

0

8 7 6 5 4 3 2 1 1

Z

Z

Z

Z

Z

Z

Z

Z

Y



















Kita dapat menyusun korelasi antara

Y

₁ dengan

Z

i, i =1,...,8 menggunakan persamaan (5h)

diperoleh  1 1,Z Y



-0.1548,  2 1,Z Y



-0.1618,  3 1,Z Y



-0.1421,  4 1,Z Y



-0.1521,  5 1,Z Y



-0.1607,  6 1,Z Y



-0.1573 ,  7 1,Z Y



-0.0132 dan  8 1,Z Y



-0.1496. Kita menyimpulkan bahwa semua variabel mempunyai makna yang sama atau tidak ada yang dominan.

Dari hasil ini disimpulkan bahwa menggunakan standardisasi variabel tidak dapat menunjukkan dominasi salah satu variabel. Hal ini juga ditunjukkan pada literatur (Johnson and Wichern, 2002) . Pemilihan variabel dengan standarisasi dilakukan bila data mempunyai perbedaan yang sangat signifikan ataupun dengan satuan yang berbeda. Hal ini belum diselidiki lebih lanjut.

KESIMPULAN DAN SARAN

Pada makalah ini telah ditunjukkan pemilihan variabel dominan dengan menggunakan Principal

Component Analysis untuk 8 variabel .Variabel tersebut adalah pertanian, industri dasar, aneka

industri, barang konsumsi, keuangan, pertambangan, properti, dan perdagangan. Seluruh variabel diuji untuk mendapatkan variabel yang dominan. Diperoleh bahwa properti dan perdagangan adalah

677

variabel yang dominan yang ditunjukkan dengan variansi terbesar melalui Principal Component

Analysis.

Analisa dapat pula dilakukan dengan menstandarisasi variabel menggunakan persamaan (5c) sehingga komponen prinsip merupakan kombinasi linear antar variabel yang telah distandarisasi menurut Teorema 6. Diperoleh bahwa dominasi variabel tidak dapat dikenali.

DAFTAR PUSTAKA

[1] Johnson ,R.A., and Wichern, D.W. 2002. Applied Multivariate Statistical Analysis, 6th ed. Prentice Hall, ISBN 0-13-187715-1.

[2] Lay, D. C. 2003. Linear Algebra and Ist Applications, Third Edition, Addison Wesley, pp.482-491.

[3] Parhusip H. A., dan Siska A. 2009. Principal Component Analysis (PCA) untuk

Analisis Perlakukan Pemberian Pakan dan Mineral terhadap Produksi Susu Sapi,

Prosiding Seminar Nasioanal Matematika UNPAR, ISSN 1907-3909, Vol 4, hal.AA

42-51.

[3] Peressini, A.L., Sullivan, F.E.,Uhl, J.J.,1988. The Mathematics of Nonlinear Programming, Springer-Verlag, New-York.