ESTIMASI BERBASIS MCMC UNTUK RETURNS VOLATILITY DI PASAR VALAS INDONESIA MELALUI MODEL ARCH BERDISTRIBUSI NORMAL DAN STUDENT-T

ESTIMASI BERBASIS MCMC UNTUK RETURNS VOLATILITY

DI PASAR VALAS INDONESIA MELALUI MODEL ARCH

BERDISTRIBUSI NORMAL DAN STUDENT-T

Oleh,

IMAM MALIK SAFRUDIN

NIM : 662011001

TUGAS AKHIR

Diajukan kepada Program Studi Matematika, Fakultas Sains dan Matematika

guna memenuhi sebagian dari persyaratan untuk mencapai gelar Sarjana Sains

Program Studi Matematika

Fakultas Sains dan Matematika

Universitas Kristen Satya Wacana

Salatiga

2015

v

MOTTO

Esensi hidup adalah shalat dan bertemu dengan Allah SWT.

(sahabat saya, Mumun Majnun)

vi

PERSEMBAHAN

Dipersembahkan untuk

My Family

vii

KATA PENGANTAR

Bismillahirrahmanirrahim,

Assalamualaikum wa Rahmatullah wa Barakatuh,

Penulis mengucapkan rasa syukur kehadirat Allah SWT atas limpahan segala Rahmat

dan HidayahNya, sholawat serta salam semoga tercurahkan kepada junjungan Nabi besar

Muhammad SAW. Sehingga penulis dapat menyelesaikan tugas akhir (skripsi) sebagai syarat

menyelesaikan Studi Strata 1 (S1) di Program Studi Matematika pada Fakultas Sains dan

Matematika, Universitas Kristen Satya Wacana.

Skripsi ini terdiri dari dua makalah. Makalah pertama berjudul “Estimasi Berbasis

MCMC untuk Returns Volatility di Pasar Valas Indonesia melalui Model ARCH” dan

makalah kedua berjudul “Estimasi MCMC untuk Return Volatility dalam Model ARCH

dengan Return Error berdistribusi Student-t” yang telah dipublikasikan dalam Seminar

Nasional Matematika dan Pendidikan Matematika dengan tema “Peran Matematika &

Pendidikan Matematika Abad 21” pada tanggal 9 Mei 2015 yang diselenggarakan oleh

Program Studi Pendidikan Matematika, Universitas Muhammadiyah Purworejo.

Penulisan skripsi ini tidak terlepas dari bantuan dari berbagai pihak yang telah

memberikan dorongan kepada penulis baik itu berupa materil maupun spiritual. Untuk itu

dalam kesempatan ini penulis menyampaikan ucapan terima kasih kepada:

1. Dr. Suryasatriya Trihandaru, M.Sc.nat. selaku Dekan Fakultas Sains dan Matematika.

2. Dr. Bambang Susanto, MS selaku Ketua Program Studi Matematika.

3. Dra. Lilik Linawati, M.Kom. selaku Wali Studi yang selalu memberikan banyak

saran dan nasihat kepada penulis.

4. Didit Budi Nugroho, D.Sc. selaku pembimbing utama dan Dr. Adi Setiawan, M.Sc.

selaku pembimbing pendamping yang dengan sabar membimbing, mengarahkan dan

memberikan motivasi kepada penulis selama proses penulisan skripsi ini sehingga

laporan skripsi ini dapat diselesaikan dengan baik.

5. Dosen pengajar di Program Studi Matematika, Dr. Bambang Susanto, MS, Dra. Lilik

Linawati, M.Kom., Dr. Adi Setiawan, M.Sc, Tundjung Mahatma, M.Kom, Didit Budi

Nugroho, D.Sc., Dr. Hanna Arini Parhusip, M.Sc., Leopoldus Ricky Sasongko, M.Si

yang telah memberikan ilmu pengetahuan kepada penulis selama studi di FSM

UKSW serta Pak Edy sebagai Laboran yang telah memberikan bantuan kepada

penulis.

viii

6. Staf TU FSM: Mbak Eny, Bu Ketut dan Mas Basuki.

7. Family atas do’a yang telah diberikan.

8. Teman-teman BSM (Basecamp Samping Masjid): Aziz, Azhar dan Icol.

9. Teman seperjuangan Progdi Matematika 2011: Dewi, Daivi, Purwoto, Dwi, Titis,

Priska, dan Kevin.

Semoga Allah SWT memberikan balasan atas segala amal baik yang telah membantu penulis

dalam menyelesaikan skripsi.

Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan. Oleh sebab itu

penulis sangat mengharapkan kritik dan saran yang membangun untuk penulis. Akhirnya

semoga Allah SWT meridhoi amal kita semua. Amin.

Salatiga, 17 Juni 2015

ix

DAFTAR ISI

Lembar Pengesahan ... ii

Lembar Pernyataan Keaslian ... iii

Lembar Pernyataan Bebas Royalty dan Publikasi ...iv

Motto ... v

Persembahan ...vi

Kata Pengantar ... vii

Daftar Isi ...ix

Daftar Lampiran ... x

Abstrak ...xi

Pendahuluan ... 1

Makalah I: Estimasi Berbasis MCMC untuk Returns Volatility di Pasar Valas

Indonesia melalui Model ARCH

Makalah II: Estimasi MCMC untuk Return Volatility dalam Model ARCH dengan

Return Error Berdistribusi Student-t

x

DAFTAR LAMPIRAN

Lampiran 1: Skema MCMC untuk model ARCH berdistribusi Student-t

Lampiran 2: Kode Matlab

xi

ABSTRAK

Studi ini membangun suatu algoritma Markov chain Monte Carlo (MCMC) untuk

mengestimasi returns volatility dalam model ARCH dengan returns error berdistribusi

normal dan student-t. Metode Metropolis–Hastings digunakan dalam MCMC untuk

memperbarui nilai-nilai parameter model. Model dan algoritma diaplikasikan menggunakan

data harian kurs beli yen Jepang, dolar Amerika, dan euro Eropa terhadap rupiah Indonesia

pada periode 5 Januari 2009 sampai dengan 31 Desember 2014 yang diambil dari laman Bank

Indonesia. Studi empiris menunjukkan bahwa metode yang dibangun sangat efisien dan

memberikan hasil estimasi yang serupa dengan hasil Matlab untuk kasus model berdistribusi

normal. Sementara itu untuk kasus model dengan returns error berdistribusi student-t

ditunjukkan adanya bukti sangat kuat untuk penggunaan distribusi student-t pada ketiga data

di atas.

1

PENDAHULUAN

1. Latar Belakang

Menurut Hady (seperti yang dirujuk dalam Nurjanah (2005)), pasar valuta asing dapat

diartikan sebagai suatu wadah atau sistem dimana perorangan, perusahaan, dan bank dapat

melakukan transaksi keuangan internasional dengan jalan melakukan pembelian atau

permintaan, penjualan dan penawaran. Dalam referensi keuangan ekonomi internasional,

valuta asing (foreign exchange atau disingkat forex) adalah mata uang asing atau alat

pembayaran lainnya yang didasarkan pada kurs resmi yang telah ditetapkan oleh bank sentral

(Khalwaty dalam Nurjanah (2005)). Sementara itu harga/nilai dimana mata uang suatu negara

dipertukarkan dengan mata uang negara lain disebut nilai tukar (kurs).

Pada umumnya, para pelaku ekonomi di pasar valuta asing dan pasar modal memerlukan

pengukuran volatiy harga aset (Aklimawati dan Wahyudi, 2013). Taksiran volatility

diperlukan dalam strategi keuangan, misalnya untuk penghitungan harga opsi (kontrak jual

beli aset). Secara khusus, volatility adalah akar kuadrat dari variansi (besaran yang

menunjukkan besarnya penyebaran data pada suatu kelompok data).

Kebanyakan studi keuangan melibatkan return (perubahan logaritma harga aset)

daripada harga aset. Campbell dkk. (seperti dirujuk dalam Tsay (2010)), memberikan dua

alasan mengapa menggunakan return. Salah satunya yaitu runtun return lebih mudah untuk

ditangani dari pada runtun harga, karena return memiliki sifat statistik yang lebih menarik.

Pemodelan volatility pada return aset diawali dengan klas autoregressive conditional

heteroscedasticity (ARCH) yang diperkenalkan oleh Engle (1982). Nastiti (2012) dan

Aklimawati–Wahyudi (2013) mendiskusikan volatility yang mengikuti model ARCH

berturut-turut pada saham dan komoditas kakao yang mengasumsikan returns error

berdistribusi normal dan model diselesaikan dengan metode pengali Lagrange. Dalam studi

ini akan difokuskan pada model volatility menggunakan ARCH model dengan

mengasumsikan bahwa returns error berdistribusi normal dan student-t. Selanjutnya model

akan diselesaikan dengan menggunakan metode Markov chain Monte Carlo (MCMC). Carlin

dan Chib (1995) menjelaskan bahwa metode MCMC dapat memudahkan pemodelan yang

cukup kompleks dalam analisis Bayes.

Studi empiris terhadap volatility dilakukan dengan menggunakan data kurs beli Euro

(EUR), Japanese Yen (JPY), dan US Dollar (USD) terhadap rupiah Indonesia (IDR) atas

periode 5 Januari 2009 sampai dengan 31 Desember 2014 yang diambil dari laman Bank

Indonesia (BI).

2

2. Rumusan Masalah

Bagaimana menganalisis returns volatility dalam pasar valuta asing Indonesia dengan

menggunakan model ARCH.

3. Tujuan

Untuk mencapai analisis di atas, studi ini secara khusus bertujuan untuk:

(i) Menyajikan model ARCH untuk volatility dengan asset returns error berdistribusi

normal dan student-t.

(ii) Menyediakan algoritma MCMC untuk mengestimasi volatility dalam model ARCH.

(iii) Mendapatkan analisis volatility untuk kurs beli valuta asing terhadap IDR menggunakan

data nyata.

4. Batasan Masalah

Studi ini mempunyai batasan-batasan seperti berikut:

(i) Analisis difokuskan pada data kurs beli yen Jepang (JPY), Dolar Amerika (USD) dan

euro Eropa (EUR), dan terhadap rupiah periode 5 Januari 2009–31 Desember 2014 yang

diambil dari arsip Bank Indonesia (BI).

(ii) Penghitungan menggunakan alat bantu Matlab R2012a.

5. Hasil Penelitian

Hasil penelitian ini dituangkan dalam dua makalah yang telah dipublikasikan dalam

Seminar Nasional Matematika dan Pendidikan Matematika dengan tema “Peran Matematika

& Pendidikan Matematika Abad 21” pada tanggal 9 Mei 2015 yang diselenggarakan oleh

Program Studi Pendidikan Matematika, Universitas Muhammadiyah Purworejo, dan termuat

dalam prosiding ber-ISSN 2459-962X Vol. 1 No. 1 2015. Kedua makalah tersebut berjudul:

1. “Estimasi Berbasis MCMC untuk Returns Volatility di Pasar Valas Indonesia melalui

Model ARCH”, halaman 29



33.

2. “Estimasi MCMC untuk Return Volatility dalam Model ARCH dengan Return Error

Berdistribusi Student-t”, halaman 34



39.

6. Kesimpulan

Berdasarkan bahasan dari kedua makalah dapat disimpulkan sebagai berikut:

1. Algoritma MCMC yang dibangun menghasikan simulasi yang sangat efisien.

2. Hasil empiris menunjukkan bukti yang sangat kuat untuk penggunaan distribusi

3

7. Hasil Review

Paper 1: Di halaman kedua kolom 1 baris ke-26 tertulis “=”, seharusnya “∝”.

Paper 1: Di halaman kedua kolom 2 baris ke-15 tertulis “𝜆”, seharusnya “𝜆𝑎”.

Paper 1 dan 2: Kata “return” seharusnya “returns”.

Paper 2: Di halaman kedua kolom 1 baris ke-15 tertulis “𝒛 = (𝑧, 𝑧

2, … , 𝑧𝑇)”, seharusnya “𝒛 = (𝑧1, 𝑧2, … , 𝑧𝑇)”.

Paper 2: halaman kedua kolom 2 baris ke-20 tertulis “=”, seharusnya “∝”.

Paper 2: Ditambahkan daftar pustaka:

Safrudin, I., M., Nugroho, D., B., dan Setiawan, A. (2015). Estimasi Berbasis

MCMC untuk Returns Volatility di Pasar Valas Indonesia melalui Model ARCH,

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika UMP, 1(1),

29



33.

Notasi:

𝑁

: Menyatakan distribusi normal

𝑁

_[𝑎,𝑏]

: Menyatakan distribusi normal terpotong pada [a,b]

𝐼𝐺

: Menyatakan distribusi inverse gamma

𝐺

: Menyatakan distribusi gamma

Daftar Pustaka

Aklimawati, L. dan Wahyudi, T. 2013. Estimasi Volatilitas Return Harga Kakao

Menggunakan Model ARCH dan GARCH, Pelita Perkebunan 29 (2), pp. 142158.

Carlin, B. P., dan Chib, S. (1995). Bayesian model choice via Markov chain Monte Carlo

methods, Journal of The Royal Statistical Society, 57 (3), pp. 473–484.

Engle, R. F. (1982). Autoregressive conditional heteroskedasticity with estimates

of the variance of the united kingdom inflation. Econometrica, 50, pp. 987–1007.

Nastiti, K. L. A. dan Suharsono A. (2012). Analisis volatilitas saham perusahaan go public

dengan metode ARCHGARCH. Jurnal Sains dan Seni ITS, 1, (1), pp. D259D264.

Nurjanah, E. (2005). Pengaruh Nilai Tukar Rupiah atas Dollar AS Terhadap Tingkat Inflasi

di Indonesia pada Periode 1999-2004 (Data Diperoleh Pada Bank Indonesia). Skripsi,

UNIKOM, Bandung.

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

langkah (Nugroho, 2014), yaitu membangun rantai Markov dan menggunakan metode Monte Carlo untuk meringkas distribusi posterior pada parameter sebagai keluaran MCMC.

Dimisalkan 𝑹 = (𝑅1, 𝑅2, … , 𝑅𝑇) dan 𝝈 = (𝜎1, 𝜎2, … , 𝜎𝑇). Berdasarkan Teorema Bayes (lihat Koop dkk. (2007)), distribusi gabungan untuk model di atas yaitu

𝑝(𝑎, 𝑏, 𝝈|𝑹) = 𝑝(𝑹|𝝈) ∙ 𝑝(𝑎, 𝑏), dimana 𝑝(𝑹|𝝈) adalah fungsi likelihood dan 𝑝(𝑎, 𝑏) adalah distribusi prior pada (𝑎, 𝑏). Untuk memenuhi kendala parameter a dan b, ditetapkan prior seperti berikut:

𝑎~exp(𝜆) dan 𝑏~𝐵𝑒𝑡𝑎(𝛼, 𝛽), maka dipunyai distribusi gabungan yaitu 𝑝(𝑎, 𝑏, 𝝈|𝑹) ∝ ∏ 𝜎𝑡−1exp {− 𝑅_𝑡2 2𝜎_𝑡2} 𝑇 𝑡=1 ∙ exp{−𝜆𝑎} ∙ 𝑏𝛼−1(1 − 𝑏)𝛽−1 = (1 − 𝑏 𝑎 ) 1 2 exp {−(1 − 𝑏)𝑅1 2 2𝑎 } ∏ (𝑎 + 𝑏𝑅𝑡−12 ) − 1 2_{∙ exp {−} 𝑅𝑡2 2(𝑎+𝑏𝑅_𝑡−12 )} 𝑇 𝑡=2 ∙ exp{−𝜆𝑎} ∙ 𝑏𝛼−1_{(1 − 𝑏)}𝛽−1_.

atau dengan pengambilan logaritma natural diperoleh ln 𝑝(𝑎, 𝑏|𝑹) ∝1 2ln 1 − 𝑏 𝑎 − (1 − 𝑏)𝑅12 2𝑎 −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ 𝑅_𝑡2 𝑎 + 𝑏𝑅𝑡−12 𝑇 𝑡=2 − 𝜆𝑎 +(𝛼 − 1) ln 𝑏 + (𝛽 − 1) ln(1 − 𝑏). (1)

Pembangkitan nilai parameter a

Berdasarkan persamaan (1), log distribusi posterior untuk a dinyatakan oleh

𝐹(𝑎) = ln 𝑝(𝑎|𝑏, 𝑹) ∝ −1 2ln 𝑎 − (1 − 𝑏)𝑅12 2𝑎 −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ 𝑅𝑡2 𝑎 + 𝑏𝑅𝑡−12 𝑇 𝑡=2 − 𝜆.

Masalah yang muncul di sini yaitu posterior tersebut tidak mengikuti suatu distribusi tertentu. Karena itu a dibangkitkan menggunakan metode Independence Chain Metropolis–Hastings (IC-MH) yang

diperkenalkan oleh Tierney (1994) seperti berikut:

Langkah 1: Menentukan proposal untuk a, yaitu 𝑎∗_~𝑁

(0,1](𝜇𝑎∗, 𝑉𝑎∗)

Langkah 2: Menghitung rasio 𝑟(𝑎, 𝑎∗) =𝑝(𝑎

∗_{|𝑏, 𝑹)} 𝑝(𝑎|𝑏, 𝑹).

Langkah 3: Membangkitkan 𝑢 dari distribusi seragam [0,1].

Langkah 4: Jika 𝑢 < min{1, 𝑟(𝑎, 𝑎∗)}, maka proposal diterima, jika tidak, maka proposal ditolak.

Rata-rata 𝜇𝑎∗ dan variansi 𝑉𝑎∗ dicari dengan menggunakan metode yang didasarkan pada tingkah laku distribusi di sekitar modus (lihat Albert (2009)). Modus 𝑎̂ dari 𝐹(𝑎), artinya 𝐹′(𝑎̂) = 0, dicari menggunakan metode bagi dua. Selanjutnya diambil 𝜇𝑎∗ = 𝑎̂ dan 𝑉𝑎∗= −[𝐹′′(𝑎̂)]−1. Masalahnya adalah 𝐹′′(𝑎̂) bisa bernilai positif, karena itu diambil 𝑉𝑎∗= −[𝐷𝑎(𝑎̂)]−1 dengan

𝐷𝑎(𝑎̂) = min {−0.0001, 𝐹′′(𝑎̂) }.

Pembangkitan nilai parameter b

Berdasarkan persamaan (1), log distribusi posterior untuk b dinyatakan oleh

𝐹(𝑏) = ln 𝑝(𝑏|𝑎, 𝑹) ∝ −1 2ln(1 − 𝑏) − (1 − 𝑏)𝑅₁2 2𝑎 −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ 𝑅𝑡2 𝑎 + 𝑏𝑅𝑡−12 𝑇 𝑡=2 +(𝛼 − 1) ln 𝑏 + (𝛽 − 1) ln(1 − 𝑏),

yang tidak mengikuti suatu distribusi tertentu. Karena itu nilai parameter b dibangkitkan menggunakan cara yang sama seperti pada pembangkitan nilai parameter a.

Metode MCMC mensimulasi suatu nilai baru untuk setiap parameter dari distribusi posteriornya dengan mengasumsikan bahwa nilai saat ini untuk parameter lain adalah benar. Sacara ringkas skema MCMC yaitu

(i)

Inisialisasi a dan b.

(ii)

Membangkitkan sampel a dengan metode IC-MH.

(iii) Membangkitkan sampel b dengan metode

IC-MH.

(iv) Menghitung variansi (volatility kuadrat):

𝜎𝑡2 = 𝑎 + 𝑏𝑅𝑡−12 .

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

1. HASIL DAN PEMBAHASAN 4.1 Data Pengamatan

Selanjutnya model dan metode di atas diaplikasikan pada data kurs beli Euro (EUR), Japanese Yen (JPY), dan US Dollar (USD) terhadap Rupiah atas periode 5 Januari 2009 sampai dengan 31 Desember 2014 yang terdiri dari 1472 observasi. Dalam penelitian ini penghitungan dilakukan dengan alat bantu software Matlab 2012a. Gambar 1 menampilkan plot runtun waktu untuk returns dan Tabel 1 menyajikan statistik deskriptif.

Gambar 1. Plot runtun waktu returns harian untuk kurs beli JPY, USD, dan EUR terhadap Rupiah dari Januari 2009 sampai Desember 2014.

Tabel 1. Statistik deskriptif dari returns harian untuk kurs beli JPY, USD, dan EUR terhadar Rupiah dari Januari 2009 sampai Desember 2014. Mata Uang Mean SD JB Test (normali tas) LB Q test (auto korelasi) JPY – 0.004 0.363 tidak normal tidak ada korelasi USD – 0.004 0.215 tidak

normal ada korelasi EUR 0.000 0.294 tidak

normal

tidak ada korelasi

4.2 Pengaturan MCMC

Algoritma MCMC dijalankan dengan menggunakan 15000 iterasi, dimana 5000 iterasi pertama dihilangkan dan sisanya, N = 10000, disimpan untuk menghitug rata-rata posterior, simpangan baku, interval Bayes, numerical standard error (NSE), dan diagnosa konvergensi. Di sini, dipilih interval highest posterior density (HPD) yang disajikan oleh Chen dan Shao (1999) sebagai pendekatan

untuk interval Bayes. Diagnosa konvergensi dilakukan dengan menghitung integrated autocorrelation time (IACT), lihat Geweke (2005), untuk mengetahui berapa banyak sampel yang harus dibangkitkan untuk mendapatkan sampel yang saling bebas (seberapa cepat konvergensi simulasi). Sementara itu konvergensi rantai Markov diperiksa berdasarkan pada uji z-score Geweke (1992) dan NSE dihitung menggunakan metode yang disajikan oleh Geweke (2005).

Dalam aplikasi algoritma MCMC, model dilengkapi dengan prior dimana 𝜆 = 1, 𝛼 = 2.5, dan 𝛽 = 3. Untuk nilai-nilai awal parameter ditetapkan 𝑎0= 𝑏0= 0.1.

4.3 Estimasi Parameter

Tabel 2, 3 dan 4 meringkas hasil simulasi posterior parameter dalam model ARCH(1) berturut-turut untuk data kurs beli JPY, USD, dan EUR terhadap Rupiah. p-value yang berasosiasi dengan Geweke’s convergence diagnostic (G-CD) mengindikasikan bahwa semua rantai Markov sudah konvergen. Nilai-nilai IACT menunjukkan bahwa metode IC-MH adalah sangat efisien.

Tabel 2. Ringkasan hasil simulasi posterior untuk data kurs beli JPY terhadap Rupiah. LB dan UB menyatakan berturut-turut batas bawah dan batas atas interval HPD 95%.

Parameter

a

b

Matlab

0.0994

0.2619

Mean

0.1022

0.2548

SD

0.0050

0.0464

LB

0.0928

0.1648

UB

0.1121

0.3446

IACT

1.4620

1.2613

NSE

0.0000

0.0005

G-CD

0.0036

0.0648

p-value

0.9971

0.9484

CPU time (detik): 131.14

Tabel 3. Ringkasan hasil simulasi posterior untuk data kurs beli USD terhadap Rupiah.

Parameter

a

b

Matlab

0.0237

0.6532

Mean

0.0244

0.6255

SD

0.0012

0.0682

LB

0.0220

0.4903

UB

0.0267

0.7547

IACT

1.0000

1.0000

0 500 1000 1500 -2 0 2 JPY k u rs b e li 0 500 1000 1500 -2 0 2 USD k u rs b e li 0 500 1000 1500 -2 0 2 EUR waktu k u rs b e li

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

NSE

0.0000

0.0006

G-CD

– 0.0036

– 0.0260

p-value

0.9971

0.9792

CPU time (detik): 137.72

Tabel 4. Ringkasan hasil simulasi posterior untuk data kurs beli EUR terhadap Rupiah

Parameter

a

B

Matlab

0.0704

0.1878

Mean

0.0713

0.1900

SD

0.0030

0.0372

LB

0.0650

0.1186

UB

0.0771

0.2630

IACT

1.0000

1.0000

NSE

0.0000

0.0004

G-CD

– 0.0159

0.0047

p-value

0.9873

0.9962

CPU time (detik): 148.27

Plot sampel posterior dan histogram distribusi posterior parameter-parameter a dan b ditampilkan berturut-turut pada Gambar 2 dan Gambar 3. Plot sampel mengindikasikan bahwa sampel berfluktuasi disekitar rata-rata posterior, yang berarti bahwa sampel telah bercampur dengan baik (good mixing).

Gambar 2. Plot sampel untuk parameter a dan b pada model ARCH(1) untuk returns kurs beli JPY (atas), USD (tengah), dan EUR (bawah) terhadap Rupiah dari Januari 2009 sampai Desember 2014.

Gambar 3. Histogram distribusi posterior parameter a dan b pada model ARCH(1) untuk returns kurs beli JPY (atas), USD (tengah), dan EUR (bawah) terhadap Rupiah dari Januari 2009 sampai Desember 2014.

Terkait dengan estimasi parameter, hasil menunjukkan bahwa nilai estimasi a dan b serupa dengan hasil yang diperoleh dari penggunaan fungsi garch(p,q) di Matlab. Rata-rata posterior untuk variansi (volatility kuadrat) returns disajikan dalam Gambar 4. Diperoleh bahwa variansi untuk returns kurs beli JPY, USD, dan EUR terhadap rupiah berturut-turut yaitu 0.102–0.984, 0.024–1.080, dan 0.071–0.430, dimana rata-ratanya berturut-turut yaitu 0.136, 0.053, 0.088. Nilai variansi tertinggi terjadi pada periode April 2013 untuk JPY, Februari 2009 untuk USD, dan September 2011 untuk EUR.

Gambar 4. Plot runtun waktu variansi untuk returns kurs beli JPY, USD, dan EUR terhadap Rupiah dari Januari 2009 sampai Desember 2014.

Jadi, model volatility untuk returns kurs beli JPY, USD, dan EUR terhadap Rupiah berturut-turut: 𝜎𝑡2= 0.1022 + 0.2548𝑅𝑡−12 , 𝜎𝑡2= 0.0244 + 0.6255𝑅𝑡−12 , 𝜎𝑡2= 0.0713 + 0.1900𝑅𝑡−12 . 0 5000 10000 0.08 0.1 0.12 a 0 5000 10000 0.2 0.4 b 0 5000 10000 0.02 0.025 0.03 0 5000 10000 0.5 1 0 5000 10000 0.06 0.07 0.08 0 5000 10000 0 0.2 0.4 0.050 0.1 0.15 500 1000 1500 a 0 0.2 0.4 0.6 0.8 0 500 1000 1500 b 0.0150 0.02 0.025 0.03 500 1000 1500 0.2 0.4 0.6 0.8 1 0 500 1000 0.060 0.07 0.08 0.09 500 1000 0 0.1 0.2 0.3 0.4 0 500 1000 1500 0 500 1000 1500 0 0.5 1 JPY _t2 0 500 1000 1500 0 1 2 USD  t 2 0 500 1000 1500 0 0.5 EUR waktu  t 2

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

2. KESIMPULAN

Studi ini menyajikan model ARCH(1) untuk returns kurs beli JPY, USD, dan EUR terhadap Rupiah. Algoritma MCMC yang efisien dibangun untuk membangkitkan sampel dari distribusi posterior model. Hasil empiris menunjukkan bahwa rata-rata volatility untuk returns kurs beli JPY adalah yang tertinggi.

Model yang disajikan dalam studi ini bisa diperluas dengan memperhatikan distribusi tak normal untuk returns error. Selain itu, model bisa diperluas ke model GARCH.

3. REFERENSI

1. Albert, J. (2009). Bayesian computation with R, 2nd ed., Springer.

2. Carlin, B. P., dan Chib, S. (1995). Bayesian model choice via Markov chain Monte Carlo methods, Journal of The Royal Statistical Society, 57 (3), 473–484.

3. Casella, G. dan Berger R., L. (2002). Statistical inference, Thomson Learning, Duxbury.

4. Chen, M. H. dan Shao, Q. M. (1999). Monte Carlo estimation of Bayesian

credible and HPD

intervals. Journal of Computational and Graphical Statistics, 8, 69–92.

5. Engle, R. F. (1982). Autoregressive conditional heteroskedasticity with estimates

of the variance of the united kingdom inflation. Econometrica, 50, 987–1007. 6. Geweke, J. (1992). Evaluating the

accuracy of sampling-based approaches to the calculation of posterior moments, Bayesian Statistics 4 (eds. J. M. Bernardo, J. O. Berger, A. P. Dawid dan A. F. M. Smith), 169–194.

7. Geweke, J. (2005). Contemporary Bayesian econometrics and statistics. John Wiley & Sons.

8. Jones, C. P., and Wilson, J. W. (1989). Is stock price volatility increasing?, Financial Analysts Journal, 45 (6), 20– 26.

9. Koop. G., Poirier, D. J. dan Tobias, J. L. (2007). Bayesian econometri methods. Cambridge University Press, New York.

10. Muklis, I. (2011). Analisis volatilitas nilai tukar mata uang Rupiah terhadap dolar. Journal of Indonesian Apllied Economics, 5 (2), 172–182.

11. Nastiti, K. L. A. dan Suharsono A. (2012). Analisis volatilitas saham perusahaa go public dengan metode ARCHGARCH. Jurnal Sains dan Seni ITS, 1, (1), D259D264.

12. Nugroho, D. B. (2014). Realized stocastic volatility model using generalized student’s t-error

distributions and power

transformations, Dissertation. Kwansei Gakuin University, Japan.

13. Tierney, L. (1994). Markov chain for exploring posterior distributions.

Annals of Statistics,

22 (4), 1701–1762.

14. Tsay, R. S., (2010). Analysis of financial time series. John Willey and Sons, Inc. New York.

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

𝑝(𝑎, 𝑏, 𝑣, 𝒛, 𝝈|𝑹)

= 𝑝(𝑹|𝒛, 𝝈) ∙ 𝑝(𝒛|𝑣) ∙ 𝑝(𝑎, 𝑏, 𝑣),

dimana 𝑝(𝑹|𝒛, 𝝈) adalah fungsi likelihood dan 𝑝(𝑎, 𝑏, 𝑣) adalah distribusi prior pada (𝑎, 𝑏, 𝑣). Selanjutnya ditetapkan prior seperti berikut:

𝑎~exp(𝜆), 𝑏~𝐵𝑒𝑡𝑎(𝛼𝑏, 𝛽𝑏), 𝑣 = 𝐺(𝛼𝜈, 𝛽𝜈), dimana prior (a,b) tersebut dipilih untuk memenuhi kendala-kendala model. Sekarang dipunyai distribusi gabungan yaitu

𝑝(𝑎, 𝑏, 𝑣, 𝒛|𝑹) ∝ (1−𝑏_𝑎 ) 1 2 𝑧₁− 1 2_{exp {−}(1−𝑏)𝑅12 2𝑎𝑧1 } ∙ (𝑣 2) 𝑣𝑇 2 [Γ (𝑣 2)] −𝑇 ∏ (𝑎 + 𝑏𝑅_𝑡−12 ₎ −1_2𝑧 𝑡 −1₂ 𝑇 𝑡=2 exp {− 𝑅𝑡2 2(𝑎+𝑏𝑅_𝑡−12 )𝑧𝑡} ∏ 𝑧𝑡− 𝑣 2−1 𝑇 𝑡=1 exp (− 𝑣 2𝑧𝑡 ) ∙ exp{−𝜆𝑎} ∙ 𝑏𝛼−1_{(1 − 𝑏)}𝛽−1_{∙ 𝑣}𝛼𝑣−1_exp(−𝛽 𝑣𝑣). atau dengan pengambilan logaritma natural diperoleh ln 𝑝(𝑎, 𝑏, 𝜈, 𝒛|𝑹) ∝1 2ln 1 − 𝑏 𝑎 − 1 2ln(𝑧1) − (1 − 𝑏)𝑅12 2𝑎𝑧1 +𝑣𝑇 2 ln ( 𝑣 2) − 𝑇 ln (Γ ( 𝑣 2)) −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ ln(𝑧𝑡) 𝑇 𝑡=2 −1 2∑ 𝑅𝑡2 (𝑎 + 𝑏𝑅_𝑡−12 _)𝑧 𝑡 𝑇 𝑡=2 − (𝑣 2+ 1) ∑ ln(𝑧𝑡) 𝑇 𝑡=1 −𝑣 2∑ 𝑧𝑡 −1 𝑇 𝑡=1 − 𝜆𝑎 +(𝛼𝑏− 1) ln 𝑏 + (𝛽𝑏− 1) ln(1 − 𝑏) +(𝛼𝑣− 1) ln 𝑣 − 𝛽𝑣𝑣. (1) Pembangkitan parameter a

Berdasarkan persamaan (1), log distribusi posterior untuk a dinyatakan oleh

𝐹(𝑎) = ln 𝑝(𝑎|𝑏, 𝒛, 𝑹) −1 2ln 𝑎 − (1 − 𝑏)𝑅₁2 2𝑎𝑧1 −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ 𝑅𝑡2 (𝑎 + 𝑏𝑅_𝑡−12 _)𝑧 𝑡 𝑇 𝑡=2 − 𝜆𝑎

Masalah yang muncul di sini yaitu posterior tersebut tidak mengikuti suatu distribusi tertentu. Oleh karena itu, a dibangkitkan menggunakan metode Independence Chain Metropolis–Hastings (IC-MH) yang diperkenalkan oleh Tierney (1994) seperti berikut:

Langkah 1: Menentukan proposal untuk a, yaitu 𝑎∗_~𝑁

(0,1](𝜇𝑎∗, 𝑉𝑎∗)

Langkah 2: Menghitung rasio 𝑟(𝑎, 𝑎∗) =𝑝(𝑎

∗_{|𝑏, 𝑹)} 𝑝(𝑎|𝑏, 𝑹).

Langkah 3: Membangkitkan 𝑢 dari distribusi seragam [0,1].

Langkah 4: Jika 𝑢 < min{1, 𝑟(𝑎, 𝑎∗)}, maka proposal diterima, jika tidak, maka proposal ditolak.

Rata-rata 𝜇𝑎∗ dan variansi 𝑉𝑎∗ dicari dengan menggunakan metode yang didasarkan pada tingkah laku distribusi di sekitar modus (lihat Albert (2009)). Modus 𝑎̂ dari 𝐹(𝑎), artinya 𝐹′(𝑎̂) = 0, dicari menggunakan metode bagi dua. Selanjutnya diambil 𝜇𝑎∗= 𝑎̂ dan 𝑉𝑎∗= −[𝐹′′(𝑎̂)]−1_{. Masalahnya adalah 𝐹′′(𝑎̂) bisa} bernilai positif, karena itu diambil 𝑉𝑎∗= −[𝐷𝑎(𝑎̂)]−1 dengan

𝐷𝑎(𝑎̂) = min {−0.0001, 𝐹′′(𝑎̂) }.

Pembangkitan parameter b

Berdasarkan persamaan (1), log distribusi posterior untuk b dinyatakan oleh

𝐹(𝑏) = ln 𝑝(𝑏|𝑎, 𝒛, 𝑹) ∝1 2ln(1 − 𝑏) − (1 − 𝑏)𝑅12 2𝑎𝑧1 −1 2∑ ln(𝑎 + 𝑏𝑅𝑡−1 2 ₎ 𝑇 𝑡=2 −1 2∑ 𝑅𝑡2 (𝑎 + 𝑏𝑅_𝑡−12 _)𝑧 𝑡 𝑇 𝑡=2 +(𝛼𝑏− 1) ln 𝑏 + (𝛽𝑏− 1) ln(1 − 𝑏),

yang tidak mengikuti suatu distribusi tertentu. Karena itu nilai parameter b dibangkitkan menggunakan cara yang sama seperti pada pembangkitan parameter a.

Pembangkitan nilai parameter 𝑣

Berdasarkan persamaan (1), log distribusi posterior untuk 𝑣 dinyatakan oleh

𝐹(𝑣) = ln 𝑝(𝜈|𝑎, 𝑏, 𝒛, 𝑹) ∝𝑣𝑇 2 ln ( 𝑣 2) − 𝑇 ln (Γ ( 𝑣 2)) −𝑣 2∑[ln(𝑧𝑡) + 𝑧𝑡 −1_] 𝑇 𝑡=1 +(𝛼𝑣− 1) ln 𝑣 − 𝛽𝑣𝑣,

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

yang tidak mengikuti suatu distribusi tertentu. Oleh karena itu, parameter 𝑣 dibangkitkan menggunakan cara yang sama seperti pada pembangkitan parameter a, dimana proposalnya yaitu 𝑣∗~𝑁[3,40](𝜇𝜈∗, 𝑉𝑣∗).

Pembangkitan nilai vektor parameter z

Berdasarkan persamaan (1), distribusi posterior untuk z dinyatakan oleh

𝑝(𝒛|𝑎, 𝑏, 𝑣, 𝑹) ∝ 𝑧1− 𝑣+1 2 −1_{exp (−}(1 − 𝑏)𝑅1 2_{+ 𝑎𝑣} 2𝑎𝑧1 ) ∏ 𝑧_𝑡− 𝑣+1 2 −1_{exp {−}𝑅𝑡 2_{+ (𝑎 + 𝑏𝑅} 𝑡−12 )𝑣 2(𝑎 + 𝑏𝑅_𝑡−12 )𝑧𝑡 } 𝑇 𝑡=2 .

Dalam kasus ini, 𝒛 bisa dibangkitkan secara langsung dari distribusi invers gamma, yaitu 𝑧1~𝐼𝐺 ( 𝑣 + 1 2 , (1 − 𝑏)𝑅₁2_{+ 𝑎𝑣} 2𝑎 ), 𝑧𝑡~𝐼𝐺 ( 𝑣 + 1 2 , 𝑅𝑡2+ (𝑎 + 𝑏𝑅𝑡−12 )𝑣 2(𝑎 + 𝑏𝑅_𝑡−12 ₎ ), untuk 𝑡 = 2,3 … , 𝑇.

Metode MCMC mensimulasi suatu nilai baru untuk setiap parameter dari distribusi posteriornya dengan mengasumsikan bahwa nilai saat ini untuk parameter lain adalah benar. Sacara ringkas skema MCMC untuk model dalam studi ini yaitu

(i)

Inisialisasi a, b, dan 𝑣.

(ii)

Membangkitkan sampel z secara langsung.

(iii) Membangkitkan sampel 𝑣 dengan metode

IC-MH.

(iv) Membangkitkan sampel a dengan metode

IC-MH.

(v)

Membangkitkan sampel b dengan metode IC-MH.

(vi) Menghitung variansi (volatility kuadrat):

𝜎𝑡2 = 𝑎 + 𝑏𝑅𝑡−12 .

1. HASIL DAN PEMBAHASAN 4.1 Data Pengamatan

Selanjutnya model dan metode di atas diaplikasikan pada data kurs beli Euro (EUR), Japanese Yen (JPY), dan US Dollar (USD) terhadap Rupiah atas periode 5 Januari 2009 sampai dengan 31 Desember 2014 yang terdiri dari 1472 observasi. Dalam penelitian ini penghitungan dilakukan dengan alat bantu

software Matlab 2012a. Lihat Safrudin dkk. (2015) untuk plot runtun waktu untuk returns dan statistik deskriptif.

4.2 Pengaturan MCMC

Algoritma MCMC dijalankan dengan menggunakan 15000 iterasi, dimana 5000 iterasi pertama dihilangkan dan sisanya, N = 10000, disimpan untuk menghitug rata-rata posterior, simpangan baku, interval Bayes, numerical standard error (NSE), dan diagnosa konvergensi. Di sini, dipilih interval highest posterior density (HPD) yang disajikan oleh Chen dan Shao (1999) sebagai pendekatan untuk interval Bayes. Diagnosa konvergensi dilakukan dengan menghitung integrated autocorrelation time (IACT), lihat Geweke (2005), untuk mengetahui berapa banyak sampel yang harus dibangkitkan untuk mendapatkan sampel yang saling bebas (seberapa cepat konvergensi simulasi). Sementara itu konvergensi rantai Markov diperiksa berdasarkan pada uji z-score Geweke (1992) dan NSE dihitung menggunakan metode yang disajikan oleh Geweke (2005).

Dalam aplikasi algoritma MCMC, model dilengkapi dengan prior dimana 𝜆 = 1, 𝛼𝑏 = 2.5, 𝛽𝑏= 3, 𝛼𝑣= 16 dan 𝛽𝑣= 0.8. Untuk nilai-nilai awal parameter ditetapkan 𝑎0= 𝑏0= 0.1 dan v = 20.

4.3 Estimasi Parameter

Tabel 1, 2 dan 3 meringkas hasil simulasi posterior parameter dalam model ARCH(1), dimana returns error berdistribusi Student-t, berturut-turut untuk data kurs beli JPY, USD, dan EUR terhadap IDR. p-value yang berasosiasi dengan Geweke’s convergence diagnostic (G-CD) mengindikasikan bahwa semua rantai Markov sudah konvergen. Nilai-nilai IACT menunjukkan bahwa metode IC-MH adalah sangat efisien.

Tabel 1. Ringkasan hasil simulasi posterior untuk data kurs beli JPY terhadap IDR. LB dan UB menyatakan berturut-turut batas bawah dan batas atas interval HPD 95%. Parameter a b v Mean 0.0547 0.2180 5.1708 SD 0.0030 0.0414 0.5779 LB 0.0495 0.1386 4.0913 UB 0.0598 0.2998 6.3289 IACT 8.1819 5.9936 22.9946

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015

NSE 0.0000 0.0009 0.0233 G-CD – 0.0063 0.0686 0.1160 p-value 0.9949 0.9453 0.9076 CPU time (detik): 313.795

Tabel 2. Ringkasan hasil simulasi posterior untuk data kurs beli USD terhadap IDR.

Parameter a b v Mean 0.0078 0.3809 3.1140 SD 0.0004 0.0497 0.2386 LB 0.0069 0.2882 2.6469 UB 0.0087 0.4832 3.5717 IACT 1.0000 5.3140 10.0292 NSE 0.0000 0.0011 0.0070 G-CD – 0.0059 – 0.0003 – 0.1576 p-value 0.9953 0.9998 0.8747 CPU time (detik): 295.673

Tabel 3. Ringkasan hasil simulasi posterior untuk data kurs beli EUR terhadap IDR.

Parameter A b v Mean 0.0546 0.1612 10.4858 SD 0.0026 0.0353 1.6553 LB 0.0502 0.0958 7.6162 UB 0.0595 0.2339 13.9917 IACT 12.2060 5.2695 66.3636 NSE 0.0000 0.0007 0.0799 G-CD 0.0045 0.0408 0.3283 p-value 0.9964 0.9674 0.7427 CPU time (detik): 285.506

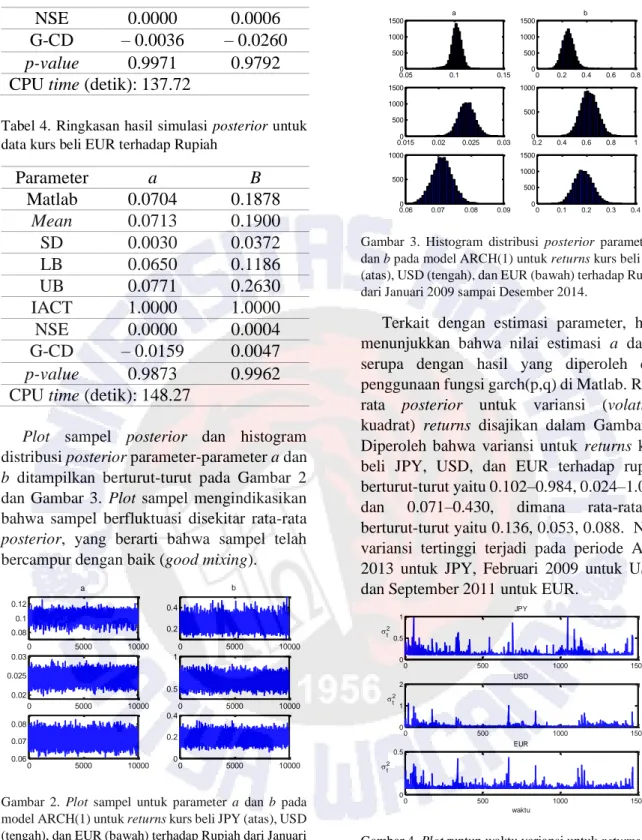
Plot sampel posterior dan histogram distribusi posterior parameter-parameter a dan b ditampilkan berturut-turut pada Gambar 1 dan Gambar 2. Plot sampel mengindikasikan bahwa sampel berfluktuasi disekitar rata-rata posterior, yang berarti bahwa sampel telah bercampur dengan baik (good mixing).

Gambar 1. Plot sampel untuk parameter a, b, dan v pada model ARCH(1) untuk returns kurs beli JPY (atas), USD

(tengah), dan EUR (bawah) terhadap IDR dari Januari 2009 sampai Desember 2014.

Gambar 2. Histogram distribusi posterior parameter a, b, dan v pada model ARCH(1) untuk returns kurs beli JPY (atas), USD (tengah), dan EUR (bawah) terhadap Rupiah dari Januari 2009 sampai Desember 2014.

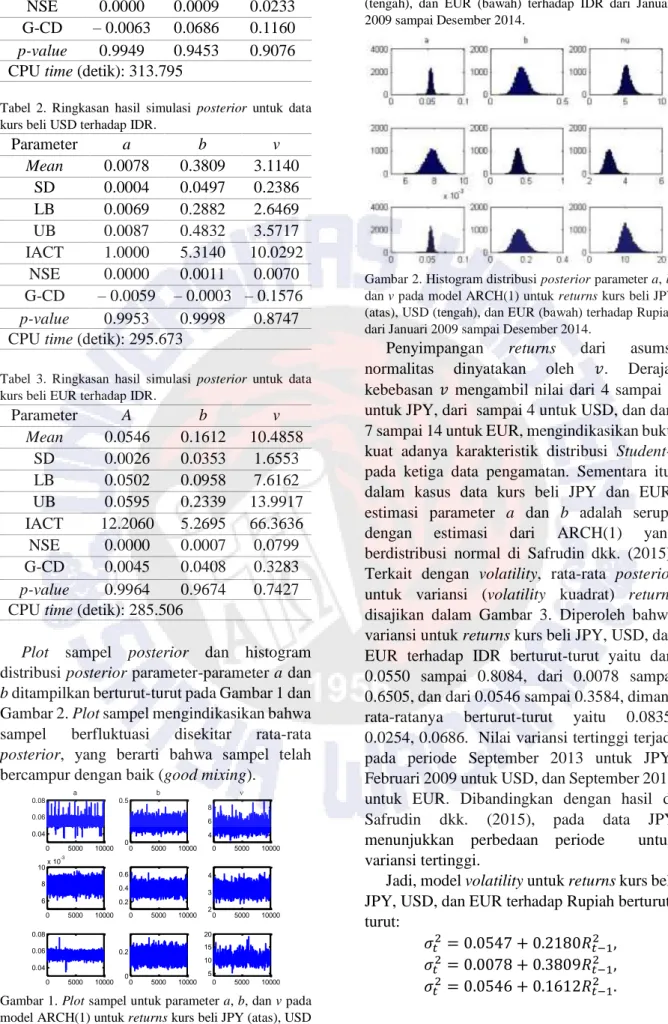
Penyimpangan returns dari asumsi normalitas dinyatakan oleh 𝑣. Derajat kebebasan 𝑣 mengambil nilai dari 4 sampai 7 untuk JPY, dari sampai 4 untuk USD, dan dari 7 sampai 14 untuk EUR, mengindikasikan bukti kuat adanya karakteristik distribusi Student-t pada ketiga data pengamatan. Sementara itu, dalam kasus data kurs beli JPY dan EUR, estimasi parameter a dan b adalah serupa dengan estimasi dari ARCH(1) yang berdistribusi normal di Safrudin dkk. (2015). Terkait dengan volatility, rata-rata posterior untuk variansi (volatility kuadrat) returns disajikan dalam Gambar 3. Diperoleh bahwa variansi untuk returns kurs beli JPY, USD, dan EUR terhadap IDR berturut-turut yaitu dari 0.0550 sampai 0.8084, dari 0.0078 sampai 0.6505, dan dari 0.0546 sampai 0.3584, dimana rata-ratanya berturut-turut yaitu 0.0835, 0.0254, 0.0686. Nilai variansi tertinggi terjadi pada periode September 2013 untuk JPY, Februari 2009 untuk USD, dan September 2011 untuk EUR. Dibandingkan dengan hasil di Safrudin dkk. (2015), pada data JPY menunjukkan perbedaan periode untuk variansi tertinggi.

Jadi, model volatility untuk returns kurs beli JPY, USD, dan EUR terhadap Rupiah berturut-turut: 𝜎𝑡2= 0.0547 + 0.2180𝑅𝑡−12 , 𝜎𝑡2= 0.0078 + 0.3809𝑅𝑡−12 , 𝜎𝑡2= 0.0546 + 0.1612𝑅𝑡−12 . 0 5000 10000 0.04 0.06 0.08 a 0 5000 10000 0 0.5 b 0 5000 10000 4 6 8  0 5000 10000 6 8 10x 10 -3 0 5000 10000 0.2 0.4 0.6 0 5000 10000 2 3 4 0 5000 10000 0.04 0.06 0.08 0 5000 10000 0 0.2 0 5000 10000 5 10 15 20

Prosiding Seminar Nasional Matematika dan Pendidikan Matematika 2015 Gambar 3. Plot runtun waktu variansi untuk returns kurs

beli JPY, USD, dan EUR terhadap IDR dari Januari 2009 sampai Desember 2014.

2. KESIMPULAN

Studi ini menyajikan model ARCH(1) dengan returns error berdistribusi Student-t untuk returns kurs beli JPY, USD, dan EUR terhadap IDR. Algoritma MCMC yang efisien dibangun untuk membangkitkan sampel dari distribusi posterior model. Hasil empiris menunjukkan bukti sangat kuat untuk penggunaan distribusi Student-t pada ketiga data tersebut.

Model yang disajikan dalam studi ini bisa diperluas dengan memperhatikan distribusi Student-t yang umum, seperti non-central Student-t dan generalized skew Student-t yang mengakomodasi heavy tails dan skewness. Lebih lanjut model bisa diperluas ke model GARCH.

3. REFERENSI

1. Bollerslev, T. (1987). A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return, Review of Economics and Statistics, 69, 542–547.

2. Casella, G. dan Berger R., L. (2002). Statistical inference, Thomson Learning, Duxbury.

3. Chen, M. H. dan Shao, Q. M. (1999). Monte Carlo estimation of Bayesian credible and HPD intervals. Journal of Computational and Graphical Statistics, 8, 69–92.

4. Engle, R. F. (1982). Autoregressive conditional heteroskedasticity with estimates of the variance of the united

kingdom inflation. Econometrica, 50, 987–1007.

5. Geweke, J. (1992). Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments, Bayesian Statistics 4 (eds. J. M. Bernardo, J. O. Berger, A. P. Dawid dan A. F. M. Smith), 169–194.

6. Geweke, J. (2005). Contemporary Bayesian econometrics and statistics. John Wiley & Sons.

7. Koop. G., Poirier, D. J. dan Tobias, J. L. (2007). Bayesian econometri methods. Cambridge University Press, New York. 8. Nugroho, D. B. (2014). Realized stocastic volatility model using generalized student’s t-error distributions and power transformations, Dissertation. Kwansei Gakuin University, Japan.

9. Tierney, L. (1994). Markov chain for exploring posterior distributions. Annals of Statistics, 22 (4), 1701–1762.

10. Tsay, R. S., (2010). Analysis of financial time series. John Willey and Sons, Inc. New York.

Lampiran 1. Skema MCMC untuk model ARCH berdistribusi Student-t

1.

Inisialisasi a, b, dan 𝜈.

2.

Pembangkitan 𝒛|𝑎, 𝑏, 𝑣, 𝑹.

Distribusi posterior bersyarat untuk z diberikan oleh

𝑝(𝒛|𝑎, 𝑏, 𝑣, 𝑹)

∝ 𝑧

₁−𝑣+12 −1

_{exp (−}

(1 − 𝑏)𝑅

1 2

_{+ 𝑎𝑣}

2𝑎𝑧

₁

) ∏

𝑧

𝑡 −𝑣+1₂ −1

exp {−

𝑅

𝑡 2

_{+ (𝑎 + 𝑏𝑅}

𝑡−12

)𝑣

2(𝑎 + 𝑏𝑅

_𝑡−12

_)𝑧

𝑡

}

𝑇 𝑡=2

.

Dalam kasus ini, 𝒛 bisa dibangkitkan secara langsung dari distribusi inverse gamma,

yaitu 𝑧

1

~𝐼𝐺 (

𝑣+1 2

,

(1−𝑏)𝑅12+𝑎𝑣 2𝑎

) dan 𝑧

𝑡

~𝐼𝐺 (

𝑣+1 2

,

𝑅_𝑡2+(𝑎+𝑏𝑅_𝑡−12 )𝑣 2(𝑎+𝑏𝑅_𝑡−12 )

), untuk 𝑡 = 2,3 … , 𝑇.

3.

Pembangkitan 𝜈|𝒛

Distribusi posterior bersyarat untuk v diberikan oleh

𝑝( 𝜈|𝒛) ∝ (

𝑣 2

)

𝑣𝑇 2

[Γ (

𝑣 2

)]

−𝑇

∏

𝑧

𝑡− 𝑣 2−1 𝑇 𝑡=1

exp (−

𝑣 2𝑧𝑡

) 𝑣

𝛼_𝑣−1

_exp(−𝛽

𝑣

𝑣).

Nilai 𝑣 dibangkitkan menggunakan metode IC-MH, yang mana proposal untuk 𝑣 yaitu

𝑣

∗

~𝑁

_[3,40]

(𝜇

_𝜈∗

, 𝑉

_𝑣∗

) dan probabilitas penerimaannya yaitu min {1,

𝑝(

𝑣

∗|

𝒛

)

𝑝(

𝑣

|

𝒛

)

}. Diambil

logaritma distribusi posterior bersyarat untuk 𝑣:

𝐹(𝑣) = ln 𝑝(𝜈|𝒛)

∝

𝑣𝑇

2

ln (

𝑣

2

) − 𝑇 ln (Γ (

𝑣

2

)) −

𝑣

2

∑[ln(𝑧

𝑡

) + 𝑧

𝑡 −1

_]

𝑇 𝑡=1

+ (𝛼

_𝑣

− 1) ln 𝑣

− 𝛽

_𝑣

𝑣,

Dicari modus posterior 𝑣̂ dari 𝐹(𝑣), artinya bahwa 𝐹′(𝑣̂) = 0, berdasarkan metode bagi

dua. Rata-rata

𝜇

_𝑣∗

dan variansi

𝑉

_𝑣∗

ditentukan dengan menggunakan metode yang

didasarkan pada tingkah laku distribusi di sekitar modus (atau modus hampiran). Dicatat

bahwa derivatif pertama dan kedua dari 𝐹(𝑣) berturut-turut yaitu

𝐹

′

(𝑣) =

𝑇

2

[ln (

𝑣

2

) + 1 − ψ (

𝑣

2

)] −

1

2

∑[ln(𝑧

𝑡

) + 𝑧

𝑡 −1

_]

𝑇 𝑡=1

+

𝛼

𝑣

− 1

𝑣

− 𝛽

𝑣

,

dimana ψ(𝑥) =

𝑑 lnΓ(𝑥) 𝑑𝑥

, dan

𝐹

′′

_{(𝑣) =}

𝑇

2𝑣

−

𝑇

4

ψ

′

₍

𝑣

2

) −

𝛼

𝑣

− 1

𝑣

2

.

Selanjutnya diambil

𝜇

𝑣∗

= 𝑣̂ dan 𝑉

𝑣∗

= −[𝐹

′′

(𝑣̂)]

−1

. Masalahnya adalah

𝐹′′(𝑣̂) bisa

bernilai

positif,

karena

itu

diambil

𝑉

𝑣∗

= −[𝐷

𝑣

(𝑣̂)]

−1

dengan

𝐷

𝑣

(𝑣̂) =

min {−0.0001, 𝐹′′(𝑣̂) }.

4.

Pembangkitan 𝑎|𝑏, 𝒛, 𝑹

Distribusi posterior bersyarat untuk a diberikan oleh

𝑝(𝑎|𝑏, 𝒛, 𝑹) ∝ (

1 − 𝑏

𝑎

)

1 2

exp {−

(1 − 𝑏)𝑅

1 2

2𝑎𝑧

1

}

∏

(𝑎 + 𝑏𝑅

_𝑡−12

₎

−1₂

_𝑧

𝑡 −1₂

exp {−

𝑅𝑡2 2(𝑎+𝑏𝑅_𝑡−12 )𝑧_𝑡

}

𝑇 𝑡=2

exp{−𝜆𝑎}.

Nilai a dibangkitkan menggunakan metode IC-MH, yang mana proposal untuk a yaitu

𝑎

∗

~𝑁(𝜇

𝑎∗

, 𝑉

𝑎∗

) dan probabilitas penerimaannya yaitu min {1,

𝑝(

𝑎

∗|

𝑏, 𝒛, 𝑹

)

𝑝(

𝑎

|

𝑏, 𝒛, 𝑹

)

}. Diambil

logaritma distribusi posterior bersyarat untuk a:

𝐹(𝑎) = ln 𝑝(𝑎|𝑏, 𝒛, 𝑹) ∝ −

1

2

ln 𝑎 −

(1 − 𝑏)𝑅

₁2

2𝑎𝑧

1

−

1

2

∑

ln(𝑎 + 𝑏𝑅

𝑡−1 2

₎

𝑇 𝑡=2

−

1 2

∑

𝑅_𝑡2 (𝑎+𝑏𝑅_𝑡−12 )𝑧𝑡 𝑇 𝑡=2

− 𝜆𝑎.

Dicari modus posterior 𝑎̂ dari 𝐹(𝑎), artinya bahwa 𝐹′(𝑎̂) = 0, berdasarkan metode bagi

dua. Dicatat bahwa derivatif pertama dan kedua dari 𝐹(𝑎) berturut-turut yaitu

𝐹

′

_{(𝑎) =}

𝑑𝐹(𝑎)

𝑑𝑎

= −

1

2𝑎

+

(1 − 𝑏)𝑅

₁2

2𝑎

2

_𝑧

1

−

1

2

∑

1

𝑎 + 𝑏𝑅

_𝑡−12 𝑇 𝑡=2

+

1

2

∑

𝑅

_𝑡2

(𝑎 + 𝑏𝑅

_𝑡−12

₎

2

_𝑧

𝑡 𝑇 𝑡=2

− 𝜆

𝐹

′

_{′(𝑎) =}

𝑑

2

_𝐹(𝑎)

𝑑𝑎

2

=

1

2𝑎

2

−

(1 − 𝑏)𝑅

₁2

2𝑎

3

_𝑧

1

+

1

2

∑

1

(𝑎 + 𝑏𝑅

_𝑡−12

₎

2 𝑇 𝑡=2

− ∑

𝑅

𝑡 2

(𝑎 + 𝑏𝑅

_𝑡−12

₎

3

_𝑧

𝑡 𝑇 𝑡=2

.

Selanjutnya diambil

𝜇

𝑎∗

= 𝑎̂ dan 𝑉

_𝑎∗

= −[𝐹′′(𝑎̂)]

−1

. Masalahnya adalah

𝐹′′(𝑎̂) bisa

bernilai

positif,

karena

itu

diambil

𝑉

𝑎∗

= −[𝐷

𝑎

(𝑎̂)]

−1

dengan

𝐷

𝑎

(𝑎̂) =

min {−0.0001, 𝐹′′(𝑎̂) }.

5.

Pembangkitan b

Distribusi posterior bersyarat untuk b diberikan oleh

𝑝(𝑏|𝑎, 𝒛, 𝑹) ∝ (

1 − 𝑏

𝑎

)

1 2

exp {−

(1 − 𝑏)𝑅

1 2

2𝑎𝑧

1

}

∏

(𝑎 + 𝑏𝑅

_𝑡−12

₎

−1₂

_𝑧

𝑡 −1₂

exp {−

𝑅𝑡2 2(𝑎+𝑏𝑅_𝑡−12 )𝑧_𝑡

}

𝑇 𝑡=2

𝑏

𝛼−1

(1 − 𝑏)

𝛽−1

_.

Nilai b dibangkitkan menggunakan metode IC-MH, yang mana proposal untuk b yaitu

𝑏

∗

~𝑁(𝜇

𝑏∗

, 𝑉

𝑏∗

) dan probabilitas penerimaannya yaitu min {1,

𝑝(

𝑏

∗|

𝑎, 𝒛, 𝑹

)

𝑝(

𝑏

|

𝑎, 𝒛, 𝑹

)

}. Diambil

logaritma distribusi posterior bersyarat untuk b:

𝐹(𝑏) = ln 𝑝(𝑏|𝑎, 𝒛, 𝑹)

∝

1

2

ln(1 − 𝑏) −

(1 − 𝑏)𝑅

₁2

2𝑎𝑧

1

−

1

2

∑

ln(𝑎 + 𝑏𝑅

𝑡−1 2

₎

𝑇 𝑡=2

−

1

2

∑

𝑅

_𝑡2

(𝑎 + 𝑏𝑅

_𝑡−12

_)𝑧

𝑡 𝑇 𝑡=2

+ (𝛼

_𝑏

− 1) ln 𝑏 + (𝛽

_𝑏

− 1) ln(1 − 𝑏)

Dicari modus posterior 𝑏̂ dari 𝐹(𝑏), artinya bahwa 𝐹′(𝑏̂) = 0, berdasarkan metode bagi

dua. Dicatat bahwa derivatif pertama dan kedua dari 𝐹(𝑏) berturut-turut yaitu

𝐹

′

(𝑏) =

𝑑𝐹(𝑏)

𝑑𝑏

= −

1

2(1 − 𝑏)

+

𝑅

₁2

2𝑎𝑧

1

−

1

2

∑

𝑅

_𝑡−12

𝑎 + 𝑏𝑅

_𝑡−12 𝑇 𝑡=2

+

1

2

∑

𝑅

_𝑡−12

𝑅

_𝑡2

(𝑎 + 𝑏𝑅

_𝑡−12

₎

2

_𝑧

𝑡 𝑇 𝑡=2

+

𝛼

𝑏

− 1

𝑏

−

𝛽

_𝑏

− 1

1 − 𝑏

,

𝐹

′′

(𝑏) =

𝑑

2

_𝐹(𝑏)

𝑑𝑏

2

= −

1

2(1 − 𝑏)

2

+

1

2

∑

𝑅

_𝑡−14

(𝑎 + 𝑏𝑅

_𝑡−12

₎

2 𝑇 𝑡=2

− ∑

𝑅

𝑡−1 4

_𝑅

𝑡2

(𝑎 + 𝑏𝑅

_𝑡−12

₎

3

_𝑧

𝑡 𝑇 𝑡=2

−

𝛼

𝑏

− 1

𝑏

2

−

𝛽

𝑏

− 1

(1 − 𝑏)

2

.

Selanjutnya diambil

𝜇

_𝑏∗

= 𝑏̂ dan 𝑉

_𝑏∗

= −[𝐹′′(𝑏̂)]

−1

. Masalahnya adalah

𝐹′′(𝑏̂) bisa

bernilai

positif,

karena

itu

diambil

𝑉

_𝑎∗

= −[𝐷

_𝑏

(𝑏̂)]

−1

dengan

𝐷

_𝑏

(𝑏̂) =

Lampiran 2. Kode Matlab

Lampiran 2.1 Kode Matlab untuk Estimasi Model ARCH Berdistribusi Normal

2.1.1 Kode Utama

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 function hasil=arch_mcmc(Rt,HP)

% Tujuan: Mengestimasi parameter-parameter dalam model ARCH % R_t = sigma_t*epsilon_t, epsilon_t~N(0,1)

% sigma_t^2 = a + b*R_{t-1}^2

% ---% Algoritma: MCMC

% ---% Masukan: Rt = Return = 100*[log(S_t)-log(S_{t-1}],

% dimana S_t = nilai kurs pada saat t

% HP = Hyperparameter = [lambda alpha beta], untuk prior % a ~ exp(lambda) dan b ~ beta(alpha,beta)

% ---% Keluaran: hasil.av = sampel-sampel parameter a

% hasil.bv = sampel-sampel parameter b % Ditulis oleh Imam Malik Safrudin (FSM UKSW) % CP: imammaliks@live.com % --- Inisialisasi T = length(Rt); % prior untuk a lamd = HP(1); % prior untuk b alp = HP(2); bet = HP(3); % nilai awal a = 0.1; b = 0.1; % banyaknya replikasi Nits = 15000; BI = 5000; N = Nits-BI;

% alokasi penyimpanan sampel

av = zeros(N,1); bv = zeros(N,1); vol = zeros(T,1);

% --- Algoritma MCMC. Step 1: Membangkitkan Rantai Markov

tic

for its = 1:Nits

% --- pembangkitan sampel a

% mencari rata-rata dan variansi untuk distribusi proposal

hp1 = lamd;

m_a = bisection(Rt,a,b,hp1,'a'); %rata-rata dengan metode bagi dua

d2a = 0.5/m_a^2-0.5*(1-b)*Rt(1)^2/m_a^3...

-0.5*sum((2*Rt(2:end).^2-m_a-b*Rt(1:end-1).^2)...

./(m_a+b*Rt(1:end-1).^2).^3); Da = min(-0.0001,d2a);

s2_a =-1/Da; % variansi

% algoritma IC-MH

% 1: pembangkitan proposal a*

pr = truncnormrnd(1,m_a,sqrt(s2_a),1e-4,1);

% 2: mengevaluasi probabilitas penerimaan

log_pa = -0.5*log(pr)-0.5*(1-b)*Rt(1)^2/pr...

-0.5*sum(log(pr+b*Rt(1:end-1).^2))...

62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 post_pr = exp(log_pa); log_pa = -0.5*log(a)-0.5*(1-b)*Rt(1)^2/a... -0.5*sum(log(a+b*Rt(1:end-1).^2))... -0.5*sum(Rt(2:end).^2./(a+b*Rt(1:end-1).^2))-lamd*a; %F(a) post_o = exp(log_pa); ratio = post_pr/post_o; ap = min(1,ratio);

% 3: pembangkitan bilangan acak seragam

u = rand(1);

% 4: pembaruan

if u <= ap, a = pr; end

% --- pembangkitan sampel b

% mencari rata-rata dan variansi untuk distribusi proposal

mup = alp; Vp = bet; hp1 = [mup Vp]; m_b = bisection(Rt,a,b,hp1,'b'); % rata-rata d2b = -0.5/(1-m_b)^2+0.5*sum((Rt(1:end-1).^4)... ./((a+m_b*Rt(1:end-1).^2).^2))... -sum(((Rt(1:end-1).^4).*(Rt(2:end).^2))... ./((a+m_b*Rt(1:end-1).^2).^3))... -(alp-1)/m_b^2-(bet-1)/(1-m_b)^2; Db = min(-0.0001,d2b); s2_b = -1/Db; % variansi % algoritma IC-MH % 1: pembangkitan proposal b* pr = truncnormrnd(1,m_b,sqrt(s2_b),0,1);

% 2: mengevaluasi probabilitas penerimaan

log_pb = 0.5*log(1-pr)-0.5*(1-pr)*Rt(1)^2/a... -0.5*sum(log(a+pr*Rt(1:end-1).^2))... -0.5*sum(Rt(2:end).^2./(a+pr*Rt(1:end-1).^2))... +(alp-1)*log(pr)+(bet-1)*log(1-pr); % F(pr) post_pr = exp(log_pb); log_pb = 0.5*log(1-b)-0.5*(1-b)*Rt(1)^2/a... -0.5*sum(log(a+b*Rt(1:end-1).^2))... -0.5*sum(Rt(2:end).^2./(a+b*Rt(1:end-1).^2))... +(alp-1)*log(b)+(bet-1)*log(1-b); %F(b) post_o = exp(log_pb); ratio = post_pr/post_o; ap = min(1,ratio);

% 3: pembangkitan bilangan acak seragam

u = rand(1); % 4: pembaruan if u <= ap, b = pr; end % pengestimasian sigma Volt = a+b*Rt(1:end-1).^2; Volt = [a/(1-b); volt];

% simpan a dan b if its > BI av(its-BI,1) = a; bv(its-BI,1) = b; vol = ((its-BI-1)*vol+volt)/(its-BI); end end toc

% --- Algoritma MCMC. Step 2: Menghitung rata-rata Monte Carlo

draws = [av bv]; MP = mean(draws); SP = std(draws);

130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175

% ===== Integrated Autocorrelation Time (IACT) ============================ % Berapa banyak sampel yang harus dibangkitkan untuk mendapatkan sampel % yang independen (seberapa cepat konvergensi simulasi)

resultsIAT = IACT(draws); IAT = [resultsIAT.iact];

% ===== Uji Konvergensi Geweke ============================================

idraw1 = round(.1*N); resultCV = momentg(draws(1:idraw1,:)); meansa = [resultCV.pmean]; nsea = [resultCV.nse1]; idraw2 = round(.5*N)+1; resultCV = momentg(draws(idraw2:N,:)); meansb = [resultCV.pmean]; nseb = [resultCV.nse1]; CD = (meansa - meansb)./sqrt(nsea+nseb); onetail = 1-normcdf(abs(CD),0,1); pV = 2*onetail;

% ===== 95% Highest Posterior Density (HPD) Interval ======================

resultsHPD = HPD(draws,0.05); LB = [resultsHPD.LB];

UB = [resultsHPD.UB];

% ===== Numerical Standard Error (NSE) ====================================

resultsNSE = NSE(draws); NSEd = [resultsNSE.nse];

%====================== Mengatur hasil pencetakan =========================

%--- Statistik Parameter:

in.cnames = char('a','b');

in.rnames = char('Parameter','Mean','SD','LB','UB','IACT','NSE','G-CD', 'p-Value');

in.fmt = '%16.6f';

tmp = [MP; SP; LB; UB; IAT; NSEd; CD; pV];

fprintf(1,’Estimasi menggunakan MCMC dan Uji Diagnosa\n'); % cetak hasil

mprint(tmp,in); hasil.vol = vol; hasil.av = av; hasil.bv = bv;

2.1.2 Kode bisection

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

function mab = bisection(Rt,a,b,hp1,par)

% Tujuan : Mencari akar dari F’(a)=0 atau F’(b)=0 menggunakan metode % bagi dua % % ---% Masukan : Rt = return % a = nilai a % b = nilai b % hp1 = nilai prior

% par = 'a' atau 'b'

% --- % keluaran : mab = akar penyelesaian

eps_step = 1e-2;

if par == 'a'

bb = 1e-3; ba = 1;

19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 bb = 0; ba = 1; end

if diffARCH(Rt,a,b,hp1,bb,par) == 0 % derivatif pertama

mab = bb; return;

elseif diffARCH (Rt,a,b,hp1,ba,par) == 0

mab = ba; return;

elseif diffARCH(Rt,a,b,hp1,ba,par)*diffARCH(Rt,a,b,hp1,bb,par) > 0 error( 'diffARCH(ba) dan diffARCH(bb) tidak mempunyai tanda berlawanan' );

end

while abs(bb - ba) >= eps_step c = (ba + bb)/2; if diffARCH(Rt,a,b,hp1,c,par) == 0 mab = c; return; elseif diffARCH(Rt,a,b,hp1,c,par)*diffARCH(Rt,a,b,hp1,ba,par) < 0 bb = c; else ba = c; end end mab = c;

2.1.3 Kode untuk turunan pertama F(a) dan F(b)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

function Fab = diffARCH(Rt,a,b,hp1,bts,par)

% Tujuan : Mengitung F’(a) atau F’(b) % % ---% Masukan : Rt = return % a = nilai a % b = nilai b % hp1 = nilai prior

% bts = batas kiri/kanan interval pada metode bagi dua

% par = 'a' atau 'b'

% --- % keluaran : Fab = nilai turunan pertama

if par == 'a'% derivatif pertama terhadap a

a = bts; lamd = hp1;

Fab = -1/(2*a)+(1-b)*Rt(1)^2/(2*a^2)...

-0.5*sum((a+b*Rt(1:end-1).^2-Rt(2:end).^2)...

./(a+b*Rt(1:end-1).^2).^2)-lamd;

elseif par == 'b' % derivatif pertama terhadap b

b = bts; alp = hp1(1); bet=hp1(2); Fab = -1/(2*(1-b))+Rt(1)^2/2*a... -0.5*sum(Rt(1:end-1).^2./(a+b*Rt(1:end-1).^2)) ... +0.5*sum(Rt(1:end-1).^2.*Rt(2:end).^2 ./((a+b*Rt(1:end-1).^2).^2))+(alp-1)/b-(bet-1)/(1-b); end

2.1.4 Kode Pendukung

Kode truncnormrnd, IACT, momentg, HPD, NSE, dan mprint dapat dilihat dalam

Nugroho (2014).

Lampiran 2.2 Kode Matlab untuk Estimasi Model ARCH Berdistribusi Student-t

2.2.1 Kode Utama

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 function hasil=archt_mcmc(Rt,HP)

% Tujuan: Mengestimasi parameter-parameter dalam model ARCH % R_t = sigma_t*z_t^0.5*eta_t, eta_t~N(0,1)

% sigma_t^2 = a + b*R_{t-1}^2

% ---% Algoritma: MCMC

% ---% Masukan: Rt = Return = 100*[log(S_t)-log(S_{t-1}],

% dimana S_t = nilai kurs pada saat t

% HP = Hyperparameter = [lambda alpha beta], untuk prior % a ~ exp(lambda) dan b ~ beta(alpha_b,beta_b)

% ---% Keluaran: hasil.vol = sampel-sampel parameter vol

% Hasil.zv = sampel-sampel parameter z_t % hasil.av = sampel-sampel parameter a % hasil.bv = sampel-sampel parameter b % Hasil.nuv = sampel-sampel parameter nu % Ditulis oleh Imam Malik Safrudin (FSM UKSW) % CP: imammaliks@live.com % --- I: Inisialisasi T = length(Rt); % prior untuk a lamd = HP(1); % prior untuk b alp = HP(2); bet = HP(3); % prior untuk nu alpnu = HP(4); betnu = HP(5); % nilai awal a = 0.1; b = 0.1; nu = 20; % banyaknya replikasi Nits = 15000; BI = 5000; N = Nits-BI;

% alokasi penyimpanan sampel

av = zeros(N,1); bv = zeros(N,1); nuv = zeros(N,1); zv = zeros(T,1); vol = zeros(T,1);

% --- Algoritma MCMC. Step 1: Membangkitkan Rantai Markov

tic

for its = 1:Nits % --- pembangkitan sampel z alpz = (nu+1)/2; betz1 = 0.5*((1-b)*Rt(1)^2+a*nu)/a; betz2T = (Rt(2:end).^2+(a+b*Rt(1:end-1).^2)*nu)... ./(2*(a+b*Rt(1:end-1).^2)); betz = [betz1; betz2T];

z = 1./gamrnd(alpz,1./betz);

% --- pembangkitan sampel nu

% mencari rata-rata dan variansi untuk proposal bersyarat

Hpv = [alpnu betnu];

65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 d2v = 0.5*T/mv-T/4*psi(1,mv/2)-(alpnu-1)/mv^2; Dv = min(-0.0001,d2v); s2v = -1/Dv; %variansi % algoritma IC-MH

% 1: pembangkitan proposal nu*

pr = truncnormrnd(1,mv,sqrt(s2v),2.1,40);

% 2: mengevaluasi probabilitas penerimaan

log_pv = 0.5*pr*T*log(pr/2)-T*gammaln(pr/2)-pr/2... *sum(log(z)+1./z)+(alpnu-1)*log(pr)-betnu*pr; post_pr = exp(log_pv); log_pv = 0.5*nu*T*log(nu/2)-T*gammaln(nu/2)-nu/2... *sum(log(z)+1./z)+(alpnu-1)*log(nu)-betnu*nu; post_o = exp(log_pv); ratio = post_pr/post_o; ap = min(1,ratio);

% 3: pembangkitan variabel acak seragam

u = rand(1); % 4: pembaruan if u <= ap, nu = pr; end nu % --- pembangkitan sampel a

% mencari rata-rata dan variansi untuk distribusi proposal

hp1 = lamd;

m_a = bisection_st(Rt,a,b,hp1,z,'a'); % rata-rata

d2a = 1/(2*m_a^2)-0.5*(1-b)*Rt(1)^2/(m_a^3*z(1))+0.5*...

sum(1./(m_a+b*Rt(1:end-1).^2).^2)-...

sum(Rt(2:end).^2./((m_a+b*Rt(1:end-1).^2).^3.*z(2:end))); Da = min(-0.0001,d2a);

s2_a = -1/Da; % variansi

% algoritma IC-MH

% 1: pembagkitan proposal a*

pr = truncnormrnd(1,m_a,sqrt(s2_a),1e-4,1);

% 2: mengevaluasi probabilitas penerimaan

log_pa = -0.5*log(pr)-0.5*(1-b)*Rt(1)^2/(pr*z(1))-... 0.5*sum(log(pr+b*Rt(1:end-1).^2))-... 0.5*sum(Rt(2:end).^2./((pr+b*Rt(1:end-1).^2).*z(2:end)))-... lamd*pr; % F(pr) post_pr = exp(log_pa); log_pa = -0.5*log(a)-0.5*(1-b)*Rt(1)^2/(a*z(1))-... 0.5*sum(log(a+b*Rt(1:end-1).^2))-... 0.5*sum(Rt(2:end).^2./((a+b*Rt(1:end-1).^2).*z(2:end)))-... lamd*a; % F(a) post_o = exp(log_pa); ratio = post_pr/post_o; ap = min(1,ratio);

% 3: pembangkitan variabel acak seragam

u = rand(1); % 4: pembaruan

if u <= ap, a = pr; end

% --- pembangkitan sampel b

% mencari rata-rata dan variansi untuk distribusi proposal

mup = alp; Vp = bet; hp1 = [mup Vp]; m_b = bisection_st(Rt,a,b,hp1,z,'b'); % rata-rata d2b = -0.5/(1-m_b)^2+0.5*sum((Rt(1:end-1).^4)... ./((a+m_b*Rt(1:end-1).^2).^2))... -sum(((Rt(1:end-1).^4).*(Rt(2:end).^2))... ./((a+m_b*Rt(1:end-1).^2).^3.*z(2:end)))... -(alp-1)/m_b^2-(bet-1)/(1-m_b)^2; Db = min(-0.0001,d2b);

133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 s2_b = -1/Db; % variansi % algoritma IC-MH % 1: pembangkitan proposal b* pr = truncnormrnd(1,m_b,sqrt(s2_b),0,1);

% 2: mengevaluasi probabilitas penerimaan

log_pb = 0.5*log(1-pr)-0.5*(1-pr)*Rt(1)^2/(a*z(1))-... 0.5*sum(log(a+pr*Rt(1:end-1).^2))-... 0.5*sum(Rt(2:end).^2./(a+pr*Rt(1:end-1).^2.*z(2:end)))... +(alp-1)*log(pr)+(bet-1)*log(1-pr); % F(pr) post_pr = exp(log_pb); log_pb = 0.5*log(1-b)-0.5*(1-b)*Rt(1)^2/(a*z(1))-... 0.5*sum(log(a+b*Rt(1:end-1).^2))-... 0.5*sum(Rt(2:end).^2./(a+b*Rt(1:end-1).^2.*z(2:end)))... +(alp-1)*log(b)+(bet-1)*log(1-b); %F(b) post_o = exp(log_pb); ratio = post_pr/post_o; ap = min(1,ratio);

% 3: pembangkitan variabel acak seragam

u = rand(1); % 4: pembaruan if u <= ap, b = pr; end % pengestimasian sigma volt = a+b*Rt(1:end-1).^2; volt = [a/(1-b); volt]; % simpan a dan b if its > BI av(its-BI,1) = a; bv(its-BI,1) = b; nuv(its-BI,1) = nu; zv = ((its-BI-1)*zv+z)/(its-BI); vol = ((its-BI-1)*vol+volt)/(its-BI); end end toc

% --- Algoritma MCMC. Step 2: Menghitung rata-rata Monte Carlo

draws = [av bv nuv]; MP = mean(draws); SP = std(draws);

% ===== Integrated Autocorrelation Time (IACT) ============================ % Berapa banyak sampel yang harus dibangkitkan untuk mendapatkan sampel % yang independen (seberapa cepat konvergensi simulasi)

resultsIAT = IACT(draws); IAT = [resultsIAT.iact];

% ===== Uji Konvergensi Geweke ============================================

idraw1 = round(.1*N); resultCV = momentg(draws(1:idraw1,:)); meansa = [resultCV.pmean]; nsea = [resultCV.nse1]; idraw2 = round(.5*N)+1; resultCV = momentg(draws(idraw2:N,:)); meansb = [resultCV.pmean]; nseb = [resultCV.nse1]; CD = (meansa - meansb)./sqrt(nsea+nseb); onetail = 1-normcdf(abs(CD),0,1); pV = 2*onetail;

% ===== 95% Highest Posterior Density (HPD) Interval ======================