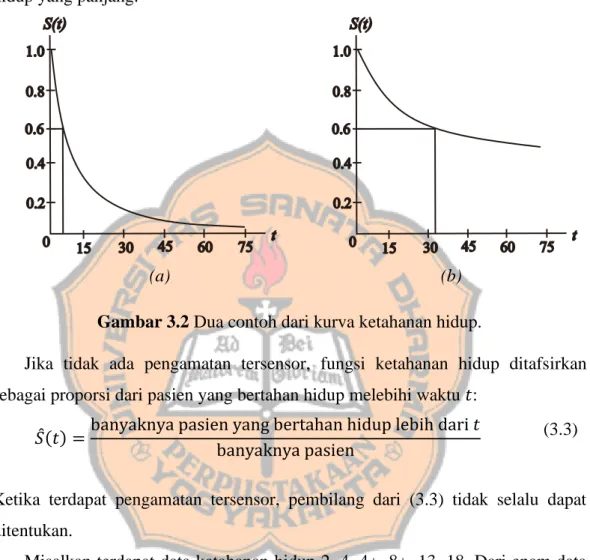
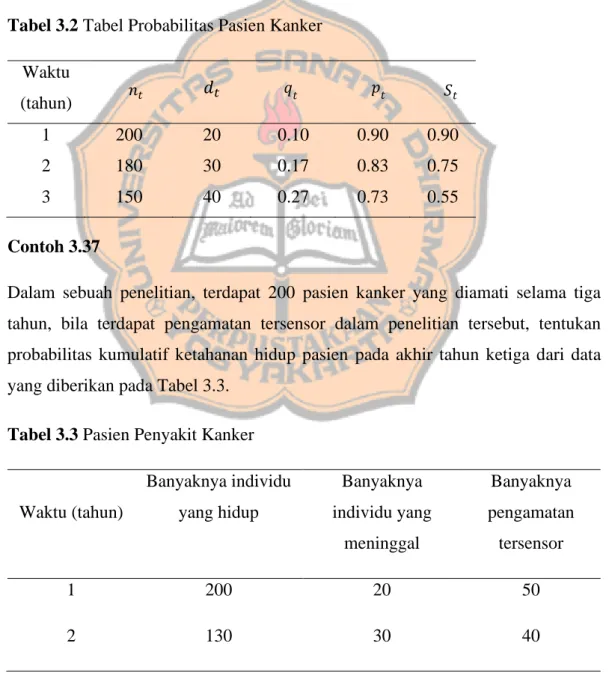
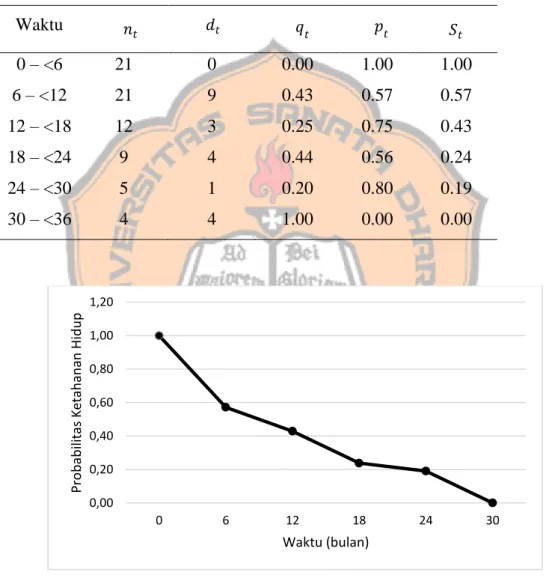
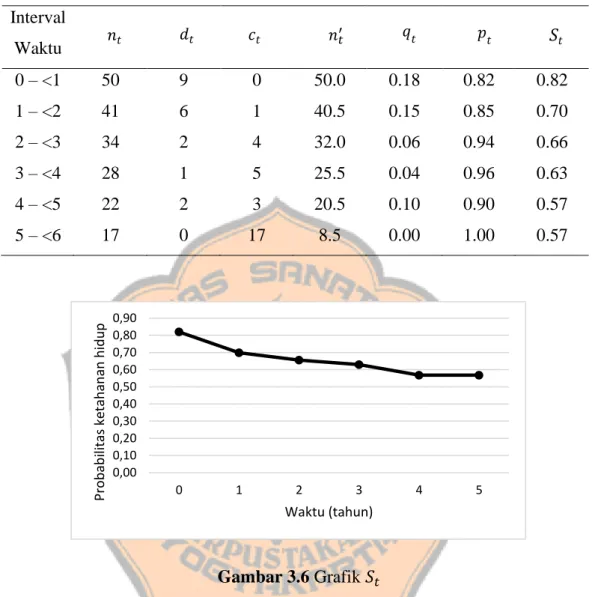
METODE TABEL KEHIDUPAN UNTUK MENENTUKAN FUNGSI KETAHANAN HIDUP
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Theresia Ardya Resti Pradwiningtyas NIM: 163114006
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA 2020
Life Table Method to Determine Survival Function
Thesis
Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Mathematics
Mathematics Study Program
Written by:
Theresia Ardya Resti Pradwiningtyas Student ID: 163114006
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
vi MOTTO
“Inilah Aku, Utuslah Aku!” (Yesaya 6:8)
“Janganlah katakan: Aku ini masih muda, tetapi kepada siapa pun engkau Kuutus, haruslah engkau pergi, dan apa pun yang Kuperintahkan kepadamu, haruslah kausampaikan. Janganlah takut kepada mereka, sebab Aku menyertai engkau,
vii
HALAMAN PERSEMBAHAN Karya ini kupersembahkan untuk:
Tuhan Yesus Kristus, kedua orang tua dan keluargaku, almamaterku dan semua orang yang menyayangi dan selalu mendoakanku.
ix ABSTRAK
Analisis ketahanan hidup merupakan metode statistika yang mengamati tentang kejadian dan waktu kejadian dari awal sampai berakhirnya suatu kejadian. Data ketahanan hidup dapat meliputi waktu bertahan hidup, respon terhadap obat yang diberikan dan karakteristik pasien terkait dengan respon, ketahanan hidup, dan perkembangan suatu penyakit. Data ketahanan hidup biasanya tidak dapat diketahui sepenuhnya, hal ini disebut dengan pengamatan tersensor. Metode tabel kehidupan digunakan untuk menduga ketahanan hidup pasien. Dalam aplikasi metode tabel kehidupan digunakan data pasien kanker payudara pada tahun 2014-2016 di Rumah Sakit Panti Rapih Yogyakarta.
Pada tugas akhir ini, dibentuk tabel kehidupan pasien kanker payudara yang mengikuti kemoterapi dan yang tidak mengikuti kemoterapi dengan interval waktu tertentu. Tabel kehidupan memberikan penduga ketahanan hidup pasien kanker payudara yang mengikuti kemoterapi dan yang tidak mengikuti kemoterapi. Dari pembahasan, dapat disimpulkan bahwa probabilitas ketahanan pasien kanker payudara pada tahun 2014-2016 di Rumah Sakit Panti Rapih Yogyakarta yang mengikuti kemoterapi memiliki peluang bertahan hidup yang lebih tinggi daripada pasien yang tidak mengikuti kemoterapi. Kemoterapi dapat meningkatkan waktu ketahanan hidup atau dapat memperpanjang waktu hidup pasien kanker payudara. Kata Kunci: tabel kehidupan, tersensor, kemoterapi
x ABSTRACT
Survival Analysis is a statistical method that observes events and time of events from the beginning to the end of the event. Survival data may include survival time, responding to the medicine given, and patient response characteristics, survival and disease progression. Survival data is generally not fully known, this is called censored observation. The life table method is used to estimate the survival of the patient. Data from breast cancer patients at (the) Panti Rapih Hospital, Yogyakarta in 204-2016 were used for the application of the life table method.
In this final project, a life table was established for a patient with breast cancer who do not take chemotherapy and does not take chemotherapy at specific time intervals. The life table provides a survival estimator from a patient with breast cancer who take chemotherapy and do not take chemotherapy. From the discussion, It can be concluded that the recovery probability of breast cancer patients at the Panti Rapih Hospital, Yogyakarta in 2014-2016 who took chemotherapy has a higher chance of survival than patients who did not take chemotherapy. Chemotherapy may increase the survival time or extend the lifetime of patients with breast cancer.
xiii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
MOTTO ... vi
HALAMAN PERSEMBAHAN ... vii
LEMBAR PERNYATAAN PERSETUJUAN ... viii
ABSTRAK ... ix
ABSTRACT ... x
KATA PENGANTAR ... xi
DAFTAR ISI ... xiii
BAB I PENDAHULUAN...1
A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 2 C. Batasan Masalah ... 3 D. Tujuan Penulisan ... 3 E. Manfaat Penulisan ... 3 F. Metode Penelitian ... 3 G. Sistematika Penulisan ... 3
BAB II DISTRIBUSI PROBABILITAS...6
A. Probabilitas ... 6
1. Probabilitas dari Suatu Kejadian ... 6
2. Probabilitas Bersyarat ... 7
3. Variabel Acak ... 9
B. Distribusi Probabilitas ... 10
1. Distribusi Probabilitas Diskrit... 10
2. Distribusi Probabilitas Kontinu ... 13
3. Nilai Harapan ... 15
4. Variansi ... 20
5. Fungsi Pembangkit Momen ... 23
6. Metode Fungsi Pembangkit Momen ... 26
xiv
D. Teorema Limit Pusat... 34
E. Pendugaan Parameter... 35
F. Metode Kemungkinan Maksimum (Maximum Likelihood) ... 41
BAB III METODE TABEL KEHIDUPAN ... 43
A. Analisis Ketahanan Hidup ... 43
B. Data Tersensor ... 44
1. Penyensoran Kanan ... 44
2. Penyensoran Kiri ... 45
3. Penyensoran Interval ... 46
C. Fungsi Ketahanan Hidup (Survival Function) ... 46
D. Fungsi Densitas Ketahanan Hidup... 49
E. Fungsi Hazard (Hazard Function) ... 50
F. Distribusi Waktu Ketahanan Hidup Waktu Kontinu ... 55
G. Distribusi Waktu Ketahanan Hidup Waktu Diskrit ... 57
H. Tabel Kehidupan ... 59
1. Tabel Kehidupan Populasi ... 59
2. Tabel Kehidupan Klinis ... 65
I. Fungsi Ketahanan Hidup berdasarkan Tabel Kehidupan ... 71
BAB IV APLIKASI METODE TABEL KEHIDUPAN UNTUK MENENTUKAN FUNGSI KETAHANAN HIDUP ... 80
A. Kanker... 80
B. Sumber Data ... 82
C. Ketahanan Hidup Pasien Penderita Kanker Payudara ... 85
1. Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016 ... 86
2. Ketahanan Hidup Pasien Kanker Payudara 2014-2016 yang Tidak Mengikuti Kemoterapi. ... 87
3. Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016 yang Mengikuti Kemoterapi. ... 89
4. Perbandingan Ketahanan Hidup Pasien Kanker Payudara Tahun 2014-2016 yang Mengikuti Kemoterapi dan Tidak Mengikuti Kemoterapi. ... 90
5. Ketahanan Hidup Pasien Kanker Payudara Stadium 2 Tahun 2014-2016 ...91
6. Ketahanan Hidup Pasien Kanker Payudara Stadium 3 Tahun 2014-2016 ...92
7. Ketahanan Hidup Pasien Kanker Payudara Stadium 4 Tahun 2014-2016. ...92
xv
8. Ketahanan Hidup Pasien Kanker Payudara Stadium 4 yang Tidak
Mngikuti Kemoterapi Tahun 2014-2016... 93
9. Ketahanan Hidup Pasien Kanker Payudara Stadium 4 yang Mngikuti Kemoterapi Tahun 2014-2016. ... 95
10. Perbandingan Ketahanan Hidup Pasien Kanker Payudara Stadium 4 yang Tidak Mngikuti Kemoterapi dan Mengikuti Kemoterapi Tahun 2014-2016...96
11. Perbandingan Ketahanan Hidup Pasien Kanker Payudara Stadium 4 yang Tidak Mngikuti Kemoterapi dan Mengikuti Kemoterapi Tahun 2014-2016...98
12. Perbandingan Ketahanan Hidup Pasien Kanker Payudara Stadium 4 yang Tidak Mngikuti Kemoterapi dan Mengikuti Kemoterapi Tahun 2014-2016...99
BAB V PENUTUP ... 102
DAFTAR PUSTAKA ... 104
1 BAB I PENDAHULUAN A. Latar Belakang Masalah
Penyakit kanker merupakan salah satu penyakit yang angka kematiannya te-rus meningkat di dunia. Kanker paru-paru, payudara, kolorektal, prostat, kulit dan perut adalah jenis kanker yang paling umum terjadi. Kematian yang disebabkan oleh kanker disebabkan oleh beberapa faktor risiko antara lain indeks massa tumbuh yang tinggi, faktor genetik, faktor karsinogen diantaranya yaitu zat kimia, radiasi, virus, hormon, dan iritasi kronis, serta faktor perilaku atau gaya hidup diantaranya pola makan yang tidak sehat, konsumsi alkohol, dan kurang aktivitas fisik. Salah satu metode utama yang digunakan untuk mengatasi kanker yaitu kemoterapi.
Analisis ketahanan hidup merupakan sebuah metode statistika yang mempelajari kejadian dan waktu kejadian. Waktu ketahanan hidup didefinisikan secara luas sebagai waktu terjadinya suatu kejadian. Dalam bidang kesehatan, kejadian yang dimaksud seperti kambuhnya suatu penyakit, kesembuhan dari penyakit yang diderita bahkan kematian seseorang. Fungsi ketahanan adalah peluang seseorang dapat bertahan lebih dari waktu yang ditentukan.
Tabel Kehidupan merupakan tabel yang memberikan pengukuran untuk angka kematian dan menggambarkan ketahanan hidup dalam suatu populasi. Terdapat dua jenis tabel kehidupan, yang pertama tabel kehidupan populasi dan tabel kehidupan klinis. Tabel kehidupan populasi digunakan untuk menggambarkan angka kematian suatu populasi tertentu. Tabel kehidupan klinis merupakan tabel yang dikonstruksikan untuk pasien.
Data yang diperoleh dapat berupa data tidak tersensor atau data tersensor. Data tidak tersensor merupakan data yang dapat tercatat secara lengkap dan jelas yang diperoleh dari setiap perkembangan individu dalam sampel dari awal penelitian sampai individu yang mengalami kegagalan (meninggal dunia). Dalam kenyataannya, pengamatan yang dilakukan dari setiap individu dalam sampel membutuhkan waktu yang sangat lama, sehingga menjadi tidak efisien. Data seperti
ini disebut dengan data tersensor. Data tersensor merupakan data yang tidak dapat tercatat secara lengkap dan jelas dari awal penelitian sampai penelitian berakhir. Banyak faktor yang dapat menyebabkan data tidak dapat tercatat secara lengkap. Faktor-faktor tersebut antara lain individu yang diamati tidak mengalami kejadian sampai penelitian berakhir, misalkan individu telah dinyatakan sembuh sebelum penelitian berakhir, selanjutnya individu menghilang selama masa penelitian berlangsung, misalkan individu yang sedang diteliti pindah atau menolak untuk diamati, dan individu terpaksa diberhentikan dari penelitian karena meninggal sebelum penelitian berkahir.
Dalam tugas akhir ini, penulis menggunakan data hasil penelitian Girik Allo, Caecilia B. (2017). Data yang digunakan merupakan data yang diperoleh dari hasil data rekam medik rumah sakit yaitu pasien penderita kanker payudara pada tahun 2014-2016 di Rumah Sakit Panti Rapih Yogyakarta. Data yang telah didapat kemudian dikelompokkan antara penderita kanker payudara yang melakukan kemoterapi dan yang tidak melakukan kemoterapi. Selanjutnya, dengan menggunakan metode tabel kehidupan akan dicari peluang bertahan hidup penderita kanker yang melakukan kemoterapi dan yang tidak melakukan kemoterapi. Dari peluang yang dihasilkan, dapat dilihat apakah dengan melakukan kemoterapi peluang bertahan hidup lebih besar daripada yang tidak melakukan kemoterapi.
B. Rumusan Masalah
Perumusan masalah dalam tugas akhir ini adalah sebagai berikut: 1. Apa itu metode tabel kehidupan?
2. Bagaimana menentukan fungsi-fungsi dasar untuk mengonstruksi metode tabel kehidupan?
3. Bagaimana konstruksi metode tabel kehidupan dalam bidang kesehatan, khususnya untuk menduga ketahanan hidup pasien?
C. Batasan Masalah
Batasan masalah dalam tugas akhir ini adalah sebagai berikut: 1. Data yang digunakan merupakan data tersensor acak.
2. Teorema Ketunggalan Distribusi Probabilitas tidak dibuktikan.
3. Teori probabilitas yang dibahas hanya yang berkaitan dengan materi pokok. 4. Data yang digunakan dalam analisis bab IV menggunakan data hasil penelitian
dari Girik Allo, Caecilia B.(2017). D. Tujuan Penulisan
Tujuan penulisan dalam tugas akhir ini adalah:
1. Mengetahui model yang digunakan dalam metode tabel kehidupan dalam bidang kesehatan.
2. Dapat menentukan fungsi-fungsi dasar untuk mengkonstruksi metode tabel kehidupan.
3. Mengetahui penerapan metode tabel kehidupan untuk menduga ketahanan hidup pasien.
E. Manfaat Penulisan
Manfaat yang diharapkan dari penulisan tugas akhir ini adalah menambah wawasan mengenai ilmu statistik dalam hal penerapan metode tabel kehidupan kepada penulis khususnya dan kepada pembaca pada umumnya.
F. Metode Penelitian
Metode penulisan yang digunakan dalam tugas akhir ini adalah studi pustaka. Studi pustaka dilakukan dengan cara mencari dan membaca buku-buku atau jurnal-jurnal yang isinya berkaitan dengan analisis data ketahanan hidup dengan metode tabel kehidupan.
G. Sistematika Penulisan
BAB I PENDAHULUAN A. Latar Belakang Masalah B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian G. Sistematika Penulisan
BAB II DISTRIBUSI PROBABILITAS A. Probabilitas
B. Distribusi Probabilitas
C. Distribusi Probabilitas Multivariat D. Teorema Limit Pusat
E. Pendugaan Parameter
F. Metode Kemungkinan Maksimum BAB III METODE TABEL KEHIDUPAN A. Analisis Ketahanan Hidup
B. Data Tersensor
C. Fungsi Ketahanan Hidup (Survival Function) D. Fungsi Densitas Ketahanan Hidup
E. Fungsi Hazard (Hazard Function)
F. Distribusi Waktu Ketahanan Hidup Waktu Kontinu G. Distribusi Waktu Ketahanan Hidup Waktu Diskrit H. Tabel Kehidupan
I. Fungsi Ketahanan Hidup berdasarkan Tabel Kehidupan
BAB IV APLIKASI METODE TABEL KEHIDUPAN UNTUK MENENTUKAN FUNGSI KETAHANAN HIDUP A. Kanker
B. Sumber Data
C. Ketahanan Hidup Pasien Penderita Kanker Payudara BAB V PENUTUP
A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
6 BAB II
DISTRIBUSI PROBABILITAS A. Probabilitas
1. Probabilitas dari Suatu Kejadian Definisi 2.1
Misalkan 𝑆 adalah ruang sampel dari sebuah eksperimen. Untuk kejadian 𝐴 di dalam 𝑆 (𝐴 adalah subset dari 𝑆), maka yang disebut 𝑃(𝐴) adalah peluang kejadian 𝐴, bila memenuhi aksioma berikut:
Aksioma 1: 𝑃(𝐴) ≥ 0. Aksioma 2: 𝑃(𝑆) = 1.
Aksioma 3: Jika 𝐴1, 𝐴2, 𝐴3, … adalah barisan kejadian yang saling asing (𝐴𝑖 ∩ 𝐴𝑗 =
∅, 𝑖 ≠ 𝑗), maka 𝑃(𝐴1∪ 𝐴2 ∪ 𝐴3∪ … ) = ⋃𝑖=1∞ 𝑃(𝐴𝑖) = ∑∞𝑖=1𝑃(𝐴𝑖).
Contoh 2.1
Sebuah kendaraan sampai pada sautu perempatan dapat belok ke kanan, belok ke kiri atau terus. Sebuah eksperimen mengobservasi pergerakan dari kendaraan tersebut melalui perempatan.
a. Daftarkan anggota ruang sampel dari percobaan tersebut!
b. Jika titik-titik sampel berpeluang sama. Tentukan peluang masing-masing kejadian!
Jawab:
a. Ruang sampel percobaan 𝑆 adalah {𝐸1, 𝐸2, 𝐸3}
Didefinisikan 𝐸1 adalah kejadian kendaraan belok kanan, 𝐸2 adalah kejadian
kendaraan belok kiri dan 𝐸3 adalah kejadian kendaraan terus. b. 𝑃(𝑆) = {𝑃(𝐸1), 𝑃(𝐸2), 𝑃(𝐸3)}.
Diketahui bahwa 𝑃(𝐸1) = 𝑃(𝐸2) = 𝑃(𝐸3).
𝑃(𝑆) = 𝑃(𝐸1) + 𝑃(𝐸2) + 𝑃(𝐸3).
𝑃(𝐸1) + 𝑃(𝐸2) + 𝑃(𝐸3) = 1. 𝑃(𝐸1) + 𝑃(𝐸1) + 𝑃(𝐸1) = 1. 3𝑃(𝐸1) = 1. 𝑃(𝐸1) =13. Sehingga diperoleh: 𝑃(𝐸1) = 𝑃(𝐸2) = 𝑃(𝐸3) =1 3.
Jadi, masing-masing kegiatan memiliki peluang 1
3.
2. Probabilitas Bersyarat Definisi 2.2
Peluang bersyarat adalah suatu kejadian 𝐴, bila diketahui kejadian 𝐵 terjadi, adalah 𝑃(𝐴|𝐵) =𝑃(𝐴 ∩ 𝐵)
𝑃(𝐵) ,
asalkan 𝑃(𝐵) > 0. Simbol 𝑃(𝐴|𝐵) dibaca “Probabilitas bersyarat 𝐴 jika diketahui kejadian 𝐵 terjadi”.
Contoh 2.2
Kita melemparkan dua dadu seimbang, dan misalkan 𝐴 adalah kejadian jumlahan angka yang muncul dari kedua dadu adalah 8, dan 𝐵 adalah kejadian angka pertama yang muncul adalah 3. Hitunglah 𝑃(𝐴|𝐵).
Solusi
Elemen-elemen dari kejadian 𝐴 dan 𝐵 adalah
𝐴 = {(2,6), (6,2), (3,5), (5,3), (4,4)}. dan 𝐵 = {(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)}. Diperoleh 𝐴 ∩ 𝐵 = {3,5)} Sehingga 𝑃(𝐴) = 5 36,
𝑃(𝐵) = 6 36= 1 6, dan 𝑃(𝐴 ∩ 𝐵) = 1 36.
Maka dari itu,
𝑃(𝐴|𝐵) = 𝑃(𝐴∩𝐵) 𝑃(𝐵) = 1 36 ⁄ 1 6 ⁄ = 1 6. Definisi 2.3
Dua kejadian 𝐴 dan 𝐵 dikatakan saling bebas jika salah satu dari syarat berikut terpenuhi:
𝑃(𝐴|𝐵) = 𝑃(𝐴), 𝑃(𝐵|𝐴) = 𝑃(𝐵), 𝑃(𝐴⋂𝐵) = 𝑃(𝐴)𝑃(𝐵). Jika tidak, 𝐴 dan 𝐵 saling bergantung.
Contoh 2.3
Dari Contoh 2.2 apakah kejadian 𝐴 dan 𝐵 saling bebas? Solusi:
Dari Contoh 2.2 diperoleh 𝑃(𝐴) = 5 36, 𝑃(𝐵) = 6 36= 1 6, dan 𝑃(𝐴 ∩ 𝐵) = 1 36. Sehingga, 𝑃(𝐴 ∩ 𝐵) = 1 36 ≠ 𝑃(𝐴)𝑃(𝐵) Jadi, kejadian 𝐴 dan 𝐵 tidak saling bebas.
3. Variabel Acak Definisi 2.4
Variabel acak 𝑋 adalah fungsi yang didefinisikan pada ruang sampel 𝑆, yang memetakan setiap elemen dalam 𝑆 ke bilangan real, 𝑋(𝜔) = 𝑥, dengan 𝜔 di dalam 𝑆.
Definisi 2.5
Variabel acak 𝑋 dikatakan diskrit jika nilai-nilainya berhingga atau tak berhingga terbilang dari nilai-nilai yang berbeda. Jika tidak memenuhi kondisi tersebut, maka variabel acak 𝑋 dikatakan kontinu.
Contoh 2.4
Sebuah dadu empat sisi memiliki nomor yang berbeda, 1, 2, 3, atau 4 terletak pada setiap sisi. Pada setiap pelemparan yang diberikan, kejadian untuk masing-masing keempat angka tersebut memiliki kemungkinan yang sama. Sebuah permainan terdiri dari melempar dadu dua kali, dan skornya adalah maksimum dari kedua angka yang terjadi.
Solusi:
Dari informasi tersebut dapat diketahui himpunan nilai yang mungkin terjadi dan menentukan variabel acak. Jika 𝜔 = (𝑖, 𝑗), dimana 𝑖, 𝑗 ∈ {1, 2, 3, 4}, maka 𝑋(𝜔) = 𝑚𝑎𝑘𝑠(𝑖, 𝑗). Ruang sampel, 𝑆, dan 𝑋 diilustrasikan pada Gambar 2.1.
Ruang sampel percobaan adalah 𝑆 =
{(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}. Setiap elemen dari 𝑆 dipetakan ke ℝ adalah variabel acak 𝑋 seperti berikut:
𝑆 (1,4) (2,4) (3,4) (4,4) (1,3) (2,3) (3,3) (4,3) (1,2) (2,2) (3,2) (4,2) (1,1) (2,1) (3,1) (4,1) 𝑋 1 2 3 4 𝑥 B. Distribusi Probabilitas 1. Distribusi Probabilitas Diskrit Definisi 2.6
Distribusi probabilitas untuk variabel diskrit 𝑋 dapat direpresentasikan dengan rumus, tabel, atau grafik yang memberikan 𝑝(𝑥) = 𝑃(𝑋 = 𝑥) untuk semua 𝑥. Contoh 2.5
Terdapat tiga pria dan tiga wanita. Dipilih dua secara acak pekerjaan khusus di sebuah perusahaan. 𝑋 adalah banyaknya wanita yang dipilih. Tentukan distribusi probabilitas dari 𝑋.
Solusi:
𝑋: banyaknya wanita yang terpilih. Hanya akan dipilih dua secara acak, sehingga kemungkinan nilai 𝑋 adalah 0 , 1, atau 2.
𝑋 = 0 → 𝑃(0) =( 3 0)( 3 2) (62) = 1 5 𝑋 = 1 → 𝑃(1) =( 3 1)( 3 1) (62) = 3 5 𝑋 = 2 → 𝑃(2) = ( 3 2) (62)= 1 5 Tabel 2.1 Distribusi Probabilitas Contoh 2.5
𝑥 𝑝(𝑥)
0 1/5
1 3/5
2 1/5
Definisi 2.7
Untuk setiap distribusi probabilitas diskrit, memenuhi pernyataan berikut: 1. 0 ≤ 𝑝(𝑥) ≤ 1, untuk semua 𝑥.
2. ∑𝑥𝑝(𝑥) = 1. Definisi 2.8
Fungsi distribusi kumulatif variabel acak 𝑋 didefinisikan sebagai berikut 𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥)
= ∑𝑋≤𝑥𝑝(𝑥), untuk −∞ < 𝑥 < ∞ Contoh 2.6
Tentukan fungsi distribusi kumulatif dari variabel acak 𝑋 pada Contoh 2.5. Solusi:
Dari Contoh 2.5 diperoleh 𝑃(0) =1
5, 𝑃(1) = 3 5, dan 𝑃(2) = 1 5. Selanjutnya akan dicari 𝐹(0), 𝐹(1), dan 𝐹(2).
𝐹(0) =1 5, 𝐹(1) = 1 5+ 3 5= 4 5, 𝐹(2) = 1 5+ 3 5+ 1 5= 1, sehingga 𝐹(𝑥) = { 0 , 𝑥 < 0 1 5 , 0 ≤ 𝑥 < 1 4 5 ,1 ≤ 𝑥 < 2 1 , 𝑥 ≥ 2 Definisi 2.9
Percobaan Binomial memiliki sifat-sifat berikut: 1. Percobaan terdiri atas 𝑛 ulangan yang identik.
2. Masing-masing ulangan menghasilkan salah satu dari dua kemungkinan hasil, yaitu “sukses” atau “gagal”.
3. Peluang sukses dari setiap ulangan adalah 𝑝, peluang gagal adalah 𝑞 = 1 − 𝑝. 4. Antar ulangan saling bebas.
5. Variabel acak 𝑋 merupakan banyaknya sukses dari 𝑛 ulangan Contoh 2.7
Sebuah mata uang seimbang dilemparkan sebanyak tiga kali. Untuk mendapatkan tepat dua angka yaitu AAG, AGA dan GAA kita dapatkan peluangnya adalah 3
8.
Apakah hal tersebut merupakan percobaan Binomial? Solusi:
Untuk mengetahui apakah hal tersebut merupakan percobaan Binomial, harus ditentukan apakah lima persyaratan dari Definisi 2.9 terpenuhi atau tidak.
1. Terdapat 𝑛 = 3 kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah 1
2 di setiap percobaannya.
Definisi 2.10
Variabel acak 𝑋 dikatakan memiliki distribusi probabilitas Binomial berdasarkan 𝑛 ulangan dengan probabilitas sukses 𝑝 jika dan hanya jika
𝑝(𝑥) = (𝑛𝑥)𝑝𝑥𝑞𝑛−𝑥, 𝑥 = 0, 1, 2, . . . , 𝑛 dan 0 ≤ 𝑝 ≤ 1.
Contoh 2.8
Diketahui bahwa sekrup yang diproduksi oleh mesin tertentu akan rusak dengan probabilitas 0.01 secara independen satu sama lain. Jika kita memilih secara acak 10 sekrup yang diproduksi oleh mesin tersebut, berapa probabilitas setidaknya dua sekrup akan rusak?
Solusi:
𝑋: banyaknya sekrup yang rusak dari 10 sekrup yang diambil secara acak. Diketahui 𝑝 = 0.01 𝑞 = 1 − 𝑝 = 1 − 0.01 = 0.99 𝑃(𝑋 ≥ 2) = ∑ (10 𝑥) (0.01) 𝑥(0.99)10−𝑥 10 𝑥=2 = 1 − [𝑃(𝑋 = 0) + 𝑃(𝑋 = 1)] = 0.004.
2. Distribusi Probabilitas Kontinu Definisi 2.11
Fungsi 𝑓(𝑥) dikatakan sebagai distribusi probabilitas variabel acak kontinu (Fungsi Densitas) jika memenuhi:
1. ∫−∞∞ 𝑓(𝑥)𝑑𝑥 = 1, 2. 𝑓(𝑥) ≥ 0
Contoh 2.9
Misalkan 𝑋 merupakan variabel acak kontinu dengan fungsi probabilitas densitas sebagai berikut
𝑓(𝑥) = {3𝑥2, 0 ≤ 𝑥 < 1 0 , selainnya. Buktikan bahwa𝑓(𝑥) adalah fungsi probabilitas densitas. Solusi:
Akan dibuktikan 𝑓(𝑥) memenuhi Definisi 2.11 1. 𝑓(𝑥) ≥ 0 jelas terlihat dari definisi 𝑓(𝑥). 2. ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 3𝑥1 2𝑑𝑥 0 ∞ −∞ = 𝑥 3| 0 1 = 1 − 0 = 1.
Jadi, terbukti bahwa 𝑓(𝑥) adalah fungsi probabilitas densitas. Definisi 2.12
Fungsi distribusi kumulatif 𝐹(𝑥) dari variabel acak kontinu 𝑋 adalah 𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) = ∫ 𝑓(𝑡)𝑑𝑡
𝑥
−∞
. Akibat dari definisi 2.12
Jika kita memiliki fungsi distribusi kumulatif 𝐹(𝑥), maka kita punya 𝑃(𝑎 < 𝑋 < 𝑏) = 𝐹(𝑏) − 𝐹(𝑎) dan
𝑑𝐹(𝑥)
𝑑𝑥 = 𝑓(𝑥) jika turunannya ada.
Contoh 2.10
Tentukan fungsi distribusi kumulatif dari Contoh 2.9 dan tentukan 𝑃(0 < 𝑋 < 1). untuk 𝑥 < 0 𝐹(𝑥) = ∫ 0 𝑑𝑡 = 0 𝑥 −∞ . untuk 0 ≤ 𝑥 < 1 𝐹(𝑥) = ∫ 𝑓(𝑡)𝑑𝑡 = ∫ 0𝑑𝑡 + ∫ 3𝑡2𝑑𝑡 𝑥 0 = 0 + 𝑡3| 0𝑥= 𝑥3 0 −∞ 𝑥 −∞ . untuk 𝑥 ≥ 1
𝐹(𝑥) = ∫ 𝑓(𝑡)𝑑𝑡 = ∫ 0𝑑𝑡 + ∫ 3𝑡2𝑑𝑡 + ∫ 0𝑑𝑡 𝑥 1 1 0 = 0 + 𝑡3+ 0|01 = 1 0 −∞ 𝑥 −∞ . Jadi, 𝐹(𝑥) = { 0, 𝑥 < 0 𝑥3, 0 ≤ 𝑥 < 1 1, 𝑥 ≥ 1 Sekarang 𝑃(0 < 𝑋 < 1) = 𝐹(1) − 𝐹(0) = 1 − 0 = 1. Definisi 2.13
Variabel acak 𝑋 dikatakan berdistribusi Normal dengan parameter 𝜇 dan 𝜎 bila fungsi probabilitas densitasnya adalah
𝑓(𝑥) = 1 √2𝜋𝜎𝑒 −12(𝑥−𝜇𝜎 )2 , −∞ < 𝑥 < ∞, 𝜎 > 0. 3. Nilai Harapan Definisi 2.14
Misalkan 𝑋 adalah variabel acak diskret dengan fungsi probabilitas 𝑝(𝑥). Nilai harapan dari 𝑋 dinotasikan dengan 𝐸(𝑋), didefinisikan sebagai
𝜇 = 𝐸(𝑋) = ∑ 𝑥𝑝(𝑥)
𝑥
Contoh 2.11
Tentukan nilai harapan dari Contoh 2.5 Solusi: 𝐸(𝑋) = 01 5+ 1 3 5+ 2 1 5= 1. Definisi 2.15
𝐸(𝑋) = ∫ 𝑥𝑓(𝑥)𝑑𝑥
∞
−∞
asalkan integral ada. Contoh 2.12
Tentukan nilai harapan dari Contoh 2.9 Solusi: 𝐸(𝑋) = ∫ 𝑥3𝑥2𝑑𝑥 1 0 = ∫ 3𝑥3𝑑𝑥 =3 4. 1 0 Teorema 2.1
Misalkan 𝑋 adalah variabel acak diskrit dengan fungsi probabilitas 𝑝(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋. Maka
𝐸[𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]. Bukti: 𝐸[𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = ∑[𝑔1(𝑥) + 𝑔2(𝑥) + ⋯ + 𝑔𝑘(𝑥)] 𝑥 𝑓(𝑥) = ∑[𝑔1(𝑥)𝑓(𝑥) + 𝑔2(𝑥)𝑓(𝑥) + ⋯ + 𝑔𝑘(𝑥)𝑓(𝑥)] 𝑥 = ∑ 𝑔1(𝑥)𝑓(𝑥) 𝑥 + ∑ 𝑔2(𝑥)𝑓(𝑥) 𝑥 + ⋯ + ∑ 𝑔𝑘(𝑥)𝑓(𝑥) 𝑥 = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]. ∎ Teorema 2.2
Misalkan 𝑋 adalah variabel acak kontinu dengan fungsi probabilitas 𝑓(𝑥) dan 𝑔1(𝑋), 𝑔2(𝑋), … , 𝑔𝑘(𝑋) adalah 𝑘 fungsi dari 𝑋. Maka
𝐸[𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]. Bukti:
𝐸[𝑔1(𝑋) + 𝑔2(𝑋) + ⋯ + 𝑔𝑘(𝑋)] = ∫ [𝑔1(𝑥) + 𝑔2(𝑥) + ⋯ + 𝑔𝑘(𝑥)]𝑓(𝑥)𝑑𝑥 ∞ −∞ = ∫ [𝑔1(𝑥)𝑓(𝑥) + 𝑔2(𝑥)𝑓(𝑥) + ⋯ + 𝑔𝑘(𝑥)𝑓(𝑥)]𝑑𝑥 ∞ −∞ = ∫ 𝑔1(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ + ∫ 𝑔2(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ + ⋯ + ∫ 𝑔𝑘(𝑥)𝑓(𝑥)𝑑𝑥 ∞ −∞ = 𝐸[𝑔1(𝑋)] + 𝐸[𝑔2(𝑋)] + ⋯ + 𝐸[𝑔𝑘(𝑋)]. ∎ Teorema 2.3
Misalkan 𝑋 merupakan variabel acak dan diberikan konstanta tak nol 𝑐, maka 𝐸(𝑐) = 𝑐.
Bukti:
Untuk variabel acak diskrit. Berdasarkan Definisi 2.14
𝐸(𝑐) = ∑ 𝑐𝑃(𝑥) = 𝑐 ∑ 𝑝(𝑥)
𝑥 𝑥
Menurut Definisi 2.7 ∑𝑥𝑝(𝑥) = 1 sehingga,
𝐸(𝑐) = 𝑐(1) = 𝑐. ∎
Untuk variabel acak kontinu Berdasarkan Definisi 2.15 𝐸(𝑐) = ∫ 𝑐𝑓(𝑥)𝑑𝑥 = 𝑐 ∫ 𝑓(𝑥)𝑑𝑥 ∞ −∞ ∞ −∞
Menurut Definisi 2.11 ∫−∞∞ 𝑓(𝑥)= 1 sehingga,
Teorema 2.4
Misalkan 𝑋 merupakan variabel acak dan diberikan konstanta tak nol 𝑐, maka 𝐸(𝑐𝑋) = 𝑐𝐸(𝑋).
Bukti:
Untuk variabel acak diskrit
Berdasarkan Definisi 2.14
𝐸(𝑐𝑋) = ∑ 𝑐𝑥𝑝(𝑥) =
𝑥
𝑐 ∑ 𝑥𝑝(𝑥)
𝑥
Menurut Definisi 2.14 𝐸(𝑋) = ∑ 𝑥𝑝(𝑥)𝑥 sehingga,
𝐸(𝑐𝑋) = 𝑐𝐸(𝑋). ∎
Untuk variabel acak kontinu Berdasarkan Definisi 2.15 𝐸(𝑐𝑋) = ∫ 𝑐𝑥𝑓(𝑥)𝑑𝑥 = 𝑐 ∫ 𝑥𝑓(𝑥) ∞ −∞ ∞ −∞ 𝑑𝑥 Menurut Definisi 2.15 𝐸(𝑋) = ∫−∞∞ 𝑥𝑓(𝑥)𝑑𝑥 sehingga,
𝐸(𝑐𝑋) = 𝑐𝐸(𝑋). ∎
Teorema 2.5
Misalkan 𝑋 merupakan variabel acak dengan fungsi probabilitas 𝑓(𝑥) dan diberikan konstanta tak nol 𝑐 dan 𝑑, maka 𝐸(𝑐𝑋 + 𝑑) = 𝑐𝐸(𝑋) + 𝑑.
Bukti:
Dengan menggunakan Teorema 2.3 dan Teorema 2.4 didapat 𝐸(𝑐𝑋 + 𝑑) = 𝐸(𝑐𝑋) + 𝐸(𝑑)
= 𝑐𝐸(𝑋) + 𝐸(𝑑)
Teorema 2.6
Jika 𝑋 merupakan variabel acak Binomial dengan 𝑛 percobaan dan probabilitas suskes 𝑝, maka
𝐸(𝑋) = 𝜇 = 𝑛𝑝. Bukti:
Berdasarkan Definisi 2.10 dan Definisi 2.14 𝐸(𝑋) = ∑ 𝑥𝑝(𝑥) = ∑ 𝑥 (𝑛 𝑥) 𝑝 𝑥 𝑛 𝑥=0 𝑥 (1 − 𝑝)𝑛−𝑥 karena jumlahan pertama yaitu ketika 𝑥 = 1 maka didapat,
𝐸(𝑋) = ∑ 𝑥 𝑛! (𝑛 − 𝑥)! 𝑥!𝑝 𝑥(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=1 = ∑ 𝑥 𝑛! (𝑛 − 𝑥)! 𝑥(𝑥 − 1)!𝑝 𝑥(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=1 = ∑ 𝑛! (𝑛 − 𝑥)! (𝑥 − 1)!𝑝 𝑥(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=1 = ∑ 𝑛(𝑛 − 1)! (𝑛 − 𝑥)! (𝑥 − 1)!𝑝 𝑥(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=1 misalkan 𝑧 = 𝑥 − 1, 𝐸(𝑋) = 𝑛𝑝 ∑ (𝑛 − 1)! (𝑛 − 𝑥)! (𝑥 − 1)!𝑝 𝑥−1(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=1 = 𝑛𝑝 ∑ (𝑛 − 1)! (𝑛 − 1 − 𝑧)! 𝑧!𝑝 𝑧(1 − 𝑝)𝑛−1−𝑧 𝑛−1 𝑧=0 = 𝑛𝑝 ∑ (𝑛 − 1 𝑧 ) 𝑝 𝑧(1 − 𝑝)𝑛−1−𝑧 𝑛−1 𝑧=0
Perhatikan bahwa 𝑝(𝑧) = (𝑛−1𝑧 )𝑝𝑧(1 − 𝑝)𝑛−1−𝑧 merupakan fungsi probabilitas
Binomial. Maka ∑𝑛−1𝑧=0(𝑛−1𝑧 )𝑝𝑧(1 − 𝑝)𝑛−1−𝑧 = 1, dan menunjukkan bahwa
4. Variansi Definisi 2.16
Misalkan 𝑋 merupakan variabel acak dengan rata-rata 𝐸(𝑋) = 𝜇, variansi dari variabel acak 𝑋 didefinisikan sebagai nilai harapan dari (𝑋 − 𝜇)2 yaitu,
𝑉(𝑋) = 𝐸[(𝑋 − 𝜇)2]
Standar deviasi dari 𝑋 adalah akar kuadrat positif dari 𝑉(𝑋). Contoh 2.13
Distribusi probabilitas untuk variabel acak 𝑋 diperlihatkan dalam Tabel 2.2. Tentukan rata-rata, variansi, dan standar deviasi dari 𝑋.
Tabel 2.2 Distribusi Probabilitas untuk 𝑋
𝑥 𝑝(𝑥) 0 1/8 1 1/4 2 3/8 3 1/4 Solusi:
Dengan menggunakan Definisi 2.14 dan Definisi 2.16
𝜇 = 𝐸(𝑋) = ∑ 𝑥𝑝(𝑥) = (0)(1 8)⁄ + (1)(1 4)⁄ + (2)(3 8)⁄ + (3)(1 4) = 1.75⁄ 3 𝑥=0 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = ∑(𝑥 − 𝜇)2𝑝(𝑥) 3 𝑥=0 = (0 − 1.75)2(1 8)⁄ + (1 − 1.75)2(1 4)⁄ + (2 − 1.75)2(3 8)⁄ + (3 − 1.75)2(1 8)⁄ = 0.9375 𝜎 = √𝜎2 = √0.9375 = 0.97.
Teorema 2.7
Jika 𝑋 merupakan variabel acak dengan fungsi probabilitas 𝑓(𝑥) dan rata-rata 𝜇 = 𝐸(𝑋), maka 𝑉(𝑋) = 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸(𝑋2) − 𝜇2. Bukti: 𝜎2 = 𝐸[(𝑋 − 𝜇)2] = 𝐸(𝑋2− 2𝜇𝑋 + 𝜇2) = 𝐸(𝑋2) − 𝐸(2𝜇𝑋) + 𝐸(𝜇2) = 𝐸(𝑋2) − 2𝜇𝐸(𝑋) + 𝐸(𝜇2) = 𝐸(𝑋2) − 2𝜇2+ 𝜇2 = 𝐸(𝑋2) − 𝜇2 ∎ Contoh 2.14
Tentukan variansi dari variabel acak 𝑋 dari Contoh 2.13. Solusi:
Telah ditemukan pada Contoh 2.13 bahwa rata-rata 𝜇 = 1.75. Karena 𝐸(𝑋2) = ∑ 𝑥2𝑝(𝑥) =
𝑥
(02)(1 8)⁄ + (12)(1 4)⁄ + (22)(3 8)⁄ + (32)(1 4) = 4,⁄ Dengan menggunakan Teorema 2.7 didapat
𝜎2 = 𝐸(𝑋2) − 𝜇2 = 4 − (1.75)2 = 0.9375.
Teorema 2.8
Jika 𝑋 merupakan variabel acak dan 𝑐 merupakan suatu konstanta maka 𝑉(𝑐𝑋) = 𝑐2𝑉(𝑋). Bukti: 𝑉(𝑐𝑋) = 𝐸(𝑐𝑋 − 𝑐𝜇)2 = 𝐸[𝑐(𝑋 − 𝜇)]2 = 𝐸[𝑐2(𝑋 − 𝜇)2] = 𝑐2𝐸(𝑋 − 𝜇)2
= 𝑐2𝑉(𝑋). ∎
Teorema 2.9
Misalkan 𝑋 merupakan variabel acak Binomial dengan 𝑛 percobaan dan probabilitas sukses 𝑝, maka
𝜎2 = 𝑉(𝑋) = 𝑛𝑝𝑞.
Bukti:
Dari Teorema 2.7 kita tahu bahwa 𝑉(𝑋) = 𝜎2 = 𝐸(𝑋2) − 𝜇2. Sehingga 𝜎2 dapat
dihitung jika kita menentukan 𝐸(𝑋2)
𝐸(𝑋2) = ∑ 𝑥2𝑝(𝑥) 𝑛 𝑥=0 = ∑ 𝑥2(𝑛 𝑥) 𝑝 𝑥𝑞𝑛−𝑥 = ∑ 𝑥2 𝑛! 𝑥! (𝑛 − 𝑥)! 𝑛 𝑥=0 𝑛 𝑥=0 𝑝𝑥𝑞𝑛−𝑥 perhatikan bahwa 𝐸[𝑋(𝑋 − 1)] = 𝐸(𝑋2− 𝑋) = 𝐸(𝑋2) − 𝐸(𝑋) sehingga 𝐸(𝑋2) = 𝐸[𝑋(𝑋 − 1)] + 𝐸(𝑋) = 𝐸[𝑋(𝑋 − 1)] + 𝜇. Dalam kasus, 𝐸[𝑋(𝑋 − 1)] = ∑ 𝑥(𝑥 − 1) 𝑛! 𝑥! (𝑛 − 𝑥)! 𝑛 𝑥=0 𝑝𝑥(1 − 𝑝)𝑛−𝑥. Ketika 𝑥 = 0 dan 𝑥 = 1 jumlahannya akan sama dengan nol, maka
𝐸[𝑋(𝑋 − 1)] = ∑ 𝑥(𝑥 − 1) 𝑛! 𝑥! (𝑛 − 𝑥)!
𝑛
𝑥=2
𝑝𝑥(1 − 𝑝)𝑛−𝑥. misalkan 𝑧 = 𝑥 − 2 untuk memperoleh
𝐸[𝑋(𝑋 − 1)] = 𝑛(𝑛 − 1)𝑝2∑ (𝑛 − 2)! (𝑥 − 2)! (𝑛 − 𝑥)!𝑝 𝑥−2(1 − 𝑝)𝑛−𝑥 𝑛 𝑥=2 = 𝑛(𝑛 − 1)𝑝2∑ (𝑛 − 2)! 𝑧! (𝑛 − 2 − 𝑧)!𝑝 𝑧(1 − 𝑝)𝑛−2−𝑧 𝑛−2 𝑧=0 = 𝑛(𝑛 − 1)𝑝2∑ (𝑛 − 2 𝑧 ) 𝑝 𝑧(1 − 𝑝)𝑛−2−𝑥 𝑛−2 𝑧=0 .
Perhatikan bahwa 𝑝(𝑧) = (𝑛−2𝑧 )𝑝𝑧𝑞𝑛−2−𝑥 adalah fungsi probabilitas Binomial dengan (𝑛 − 2) percobaan. Maka ∑𝑛−2𝑧=0𝑝(𝑧) = 1 dan
𝐸[𝑋(𝑋 − 1)] = 𝑛(𝑛 − 1)𝑝2. Sehingga, 𝐸(𝑋2) = 𝐸[𝑋(𝑋 − 1)] + 𝜇 = 𝑛(𝑛 − 1)𝑝2 + 𝑛𝑝 dan 𝜎2 = 𝐸(𝑋2) − 𝜇2 = 𝑛(𝑛 − 1)𝑝2 + 𝑛𝑝 − 𝑛2𝑝2 = 𝑛𝑝[(𝑛 − 1)𝑝 + 1 − 𝑛𝑝] = 𝑛𝑝(1 − 𝑝) = 𝑛𝑝𝑞. ∎ 5. Fungsi Pembangkit Momen
Definisi 2.17
Fungsi pembangkit momen 𝑚(𝑡) untuk variabel acak 𝑋 didefinisikan sebagai 𝑚(𝑡) = 𝐸(𝑒𝑡𝑋). Kita katakan bahwa fungsi pembangkit momen untuk 𝑋 ada jika
terdapat konstanta positif 𝑏 sedemikian sehingga 𝑚(𝑡) berhingga untuk |𝑡| ≤ 𝑏. Teorema 2.10
Jika 𝑚(𝑡) ada, maka untuk setiap bilangan positif 𝑘, 𝑑𝑘𝑚(𝑡) 𝑑𝑡𝑘 | 𝑡=0 = 𝑚(𝑘)(0) = 𝜇′𝑘. Bukti: 𝑑𝑘𝑚(𝑡)
𝑑𝑡𝑘 atau 𝑚(𝑘)(𝑡) adalah turunan ke-𝑘 dari 𝑚(𝑡) yang berhubungan dengan 𝑡.
Karena 𝑚(𝑡) = 𝐸(𝑒𝑡𝑋) = 1 + 𝑡𝜇′1+ 𝑡2 2!𝜇′2+ 𝑡3 3!𝜇′3+ ⋯, didapat 𝑚(1)(𝑡) = 𝜇′1 + 2𝑡 2!𝜇′2+ 3𝑡 3! 𝜇′3+ ⋯,
𝑚(2)(𝑡) = 𝜇′2+2𝑡 2!𝜇′3 + 3𝑡2 3! 𝜇′4+ ⋯, secara umum, 𝑚(𝑘)(𝑡) = 𝜇′𝑘+2𝑡 2!𝜇′𝑘+1+ 3𝑡2 3! 𝜇′𝑘+2+ ⋯, Ketika 𝑡 = 0 pada masing-masing turunan, didapatkan
𝑚(1)(0) = 𝜇′1, 𝑚(2)(0) = 𝜇′2,
secara umum,
𝑚(𝑘)(0) = 𝜇′𝑘. ∎
Contoh 2.15
Tentukan fungsi pembangkit momen dari Distribusi Normal. Solusi: 𝑓(𝑥) = 1 √2𝜋𝜎𝑒 −12(𝑥−𝜇𝜎 )2 𝑀𝑋(𝑡) = ∫ 𝑒𝑡𝑥 ∞ −∞ 1 √2𝜋𝜎𝑒 −12(𝑥−𝜇𝜎 )2 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒− 1 2( 𝑥2−2𝜇𝑥+𝜇2 𝜎2 ) 𝑒𝑡𝑥 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒( −𝑥2+2𝜇𝑥−𝜇2 2𝜎2 )𝑒𝑡𝑥 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒( −𝑥2+2𝜇𝑥−𝜇2+2𝜎2𝑡𝑥 2𝜎2 ) 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒−2𝜎12(𝑥2−2𝜇𝑥−2𝜎2𝑡𝑥+𝜇2) 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒− 1 2𝜎2[𝑥2−2𝑥(𝜇+𝜎2𝑡)+𝜇2] 𝑑𝑥
= ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒− 1 2𝜎2[(𝑥−(𝜇+𝜎2𝑡)) 2 −2𝜇𝜎2𝑡−𝜎4𝑡2] 𝑑𝑥 = ∫ 1 √2𝜋𝜎 ∞ −∞ 𝑒− 1 2𝜎2(𝑥−(𝜇+𝜎2𝑡)) 2 (−2𝜇𝜎2𝑡−𝜎4𝑡2 2𝜎2 ) 𝑑𝑥 = 𝑒𝜇𝑡+𝜎 2𝑡2 2 ∫ 𝑓(𝑥) ∞ −∞ 𝑑𝑥 = 𝑒𝜇𝑡+𝜎 2𝑡2 2 Teorema 2.11
Jika 𝑋 merupakan variabel acak berdistribusi Normal dengan parameter 𝜇 dan 𝜎, maka
𝐸(𝑋) = 𝜇 dan 𝑉(𝑋) = 𝜎2. Bukti:
Akan ditunjukkan dengan menggunakan metode fungsi pembangkit momen dari Distribusi Normal. 𝐸(𝑋) = 𝑑 𝑑𝑡𝑚𝑋(𝑡)|𝑡=0 = 𝑑 𝑑𝑡𝑒 𝜇𝑡+𝜎 2𝑡2 2 | 𝑡=0 = (𝜇 + 𝜎2𝑡) (𝑒𝜇𝑡+𝜎 2𝑡2 2 )| 𝑡=0 = (𝜇 + 0)(𝑒0) = 𝜇 𝐸(𝑋2) = 𝑑 𝑑2𝑡𝑚𝑋(𝑡)| 𝑡=0 = 𝜎2𝑒𝜇𝑡+𝜎 2𝑡2 2 + (𝜇 + 𝜎2𝑡)(𝜇 + 𝜎2𝑡) (𝑒𝜇𝑡+ 𝜎2𝑡2 2 )| 𝑡=0 = 𝜎2+ 𝜇2
𝑉(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2
= (𝜎2+ 𝜇2) − 𝜇2
= 𝜎2. ∎
6. Metode Fungsi Pembangkit Momen Teorema 2.12 Teorema Ketunggalan
Misalkan 𝑚𝑋(𝑡) dan 𝑚𝑌(𝑡) merupakan fungsi pembangkit momen dari variabel
acak 𝑋 dan 𝑌. Jika kedua fungsi pembangkit momen ada dan 𝑚𝑋(𝑡) = 𝑚𝑌(𝑡) untuk
semua nilai dari 𝑡, maka 𝑋 dan 𝑌 memiliki distribusi probabilitas yang sama. Bukti:
Bukti dapat dilihat pada skripsi Julie, H. (1999). Teorema Limit Pusat Lindenberg dan Terapannya. Skripsi.
𝐹(𝑥) = 𝐺(𝑥). (Skripsi halaman 54).
Berdasarkan teorema ketunggalan terdapat korespondensi satu-satu antara fungsi pembangkit momen dengan fungsi probabilitas.
Contoh 2.16
Andaikan 𝑋 berdistribusi Normal dengan rata-rata 𝜇 dan variansi 𝜎2, bila 𝑍 = 𝑋̅−𝜇
𝜎 √𝑛⁄ ,
tunjukkan bahwa 𝑍 merupakan distribusi Normal standar dengan rata-rata 0 dan variansi 1. Solusi: 𝑚𝑍(𝑡) = 𝐸[𝑒𝑍𝑡] = 𝐸 [𝑒( 𝑋̅−𝜇 𝜎 √𝑛⁄ )𝑡]
= 𝐸 [𝑒 𝑋̅𝑡 𝜎 √𝑛⁄ (𝑒 −𝜇𝑡 𝜎 √𝑛⁄ ) ] = 𝑒 𝜇𝑡 𝜎 √𝑛⁄ [𝐸 (𝑒 𝑋̅𝑡 𝜎 √𝑛⁄ )] misal 𝑡′= 𝑡 𝜎 √𝑛⁄ = 𝑒−𝜇𝑡′[𝐸(𝑒𝑋̅𝑡)] = 𝑒−𝜇𝑡′[𝐸 (𝑒𝑋1𝑡 ′ 𝑛 𝑒 𝑋2𝑡′ 𝑛 … 𝑒 𝑋𝑛𝑡′ 𝑛 )] = 𝑒−𝜇𝑡′𝑚𝑋̅(𝑡′) = 𝑒−𝜇𝑡′(𝑒𝜇𝑡′+𝜎 2𝑡′2 2 ) = 𝑒 −𝜇𝑡 𝜎 √𝑛⁄ 𝑒 ( 𝜇𝑡 𝜎 √𝑛⁄ + ( 𝑡2 𝜎2⁄𝑛)𝜎2 2 )𝑛 = 𝑒 −𝜇𝑡 𝜎 √𝑛⁄ (𝑒 𝜇𝑡 𝜎 √𝑛⁄ ) (𝑒𝑡 2𝑛 2𝑛) = 𝑒𝑡 2 2
𝑚𝑍(𝑡) akan sama dengan fungsi pembangkit momen dari Distribusi Normal apabila
𝜇 = 0 dan 𝜎2 = 1, sehingga menurut Teorema 2.12 𝑍 berdistribusi Normal standar
dengan 𝜇 = 0 dan 𝜎2 = 1. Teorema 2.13
Misalkan 𝑋1, 𝑋2, … , 𝑋𝑛 adalah variabel acak yang saling bebas dengan fungsi
pembangkit momen 𝑚𝑋1(𝑡), 𝑚𝑋2(𝑡), … , 𝑚𝑋𝑛(𝑡). Jika 𝑈 = 𝑋1+ 𝑋2+ ⋯ + 𝑋𝑛,
Bukti: 𝑚𝑈(𝑡) = 𝐸(𝑒𝑢𝑡) = 𝐸[𝑒(𝑋1+𝑋2+⋯+𝑋𝑛)𝑡] = 𝐸[(𝑒𝑋1𝑡) × (𝑒𝑋2𝑡) × … × (𝑒𝑋𝑛𝑡)] = 𝐸(𝑒𝑋1𝑡) × 𝐸(𝑒𝑋2𝑡) × … × 𝐸(𝑒𝑋𝑛𝑡) = 𝑚𝑋1(𝑡) × 𝑚𝑋2(𝑡) × … × 𝑚𝑋𝑛(𝑡). ∎
C. Distribusi Probabilitas Multivariat Definisi 2.18
Misalkan 𝑋 dan 𝑌 merupakan variabel acak diskrit, maka fungsi probabilitas 𝑓(𝑥, 𝑦) = 𝑃(𝑋 = 𝑥, 𝑌 = 𝑦) disebut fungsi probabilitas bersama dari 𝑋 dan 𝑌, untuk −∞ < 𝑥 < ∞, −∞ < 𝑦 < ∞.
Contoh 2.17
Dalam suatu kelas terdapat 2 siswa Amerika Afrika (berkulit hitam), 2 siswa berkulit putih, dan 3 siswa Hispanic Amerika. Jika 2 siswa diambil secara acak dari kelas tersebut, dan jika 𝑋 merupakan banyaknya siswa berkulit hitam, dan 𝑌 merupakan banyaknya siswa berkulit putih, tentukan fungsi probabilitas bersama dari variabel acak 𝑋 dan 𝑌.
Solusi:
Terdapat 7 siswa di dalam kelas tersebut, sehingga ada (72) = 21 cara untuk mengambil 2 siswa dari 7 siswa.
Banyaknya cara mengambil 0 siswa berkulit hitam, 0 siswa berkulit putih, dan 2 siswa Hispanic Amerika adalah (20)(20)(32) = 3 cara, sehingga (𝑋 = 0, 𝑌 = 0) = 𝑝(0,0) =( 2 0)(20)(32) (72) = 3 120 .
Cara yang sama dapat dilakukan dengan mencari semua kemungkinan nilai 𝑋 dan 𝑌. Tabel 2.3 memperlihatkan semua fungsi probabilitas bersama dari variabel acak 𝑋 dan 𝑌.
Definisi 2.19
Misalkan 𝑋 dan 𝑌 merupakan variabel acak diskrit dengan fungsi probabilitas bersama 𝑝(𝑥, 𝑦), maka
1. 𝑝(𝑥, 𝑦) ≥ 0 untuk semua 𝑥 dan 𝑦. 2. ∑𝑥,𝑦𝑝(𝑥, 𝑦) = 1. Tabel 2.3 𝑌 𝑋 0 1 2 0 3 120 6 120 1 120 1 6 120 4 120 0 2 1 120 0 0 Definisi 2.20
Setiap variabel acak 𝑋 dan 𝑌 fungsi distribusi bersama 𝐹(𝑥, 𝑦) adalah 𝐹(𝑥, 𝑦) = 𝑃(𝑋 ≤ 𝑥, 𝑌 ≤ 𝑦), −∞ < 𝑥 < ∞, −∞ < 𝑦 < ∞. Contoh 2.18
Tentukan 𝐹(1,1) untuk Contoh 2.17 Solusi:
Untuk dua variabel diskrit 𝑋 dan 𝑌, 𝐹(𝑥, 𝑦) diberikan dengan 𝐹(𝑥, 𝑦) = ∑ ∑ 𝑓(𝑡1, 𝑡2).
𝑡2≤𝑦
𝑡1≤𝑥
Sehingga 𝐹(1,1) = 𝑝(0,0) + 𝑝(0,1) + 𝑝(1,0) + 𝑝(1,1) = 19
Definisi 2.21
Misalkan 𝑋 dan 𝑌 merupakan variabel acak kontinu dengan fungsi distribusi bersama 𝐹(𝑥, 𝑦). Jika terdapat fungsi nonnegatif 𝑓(𝑥, 𝑦) seperti
𝐹(𝑥, 𝑦) = ∫ ∫ 𝑓(𝑡1, 𝑡2)𝑑𝑡2𝑑𝑡1 𝑦 −∞ 𝑥 −∞ ,
untuk semua −∞ < 𝑥 < ∞, −∞ < 𝑦 < ∞, maka 𝑋 dan 𝑌 disebut variabel acak kontinu bersama. Fungsi 𝑓(𝑥, 𝑦) disebut fungsi densitas probabilitas bersama. Definisi 2.22
Misalkan 𝑋 dan 𝑌 merupakan variabel acak kontinu dengan fungsi probabilitas bersama 𝑓(𝑥, 𝑦), maka
1. 𝑓(𝑥, 𝑦) ≥ 0 untuk semua 𝑥 dan 𝑦. 2. ∫−∞∞ ∫−∞∞ 𝑓(𝑥, 𝑦) = 1.
Contoh 2.19
Bensin harus disimpan dalam tangki curah pada awal minggu dan kemudian dijual kepada pelanggan. Misalkan 𝑋 menunjukkan kapasitas tangki curah yang tersedia setelah tangki diisi pada awal minggu dan 𝑌 menunjukkan kapasitas tangki curah yang dijual selama satu minggu dengan fungsi densitas bersama sebagai berikut:
𝑓(𝑥, 𝑦) = {3𝑥2, 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1 0, selainnya.
Tunjukkan bahwa fungsi densitas bersamanya memenuhi Definisi 2.22 Solusi:
1. Dapat dilihat jelas bahwa 𝑓(𝑥, 𝑦) ≥ 0 untuk semua 𝑥 dan 𝑦. 2. Akan ditunjukkan bahwa ∫ ∫ 3𝑥01 01 2𝑑𝑥𝑑𝑦 = 1.
∫ ∫ 3𝑥2𝑑𝑥𝑑𝑦 1 0 1 0 = ∫(𝑥3|01) 1 0 𝑑𝑦 = ∫ 1 1 0 𝑑𝑦
= 𝑦|01 = 1. Definisi 2.23
Misalkan 𝑋 dan 𝑌 memiliki fungsi probabilitas bersama 𝑓(𝑥, 𝑦), maka 𝑋 dan 𝑌 dikatakan saling bebas jika dan hanya jika
𝑓(𝑥, 𝑦) = 𝑓𝑋(𝑥)𝑓𝑌(𝑦) untuk semua pasangan bilangan real 𝑥 dan 𝑦.
Contoh 2.20 Misalkan
𝑓(𝑥, 𝑦) = {3𝑥, 0 ≤ 𝑦 ≤ 𝑥 ≤ 1, 0, selainnya. a. Tentukan 𝑓𝑋(𝑥) dan 𝑓𝑌(𝑦).
b. Apakah 𝑋 dan 𝑌 saling bebas? Solusi:
a. Kita perhatikan untuk setiap 𝑥, 𝑦 bervariasi dari 0 ke 𝑥 (0 < 𝑦 < 𝑥), maka dari itu
𝑓𝑋(𝑥) = ∫ 3𝑥 𝑑𝑦 = 3𝑥(𝑦|0𝑥) = 3𝑥2, 0 < 𝑥 < 1. 𝑥
0
Demikian pula, untuk setiap 𝑦, 𝑥 bervariasi dari 𝑦 ke 1 𝑓𝑌(𝑦) = ∫ 3𝑥 𝑑𝑥 =3𝑥 2 2 |𝑦 1 = 3 2 1 𝑦 −3𝑦 2 2 = 3 2(1 − 𝑦 2), 0 < 𝑦 < 1.
b. Untuk memeriksa sifat saling bebas dari 𝑋 dan 𝑌 𝑓𝑋(1)𝑓𝑌(1 2) = (3) ( 9 8) = 27 8 ≠ 3 = 𝑓 (1, 1 2). Jadi, 𝑋 dan 𝑌 tidak saling bebas.
Definisi 2.24
Misalkan 𝑔(𝑋1, 𝑋2, … , 𝑋𝑘) merupakan fungsi dari variabel acak diskrit, 𝑋1, 𝑋2, … , 𝑋𝑘 yang memiliki fungsi probabilitas 𝑝(𝑥1, 𝑥2, … , 𝑥𝑘). Maka nilai harapan dari 𝑔(𝑋1, 𝑋2, … , 𝑋𝑘)
𝐸[𝑔(𝑋1, 𝑋2, … , 𝑋𝑘)] = ∑ … ∑ ∑ 𝑔(𝑥1, 𝑥2, … , 𝑥𝑘)𝑝(𝑥1, 𝑥2, … , 𝑥𝑘).
𝑥1
𝑥2
𝑥𝑘
Jika 𝑋1, 𝑋2, … , 𝑋𝑘 merupakan variabel acak kontinu dengan fungsi densitas bersama 𝑓(𝑥1, 𝑥2, … , 𝑥𝑘), maka 𝐸[𝑔(𝑋1, 𝑋2, … , 𝑋𝑘)] = ∫ … ∫ ∫ 𝑔(𝑥1, 𝑥2, … , 𝑥𝑘)𝑓(𝑥1, 𝑥2, … , 𝑥𝑘)𝑑𝑥1𝑑𝑥2… 𝑑𝑥𝑘 ∞ −∞ ∞ −∞ ∞ −∞ . Contoh 2.21
Misalkan 𝑋1 dan 𝑋2 memiliki fungsi densitas bersama sebagai berikut 𝑓(𝑥1, 𝑥2) = {3𝑥1, 0 ≤ 𝑥0, selainnya1 ≤ 1,0 ≤ 𝑥2 ≤ 1
Tentukan 𝐸(𝑋1, 𝑋2)
Solusi:
Dari Definisi 2.24 didapat
𝐸(𝑋1, 𝑋2) = ∫ ∫ 𝑥1𝑥2 ∞ −∞ ∞ −∞ 𝑓(𝑥1, 𝑥2)𝑑𝑥1𝑑𝑥2 = ∫ ∫ 𝑥1𝑥2 1 0 1 0 (3𝑥1)𝑑𝑥1𝑑𝑥2 = ∫ ∫ 3𝑥12𝑥2 1 0 𝑑𝑥1𝑑𝑥2 1 0 = ∫ 𝑥2(𝑥13] 0 1) 1 0 𝑑𝑥2 = ∫ 𝑥2𝑑𝑥2 1 0 =1 2𝑥2 2] 0 1 =1 2.
Teorema 2.14
Jika 𝑋 dan 𝑌 merupakan variabel acak yang saling bebas dan 𝑔(𝑥) dan ℎ(𝑦) merupakan fungsi dari 𝑋 dan 𝑌, maka
𝐸[𝑔(𝑋)ℎ(𝑌)] = 𝐸[𝑔(𝑋)]𝐸[ℎ(𝑌)]. Bukti:
Untuk variabel diskrit
𝐸[𝑔(𝑋)ℎ(𝑌)] = ∑ ∑ 𝑔(𝑥)ℎ(𝑦)𝑓(𝑥, 𝑦) ∀𝑦 ∀𝑥 = ∑ ∑ 𝑔(𝑥)ℎ(𝑦) ∀𝑦 ∀𝑥 𝑓1(𝑥)𝑓2(𝑦) = [∑ 𝑔(𝑥)𝑓1(𝑥) ∀𝑥 ] [∑ ℎ(𝑦)𝑓2(𝑦) ∀𝑦 ] = 𝐸[𝑔(𝑋)]𝐸[ℎ(𝑌)] ∎ Untuk variabel kontinu
𝐸[𝑔(𝑋)ℎ(𝑌)] = ∫ ∫ 𝑔(𝑥)ℎ(𝑦)𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 ∞ −∞ ∞ −∞ = ∫ ∫ 𝑔(𝑥)ℎ(𝑦)𝑓1(𝑥)𝑓2(𝑦)𝑑𝑥𝑑𝑦 ∞ −∞ ∞ −∞ = [ ∫ 𝑔(𝑥)𝑓1(𝑥) ∞ −∞ 𝑑𝑥] [ ∫ ℎ(𝑦)𝑓2(𝑦) ∞ −∞ 𝑑𝑦] = 𝐸[𝑔(𝑋)]𝐸[ℎ(𝑌)] ∎
D. Teorema Limit Pusat Teorema 2.15
Misalkan 𝑋 dan 𝑋1, 𝑋2, 𝑋3, … adalah variabel acak dengan fungsi pembangkit momen 𝑚(𝑡) dan 𝑚1(𝑡), 𝑚2(𝑡), 𝑚3(𝑡), …
Jika
lim
𝑛→∞𝑚𝑛(𝑡) = 𝑚(𝑡), ∀𝑡 ∈ ℝ
maka fungsi distribusi dari 𝑋𝑛 akan konvergen ke fungsi distribusi dari 𝑋, 𝑛 → ∞. Bukti:
Bukti terdapat pada buku Williams, David. 1991. Probability with Martingales. New York: Cambridge University Press. (Halaman 185).
Teorema 2.16
Misalkan 𝑋1, 𝑋2, … 𝑋𝑛 merupakan variabel acak berdistribusi indentik dan saling bebas dengan 𝐸(𝑌𝑖) = 𝜇 dan 𝑉(𝑌𝑖) = 𝜎2 < ∞. Didefinisikan
𝑈𝑛 = ∑ 𝑌𝑖 − 𝑛𝜇 𝑛 𝑖=1 𝜎√𝑛 = 𝑌̅ − 𝜇 𝜎 𝑛⁄ dimana 𝑌̅ = 1 𝑛∑ 𝑌𝑖 𝑛 𝑖=1 .
Maka fungsi distribusi dari 𝑈𝑛 konvergen ke fungsi Disribusi Normal Standar saat 𝑛 → ∞ adalah lim 𝑛→∞𝑃(𝑈𝑛 ≤ 𝑢) = ∫ 1 √2𝜋𝑒 −𝑡2⁄2 𝑑𝑡 𝑢 −∞ untuk semua 𝑢. Bukti: 𝑈𝑛 = √𝑛 (𝑌̅ − 𝜇 𝜎 ) = 1 √𝑛( ∑𝑛𝑖=1𝑌𝑖 − 𝑛𝜇 𝜎 ) = 1 √𝑛∑ 𝑍𝑖 𝑛 𝑖=1 , dimana 𝑍𝑖 =𝑌𝑖 − 𝜇 𝜎
Karena variabel acak 𝑌𝑖 saling bebas dan distribusi identik, 𝑍𝑖, 𝑖 = 1, 2, … , 𝑛 saling bebas dan berdistribusi identik dengan 𝐸(𝑍𝑖) = 0 dan 𝑉(𝑍𝑖) = 1.
Fungsi pembangkit momen dari jumlah variabel acak adalah hasil kali dari fungsi pembangkit momen,
𝑚∑ 𝑍𝑖(𝑡) = 𝑚𝑍1(𝑡) × 𝑚𝑍2(𝑡) × … 𝑚𝑍𝑛(𝑡) = [𝑚𝑍𝑖(𝑡)] 𝑛 dan 𝑚𝑈𝑛(𝑡) = 𝑚∑ 𝑍𝑖( 𝑡 √𝑛) = [𝑚𝑍𝑖( 𝑡 √𝑛)] 𝑛 . Dengan Teorema Taylor didapat
𝑚𝑍1(𝑡) = 𝑚𝑍1(0) + 𝑚′𝑍1(0)𝑡 + 𝑚′′𝑍1(𝜉)𝑡
2
2 , dimana 0 < 𝜉 < 𝑡, dan karena 𝑚𝑍1(𝑡) = 𝐸(𝑒0𝑍1) = 𝐸(1) = 1, dan 𝑚′
𝑍1(0) = 𝐸(𝑍1) = 0, 𝑚𝑍1(𝑡) = 1 + 𝑚′′𝑍1(𝜉) 2 𝑡 2, dimana 0 < 𝜉 < 𝑡. Sehingga, 𝑚𝑈𝑛(𝑡) = [1 +𝑚′′𝑍1(𝜉𝑛) 2 ( 𝑡 √𝑛) 2 ] 𝑛 = [1 +𝑚′′𝑍1(𝜉𝑛) 𝑡 2⁄2 𝑛 ] 𝑛 , dimana 0 < 𝜉𝑛 < 𝑡 √𝑛. Perhatikan bahwa 𝑛 → ∞, 𝜉𝑛 → 0 dan 𝑚′′𝑍1(𝜉𝑛) 𝑡
2⁄ → 𝑚2 ′′
𝑍1(0) 𝑡
2⁄ =2
𝐸(𝑍12) 𝑡2⁄ = 𝑡2 2⁄ karena 𝐸(𝑍2
12) = 𝑉(𝑍1) = 1. Ingat bahwa jika
lim 𝑛→∞𝑏𝑛 = 𝑏 maka lim𝑛→∞(1 + 𝑏𝑛 𝑛) 𝑛 = 𝑒𝑏. Maka lim 𝑛→∞𝑚𝑈𝑛(𝑡) = lim𝑛→∞[1 + 𝑚′′𝑍1(𝜉𝑛) 𝑡 2⁄2 𝑛 ] 𝑛 = 𝑒𝑡2⁄2,
fungsi pembangkit momen untuk variabel acak Normal standar. Dengan menggunakan Teorema 2.15, kita dapatkan bahwa 𝑈𝑛 mempunyai fungsi distribusi yang konvergen ke fungsi distribusi Normal standar.
E. Pendugaan Parameter
Pendugaan parameter adalah bagian dari statistik inferensi yang merupakan suatu cara untuk memprediksi karakteristik dari suatu populasi berdasarkan sampel yang diambil. Informasi yang didapatkan dalam sampel dapat digunakan untuk menghitung nilai penduga titik, penduga selang, atau keduanya.
Definisi 2.25
Penduga merupakan peraturan, yang sering dinyatakan sebagai rumus, yang memberi tahu bagaimana cara menghitung nilai pendekatan berdasarkan pengukuran yang didapat dalam sampel.
1. Pendugaan Titik
Penduga titik merupakan salah satu nilai tunggal yang dengan sebaik-baiknya menduga nilai parameter yang tak diketahui.
Contoh 2.22
Untuk contoh, rata-rata sampel
𝑋̅ =1 𝑛∑ 𝑋𝑖
𝑛
𝑖=1
adalah salah satu penduga titik dari rata-rata populasi 𝜇. 𝑋̅ merupakan aturan dan rumus yang menjumlahkan sampel pengamatan dan membaginya dengan ukuran sampel 𝑛.
Definisi 2.26
Misalkan 𝜃̂ merupakan penduga titik dari parameter 𝜃. Maka 𝜃̂ merupakan penduga tak bias jika 𝐸(𝜃̂) = 𝜃. Jika 𝐸(𝜃̂) ≠ 𝜃, 𝜃̂ dikatakan bias.
Contoh 2.23
Misalkan 𝐸(𝜃̂1) = 𝐸(𝜃̂2) = 𝜃 dan andaikan penduga 𝜃̂3 = 𝑎𝜃̂1+ (1 − 𝑎) 𝜃̂2.
Tunjukkan bahwa 𝜃̂3 merupakan penduga tak bias dari 𝜃. Solusi: 𝐸(𝜃̂3) = 𝐸[𝑎𝜃̂1+ (1 − 𝑎)𝜃̂2] = 𝑎𝐸(𝜃̂1) + (1 − 𝑎) 𝐸(𝜃̂2) = 𝑎𝜃 + (1 − 𝑎)𝜃 = 𝑎𝜃 + 𝜃 − 𝑎𝜃 = 𝜃
Menurut Definisi 2.26 karena 𝐸(𝜃̂3) = 𝜃 maka 𝜃̂3 merupakan penduga tak bias dari
𝜃.
Definisi 2.27
Bias dari penduga titik 𝜃̂ diberikan oleh 𝐵(𝜃̂) = 𝐸(𝜃̂) − 𝜃. Definisi 2.28
Jumlah kuadrat galat dari penduga titik 𝜃̂ adalah 𝑀𝑆𝐸(𝜃̂) = 𝐸 [(𝜃̂ − 𝜃)2]. 2. Penduga Selang
Penduga selang adalah rumus untuk menentukan batas-batas interval berdasarkan pengukuran dari sampel. Penduga selang sering disebut juga selang kepercayaan. Batas bawah dan batas atas dari selang kepercayaan disebut batas kepercayaan atas dan batas kepercayaan bawah. Probabilitas bahwa selang kepercayaan akan mendekati 𝜃 disebut koefisien kepercayaan.
Misalkan 𝜃̂𝐿 dan 𝜃̂𝑈 merupakan batas bawah dan batas atas selang kepercayaan untuk sebuah parameter 𝜃. Maka
𝑃(𝜃̂𝐿 ≤ 𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼,
1 − 𝛼 adalah koefisien kepercayaan. Selang acak yang dihasilkan, didefinisikan sebagai [𝜃̂𝐿, 𝜃̂𝑈] disebut selang kepercayaan dua sisi.
Dapat dibentuk selang kepercayaan satu sisi sedemikian rupa 𝑃(𝜃̂𝐿 ≤ 𝜃) = 1 − 𝛼
dengan selang kepercayaan [𝜃̂𝐿, ∞). Demikian pula kita juga dapat memiliki
selang kepercayaan satu sisi sedemikian rupa 𝑃(𝜃 ≤ 𝜃̂𝑈) = 1 − 𝛼 dengan selang kepercayaan (−∞, 𝜃̂𝑈].
3. Metode Pivot
Metode pivot merupakan salah satu metode yang digunakan untuk menentukan selang kepercayaan. Metode ini bergantung pada kuantitas pivot yang memiliki dua karakteristik, yaitu:
1. Merupakan fungsi dari pengukuran sampel (𝑥1, 𝑥2, … , 𝑥𝑛) dan merupakan fungsi dari parameter 𝜃 yang tidak diketahui.
2. Memiliki fungsi probabilitas yang tidak bergantung pada parameter 𝜃. Contoh 2.24
Tentukan selang kepercayaan 95% bagi 𝜇 bila diketahui kuantitas pivotnya adalah 𝑍 = 𝑋̅−𝜇
𝜎 √𝑛⁄ , dengan 𝑋 berdistribusi Normal dengan rata-rata 𝜇 yang tidak diketahui
dan variansi 𝜎2 = 1.
Solusi:
Dari Contoh 2.16 telah diketahui bahwa fungsi pembangkit momen dari Z adalah 𝑚𝑍(𝑡) = 𝑒𝑡22 yang sama dengan fungsi pembangkit momen dari Distribusi Normal
apabila 𝜇 = 0 dan 𝜎2 = 1.
Fungsi probabilitas dari 𝑍 adalah 𝑓𝑍(𝑍) = 1
√2𝜋𝑒 (−1
2𝑍 2)
Syarat kuantitas pivot dipenuhi, yaitu:
1. 𝑍 merupakan fungsi dari pengukuran (𝑥1, 𝑥2, … , 𝑥𝑛) dan parameter 𝜇 yang tidak diketahui.
2. Fungsi probabilitas yaitu 𝑓𝑍 tidak bergantung pada parameter 𝜇. Selang kepercayaan 95% bagi 𝜇 adalah
𝑃(−𝑧𝛼 2⁄ < 𝑍 < 𝑧𝛼 2⁄ ) = 0.95 𝑃(−𝑧0.05 2⁄ < 𝑍 < 𝑧0.05 2⁄ ) = 0.95
Dari Tabel Distribusi Normal (Lampiran 1) diperoleh 𝑧0.05 2⁄ = 𝑧0.025= 1.96.
𝑃(−1.96 < 𝑍 < 1.96) = 0.95 𝑃 (−1.96 <𝑋̅ − 𝜇
𝑃 (−1.96 ( 𝜎 √𝑛) < 𝑋̅ − 𝜇 < 1.96 ( 𝜎 √𝑛)) = 0.95 𝑃 (−𝑋̅ − 1.96 ( 𝜎 √𝑛) < −𝜇 < −𝑋̅ + 1.96 ( 𝜎 √𝑛)) = 0.95 Jadi, selang kepercayaan 95% bagi 𝜇 adalah
𝑃 (𝑋̅ −1.96𝜎
√𝑛 < 𝜇 < 𝑋̅ + 1.96𝜎
√𝑛 ) = 0.95 4. Selang Kepercayaan untuk Sampel Besar
Jika sampel berukuran besar, maka dengan Teorema Limit Pusat, disribusi sampel dapat diasumsikan mendekati Normal. Misalkan, jika 𝜃 merupakan parameter yang tidak diketahui (seperti 𝜇, 𝑝, (𝜇1− 𝜇2), (𝑝1−
𝑝2)), maka untuk sampel yang berukuran besar, dengan Teorema Limit Pusat
𝑍 = 𝜃̂ − 𝜃 𝜎𝜃̂
mendekati Distribusi Normal Standar, dimana 𝜃̂ merupakan penduga kemungkinan maksimum dari 𝜃 dan 𝜎𝜃̂ merupakan standar deviasi. Metode
pivot dapat digunakan untuk menentukan selang kepercayaan untuk parameter 𝜃. Untuk 𝜃 = 𝜇, 𝑛 ≥ 30 dapat dikatakan besar; untuk parameter Binomial 𝑝, 𝑛 dikatakan besar jika 𝑛𝑝 dan 𝑛(1 − 𝑝) keduanya lebih besar dari 5.
Contoh 2.25
Misalkan 𝜃̂ berdistribusi Normal dengan rata-rata 𝜃 dan standar deviasi 𝜎𝜃̂ dimana
𝜎 diasumsikan diketahui. Tentukan selang kepercayaan untuk 𝜃 yang memiliki koefi sien kepercayaan sama dengan 1 − 𝛼.
Solusi:
Kuantitas pivot dari 𝜃̂ adalah
𝑍 = 𝜃̂ − 𝜃 𝜎𝜃̂
dan memiliki Distribusi Normal Standar. Pilih dua nilai ujung −𝑍𝛼 2⁄ dan 𝑍𝛼 2⁄ sehingga 𝑃(−𝑍𝛼 2⁄ ≤ 𝑍 ≤ 𝑍𝛼 2⁄ ) = 1 − 𝛼 (2.1) 𝑃 (−𝑍𝛼 2⁄ ≤ 𝜃̂ − 𝜃 𝜎𝜃̂ ≤ 𝑍𝛼 2⁄ ) = 1 − 𝛼 𝑃(−𝑍𝛼 2⁄ 𝜎𝜃̂ ≤ 𝜃̂ − 𝜃 ≤ 𝑍𝛼 2⁄ 𝜎𝜃̂) = 1 − 𝛼 𝑃(−𝜃̂−𝑍𝛼 2⁄ 𝜎𝜃̂ ≤ −𝜃 ≤ −𝜃̂ + 𝑍𝛼 2⁄ 𝜎𝜃̂) = 1 − 𝛼 𝑃(𝜃̂ − 𝑍𝛼 2⁄ 𝜎𝜃̂ ≤ 𝜃 ≤ 𝜃̂ + 𝑍𝛼 2⁄ 𝜎𝜃̂) = 1 − 𝛼 Sehingga diperoleh, 𝜃̂𝐿 = 𝜃̂ − 𝑍𝛼 2⁄ 𝜎𝜃̂ dan 𝜃̂𝑈 = 𝜃̂ + 𝑍𝛼 2⁄ 𝜎𝜃̂
Maka dari itu, selang kepercayaan (1 − 𝛼)100% untuk 𝜃 adalah 𝜃̂ ± 𝑍𝛼 2⁄ 𝜎𝜃̂.
Contoh 2.26
Enam puluh empat kendaraan diamati secara acak untuk kecepatannya (dalam mph) di jalan raya yang batas kecepatannya adalah 70 mph. Diperoleh kecepatan rata-ratanya adalah 73.3 mph. Kita asumsikan bahwa kecepatan kendaraan berdistribusi Normal dengan 𝜎 = 3.2. Tentukan selang kepercayaan 90% untuk kecepatan rata-rata sebenarnya 𝜇, dari kendaraan di jalan raya tersebut.
Solusi:
Diketahui 𝜃 = 𝜇, sedemikian sehingga 𝜃̂ = 𝑥̅ = 73.3, 𝜎 = 3.2 dan 𝛼 = 0.10 untuk sampel 𝑛 = 64.
Selang kepercayaan
𝜃̂ ± 𝑍𝛼 2⁄ 𝜎𝜃̂
menjadi
𝑥̅ ± 𝑍𝛼 2⁄ 𝜎𝜃̂
Dari Tabel Distribusi Normal (Lampiran 1) diperoleh 𝑍𝛼 2⁄ 𝜎𝜃̂ = 𝑍0.05 = 1.645.
Diperoleh batas kepercayaan bawah dan batas kepercayaan atas 𝑥̅ − 𝑍𝛼 2⁄ (
𝜎
√𝑛) = 73.3 − 1.645 ( 3.2
𝑥̅ + 𝑍𝛼 2⁄ (
𝜎
√𝑛) = 73.3 + 1.645 ( 3.2
√64) = 73.958. Jadi, selang kepercayaan 90% bagi 𝜇 adalah (72.642, 73.958 ).
F. Metode Kemungkinan Maksimum (Maximum Likelihood)
Metode kemungkinan maksimum adalah teknik yang sangat luas dipakai dalam pendugaan suatu parameter distribusi data (Dempster et al.). Metode ini merupakan alternatif bagi metode kuadrat terkecil dengan memaksimumkan fungsi kemungkinan.
Definisi 2.29
Misalkan 𝑥1, 𝑥2, … , 𝑥𝑛 merupakan sampel pengamatan yang diambil secara acak yang bersesuian dengan variabel acak 𝑋1, 𝑋2, … , 𝑋𝑛 yang distribusinya bergantung pada parameter 𝜃. Jika 𝑋1, 𝑋2, … , 𝑋𝑛 merupakan variabel acak diskrit, fungsi
likelihood dari sampel, 𝐿(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃), didefinisikan sebagai probabilitas bersama dari 𝑥1, 𝑥2, … , 𝑥𝑛. . Jika 𝑋1, 𝑋2, … , 𝑋𝑛 merupakan variabel acak kontinu, fungsi likelihood dari sampel, 𝐿(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃), didefinisikan sebagai
probabilitas bersama dari 𝑥1, 𝑥2, … , 𝑥𝑛.
Jika himpunan dari variabel acak 𝑋1, 𝑋2, … , 𝑋𝑛 merupakan sampel acak dari distribusi diskrit dengan fungsi probabilitas 𝑝(𝑥|𝜃), maka
𝐿(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃) = 𝑝(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃) = 𝑝(𝑥1|𝜃) × 𝑝(𝑥2|𝜃) × … × 𝑝(𝑥𝑛|𝜃),
Jika 𝑋1, 𝑋2, … , 𝑋𝑛 merupakan distribusi kontinu dengan fungsi densitas 𝑓(𝑥|𝜃), maka
𝐿(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃) = 𝑓(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃) = 𝑓(𝑥1|𝜃) × 𝑓(𝑥2|𝜃) × … × 𝑓(𝑥𝑛|𝜃).
Biasanya notasi likelihood dengan 𝐿(𝜃) disederhanakan menjadi 𝐿(𝑥1, 𝑥2, … , 𝑥𝑛 |𝜃).
Definisi 2.30 Metode Kemungkinan Maksimum
Misalkan fungsi kemungkinan bergantung pada 𝑘 parameter-parameter 𝜃1, 𝜃2, … , 𝜃𝑘. Penduga kemungkinan maksimum adalah nilai-nilai penduga
parameter-parameternya yang memaksimalkan fungsi kemungkinan 𝐿(𝑥1, 𝑥2, … , 𝑥𝑛|𝜃1, 𝜃2, … , 𝜃𝑘).
Contoh 2.27
Misalkan 𝑋1, … , 𝑋𝑛 merupakan sampel acak dari Distribusi Poisson dengan parameter 𝜆. Tentukan penduga kemungkinan maksimum bagi 𝜆.
Solusi:
Kita memiliki fungsi probabilitas 𝑝(𝑥) =𝜆
𝑥𝑒−𝜆
𝑥! , 𝑥 = 0,1,2, … , 𝜆 > 0. Oleh karena itu, fungsi kemungkinannya adalah
𝐿(𝜆) = ∏𝜆 𝑥𝑒−𝜆 𝑥! 𝑛 𝑖=1 = 𝜆 ∑𝑛𝑖=1𝑥𝑖𝑒−𝑛𝜆 ∏𝑛𝑖=1𝑥𝑖! ,
Untuk mempermudah perhitungan akan digunakan transformasi logaritma, karena fungsi logaritma adalah fungsi yang monoton naik, sehingga memaksimalkan 𝑙𝑛 𝐿(𝜆) berarti juga memaksimalkan 𝐿(𝜆).
ln 𝐿(𝜆) = ∑ 𝑥𝑖 𝑛 𝑖=1 𝑙𝑛 𝜆 − 𝑛𝜆 − ∑ ln(𝑥𝑖!) 𝑛 𝑖=1
dan menurunkan terhadap 𝜆, didapat 𝑑 ln 𝐿(𝜆) 𝑑𝜆 = ∑𝑛𝑖=1𝑥𝑖 𝜆 − 𝑛 dan 𝑑 ln 𝐿(𝜆) 𝑑𝜆 = 0, maka ∑𝑛𝑖=1𝑥𝑖 𝜆 − 𝑛 = 0 (2.2)
Pembuat nol untuk persamaan (2.2) adalah ∑ 𝑥𝑖
𝑛 𝑖=1 𝜆 = 𝑛, sehingga diperoleh 𝜆 =∑ 𝑥𝑖 𝑛 𝑖=1 𝑛 = 𝑥̅. Maka dari itu, penduga bagi 𝜆 adalah
43 BAB III
METODE TABEL KEHIDUPAN
A. Analisis Ketahanan Hidup
Analisis ketahanan hidup adalah metode statistika untuk mempelajari suatu kejadian dan waktu kejadian. Waktu dalam analisis ketahanan hidup dapat berupa tahun, bulan, minggu atau hari dari awal pengamatan sampai terjadinya suatu kejadian. Dalam analisis ketahanan hidup variabel waktu direpresentasikan sebagai waktu ketahanan hidup dimana variabel tersebut menunjukkan bahwa seseorang dapat bertahan untuk beberapa jangka waktu. Kita bisa juga menyebut kejadian tersebut sebagai suatu kegagalan, contohnya kematian individu.
Waktu ketahanan hidup didefinisikan secara luas sebagai waktu terjadinya suatu kejadian. Pada bidang kesehatan, kejadian dalam analisis ketahanan hidup yang dimaksud adalah kematian yang dapat disebabkan karena suatu penyakit, kambuhnya suatu penyakit saat pengobatan berlangsung atau karena munculnya suatu penyakit baru. Data ketahanan hidup dapat meliputi waktu bertahan hidup, respon terhadap obat yang diberikan dan karakteristik pasien terkait dengan respon, ketahanan hidup, dan perkembangan suatu penyakit. Ketahanan hidup difokuskan pada prediksi atau peramalan probabilitas respon, kelangsungan hidup atau rata-rata waktu hidup, membandingkan distribusi ketahanan hidup dari percobaan hewan atau pasien dan mengidentifikasi risiko dan/atau faktor prognostik terkait dengan respon, ketahanan hidup, dan perkembangan suatu penyakit. Waktu ketahanan dalam analisis ketahanan hidup dikenal juga dengan waktu kegagalan atau failure time.
Analisis ketahanan hidup sangat berguna untuk mempelajari berbagai macam peristiwa, baik secara sosial dan ilmu pengetahuan alam, termasuk timbulnya suatu penyakit, kegagalan peralatan, gempa bumi, kecelakaan mobil, pasar saham, revolusi, pemutusan hubungan kerja, kelahiran, pernikahan, perceraian, promosi, pensiun dan penangkapan. Penyesuaian suatu materi sesuai dengan kebutuhan
menyebabkan metode ini mengalami banyak perkembangan yang ditemukan oleh para peneliti di bidang yang berbeda, sehingga terdapat beberapa istilah nama yang berbeda, seperti Analisis Peristiwa Sejarah (Sosiologi), Analisis Reliabilitas (Teknik), Kegagalan Analisis Waktu (Teknik), Analisis Durasi (Ekonomi) dan Analisis Transisi (Ekonomi) (Allison, 1995).
B. Data Tersensor
Banyak peneliti menganggap analisis data ketahanan hidup hanya sebagai aplikasi dari data metode statistika konvensional untuk jenis masalah khusus: parametrik jika distribusi waktu ketahanan hidup diketahui berdistribusi Normal dan non parametrik jika distribusi waktu ketahanan hidup tidak diketahui. Asumsi ini benar jika waktu ketahanan hidup dari semua subjek diketahui. Pada umumnya, waktu ketahanan hidup tidak demikian. Misalnya, terdapat pasien yang masih bertahan atau sembuh selama pengamatan berlangsung, tetapi waktu ketahanan hidup yang tepat dari pasien tidak diketahui. Hal ini disebut sebagai pengamatan tersensor atau waktu tersensor. Penyensoran didefinisikan sebagai hilangnya pengamatan pada variabel kehidupan dalam proses pengamatan (Xian Liu, 2012).
Secara umum, penyensoran dibagi menjadi beberapa tipe, yaitu penyensoran kana, penyensoran kiri dan penyensoran interval.
1. Penyensoran Kanan
Penyensoran kanan dibagi menjadi tiga kategori yaitu penyensoran tipe I, penyensoran tipe II dan penyensoran acak.
a. Penyensoran Tipe I
Penyensoran tipe I merupakan penyensoran dimana pengamatan akan dilakukan selama waktu 𝑇 yang telah ditentukan dan akan berakhir setelah mencapai waktu 𝑇, berakhirnya waktu 𝑇 menyatakan waktu tersensor. Penyensoran tipe I merujuk pada fakta bahwa semua pengamatan memiliki waktu yang sama. Bahkan pengamatan yang tidak disensor dikatakan untuk memiliki waktu tersensor. Penyensoran tipe I biasanya berhubungan dengan jangka pengamatan yang telah ditentukan sebelumnya. Secara matematis,