Bab VIII Aspek Kosmologi Teori Skalar-Vektor-Tensor
VIII.1 Pendahuluan
Kemungkinan invarian Lorentz dilanggar pada energi-energi tinggi dalam teori 4-dimensi dengan konsekuensi yang dapat diuji (Mattingly dan Vucetich, 2005) telah menjadi sebuah subjek riset yang sangat menarik akhir-akhir ini. Hasil-hasil tentatif dari gravitasi kuantum dan teori string menunjukan bahwa ada sebuah keadaan dasar (ground state) yang tidak invarian Lorentz. Teori string juga memprediksikan bahwa alam semesta dengan koordinat non komutatif (Connes, dkk., 1998) menuju sebuah pelanggaran invarian Lorentz (Carrol, dkk., 2001). Dari observasi astrofisika menunjukan bahwa keberadaan sinar kosmik energi tinggi disekitar ambang Greisen-Zatsepin-Kuzmin (GZK) dapat dijelaskan melalui pelanggaran invarian Lorentz (Chrisholm dan Kolb, 2004). Dari kebanyakan riset yang mengeksplorasi kemungkinan pelanggaran Lorentz terfokus pada fisika non gravitasional, yaitu ruang-waktu datar. Dalam ruang-waktu datar, pelanggaran Lorentz digambarkan oleh kopling konstan dari tensor yang tidak memenuhi simetri Lorentz. Untuk memformulasikan pelanggaran invarian Lorentz dalam ruang-waktu lengkung tanpa melanggar prinsip-prinsip kovariansi dari tensor maka tensor tersebut dipandang sebagai medan dinamik yang memenuhi persamaan-persamaan medan efektif.
Bab ini bertujuan untuk memberikan sebuah implementasi pelanggaran Lorentz dalam fisika gravitasional dengan meninjau sebuah medan vektor yang memiliki nilai ekspektasi vakum yang tidak lenyap dan mengkopel medan vektor dengan gravitasi atau medan-medan materi. Jika medan-medan materi adalah sebuah medan skalar maka teori yang dihasilkan adalah teori gravitasi skalar-vektor-tensor pelanggaran Lorentz. Kasus khusus dari teori ini tanpa medan skalar pertama kali diperkenalkan oleh Kostelecky dan Samuel (1989). Dalam konteks berbeda, Bekenstein (2004) juga mengkaji teori gravitasi dengan sebuah medan vektor untuk menjelaskan efek dari materi gelap. Medan vektor dapat menentukan sebuah kerangka universal pada setiap titik di dalam ruang-waktu dan setiap
medan-medan materi yang terkopel dengan medan ini akan mengalami pelanggaran invarian Lorentz lokal (Colladay dan Kostelecky, 1998).
Di dalam bab ini pula dipelajari beberapa akibat kosmologi dari pelanggaran Lorentz dalam konteks skalar-vektor-tensor. Pertama dibahas formulasi umum dari teori skalar-vektor-tensor pelanggaran Lorentz dengan meninjau kopling antara medan skalar dan medan vektor adalah bergantung waktu. Evolusi waktu dari parameter-parameternya dapat dipandang sebagai sebuah konsekuensi dari dinamika medan skalar. Kemudian dengan menggunakan persamaan-persamaan dinamika, diturunkan persamaan keadaan dalam ungkapan parameter vektor kopling. Konsekuensi kosmologi dari medan skalar menggelinding yaitu inflasi dibahas untuk beberapa model yang diberikan. Akhirnya, titik-titik kritis dari sistem global ditinjau untuk mempelajari stabilitas sistem.
VIII.2 Teori Gravitasi Skalar-Vektor-Tensor
Di dalam sub bab ini dibahas skema dari teori skalar-vektor-tensor dengan meninjau alam semesta 4-dimensi di mana ada derajat kebebasan non-gravitasional dalam kerangka kerja teori gravitasi skalar-vektor-tensor Asumsikan bahwa ada simetri Lorentz yang dilanggar secara spontan dengan nilai ekspektasi dari sebuah medan vektor diberikan oleh .
Tinjau sebuah aksi sebagai jumlah dari tiga aksi yang berbeda
(VIII.1) di mana aksi untuk medan tensor, , medan vektor, , dan medan skalar, , berturut-turut diberikan sebagai berikut:
(VIII.2)
(VIII.3)
Disini ( ) adalah parameter sembarang dan adalah rapat Lagrangian medan skalar dinyatakan sebagai fungsi dari metrik dan medan skalar . λ adalah sebuah pengali Lagrange yang memberikan kendala medan vektor menjadi serupa waktu. Selanjutnya aksi (VIII.1) dapat dipandang sebagai sebuah aksi yang menggambarkan teori gravitasi skalar-vektor-tensor. Pada persamaan (VIII.3), oleh nilai ekspektasi vakum, medan vektor memenuhi sebuah kendala
(VIII.5) Selanjutnya pula, telah diambil medan vektor sebagai sebuah vektor tak berdimensi dan akibatnya parameter memiliki dimensi kuadrat massa. Dengan kata lain, memberikan deskripsi skala massa pada perusakan simetri. Secara prinsip, kerangka acuan diam khusus pada setiap titik dalam ruang-waktu ditentukan oleh medan vektor yang melanggar simetri Lorentz.
Solusi persamaan gerak dapat diperoleh dengan mengasumsikan bahwa alam semesta memiliki sifat homogen dan isotropik. Untuk itu, metrik ruang-waktu dapat dipilih metrik Friedmann-Robertson-Walker:
(VIII.6) Faktor skala dari alam semesta ditentukan oleh . Karena adalah medan vektor yang dinamik maka persamaan kendala (VIII.5) menghasilkan
(VIII.7) Variasi aksi persamaan (VIII.1) terhadap metric menghasilkan persamaan medan Einstein berikut ini:
(VIII.8) di mana adalah tensor energi-momentum total, . dan berturut-turut menyatakan tensor energi-momentum medan vektor dan medan skalar yang didefinisikan melalui perumusan standar
(VIII.9) Komponen waktu dan komponen ruang dari tensor energi-momentum total diberikan oleh
(VIII.10) di mana rapat energi dan tekanan dari medan vektor adalah
(VIII.11)
Sebagai catatan bahwa kopling parameter tidak memberikan kontribusi dinamik. Di dalam persamaan (VIII.11), tanda aksen menyatakan turunan dari setiap kuantitas terhadap , sehingga dihubungkan dengan turunan terhadap waktu oleh persamaan berikut:
(VIII.12) Kuantitas menyatakan parameter Hubble. Dari persamaan (VIII.11) dapat dilihat bahwa persamaan energi untuk medan vektor diberikan oleh
(VIII.13) Untuk mempertahankan hukum kekekalan energi total,
(VIII.14) maka persamaan energi untuk medan skalar memenuhi
(VIII.15)
Persamaan energi total (VIII.14) dapat diperoleh melalui ketidakdivergenan secara kovarian tensor energi-momentum total sebagai akibat dari lenyapnya divergensi tensor Einstein secara geometrik yaitu dari kontraksi geometrik identitas Bianchi. Ruas kanan persamaan (VIII.13) dan persamaan (VIII.14) dipandang sebagai sebuah suku interaksi antara medan vektor dan medan skalar sebagai akibat dari kopling parameter yang bergantung pada medan skalar dan tentunya juga terhadap waktu.
Dengan memanfaatkan komponen waktu dan komponen ruang persamaan (VIII.10) dan persamaan Einstein (VIII.8), dapat diperoleh dua buah persamaan bebas yang dinamakan sebagai persamaan Friedmann sebagai berikut:
(VIII.16) (VIII.17) Kedua persamaan Friedmann di atas dapat ditulis kembali dalam bentuk yang lebih sederhana:
(VIII.18)
(VIII.19) Suku kedua pada ruas kanan persamaan (VIII.19) adalah sebuah akibat dari medan vektor kopling yang tidak konstan. Jika , tanpa medan vektor, persamaan (VIII.18) dan persamaan (VIII.19) tidak lain adalah persaman gerak untuk teori skalar-tensor. Sedangkan, jika , persamaan tersebut menjadi persamaan yang telah dipelajari oleh Carrol dan Lim (2004).
Dengan menggunakan persamaan (VIII.18) dan persamaan (VIII.15) dapat diperoleh tiga buah persamaan berikut:
(VIII.20)
(VIII.21)
(VIII.22) di mana
(VIII.23) dan adalah persamaan keadaan dari medan skalar. Dapat pula dilihat bahwa persamaan-persamaan (VIII.20) – (VIII.22) memenuhi kendala:
(VIII.24) dan juga oleh persamaan Friedmann (VIII.19). Solusi dari sistem persamaan (VIII.21) – (VIII.23) dan (VIII.24) bergantung pada model yang ditinjau dan jenis
materi yang ada dalam alam semesta. Solusi umum persamaan-persamaan tersebut adalah:
(VIII.25)
(VIII.26)
(VIII.27) Jika fungsi-fungsi dan diberikan, maka dapat diperoleh evolusi parameter Hubble dalam pelanggaran Lorentz. Misalnya, konstanta kosmologi adalah suatu fluida yang memiliki persamaan keadaan konstan . Sehingga persamaan di atas memiliki solusi: , dan di mana dan masing-masing merupakan fungsi dari . Jika merupakan parameter konstan dari suatu bentuk fluida dan diberikan, persamaan (VIII.25) - (VIII.27) dapat digunakan untuk menentukan kopling vektor dan rapat energi medan skalar
, kemudian potensial dari medan skalar dapat ditentukan.
VIII.3 Persamaan Dinamika Medan Skalar
Jika bentuk Lagrangian dari sebuah medan skalar diberikan di dalam ruang-waktu FRW, maka dapat diperoleh persamaan gerak untuk medan skalar dengan memanfaatkan persamaan-persamaan (VIII.15) dan (VIII.20) – (VIII.22). Untuk itu, tinjau sebuah rapat Lagrangian dari sebuah medan skalar yang memiliki potensial di dalam persamaan (VIII.1),
(VIII.28) di mana dan untuk medan skalar biasa. Sedangkan
untuk medan skalar phantom. Dengan asumsi bahwa medan skalar adalah homogen, sebagai fungsi dari waktu, maka maka rapat energi dan tekanan dapat diperoleh, yaitu
(VIII.29) (VIII.30)
Dari kedua persamaan di atas, parameter persamaan keadaan diberikan oleh (VIII.31) Substitusi persamaan (VIII.29) ke dalam persamaan (VIII.18), maka persamaan Friedmann dapat dinyatakan kembali dalam bentuk
(VIII.32) Kemudian dengan mengambil turunan persamaan (VIII.18) terhadap serta menggunakan persamaan (VIII.15), dapat diperoleh persamaan gerak untuk medan skalar:
(VIII.33) Selanjutnya, turunan terhadap dari persamaan (VIII.32) dan dengan memanfaatkan persamaan (VIII.33), persamaan gerak medan skalar menjadi
(VIII.34) Substitusi (VIII.34) ke dalam persamaan Friedmann, menghasilkan ungkapan untuk potensial medan skalar
(VIII.35) Di dalam persamaan di atas, parameter Hubble, , dinyatakan sebagai fungsi dari medan skalar , . Dari persamaan (VIII.20), persamaan keadaan untuk medan skalar dapat ditulis kembali dalam bentuk
(VIII.36) Persamaan-persamaan (VIII.34) dan (VIII.36) adalah dua buah persamaan yang dapat digunakan untuk memperoleh solusi medan skalar dan persamaan keadaannya . Hal ini dapat dikerjakan jika parameter Hubble dan vektor kopling diketahui. Dengan menentukan kedua parameter tersebut, dapat diperoleh solusi eksak persamaan-persamaan (VIII.34) dan (VIII.36). Persamaan-persamaan tersebut dapat dimanfaatkan untuk memperoleh kuantitas-kuantitas fisis berikut: potensial , energi kinetik ( ), rapat energi ( ) dan tekanan ( ),
(VIII.37)
VIII.3.1 Solusi Eksak dan Evolusi Medan Skalar
Pertama diselesaikan persamaan-persamaan (VIII.34) dan (VIII.36) untuk , , , dan , yang memerlukan dua buah kuantitas harus diketahui. Berikut ini dicari solusi-solusi eksak dari persamaan keadaan medan skalar untuk kopling vektor kudratik medan skalar. Zlatev, dkk., (1999) telah mempelajari persamaan keadaan medan skalar dalam konteks kosmologi dengan medan skalar sebagai medan tracker serta ditinjau pula beberapa jenis potensial yang menghasilkan dinamika persamaan keadaan.
Tinjau sebuah model berikut ini:
(VIII.38)
di mana dan adalah parameter-parameter konstan. Setelah mengintegrasi persamaan (VIII.34) maka persamaan evolusi untuk medan skalar diberikan oleh:
(VIII.39) Di dalam persamaan di atas adalah sebuah konstanta. Kemudian persamaan keadaan medan skalar menjadi
(VIII.40)
Evolusi dari potensial, energi kinetik, rapat energi dan tekanan berturut-turut adalah
(VIII.41)
Solusi-solusi yang diberikan pada persamaan di atas sepenuhnya terkait dengan pelangggaran Lorentz yang dinyatakan oleh kopling parameter . Dari model yang diberikan oleh persamaan (VIII.38), evolusi kosmik dimulai dari faktor skala
yang konstan kemudian bertambah secara eksponensial, . Vektor kopling mulai dari medan skalar yang konstan, , kemudian menurun secara eksponensial untuki medan skalar biasa dan untuk kasus medan phantom evolusi dari vektor kopling menjadi menurun. Sedangkan potensial, energi kinetik, rapat energi dan tekanan adalah fungsi-fungsi eksponensial terhadap waktu dan kuantitas tersebut menurun untuk medan skalar biasa. Untuk medan phantom potensial dan rapat energinya bertambah secara eksponensial. Energi kinetik dan tekanan untuk medan skalar biasa mulai dengan besaran negatif. Persamaan keadaan menjadi besaran yang tidak dinamik dan hanya bergantung pada nilai dari parameter kopling baik untuk medan skalar biasa maupun medan phantom. Agar ekspansi yang dipercepat dapat terjadi maka parameter kopling memiliki nilai untuk medan skalar biasa. Dari hasil observasi, persamaan keadaan memiliki nilai lebih kecil dari . Jadi nilai dapat dipilih sesuai dengan hasil observasi. Untuk kasus di mana dan
, juga diperoleh persamaan keadaan yang konstan,
(VIII.42) Syarat bagi alam semesta yang dipercepat atau menghasilkan
(VIII.43) Untuk model di atas diperoleh ekspansi fungsi pangkat yang memiliki bentuk
(VIII.44) di mana pangkatnya didefinisikan oleh
(VIII.45) Evolusi dari medan skalar diberikan oleh
VIII.3.2 Dinamika Persamaan Keadaan
Tinjau sebuah model di mana vektor kopling diberikan dalam bentuk fungsi pangkat dari medan skalar
( )
0, ,
n
H =H β φ =mφ n>2. (VIII.47) Disini , m dan n adalah parameter-parameter konstan. Dengan mengikuti
langkah-langkah penurunan sebelumnya, evolusi dari medan skalar diperoleh sebagai berikut 0 H
( )
(
)
(
)
( ) 0 1 2 2 0 0 0 1 2 2 n n t mnH n t t φ φ η φ − − = ⎡ + − − ⎤ ⎣ ⎦ , (VIII.48)dan vektor kopling diberikan oleh
( )
(
)
(
)
( ) 0 2 2 0 0 0 1 2 2 n n n n m t mnH n t t φ β η φ − − = ⎡ + − − ⎤ ⎣ ⎦ . (VIII.49)Sedangkan persamaan keadaan (VIII.36) menghasilkan
( )
(
2 0)
2(
)
2 0 0 4 3 1 1 2 2 n n mn t mnH n t t η φ ω η φ − − = − + + − − 0 . (VIII.50)Potensial, energi kinetik, rapat energi dan tekanan medan skalar memilki solusi
( )
(
)
(
)
2 2 2 2 0 0 0 2 0 0 0 2 3 3 1 1 2 2 n n mn V t mH mnH n t t η φ φ η φ − − ⎡ ⎤ = ⎢ − ⎥× + − − ⎣ ⎦(
)
2(
)
( 2) 0 0 0 1 1 2ηmnH n 2 φn− t t n n− × ⎡ + − − ⎤ ⎣ ⎦ , (VIII.51)( )
(
)
(
)
(
)
( ) ( ) 2 1 0 0 2 1 2 2 0 0 0 2 1 2 2 n n n n mnH K t mnH n t t η φ η φ − − − − = ⎡ + − − ⎤ ⎣ ⎦ , (VIII.52)( )
(
)
(
)
( ) 2 0 0 2 2 0 0 0 3 1 2 2 n n n n mH t mnH n t t φ ρ η φ − − = ⎡ + − − ⎤ ⎣ ⎦ , (VIII.53)( )
(
)
(
)
2 2 2 2 0 0 0 2 0 0 0 4 3 3 1 1 2 2 n n mn p t mH mnH n t t η φ φ η φ − − ⎡ ⎤ = ⎢− + ⎥× + − − ⎣ ⎦(
)
2(
)
( 2) 0 0 0 1 1 2ηmnH n 2 φn− t t n n− × ⎡ + − − ⎤ ⎣ ⎦ . (VIII.54)Dari solusi-solusi di atas bahwa model (VIII.47) menggambarkan dinamika evolusi yang dimulai dari faktor skala yang konstan kemudian naik secara eksponensial, . Vektor kopling juga mulai dari nilai yang konstan 0 0 ( ) exp[ ( )] a t =a H t−t0 2 0
mφ . Persamaan keadaan menjadi dinamik baik untuk medan skalar biasa maupun medan phantom. Kemudian, potensial, energi kinetik, rapat energi dan tekanan menurun untuk medan skalar biasa sedangkan untuk medan phantom potensial dan rapat energi bertambah besar.
VIII.4 Skenario Inflasi Pelanggaran Lorentz
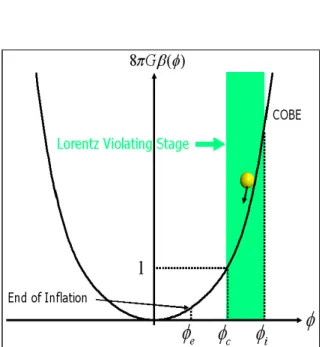
Pelanggaran Lorentz di dalam skenario inflasi dapat dibedakan menjadi dua bagian: daerah gelindingan perlahan (slow-roll) pelanggaran Lorentz, 8π βG >>1, dan daerah gelindingan perlahan standar, 8π βG <<1. Kasus pertama terkait dengan β β= pada persamaan (VIII.23) dan kasus kedua terkait dengan
1
(8 G) β = π −
yang menggambarkan inflasi standar.
Di dalam sub bab ini ditinjau skenario inflasi medan skalar yang didasarkan atas teori skalar-vektor-tensor. Vektor kopling dan potensial diberikan sebagai model dan dinamikanya digambarkan oleh persamaan Friedmann dan persamaan gerak medan skalar. Dari hasil yang diperoleh pada sub Bab VIII.2, persamaan-persamaan dinamika tersebut adalah
( )
2 1 1 2 2 3 2 H H φ V φ β ⎡ ′ ⎤ = ⎢ + ⎥ ⎣ ⎦ , (VIII.55) 2 1 0 2 H H φ β β β ′ ′ ′ + + = , (VIII.56) , , 2 3 V 3 H H H φ φ φ′′+ ′φ′+ φ′+ + β =0. (VIII.57) Persamaan-persamaan dinamika di atas menghasilkan nilai kritis dari medan skalar (lihat Gambar VIII.1) yang didefinisikan oleh( )
8π β φG c =1. (VIII.58)
Sebagai contoh, parameter kopling dengan bentuk β =nφ2 maka persamaan (VIII.58) menghasilkan
8 pl c M n φ π = . (VIII.59)
Gambar VIII.1 Sebuah titik kritis di mana kopling antara vektor pelanggaran Lorentz dan medan skalar menjadi tidak efektif (Kanno dan Soda, 2006).
Misalkan φi menyatakan nilai awal dari medan skalar. Dengan mengambil ~ 3
i Mpl
φ , syarat φ φi > c menghasilkan parameter kopling n>1/(72 ) ~ 1/ 226π agar terjadi inflasi pelanggaran Lorentz. Sedangkan jika φ φi < c , efek dari pelanggaran Lorentz dapat diabaikan. Berikut ini ditinjau sebuah model vektor kopling yang diberikan oleh
( )
mn
β φ = φ , (VIII.60)
dengan m dan n adalah parameter-parameter. Untuk model ini, nilai kritis dari medan skalar adalah
1 2 8 m pl c M n φ π ⎛ ⎞ = ⎜⎜ ⎟⎟ ⎝ ⎠ , dan
(
)
2 8 3 pl m pl M n M π > . (VIII.61) Ada beberapa tipe potensial yang dapat menghasilkan inflasi dalam kosmologi standar. Di dalam skenario teori scalar-vektor-tensor, inflasi dapat terjadi tanpa potensial (Kanno dan Soda, 2006). Pada pasal berikut ini ditinjau dua tipe potensial yaitu potensial fungsi pangkat kebalikan (inverse power-law potential)dan potensial fungsi pangkat (power-law potential). Solusi dan analisanya dibahas untuk masing-masing daerah inflasi.
VIII.4.1 Potensial Fungsi Pangkat Kebalikan Tinjau sebuah potensial dalam bentuk
( )
4V φ =μ φ+ν −ν. (VIII.62) Disini μ dan ν adalah konstanta-konstanta. Model potensial fungsi pangkat kebalikan dalam kosmologi standar dapat menghasilkan perturbasi tensor untuk fluktuasi medan skalar skala-invarian (Barrow, 1990) dan juga dapat dihasilkan dalam model supersimetrik QCD (Binetruy, 1999).
VIII.4.1.1 Daerah Gelindingan Perlahan Pelanggaran Lorentz
Untuk nilai medan skalar φ yang cukup besar, fungsi kopling β(φ) dan fungsi potensial V(φ) keduannya memberikan kontribusi dalam model yang ditinjau. Selama inflasi, efek pelanggaran Lorentz terhadap dinamika inflasi juga besar. Dalam daerah pelanggaran Lorentz persamaan Friedmann dan persamaan gerak medan skalar diberikan oleh
( )
2 1 1 2 2 3 2 H H φ V φ β ⎡ ′ ⎤ = ⎢ + ⎥ ⎣ ⎦, (VIII.63) 2 1 0 2 H H φ β β β ′ ′ ′ + + = , (VIII.64) , , 2 3 V 3 H H H φ φ φ′′+ ′φ′+ φ′+ + β =0. (VIII.65) Ketika terjadi inflasi, faktor skala menghasilkan sebuah percepatan dan medan skalar berevolusi lebih lambat dibandingkan dengan ekspansi alam semesta. Sehingga medan skalar memenuhi syarat menggelinding perlahan2 2
H φ′ << V, φ′′<<φ′, φ′2<<β dan β′<<β. (VIII.66) Dengan syarat ini persamaan (VIII.63) – (VIII.65) menjadi
2 H ~ 3 V β , φ′~ , V, V φ φ β β β ⎛ ⎞ − ⎜ + ⎝ ⎠⎟. (VIII.67)
Dari model yang diberikan, potensial oleh persamaan (VIII.62) dan kopling vektor oleh persamaan (VIII.60), maka dapat diperoleh
( 4 2 3 m H n ν ν μ + φ − + = ), (VIII.68)
(
)
(m 1) n m φ′ = − −ν φ − . (VIII.69)Solusi dari medan skalar sebagai fungsi dari faktor skala dapat diperoleh dengan mengintegrasi persamaan (VIII.69),
( )
2(
)(
)(
)
1( 2) 2 m , m i n m m i m 2,m φ α =⎡φ − + − −ν α α− ⎤− − ≠ ≠ν ⎣ ⎦ , (VIII.70)dengan φ α α
(
= 1)
≡φi adalah suatu konstanta. Persamaan Friedmann menjadi(
)(
)(
)
( ) ( ) 4 2 2 2 2 3 m m m i H n m m n ν ν μ + φ ν α α i + − − ⎡ = ⎣ + − − − ⎤⎦ . (VIII.71)Agar solusi yang diberikan oleh persamaan (VIII.70) memenuhi syarat gelindingan perlahan (VIII.66) selama terjadi pelanggaran Lorentz, maka pangkat m dari kopling vektor memenuhi m>2 karena:
2
φ′ (~α−2 1( −m) (2−m))<<β(~αm(2−m)), (VIII.72) β′(~α−2 1(−m) (2−m))<<β(~αm(2−m)). (VIII.73) Ekspansi alam semesta yang terjadi pada daerah pelanggaran Lorentz diberikan oleh evolusi faktor skala,
( )
(
)(
)
1( 1) 1 1 1 exp 1 , 0 D i D i a t B AC D t t C a C C B − − − ⎧ ⎫ ⎪ ⎛ ⎞ ⎪ = ⎨− + ⎜ − − − ⎟ ⎬ ≠ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ , (VIII.74)dengan A, B, C dan D adalah konstanta-konstanta yang didefinisikan sebagai berikut:
(
)(
)
(
)
4 2 , , 2 , 3 2 m i m A B C n m m D n m ν 2 μ + φ ν ν − + = = = − − = − . (VIII.75) Dengan memanfaatkan persamaan-persamaan (VIII.70), (VIII.71) dan (VIII.74) maka evolusi waktu dari kuantitas-kuantitas medan skalar, parameter Hubble dan kopling vektor berturut-turut adalah( )
1(
)(
)
1( 1)( 2) 1 1 D m i D t AC D t t B φ − − − ⎛ =⎜ − − − ⎝ ⎠ ⎞ ⎟ , (VIII.76)( )
1(
)(
)
( 1) 1 1 D D i D H t A AC D t t B − − − ⎛ = ⎜ − − − ⎝ ⎠ ⎞ ⎟ , (VIII.77)( )
1(
)(
)
( 1)( 2) 1 1 m D m i D t n AC D t t B β = ⎛⎜ − − − − − − ⎝ ⎠ ⎞ ⎟ . (VIII.78)Evolusi dari rapat energi medan skalar diberikan oleh
( )
2(
)(
)
( 2 ( 2)) ( 1)( 2) 1 1 3 1 m D m D m i D t V nA AC D t t B ρ − − − − − ⎛ ⎞ = ⎜ − − − ⎟ ⎝ ⎠ . (VIII.79)Persamaan (VIII.77) menunjukkan bahwa parameter Hubble menurun selama terjadi inflasi, hal ini adalah sebuah konsekuensi dari pelanggaran Lorentz.
Setelah mensubstitusikan persamaan (VIII.60) ke persamaan (VIII.67) maka untuk m=2,ν ≠2 evolusi dari medan skalar diberikan oleh
( )
n(2 )( i)ie
ν α α
φ α =φ − − −
, (VIII.80)
dengan φ α α
(
= i)
≡φi. Agar solusi ini memenuhi syarat gelindingan perlahan maka(
)
2 1 2 n ν < − . (VIII.81)Sehingga kisaran dari parameter n di mana inflasi pelanggaran Lorentz terjadi adalah
(
)
21 1
226< <n 2−ν . (VIII.82)
Parameter Hubble sebagai fungsi dari faktor skala diberikan oleh
( )
( 2 4)( 2 2 n i i H α =H e− ν − α α− ), (VIII.83) di mana ( ) 4 2 2 3 i i H n ν ν μ φ + + = . (VIII.84)Faktor skala juga dapat diungkapkan sebagai fungsi dari medan skalar
( )
( )
1n( 2) i i a t t a ν φ φ − ⎡ ⎤ = ⎢ ⎥ ⎣ ⎦ . (VIII.84)Sehingga evolusi waktu dari kuantitas-kuantitas fisis dapat dirangkum sebagai berikut:
( )
(
)
(
)
1 ( 2 ) 2 2 4 n i i i a t n H t t a ν ν −4 ⎡ =⎣ − − ⎤⎦ , (VIII.85)( )
(
)
(
)
1( 2) 2 2 4 i i i t n H t t ν φ ν φ + ⎡ =⎣ − − ⎤⎦ , (VIII.86)( )
(
2)
(
)
2 4 i i H t n t H = ν − −t , (VIII.87)( )
(
)
(
)
2( 2) 2 2 2 4 i i i t n H t t n ν β ν φ + ⎡ =⎣ − − ⎤⎦ . (VIII.88)Dan evolusi dari rapat energi medan skalar adalah
( )
4(
)
(
)
( 2) 2 2 4 i i i t n H t t ν ν ν μ ρ ν φ + − + ⎡ = ⎣ − − ⎤⎦ . (VIII.89)VIII.4.1.2 Daerah Gelindingan Perlahan Standar
Setelah medan skalar melewati nilai kritis φc, dinamika inflasi ditentukan oleh potensial V. Untuk daerah gelindingan perlahan standar persmaan Friedmann dan persamaan gerak medan skalar menjadi
2 8 1 2 2 3 2 G H = π ⎡⎢ H φ′ +V⎤⎥ ⎣ ⎦, (VIII.90) 2 4 H G H π φ ′ ′ + =0, (VIII.91) , 2 3 V H H H φ φ′′+ ′φ′+ φ′+ =0. (VIII.92) Syarat gelindingan perlahan standar menghasilkan persamaan gelindingan perlahan 2 H ≈ 8 3 G V π , φ′ ≈ 1 , 8 V G V φ π . (VIII.93)
Untuk potensial fungsi pangkat kebalikan, persamaan evolusi dari medan skalar inflaton dan parameter Hubble sebagai fungsi dari faktor skala adalah
( )
(
2 2 4 c G c)
ν φ α φ α α π = + − , (VIII.94)( )
(
)
2 2 8 4 2 3 c 4 G H G c ν ν π ν α μ φ α α π − + ⎡ ⎤ = ⎢ + − ⎥ ⎣ ⎦ . (VIII.95)Solusi untuk faktor skala diperoleh
( )
4(
2( )
2 exp c c a t G t a π φ φ ν)
⎡ ⎤ = ⎢ − ⎥ ⎣ ⎦. (VIII.96)Ketika syarat gelindingan perlahan dilanggar maka inflasi pada daerah standar berakhir dan alam semesta mulai dengan periode pemanasan kembali (reheating). Persamaan-persamaan evolusinya diberikan oleh
( )
(
(
)(
)
( ))
1 1 1 1 exp s Ds 1 Ds s s s s c c s s a t B B A C D t t a C C + + ⎧ ⎫ = ⎨− + + + − ⎬ ⎩ ⎭, (VIII.97)( )
(
1(
)(
)
)
1 2( 1) 1 s s D D s s s s c t B A C D t t φ = + + + − + , (VIII.98)( )
(
1(
)(
)
)
( 1) 1 s s s D D D s s s s s c H t = A B + +A C D + t−t + . (VIII.99)( )
3 2(
1(
)(
)
)
2 ( ) 1 8 s s s D D D s s s s s s c s A C t B A C D t t D ρ ⎛ ⎞ + +1 = ⎜ ⎟ + + − ⎝ ⎠ , (VIII.100) di mana 4 2 8 , , , 3 4 s s c s G A B C G ν 4 s D π μ φ ν ν π + = = = = . (VIII.101)Berbeda dengan daerah inflasi pelanggran Lorentz pada daerah gelindingan perlahan standar, parameter Hubble bertambah besar selama evolusi. Kuantitas lain yang dihitung selama fasa inflansi adalah jumlah e-folding. Jumlah e-folding total diberikan oleh
(
)(
)
( ) 1 1 1 1 1 1 D c i D B N AC D t C C B t − − − ⎛ ⎞ = − + ⎜ − − − ⎟ ⎝ ⎠ 1(
s 1(
1)(
)
)
1( s 1) D D s s s s s e c s s B B A C D t t C C + + − + + + −(
2 2)
(
2 2 1 4 , m m c i e c G C)
π φ φ φ ν − − = − + −φ . (VIII.102) untuk m>2,ν ≠m dan(
2)
(
2)
2(
)
1 log 4 4 i c i N n H n ν ν t t ⎡ ⎤ = ⎣ − − ⎦ −(
(
)(
)
)
( ) 1 1 1 1 1 s s D D s s s s s e c s s B B A C D t t C C + + − + + + −(
21)
log 4(
2 2 , i e c c G n φ π φ φ)
ν φ ν ⎛ ⎞ = ⎜ ⎟+ − ⎝ ⎠ − (VIII.103)untuk m=2,ν ≠2. Di dalam persamaan-persamaan di atas, suku pertama adalah kontribusi dari daerah inflasi pelanggaran Lorentz dan suku kedua adalah kontribusi dari daerah inflasi standar. Sebuah contoh, jika nilai-nilai parameter diambil sebagai berikut: N = 70, n = 10-2, m = 2 dan ν = 1. Jika φe ~ 0.3 Mpl
adalah besaran medan skalar pada akhir inflasi maka diperoleh nilai kritisnya φc ~2Mpl dan besaran ini masih lebih kecil dari φi~ 2.5Mpl. Sehingga kontribusi dari akhir inflasi masih relevan.
VIII.4.2 Potensial Fungsi Pangkat
Pada pasal ini ditinjau untuk potensial fungsi pangkat, dibatasi hanya pada pangkat dua, yaitu
( )
1 2 22
V φ = M φ . (VIII.104)
VIII.4.2.1 Daerah Gelindingan Perlahan Pelanggaran Lorentz
Untuk model potensial yang diberikan oleh persamaan (VIII.104) dan memanfaatkan syarat gelindingan perlahan, maka persamaan gelindingan perlahan pada daerah pelanggaran Lorentz adalah
( ) 2 2 2 6 m M H n φ − − = , (VIII.105)
(
)
( 1) 2 m n m φ′ = − + φ − . (VIII.106)Solusi untuk medan skalar diberikan oleh
( )
(
)
(
)
1 2( ) 2 2 4 m m i n m φ α =⎡φ − + − α α− − ⎣ i ⎤⎦ , (VIII.107) untuk m≠2 dan( )
4n( i) ie α α φ α =φ − − , (VIII.108)untuk m=2. Skenario untuk kasus m=2 telah dikaji oleh Kanno dan Soda (2006), diperoleh bahwa parameter Hubble menjadi konstan selama inflasi daerah
pelanggaran Lorentz. Disini akan dibahas untuk kasus m≠2 dan parameter Hubble diberikan oleh
( )
2(
)
(
2 2 2 4 6 m i M H n m n i)
α = ⎡φ − + − α −α ⎤ ⎣ ⎦, (VIII.109)dan solusi untuk faktor skala diberikan oleh
( )
(
2)
2( )
2 1 1 1 exp 4 m m i i a t a n m φ − t φ − ⎡ ⎛ ⎞⎤ ⎢ ⎥ = ⎜⎜ − − ⎟⎟ ⎢ ⎝ ⎠⎥ ⎣ ⎦ . (VIII.110)Seperti juga dalam kasus sebelumnya, untuk efek pelanggaran Lorentz dapat terjadi. Evolusi waktu dari persamaan (VIII.110) adalah
2 m>
( )
1 1 2 1(
)
2 2 i b t b dc t c c α α ti ⎡ ⎤ = − + ⎢ + − ⎥ ⎣ ⎦ , (VIII.111) di mana(
)
2 2 2 , 4 , , 6 m i M b c n m d m n φ − = = − = >2. (VIII.112)Dengan memanfaatkan solusi (VIII.111) maka diperoleh
( )
(
)
2 1 2 1 1 exp 2 i i a t b b dc t t a c c ⎧ ⎫ ⎪ ⎡ ⎤ ⎪ = ⎨− + ⎢ + − ⎥ ⎬ ⎣ ⎦ ⎪ ⎪ ⎩ ⎭, (VIII.113)( )
1 2 1(
)
2( 2) 2 m i t b dc t t φ =⎡ + − − − ⎢⎣ ⎦ ⎤ ⎥ , (VIII.114)( )
1 2 1(
)
2 i H t =d b⎡⎢ + dc t−t ⎤⎥ ⎣ ⎦, (VIII.115)( )
1 2 1(
)
2 ( 2) 2 m m i t n b dc t t β − − ⎡ ⎤ = ⎢ + − ⎥ ⎣ ⎦ , (VIII.116)( )
2 1 2 1(
)
4( 2) 3 2 m i t nd b dc t t ρ = ⎡ + − − − ⎢⎣ ⎦ ⎤ ⎥ , (VIII.117)di mana b, c, dan d adalah konstanta-konstanta positif. Hasil yang signifikan adalah parameter Hubble dan faktor skala bertambah besar selama inflasi pelanggaran Lorentz untuk m>2 . Sedangkan untuk m=2 parameter Hubble adalah konstan. Pada pasal berikut ini dapat dilihat bahwa parameter Hubble menurun dalam daerah gelindingan perlahan standar. Sehingga selama periode inflasi dapat dihasilkan spektrum dengan spektrum awal biru dan kemudian
spektrum warna merah. Hal ini dapat menjelaskan spektrum daya CMB pada skala besar yang diamati oleh WMAP (Bennet, dkk., 2003). Secara kualitatif dapat dijelaskan sebagai berikut. Ketika parameter Hubble bertambah besar maka medan skalar memiliki energi yang tinggi selama periode inflasi pelanggaran Lorentz dan dapat menghasilkan spektrum warna biru. Sebaliknya, dalam daerah gelindingan perlahan standar, parameter Hubble menurun yang berarti energi medan skalar menurun dan kemudian menghasilkan spektrum warna merah.
VIII.4.2.2 Daerah Gelindingan Perlahan Standar
Berikut ini ditinjau skenario inflasi chaotic dalam daerah gelindingan perlahan standar. Persamaan Friedmann dan persamaan gerak diberikan oleh persamaan (VIII.90) – (VIII.92). Dengan asumsi syarat gelindingan perlahan standar dipenuhi maka persamaan gelindingan perlahan diberikan oleh
2 H ≈ 4 2 2 3 G M π φ , (VIII.118) φ′ ≈ 1 1 4πGφ − . (VIII.119)
Persamaan-persamaan evolusi sebagai fungsi dari faktor skala adalah
( )
(
2 2 1 2 c G c)
φ α φ α α π = − − , (VIII.120)(
2 2 4 2 1 3 c 2 GM H G π φ α π ⎛ = ⎜ − − ⎝ αc)
⎠ ⎞ ⎟. (VIII.121)Integrasi persamaan (VIII.121) menghasilkan
( )
1 1 2 1(
)
2 2 s c s s s s s b t b d c t c c α −α = − ⎡⎢ − −tc ⎤⎥ ⎣ ⎦ . (VIII.122)Dengan memanfaatkan hubungan ini, dinamika evolusi dari alam semesta digambarkan oleh persamaan berikut:
( )
(
)
2 1 2 1 1 exp 2 s s s s c c s s a t b b d c t t a c c ⎧ ⎫ ⎪ ⎡ ⎤ ⎪ = ⎨ − ⎢ − − ⎥ ⎬ ⎣ ⎦ ⎪ ⎪ ⎩ ⎭, (VIII.123)( )
1 2 1(
2)
s s s c t b d c t t φ = − − , (VIII.124)( )
1 2 1(
)
2 s s s s c H t =d ⎡b − d c t−t ⎢⎣ ⎦ ⎤ ⎥, (VIII.125)( )
3 1 2 1(
)
2 4 2 s s s s s c c d t b d c t t ρ = ⎡⎢⎣ − − ⎦ ⎤ ⎥ , (VIII.126) di mana 2 2 1 4 , , 2 3 s c s s GM b c d G π φ π = = = . (VIII.127)Sebagaimana telah disebutkan sebelumnya, parameter Hubble menurun dalam daerah gelindingan perlahan standar. Untuk kasus potensial chaotic, jumlah total e-folding adalah
(
)
2 1 2(
)
2 1 2 1 1 1 1 2 2 s c i s s s e c s s b b N b dc t t b d c t c c c c ⎡ ⎤ ⎡ = − + ⎢ + − ⎥ + − ⎢ − − ⎣ ⎦ ⎣ t ⎤ ⎥⎦(
2)(
2 2)
(
2 1 2 4 m m c i G c e n m)
2 φ − φ − π φ = − + − −φ . (VIII.128)di mana φe adalah nilai medan scalar pada akhir inflasi. Kembali suku pertama muncul dari inflasi pada daerah pelanggaran Lorentz.
VIII.5 Analisis Ruang Fasa VIII.5.1 Sistem Dinamik
Metode sistem dinamika dapat digunakan sebagai analisis kualitatif dari sebuah model kosmologi yang terdiri dari persamaan-persamaan diferensial biasa. Interpretasi fisis untuk melengkapi sistem dinamik dipahami dari definisi-definisi variabel yang diberikan. Sebagai contoh, tinjau sebuah sistem yang terdiri dari tiga buah derajat kebebasan yaitu terdiri dari tiga buah variabel: u, v dan w, untuk menggambarkan sistem. Maka dinamika dari sistem dapat dinyatakan oleh persamaan-persamaan diferensial biasa yang terkopel:
(
, , du)
f u v w dt = , (VIII.129)(
, , dv g u v w dt =)
, (VIII.130)(
, , dw h u v w dt =)
. (VIII.131)Fungsi-fungsi f, g, dan h tidak meliputi waktu sehingga sistemnya adalah outonomous. Bentuk dari persamaan-persamaan sistem dinamik di atas dapat dimanfaatkan untuk mengidentifikasi titik-titik tetap dari sistem. Titik-titik tetap didefinisikan sebagai titik-titik di mana turunan waktu dari variabel-variabel lenyap, untuk kasus di atas adalah
(
, ,)
0 f u v w = , (VIII.132)(
, ,)
0 g u v w = , (VIII.133)(
, ,)
0 h u v w = . (VIII.134)Titik-titik tetap yang diperoleh menentukan trayektori dari sistem. Sebagai contoh, untuk sistem 1-dimensi, persamaan dinamikanya adalah
( )
dxf x
dt = . (VIII.135)
Maka titik-titik tetap diperoleh dengan mengambil f x
( )
=0.VIII.5.2 Sistem Dinamik Medan Skalar
Pada pasal ini dibahas struktur global dari dinamika sistem melalui analisis bidang fasa dan menghitung evolusi kosmologi secara numerik. Dengan memperkenalkan variabel-variabel berikut: 2 , 3 6 V x y H φ , β β ′ ≡ ≡ (VIII.136) , 1 , 2 V V , , φ φ β λ λ β β ≡ ≡ − (VIII.137) , 1 2 2 , , , VV V , 2 φφ φφ φ φ ββ β Γ ≡ Γ ≡ . (VIII.138)
maka persamaan gerak medan skalar (VIII.56) dan (VIII.57) dapat dinyatakan sebagai sistem bidang-autonomous:
(
2)
(
)
1 2 3 3 1 2 2 x′ = − x −x + λ λ+ y , (VIII.139)(
1 2)
3 3 2 y′ =⎡⎢ x− λ λ+ ⎤x ⎣ ⎦⎥ y, (VIII.140)2 1 1 1 1 6 2 x λ′ = − λ ⎛⎜Γ − ⎝ ⎠ ⎞ ⎟ , (VIII.141) 2 1 2 2 2 2 6 1 2 x λ λ λ λ ⎡ ⎛ ⎞⎤ ′ = − ⎢Γ − −⎜ ⎟⎥ ⎝ ⎠ ⎣ ⎦ . (VIII.142)
Sebuah aksen menyatakan turunan terhadap logaritme dari faktor skala, α =lna. Fungsi-fungsi λ φ1( ) dan λ φ2( ) masing-masing menentukan vektor kopling dan potensial. Persamaan Friedmann (VIII.55) menjadi
2 2
1
x +y = . (VIII.143)
Persamaan keadaan medan skalar dapat diungkapkan dalam varibel-variabel baru
2 2 2 p 2 x y x y φ φ φ ω ρ − = = + . (VIII.144) Ungkapan 2
x mengandung informasi untuk ekspansi oleh energi kinetik medan skalar dan y2 oleh potensial dalam skenario pelanggaran Lorentz.
Dalam sistem autonomous, persamaan-persamaan (VIII.139) – (VIII.142) dapat dinyatakan dalam bentuk x’ = f(x) di mana x(x, y,λ1,λ2), dan titik-tritik tetap yang dinamakan dengan titik-titik kritis x0 adalah solusi dari sistem persamaan f(x0) = 0. Untuk menentukan stabilitas dari sistem, gangguan dilakukan disekitar titik-titik kritis dalam bentuk x = x0 + u dan menghasilkan persamaan gerak u’ = M u, di mana 0 i ij j x f M x ∂ = ∂ . (VIII.145)
Untuk persamaan-persamaan dinamika (VIII.139) – (VIII.142), u adalah sebuah vektor kolom yang terdiri dari gangguan x, y,λ1,λ2 . Jadi Mij adalah sebuah matrik 4 x 4. Stabilitas dari titik-titik kritis ditentukan oleh nilai-nilai eigen μi dari matrik M pada titik kritis. Titik kritis dikatakan stabil jika nilai-nilai eigen dari M adalah riil negatif Re(μi)<0 dan tidak stabil jika Re(μi)>0 dan jika tidak memenuhi keduannya, titik kritis dikatakan titik balik (saddle point).
( )
2( )
1,
2
m V M2 2
β φ = φ φ = φ , (VIII.146) dengan m dan M adalah parameter-parameter. Substitusi persamaan ini ke persamaan-persamaan (VIII.137) dan (VIII.138) menghasilkan
1 2 1 2 1 2 , 2 m λ λ= = − Γ = Γ = . (VIII.147)
Dan secara trivial dipenuhi untuk persamaan-persamaan (VIII.141) dan (VIII.142). Persamaan (VIII.139) dan persamaan (VIII.140) dapat diyatakan dalam persamaan tunggal
(
1 2)
(
2)
3 3 1 2 x′ = −⎡⎢ x− λ λ+ ⎤⎥ −x ⎣ ⎦(
2)
3x 2 6m 1 x ⎡ ⎤ = −⎣ + ⎦ − . (VIII.148)Solusi-solusi pelanggaran Lorentz dapat diperoleh dari persamaan
2 1 3 6 H x x H λ ′ = − + . (VIII.149)
Suku kedua ruas kanan persamaan ini muncul akibat dari pelanggaran Lorentz. Titik-titik kritis ( ,x y0 0)dari sistem adalah
,
(1, 0) ( 1, 0)− dan (− 8 / 3, 1 8 / 3m − m ). (VIII.150) Titik-titik kritis (1, 0) atau ( 1, 0)− berhubungan dengan solusi-solusi didominasi oleh suku kinetik pelanggaran Lorentz dan titik kritis (− 8 / 3, 1 8 / 3m − m ) berhubungan dengan solusi potensial-kinetik pelanggaran Lorentz. Dengan mengintegrasi persamaan (VIII.149), solusi untuk parameter Hubble diberikan oleh exp H p α ⎛ ∝ ⎜− ⎝ ⎠ ⎞ ⎟. (VIII.151)
Solusi ini berhubungan dengan alam semesta mengembang dengan faktor skala diberikan oleh ( ) ~ p a t t , 2 2 0 1 0 0 1 1 3 6 3 2 6 p 0 x λx x mx ≡ = − + . (VIII.152)
Sehingga titik kritis x0 = ±1 menghasilkan m>1/ 6 dan titik kritis x0 = − 8m/ 3 menghasilkan m<1/16.
Gangguan linier disekitar titik x0+ = +1dan x0− = −1 berturut-turut menghasilkan
nilai-nilai eigen μ+ = +6 4 6m dan μ− = −6 4 6m. Jadi untuk nilai m positif, selalu tidak stabil dan
0 1
x+ = + x0− = −1 adalah stabil untuk tetapi tidak
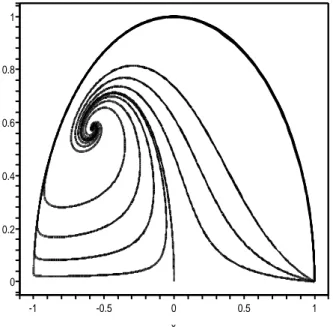
stabil untuk . 3/ 8 m> 3/ 8 m< 0.2 0 x 1 0.5 0 -0.5 -1 y 1 0.8 0.6 0.4
Gambar VIII.2 Bidang fasa solusi dominasi kinetik pelanggaran Lorentz.
0.2 0 x 1 0.5 0 -0.5 -1 y 1 0.8 0.6 0.4
Kemudian gangguan liniear disekitar titik potensial-kinetik pelanggaran Lorentz menghasilkan nilai eigen μ =8m−3 , dan memberikan solusi stabil untuk
. Gambar VIII.2 dan Gambar VIII.3 menunjukan kurva bidang fasa untuk dan . Trayektori dibatasi di dalam lingkaran .
3/ 8 m<
3/ 8
m> m<3/ 8 x2 +y2 =1
Dalam model (VIII.146), persamaan keadaan medan skalar diberikan oleh 16 1 3 m φ ω = − + , (VIII.153)
yaitu ditentukan oleh parameter m dari vektor kopling, dan selalu memenuhi 1
φ
ω > − untuk m positif.
VIII.6 Rangkuman
Dalam bab ini telah diperoleh perumusan kosmologi dari teori gravitasi skalar-vektor-tensor dengan medan vektor serupa waktu. Dengan asumsi bahwa medan-medan adalah homogen, rapat energi dan tekanan dari medan-medan skalar diperoleh dan persamaan (VIII.20) – (VIII.22) bersama-sama dengan persamaan Friedmaan dapat digunakan untuk menggambarkan solusi-solusi kosmologi.
Di dalam sub Bab VIII.3, solusi eksak persamaan keadaan diperoleh dari model parameter Hubble dan vektor kopling fungsi pangkat. Persamaan keadaan non dinamik diperoleh untuk n = 2 dan n > 2 menjadi dinamik. Untuk kasus ini medan skalar terkait dengan pelanggaran Lorentz dan persamaan keadaan dari medan skalar ditentukan oleh parameter kopling vektor.
Inflasi pelanggaran Lorentz yang dibahas di dalam sub Bab VIII.4 menunjukkan bahwa untuk potensial fungsi pangkat kebalikan, evolusi parameter Hubble menurun pada daerah pelanggaran Lorentz dan bertambah besar pada daerah gelindingan perlahan standar. Untuk kasus potensial fungsi pangkat, potensial chaotic, evolusi parameter Hubble menurun pada daerah pelanggaran Lorentz dan bertambah besar pada daerah gelindingan perlahan standar.
Vektor kopling kuadratik dan potensial chaotic berhubungan dengan nilai-nilai konstan λ λ1= 2 = −2 m dan Γ = Γ =1 2 1/ 2. Untuk kasus sebaliknya jika λ1 dan
2
λ dibuat konstan, ditemukan bahwa bentuk vektor kopling masih dalam fungsi kuadratik dari medan skalar sedangkan potensial sebagai fungsi dari medan skalar adalah fungsi pangkat V ~φ2γ dan Γ =1 1/ 2, Γ = −2 1 1/(2 )γ di mana γ λ λ= 2/ 1. Di dalam sub Bab VIII.5, dipelajari perilaku atraktor dari medan skalar penyebab inflasi dalam konteks pelanggaran Lorentz. Diperoleh bahwa ada solusi-solusi stabil dari evolusi alam semesta. Ada tiga buah titik kritis yang diperoleh yaitu: dua buah solusi ketika suku kinetik menjadi dominan dan satu buah solusi ketika suku kinetik-potensial menjadi dominan. Bergantung dari kopling parameter, jika salah satu dari titik kritis adalah stabil maka titik kritis yang lain menjadi tidak stabil. Alam semesta kemudian berevolusi dari keadaan yang tidak stabil menuju ke salah satu titik kritis yang stabil.