Kajian Lintasan Orbit Pada Turbin Angin Savanius Tipe Rotor Helix Dengan Menggunakan Software Matlab 2014

BAB 2

TINJAUAN PUSTAKA

2.1.Turbin Angin

Turbin angin merupakan sebuah alat yang digunakan dalam sistem konversi energi angin (SKEA). Turbin angin berfungsi merubah energi kinetik angin menjadi energi mekanik berupa putaran poros. Putaran poros tersebut kemudian digunakan untuk beberapa hal sesuai dengan kebutuhan seperti memutar dinamo atau generator untuk menghasilkan listrik atau menggerakkan pompa untuk pengairan. [6]. Bagian-bagian turbin dapat dilihat pada Gambar 2.1.

Gambar 2.1. Konstruksi turbin angin [7].

Keterangan gambar:

1. Arah angin pada HAWT tipe upwind

2. Diameter rotor

3. Hub height

4. Rotorblade

5. Gear box

6. Generator

7. Nacelle

8. Tower pada HAWT

9. Arah angin pada HAWT tipe downwind

10. Tinggirotor

11. Tower pada VAWT 12. Equator height

Pemanfaatan energi angin telah dilakukan sejak lama. Pertama kali digunakan untuk menggerakkan perahu di sungai Nil sekitar 5000 SM. Penggunaan kincir sederhana telah dimulai sejak permulaan abad ke-7 dan tersebar diberbagai negara seperti Persia, Mesir, dan Cina dengan berbagai desain. Di Eropa, kincir angin mulai dikenal sekitar abad ke-11 dan berkembang pesat saat revolusi industri pada awal abad ke-19 [7].

Desain dari kincir/turbin angin sangat banyak macam jenisnya, berdasarkan bentuk rotor, kincir angin dibagi menjadi dua tipe, yaitu turbin angin sumbu mendatar (horizontal axis windturbine) dan turbin angin sumbu vertikal (vertical axis wind turbine) [5]

Salah satu komponen utama dari turbin angin adalah rotor. Rotor ini berfungsi mengkonversi gerak linear angin menjadi gerak putar sudu turbin. Untuk klasifikasi berdasarkan fungsi gaya aerodinamis, merujuk pada gaya utama yang menyebabkan rotor berputar. Berdasarkan fungsi gaya aerodinamis, rotor

terbagi menjadi dua, yaitu rotor tipe drag dan rotor tipe lift.

1. Rotor tipe drag, memanfaatkan efek gaya hambat atau drag sebagai gaya

penggerak rotor.

2. Rotor tipe lift, memanfaatkan efek gaya angkat sebagai gaya penggerak rotor.

Gaya ini terjadi akibat angin yang melewati profile rotor.

Vertical Axis Wind Turbine (VAWT) merupakan turbin angin sumbu tegak

yang gerakan poros dan rotor sejajar dengan arah angin, sehingga rotor dapat berputar pada semua arah angin. Ada tiga tipe rotor pada turbin angin jenis ini, yaitu: Savonius, Darrieus, dan H rotor. Turbin Savonius memanfaatkan gaya drag

sedangkan Darrieus dan H rotor memanfaatkan gaya lift. Turbin angin sumbu vertical dan beberapa aplikasinya dapat dilihat pada Gambar 2.2. dan 2.3.

VAWT awalnya lebih berkembang untuk konversi energi mekanik, tetapi seiring dengan perkembangan desain, turbin tipe ini banyak digunakan untuk konversi energi listrik skala kecil.

VAWT juga mempunyai beberapa kelebihan dan kekurangan. Kelebihannya, yaitu memiliki torsi tinggi sehingga dapat berputar pada kecepatan angin rendah, dinamo atau generator dapat ditempatkan di bagian bawah turbin sehingga mempermudah perawatan, tidak bising, dan kerja turbin tidak dipengaruhi arah angin. Kekurangannya yaitu kecepatan angin di bagian bawah sangat rendah sehingga apabila tidak memakai tower akan menghasilkan putaran yang rendah, dan efisiensi lebih rendah dibandingkan HAWT.

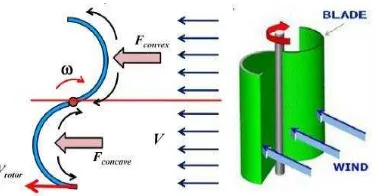
2.2.Turbin Angin Savonius

Salah satu jenis turbin angin sumbu vertikal (VAWT) yang dapat digunakan pada angin dengan kecepatan rendah adalah turbin angin Savonius. Turbin ini ditemukan oleh sarjana Finlandia bernama Sigurd J. Savonius pada tahun 1922. Konstruksi turbin sangat sederhana, tersusun dari dua buah sudu

setengah silinder. Pada perkembangannya turbin Savonius ini banyak mengalami perubahan bentuk rotor, seperti yang terlihat pada Gambar 2.6.

Gambar 2.3. Rotor tipe U dan Helix

Pada gambar 2.6 merupakan penjelasan angin mendorong rotor turbin angin memutar lengan.

Turbin angin savonius memili banyak variasi salah satunya tipe rotorhelix

seperti di bawah ini

Gambar 2.5 RotorSavonius berbentuk heliks [12]

Rotor Savonius tipe ini pertama kali dikenalkan tahun 2006 oleh suatu perusahaan bernama “Helix Wind”. Rotor ini memiliki desain yang tidak biasa, yaitu berbentuk helix. Namun bentuk helix disini memiliki keuntungan antara lain memiliki getaran yang halus karena variasi torsinya relatif merata untuk setiap

bucket, dan juga memiliki torsi yang baik. Tetapi rotor tipe ini memiliki geometri yang relatif rumit, sehingga sulit dalam pembuatan [13].

2.3. Analisa Getaran

Analisa getaran merupakan salah satu alat yang sangat bermanfaat sebagai prediksi awal terhadap adanya masalah pada mekanikal, elektrikal dan proses pada peralatan, mesin-mesin dan sistem proses yang kontinu di pabrik. Sehingga analisa getaran saat ini menjadi pilihan teknologi predictive maintenance yang paling sering digunakan [9].

Disamping manfaatnya dalam hal predictive maintenance, teknik analisa getaran juga digunakan sebagai teknik untuk mendiagnosa, yang dapat

diaplikasikan antara lain untuk: acceptance testing, pengendalian mutu, mendeteksi bagian yang mengalami kelonggaran, pengendalian kebisingan,

mendeteksi adanya kebocoran, desain dan rekayasa mesin, dan optimasi produksi.

2.3.1. Konsep Analisa Getaran

gerakan sesaat (displacement, velocity, dan acceleration ) sebagai fungsi waktu. Sinyal yang demikian disebut sebagai time history. Suatu sample data didefinisikan sebagai time history dari pengukuran getaran tunggal x(t) dalam durasi tertentu.

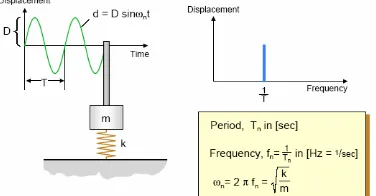
Getaran diartikan sebagai gerak osilatif disekitar posisi tertentu. Untuk getaran sebuah titik akibat operasi mesin, analisa getaran didasarkan pada peristiwa gerak osilatif yang periodik. Gerak periodik adalah suatu gerak gelombang yang berulang dalam selang waktu tertentu. Bentuk paling sederhana dari gerak periodik adalah gerak harmonik. Berikut adalah gerak sederhana fenomena getaran dapat dilihat pada sebuah pegas yang salah satu ujungnya dijepit dan ujung lainnya diberi massa M seperti gambar 2.1. berikut.

Gambar 2.6. Getaran pada sistim pegas-Massa sederhana[16].

Mula-mula sistem dalam keadaan setimbang (gambar 2.11.a). Jika massa diberi gaya F maka massa akan turun sampai batas tertentu (gambar 2.11.b). Perpindahan maksimum posisi massa bergantung pada besarnya gaya F, massa dan kekuatan tarik pegas melawan gaya F tersebut. Jika gaya sebesar F tidak dikenakan lagi pada massa, maka massa akan ditarik ke atas oleh pegas karena tenaga potensial yang tersimpan dalam pegas (gambar 2.11.c). Massa akan kembali ke posisi kesetimbangan, selanjutnya bergerak ke atas sampai batas tertentu. Perpindahan maksimum ke atas dipengaruhi oleh kekuatan tarik pegas

dan massa benda. Proses tersebut akan berulang sampai tidak ada pengaruh gaya luar pada sistem. Gerakan massa naik turun ini disebut osilasi mekanis. Berkaitan

2.3.2. Karakteristik Getaran

Kondisi mesin dan kerusakan mekanis dapat diketahui dengan mempelajari karakteristik getarannya. Pada suatu sistem pegas-massa, karakteristik getaran dapat dipelajari dengan membuat grafik pergerakan beban terhadap waktu, seperti terlihat pada Gambar 2.12.

Gambar 2.7. Karakteristik getaran[14].

Gerak beban dari posisi netralnya ke batas atas kemudian kembali ke posisi netral (kesetimbangan) dan bergerak lagi ke batas bawah kemudian kembali ke posisi kesetimbangan, menunjukkan gerakan satu siklus. Waktu untuk melakukan gerak satu siklus ini disebut periode, sedangkan jumlah siklus yang dihasilkan dalam satu interval waktu tertentu disebut frekuensi. Dalam analisis getaran mesin, frekuensi lebih bermanfaat karena berhubungan dengan putaran (rpm) suatu mesin.

2.3.3. Frekuensi Getaran

Frekuensi adalah jumlah siklus pada tiap satuan waktu. Besarnya dapat

dinyatakan dengan siklus per detik (cycles per second/cps) atau siklus per menit (cycles per minute/cpm). Frekuensi getaran penting diketahui dalam analisis getaran mesin untuk menunjukkan masalah yang terjadi pada mesin tersebut. Dengan mengetahui frekuensi getaran, akan memungkinkan untuk dapat mengidentifikasikan bagian mesin yang salah (fault) dan masalah yang terjadi.

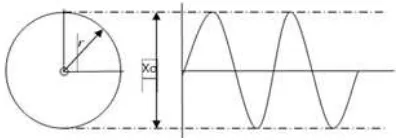
2.3.4. Amplitudo (Perpindahan, Kecepatan, dan Percepatan)

Perpindahan (displacement), kecepatan (velocity), dan percepatan (acceleration) diukur untuk menentukan besar dan kerasnya suatu getaran. Biasanya diwakili dengan pengukuran amplitudo getaran.

Gambar 2.13. adalah model amplitude yang memperlihatkan hubungan dari gerakan poros yang berputar dengan amplitude r.

Gambar 2.8 Model amplitudo

Perpindahan (displacement) adalah gerakan suatu titik dari suatu tempat ke tempat lain yang mengacu pada suatu titik tertentu yang tidak bergerak (tetap). Dalam pengukuran getaran mesin, sebagai standar digunakan jarak perpindahan puncak ke puncak (peak to peak displacement), seperti terlihat pada gambar 2.14. Contohnya adalah perpindahan poros karena gerak putarnya. Jika perpindahan

poros terlalu besar sampai melebihi batas “clearance” bantalan akan

mengakibatkan rusaknya bantalan.

Kecepatan (velocity) merupakan perubahan jarak per satuan waktu. Kecepatan gerak mesin selalu dinyatakan dalam kecepatan puncak (peak velocity). Kecepatan puncak gerakan terjadi pada simpul gelombang. Dalam getaran, kecepatan merupakan parameter penting dan efektif, karena dari data kecepatan

akan dapat diketahui tingkat getaran yang terjadi.

Percepatan (acceleration) adalah perubahan kecepatan per satuan waktu. Percepatan berhubungan erat dengan gaya. Gaya yang menyebabkan getaran pada bantalan mesin atau bagian-bagian lain dapat ditentukan dari besarnya getaran.

Hubungan antara perpindahan dan waktu untuk gerak harmonik dapat dinyatakan secara matematik sebagai berikut :

= � � � ... (2.1)

Dimana perpindahan maksimum diekspresikan sebagai X

0, yang juga

frekuensi, yang diberi notasi f dan didefinisikan sebagai jumlah siklus per satuan waktu. Satuan yang umum digunakan untuk f adalah siklus per menit (cpm) atau siklus per detik (cps, Hz). Kecepatan dan percepatan gerak harmonik dapat diperoleh dengan differensiasi. Dengan menggunakan notasi titik untuk turunannya, maka didapat :

Kecepatan (Velocity) mm/s

= �_�� = �� cos � ... (2.2)

Percepatan (Acceleration) mm/s2

= �_��2₂ = − �� sin � ... (2.3)

1g= 9,807m/s2

Dengan amplitudo dapat terbaca indikasi beratnya kerusakan pada mesin dan dapat digunakan untuk mengukur beberapa masalah getaran. Bagaimanapun

unit yang pasti mengacu pada respon getaran frekuensi. Gambar 2.14. menunjukkan Displacement dan Frequency.

Gambar 2.9. Displacement dan Frequency

Perpindahan (displacement) mengindikasikan berapa jauh suatu objek bergetar, kecepatan (velocity) mengindikasikan berapa cepat objek bergetar dan percepatan (acceleration) suatu objek bergetar terkait dengan gaya penyebab getaran.

2.3.5. Fasa (phase)

lain, kecepatan mendahului 0 terhadap perpindahan, sedangkan percepatan

tertinggal 0 terhadap perpindahan.

Gambar 2.10. Beda fasa antara perpindahan, percepatan, Dan percepatan

Pengukuran fasa memberikan cara untuk menentukan bagaimana suatu elemen bergetar relatif terhadap elemen lain. Pembandingan gerak relatif dari dua atau lebih elemen mesin sering diperlukan dalam diagnosis kerusakan spesifik suatu mesin. Sebagai contoh, bila analisis menyatakan bahwa getaran suatu mesin tidak sefasa dengan getaran base-nya, maka mungkin terjadi kelonggaran baut atau kelonggaran mesin dari base-nya.

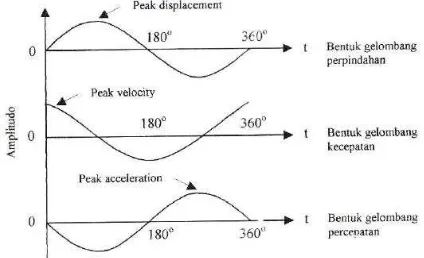
Jadi kecepatan dan percepatan juga harmonik dengan frekuensi osilasi yang sama, tetapi memiliki beda phasa terhadap perpindahan, berturut-turut

dengan � dan π radian. Gambar 2.16 adalah hubungan displecemen, velocity dan

acceleration.

Gambar 2.11. Hubungan phasa perpindahan, kecepatan, dan percepatan pada gerak harmonik

Tabel 2.1. Satuan yang digunakan tiap karakteristik Karateristik

Getaran

Satuan

Metrik British

Perpindahan microns peak to peak ( 1 µm = 0.001 mm )

Sumber: Maintenance Engineering Handbook, Mobley

2.4. Rotor Orbit Trajectories

Rotor orbit trajectories secara khusus digunakan untuk analisa pada

lateral rotor vibration (LRV), yang memberikan tambahan informasi diagnosa

komponen mesin yang bermanfaat untuk analisa trouble shooting. Hal ini terutama untuk mengindentifikasi penyebab natural dari masalah getaran pada mesin-mesin berputar. LRV, juga disebut transverse rotor vibration adalah gerak orbit pada bidang radial terhadap sumbu putar rotor. Model sederhana dari LRV yaitu gerakan orbit rotor yang memiliki dua derajat kebebasan (degree of freedom), seperti yang ditampilkan pada Gambar 2.12.Pada model ini, masa rotor m, dapat berubah posisi pada bidang radial x-y. Massa ini terhubung dengan struktur melalui pegas dan peredam yang tereksitasi oleh gaya radial yang berubah terhadap waktu, misalnya gaya akibat massa unbalance[13]

Dua persamaan gerak dari model ini yang dipengaruhi oleh gaya eksitasi yang berasal dari F = ma , maka diperoleh,

+ + � = �0cos � ... (2.4)

+ + � = �0sin � ... (2.5)

Pada kondisi isotropik, yaitu � = � ≡ � dan = ≡ , maka

persamaan 2.4 dan 2.5 dapat di tulis dalam bentuk matrix,

[ ] { } + [ _{] { } + [� �]{ } = {}�_� } ... (2.6)

Untuk menggambarkan resultan dari perpindahan sistem pada persamaan

(2.6) yang bergetar pada sumbu x dan y dengan frekuensi yang sama � , maka setiap gerak harmonik dapat disajikan sebagai vektor dan berlaku penjumlahan vektor. Apabila dianggap bahwa massa m dari kondisi unbalance dianggap berosilasi secara simultan dengan gerak harmonik sederhana yang memiliki frekuensi yang sama menurut sumbu x dan y. Maka perpindahan dari partikel

konstanta, Dengan mengembangkan argumen dari sinus, maka diperoleh :

= sin � � + � sin �

Dengan melakukan perkalian kuadrat dan penjumlahan terhadap persamaan (2.9) dan (2.10) maka,

in (� − � ) = 22+

2

yang merupakan persamaan umum sebuah lingkaran elips

Biasanya sumbu utama dari elipse akan menunjuk terhadap sumbu x dan y, tetapi hal ini akan menjadi sumbu utama ketika ada perbedaan fase � − � = �/ maka persamaan (2.11) menjadi bentuk yang lebih dikenal,

2

2+

2

2 = ... (2.12)

Jika X=Y=A, maka persamaan (2.12) menjadi + = . Saat � − � = , �. 4 �. Dan seterusnya, maka akan diperoleh persamaan

=

yang merupakan suatu garis lurus yang memiliki kemiringan Y/X. Kembali lagi untuk � − � = �, �, � dan seterusnya, akan diperoleh:

=

yang merupakan suatu garis lurus namum dengan kemiringan yang berlawanan. Lintasan jejak partikel ini dapat dilihat pada Gambar 2.11 dan secara mudah dapat digambarkan dengan menggunakan program simulasi matematika Matlab versi 6.1.

Untuk menggambarkan kurva dua dimensi dari fungsi x dan y dengan

menggunakan Matlab versi 6.1. digunakan perintah ”ezplot”. Berdasarkan fungsi dasar pada persamaan (2.7 dan 2.8), maka kurva koordinat diketahui:

(x, y) = sin(t),sin(t +�),

Dimana � = ,�,�, � , �, �, �, �, �

Dengan memberikan perintah kedalam MatLab versi 6.1 untuk tiap φ , yaitu:

>> ezplot('sin(t)','sin(t+� )')

Gambar 2.13 Berbagai lintasan orbit dalam sistem getaran yang simultan pada sumbu yang tegak lurus dimana gerak harmonik sederhana memiliki frekuensi yang sama[8].

Untuk menggambarkan gerak partikel unbalance dalam ruang tiga dimensi, persamaan fungsi ditambahkan dalam arah sumbu z. sehingga ada persamaan gerak harmonik sederhana ketiga, yaitu:

= sin � + � ... (2.13) Apabila X=Y=Z=A, maka kurva koordinat dalam dimensi ruang adalah:

(x, y, z) = sin(t),sin(t +δ ),sin(t) ,

perintah yang dituliskan kedalam MatLab versi 6.1 untuk φ\�=π/2 , yaitu:

>> ezplot3(’sin(t)’,’sin(t+π 2 )’,’sin(t)’)

akan menghasilkan lintasan orbit dalam dimensi ruang dengan pada frekuensi yang sama seperti yang ditunjukkan pada Gambar 2.12.

2.5.Metode lintasan Orbit (Pola Lissajous)

Sebagai metode analisa tambahan kadang-kadang diterapkan analisa orbit (pola Lissajous) karena pada umumnya pada instalsai non-contact pickup untuk suatu pengukuran pada daerah bearing yang mendeteksi tingkat vibrasi pada arah

axial.[18]

Sehingga rekomendasi pengukuran yang lengkap dengan arah vibrasi axial

tidak dapat dilakukan. Untuk non-contact pick-up pada umumnya dipasang permanen untuk mendeteksi vibrasi langsung pada shaft mesin-mesin yang penggunaannya cukup kritis, instalasinya berupa probe pada arah radial (horisontal dan vertikal) yang keduanya dipisahkan oleh sudut 90 derajat.[18]

Di sini analisa orbit dapat dilakukan, sebagai tambahan untuk analisa spektrum. Para praktisi telah melakukan penelitian mengenai kegunaan metoda orbit (pola Lissajous) dan berhasil mendapat kesimpulan terhadap bentuk bentuk orbit dalam hubungannya dengan kerusakan bagian-bagian mesin yang diukur dan dianalisa vibrasinya. Bentuk karakteristik pola Lissajous sebagai berikut:

1.Unbalance

Suatu keadaan unbalance pada rotary machine ditunjukkan oleh pola

Lissajous sebagai vibrasi yang besar pada frekuensi 1×RPM dengan menganggap bahwa vibrasi pada frekuensi yang lain sangat kecil dan tidak berarti.[18]

Bentuknya dapat betul-betul bulat atau sedikit lonjong (elips) dan di dalam pola yang terbentuk akan terlihat satu bush spot yang menunjukkan bahwa vibrasi

yang besar hanya terjadi pada frekuensi 1×RPM. Gambar pola Lissajousnya diberikan di bawah ini.[18]

2.Misalignment

Misalignment yang terjadi pada rotary machine akan menyebabkan vibrasi yang utama pada frekuensi 1×RPM yaitu sekitar yang diikuti dengan munculnya

vibrasi pads 2×RPM, 3×RPM, dan harmonik yang lebih tinggi lagi. Di dalam gambar pola Lissajousnya akan memberikan bentuk elips pipih seperti pisang atau bahkan bentuk pisang yang melengkung.[18]

Bentuk elips pipih selain memberikan kemungkinan vibrasi yang disebabkan oleh keadaan Misalignment, tetapi juga dapat disebabkan oleh kerusakan bearing

atau kemungkinan terjadinya resonansi.[18]

Gambar 2.16. Pola Lissajous pads rotary machine yang mengalami Misalignment[18]

3.Oil Whirl

Misalignment akan menyebabkan vibrasi yang utama pada frekuensi di

bawah 1×RPM. Di dalam gambar pola Lissajousnya akan memberikan bentuk dua buah lingkaran atau elips yang ditandai dengan adanya dua buah blank spot. Bahkan karena kejadian oil whirl yang di bawah 1×RPM tidak persis 1/2×RPM,

Gambar 2.17. Pola Lissajous pads rotary machine

yang mengalami oil whirl.[18]

4. Rubbing (Gesekan)

Gambar 2.18 Pola Lissajous pada rotary machine yang mengalami hit-and-bounce rubbing.[18]

Pola semacam ini mirip dengan pola Lissajous yang terjadi pada peristiwa terjadinya oil whirl, hanya bedanya dengan peristiwa oil whirl maka di sini lingkaran yang berada di dalam tidak berputar-putar.[18]

Dengan semakin beratnya kondisi rubbing yang terjadi, yaitu yang dinamakan heavy rubbing atau full rubbing, dan ditambah lagi dengan frekuensi resonansi, frekuensi harmonik, serta random frekuensi non-syncronous, maka

akan menghasilkan pola Lissajous yang sangat kompleks.[18]

2.6.Fast Fourier Transform (FFT)

gelombang berbasis waktu (time domain) dirubah menjadi gelombang sebagai fungsi dari frekuensi. Sehingga jika dilhat pada gambar dibawah ini; gelombang fungsi frekuensi dilihat sebagai fungsi amplitude (sumbu Y) dan frekuensi (sumbu Z). Proses transformasi dari gelombang berbasis waktu ke gelombang berbasis frekuensi dapat dilakukan oleh sebuah alat analyzer.[19]

Gambar 2.10: Gelombang Frekuensi[19]

Sebagai contoh grafik dibawah ini menunjukkan gambar gelombang fungsi waktu (Time Waveform) dari Turbin Uap berkapasitas 40 MW. Untuk menarik kesimpulan dari grafik ini sangat tidak mudah, kita tidak bisa menjawab pertanyaan apakah yang menyebabkan getaran, meskipun kita mungkin bisa memperoleh informasi tingkat keparahan dari vibrasi pada Turbin ini.[19]

Gambar 2.12: Time Waveform Turbin[19]

informasi apa yang menjadi penyebab vibrasi dan amplitude menunjukkan tingkat keparahannya. [19]

Gambar 2.13: Spectrum Data

Gambar 2.14: Transform FFT [19]

2.6.1. Unbalance (Sinyal Satu Kali Putaran)

Unbalance dicirikan dengan sinyal yang muncul pada frekuensi tunggal, dengan amplitude yang sama besar pada keseluruhan arah radial. Pada unbalance murni, vibrasi akan muncul dalam bentuk gelombang sinus pada kecepatan mesin, dituliskan sebagai 1×RPM. Vibrasi terjadi ketika pusat masa dari suatu elemen

yang berputar tidak sesumbu dengan susunan elemen putar. Amplitude akan terus membesar dengan terus bertambahnya kecepatan elemen dan akan mencapai kecepatan kritis dari elemen putar. Berikut adalah pola spectrum yang akan terjadi apabila unbalance: [19]

2.6.2 Misalignment (Sinyal Pada Dua kali Putaran)

Para ahli sepakat bahwa penyebab dari 70 hingga 75 persen dari getaran disebabkan oleh Misalignment. Dan seringkali vibrasi yang disebabkan oleh

Misalignment sering disalah artikan sebagai unbalance. Hal ini bisa anda pahami jika kita mengerti tahap-tahap terjadinya unbalance akibat munculnya

misalignement seperti yang dijelaskan pada tahapan berikut ini : 1.Ciri Misalignment:

a. Mempunyai komponen getaran pada frekuensi 2×putaran poros

b. Menyebabkan getaran dalam arah aksial 2.Misalignment berasal dari:

a. Preload dari poros bengkok atau bantalan yang tidak mapan b. Sumbu poros pada kopling tidak segaris

3.Misalignment terjadi karena adanya pergeseran atau penyimpangan salah satu bagian mesin dari garis pusatnya. Misalignment sendiri mengakibatkan getaran dalam arah axial. Misalignment merupakan penyebab kedua terjadinya vibrasi meskipun telah digunakan flexible couplings dan self aligning bearing.

4. Setiap elemen berputar (Rotating element) memiliki sejumlah unbalance. Setiap manufaktur memiliki toleransi terhadap unbalance ini. Untuk mencapai kondisi keseimbangan yang sempurna adalah sangat sulit dan mahal, yang hanya dilkukan untuk aplikasi-aplikasi tertentu seperti kapal selam nuklir misalnya.

5. Ketidak seimbangan yang kecil ini kemudian diredam atau diserap dengan menggunakan rolling element bearings yang memiliki clearance diantara bagian yang tetap dan bagian berputarnya sekitar 0.0005 “ atau bahkan untuk

beberapa aplikasi praktis tidak ada clearance sama sekali.

6. Ketika unit-unitnya mengalami kondisi Misalignment, elemen-elemennya

mengalami tarikan dan tekanan melalui kopling dan menghasilkan keausan yang tidak dinginkan pada bearings. Dengan segera keausan ini akan membuat

clearance antara element putar dan race-nya membesar. Sehingga kemudia bearings tidak lagi mampu bertindak sebagai damper yang menjaga unbalance

Tahap akhir dicapai ketika seorang yang memahami getaran menyimpulkan bahwa getaran terjadi akibat adanya unbalance, sehingga dilakukan langkah koreksi untuk memperbaiki keseimbangan elemen-elemen putar. Tanpa diagnose yang tepat masalah getaran ini akan kembali muncul, seperti yang dijelaskan pada tahap sebelumnya, bahwa misalignemet-lah ternyata yang meneyebabkan timbulnya unbalance. Secara statistic menunjukkan bahwa sekitar 12% pekerjaan harus diulang dan biaya menjadi naik, karena salah

diagnose. Beberapa gambaran terjadinya misaligment dan pola spektrum yang terjadi apabila misaligment terjadi pada pompa yang mengalami kerusakan

Gambar2.20: Posisi Misaligment

2.7.3. Mechanical looseness

Karakteristik dominan dari kehilangan mekanis adalah munculnya

multiple harmonic pada beberapa kecepatan operasi. Kecepatan operasi dari suatu komponendituliskan sebagai 1, misalnya adalah 1800 CPM. Harmonic ke-2 adalah 2×(3600 CPM) dan harmonic ke-3 adalah 3×(5400 CPM), dan seterusnya.

Pada kasus kehilangan mekanis, amplitudo terbesar akan terjadi dekat dengan sumber masalah.[19]

Gambar2.22: Pola SpectrumMechanical Looseness [17]