Directory UMM :Journals:Journal_of_mathematics:OTHER:

INFERIOR AND SUPERIOR SETS WITH RESPECT TO AN

ARBITRARY SET

S

FROM

INd

USED IN THE

MULTIDIMENSIONAL INTERPOLATION THEORY

by

Nicolae Crainic

Abstract: Among the necessary and useful notions for the elaboration of some multidimensional interpolation schemes, there is the one of inferior (superior) set with respect to an arbitrary set S from INd, d ≥1. That is why we proposed in the current paper to approach some notions related to these sets, by definitions, remarks, theorems and examples. After the definition of inferior (superior) sets, we show a disjoint decomposition of the set S

⊂

INdwith inferior (superior) sets, which by coalescences and under some conditions (theorem 1), leads to inferior (superior) sets too. Next, we define two total order relations on

S

⊂

d

IN which are more often used in the interpolation theory and we study the relation between the first (last) elements of Sand the inferior (superior) sets of this set (theorem 2).

Notations: Throughout this paper we use the notation INd to denote the set

} , 1 , ,

0 / ) ,..., , (

{i= i₁ i₂ i_d i_k ≥ i_k ∈IN k = d , we put i =i₁ +i₂ +...+i_d for any

∈

i

INd, and the pairs

(

S

,

ρ

)

stand for subsets S

⊂

INd together with relations

"

"

ρ

.

Definition 1: Given i=(i₁,i₂,...,i_d)∈INd, j=(j₁, j₂,..., j_d)∈INd, we

say that

i

≤

j

, if

0

≤

i

k

≤

j

k, for any

k

=

1

,

d

. Remarks:

1.1 The relation “

≤

” is reflexive, anti- symmetric and transitive, i.e. it is an order relation on INd. We use the same symbol “

≤

” to denote the relation

induced on (arbitrary) subsets S

⊂

INd. Unless otherwise specified, we will consider such subsets S to be endowed with the relation “

≤

”.

1.2 We will also denote by

S

_α the set

α

Definition 2: We say thatS ⊂INdis an inferior set with respect to INd if,

for any

i

∈

S

, j∈INdwith

j

≤

i

, we have

j

∈

S

too. Similarly, we say that S is

a superior set with respect to INd if for any i∈INd ,

j

∈

S

with

j

≤

i

, we have

S

∈

i

.

Remarks:

2.1. Similarly, one can define the notion of inferior (superior) sets with respect to arbitrary subsets S

⊂

INd.

2.2 Often we simply say inferior, respectively superior set, without indicating the set to which it is an inferior, respectively superior, this fact being implied. In genera, in these situations, it is implied that it is with respect to eitherINd, or the set itself.

Proposition 1: If

S

⊂

IN

d and X ⊂S is inferior (superior) with respect to S, then S \X is superior (inferior) with respect to S.

Proof: Let

X

be an inferior set with respect to S,

i

∈

S

\

X

,

j

∈

S

and

j

i

≤

. If

j

∉

S

\

X

, then

j

∈

X

, hence, since

X

is inferior and

i

≤

j

,

S

X

S

⊂

∈

\

i

, it follows that

j

∈

S

\

X

. The second part of the proposition can be proven similarly.

Remarks:

3.1 For any

α

=

(

α

₁

,

α

₂

,...,

α

_d

)

∈

S

, the

S

_α is superior with respect to S, and S\

S

_α is inferior with respect to S.

3.2 The empty set is inferior, respectively superior with respect to any set S

⊂

INd.

3.3 Any set S from INd is inferior, respectively superior with respect to itself.

3.4 The relation "is inferior with respect to" defines an order on the set of subsets of INd, while the relation "is superior with respect to" does not (because it is not transitive).

3.5 If

X

i

⊂

IN

d and

X

i is inferior (respectively superior) with

respect to

X

i₊₁ for any

i

=

1

,

n

−

1

, then

X

1

⊂

X

2

⊂

...

⊂

X

n, (respectively

n

X

X

The remarks 3.1 and 3.2 are obvious from the definitions, while the remark 3.3 results from 3.1 for

S

'=Ø. The reflexivity of the relation “inferior with respect to”, results from 3.3 too. All other remarks result rather easily from the previous definitions.

Theorem 1: If

S

1

∪

S

2

∪

...

∪

S

nis a disjoint cover of S

d

IN

⊂

, so that

i

S

is inferior (superior) with respect to

S

i

∪

...

∪

S

n for any

i

=

1

,

n

, then

1.

S

k

∪

S

l is inferior (superior) with respect to

S

k

∪

S

l

∪

...

∪

S

n 2.

S

k

∪

...

∪

S

l is inferior (superior) with respect to

S

k

∪

...

∪

S

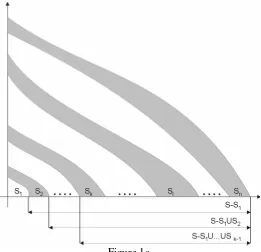
n, for any 1≤k ≤l ≤n. [image:3.595.176.437.294.546.2]

Proof: 1. The decomposition of S

⊂

IN

2for the inferior sets case is shown in Figure 1 a, while Figure 1b depicts the case for superior sets where each pair of curves limits points of natural coordinates from S.

[image:4.595.108.485.67.567.2]

Figure 1b

Given

i

∈

S

k

∪

S

l,

j

∈

S

k

∪

S

l

∪

...

∪

S

n with

j

≤

i

, it follows that (

i

∈

S

k,

j

∈

S

k

∪

S

l

∪

...

∪

S

n with

j

≤

i

) or (

i

∈

S

l,

j

∈

S

k

∪

S

l

∪

...

∪

S

n with

i

j

≤

).

If (

i

∈

S

k,

j

∈

S

k

∪

S

l

∪

...

∪

S

n with

j

≤

i

), it follows that (

i

∈

S

k,

n l

k

S

S

S

∪

∪

∪

∈

...

j

⊂

S

k

∪

S

k+1

∪

...

∪

S

n with

j

≤

i

) and because according to the hypothesis

S

k is inferior with respect to

S

k

∪

...

∪

S

n, it results that

j

∈

S

k, i.e.

l k

S

S

∪

∈

j

.

Given (

i

∈

S

l,

j

∈

S

k

∪

S

l

∪

...

∪

S

n with

j

≤

i

), it follows that (

i

∈

S

l,

k

S

∈

j

with

j

≤

i

), or (

i

∈

S

l,

j

∈

S

l

∪

...

∪

S

n with

j

≤

i

), and thus

j

∈

S

k or

l

S

∈

j

, i.e.

j

∈

S

k

∪

S

l. We relied also on the hypothesis that

S

l is inferior with respect to

S

l

∪

...

∪

S

n.

In both possible cases discussed previously it results that

j

∈

S

k

∪

S

l. Also according to the definition 2, it follows that

S

k

∪

S

l is inferior with respect to

n l

k

S

S

2. The second point of the theorem results applying successively the first one. Also the situation regarding the superior set can be proven either similarly to the previous one, using the hypothesis and the definition 2, or using the proposition 1.

Remarks:

4.1 The point 1 of the theorem can be extended to more then two "isolated" set (not necessary consecutive)

4.2 The statement "

S

_i is inferior (superior) with respect to

n l

k

S

S

S

∪

∪

...

∪

", is equivalent to "

S

_i is inferior (superior) with respect to

)

...

(

\

S

₁

∪

∪

S

_i−1

S

”, which is more often used in practice.

It is worthwhile to notice that the relation

"

≤

"

defined between the elements of the set INd(definition 1) and used when defining an inferior (superior) subset of

S

⊂

INd, is not a complete order relation on this set. This means that the relation

"

"

≤

is not sufficient for ordering all elements of the set INdor S

⊂

INd. More

concrete, if we use the relation

"

≤

"

, (0,0)∈IN2 can be followed by (0,1)∈IN2 and by (1,0)∈IN2 without any way of comparing these two elements between them. Next

we will define two total order relations on the set S

⊂

INdand the first discussed one will be the lexicographic one.

Definition 3: Given i=(i1,i2,...,id)∈INd,

d d IN j

j

j ∈

=( ₁, ₂,..., )

j we

say that i«

j

, if

i

₁

<

j

₁, or

i

₁

=

j

₁ and

i

₂

<

j

₂… or

i

₁

=

j

₁…

i

d−1

=

j

d−1 and

d d

j

i

≤

.

Definition 4: Given i=(i1,i2,...,id)∈INd,

d d IN j

j

j ∈

=( ₁, ₂,..., )

j , we

say that

i

p

j

, if i < j or i = j and i«

j

. Remarks

5.1. On IN1, the relations from definitions 3 and 4 coincide with the relation from the definition 1.

5.2. The relations defined by 3 and 4 are total order relations on INd

and on any S

⊂

INd. In other words, with any of these two relations, the elements of d

5.4. The elements of

X

⊂S are the first X elements of

(

S

,

ρ

)

, with respect to the relation

ρ

∈

{"

p

"

,”«”}, if for any i∈X,

j

∈

S

\

X

, it follows that

i

ρ

j

, and the elements of

Y

⊂S are the last Y elements of

(

S

,

ρ

)

with respect to the relation

ρ

∈

{"

p

"

,”«”}, if for any i∈Y ,

j

∈

S

\

Y

, it results

j

ρ

i

.

5.5. It is easy to notice that we can also define other total

relations on

d

IN

The usage of one of the two previous relations depends on

S

⊂

INd

and the problem to be solved.

Proposition 2: Let i,

j

∈

S

and

ρ

∈

{"

p

"

,”«”}.

2.1. If

i

≤

j

, then

i

ρ

j

, but not conversely. If

i

p

j

, this does not imply i«

j

, and conversely.

2.2. The statement ”elements of

X

⊂Sare the first X elements of

)

,

(

S

ρ

with respect to the relation

ρ

∈

{"

p

"

,”«”}” is equivalent to ”for any i∈X,

S

∈

j

with

j

ρ

i

, then

j

∈

X

”. The assertion ”the elements Y ⊂S are the last Y elements of

(

S

,

ρ

)

, with respect to the relation

ρ

∈

{"

p

"

,”«”}” is equivalent to “for any i∈Y ,

j

∈

S

with

i

ρ

j

, then

j

∈

Y

”.

Proof: 1. The first part of this proposition results easily by combining the definitions 1, 3 and 4. The other sentences are justified by counter examples. Thus, for

)

3

,

1

(

,

(

2

,

1

)

2

IN

∈

,

(

1

,

3

)

«

(

2

,

1

)

and

(

1

,

3

)

is not in the relation

"

≤

"

, respectively

"

"

p

with

(

2

,

1

)

. Also, if (3,1), (2,4)

∈

IN

2, (3,1)p(2,4) and (3,1) are not in the relation

"

≤

"

, respectively ”«” with (2,4).

2. Assume that the elements of

X

⊂S are the first X elements of

(

S

,

ρ

)

, in the relation

ρ

∈

{"

p

"

,”«”}, and the assertion “for any i∈X,

j

∈

S

with

j

ρ

i

, then

j

∈

X

” is false. Then we would have i∈X,

j

∈

S

with

j

ρ

i

, and

X

∉

j

, i.e. we would have i∈X ,

j

∈

S

\

X

with

j

ρ

i

. In addition, we would have that i∈X,

j

∈

S

\

X

implies

i

ρ

j

(according to the observation 5.4), that is

i

=

j

(

"

ρ

"

being anti-symmetric). This is impossible because this would mean that

X

and

X

S\ have i in common, hence the assertion can not be false. The other assertions can be similarly justified.

Theorem 2: IfS=

(

S

,

ρ

)

is a total ordered set fromINdwith the relation

"

{"

p

∈

ρ

,”«”} and if the elements of

X

are the first X elements of

(

S

,

ρ

)

, then

X

is inferior with respect to S, and if the elements of Yare the last Y elements of

)

,

(

S

ρ

, then Y is a superior set with respect to S.

Proof: Let the elements of

X

be the first elements of S in the relation

"

{"

p

∈

ρ

,”«”}. Let

i

∈

X

,

j

∈

S

with

j

≤

i

. Since, according to proposition 2, if

i

j

≤

then

j

ρ

i

, then from “

i

∈

X

,

j

∈

S

with

j

≤

i

” it follows that “

i

∈

X

,

S

∈

j

with

j

ρ

i

”. From this deduction according to proposition 2, we infer that

X

∈

j

(the elements of

X

are the first elements of S). We have that, if

i

∈

X

,

S

∈

j

with

j

≤

i

then

j

∈

X

, which according to the definition 2, is the same with the fact that

X

is an inferior set with respect to S.

The last part of the theorem can be proved by analogy with the first one. Its proof can be made using the proposition 1, as well as the results of the first part. Thus, if the elements of

Y

are the last Y elements of

(

S

,

ρ

)

, and because

S Y S

Y + \ = , it results that the elements of S\Y are the first S\Y elements of

)

,

(

S

ρ

. Thus, according to the first part of the theorem, S \Y is inferior with respect to S, which according to proposition 1, implies that

S

\

(

S

\

Y

)

=

Y

is superior with respect toS.

Remarks

6.1. Given

ρ

∈

{"

p

"

,”«”}, α∈

(

S

,

ρ

)

, the set

{

i

∈

(

S

,

ρ

)

/

i

ρ

α

}

is inferior with respect toS, but the set

{

i

∈

(

S

,

ρ

)

/

α

ρ

i

}

is superior with respect toS, because the elements of these sets are the first, respectively the last elements of

)

,

(

S

ρ

.

6.2. In general, the previous theorem has no reciprocity. Thus, the set

)}

0

,

2

(

),

0

,

1

(

),

1

,

0

(

),

0

,

0

{(

=

X

is inferior with respect to

S=

(

S

,

p

)

=

(

T

₂2

,

p

)

=

{(

0

,

0

),

(

0

,

1

),

(

1

,

0

),

(

0

,

2

),

(

1

,

1

),

(

2

,

0

)}

, and the four elements of

X

are not also the first four elements of

(

T

₂2

,

p

)

. Also

X

=

{(

0

,

0

),

(

0

,

1

),

(

1

,

0

)}

is inferior with respect to S=(S,«)=

(

T

₂2

,

«)=

{(

0

,

0

),

(

0

,

1

),

(

0

,

2

),

(

1

,

0

),

(

1

,

1

),

(

2

,

0

)}

, and the three elements of

X

are not also the first ones of

(

T

₂2

,

«). The set

)}

0

,

2

(

),

1

,

1

(

),

0

,

1

{(

=

6.3. According to observation 5.4, proposition 2.2 and theorem 2, if

S

=

(

S

,

ρ

)

is a total ordered set from

d

IN

and if

S

₁

∪

S

₂

∪

...

∪

S

_n

is a disjoint

cover of

S

⊂

IN

d

so that the elements of

S

_i

are the first (last)

S_i

elements of

n i

S

S

∪

...

∪

for any

i

=

1

,

n

, then it follows that

S

_k

∪

S

_l

is inferior (superior)

with respect to

S

_k

∪

S

_l

∪

...

∪

S

_n

and that

S

_k

∪

...

∪

S

_l

is inferior (superior)

with respect to

S

_k

∪

...

∪

S

_n

, for any

1≤k ≤l ≤n

. In the same conditions, we

have that the elements of the set

S

_k

∪

S

_l

are the first (last)

S_k ∪S_l

elements

of the set

S

_k

∪

S

_l

∪

...

∪

S

_n

, and the elements of the set

S

_k

∪

...

∪

S

_l

are the

first (last)

S_k ∪...∪S_l

elements of the set

S

_k

∪

...

∪

S

_n

for any

1≤k ≤l ≤n

.

REFERENCES

[1] Jia, Rong-Quing and Sharma, A., Solvability of some multivariate interpolation problems, 1990

[2] Rudolf A. Lorentz, Multivariate Birkhoff Interpolation, Springer – Verlag Berlin Heidelberg 1992

Author: