i
MODEL SIR PENYEBARAN PENYAKIT LEPTOSPIROSIS
Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Pendidikan
Program Studi Pendidikan Matematika
Oleh:
Symphorianus Faming Patrianto
NIM: 111414100
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
iv
HALAMAN PERSEMBAHAN
“Nothing is impossible.
Anything can happen as long as we
believe.”
Skripsi ini kupersembahkan untuk,
Kedua orang tua tercinta,
Kakakku Nicasius Ade dan adik sepupuku Faida Fitria,
Yang selalu memberikan doa dan dukungan dalam semua hal
Patner terbaikku: Gisela Laurenti Delani Winarto
Semoga menjadi patner terbaik untuk saat ini dan di masa depan
v
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini
tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan
dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 21 Januari 2016
Penulis,
vi ABSTRAK
Model SIR (Susceptibles-Infectious-Recovered) merupakan model epidemi yang pertama kali diperkenalkan oleh W.O. Kennack dan McKendrick. Pada model ini anggota dari populasi dibagi menjadi tiga kelas yaitu Susceptibles,Infectious, dan Recovered.
Model SIR ini telah digunakan oleh B. Pimphunchat et al pada penelitian sebelumnya dengan studi kasus tentang penyebaran penyakit leptospirosis di Thailand. Model SIR ini digunakan berdasarkan asumsi yang telah disusun dan sesuai dengan perilaku epidemi penyakit tersebut. Akan tetapi, tidak menutup kemungkinan model epidemi lain juga dapat digunakan seperti model epidemi SEIR, SIS, dan MSIR.
Pada tulisan ini akan melengkapi penelitian sebelumnya dengan menambahkan dua kelas populasi yaitu manusia rentan dan vektor rentan. Berdasarkan asumsi-asumsi, disusun model SIR dengan lima kelas populasi, yaitu kelompok manusia yang rentan terinfeksi penyakit ( ), kelompok manusia yang terinfeksi oleh penyakit ( ), kelompok manusia yang telah sembuh dari penyakit ( ), kelompok vektor yang rentan terinfeksi penyakit ( ), dan kelompok vektor yang terinfeksi oleh penyakit ( ).
Sebagai hasil penelitian diperoleh model dengan lima variabel sebagai berikut:
.
Dari model di atas diperoleh dua titik kesetimbangan yang merupakan titik dimana sistem berada pada keadaan setimbang, yaitu titik kesetimbangan endemik penyakit dan titik kesetimbangan bebas penyakit. Setelah itu, dilakukan analisis kestabilan pada titik kesetimbangan untuk mengetahui kestabilan dari titik kesetimbangan dengan linearisasi sistem menggunakan matriks jacobian diperoleh nilai-nilai eigen dari masing-masing titik kesetimbangan. Dari analisis kestabilann diperoleh bahwa titik kesetimbangan endemik penyakit tidak stabil sehingga penyakit tidak bersifat endemik sedangkan titik kesetimbangan bebas penyakit stabil asimptotik jika angka kematian vektor lebih tinggi dari angka kelahirannya atau sehingga penyakit tidak menyebar pada populasi.
vii ABSTRACT
SIR (Susceptibles-Infectious-Removed) model is a epidemic model who has been introduced by W.O. Kennack and McKendrick. In this model, population is devided into three subgroups; Susceptible, Infectious, and Removed. This model was used by B. Pimphunchat et al in their journal by study case of spread of leptospirosis in Thailand. SIR model was used to discribe the spread of this desease based by the assumptions and this model is compatible to describe the desease behaviour. Nevertheles, another models can used to describe this desease too, like SIS, SEIR, and MSIR.
This paper was made to complete the last research by add two groups of population to this model, there are group of susceptible humans and group of susceptible vectorns. By the assumptions, it was constructed SIR model by five groups of populations; group of susceptible humans ( ), group of infected humans ( ), group of recovered humans ( ), group of susceptable vectors ( ), and group of infected vectors ( ).
The result of the research was a mathematic model wih five variables, there are:
.
Two equilibrium points were found , there are desease-free equilibrium point and endemic equilibrium point. Then stability analysis was done by linearized method using jacobian matrix to get the eigenvalues for every equilibrium points. From stability analysis, we found that the endemic equilibrium point was unstable, so, the desease was not endemic, but the desease-free equilibrium point was asymptotically stable if natural birth rate of vectors is less than natural death rate of vectors or , so, over a long time, the population in the desease-free state.
viii
LEMBAR PERNYATAAN PERSETUJUAN
PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Yang bertandatangan di bawah ini, saya mahasiswa Universitas Sanata
Dharma dengan:
Nama : Symphorianus Faming Patrianto
NIM : 111414100
Dengan pengembangan ilmu pengetahuan, saya memberikan karya ilmiah
saya kepada Perpustakaan Universitas Sanata Dharma dengan judul:
MODEL SIR PENYEBARAN PENYAKIT LEPTOSPIROSIS
Beserta perangkat yang diperlukan, bila ada. Dengan demikian, saya
memberikan hak untuk menyimpan, mengalihkan ke dalam bentuk media lain,
mengelolanya dalam bentuk pangkalan data, mendistribusikannya secara terbatas,
dan mempublikasikannya di internet atau media lain untuk kepentingan akademis
tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya
selama tetap mencantumkan nama saya sebagai penulis kepada Perpustakaan
Universitas Sanata Dharma. Demikian pernyataan ini saya buat dengan
sebenarnya.
Dibuat di Yogyakarta
Pada tanggal 21 Januari 2016
Yang menyatakan,
ix
KATA PENGANTAR
Puji dan syukur penulis haturkan kepada Tuhan Yang Maha Esa, atas
segala berkat dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi ini.
Dalam penyusunan skripsi ini, penulis menemukan banyak kesulitan, akan
tetapi atas bantuan dan dukungan dari banyak pihak akhirnya penulis dapat
menyelesaikan skripsi ini. Oleh karena itu, penulis ingin mengucapkan terima
kasih kepada:
1. Bapak Beni Utomo, M.Sc., selaku dosen pembimbing skripsi yang dengan
sabar memberi bimbingan, meluangkan waktu dan pikiran dalam
menyusun skripsi ini.
2. Ibu Veronika Fitri Rianasari, M.Sc., selaku dosen pembimbing akademik
yang telah memberikan banyak bimbingan dalam hal akademik dan
perkuliahan.
3. Bapak dan Ibu dosen Program Studi Pendidikan Matematika yang telah
memberikan ilmu yang sangat berguna dan bermanfaat bagi penulis.
4. Kedua orang tuaku, kakakku Nicasius Ade Patrianto, dan adik sepupuku
Faida Fitria Fatma yang senantiasa selalu memberikan doa dan dukungan
dalam segala hal.
5. Sahabat-sahabat: Danik, Lilik, Yoga, Fian, Chris, Yosa, dan Ditya, terima
kasih untuk kebersamaan selama proses kuliah, saling berbagi dalam suka
x
6. Patner terbaik, Gisela Laurenti Delani Winarto yang selalu memberikan
semangat, dukungan, dan sebagai tempat curahan hati.
7. Teman-teman seperjuangan Prodi Pendidikan Matematika angkatan 2011
dalam kebersamaan, semangat, doa, dan segala bantuan kepada penulis.
8. Semua pihak yang tidak dapat disebutkan satu per satu, yang terlibat
dalam proses penyusunan skripsi ini.
Penulis menyadari bahwa masih banyak kekurangan dalam penyusunan
skripsi ini. Oleh karena itu, penulis mengharapkan saran dan kritik demi
penyempurnaan skripsi ini. Akhirnya, penulis berharap semoga skripsi ini dapat
berguna bagi pembaca.
Yogyakarta, 09 Desember 2015
xi DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING .... Error! Bookmark not defined. HALAMAN PENGESAHAN ... ii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
ABSTRAK ... vi
ABSTRACT ... vii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR TABEL ... xiii
DAFTAR GAMBAR ... xiv
BAB I PENDAHULUAN ... 1 A. LATAR BELAKANG ... 1 B. RUMUSAN MASALAH ... 3 C. BATASAN MASALAH ... 4 D. TUJUAN PENULISAN ... 4 E. MANFAAT PENULISAN ... 4 F. SISTEMATIKA PENULISAN ... 5
xii
BAB II LANDASAN TEORI ... 7
A. MODEL MATEMATIKA ... 7
B. SISTEM LINEAR DAN MATRIKS ... 11
C. PERSAMAAN DIFERENSIAL ... 18
D. TEORI SISTEM DINAMIK ... 22
BAB III MODEL PENYEBARAN PENYAKIT LEPTOSPIROSIS ... 30
A. PENYEBARAN PENYAKIT LEPTOSPIROSIS ... 30
B. MODEL MATEMATIKA UNTUK PENYEBARAN PENYAKIT LEPTOSPIROSIS ... 32
C. FORMULASI MODEL ... 37
BAB IV ANALISIS KESTABILAN ... 46
A. TITIK KESETIMBANGAN ... 47 B. ANALISIS KESTABILAN ... 52 C. SIMULASI MODEL ... 58 BAB V PENUTUP ... 67 A. KESIMPULAN ... 67 B. SARAN ... 68 DAFTAR PUSTAKA ... 69 LAMPIRAN ... 70
xiii
DAFTAR TABEL
Tabel 3. 1. Daftar Variabel-variabel ... 35
Tabel 3. 2. Daftar Parameter-parameter ... 36
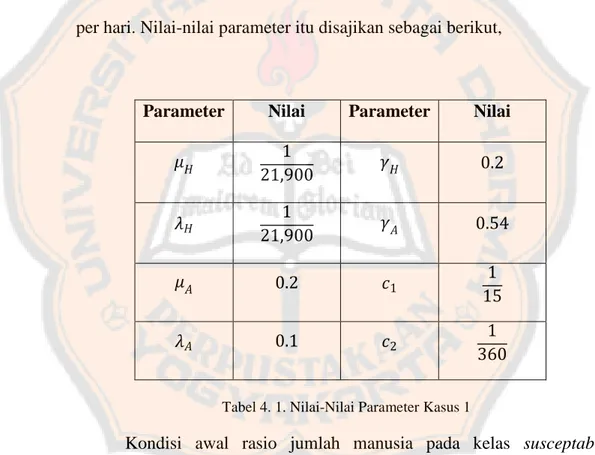
Tabel 4. 1. Nilai-nilai Parameter Kasus 1 ... 59
xiv
DAFTAR GAMBAR
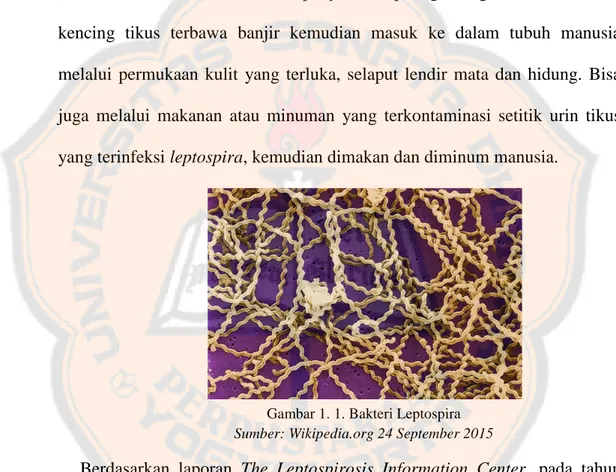
Gambar 1. 1. Bakteri Leptospira ... 2
Gambar 3. 1. Tikus sebagai Penyebar Utama ... 30
Gambar 3. 2. Siklus Penyebaran Penyakit Leptospirosis ... 31
Gambar 3. 3. Diagram Penyebaran Penyakit Leptospirosis ... 37
Gambar 3. 4. Diagram Jumlah Total Populasi Manusia ... 38
Gambar 3. 5. Diagram Jumlah Total Populasi Vektor ... 38
Gambar 4. 1. Grafik Dinamika Populasi Vektor dan Manusia ... 60
1 BAB I PENDAHULUAN
A. LATAR BELAKANG
Perkembangan dan kemajuan dunia modern ini berkaitan erat dengan
semakin berkembangnya ilmu pengetahuan, salah satunya dalam bidang
matematika. Perkembangan ilmu pengetahuan dalam bidang matematika
memberikan dampak positif dalam kehidupan manusia. Matematika banyak
digunakan dalam berbagai bidang, termasuk ilmu pengetahuan alam, rekayasa
medis, dan ilmu pengetahuan sosial. Selain itu, matematika juga banyak
diaplikasikan pada seluruh aspek kehidupan manusia sehari-hari. Peran
matematika pada masalah kehidupan sehari-hari maupun pada bidang ilmu
lain disajikan dalam pemodelan matematika dan direpresentasikan dalam
bentuk model yaitu model matematika.
Secara umum, model matematika merupakan sekumpulan persamaan atau
pertidaksamaan yang mengungkapkan perilaku suatu permasalahan yang
nyata (Ekawati, 2012). Model matematika dibuat berdasarkan asumsi-asumsi.
Kemudian model matematika tersebut dianalisis agar model yang telah dibuat
representatif terhadap permasalahan yang dibahas. Berbagai masalah yang
terjadi dan timbul dari berbagai bidang ilmu, misalnya bidang kesehatan,
biologi, ekonomi, dan lain sebagainya dapat dibuat model matematikanya.
penyebaran penyakit leptospirosis. Penyakit leptospirosis merupakan penyakit menular yang disebabkan oleh bakteri patogen Spirochetes dari genus Leptospira, yang dapat ditularkan secara langsung maupun tidak langsung dari hewan ke manusia. Penyakit ini dapat ditularkan melalui air
(water borne disease). Penularan penyakit ini paling sering melalui tikus. Air kencing tikus terbawa banjir kemudian masuk ke dalam tubuh manusia
melalui permukaan kulit yang terluka, selaput lendir mata dan hidung. Bisa
juga melalui makanan atau minuman yang terkontaminasi setitik urin tikus
yang terinfeksi leptospira, kemudian dimakan dan diminum manusia.
Berdasarkan laporan The Leptospirosis Information Center, pada tahun 2000 case fatality rate (CFR) leptospirosis di Indonesia menempati urutan ketiga di dunia (16,7%). Sementara menurut Depkes RI (2009), leptospirosis di Indonesia pada rentang 2004-2010 cenderung mengalami peningkatan,
baik dari jumlah kasus maupun kematian dengan insiden tertinggi terjadi pada
tahun 2007.
Model matematika yang akan dibahas dalam tulisan ini adalah model
penyebaran penyakit leptospirosis yang dimodelkan dalam bentuk SIR
Gambar 1. 1. Bakteri Leptospira
(Susceptibles-Infectious-Removed). Model SIR digunakan karena model ini sesuai dengan perilaku epidemi penyakit ini yaitu rentan penyakit, terinfeksi,
dan kemudian sembuh. Selain itu, model SIR ini lebih mudah dalam
penerapannya karena setiap populasi hanya dibagi menjadi tiga kelas. Model
SIR ini menggambarkan bahwa individu yang rentan terserang penyakit
menjadi individu yang terinfeksi penyakit, kemudian sembuh dengan
kekebalan sementara terhadap penyakit tersebut. Berdasarkan populasinya,
model SIR ini dibagi dua yaitu populasi manusia dan populasi vektor.
Populasi manusia dibagi menjadi tiga kelas yaitu kelas populasi manusia yang
rentan terhadap penyakit ( ), kelas populasi manusia yang terinfeksi
penyakit ( ), dan kelas populasi manusia yang sembuh dan kebal penyakit
( ). Dan populasi vektor dibagi menjadi dua kelas yaitu kelas populasi
vektor yang rentan penyakit ( ) dan kelas populasi vektor yang terinfeksi
penyakit ( ).
Dalam tugas akhir ini, akan dianalisis model penyebaran penyakit
leptospirosis untuk mengetahui perilaku penyebaran penyakit ini dengan melakukan analisis kestabilan model pada keadaan bebas penyakit dan pada
saat penyakit menyebar.
B. RUMUSAN MASALAH
Pokok permasalahan yang akan dibahas dalam tulisan ini yaitu:
2. Bagaimana menentukan titik-titik kesetimbangan dan melakukan analisis
kestabilan di titik kesetimbangan?
C. BATASAN MASALAH
Pada penulisan ini, masalah yang akan dibahas hanya dibatasi pada
penyebaran penyakit leptospirosis dengan model SIR (Susceptibles, Infectious, Recovered). Jumlah populasi manusia dan vektor diasumsikan tetap atau konstan.
D. TUJUAN PENULISAN
Berdasarkan perumusan masalah, penulisan ini bertujuan untuk:
1. Memodelkan penyebaran penyakit leptospirosis.
2. Menentukan titik kesetimbangan dan melakukan analisis kestabilan di
titik kesetimbangannya.
E. MANFAAT PENULISAN
Manfaat yang diambil dari tulisan ini adalah untuk memperoleh
pengetahuan tentang perilaku penyebaran penyakit leptospirosis pada populasi dengan model matematika.
F. SISTEMATIKA PENULISAN
BAB I PENDAHULUAN
Bab ini membahas mengenai latar belakang masalah, rumusan
masalah, batasan masalah, tujuan penulisan, manfaat penulisan, dan
sistematika penulisan.
BAB II LANDASAN TEORI
Bab ini membahas mengenai teori-teori penunjang yang akan
digunakan dalam pembentukan model dan analisis kestabilan
model. Teori-teori yang digunakan yaitu teori-teori aljabar linear
dan sistem persamaan linear, sistem persamaan diferensial, serta
teori sistem dinamik.
BAB III MODEL PENYEBARAN PENYAKIT LEPTOSPIROSIS
Bab ini membahas penyebaran penyakit leptospirosis dengan model SIR. Menentukan asumsi-asumsi yang digunakan untuk
menyusun model matematika dan menyusun model matematika
SIR berdasarkan asumsi-asumsi.
BAB IV ANALISIS KESTABILAN
Bab ini membahas tentang menentukan titik kesetimbangan model
matematika SIR. Melakukan analisis kestabilan model berdasarkan
BAB V PENUTUP
Bab ini berisi kesimpulan sebagai jawaban dari rumusan masalah
yang diajukan. Selain itu, berisi saran untuk pengembangan tulisan
7 BAB II
LANDASAN TEORI
A. MODEL MATEMATIKA
Model matematika merupakan salah satu alat yang dapat membantu
mempermudah penyelesaian masalah dalam kehidupan nyata.
Masalah-masalah tersebut dapat dibawa ke dalam model matematis dengan
menggunakan asumsi-asumsi tertentu (Ripno Juli, 2012).
Secara umum, epidemi adalah timbulnya suatu penyakit yang menimpa
sekelompok masyarakat atau suatu wilayah dengan angka kejadian yang
melebihi angka normal dari kejadian penyakit tersebut (Ripno Juli, 2012).
Model epidemi merupakan model matematika yang digunakan untuk melihat
laju penyebaran penyakit. Kondisi epidemi terjadi ketika ada salah satu
individu rentan pada populasi tersebut, maka populasi tersebut memiliki
peluang menjadi populasi rentan, dan kemungkinan besar infeksi tersebut
akan mewabah pada populasi tersebut. Sehingga pada akhirnya seluruh
individu dalam populasi berpeluang terinfeksi. Beberapa model matematika
epidemi diantaranya:
1. Model SIR
Model SIR pada awalnya diperkenalkan oleh W.O. Kennack dan
McKendrick dalam makalahnya yang berjudul “A Contribution to the Mathematical Theory of Epidemics”, yang kemudian muncul dalam
Rangkuman tersebut dituliskan secara lengkap oleh Murray. Dalam
model epidemik SIR, anggota dari populasi manusia dibagi menjadi tiga
kelas, yaitu: suspek dengan simbol S, terinfeksi dengan simbol I, dan
sembuh atau recovery dengan simbol R, yang masing-masing diberikan
dalam bentuk S, I, dan R. Jumlah total dari keseluruhan kelompok tersebut adalah
atau susceptable dalam pemodelan SIR merupakan individu yang tidak terinfeksi tetapi golongan ini rentan terinfeksi penyakit. Oleh
karena itu, golongan ini juga memiliki kemungkinan untuk menjadi
terinfeksi menjadi atau infected.
atau infected merupakan individu yang dapat menyebarkan penyakit pada individu yang susceptable waktu yang diperlukan oleh penderita infeksi penyakit dinamakan periode penyakit. Setelah
mengalami periode penyakit kemudian individu ini pindah dan menjadi
individu yang sembuh atau recovered.
atau recovered merupakan individu yang telah sembuh atau kebal dalam kehidupannya.
Model SIR umumnya ditulis dalam bentuk persamaan diferensial
biasa, yang merupakan salah satu bagian model deterministik dengan
waktu kontinu. Laju perubahan jumlah individu terinfeksi didefinisikan
sebagai , dengan merupakan laju penularan penyakit sedangkan merupakan nilai laju penyembuhan. Individu yang
terinfeksi diasumsikan dapat kembali sembuh dengan probabilitas
konstan sepanjang waktu, yang kemudian berubah secara konstan dengan
laju penyembuhan per kapita yang dinotasikan sebagai dan
keseluruhannya disimbolkan sebagai . Secara skematik dapat digambarkan sebagai berikut:
Laju perubahan jumlah individu yang rentan dipengaruhi oleh
banyaknya individu yang tertular penyakit oleh individu yang terinfeksi
dengan laju penularan . Laju perubahan jumlah individu yang terinfeksi
dipengaruhi oleh banyaknya individu yang rentan tertular penyakit
menjadi terinfeksi dan banyaknya individu yang terinfeksi menjadi
sembuh dengan laju penyembuhan β. Laju perubahan jumlah individu
yang sembuh dipengaruhi oleh banyaknya individu yang terinfeksi
menjadi sembuh dengan laju penyembuhan β, sehingga dari diagram
tersebut dapat dibentuk dalam persamaan diferensial sebagai berikut:
(2.1)
Persamaan ini menggambarkan mengenai transisi masing-masing
individu dari ke lalu ke . Dengan menambahkan sistem persamaan
(2.1) dapat ditunjukkan bahwa total populasi adalah konstan.
2. Model SI
Model SI adalah bentuk sederhana dari model SIR klasik. Pada
beberapa kasus infeksi tidak diperlukan adanya kelas populasi
recovered. Misalnya, bisa jadi individu yang telah terinfeksi sama sekali tidak dapat sembuh. Secara skematik dapat digambarkan sebagai berikut:
Dalam model SI, anggota dari populasi manusia hanya dibagi
menjadi dua kelas, yaitu: suspek dengan simbol S dan terinfeksi dengan
simbol I. Jumlah total dari keseluruhan kelompok tersebut adalah
3. Model SEIR
Model SEIR menggunakan pertimbangan bahwa adanya periode
ekspose atau tersembunyi dari penyakit. Beberapa penyakit mempunyai
sebuah fase tersembunyi atau belum terlihat, pada waktu dimana individu
dikatakan telah terinfeksi tetapi tidak menginfeksi dilambangkan dengan
simbol . Secara skematik dapat digambarkan sebagai berikut:
Dalam model SEIR, anggota dari populasi manusia dibagi menjadi
empat kelas, yaitu: suspek dengan simbol S , ekspose dengan simbol ,
susceptables infected
terinfeksi dengan simbol I, dan sembuh dengan simbol . Jumlah total
dari keseluruhan kelompok tersebut adalah
4. Model MSIR
Model MSIR menggunakan anggapan bahwa untuk beberapa kasus
penyakit dimana seorang individu terlahir dengan kekebalan pasif dari
ibunya. Individu yang memiliki kekebalan pasif ini disimbolkan dengan
. Secara skematik dapat digambarkan sebagai berikut:
Dalam model MSIR, anggota dari populasi manusia hanya dibagi
menjadi empat kelas, yaitu: bayi dengan kekebalan pasif dengan simbol
, suspek dengan simbol , terinfeksi dengan simbol , dan sembuh
dengan simbol . Jumlah total dari keseluruhan kelompok tersebut
adalah
B. SISTEM LINEAR DAN MATRIKS
1. Sistem persamaan linear
Definisi 2.1. (Howard Anton, 1988). Sistem persamaan linear adalah suatu himpunan berhingga dari persamaan-persamaan linear dalam
peubah .
Bentuk umum dari sistem persamaan linear yang terdiri dari
persamaan linear dengan bilangan tak diketahui dapat dituliskan
sebagai
di mana , , , adalah bilangan-bilangan tak diketahui sedangkan
dan menyatakan konstanta-konstanta. Sistem persamaan linear di atas
dapat dituliskan juga dalam bentuk matriks.
Contoh 1:
2. Matriks
Definisi 2.2. (Howard Anton, 1988). Matriks adalah susunan segiempat dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut
dinamakan entri dalam matriks.
Ukuran matriks dapat dijelaskan dengan menyatakan banyaknya m
baris dan banyaknya n kolom yang terdapat dalam matriks tersebut. Jika
adalah sebuah matriks berukuran dengan untuk entrinya pada baris dan kolom , maka dapat dituliskan sebagai
[ ] atau [ ] Contoh 2: * +
Matriks mempunyai 3 baris dan 2 kolom sehingga ukurannya adalah
. Jadi matriks adalah matriks .
[ ]
Matriks mempunyai 3 baris dan 3 kolom sehingga ukurannya adalah
. Jadi matriks adalah matriks atau dapat juga disebut sebagai matriks persegi.
Jika adalah suatu matriks persegi berukuran , maka memiliki skalar khusus yang disebut determinan . Biasanya
dilambangkan dengan ( ) atai | |.
3. Determinan matriks
Definisi 2.3. (Howard Anton, 1988). Misalkan adalah matriks persegi. Fungsi determinan ( ) didefinisikan sebagai jumlah semua hasil kali elementer bertanda dari . Jumlah ( ) dinamakan determinan.
Contoh 3:
* +
[ ]
Determinan-determinan matriks di atas, yaitu
( ) (* +) | | ( ) ([ ]) ( ) ( ) ( )
Akan tetapi, metode tersebut tidak berlaku untuk determinan
matriks yang lebih tinggi. Oleh karena itu, determinan juga dapat
dihitung dengan sebuah metode yaitu ekspansi kofaktor.
4. Ekspansi Kofaktor
Definisi 2.4. (Howard Anton, 1988).Jika adalah suatu matriks persegi, maka minor entri dinyatakan oleh dan didefinisikan sebagai
determinan submatriks dari yang diperoleh setelah menghilangkan
baris ke- dan kolom ke- . Bilangan ( ) dinyatakan oleh dan disebut kofaktor entri .
Contoh 4:
[
]
Minor entri adalah
| |
Kofaktor adalah
( )
Pada contoh 3, determinan dari matriks yang berukuran adalah ( )
yang dapat dituliskan kembali sebagai ( ) ( ) ( ) ( ).
Karena pernyataan-pernyataan dalam kurung adalah kofaktor-kofaktor
, , dan maka diperoleh
( )
sehingga determinan matriks dapat ditulis
( )
Teorema 2.1. (Howard Anton, 1988). Determinan matriks yang berukuran dapat dihitung dengan mengalikan entri-entri dalam suatu baris (atau kolom) dengan kofaktornya dan menambahkan
hasil-hasil kali yang dihasil-hasilkan; yaitu, untuk setiap dan maka,
( )
(perluasan kofaktor di sepanjang kolom ke- )
dan
( )
(perluasan kofaktor di sepanjang baris ke- ).
Contoh 5:
[
]
Hitung ( ) dengan perluasan kofaktor di sepanjang baris pertama. Penyelesaian. ( ) | | | | | | | | ( ) ( )
Suatu matriks persegi atau matriks berukuran memiliki suatu nilai karakteristik. Nilai karakteristik dari matriks ini disebut dengan nilai eigen.
5. Nilai Eigen
Definisi 2.5. (Howard Anton, 1988). Jika adalah matriks , maka vektor tak nol di dalam dinamakan vektor eigen (eigenvector) dari
jika adalah kelipatan skalar dari yakni,
untuk suatu skalar . Skalar dinamakan nilai eigen (eigenvalue) dari dan dikatakan vektor eigen yang bersesuaian dengan .
Jika adalah nilai eigen dari yang bersesuaian dengan , maka
, sehingga perkalian oleh akan memperbesar , atau membalik arah , yang bergantung pada nilai , sedangkan untuk mencari nilai
eigen matriks yang berukuran maka kita menulis kembali
sebagai
atau secara ekuivalen
( )
Supaya menjadi nilai eigen, maka harus ada penyelesaian tak nol dari
persamaan ini. Persamaan ini akan mempunyai penyelesaian tak nol jika
dan hanya jika
( )
Ini dinamakan persamaan karakteristik ; skalar yang memenuhi
persamaan ini adalah nilai eigen dari . Bila diperluas, maka determinan
( ) adalah polinom yang dinamakan polinom karakteristik dari . Jika adalah matriks , maka polinom karakteristik harus
memenuhi dan koefisien adalah , sehingga polinom karakteristik
dari matriks berbentuk
( )
Contoh 6:
Carilah nilai-nilai eigen dari matriks
* +
Penyelesaian. Karena
*
+ * + * +
Maka polinom karakteristik dari adalah
( ) * +
Dan persamaan karakteristik dari adalah
Penyelesaian-penyelesaian persamaan ini adalah dan ; inilah nilai-nilai eigen dari . Lebih lanjut, matriks dan nilai eigen akan banyak
digunakan untuk mencari penyelesaian suatu sistem persamaan
diferensial.
C. PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah persamaan yang mengandung derivatif
(turunan) satu atau lebih fungsi yang tidak diketahui (William E Boyce,
Contoh 7: ( ) ( ) ( )
Persamaan diferensial diklasifikasikan menjadi dua, yaitu persamaan
diferensial biasa dan persamaan diferensial parsial.
1. Persamaan Diferensial Biasa
Jika fungsi yang tidak diketahui tergantung dari satu variabel bebas
saja maka persamaan diferensial yang terbentuk disebut persamaan
diferensial biasa.
Contoh 8:
2. Persamaan Diferensial Parsial
Jika fungsi yang tidak diketahui tergantung dari beberapa variabel
bebas maka persamaan diferensial yang terbentuk disebut persamaan
diferensial parsial. Contoh 9: ( ) ( ) ( ) ( ) ( )
3. Persamaan Diferensial Linear dan Tak Linear
Persamaan diferensial biasa ( ̇ ( )) , dikatakan linear jika adalah linear dalam variabel-variabel ̇ ( ). Definisi serupa juga berlaku untuk persamaan diferensial parsial. Jadi persamaan
umum persamaan diferensial biasa linear orde n diberikan dengan
( ) ( ) ( ) ( ) ( )
Persamaan yang tidak dalam bentuk di atas merupakan persamaan tak
linear.
Contoh 8:
a.
( ), merupakan persamaan diferensial linear.
b.
, merupakan persamaan diferensial tak linear
karena suku dan .
4. Persamaan Diferensial Homogen dan Nonhomogen
Suatu persamaan diferensial yang mempunyai bentuk umum
( ) ( ) ( ) disebut homogen jika ( ) . Jika ( )
tersebut berbentuk fungsi exponensial, trigonometri, ataupun fungsi
polynomial dan ( ) maka persamaan diferensial tersebut dikatakan nonhomogen.
Contoh 9:
5. Penyelesaian Persamaan Diferensial
Penyelesaian dari persamaan diferensial biasa
( ) ( ( )) dalam interval adalah sebuah
fungsi sedemikian sehingga ( ) ( ) ( )( ) ada dan memenuhi
( )( ) * ( ) ( ) ( )( )+
untuk setiap dalam . Contoh 10:
Selesaikan Persamaan Diferensial berikut:
Persamaan di atas dapat ditulis sebagai:
Bila kedua ruas diintegralkan maka
∫ ∫
Sehingga diperoleh
atau
dengan
Jika diketahui nilai awal ( ) dan bila disubtitusikan ke persamaan
dan diperoleh , sehingga persamaan menjadi: ( )
D. TEORI SISTEM DINAMIK
Teori sistem adalah suatu ilmu yang mempelajari tentang sistem sebagai
obyeknya (Rudolfh Stitchweh, 2011). Sistem dinamik adalah sistem yang
memiliki struktur dan aktivitas yang ditandai dengan pola perilaku yang
berubah-ubah sepanjang waktu (Vincent Gazpers). Teori sistem dinamik
merupakan bidang matematika terapan yang digunakan untuk memeriksa
perilaku sistem dinamik, biasanya menggunakan persamaan diferensial. Teori
ini membahas perilaku kualitatif jangka panjang sistem dan pemecahan
persamaan gerak dari sistem yang terutama bersifat mekanik di alam.
1. Sistem Persamaan Diferensial
Sistem persamaan diferensial adalah suatu sistem yang memuat
persamaan diferensial dengan buah fungsi yang tidak diketahui,
dimana . Bentuk umum dari sistem persamaan diferensial dapat dituliskan sebagai berikut:
̇ ( ) ̇ ( ) ̇ ( )
Sistem di atas dapat ditulis sebagai
[ ̇ ( ) ̇ ( ) ̇ ( ) ] [ ] [ ( ) ( ) ( ) ] [ ( ) ( ) ( )] atau ̇ ( ).
2. Sistem Homogen
Sistem persamaan diferensial ̇ ( ) disebut homogen jika
( ) dan tidak homogen jika ( ) . Sistem homogen dari persamaan diferensial linear orde satu dengan koefisien real, secara
umum dapat ditulis sebagai:
̇ ̇ ̇
Sistem persamaan di atas dapat di tulis sebagai ̇ , dengan
( ) [ ( ) ( ) ( ) ] [ ] 3. Kestabilan
Definisi 2.6. (D.Gilliam, 1999). Suatu persamaan diferensial ̇( )
( ( )), dimana ( ) . Misal ( ) merupakan penyelesaian dari persamaan, dengan kondisi awal ( ) . Misal
) merupakan penyelesaian dari persamaan diferensial. a. Penyelesaian stabil di ) jika untuk setiap , ada
sedemikian sehingga | ( ) | , penyelesaian ( ) terdefinisi untuk setiap ) dan
| ( ) ( )| , .
b. stabil asimptotik di ) jika stabil dan untuk setiap , ada sedemikian sehingga | ( ) | ,
| ( ) ( )| .
c. tidak stabil jika ada sedemikian sehingga untuk setiap dimana ada dengan | ( ) | sedemikian sehingga
| ( ) ( )| untuk ).
Kestabilan digunakan untuk menentukan apakah sistem tersebut
stabil atau tidak dengan menguji kestabilan dari titik kesetimbangannya.
4. Titik Kesetimbangan (equilibrium)
Diberikan sistem persamaan diferensial ̇ , titik kesetimbangan (equilibrium) adalah suatu penyelesaian yang memenuhi
̇ . Berdasarkan persamaan ̇ di mana adalah matriks berukuran , penyelesaiannya adalah ( ) , ( ) dan
adalah nilai-nilai eigen dari berlaku
Teorema 2.2. adalah sebuah matriks dan adalah nilai-nilai eigen dari . Misalkan bahwa ( ) di mana dan bernilai real untuk Ada suatu konstanta sedemikian sehingga
‖ ‖ , .
Berdasarkan dari teorema 2.2, maka berlaku pula
Teorema 2.3. adalah sebuah matriks dan misalkan semua nilai eigen dari berniali real dan kurang dari atau sama dengan nol, dan nilai
eigen dengan nilai nol adalah simpel. Maka, ada suatu konstanta
‖ ‖ , .
Nilai-nilai eigen dari matriks menggolongkan kestabilan dari titik
kesetimbangan sistem persamaan diferensial ̇ .
Teorema 2.4 (C. C. Remsing, 2006). Suatu sistem stabil netral jika dan hanya jika beberapa nilai eigen dari bernilai real tak-positif dan paling
sedikit satu nilai eigen yang bernilai nol.
a. Suatu sistem stabil asimptotik jika dan hanya jika adalah sebuah
matriks yang stabil yaitu setiap nilai eigen dari bernilai real
negatif.
b. Suatu sistem tidak stabil jika dan hanya jika beberapa nilai eigen dari
bernilai real positif.
Bukti:
a. Misalkan ( ) , berdasarkan teorema 2.3 ada suatu konsatanta sedemikian sehingga
‖ ‖ , .
Misal penyelesaian , diberikan , ambil . Jika adalah kondisi awal dengan | | | | , maka
| ( )| | | ‖ ‖ | | | | ( )
Sehingga | ( )| . Jadi, sistem tersebut stabil atau stabil netral.
b. Misalkan ( ) , maka sistem dalam keadaan stabil berdasarkan bukti sebelumnya. Ambil suatu bilangan real
, sedemikian sehingga ( ) untuk semuaa nilai eigen dari . Berdasarkan teorema 2.2, ada suatu konsatanta
sedemikian sehingga
‖ ‖ , .
Maka untuk kondisi awal ,
| ( )| | | ‖ ‖ | | | | , .
Karena bernilai negatif, saat . Sehingga
( ) . Jadi, sistem tersebut stabil asimptotik.
c. Misalkan nilai eigen dengan Misalkan adalah suatu vektor eigen dari . Penyelesaian dari sistem dengan
kondisi awal dalah . Diberikan , misal
| | maka | | . Dengan kata lain, penyelesaian
( ) dari sistem dengan kondisi awal adalah ( )
. Sehingga | ( )| ( ) . Karena
maka | ( )| saat . Jadi, sistem tidak stabil. Contoh 11:
Diketahui sistem persamaan diferensial sebagai berikut:
( ) *
+ ( )
Titik kesetimbangan (equilibrium) akan diperoleh jika dan , maka
Diperoleh ( ) ( ) Dari matriks *
+ akan dicari nilai eigennya, yaitu * + * + *
+
Maka polinom karakteristik dari adalah
( ) *
+
Dan persamaan karakteristik dari adalah
Maka diperoleh nilai dan
Kedua nilai eigen dari matriks bernilai negatif, maka berdasarkan
teorema (2.4) titik kesetimbangannya stabil asimptotik. Akan tetapi, jika
sistem tidak linear, maka untuk menentukan kestabilan sistem tersebut
dilakukan dengan dengan linearisasi sistem.
5. Linearisasi Sistem
Definisi 2.7. (Lawrence Perko, 2001). Titik dinamakan titik kesetimbangan atau titik kritis dari ̇ ( ) jika ( ) . Titik
kesetimbangan dinamakan titik kesetimbangan hiperbolik dari
̇ ( ) jika tidak ada nilai eigen dari matrik ( ) bernilai nol. Sistem linear ̇ dengan matriks ( ) linearisasi dari
̇ ( ) pada . Linearisasi sistem ̇ ( ) menggunakan matriks Jacobian.
Teorema 2.5. Jika dapat diturunkan pada , maka turunan parsial , semua ada pada dan untuk semua ,
( ) ∑
( )
Jika ( ̅) adalah fungsi yang dapat diturunkan, turunan ( ̅) diberikan oleh matriks Jacobian ,
( ̅) * ( ̅)+ [ ( ̅) ( ̅) ( ̅) ( ̅) ( ̅) ( ̅) ( ̅) ( ̅) ( ̅)]
Kriteria kestabilan sistem non linear ̇ ( ) dapat ditentukan dengan nilai eigen dari matriks Jacobian ( ̅).
Teorema 2.6. (Olsder, 1994). Diberikan matriks Jacobian ( ̅) dari sistem non linear ̇ ( ) dengan nilai eigen .
a. Stabil asimptotik lokal, jika semua nilai eigen dari matriks ( ̅) bernilai negatif.
b. Tidak stabil, jika terdapat paling sedikit satu nilai eigen matriks
( ̅) bernilai positif. Bukti:
Jika adalah matriks , maka berlaku . Diberikan nilai awal , maka solusinya adalah .
a. Jika semua nilai eigen dari ,
( ) , untuk
maka nilai saat , sehingga semua nilai dari mendekati titik kesetimbangannya. Jadi, sistem stabil asimptotik
lokal.
b. Jika ada nilai eigen dari
( ) , untuk
maka nilai atau tidak mendekati nol saat , sehingga nilai dari menjauhi titik kesetimbangannya dan bergerak menuju . Jadi, sistem tidak stabil.
30 BAB III
MODEL PENYEBARAN PENYAKIT LEPTOSPIROSIS
A. PENYEBARAN PENYAKIT LEPTOSPIROSIS
Penyakit leptospirosis merupakan penyakit menular yang disebabkan oleh bakteri patogen Spirochetes dari genus Leptospira, yang dapat ditularkan secara langsung maupun tidak langsung dari hewan ke manusia. Leptospirosis merupakan penyakit yang dapat ditularkan melalui air (water borne disease). Urin (air kencing) dari individu yang terserang penyakit ini merupakan
sumber utama penularan, baik pada manusia maupun pada hewan.
Kemampuan Leptospira untuk bergerak dengan cepat dalam air menjadi salah satu faktor penentu utama ia dapat menginfeksi induk semang yang baru.
Penyakit ini memasuki masa puncaknya ketika musim hujan. Hujan deras
akan membantu penyebaran penyakit ini, terutama di daerah banjir.
Gambar 3. 1. Tikus sebagai Penyebar Utama
Penularan penyakit ini bisa melalui hewan mamalia. Namun, Sejauh ini
tikus merupakan penyebar utama leptospirosis karena bertindak sebagai inang alami dan memiliki daya reproduksi tinggi. Air kencing tikus terbawa banjir
kemudian masuk ke dalam tubuh manusia melalui permukaan kulit yang
terluka, selaput lendir mata dan hidung. Bisa juga melalui makanan atau
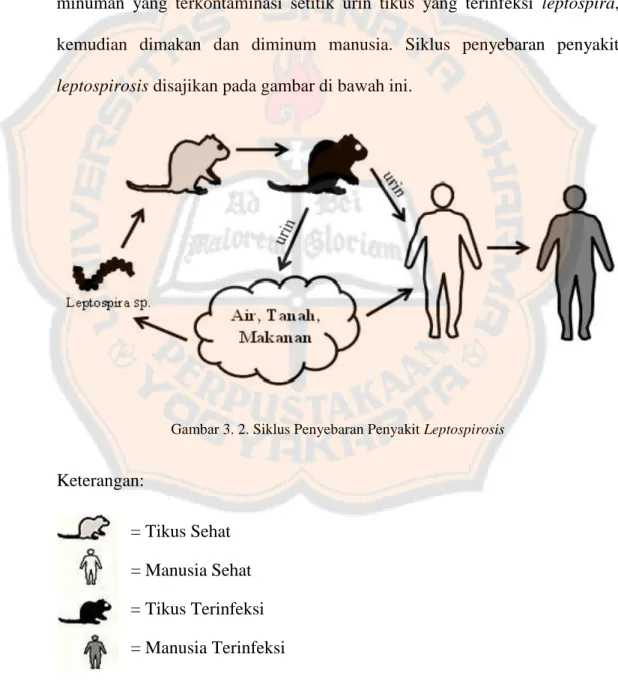
minuman yang terkontaminasi setitik urin tikus yang terinfeksi leptospira, kemudian dimakan dan diminum manusia. Siklus penyebaran penyakit
leptospirosis disajikan pada gambar di bawah ini.
Gambar 3. 2. Siklus Penyebaran PenyakitLeptospirosis
Keterangan:
= Tikus Sehat
= Manusia Sehat
= Tikus Terinfeksi
Tanda-tanda dan gejala leptospirosis biasanya muncul tiba-tiba, sekitar 7 sampai 14 hari setelah seseorang terinfeksi, dan dalam beberapa kasus, tanda
dan gejala tersebut mungkin muncul sebelum atau sesudahnya. Leptospirosis tidak menular langsung dari pasien ke pasien. Masa inkubasi leptospirosis adalah dua hingga 26 hari. Sekali berada di aliran darah, bakteri ini bisa
menyebar ke seluruh tubuh dan mengakibatkan gangguan khususnya hati dan
ginjal. Ada dua jenis utama leptospirosis:
1. Leptospirosis ringan: pasien mengalami nyeri otot, menggigil dan mungkin sakit kepala seperti gejala flu. Rata-rata 90% dari kasus
leptospirosis tergolong jenis ini.
2. Leptospirosis berat: dapat mengancam jiwa. Ada risiko kegagalan organ dan pendarahan internal. Jenis leptospirosis ini terjadi ketika bakteri menginfeksi ginjal, hati dan organ utama lainnya.
Cara pengobatan penyakit leptospirosis ini pada manusia adalah dengan memberikan obat antibiotik secara rutin kepada pasien yang terinfeksi
leptospirosis baik yang ringan maupun berat.
B. MODEL MATEMATIKA UNTUK PENYEBARAN PENYAKIT LEPTOSPIROSIS
Model matematika yang akan digunakan dalam memodelkan penyebaran
penyakit leptospirosis ini adalah model SIR (Susceptables, Infective, Recovered). Model SIR digunakan karena model ini sesuai dengan perilaku epidemi penyakit ini yaitu rentan penyakit, terinfeksi, dan kemudian sembuh.
Selain itu, model SIR ini lebih mudah dalam penerapannya karena setiap
populasi hanya dibagi menjadi tiga kelas. Model SIR ini menggambarkan
bahwa individu yang rentan terserang penyakit menjadi individu yang
terinfeksi penyakit, kemudian sembuh dengan kekebalan sementara terhadap
penyakit tersebut . Model SIR ini dibagi menjadi dua populasi, yaitu populasi
manusia dan populasi vektor, istilah “vektor” yang dimaksud adalah tikus,
karena sebagai sarana penyebaran penyakit . Populasi manusia dibagi ke
dalam tiga kelas populasi yaitu kelas populasi manusia yang rentan adalah
setiap individu dari populasi manusia yang belum terinfeksi tetapi rentan
terinfeksi penyakit, kelas populasi manusia yang terinfeksi adalah setiap
individu dari populasi manusia yang telah tertular atau terinfeksi penyakit,
dan kelas populasi manusia yang bebas penyakit adalah setiap individu dari
populasi manusia yang telah sembuh dari penyakit dengan antibiotik atau
sedang diisolasi sedangkan populasi vektor dibagi menjadi dua kelas yaitu
kelas populasi vektor yang rentan adalah setiap individu dari populasi tikus
yang belum terinfeksi tetapi rentan terinfeksi penyakit dan kelas populasi
vektor yang terinfeksi adalah setiap individu dari populasi tikus yang telah
terinfeksi penyakit dan dapat menularkannya. Pembentukan model ini
dibatasi oleh beberapa asumsi. Asumsi-asumsi yang digunakan dalam model
penyebaran penyakit leptospirosis sebagai berikut:
1. Jumlah populasi manusia dan vektor adalah tetap atau konstan.
2. Angka kematian alami tetap, berakibat sama untuk semua kelas populasi.
4. Setiap Individu tidak dipengaruhi oleh umur atau status penyakit
sehingga data setiap individu sama.
5. Setiap individu yang baru lahir dianggap tidak memiliki kekebalan dan
mudah terserang penyakit dengan segera.
6. Manusia yang terinfeksi leptospirosis ringan dan berat tidak dibedakan. 7. Manusia yang rentan yang terinfeksi oleh vektor yang terinfeksi dapat
segera menjadi manusia yang terinfeksi tanpa membutuhkan waktu
inkubasi.
8. Manusia yang rentan dapat terinfeksi oleh vektor terinfeksi tetapi tidak
dapat terinfeksi oleh manusia lain yang telah terinfeksi.
9. Masa inkubasi penyakit tidak diperhatikan.
10.Hanya terdapat satu macam penularan dengan penyakit yang sama.
11.Vektor yang rentan dapat dengan segera menjadi vektor terinfeksi tanpa
membutuhkan masa inkubasi.
12.Manusia yang terinfeksi dapat disembuhkan dengan menggunakan
antibiotik.
13.Angka penularan leptospirosis dari vektor yang terinfeksi ke manusia yang rentan berubah-ubah berdasarkan jumlah curah hujan yang turun.
14.Kedua populasi homogen yang berarti setiap individu mempunyai
kemungkinan yang sama dalam melakukan kontak dengan individu lain.
Adapun variabel-variabel dan parameter-parameter yang digunakan dalam
Variabel Keterangan
Jumlah populasi manusia pada waktu
Jumlah manusia yang rentan terinfeksi
pada waktu
Jumlah manusia yang terinfeksi pada
waktu
Jumlah manusia yang telah sembuh,
bebas dari penyakit, atau kebal dari
infeksi virus yang sedang mewabah
pada waktu
Jumlah populasi vektor pada waktu
Jumlah vektor yang rentan terinfeksi
pada waktu
Jumlah vektor yang terinfeksi pada
waktu
Tabel 3. 1. Daftar Variabel-variabel
Parameter Keterangan
Angka kelahiran alami manusia
Angka kematian alami manusia
Angka kematian alami vektor
Angka penularan penyakit dari vektor
yang terinfeksi ke manusia yang rentan
Angka penularan penyakit dari vektor
yang terinfeksi ke manusia yang rentan
Angka kesembuhan individu yang
sembuh dengan antibiotik dan menjadi
kebal
Angka perubahan individu yang kebal
menjadi rentan kembali
Tabel 3. 2. Daftar Parameter-parameter
Setiap manusia yang baru lahir ( ) sehat tetapi rentan terinfeksi penyakit. Manusia yang rentan dapat tertular penyakit oleh vektor yang
terinfeksi menjadi terinfeksi dengan angka penularan dan dapat meninggal
( ). Manusia yang terinfeksi akan menjadi sembuh dengan antibiotik dengan angka kesembuhan dan dapat juga meninggal ( ). Manusia yang telah sembuh atau kebal terhadap penyakit akan kembali menjadi rentan ( ) dan dapat meninggal ( ).
Sedangkan setiap vektor yang baru lahir ( ) ada yang rentan terhadap penyakit dan ada yang terinfeksi, sesuai dengan kondisi induknya. Vektor
yang rentan penyakit dapat segera terinfeksi dengan angka penularan dan
dapat mati ( ). Vektor yang telah terinfeksi tidak dapat menjadi sembuh dan akan mati ( ).
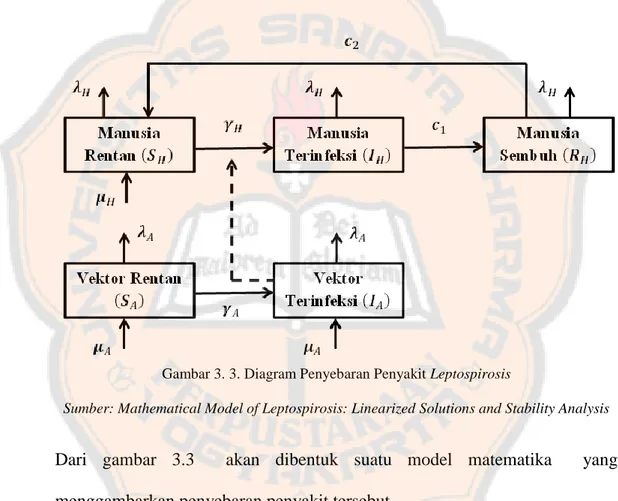
Sebagaimana telah dijelaskan dalam gambar 3.2 mengenai siklus
penyebaran penyakit leptospirosis dari tikus ke manusia dan asumsi-asumsi yang telah dibuat, serta dengan variabel-variabel dan parameter-parameter
yang telah ditentukan, secara skematis dinamika penyebaran penyakit
leptospirosis dapat disajikan dalam bagan di bawah ini.
Gambar 3. 3. Diagram Penyebaran PenyakitLeptospirosis
Sumber: Mathematical Model of Leptospirosis: Linearized Solutions and Stability Analysis
Dari gambar 3.3 akan dibentuk suatu model matematika yang
menggambarkan penyebaran penyakit tersebut.
C. FORMULASI MODEL
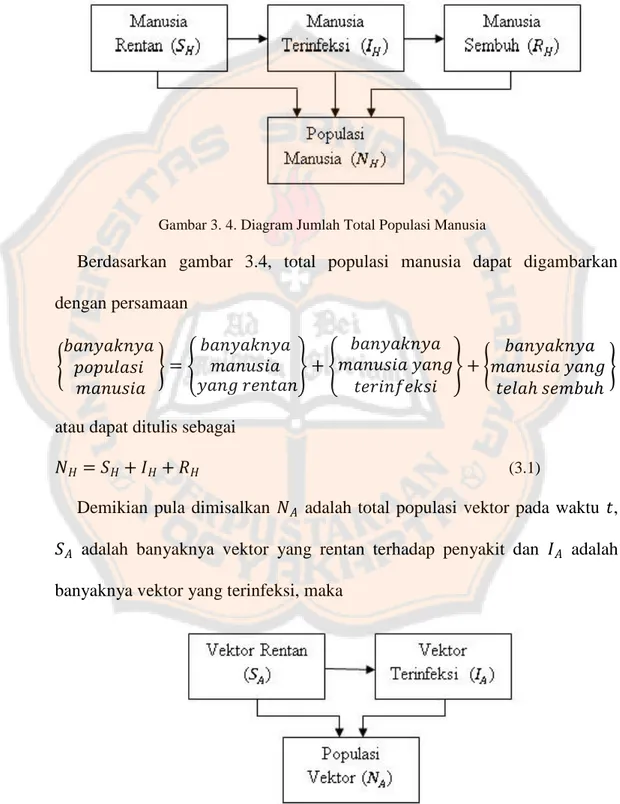
Misalkan adalah total populasi manusia pada waktu , adalah
banyaknya manusia yang terinfeksi, dan adalah banyaknya manusia yang
telah sembuh, maka
Berdasarkan gambar 3.4, total populasi manusia dapat digambarkan
dengan persamaan { } { } { } { }
atau dapat ditulis sebagai
(3.1)
Demikian pula dimisalkan adalah total populasi vektor pada waktu ,
adalah banyaknya vektor yang rentan terhadap penyakit dan adalah
banyaknya vektor yang terinfeksi, maka
Gambar 3. 4. Diagram Jumlah Total Populasi Manusia
Berdasarkan gambar 3.5, total populasi vektor dapat digambarkan dengan persamaan { } { } { }
atau dapat ditulis
(3.2)
Misalkan adalah banyaknya populasi manusia yang rentan pada waktu
. Berdasarkan gambar 3.3, laju perubahan populasi manusia yang rentan
dapat digambarkan dengan persamaan
{ } { } { }
Jumlah manusia yang masuk ke populasi rentan dipengaruhi oleh
banyaknya individu yang lahir dalam populasi dengan angka kelahiran
dan banyaknya individu dalam populasi bebas penyakit ( ) yang menjadi
rentan kembali dengan angka ,
{ }
Dan jumlah manusia yang keluar dari populasi rentan dipengaruhi oleh
banyaknya individu rentan yang terinfeksi oleh tikus (vektor) yang terinfeksi
terinfeksi ke manusia yang rentan sebanyak dan jumlah individu yang
meninggal dalam populasi rentan dengan angka kematian ,
{ }
Sehingga laju perubahan populasi manusia yang rentan adalah
( ) ( )
Maka diperoleh persamaan
(3.3)
Dimisalkan adalah banyaknya populasi manusia yang terinfeksi pada
waktu . Berdasarkan gambar 3.3, laju perubahan populasi manusia yang
terinfeksi dapat digambarkan dengan persamaan
{ } { } { }
Jumlah manusia yang masuk ke populasi terinfeksi dipengaruhi oleh
banyaknya individu rentan yang terinfeksi oleh tikus (vektor) yang terinfeksi
( ) denganangka penularan penyakit leptospirosis dari vektor yang terinfeksi ke manusia yang rentan sebanyak ,
{ }
Dan jumlah manusia yang keluar dari populasi rentan dipengaruhi oleh
kesembuhan dan jumlah individu dari populasi terinfeksi yang meninggal
dengan angka kematian ,
{ }
Sehingga laju perubahan populasi manusia yang terinfeksi adalah
( ) ( )
Maka diperoleh persamaan
(3.4)
Dimisalkan pula adalah banyaknya populasi manusia yang bebas
penyakit pada waktu . Berdasarkan gambar 3.3, laju perubahan populasi
manusia yang bebas penyakit dapat digambarkan dengan persamaan
{ } { } { }
Jumlah manusia yang masuk ke populasi bebas penyakit dipengaruhi oleh
banyaknya individu yang terinfeksi atau sakit menjadi sembuh dengan angka
kesembuhan , { }
Dan jumlah manusia yang keluar dari populasi bebas penyakit dipengaruhi
rentan kembali dengan angka dan jumlah individu dari populasi bebas
penyakit yang meninggal dengan angka kematian ,
{ }
Sehingga laju perubahan populasi manusia yang bebas penyakit adalah
( ) ( )
Maka diperoleh persamaan
(3.5)
Misalkan adalah banyaknya populasi vektor yang rentan pada waktu .
Berdasarkan gambar 3.3, laju perubahan populasi vektor yang rentan dapat
digambarkan dengan persamaan
{ } { } { }
Jumlah vektor yang masuk ke populasi vektor rentan dipengaruhi oleh
banyaknya individu yang lahir dalam populasi vektor rentan dengan angka
kelahiran , { }
Dan jumlah vektor yang keluar dari populasi vektor rentan dipengaruhi
terinfeksi dengan angka penularan penyakit leptospirosis dari vektor yang terinfeksi ke vektor yang rentan sebanyak dan jumlah vektor yang mati
dalam populasi vektor rentan dengan angka kematian ,
{ }
Sehingga laju perubahan populasi vektor yang rentan adalah
( ) ( )
Maka diperoleh persamaan
(3.6)
Misal adalah banyaknya populasi vektor yang terinfeksi pada waktu .
Berdasarkan gambar 3.3, laju perubahan populasi vektor yang terinfeksi dapat
digambarkan dengan persamaan
{ } { } { }
Jumlah vektor yang masuk ke populasi vektor rentan dipengaruhi oleh
banyaknya individu yang lahir dalam populasi vektor terinfeksi dengan angka
kelahiran dan banyaknya vektor rentan yang terinfeksi penyakit oleh
vektor yang telah terinfeksi dengan angka penularan penyakit leptospirosis dari vektor yang terinfeksi ke vektor yang rentan sebanyak ,
{ }
Dan jumlah vektor yang keluar dari populasi vektor terinfeksi dipengaruhi
oleh jumlah vektor yang mati dalam populasi vektor rentan dengan angka
kematian , { }
Sehingga laju perubahan populasi vektor yang terinfeksi adalah
( ) ( )
Maka diperoleh persamaan
(3.7)
Dari persamaan (3.1), (3.2), (3.3), (3.4), (3.5), (3.6), dan (3.7) diperoleh
model SIR sebagai berikut:
(3.8)
Model (3.8) merupakan suatu sistem persamaan diferensial non linear
dengan lima variabel, yaitu , , , , dan . Model tersebut
menggambarkan laju perubahan populasi pada waktu untuk masing-masing
kelas yaitu populasi manusia rentan( ), manusia terinfeksi ( ), manusia sembuh ( ), vektor rentan( ), dan vektor terinfeksi ( ).
46 BAB IV
ANALISIS KESTABILAN
Pada bab ini akan dibahas mengenai analisis kestabilan model yang telah
diperoleh pada bab sebelumnya. Analisis dilakukan dengan cara mencari titik
kesetimbangan dari sistem persamaan (3.8) yang kemudian akan diuji
kestabilannya. Uji kestabilan titik kesetimbangan dilakukan untuk melihat
kestabilan dari sistem atau model yang telah dibuat.
Berdasarkan sistem persamaan (3.8), banyaknya populasi manusia ( ) adalah sehingga diperoleh dan banyaknya populasi vektor adalah sehingga
diperoleh sehingga dan untuk bilangan bulat positif. Berdasarkan asumsi bahwa jumlah kedua populasi konstan, sistem (3.8)
dapat diskala ke total populasi dan untuk menyederhanakan sistem (3.8).
Banyaknya individu masing-masing kelompok dinyatakan sebagai berikut:
, , , , , , dan .
Dari persamaan di atas, diperoleh:
dan
sehingga sistem persamaan (3.8) diperoleh sebagai berikut:
(4.1)
Kemudian sistem persamaan (4.1) akan dianalisis kestabilannya dengan terlebih
dahulu menentukan titik kesetimbangannya.
A. TITIK KESETIMBANGAN
Dari sistem persamaan (4.1) akan dicari titik kesetimbangannya, yaitu
dengan . Sehingga diperoleh
(4.2)
(4.3)
(4.4)
(4.5)
(4.6)
Dari persamaan (4.2) diperoleh
( ) ( )
Dari persamaan (4.3) diperoleh
( ) ( )
Dari persamaan (4.4) diperoleh
( )
( )
Dari persamaan (4.5) diperoleh
( ) Untuk kasus , Persamaan (4.6) menjadi: ( ) ( )
Subtitusikan persamaan ( ) ke ( ), diperoleh:
( ) Subtitusikan ( ) ( ) ke ( ), diperoleh: ( )
( ) Subtitusikan ( ) ke ( ), diperoleh: ( ) Subtitusikan ( ) ke ( ), diperoleh: ( )
Sehingga diperoleh titik kesetimbangan bebas penyakit
( ) ( ).
Titik kesetimbangan endemik ditentukan dengan asumsi dengan
( ). Sehingga (4.7) (4.8) (4.9) (4.10) (4.11)
Untuk kasus , maka Persamaan (4.7) diperoleh:
( ) * ( )+ ( ) ( ) Persamaan (4.8) diperoleh: ( ) ( ) ( ) ( ) ( )
Dari persamaan (4.9), diperoleh:
( ) ( ) Subtitusikan ( ) ke ( ), diperoleh: ( ) ( ) * ( )+ ( ) ( ) Subtitusikan ( ) ke ( ), diperoleh: [ ( )] ( ) ( ( ) ) [ ( ) ( ) ( ( ) )]
( ) ( )( ( ) ) ( )( ) ( ( )( )[( ) )( ) ] ( ) Subtitusikan ( ) ke ( ), diperoleh: ( ) [ ( )( ) ( )( ) ( )[( )( ) ]] ( )( ) ( ( )( )[( ) )( ) ] ( ) Subtitusikan ( ) ke ( ), diperoleh: ( ( )( ) ( )( ) ( )[( )( ) ]) ( )( ) ( ( ) ( ) )( ) ] ( )
Dari persamaan (4.11) diperoleh:
( )
( ) ( ) ( )
( ) ( ) ( )
( )
Jadi, diperoleh titik kesetimbangan endemik ( ) sebagai berikut: ( )( ) ( )( ) ( )[( )( ) ] ( )( ) ( )( ) ( )[( )( ) ] ( ) ( )( ) ( )[( )( ) ]
B. ANALISIS KESTABILAN
Dengan menggunakan linearisasi akan diperoleh analisis kestabilan
berdasarkan nilai eigen dan matriks jacobian. Matriks jacobian dari sistem
(4.1) adalah ( ) [ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ] ( ) [ ] (4.12) dengan ( ).
1. Analisis Kestabilan di Sekitar Titik Kesetimbangan Bebas Penyakit
Untuk titik kesetimbangan bebas penyakit
( ) ( ) dari matriks jacobian (4.12) diperoleh:
( ) [ ( ) ( ) ] ( ) [ ]
Menentukan nilai eigen matriks
( ( )) ( [ ] [ ]) ([ ] [ ]) [ ( ) ( ) ( ) ( )] || ( ) ( ) ( ) ( ) | |
Dengan menggunakan metode ekspansi kofaktor sepanjang baris pertama
matriks di atas diperoleh,
] ( )] ( )] ( )] ( )]
Dan diperoleh nilai-nilai eigen di titik sebagai berikut:
, , , , dan
Dari nilai-nilai eigen tersebut terlihat bahwa nilai eigen , , dan
adalah negatif. Selanjutnya, nilai dan akan dianalisis.
Akan ditunjukkan bahwa ,
Diasumsikan bahwa dan , sehingga ketika atau .
Jadi, dengan syarat maka . Akan ditunjukkan bahwa ,
Karena nilai eigen dan bernilai sama maka dengan syarat
atau .
Jadi, nilai , , , sedangkan jika
. Semua nilai eigen dari matriks ( ) bernilai negatif ketika , maka titik kesetimbangan bebas penyakit stabil asimptotik atau
dengan kata lain tidak terjadi penyebaran penyakit pada populasi.
2. Analisis Kestabilan di Sekitar Titik Kesetimbangan Endemik
Untuk titik kesetimbangan endemik ( ) sebagai berikut: ( )( ) ( )( ) ( )[( )( ) ] ( )( ) ( )( ) ( )[( )( ) ] ( ) ( )( ) ( )[( )( ) ]
dari persamaan matriks jacobian (4.12) diperoleh:
( ) [ ( ) ( ( )( ) ( )( ) ( ) ( )( ) ]) ( ( ( )( ) )( ) ( ) ( )( ) ]) ( ) ( ) ( ) ( ) ] ( ) [ ( ) ( )( ) ( )( ) ( ) ( )( ) ] ( ) ( )( ) ( )( ) ( )[( )( ) ] ]
Menentukan nilai eigen matriks
( [ ] [ ( ) ( )( ) ( )( ) ( ) ( )( ) ] ( ) ( )( ) ( )( ) ( ) ( )( ) ] ]) ( [ ] [ ( ) ( )( ) ( )( ) ( ) ( )( ) ] ( ) ( )( ) ( )( ) ( ) ( )( ) ] ]) [ ( ( )) ( )( ) ( )( ) ( )[( )( ) ] ( ) ( ) ( )( ) ( )( ) ( )[( )( ) ] ( ) ]
| | ( ( ) ) ( )( ) ( )( ) ( ) ( )( ) ] ( ) ( ) ( )( ) ( )( ) ( )[( )( ) ] ( ) ||
Dengan menggunakan metode ekspansi kofaktor sepanjang baris pertama
matriks di atas diperoleh,
Dengan nilai-nilai koefisien sebagai berikut:
( ) ( ) ( ( )) ( ) ( ) ] ( ) ] ( ( )) ( ) ( ( )) ( ) ( ) ( ) ] ( ) ( ( )) ( ) ] ( ( ))