MATEMATIKA TEKNIK 2 bab 1 Bil

Bab I

BILANGAN DAN PEUBAH KOMPLEKS

Kelengkapan

i. Kompetensi Program Studi

Pada modul ini akan dibahas mengenai bilangan kompleks dan peubah kompleks yang diharapkan dapat mengacu pada kompetensi Program Studi Teknik Elektro sebagai berikut : Kompetensi Utama : Kemampuan menerapkan pengetahuan dasar Rangkaian Listrik pada

Sistem Tenaga Listrik, Telekomunikasi serta Kendali, Komputer & Elektronika

ii. Sasaran Belajar

Mengacu pada kompetensi program studi, yaitu pengetahuan dasar atau fondasi dari ilmu keteknikan, maka diharapkan mahasiswa mempunyai pengetahuan memadai tentang bilangan kompleks sebagai dasar untuk mempelajari ilmu teknik elektro.

iii. Sasaran Pembelajaran

Proses pembelajaran pada modul bilangan kompleks diharapkan mahasiswa :

 Mengetahui perbedaan dan persamaan antara bilangan nyata dan bilangan kompleks.

 Mengetahui peran bilangan kompleks dalam menyatakan besaran-besaran dua dimensi

seperti parameter-parameter kelistrikan (arus, tegangan, impedansi dan lain-lain).  Mengetahui bentuk-bentuk bilangan kompleks serta pernyataan grafis bilagan kompleks.

 Mampu mengkonversi bilangan kompleks dari satu bentuk ke bentuk lainnya.

 Mampu melakukan aritmetika bilangan kompleks termasuk memangkatkan dan mencari akar bilangan kompleks.

 Mengetahui komplikasi bilangan kompleks dalam bentuk polar, yaitu bahwa bentuk polar

bilangan kompleks berharga banyak (multi-valued).

iv. Strategi/Metode Pembelajaran

Maple, baik di laboratorium kompuer atau di kelas dengan menggunakan computer mobile (lap top).

v. Indikator/Kriteria Penilaian

Keberhasilan sasaran belajar diketahui ketika mahasiswa mengetahui dan mencapai sasaran pembelajaran yang telah disebutkan pada bagian sasaran pembelajaran

1. Sistem Bilangan Nyata (R)

Sistem bilangan seperti yang kita kenal sekarang adalah hasil dari perkembangan dalam sejarah matematika yang merupakan bagian dari sejarah kebudayaan umat manusia. Sistem bilangan berkembang secara bertahap sejak adanya manusia berikut:

1. Bilangan asli 1, 2, 3, 4,. . , yang disebut juga bilangan bulat positip. Bilangan asli inilah yang pertama kali digunakan dalam hitung-menghitung. Simbol-simbolnya berubah dengan berubahnya waktu. Dikenal misalnya symbol bilangan Romawi I, II, III, IV. . ., Jika a dan b adalah bilangan asli, jumlah a + b dan perkalian a . b, (a) (b) atau ab juga disebut bilangan asli. Untuk alasan ini himpunan bilangan asli dikatakan tertutup di bawah operasi penjumlahan dan perkalian atau memenuhi sifat tertutup (closure) terhadap operasi-operasi ini.

2. Bilangan bulat negatip dan nol, dilambangkan dengan - 1, - 2, - 3. . . dan 0 yang masing-masing muncul untuk memungkinkan solusi dari persamaan x + b = a, dimana a dan b adalah bilangan asli. Hal ini kemudian tiba pada operasi pengurangan, atau invers dari penjumlahan, dan kita tulis sebagai x = a – b.

Himpunan bilangan bulat positip, negatip dan nol disebut HIMPUNAN BILANGAN BULAT yang tertutup di bawah operasi-operasi penjumlahan, perkalian, dan pengurangan.

3. Bilangan rasional dan pecahan seperti - 3 4 , -

8

3 . . . muncul untuk memungkinkan solusi dari persamaan seperti bx = a untuk semua bilangan bulat a dan b di mana b≠0 ini mengarah ke operasi divisi atau invers perkalian, dan kita tulis sebagai

4. Bilangan irasional seperti

_√

2 =1.41423. . . dan π = 3. 14159. . .adalah bilangan yang tidak rasional, yang tidak dapat dinyatakan dengan a/b dimana a dan b adalah bilangan bulat dan b≠0

Himpunan bilangan rasional dan irasional di sebut dengan himpunan bilangan nyata atau ril. Diasumsikan bahwa mahasiswa sudah mengetahui berbagai operasi pada bilangan nyata.

2. Garis Bilangan Nyata

Bilangan nyata atau ril dapat direpresentasikan dengan titik-titik pada garis yang disebut sumbu bilangan nyata, lihat Gambar 1.1, dimana titik yang merepresentasikan bilangan nol disebut titik asal (point of origin dan disimbolkan dengan huruf O).

−2 anggota-anggota dari himpunan bilangan nyata. Artinya setiap bilangan nyata anggota himpunan bilangan nyata diwakili oleh sebuah dan hanya sebuah titik pada garis bilangan nyata.

Jika nilai-nilai x berada dalam selang a < x <b maka selang atau interval tersebut disebut

selang terbuka, sedangkan jika a_≦ x_≦b , maka selang itu disebut selang tertutup.

Nilai mutlak dari sebuah bilangan asli a, dinotasikan dengan |a| , yang sama untuk a

3. Sistem Bilangan kompleks (C)

Tidak ada bilangan asli x yang memenuhi persamaan x2

+1=0 . Agar solusi dari persamaan itu ada maka diperkenalkanlah sistem bilangan kompleks.

Definisi bilangan kompleks: Sebuah bilangan kompleks z adalah sepasang bilangan nyata

berurutan (a,b). Jadi z = (a,b).

Bilangan kompleks direpresentasikan dengan sebuah bidang datar yang disebut BIDANG

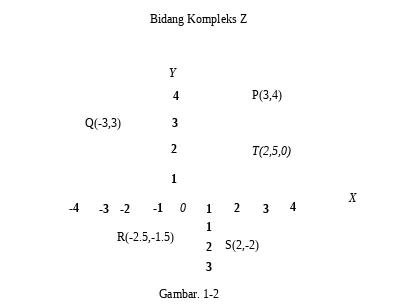
KOMPLEKS. Lihat gambar 1-2. Terdapat hubungan satu-satu (one to one) antara titik-titik pada

bidang kompleks dengan anggota-anggota himpunan bilangan kompleks C dengan catatan hal ini tidak berlaku jika bilangan-bilangan kompleks dinyatakan dalam bentuk polar (yang akan dibicarakan nanti).

Dengan sistem koordinat Kartesius yang sudah kita kenal maka bilangan kompleks dapat dinyatakan dalam bentuk z = a + bi dimana a dan b adalah bilangan asli dan i, yaitu satuan

bilangan imajiner, yang mempunyai kelengkapan i2=−1.

Jika z = a + bi , maka bilangan asli a disebut komponen nyata dari z dan b disebut

bagian khayal atau komponen imajiner dari z dan dinotasikan dengan Re

{

z} dan lm

{

z}

berturut-turut.

Jadi, jika z = a+bi maka:

Re z = a dan Im z = b

Simbol z yang menyatakan semua bilangan-bilangan kompleks disebut variabel kompleks (complex variable).

1. Dua bilangan kompleks a + bi dan c + di adalah sama jika dan hanya jika a = c dan

b = d.

2. Kita dapat mengangap bilangan asli sebagai sebuah bagian dari himpunan bilangan kompleks dengan b = Re z = 0.

3. Jika a = 0 , maka bilangan kompleks z = 0 + bi disebut bilangan imajiner asli atau

Im z = b.

4. Konjugat kompleks atau sekawan kompleks dari sebuah bilangan kompleks a + bi

adalah bilangan kompleks a-bi . Konjuget kompleks dari sebuah bilangan kompleks

z sering diindikasikan oleh ´z atau z* . Jadi: penjumlahan, dan 1 adalah elemen identitas dari perkalian.

12. Untuk setiap bilangan kompleks z1 dalam C ada bilangan unik z dalam C sedemikian sehingga z + z1 = 0; z adalah terpilih searah z1 untuk penjumlahan yang ditunjukkan oleh –z1.

13.Untuk setiap z1 dalam C ada bilangan unik z dalam C sedemikian sehingga z1z = zz1 = 1; z adalah terpilih berlawanan z1 berkenaan dengan perkalian dan ditunjukan oleh 1/z1.

4. Operasi dasar pada bilangan kompleks

1. Penjumlahan

4. Pemangkatan (perkalian sebuah bilangan kompleks dengan dirinya sendiri) 5. Pembagian

>

Tampak bahwa z1 + z2 serta z2 + z1 keduanya kompleks dan z1 + z2 = z2 + z1.

Tugas:

Perlihatkanlah berlakunya sifat 7, 8, 9, 10 dan 11 pada bagian 3.

5. Interpretasi Vektor dari Bilangan-bilangan Kompleks

Bentuk bilangan kompleks z = x + iy dapat dipandang vektor OP dengan titik asal O dan titik akhir P pada bidang kompleks Z. Titik P identik dengan bilangan kompleks tertentu (x,y), lihat gambar 1.2. Kadang-kadang kita sebut OP = x+iy sebagi vektor posisi dari P. Pada gambar 1-2 tampak pula vektor AB. Kedua vektor OP dan AB ini memiliki panjang sama atau ukuran dan arahnya sama tetapi titik awalnya berbeda, sehingga OP dan AB. Dengan kata lain kita dapat menulis OP = AB = x + iy akan tetapi hanya vektor OP yang yang memberikan titik z = (x,y) yang tepat.

y

A P

z = ( x,y)

O X

Gambar 1.2

Jumlah bilangan kompleks sebagai jumlah jajaran genjang dari jumlahan vektor

Jumlah dari bilangan kompleks berkorespondensi dengan jumlah jajaran genjang dari jumlah untuk vektor ( lihat gambar. 1-2). Dengan jumlah bilangan kompleks z1 dan z2, yang diwakili oleh vetor OA dan OB kita melengkapi jajargenjang OACB dimana untuk sudut OA dan OB berkorespondensi dengan z1 dan z2. Untuk diagonal OC dari jajargenjang

bekorespondensi dengan z1 + z2. Lihat masalah 5.

A z2 C

Z1 z1+ z2 z1

Z2 B O

Gambar. 1-2

Contoh:

Nilai Mutlak

Nilai Mutlak atau modulus dari sebuah bilangan kompleks a+bi didefinisikan sebagai

|

a+bi

|

=

√

a2+b2. Notasinya adalah mod. Jadi:

mod z = |a+bi|=

√

a2+b2.

Jika bilangan kompleks z dipandang sebagi vektor maka mod z adalah besar atau panjang atau norm dari vektor z.

Jika z₁, z₂, z₃ ,…., z_m adalah bilangan kompleks maka akan berlaku:

1.

|

z₁z₂

_|

=

|

z₁

_||

z₂

_|

atau

|

z₁z₂… z_m

_|

=

_|

z₁

_||

z₂

_|

…

_|

z_m

_|

2.

|

z1

z2

|

=

|

z1

z2

|

jika z₂≠0

4.

|

z₁+z₂

_|≧|

z₁

_|

−

_|

z₂

_|

atau

|

z₁−z₂

_|≧|

z₁

_|

−

_|

z₂

_|

Contoh:

1. Jika z = -4 + 2i, maka –

mod z =

2¿2 ¿

4¿2+¿ ¿

|−4+2i|=√¿

Dengan menggunakan software Maple maka contoh soal ini dapat diselesaikan sebagai berikut:

>

Cara lain untuk menentukan modulus dari sebuah bilangan kompleks adalah dengan menggunakan simbol harga mutlak ││. Lihat contoh berikut ini:

>

>

Catatan:

Diatas ini juga diperlihatkan 2 cara untuk mendefinisikan (artinya menentukan isi dari sebuah variable kompleks z) dalam Maple. Cara pertama hanya menggunakan operator pendefinisian :=. Cara kedua menggunakan pembentuk bilangan kompleks (complex constructor)

Complex. Perhatikan bahwa perintah-perintah dalam Maple adalah case sensitive (huruf kecil

dibedakan dengan huruf besar). Perintah untuk menghitung harga mutlak atau modulus adalah abs. Bila diinginkan bentuk decimal (floating point) dari hasil dapat ditambahkan perintah evalf.

2. Jika z1 = (4 + 3i), z2 = -5 + 7i dan z3 = -1 – 2i hitunglah z1 + z2 + z3, z1z2z3, z1/z2, z1.z2/z3, z3/(z1 + z2)

Jawab:

Untuk penyelesaian contoh 2 ini secara hitung tangan (manual) silahkan mahasiswa mengerjakannya sendiri.

3. Diketahui z = 2 – 6.5i. Hitunglah z2 _{, z}11 _{, √z} Jawab:

z2 _{= z . z = (2-6.5i) (2-6.5i) = (2x2 – 2x6.5i – 2x6.5i + 6.5x6.5 i}2₎ = 4 -26i – 42.25 = - 38.25 – 26i

Dengan Maple:

>

4. Perhatikan contoh-contoh perhitungan dengan Maple berikut ini. Carilah informasi mengenai setiap perintah Maple yang belum Anda ketahui dari fasilitas Help dari Maple. Cara tercepat untuk memperoleh informasi dalam Maple adalah dengan perintah ?. Misalnya >?seq akan menampilkan informasi mengenai perintah seq, yaitu perintah untuk menghitung barisan bilangan.

Tugas:

1. Jika z1 = (1,1), z2 = (2, -3) dan z3 = (-2, 1) hitunglah z1+z2+z3, z3-z2-z1, z1z2z3, z1/z2/z3.

2. Hitung pulalah z12_{.√z2 serta z3}3

3. Perlihatkanlah berlakunya hukum tertutup untuk penjumlahan, hukum komutatif untuk penjumlahan serta hukum asosiatif untuk penjumlahan.

6. Penyajian Grafis Dari Bilangan kompleks

Gambar 1-2 memperlihatkan sebuah bidang kompleks z dengan sistem koordinat Kartesius. Titik-titik P, Q, R, S dan T telah ditentukan dan koordinat setiap titik adalah bilangan kompleks yang direpresentasikan oleh titik bersangkutan. Titik P misalnya mempunyai koordinat (3,4)  P = (3,4) dan sesuai dengan definisi bilangan kompleks sebagai pasangan bilangan nyata berurutan maka (3,4) = 3 + 4i adalah bilangan kompleks yang secara grafis direpresentasikan oleh titik P.

Jarak antar dua bilangan z1= x1+ iy1 dan z2= x2 + iy2 didalam bidang yang kompleks diberi

oleh | z1- z2|=

√

(

x

1

−

x

2

)

2

Contoh:

1. Plotlah bilangan-bilangan kompleks 2+3i dan -3-4i pada bidang kompleks.

Jawab:

Catatan:

Perintah restart adalah untuk membersihkan memori (agar tidak berisi definisi-definisi dari session sebelumnya). Perintah with(plots) adalah untuk memanggil rutin-rutin plotting agar dimuat di memori dan siap untuk digunakan.

2. Plotlah titik-titik z = 3+5i, sekawan (conjugate) z dan –z.

Jawab:

>

>

4. Hitunglah jarak antara bilangan-bilangan kompleks 2+3i dan -3-4i pada bidang kompleks.

Jawab:

>

7. Representasi Bilangan Kompleks secara Proyeksi Stereografis

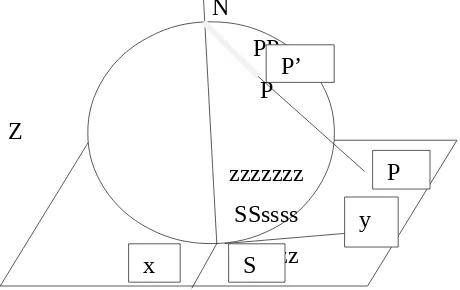
Misalnya P (gambar 1-3) sebuah titik pada bidang kompleks Z yang mewakili bilangan kompleks z1. Bola Riemann (Riemann’s sphere) adalah bola berjari-jari satu dengan kutub selatan S berimpit dengan titik asal O dari sistem koordinat Kartesius yang ditetapkan pada Z. Bila kita tarik garis PN maka garis tersebut akan memotong bola pada titik P’. Maka titik P’ merupakan proyeksi dari titik P pada bola Riemann.

Cara untuk memetakan titik pada bola disebut proyeksi stereografis. Menarik untuk mengetahui bahwa semua titik pada tak berhingga diproyeksikan ke kutub utara N.

N

Gambar 1-3 Proyeksi Stereografis dengan bola Riemann (Riemann’s sphere).

8. Bentuk Polar dari Bilangan Kompleks x

y P P’

Jika P adalah titik pada bidang kompleks yang sama dengan bilangan kompleks (x, y)

atau x +iy, maka kita lihat dari Gambar. 1-3 bahwa x=rcosθ _{, dan}

y

=

r

sin

θ

Y

P(x,y)

r

� y

X’ x X

O

Y’

Gambar. 1-4

Tampak bahwa

r

=

√

x

2

+

y

2

=|

x

+

iy

|

adalah nilai modulus atau nilai mutlak dari

z

=

x

+

iy

_{1 [dinotasikan dengan mod z atau}

|

z

|

_{]; dan} θ _{, disebut amplituda atau}

argument (penjelasan) dari

z

=

x

+

iy

[dinotasikan dengan arg z]. θ adalah sudut yang dbuiat

oleh garis OP dengan sumbu x positif.

Oleh karena itu,

z

=

x

+

iy

₁

=

r

(

cos

θ

+

i

sin

θ

)

disebut bentuk polar dari bilangan kompleks, r danθ disebut koordinat polar (kutub).

Untuk setiap bilangan kompleks z ≠ 0 terdapat hanya satu nilai yang sesuai dengan θ untuk 0 ≦ � < 2π. Namun, tambahan kelipatan interval lain sebesar 2π, misalnya - π < θ ≦ π, dapat digunakan. Dalam matematika teknik (engineering mathematics) pada umumnya kita bekerja pada nilai utama (principal value) dengan θ dalam selang 0 ≦ � < 2π.

Contoh-contoh:

1. Merubah bentuk Kartesius bilangan kompleks 3+4i ke bentuk polar dengan menggunakan Maple.

>

>

>

>

>

>

>

2. Merubah bilangan kompleks polar 2∠5 ke bentuk Kartesius:

3. Dengan Maple kita dapat juga memperoleh bentuk polar dari pernyataan seperti z = a + bI. Perhatikan contoh berikut:

>

Tugas:

1. Ubahlah ke bentuk polar 2 + 7i, -3-5i, -4+4i, 3-2i.

2. Ubahlah ke bentuk Kartesius 1∠30o_{, 3∠1, 2∠45}o_{, 4∠2,5.}

3. Diketahui bilangan-bilangan kompleks sebagai berikut:

a) 5 + 3 i b) 3 + 2 i 2 - 4 i 3 c) 6 i 2 + 3 i - 12

d) 2

(

cos

π

6 + i sin

π

6

)

_{e) 2}

(

cos

π

4 + i sin

π

4

)

_f)

_√

_{2 . e} −

π

4 i

Buatlah plottingnya dan nyatakan bilangan-bilangan kompleks di atas dalam bentuk-bentuk yang lain.

Jika

z

1

=

x

1

+

iy

1

=

r

1

(

cos

θ

1

+

i

sin

θ

1

)

_dan

z

2

=

x

2

+

iy

2

=

r

2

(

cos

θ

2

+

i

sin

θ

2

)

kita dapat menunjukkan bahwa:

z₁z₂=r₁r₂{cos(θ₁+θ₂)+isin(θ₁+θ₂)}

z₁ z₂=

r₁

r₂{cos(θ1−θ2)+isin(θ1−θ2)}

Berdasarkan (2) dapat diperlihatkan bahwa:

z

₁

z

₂

...

z

_n

=

r

₁

r

₂

... ...

r

_n

{

cos

(

θ

₁

+

θ

₂

...

+

θ

_n

)+

i

sin

(

θ

₁

+

θ

₂

...

+

θ

_n

)}

dan jika

z

1

=

z

2

=

...

=

z

n

=

z

_{ini menjadi}

z

n

={

r

(

cos

θ

+

i

sin

θ

)}

n

=

r

n

(

cos

nθ

+

i

sin

nθ

)

Persamaan (5) ini dikenal sebagai Theorema De Moivre

Contoh:

1. Hitung (5 – 3i)5 _{dengan menggunakan theorema de Moivre.}

Penyelesaian:

>

(2)

(3)

(4)

10. Akar dari Bilangan Kompleks

Sejumlah w disebut akar n dari bilangan kompleks zjika wn_{=z, dan kita tulis w=z}1/n_{. Dari} theorema De Moivre kita dapat menunjukkan bahwa jika n adalah bilangan bulat positif, maka

z

1/n

={

r

(

cos

θ

+

i

sin

θ

)}

1/n

=r1/n

{

cos

(

θ+2kπ

n

)

+isin

(

θ+2kπ

n

)

}

_{k =0,1,2, ...,n-1}

Berikut dapat diperlihatkan bahwa ada n nilai yang berbeda untuk z1/n , dengan kata lain ada n akar yg berbeda dari z, dengan syarat z ≠ 0.

Contoh:

1. Tentukan harga (1 + i ) 8 . Penyelesaian:

Jika z = (1 + i) 8 berarti: x = 1 ; y = 1  r =

√

2 dan tg = 1   =

π

4 _{sehingga dalam} bentuk polar :

z =

√

2. e

2. Berapakah akar pangkat 3 dari 8.

Penyelesaian:

Kita pasti telah tahu bahwa akar pangkat 3 dari 8 adalah 2. Itu sudah cukup jika kita menganggap 8 sebagai bilangan real. Tetapi jika kita kita menganggap 8 adalah bilangan komplekkompleks z = 8 + 0 i, maka berarti :

x = 8 ; y = 0 ;  r = 8 dan tg  = 0  = 0 ; 2 ; 4 ; 6 . . . = 2 n

Jadi:

Sebagai bilangan kompleks 8 = 8 . e i 2 n π

Jadi akar pangkat 3 dari 8 adalah:

Untuk n = 2  z

3. Hitunglah z1/4 _{jika z = -3+3i dengan menggunakan rumus Euler.}

Penyelesaian:

elementer dan mensubstitusi

x

=

iθ ,

kita peroleh

e

iθ

=

cos

θ

+

i

sin

θ e

=

2,71828

yang disebut rumus Euler. Dengan menggunakan rumus Euler ini secara sederhana kita definisikan

ez = e(x + iy) = ex eiy = ex (cos y + i sin y) = ex cos y + i ex sin y (8)

Dengan demikian bilangan kompleks z dapat dituliskan sebagai berikut ini:

z = r eiθ = r cos + i r sin θ

Jadi sampai sekarang sudah ada 4 cara yang bisa kita gunakan untuk menuliskan bilangan

kompleks z yaitu: z = (x,y) = x + iy = r∠_{θ = reiθ.}

Contoh 1:

Tuliskan -4 + 5i dalam bentuk reiθ dan hitunglah (-4+5i)7.

Penyelesaian:

Tugas: