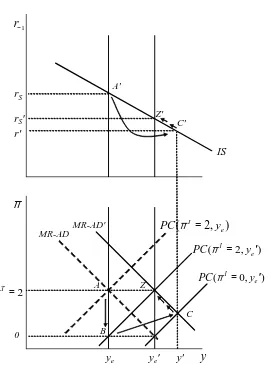
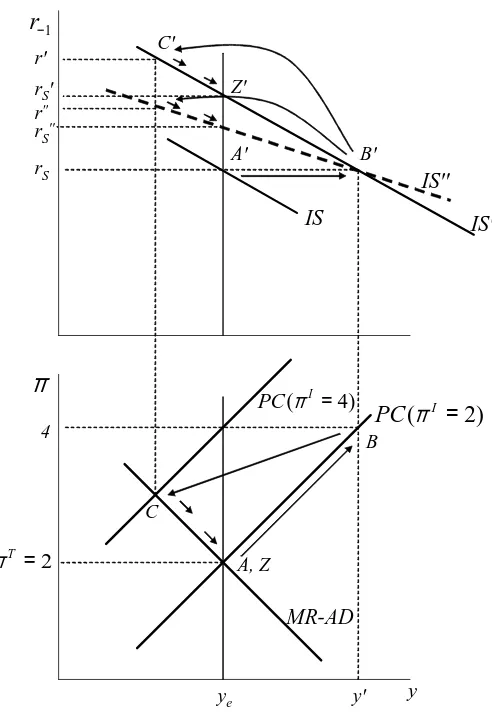
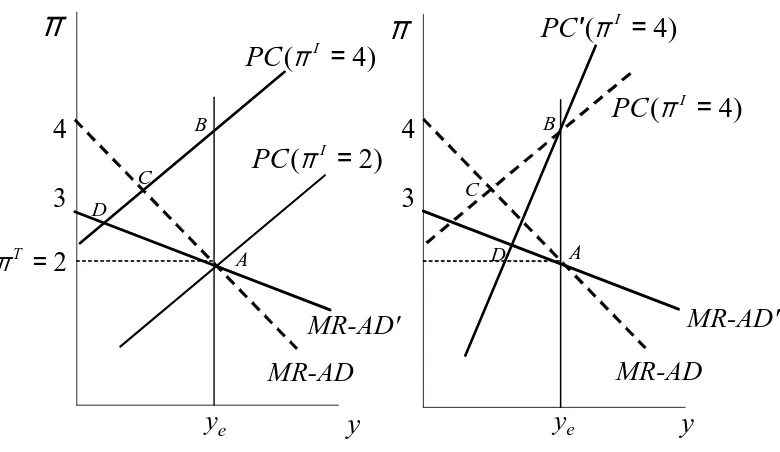
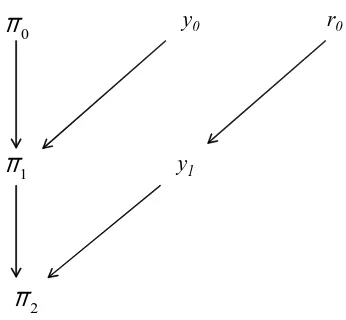
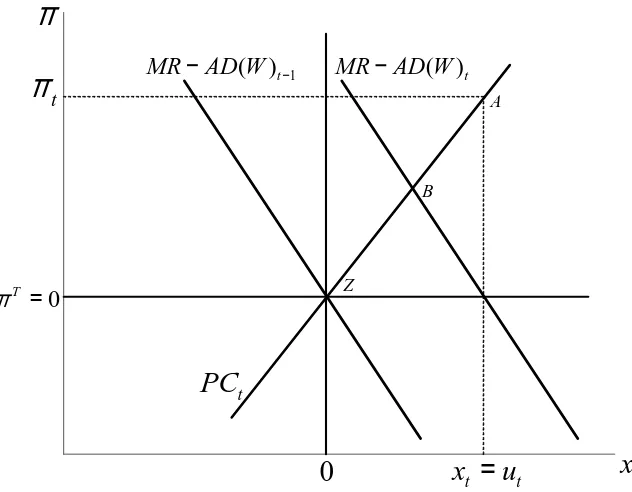
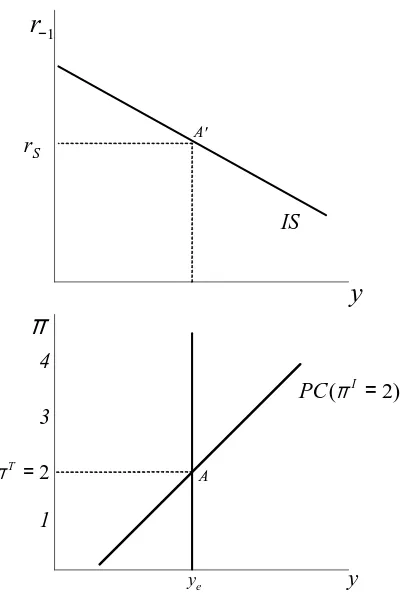
The 3 Equation New Keynesian Model A
Teks penuh
Gambar


Garis besar
Dokumen terkait
sangat kecil (2 persen) ini menunjukkan bahwa kualitas mahasiswa baru yang diterima di FE sangat baik dan seharusnya siap untuk diajarkan sebagai ilmu ekonomi
Geragai Kabupat en Tanj ung Jabung Timur Tahun Anggaran 2014, unt uk Paket Pekerj aan t ersebut diat as t el ah dil aksanakan Pembukaan Penawaran pada Tanggal 18 Jul i 2014,
The National Science Foundation (NSF) has several programs that help students work in foreign laborato- ries. The East Asia and Pacific Summer Institutes pro- gram sends about
16. Untuk korban banjir sebanyak 400 orang selama 3 hari. ) - Komunikasi dan
• Apa paradigma ilmu pengetahuan yang digunakan oleh KLH untuk merespon issu lingkungan yang timbul. • Paradigma yang dipilih menentukan strategi
(2) Dari data pada Tabel A, perhatikanlah nilai-nilai pada kolom kedua (yakni tegangan catu daya hasil pengukuran dengan multimeter) dan kolom ketiga (yakni tegangan pada
ini ditunjukkan dari probabilitas signifikansi 0.045 dan nilai ini dibawah α = 0.05, hal ini menyatakan bahwa variabel NIM tidak terdestribusi
Penelitian Mardliyyah (2016) yang melakukan penelitian tentang pengaruh pengungkapan CSR terhadap nilai perusahaan dengan profitabilitas sebagai variabel moderasi