DINAMIKA ORDE PERTAMA SISTEM NONLINIER TERKOPEL DENGAN RELASI PREDASI, MUTUAL, DAN SIKLIK (Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi)

(1)

DINAMIKA ORDE PERTAMA SISTEM NONLINIER TERKOPEL

DENGAN RELASI PREDASI, MUTUAL, DAN SIKLIK

(Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi)

Oleh:

MADA SANJAYA WS

G74103018

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2007

(2)

ABSTRAK

Mada Sanjaya WS. Dinamika Orde Pertama Sistem Nonlinier Terkopel dengan Relasi Predasi, Mutual, dan Siklik (Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi). Dibimbing oleh Husin Alatas.

Pengontrolan terhadap populasi suatu spesies tertentu diperlukan untuk menghindari berbagai bencana seperti kekurangan pangan, ledakan hama, dan kepunahan suatu spesies. Penelitian ini dilaksanakan untuk mempelajari sebuah model dinamika mangsa pemangsa menggunakan persamaan Lotka-Volterra termodifikasi melalui analisis numerik dan semi analitik. Model yang diajukan dalam penelitian ini yaitu model mutualisme antara dua spesies dengan kehadiran pemangsa, model dua mangsa satu pemangsa, dan model rantai makanan siklik serta aplikasi model dinamik pengendalian hama pertanian. Telah ditemukan bahwa model dinamika dua spesies hierarki dua tingkat dengan pendekatan persamaan Lotka-Volterra menunjukkan suatu kemiripan dengan data pengamatan fluktuasi populasi kelinci dan Lynx di mana populasi mangsa dan pemangsa berfluktuasi membentuk suatu siklus. Pada model dinamika tiga spesies ini menunjukkan banyak fenomena menarik mengenai keterkaitan antara parameter model dengan fluktuasi populasi ketiga spesies. Hipotesis yang diajukan adalah bahwa pada parameter kritis tertentu diagram fase sistem dinamika tiga spesies akan mengalami bifurkasi yang bisa menunjukan fluktuasi spesies tertentu ke arah kepunahan sementara yang lainya akan mengalami booming hingga akan mencapai keseimbangan kembali. Melalui analisis optimasi dan bifurkasi keterkaitan antara parameter-parameter sistem seperti laju kelahiran dan efektivitas serta produktivitas pemangsa terhadap populasi spesies lainya dapat ditentukan. Titik kritis terjadinya kepunahan dapat diprediksi sehingga pengontrolan bagi ahli biologi untuk memverifikasi sejauh mana kesesuaiannya dengan ekosistem tertentu dan pada akhirnya dapat membantu kita mengatasi atau setidaknya memahami proses kepunahan suatu spesies tertentu.

(3)

DINAMIKA ORDE PERTAMA SISTEM NONLINIER TERKOPEL

DENGAN RELASI PREDASI, MUTUAL DAN SIKLIK

(Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi)

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

MADA SANJAYA WS

G74103018

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2007

(4)

Judul : Dinamika Orde Pertama Sistem Nonlinier Terkopel dengan Relasi Predasi, Mutual, dan Siklik (Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi).

Nama : Mada Sanjaya WS NIM : G74103018

Menyetujui :

Pembimbing I

Dr. Husin Alatas, M.Si NIP 132206234

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, MS. NIP 131473999

(5)

RIWAYAT HIDUP

Penulis dilahirkan di Cirebon, pada tanggal 11 Oktober 1985 sebagai anak kedua dari tiga bersaudara, pasangan Waryano Sunaryo dan Eti.

Penulis menyelesaikan studinya di SMU Negeri 1 Lemah Abang-Cirebon pada tahun 2003 dan pada tahun yang sama diterima di Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis terdaftar sebagai mahasiswa Departemen Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama duduk di bangku kuliah, penulis aktif dalam berbagai kegiatan (kepanitiaan) dan organisasi intra kampus seperti menjadi anggota DKM Al Hurriyyah IPB pada tahun 2003-2004, Departemen Kerohanian Himpunan Mahasiswa Fisika (HiMaFi) IPB pada tahun 2003-2004, staff Departemen kerohanian BEM FMIPA pada tahun 2004-2005, staff Departemen Kebijakan Nasional BEM KM IPB pada tahun 2005 serta aktif sebagai ketua Rohis OMDA Cirebon pada tahun 2005. Penulis pernah menjadi asisten praktikum mata kuliah Fisika Dasar I dan II 2004-2006, penulis juga aktif mengajar private di kota Bogor, menjadi staff pengajar A-Project, Physics Challange dan Best Student Program pada tahun 2004–2006. Serta menjadi tutor di Bimbingan Belajar Bintang Pelajar Regional Bogor pada tahun 2006 sampai sekarang.

(6)

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Allah SWT yang telah melimpahkan taufik dan hidayah-Nya, sehingga penulis dapat menyelesaikan proposal yang berjudul “Dinamika Orde Pertama Sistem Nonlinier Terkopel dengan Relasi Predasi, Mutual, dan Siklik (Tinjauan Kasus Mangsa-Pemangsa pada Sistem Ekologi).”, yang dilakukan dalam rangka tugas akhir untuk memperoleh gelar Sarjana Sains pada Departemen Fisika Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Pada kesempatan ini, penulis mengucapkan banyak terima kasih dan memberikan penghargaan yang sebesar-besarnya kepada Bapak Husin Alatas atas segala bimbingan dan motivasinya yang diberikan kepada penulis untuk segera menyelesaikan penelitian ini, juga kepada Bapak Irzaman dan Bapak Kiagus Dahlan selaku penguji dari skripsi ini. Kepada orangtua dan seluruh sanak keluarga penulis, juga kepada “Dinda yang selalu berada di hatiku”, seluruh staff dan dosen Fisika khususnya, dan IPB pada umumnya. Serta seluruh pihak yang telah membantu penulis yang tak mungkin disebutkan satu-persatu, juga kepada semua teman-teman seperjuangan Fisika.

Penulis memahami bahwa tiada gading yang tak retak. Oleh karena itu, segala macam saran dan kritik yang membangun akan penulis terima dengan senang hati. Semoga apa yang disampaikan oleh penulis akan bermanfaat bagi ilmu pengetahuan.

Bogor, Maret 2007

Penulis

(7)

DAFTAR ISI

KATA PENGANTAR... i DAFTAR ISI... ii DAFTAR GAMBAR... iv DAFTAR TABEL... vi DAFTAR LAMPIRAN... vii PENDAHULUAN... . 1 Latar Belakang... 1 Tujuan... 1 TINJAUAN PUSTAKA... 1

Persamaan Differensial Orde Pertama... 1

Model Dinamik untuk Interaksi Multispesies... 1

Titik Kritis (critical point)... 2

Kontruksi Matrik Jacobi... 2

Vektor Eigen dan Nilai Eigen... 2

Model Dinamik Lotka-Volterra Dua Spesies... 2

Analisis Model Dinamik untuk Interaksi Dua Spesies... 3

Kontruksi Matriks Jacobi ... 3

Analisis Kestabilan Titik Kritis... 3

Titik Kritis T1 ... 3 Titik Kritis T2 ... 3

Orbit dan Kestabilan Sistem... 3

Kesesuaian Model dengan Hasil Pengamatan Lapangan... 4

METODOLOGI PENELITIAN... 4

Waktu dan Tempat Penelitian... 4

Peralatan ... 4 Studi Pustaka ... 4 Pembuatan Program... 4 Analisis Output………...…... 4 HASIL DAN PEMBAHASAN………...……… 5 PEMODELAN………...….…… … 5 Model Dinamik untuk Interaksi Dua Spesies Mutualistik………...……… 5

Model Dinamik untuk Interaksi Dua Spesies Mutualistik dengan Kehadiran Pemangsa………... ... 5

Model Dinamik Dua mangsa Satu Pemangsa tanpa Kompetisi Intraspesifik... 5

Model Dinamik Dua mangsa Satu Pemangsa dengan Kompetisi Intraspesifik... 6

Model Dinamik Rantai Makanan Siklik………... 6

ANALISIS MODEL………...…… 6

Model Dinamik untuk Interaksi Dua Spesies Mutualistik………...… 6

Penentuan Titik Kritis………...……. 6

Kontruksi Matriks Jacobi... 7

Titik Kritis T1... 7

Orbit dan Kestabilan Sistem... 8

Model Dinamik untuk Interaksi Dua Spesies Mutualistik dengan Kehadiran Pemangsa... ... 10

(8)

Penentuan Titik Kritis... 10

Titik Kritis T1... 11 Titik Kritis T2... 11 Titik Kritis T3... 11 Titik Kritis T4... 11 Titik Kritis T5... 12 Titik Kritis T6... 16

Model Dinamik Dua mangsa Satu Pemangsa tanpa Kompetisi Intraspesifik... 19

Titik Kritis T1... 19 Titik Kritis T2... 20 Titik Kritis T3... 20 Hasil Numerik... 20 Kasus ad = bc………...….…… 20 Kasus ad > bc………..….…… 20 Kasus ad < bc... 21

Model Dinamik Dua mangsa Satu Pemangsa dengan Kompetisi Intraspesifik... 24

Titik Kritis T1... 24 Titik Kritis T2... 24 Titik Kritis T3... 25 Titik Kritis T4... 25 Titik Kritis T5... 25 Titik Kritis T6... 25 Titik Kritis T7... 26 Hasil Numerik... 26 Parameter 1………...…………... 26 Parameter 2………...………... 26 Parameter 3... 26

Attractor Model Dinamik Dua Mangsa Satu Pemangsa………...……… 29

Hasil Eksperimen Lapangan... 30

Model Dinamik Rantai Makanan Siklik... 32

Hasil Numerik... 35

Kasus beh = fic... 35

Kasus beh > fic... 36 Kas Aplikasi Model Dinamik Pengendalian Hama pertanian... 38

Analisis Model Dinamik Pengendalian Hama pertanian... 39

Hasil Numerik... 40

Kasus ag = fb... 40

Kasus ag > fb... 41

Kasus ag < fb... 42

SIMPULAN DAN SARAN... 43

DAFTAR PUSTAKA... 43

(9)

Gambar 1. Dinamika populasi dua

spesies... 3

Gambar 2. Orbit kestabilan mangsa pemangsa dua

spesies... 4 Gambar 3. Dinamika Populasi Hare dan Lynx oleh Hudson Bay

Company... 4 Gambar 4. Orbit Kestabilan Populasi Hare’s dan Lynx oleh Hudson Bay

Company………...

... 4 Gambar 5. (a) Grafik ruang phasa bidang xy dengan kondisi awal x = 1 dan y = 1 (b)

Grafik laju populasi dengan kondisi awal x = 1 dan y =

1... 8 Gambar 6. Grafik kestabilan titik kritis T4 saat ad > bc (a) ruang phasa bidang xy

dengan memvariasikan kondisi awal dan t = 100 (a) laju populasi kondisi awal x = 2 dan y = 2 (b) laju populasi kondisi awal, x = 1 dan y = 2, dan

(c) laju populasi kondisi awal x = 2 dan y =

1... 9 Gambar 7. (a) Grafik ruang phasa bidang xy dengan kondisi awal x = 1 dan y = 1 dan

(b) grafik laju perubahan populasi dengan kondisi awal x = 1 dan y =

1... 10 Gambar 8. Grafik ruang phasa titik kritis T4 dengan kondisi awal x = 1, y = 1, z = 1, t

= 1000 dan parameter a = 2.5, b = 1, c = 1, dan d =

2.5... 11 Gambar 9. Grafik ruang phasa dengan kondisi awal x = 1 dan y =

1... 12 Gambar 10. Grafik ruang phasa titik kritis T4 dengan kondisi awal x = 1, y = 1, z = 1, t =

1000 dan parameter a = 0.5, b = 1, c = 1 dan d =

0.5... 12 Gambar 11. Grafik ruang phasa dengan kondisi awal x = 1 dan y =

1... 12 Gambar 12. Bifurkasi yang terjadi pada titik kritis T5 dengan t = 1000 dan memvariasikan

parameter yang digunakan, (a) parameter d = 1.5 dan l = 1.5 (b) parameter d = 1.2 dan l = 1.2 (c) parameter d =1 dan l = 1 (d) parameter d = 0.7 dan l = 0.7 (e) parameter d = 0.5 dan l = 0.5 serta (f) parameter d = 0.3

dan l = 0.3……….. 14

Gambar 13. Grafik Laju Perubahan Populasi pada Titik Kritis T5 dengan beberapa

parameter, (a) parameter d = 1.5 dan l = 1.5 (b) parameter d = 1.2 dan l = 1.2 (c) parameter d = 1 dan l = 1 (d) parameter d = 0.7 dan l = 0.7 (e) parameter d = 0.5 dan l = 0.5 serta (f) parameter d = 0.3 dan l =

0.3……… 15 Gambar 14. Bifurkasi yang terjadi pada titik kritis T6 dengan t = 1000 dan

memvariasikan parameter yang digunakan, (a) parameter b = 0.1 dan c = 0.1 (b) parameter b = 0.5 dan c = 0.5 (c) parameter b = 0.8, c = 0.8 (d) parameter b = 1 dan c = 1 (e) parameter b = 1.1 dan c = 1.1 serta (f)

parameter b = 1.2 dan c = 1.2………. 17

Gambar 15. Grafik Laju Perubahan Populasi pada Titik Kritis T6 dengan beberapa

parameter, (a) parameter b = 0.1 dan c = 0.1 (b) parameter b = 0.5 dan c = 0.5 (c) parameter b = 0.8 , c = 0.8 (d) parameter b = 1 dan c = 1 (e) parameter b = 1.1 dan c = 1.1 serta (f) parameter b = 1.2 dan c =

1.2……….. 18 Gambar 16. Bifurkasi yang terjadi pada model dua mangsa satu predator dengan t =

500 dan memvariasikan parameter yang digunakan, (a) parameter a = 1, b = 1, c = 1 dan d = 1 (b) parameter a = 2, b = 1, c = 1 dan d = 2 (c) parameter a = 20, b = 1, c = 1 dan d = 20 (e) parameter a = 1, b = 2, c = 2 dan d = 1 (f) parameter a = 1, b = 20, c = 20, dan d =

1……… 22 Gambar 17. Grafik Laju Perubahan Populasi pada model dua mangsa satu predator

dengan memvariasikan parameter yang digunakan, (a) parameter a = 1, b = 1, c = 1 dan d = 1 (b) parameter a = 2, b = 1, c = 1 dan d = 2 (c)

(10)

parameter a = 20, b = 1, c = 1 dan d = 20 (e) parameter a = 1, b = 2, c = 2 dan d =1 (f) parameter a = 1, b = 20, c = 20 dan d =

1... 23 Gambar 18. Bifurkasi yang terjadi pada titik kritis T7 dengan t = 1000 dan

memvariasikan parameter yang digunakan, (a) bersifat periodik dengan c = 0.003 (b) bersifat periodik dengan c = 0.004 (c) bersifat periodik dengan c = 0.005 (d) bersifat periodik dengan c = 0.006 (e) bersifat periodik dengan c = 0.007 serta (f) bersifat chaotik dengan c =

0.008... 27 Gambar 19. Laju Perubahan populasi yang terjadi pada titik kritis T7 dengan

memvariasikan parameter yang digunakan, (a) laju populasi tiga spesies dengan c = 0.003 (b) populasi tiga spesies dengan c = 0.005 (c) populasi tiga spesies dengan c = 0.008 (d) Plot x dan z terhadap waktu t dengan c = 0.003 bersifat periodik (e) Plot x dan z terhadap waktu t dengan c = 0.005 bersifat periodik (f) Plot x dan z terhadap waktu t dengan c =

0.008 bersifat chaotik... 28 Gambar 20. Attractor model dinamik dua mangsa satu pemangsa dengan kondisi awal

populasi predator divariasikan z0 = 2, z0 = 2.1 dan z0 = 2.2 sedangkan parameter c = 0.01 (a) ruang fase tiga spesies t = 3000, (b) laju populasi mangsa x, (c) laju populasi mangsa y dan (d) laju populasi pemangsa

z………... 29 Gambar 21. Attractor model dinamik dua mangsa satu pemangsa saat kondisi awal

populasi predator divariasikan z0 = 2, z0 = 2.1 dan z0 = 2.2 sedangkan parameter c = 0.01 (a) ruang fase tiga spesies, t = 3000 (b) ruang fase bidang xy, (c) ruang fase bidang yz dan (d) ruang fase bidang

xz... 30 Gambar 22. Hasil Experimental Dinamika Populasi sistem chemostat bacteria–

ciliate... 31 Gambar 23. Bifurkasi ruang phasa pada model siklik dengan t = 10 dan memvariasikan

parameter yang digunakan, (a) parameter c =0.6 (b) parameter c = 0.8 (c) parameter c = 0.96 (d) parameter c =1. 2 (e) parameter c = 1.35 (f)

parameter c = 1.6………... 33

Gambar24. Laju perubahan populasi pada model siklik dengan memvariasikan parameter yang digunakan ,(a) parameter c = 0.6 (b) parameter c = 0.8 (c) parameter c = 0.96 (d) parameter c = 1. 2 (e) parameter c = 1.35 (f) parameter c =

1.6………. 34 Gambar 25. Skema daur hidup hama ulat buah (Helicoverpa armigera) yang merusak

tanaman kapas beserta musuh

alaminya... 38

Gambar 26. Diagram rantai makanan pada tanaman

kapas... 39 Gambar 27. Orbit kestabilan pada bidang 3-dimensi kasus ag =

fb... 40

Gambar 28. Dinamika populasi tiga spesies dengan nilai awal x = 1, y = 1, z = 1.5 dan t

= 20 kasus ag = fb... 41 Gambar 29. Orbit kestabilan pada bidang 3-dimensi kasus ag >

fb... 41 Gambar 30. Dinamika populasi tiga spesies dengan nilai awal x = 2, y = 2, z = 1 dan t =

20 kasus ag > fb...

.... 41

Gambar 31. Orbit Kestabilan pada bidang 3-dimensi kasus ag <

fb... 42

Gambar 32. Dinamika populasi tiga spesies dengan nilai awal x = 2 , y = 2, z = 1 dan t =

20 kasus ag < fb...

(11)

DAFTAR TABEL

Tabel 1. Nilai-nilai parameter yang digunakan dalam titik kritis T4 Model

Mutualisme... 11 Tabel 2. Nilai-nilai parameter yang digunakan dalam titik kritis T5 Model

Mutualisme... 12 Tabel 3. Nilai-nilai parameter yang digunakan dalam titik kritis T6 Model

Mutualisme... 16 Tabel 4. Nilai-nilai parameter yang digunakan dalam Model dua mangsa satu

pemangsa... 21 Tabel 5. Nilai-nilai parameter yang digunakan dalam Model Rantai Makanan

Siklik... 35 Tabel 6. Nilai-nilai parameter yang digunakan Rantai Makanan pada Tanaman

(12)

DAFTAR LAMPIRAN

Lampiran 1. Analisis Titik Kritis Model Dinamik Tiga

Spesies... 46 Lampiran 2. Analisis Nilai Eigen Model Dinamik Tiga

Spesies... 48 Lampiran 3. Sintaks Plot Grafik Dengan Software Matlab

7... 54 Lampiran 4. Diagram Alir

(13)

PENDAHULUAN Latar Belakang

Salah satu cabang sains yang sedang berkembang dewasa ini adalah sains nonlinier. Dasar dari ilmu ini berpijak pada fakta bahwa gejala yang terjadi di alam secara umum tidak memenuhi prinsip linieritas, tetapi bersifat nonlinier.

Gejala nonlinier pertama kali diprediksi oleh Henri Poincare pada tahun 1880-an, ketika mencoba memecahkan permasalahan stabilitas dari suatu sistem dinamis, seperti gerak tiga benda langit di bawah pengaruh gaya gravitasi (rigid body problem). Pada tahun 1963 Edward Lorenz pertama kali menyelidiki gejala nonlinieritas pada sistem cuaca dengan menyederhanakan sistem cuaca yang kompleks ke bentuk persamaan yang sederhana dan berkelakuan chaotic. Gejala nonlinieritas ini dapat dianalisis melalui pendekatan system dinamik (dynamical system approach).

Selain dalam fisika, bidang lain yang terkait dengan gejala nonlinieritas antara lain adalah analisis populasi pada ekologi, analisis keuangan dalam ekonomi, reaksi kimia, ataupun analisis kriminalitas bahkan sifat nonlinieritas ini dapat dipakai juga untuk memprediksi banjir di suatu daerah dengan menggunakan asumsi tertentu. Dalam penelitian ini yang akan dikaji dengan lebih mendalam adalah fenomena nonlinieritas dalam suatu sistem ekologi.

Dengan memanfaatkan analisis sistem dinamik maka gejala nonlinieritas pada sistem ekologi dapat dipelajari dan diaplikasikan secara nyata untuk berbagai kepentingan. Pada penelitian ini akan dibahas beberapa model dinamik interaksi antara tiga spesies, yaitu interaksi dua spesies yang saling menguntungkan (Simbiosis Mutualisme) dengan kehadiran pemangsa, model dua mangsa satu pemangsa, dan model rantai makanan serta aplikasinya dalam proses pengendalian hama tanaman pertanian dengan mengembangkan musuh alaminya.

Tujuan

Penelitian ini bertujuan:

1) Mempelajari model dinamika nonlinier yang berlaku pada sistem simbiosis mutualisme, model dua mangsa satu pemangsa, dan model rantai makanan siklik.

2) Menganalisis kondisi kestabilan pada ketiga model dinamik tersebut. 3) Mengetahui bentuk kestabilan di sekitar titik kritisnya

4) Mengetahui arti fisis dari grafik yang diperoleh.

5) Mengaplikasikan model dinamik dalam pengendalian hama pada tumbuhan dengan mengembangkan musuh alaminya.

TINJAUAN PUSTAKA

1. Persamaan Differensial Orde Pertama

Sistem persamaan differensial orde pertama interaksi dua spesies dapat dinyatakan sebagai: 1 2 ( , ) ( , ) dx f x y dt dy f x y dt = = (1)

Sedangkan untuk interaksi tiga spesies dapat dinyatakan sebagai: 1 2 3 ( , , ) ( , , ) ( , , ) dx f x y z dt dy f x y z dt dz f x y z dt = = = (2) (1) f1 ,f2 dan f3 adalah fungsi kontinu bernilai real dari x dan y, dengan laju perubahan x dan y

sendiri dan tidak mengandung t di dalamnya. Sistem persamaan differensial disebut sebagai sistem persamaan differensial mandiri (Autonomous).

(14)

2. Model Dinamik untuk Interaksi Multispesies

Generalisasi dari model dinamik Lotka-Voltera klasik dari n-spesies yang berinteraksi dapat dinyatakan dengan 1 , 1, 2,3.. n i i i ij j j dx x r x dt i

α

= ⎛ ⎞ = _⎜ + _⎟ ⎝ ⎠ =

∑

(3)

3. Titik Kritis (critical point)

Analisis sistem persamaan differensial sistem dua spesies sering digunakan untuk menentukan solusi yang tidak berubah terhadap waktu, yaitu untuk tiap

dx

/

dt

=

0 ,

dy

/

dt

=

0

. Titik kritis ( * *

, y

x ) dari sistem dapat diperoleh dengan menentukan 0 / , 0 /dt= dy dt= dx (4)

Sedangkan untuk interaksi tiga spesies titik kritis (x y z*, *, ∗) dapat diperoleh dengan menentukan

/ 0, / 0, / 0

dx dt= dy dt= dz dt= (5)

4. Kontruksi Matrik Jacobi

Dengan melakukan pelinieran pada persamaan interaksi dua spesies maka diperoleh matriks Jacobi berikut ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = 2 2 1 2 2 1 1 1 x f x f x f x f Ji (6)

Sedangkan untuk interaksi tiga spesies diperoleh matrik Jacobi

1 1 1 1 2 3 2 2 2 1 2 3 3 3 3 1 2 3 i f f f x x x f f f J x x x f f f x x x ⎡∂ ∂ ∂ ⎤ ⎢_∂ _∂ _∂ ⎥ ⎢ ⎥ ⎢∂ ∂ ∂ ⎥ = ⎢_∂ _∂ _∂ ⎥ ⎢ ⎥ ⎢_∂ _∂ _∂ ⎥ ⎢_∂ _∂ _∂ ⎥ ⎣ ⎦ (7)

5. Vektor Eigen dan Nilai Eigen

Diberikan matrik dengan koefisien konstan J berukuran n× dan SPD homogen berikut: n Jx

x_&= , x(0)=x₀ (8)

Suatu vektor tak nol x dalam ruang _ℜn_{disebut vektor eigen dari J jika untuk suatu skalar}

λ

berlaku:

x

Jx=

λ

(9)

Nilai skalar

λ

dinamakan nilai eigen dari J.

(15)

0 )

(J−λI x= (10)

Dengan I matrik diagonal satuan. Persamaan (10) mempunyai solusi tak nol jika dan hanya jika 0 ) det( ) ( = J− I =J− I= pλ λ λ (11)

Persamaan (11) disebut persamaan karakteristik dari matrik Jacobi. 5. Model Dinamik Lotka-Volterra Untuk Interaksi Dua Spesies

Model mangsa-pemangsa klasik yang telah banyak dikenal adalah model Lotka-Volterra untuk dua spesies, yaitu:

dxy cy dt dy bxy ax dt dx + − = − = (12) Keterangan:

a : menunjukkan kelahiran rata-rata dari mangsa tanpa adanya pemangsa. b : merupakan jumlah mangsa yang dimangsa oleh pemangsa.

c: menunjukkan angka kematian pemangsa secara alami tanpa pengaruh ada atau tidak adanya mangsa.

d : menunjukkan jumlah kelahiran dari pemangsa yang dipengaruhi oleh adanya mangsa. Pada model mangsa-pemangsa dua spesies di atas, misalkan x menyatakan banyaknya spesies sebagai mangsa di level pertama pada waktu t, y menyatakan banyaknya spesies sebagai pemangsa di level dua pada waktu t. Dari persamaan tersebut perubahan laju populasi spesies x dipengaruhi oleh tingkat reproduksi yaitu laju pertumbuhan alami spesies tersebut. Kemudian terjadi proses pemangsaan terhadap spesies x oleh spesies y, sehingga efek yang ditimbulkan dari pemangsaan tersebut akan mempengaruhi laju populasi spesies x. Perubahan laju populasi spesies y dipengaruhi oleh laju kematian alami yang terjadi tanpa kehadiran spesies x sebagai mangsanya. Laju pemangsaan spesies x juga bergantung pada kontak atau bertemunya mangsa dan pemangsa.

Ada lima tahap yang dilakukan untuk menganalisis kondisi kastabilan pada model tersebut antara lain:

1. menentukan titk kritis

2. mengkontruksi matrik komunitas (Jacobian) dan mengevaluasinya di titik kritis yang telah diperoleh. matrik komunitas menyatakan efek dari spesies ke-j terhadap spesies ke-i di sekitar titik kritisnya

3. Menentukan nilai eigen dan menganalisis kondisi kestabilan 4. Menentukan orbit kestabilan

5. Menafsirkan secara ekologis.

6. Analisis Model Dinamik untuk Interaksi Dua Spesies Penentuan titik kritis

Sesuai persamaan (4) maka untuk interaksi dua spesies diperoleh:

0 ) ( 0 ) ( = + − = − dx c y by a x (13)

Dari persamaan tersebut diperoleh dua titik kritis sebagai berikut:

) / , / ( ) 0 , 0 ( 2 1 b a d c T T = = ₍₁₄₎

(16)

Kontruksi Matriks Jacobi

Dengan melakukan pelinieran pada persamaan (1) maka diperoleh matriks Jacobi:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + − − − = dx c dy bx by a Ji (15)

Matriks komunitas diperoleh dengan mensubstitusikan titik kritis T1 dan T2 yang telah

diperoleh ke dalam matriks Ji (15) yaitu:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = c a J 0 0 1 (16) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − = 0 0 2 b da d bc J (17)

Analisis Kestabilan Titik kritis

Kondisi kestabilan dari setiap titik kritis dapat dianalisis dan dapat dilihat dari nilai eigennya. Berikut beberapa persamaan karakteristik untuk tiap titik kritis:

[

][

]

0 ) det( ) ( ₁ 1 = − − − = − = λ λ λ λ c a I J P ₍₁₈₎ 0 ) det( ) ( 2 2 2 = J − I = +ac= P λ λ λ (19) Titik kritis T1

Nilai eigen yang diperoleh dari persamaan (18) yaitu, λ₁=a danλ₂ =−c. Agar sistem di titik T1 stabil maka harus dipenuhi syarat

λ

₁<0,

λ

₂<0. diketahui bahwa a dan c positif sehingga

mengakibatkan λ1>0,λ2<0.(dua bilangan real dengan tanda berbeda). Sehingga dari hasil ini dapat disimpulkan bahwa tipe titik kritis T1 adalah titik sadel.

Titik kritis T2

Nilai eigen yang diperoleh dari persamaan (19) yaitu, λ₁_,₂ =± aci. Jadi pada titik kritis T2

nilai eigen merupakan konjugat kompleks, karena bagian realnya sama dengan nol maka dapat disimpulkan bahwa tipe titik kritis T2 adalah titik fokus (center point).

Orbit dan Kestabilan Sistem

Bentuk kestabilan orbit dan laju perubahan populasi dua spesies hasil simulasi model diperoleh:

(17)

Gambar 2. Orbit kestabilan mangsa pemangsa dua spesies Kesesuaian Model Dengan Hasil Pengamatan Lapangan

Model mangsa Pemangsa Lotka- Volterra memprediksi suatu siklus periodik dengan perbedaan fase kecil antara populasi mangsa dengan pemangsa. Perilaku ini dapat dilihat dari pengamatan terkenal di Hudson bay Company yang mencatat jumlah mangsa kelinci (hare) dan pemangsa (lynx) dari tahun 1845-1935 berikut:

Gambar 3.Dinamika Populasi Hare dan Lynx oleh Hudson Bay Company

Gambar 4.Orbit kestabilan populasi Hare’s dan Lynx Oleh Hudson Bay Company

Secara kasar terlihat adanya kemiripan antara grafik model dinamika dua spesies dengan grafik dinamika populasi hasil observasi di alam.

METODOLOGI PENELITIAN

Waktu dan Tempat Penelitian

Penelitian telah selesai dilaksanakan di laboratorium Fisika Teori, Departemen Fisika, Institut Pertanian Bogor dimulai dari bulan September 2006 sampai dengan bulan Februari 2007. kegiatannya meliputi penelitian pendahuluan, pembuatan program, analisis output, pengolahan data, dan penyusunan laporan.

(18)

Peralatan

Peralatan yang digunakan dalam penelitian ini berupa komputer intel(R)Pentium(R) 4 CPU 3.00 GHz,512 MB of RAM. Software yang digunakan untuk proses komputasi adalah bahasa pemrograman Matlab 7.01 dari Mathwork, Inc.dan bahasa pemrograman Maple 9.5. Untuk mendukung penelitian ini sumber referensi yang digunakan selain buku (literature) juga informasi yang diperoleh dari internet yang dapat diakses dari Laboratorium.

Studi Pustaka

Studi pustaka diperlukan untuk mengetahui sejauh mana perkembangan yang telah dicapai dalam bidang yang diteliti.

Pembuatan Program

Pembuatan program dengan bahasa pemrograman Maple 9.5 dan Matlab 7.01 diperlukan untuk memudahkan perhitungan secara numerik maupun eksak juga memudahkan dalam pembuatan grafik solusi persamaan baik ruang fasenya maupun laju perubahan populasi pada model ekologi yang dibuat.

Analisis Output

Analisis output diperlukan untuk menguji apakah output yang didapat sesuai dengan teori yang ada dalam literatur. Sistematika penelitian yang lebih lengkap dapat dilihat pada lampiran 4.

HASIL DAN PEMBAHASAN

PEMODELAN

1. Model Dinamik untuk Interaksi Dua Spesies Mutualistik

Model ini mengasumsikan bahwa interaksi setiap spesies mendapat keuntungan karena berinteraksi dengan spesies yang lain. Tetapi kelangsungan hidup suatu populasi tidak bergantung pada interaksi itu (mutualisme facultatif). Sedangkan interaksi antar spesies yang sama dapat menurunkan laju pertumbuhan kedua populasi spesies, karena kedua spesies yang sama di dalam populasi berkompetisi untuk mendapatkan keuntungan dari spesies lain yang berbeda. Model tersebut dapat dinyatakan dalam bentuk persamaan logistik berikut:

0 , , 0 , ,. 1 , 0 ) ( ) ( ≥ > < < − + = + − = c b d a k j dy cx k y dt dy by ax j x dt dx (20) Dengan,

a : besarnya laju penurunan pertumbuhan spesies x akibat bertambahnya satu individu spesies x di dalam populasi.

b : besarnya laju peningkatan pertumbuhan spesies x akibat bertambahnya satu individu spesies y di dalam populasi.

c : besarnya laju peningkatan pertumbuhan spesies y akibat bertambahnya satu individu spesies x di dalam populasi

d : besarnya laju penurunan pertumbuhan spesies y akibat bertambahnya satu individu spesies y di dalam populasi

j : laju pertumbuhan intrinsik spesies x. k : laju pertumbuhan intrinsik spesies y.

2. Model Dinamik untuk Interaksi Dua Spesies Mutualistik dengan kehadiran Pemangsa. Interaksi ini dapat dinyatakan dalam bentuk persamaan logistik berikut:

(19)

) ( ) ( ) ( fy l z dt dz ez dy cx k y dt dy by ax j x dt dx + − = − − + = + − = (21) 0 , , 0 , , , , 1 , , 0< j k l< a d e f > bc≥ Dengan,

Dimana a, b, c, d, k dan l memiliki tafsiran seperti pada model (20)

e : besarnya laju penurunan spesies y akibat bertambahnya satu individu pemangsa z di dalam populasi.

f : besarnya laju peningkatan pertumbuhan pemangsa z akibat bertambahnya satu individu spesies y di dalam populasi.

l : laju penurunan intrinsik pemangsa z

3. Model Dinamik Dua Mangsa Satu Pemangsa tanpa Kompetisi Intraspesifik.

Untuk model dinamik dua mangsa satu pemangsa dapat dibentuk dengan Persamaan Lotka-Volterra yang dimodifikasi sebagai berikut:

gyz fxz ez dt dz dyz cy dt dy bxz ax dt dx + + − = − = − = (22) a,b,c,d,e,f,g >0 Dengan,

a : laju pertumbuhan intrinsik spesies x.

b : besarnya laju penurunan spesies x akibat bertambahnya satu individu pemangsa z di dalam populasi.

c : laju pertumbuhan intrinsik spesies y.

d : besarnya laju penurunan spesies x akibat bertambahnya satu individu pemangsa z di dalam populasi.

e : laju penurunan intrinsik pemangsa z.

f : besarnya laju peningkatan pertumbuhan pemangsa z akibat bertambahnya satu individu spesies x di dalam populasi.

g : besarnya laju peningkatan pertumbuhan pemangsa z akibat bertambahnya satu individu spesies y di dalam populasi.

4. Model Dinamik Dua Mangsa Satu Pemangsa dengan Kompetisi Intraspesifik.

Untuk model dinamik dua mangsa satu pemangsa dapat dibentuk dengan persamaan Lotka-Volterra yang dimodifikasi sesuai Model Gilpin (1979) sebagai berikut:

2 2 dx jx ax bxy cxz dt dy ky dy exy fyz dt dz lz gxz hyz dt = − − − = − − − = − + + (23) Dengan,

j, k dan l memiliki tafsiran seperti pada model (21)

a : besarnya laju penurunan pertumbuhan spesies x akibat bertambahnya satu individu spesies x di dalam populasi.

b : besarnya laju penurunan pertumbuhan spesies x akibat bertambahnya satu individu spesies y di dalam populasi.

(20)

d : besarnya laju penurunan pertumbuhan spesies y akibat bertambahnya satu individu spesies y di dalam populasi.

e : besarnya laju penurunan spesies y akibat bertambahnya satu individu spesies x di dalam populasi.

f : besarnya laju penurunan spesies y karena pemangsaan oleh predator z.

g : besarnya laju peningkatan pertumbuhan pemangsa z akibat bertambahnya satu individu spesies x di dalam populasi.

h : besarnya laju peningkatan pertumbuhan pemangsa z akibat bertambahnya satu individu spesies y di dalam populasi.

5. Model Dinamik Rantai Makanan Siklik

Untuk model dinamik rantai makanan siklik dapat dibentuk dengan persamaan Lotka-Volterra yang dimodifikasi sebagai berikut:

ixz hyz gz dt dz fyz exy dy dt dy cxy bxz ax dt dx − + = − + = − + = (24) Dengan,

a : laju pertumbuhan intrinsik spesies x.

b : besarnya laju peningkatan pertumbuhan spesies x akibat bertambahnya satu individu spesies z di dalam populasi.

c : besarnya laju penurunan spesies x akibat bertambahnya satu individu spesies y di dalam populasi.

d : laju pertumbuhan intrinsik spesies x.

e : besarnya laju peningkatan pertumbuhan spesies x akibat bertambahnya satu individu spesies z di dalam populasi.

f : besarnya laju penurunan spesies y akibat bertambahnya satu individu spesies z di dalam populasi.

g : laju pertumbuhan intrinsik spesies z.

h : besarnya laju peningkatan pertumbuhan spesies z akibat bertambahnya satu individu spesies y di dalam populasi

i : besarnya laju penurunan spesies z akibat bertambahnya satu individu spesies x di dalam populasi.

ANALISIS MODEL

Ada lima tahap yang dilakukan untuk menganalisis kondisi kastabilan pada kedua model tersebut antara lain:

• menentukan titik kritis

• mengkontruksi matrik komunitas (Jacobian).

• Menentukan nilai eigen dan menganalisis kondisi kestabilan. • Menentukan orbit kestabilan

• Menafsirkan secara ekologis.

1. Analisis Model Dinamik untuk Interaksi Dua Spesies Mutualistik 1.1 Penentuan titik kritis

Dari persamaan (4) diperoleh empat titik kritis sebagai berikut: a. Pilih x = 0 dan y = 0 sehingga diperoleh titik kritis T1 (0, 0).

b. Pilih j−ax+by=0 dan y = 0 maka diperoleh titik kritis T2 (j/a, 0)

(21)

d. Pilih j−ax+by=0 dan k + cx - dy = 0 maka akan diperoleh titik kritis T4 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − + bc ad ak cj bc ad bk dj ,

1.2 Kontruksi Matrik Jacobi

Dengan melakukan pelinieran pada sistem persamaan (20) maka diperoleh matrik komunitas

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + + − = dy cx k cy bx by ax j Ji 2 2 ₍₁₂₎

Matrik komunitas diperoleh dengan mensubstitusikan titik kritis T1,T2,T3 dan T4 yang telah

diperoleh ke dalam matrik Ji (11) yaitu:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = k j J 0 0 1 (13) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − = j a c k j a b j J 0 2 (14) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + = k k d c k d b j J 0 3 (15) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 22 21 12 11 4 A A A A J (16) Dengan, A11 = bc ad bk dj a − + − ( ) A12 = bc ad bk dj b − + ) ( A21 = bc ad ak cj c − + ) ( A22 = bc ad ak cj d − + − ( )

1.3 Analisis kestabilan titik kritis

Melalui persamaan (11) dapat diperoleh persamaan karakteristik pada titik kritis masing-masing, yaitu:

[

λ

][

λ

]

λ λ = J − I = j− k− P₁( ) det( ₁ ) =0 (17) 0 ] [ ) det( ) ( 2 2 = ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ ₋ − − = − = λ λ λ λ a c k j I J P (18)

[

]

0 ) det( ) ( 3 3 = − − ⎥⎦ ⎤ ⎢⎣ ⎡ ₊ ₋ = − = λ λ λ λ k k d b j I J P ₍₁₉₎ 0 ) det( ) ( 2 4 4 λ = J −λI =λ −τλ+δ = P (20) Dengan,

(22)

⎥⎦ ⎤ ⎢⎣ ⎡ − + − + ⎥⎦ ⎤ ⎢⎣ ⎡ − + − = + = = bc ad ak cj d bc ad bk dj a A A J tr ) ( ) ( ) ( 4 11 22 τ τ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + − ⎥⎦ ⎤ ⎢⎣ ⎡ − + − ⎥⎦ ⎤ ⎢⎣ ⎡ − + − = − = = bc ad ack j c bc ad k b bdj bc ad ak cj d bc ad bk dj a A A A A J 2 2 21 12 22 11 4 ) ( ) ( ) det( δ δ Titik Kritis T1

Nilai eigen dari persamaan (17) yaitu, λ1= j danλ2=k

Diketahui j dan k positif (0<j<1,0<k<1) , a, d > 0 dan b,c≥ sehingga 0 λ₁>0,danλ₂ >0 (bilangan real dengan tanda sama). Dari hasil tersebut tipe titik kritis T1 merupakan simpul yang

tidak stabil. Titik Kritis T2

Nilai eigen persamaan (18) yaitu: j a c k dan j = + − = 2 1 , λ λ

Karena (0<j<1,0<k<1) dan a, d > 0, b , c≥0 mengakibatkan λ₁<0,danλ₂ >0 (real berbeda dengan tanda berlawanan) maka titik kritis T2 adalah titik sadel yang tak stabil.

Titik Kritis T3

Nilai eigen persamaan (19) yaitu: k dan k d b j+ =− = 2 1 , λ λ

Karena ( 0 < j < 1, 0 < k <1) dan a, d > 0, b , c

≥

0

mengakibatkan λ1>0,danλ2 <0 maka titik kritis T3 merupakan sadel tak stabil.

Titik Kritis T4

Agar titik kritis T4 stabil maka harus memenuhi kriteria kestabilan berikut:τ <0,danδ >0

diketahui (0<j<1,0<k<1) , a, d > 0 dan b,c≥ sehingga kondisi 0 τ <0 terpenuhi jika ad – bc > 0 dan δ >0 sudah terpenuhi.

1.4 Orbit dan kestabilan sistem

Orbit dan model dapat diperoleh dari dua tipe dinamik, yaitu: kasus ad > bc

Dengan parameter a = 1, d = 1 , b = 0.5, c = 0.5, j = k = 0.8 dan kondisi awal bervariasi, maka diperoleh grafik ruang fase dan grafik laju populasinya sebagai berikut:

(23)

(a) (b)

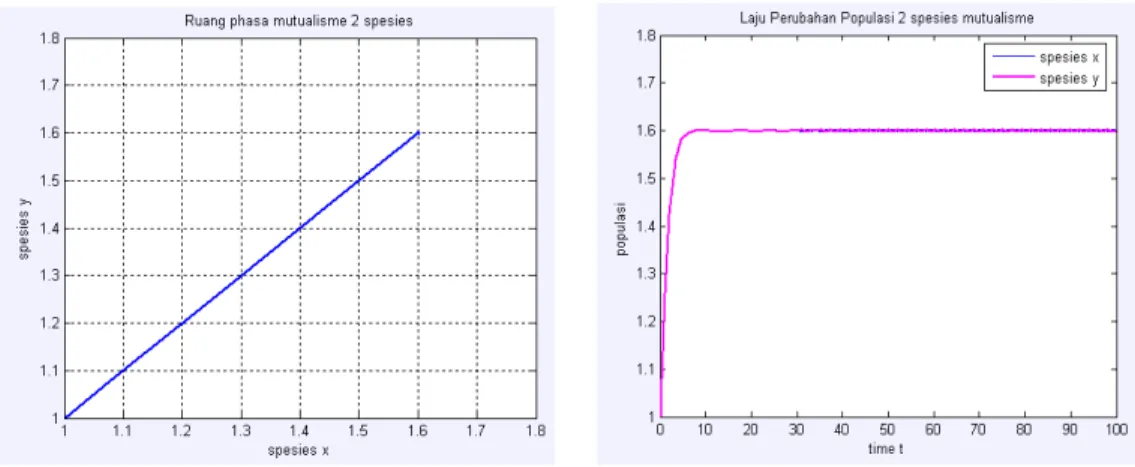
Gambar 5. (a) Grafik ruang fase bidang xy dengan kondisi awal x = 1, y = 1 dan t = 100 (b) Grafik laju populasi dengan kondisi awal x = 1 dan y = 1

Gambar 5 memperlihatkan bahwa titik kritis T1 merupakan titik simpul tak stabil, dari

Gambar 5 terlihat orbit bergerak menjauhi T1(0,0) dan bergerak menuju titik kritis

T4(1.6,1.6), sehingga titik kritis tersebut

merupakan titik simpul yang stabil. Kondisi ini diperoleh karena pada saat ad > bc maka akan diperoleh nilai eigen untuk T1 merupakan dua

buah nilai real positif λ₁>0,danλ₂>0 sedangkan untuk titik kritis T4 saat ad > bc

akan diperoleh nilai eigen berupa dua buah real negatif λ₁<0,danλ₂<0.

Gambar 6 memperlihatkan ruang fase bidang xy untuk berbagai variasi, dari gambar terlihat bahwa orbit bergerak dari kondisi awal menuju titik kritis T4. Dari gambar 6 (a) terlihat

lintasan orbit membelok, hal ini terjadi karena adanya titik kritis T2 dan T3 yang merupakan

titik sadel yang bersifat tak stabil. Saat kondisi parameter berapapun pada titik kritis T2 dan T3

akan tetap diperoleh dua buah nilai eigen real berlawananan tanda.

Gambar 6 memperlihatkan pada kondisi parameter ad > bc semua sistem bergerak menuju kestabilan asimtotik. Pada kondisi ini kedua spesies dapat hidup bersama dan bertahan hidup untuk jangka waktu tertentu dengan syarat interaksi intraspesifiknya (interaksi antaspesies itu sendiri) harus lebih besar dibandingkan dengan interaksi interspesifiknya (interaksi dengan spesies yang berbeda).

(24)

(c) (d)

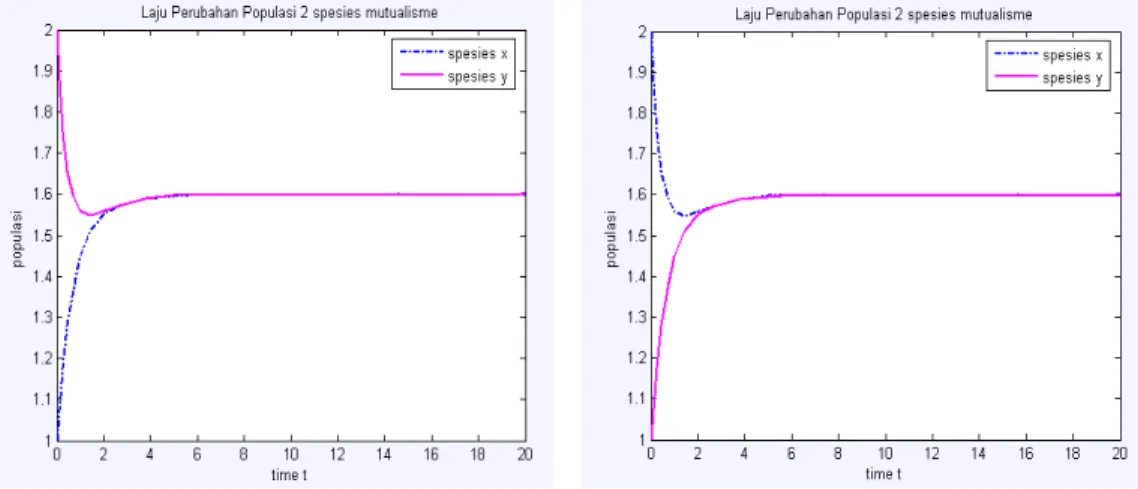
Gambar 6. Grafik kestabilan titik kritis T4 saat ad > bc (a) ruang fase bidang xy dengan

memvariasikan kondisi awal dan t = 100 (a) laju populasi kondisi awal x = 2 dan y = 2 (b) laju populasi kondisi awal x = 1 dan y = 2 dan (c) laju populasi kondisi awal x = 2 dan y = 1.

kasus ad < bc

Dengan parameter a = d = 0.5 , b = c = 1, j = k = 0.8 dan kondisi awal bervariasi, maka diperoleh grafik ruang fase dan grafik laju populasinya sebagaimana diperlihatkan pada gambar berikut.

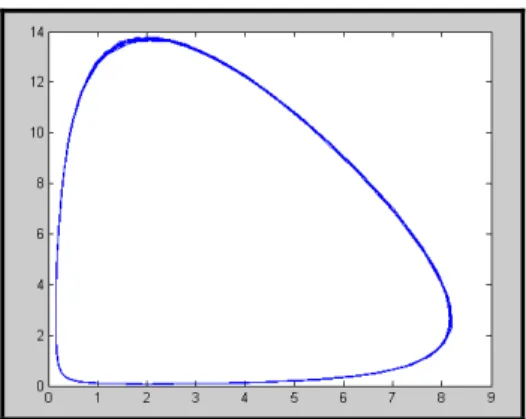
Gambar 7 memperlihatkan bahwa pada saat parameter ad < bc (interaksi interspesifiknya lebih dominan dari interaksi intraspesifik) maka ruang fase tersebut memperlihatkan perilaku dinamik yang tidak stabil, karena orbit bergerak menjauhi titik kritis T4. Pada kondisi tersebut kedua populasi

spesies memperoleh keuntungan yang berlebihan sehingga laju pertumbuhan kedua spesies mengalami peningkatan tanpa batas dan terjadi peledakan populasi.

(a)

(b)

Gambar 7.(a) grafik ruang fase bidang xy dengan kondisi awal x = 1, y = 1 dan t = 1 (b) grafik laju perubahan populasi dengan kondisi awal x = 1 dan y = 1

2. Analisis Model Dinamik Interaksi Dua Spesies Mutualistik dengan kehadiran Pemangsa

2.1 Penentuan titik kritis

Melalui persamaan (5) diperoleh titik kritis sebagai berikut:

T1 (0,0,0). (21)

T2 (j/a,0,0), (22)

(25)

T4 dj bk,cj ak , 0 ad bc ad bc + + ⎛ ⎞ ⎜ ₋ ₋ ⎟ ⎝ ⎠, (24) T5 0,l, fk dl f fe ⎛ − + ⎞ ⎜ ⎟ ⎝ ⎠ (25) T6 fj bl l afk_, _, adl cfj cbl fa f afe ⎛ + − + + ⎞ ⎜ ⎟ ⎝ ⎠ (26)

2.2 Kontruksi Matriks Jacobi

Dengan melakukan pelinieran pada persamaan 21, maka diperoleh matriks komunitas sebagai berikut:

Ji= 2 0 2 0 j ax by bx cy k cx dy ez ey fz l fy − + ⎡ ⎤ ⎢ _{+ − −} ₋ ⎥ ⎢ ⎥ ⎢ − + ⎥ ⎣ ⎦ (27)

Matrik komunitas diperoleh dengan mensubstitusikan titik kritis yang telah diperoleh ke dalam matrik Ji (19) yaitu:

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − = l k j J 0 0 0 0 0 0 1 (28) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + − = l a cj k a bj j J 0 0 0 0 0 2 (29) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + − − − + = d fk l d ek k d ckd bk j J 0 0 0 0 3 (30) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 33 32 31 23 22 21 13 12 11 4 A A A A A A A A A J (31) Dengan, ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + + − = = = − + − = − + − = − + = = − + = − + − = bc ad ak jc f l A A A bc ad ak jc e A bc ad ak jc d A bc ad ak jc c A A bc ad dj bk b A bc ad dj bk a A 33 32 31 23 22 21 13 12 11 0 0 ) ( ) ( ) ( 0 ) ( ) ( ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − + = 0 0 0 0 5 e dl fk f el f dl f cl f bl j J (32) ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 33 32 31 23 22 21 13 12 11 6 B B B B B B B B B J (33) Dengan, 11 12 13 2 1 2 2 ( ) ( ) 0 a fj bl B a f b fj bl B af B cl B f d l B f − + = + = = = − = 0 0 33 32 31 23 = + + − = = − = B ae cbl cfj adl afk B B f el B

2.3 Analisis kestabilan titik kritis Titik Kritis T1

(26)

Dari persamaan karakteristik diperoleh nilai eigen T1 yaitu:

1 j, 2 k, 3 l

λ = λ = λ = − (34)

Sehingga, karena pada titik kritis ini nilai eigen terdiri dari dua real positif dan satu real negatif maka trayektor pada titik ini merupakan titik tak stabil.

Titik Kritis T2

1 , 2 , 3

ka cj

j l

a

λ = − λ = + λ = − (35)

Diperoleh bahwa nilai eigen dari titik kritis ini terdiri dari dua nilai real negatif dan satu real positif. Sehingga aliran vektor pada titik kritis ini juga merupakan titik tak stabil. Titik Kritis T3

1 , 2 , 3

bk dj fk dl

k

d d

λ = + λ = − λ = − (36) Dari nilai eigen tersebut dapat diperoleh bahwa pada titik kritis tersebut merupakan titik tak stabil.

Titik Kritis T4

Kondisi kestabilan pada T4 terjadi saat

pemangsa punah, sehingga analisis dari titik kritis ini sama dengan model interaksi mutualisme dua spesies tanpa kehadiran pemangsa.

Untuk menganalisis kondisi kestabilan dari titik kritis T4, maka diperlukan analisis tiap

parameter yang digunakan sebagai berikut: Tabel 1. Nilai-nilai parameter yang digunakan dalam titik kritis T4 Model Mutualisme

Kasus a b c d ad > bc ad < bc 2.5 0.5 1 1 1 1 2.5 0.5 Kasus ad > bc

Pada saat ad > bc maka akan diperoleh nilai eigen sebagai berikut:

1 0.333, 2 1.000, 3 2.333

λ = − λ = − λ = −

Sehingga trayektor pada titik tersebut merupakan titik stabil.

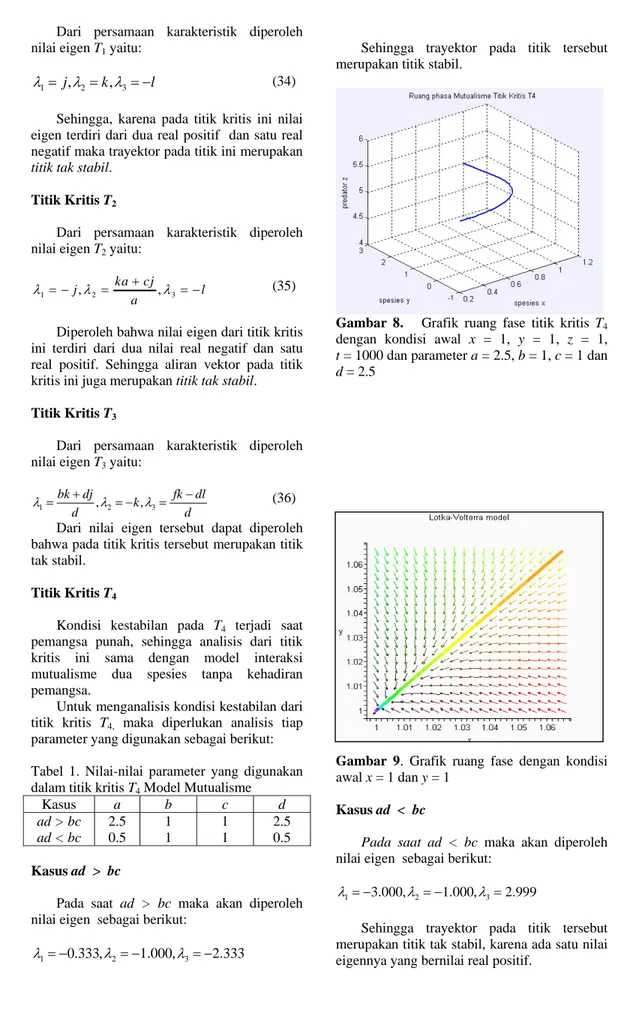
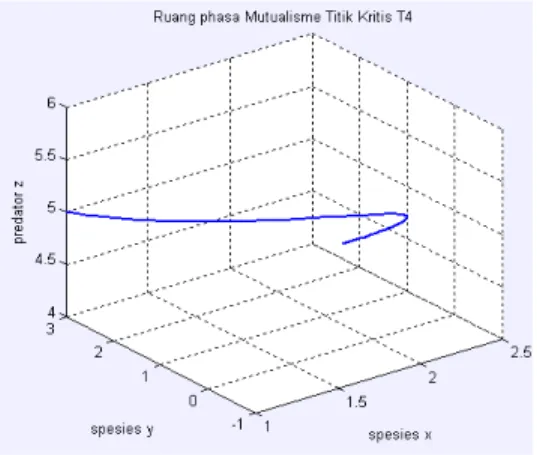
Gambar 8. Grafik ruang fase titik kritis T4

dengan kondisi awal x = 1, y = 1, z = 1, t = 1000 dan parameter a = 2.5, b = 1, c = 1 dan d = 2.5

Gambar 9. Grafik ruang fase dengan kondisi awal x = 1 dan y = 1

Kasus ad < bc

Pada saat ad < bc maka akan diperoleh nilai eigen sebagai berikut:

1 3.000, 2 1.000, 3 2.999

λ = − λ = − λ =

Sehingga trayektor pada titik tersebut merupakan titik tak stabil, karena ada satu nilai eigennya yang bernilai real positif.

(27)

Gambar 10. Grafik ruang fase titik kritis T4

dengan kondisi awal x = 1, y = 1, z = 1, t = 1000 dan parameter a = 0.5, b = 1, c = 1 dan d = 0.5

Gambar 11. Grafik ruang fase dengan kondisi awal x = 1 dan y = 1

Titik Kritis T5

Untuk menganalisis kondisi kestabilan dari titik kritis T5 maka diperlukan analisis tiap

parameter yang digunakan sebagai berikut: Tabel 2. Nilai-nilai parameter yang digunakan dalam titik kritis T5 model mutualisme

Kasus f k d l fk < dl fk < dl fk = dl fk > dl fk > dl fk > dl 1 1 1 1 1 1 1 1 1 1 1 1 1.5 1.2 1 0.7 0.5 0.3 1.5 1.2 1 0.7 0.5 0.3

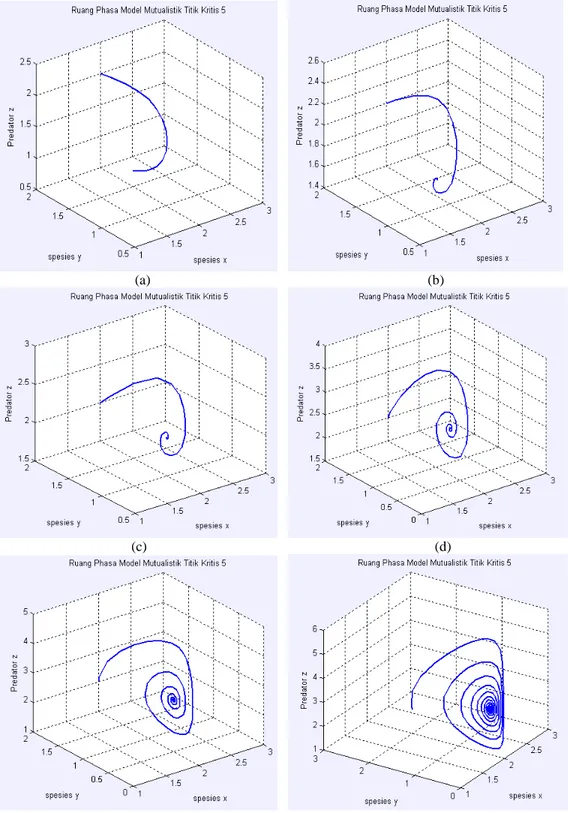
Dari beberapa parameter tersebut dapat diperoleh grafik ruang fase yang mamperlihatkan gejala bifurkasi pada titik kritis T5 .Gambar 12 memperlihatkan gejala bifurkasi

yang terjadi pada titik kritis T5. Gambar 12(a)

memperlihatkan orbit kestabilan di sekitar titik kritis T5 yang merupakan titik stabil kemudian

dengan mengubah parameter, secara perlahan titik tersebut berubah menjadi spiral yang stabil seperti yang terlihat pada gambar 12(d), 12(e) dan 12(f). Terlihat trayektor memiliki lintasan periodik spiral di sekitar titik kritis yang semakin memenuhi bidang spiral.

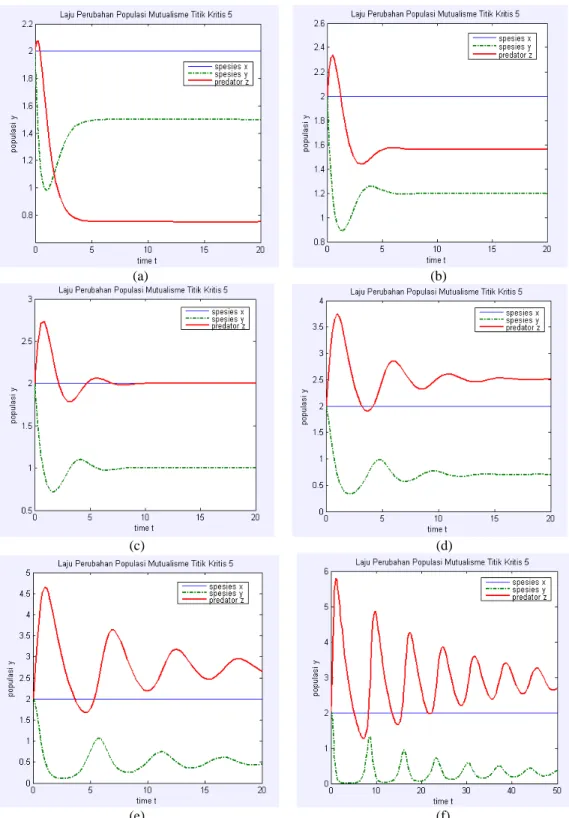
Gambar 13 memperlihatkan laju perubahan populasi ketika spesies x tetap, dari grafik tersebut terlihat ketika populasi spesies x tetap maka populasi spesies y akan mengalami penurunan secara periodik hingga mencapai keseimbangan populasi, penurunan ini disebabkan karena laju pertumbuhan populasi dipengaruhi secara mutual oleh spesies x sehingga ketika interaksi interspesifiknya berkurang dibandingkan dengan interaksi intraspesifiknya maka populasinya akan mengalami penurunan secara periodik. Dari gambar terlihat pula ketika spesies x dibuat tetap populasi pemangsa z akan mengalami penurunan juga seiring dengan menurunnya spesies y yang menjadi mangsanya sampai pada suatu keseimbangan populasi tertentu.

Analisis Titik Kritis T5

Parameter 1

Jika parameter yang dipakai adalah f = 1, k = 1, d = 1.5 dan l = 1.5 maka secara numerik diperoleh nilai eigen sebagai berikut:

1 2.500, 2 0.647, 3 -2.897

(28)

Diperoleh dua buah nilai eigen positif yang bersesuaian dengan bidang tak stabil dan satu nilai eigen real negatif yang bersesuaian dengan garis stabil, sehingga dari nilai eigen tersebut diketahui pada titik kritis tersebut dengan kondisi parameter fk < dl merupakan titik sadel.

Parameter 2

1 2.200, 2 0.302, 3 -1.742

λ = λ = λ =

Diperoleh dua buah nilai eigen positif yang bersesuaian dengan bidang tak stabil dan satu nilai eigen real negatif yang bersesuaian dengan garis stabil. Dari nilai eigen tersebut diketahui pada titik kritis tersebut dengan kondisi parameter fk < dl merupakan titik sadel.

Parameter 3

Jika parameter yang dipakai adalah f = 1, k = 1, d = 1 dan l = 1, maka secara numerik diperoleh nilai eigen sebagai berikut:

1 2.000, 2 0.000, 3 -1.000

λ = λ = λ =

Diperoleh sebuah eigen positif yang bersesuaian dengan bidang tak stabil dan satu nilai eigen real negatif yang bersesuaian dengan garis stabil. Sehingga, dari nilai eigen tersebut maka diketahui pada titik kritis tersebut dengan kondisi parameter fk = dl merupakan titik stabil.

Parameter 4

Jika parameter yang dipakai adalah f =1, k = 1, d = 0.7 dan l = 0.7 maka secara numerik diperoleh nilai eigen sebagai berikut:

1 2 3 1.700, -0.245 0.544 i -0.245-0.544 i λ λ λ = = + =

Sehingga diperoleh dua buah nilai eigen kompleks dengan bagian realnya bernilai negatif sehingga orbit yang dihasilkan membentuk sebuah bidang bersifat spiral stabil. Dan sebuah garis tak stabil yang bersesuaian dengan niali eigen real positifnya. Parameter 5

1 2 3 1.500, -0.125 0.599 i -0.125-0.599 i λ λ λ = = + =

Sehingga diperoleh dua buah nilai eigen kompleks dengan bagian realnya bernilai negatif sehingga orbit yang dihasilkan membentuk sebuah bidang bersifat spiral stabil. Dan sebuah garis tak stabil yang bersesuaian dengan niali eigen real positifnya. Parameter 6

Jika parameter yang dipakai adalah f = 1, k = 1, d = 0.3 dan l = 0.3 maka secara numerik diperoleh nilai eigen sebagai berikut:

1 2 3 1.300, -0.045 0.520 i -0.045-0.520 i λ λ λ = = + =

Sehingga diperoleh dua buah nilai eigen kompleks dengan bagian realnya bernilai negatif sehingga orbit yang dihasilkan membentuk sebuah bidang bersifat spiral stabil. Dan sebuah garis tak stabil yang bersesuaian dengan nilai eigen real positifnya.

(29)

(a) (b) (c) (d) (e) (f)

Gambar 12. Bifurkasi yang terjadi pada titik kritis T5 dengan t =1000 dan memvariasikan

parameter yang digunakan, (a) parameter d = 1.5 dan l = 1.5 (b) parameter d = 1.2 dan l = 1.2 (c) parameter d = 1 dan l = 1 (d) parameter d = 0.7 dan l = 0.7 (e) parameter d = 0.5 dan l = 0.5 serta (f) parameter d = 0.3 dan l = 0.3.

(30)

(a) (b) (c) (d) (e) (f)

Gambar 13. Grafik Laju Perubahan Populasi pada Titik Kritis T5 dengan beberapa parameter,

(a) parameter d = 1.5 dan l = 1.5 (b) parameter d = 1.2 dan l = 1.2 (c) parameter d = 1 dan l = 1 (d) parameter d = 0.7 dan l = 0.7 (e) parameter d = 0.5 dan l = 0.5 serta (f) parameter d = 0.3 dan l = 0.3.

(31)

Titik Kritis T6

Untuk menganalisis kondisi kestabilan dari titik kritis T6 maka diperlukan analisis

tiap parameter yang digunakan sebagai berikut:

Tabel 3. Nilai-nilai parameter yang digunakan dalam titik kritis T6 model mutualisme

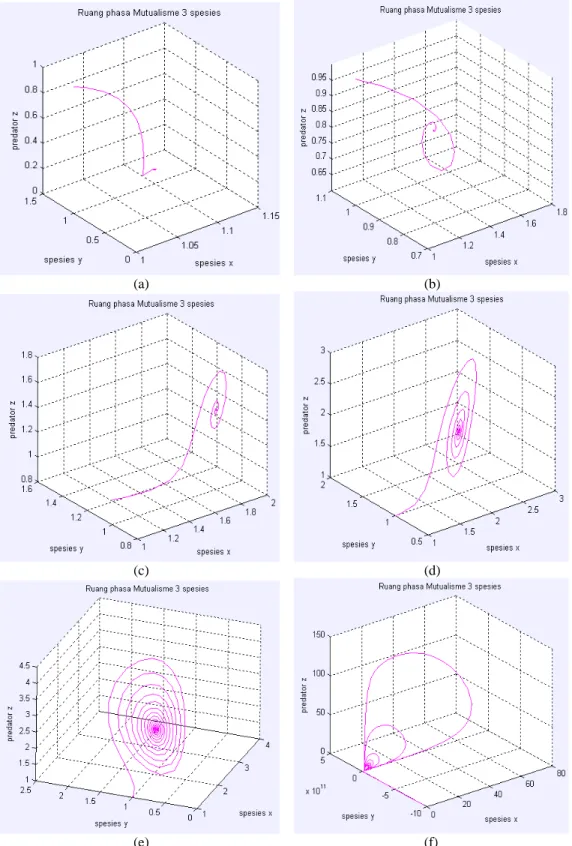
Kasus a b c d ad > bc ad > bc ad > bc ad = bc ad < bc ad < bc 1 1 1 1 1 1 0.1 0.5 0.8 1 1.1 1.2 0.1 0.5 0.8 1 1.1 1.2 1 1 1 1 1 1 Gambar 14. memperlihatkan terjadinya bifurkasi pada titik kritis T6 sesuai dengan

perubahan pada parameter yang diberikan. Pada gambar 14(a) dengan parameter b = 0.1 dan c = 0.1, di sekitar titik kritisnya masih bersifat sebagai Simpul Stabil. Sedangkan pada gambar 14(b), 14(c), 14(d), dan 14(e) memperlihatkan bahwa terjadi bifurkasi dari simpul stabil menjadi Spiral Stabil. Jika parameter yang digunakan yaitu b = 1.2 dan c = 1.2 maka orbit di sekitar titik kritis tersebut akan bersifat Spiral Tak Stabil. Sehingga pada titik kritis T6 terjadi tiga kali

bifurkasi yang memiliki sifat yang berbeda tergantung pada parameter yang digunakan.

Gambar 15 memperlihatkan laju perubahan populasi dengan memvariasikan parameter yang digunakan.pada gambar 15(a), 15(b), 15(c), 15(d), dan 15(e) memperlihatkan adanya kestabilan populasi karena parameter yang digunakan yaitu ad > bc, atau terjadinya interaksi antar spesies itu sendiri lebih besar (intraspesifik) dibandingkan dengan interaksi antar spesies yang berbeda (interspesifik) sehingga populasi ketiga spesies berada pada kondisi stabil. Sedangkan pada gambar 15(f) dengan parameter ad < bc atau interaksi antar spesies berbeda lebih besar dari interaksi antar spesies sejenis maka akan terjadi ketidakstabilan sehingga populasi ketiga spesies akan meningkat secara drastis, dalam hal ini pemangsa merupakan spesies yang paling diuntungkan sehingga populasinya meningkat paling tinggi dibandingkan spesies x dan spesies y.

Kasus ad > bc

Jika parameter yang dipakai adalah

a = 1,b = 0.1, c = 0.1, d = 1, e = 1, f = 1, g = 1, h = 1, j = 1, k = 1 , l = 1.

maka akan di peroleh nilai eigen:

1 -1.145, 2 -0.826, 3 -0.127

λ = λ = λ =

Dari nilai eigen yang diperoleh dapat dianalisis bahwa pada kondisi parameter ini maka akan diperoleh orbit di sekitar titik kritis yang bersifat simpul stabil karena nilai eigennya merupakan real negatif. Sehingga, jika interaksi antarspesiesnya lebih diperkecil maka akan diperoleh titik kritis yang bersifat simpul stabil seperti terlihat pada gambar 14(a). Pada gambar 15(a) terlihat laju perubahan populasi menuju suatu kestabilan asimtotik dimana populasi spesies x dan spesies y memiliki populasi tertinggi, sedangkan pemangsa z mengalami populasi terendah yang juga stabil.

Kasus ad = bc

a = 1.01, b = 1.01, c = 1, d = 1, e = 1, f = 1, g = 1, h = 1, j = 1, k =1, l = 1.

maka akan diperoleh nilai eigen:

1 2 3 -2.808, -0.100+1.189 i -0.100-1.189 i λ λ λ = = =

Dari nilai eigen yang diperoleh dapat dianalisis bahwa pada kondisi parameter ini maka akan diperoleh orbit di sekitar titik kritis yang bersifat spiral stabil seperti terlihat pada gambar 14(d). karena nilai eigennya merupakan kompleks dengan bagian realnya bernilai negatif sehingga bersifat stabil. Pada gambar 15(d) terlihat laju perubahan populasi menuju suatu kestabilan asymtotic dimana populasi spesies x dan pemangsa z memiliki populasi tertinggi sedangkan populasi spesies y yang menjadi mangsa dari predator z memiliki populasi yang paling rendah karena adanya pemangsaan dari pemangsa z, sedangkan interaksi interspesifiknya dan interaksi intraspesifiknya sama besar, populasi spesies y inipun menuju suatu kestabilan populasi.

(32)

(a) (b) (c) (d) (e) (f)

Gambar 14. Bifurkasi yang terjadi pada titik kritis T6 dengan t = 1000 dan memvariasikan

parameter yang digunakan, (a) parameter b = 0.1 dan c = 0.1 (b) parameter b = 0.5 dan c = 0.5 (c) parameter b = 0.8, c = 0.8 (d) parameter b = 1 dan c = 1 (e) parameter b = 1.1 dan c = 1.1 serta (f) parameter b = 1.2 dan c = 1.2.

(33)

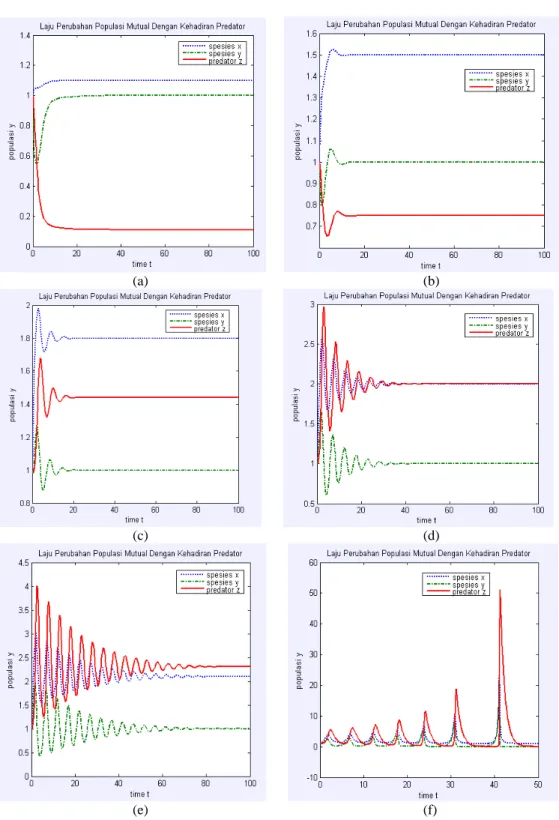
(a) (b) (c) (d) (e) (f)

Gambar 15. Grafik Laju Perubahan Populasi pada Titik Kritis T6 dengan beberapa parameter,

(a) parameter b = 0.1 dan c = 0.1 (b) parameter b = 0.5 dan c = 0.5 (c) parameter b = 0.8, c = 0.8 (d) parameter b = 1 dan c = 1 (e) parameter b = 1.1 dan c = 1.1 serta (f) parameter b = 1.2 dan c = 1.2.

(34)

Kasus ad < bc

a = 1, b = 1.2, c = 1.2, d = 1, e = 1, f = 1 , g = 1, h =1, j = 1, k = 1, l = 1.

maka akan di peroleh nilai eigen:

1 2 3 -3.237, 0. 018+1.339 i 0.018-1.339 i λ λ λ = = =

Dari nilai eigen yang diperoleh dapat dianalisis bahwa pada kondisi parameter ini maka akan diperoleh orbit di sekitar titik kritis yang bersifat spiral tak stabil sebagaimana diperlihatkan pada gambar 14(f). Karena nilai eigen yang diperoleh merupakan kompleks dengan bagian real bernilai positif sehingga bersifat tak stabil.

Gambar 15(f) memeperlihatkan laju perubahan populasi dengan parameter yang digunakan dalam hal ini yaitu ad < bc sehingga interaksi antarspesies yang berbeda lebih besar dibandingkan dengan interaksi antar spesies sejenisnya sehingga menimbulkan pengaruh pada pemangsaan spesies y oleh pemangsa z. Jadi ketika interaksi intraspesifik lebih kecil dari interaksi interspesifiknya maka pengaruh pemangsaan spesies y oleh pemangsa juga akan amat mempengaruhi kestabilan spesies x meski tak terkait secara langsung dengan pemangsa z. Spesies x dan spesies y akan mengalami fluktuasi secara periodik, sedangkan pemangsa z akan mengalami peningkatan populasi secara drastis namun tetap periodik menuju ketidakstabilan populasi.

3. Analisis Model Dinamik Dua Mangsa Satu Pemangsa tanpa Kompetisi Intraspesifik.

3.1 Penentuan titik kritis

Melalui persamaan (5) diperoleh titik kritis sebagai berikut:

T1=(0, 0, 0) (37)

T2=(0, e/g, c/d) (38)

T3=(e/f, 0, a/b) (39)

3.2 Kontruksi Matriks Jacobi

Dengan melakukan pelinieran pada persamaan (22) maka diperoleh matriks komunitas ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + + − − − − − = gy fx e gz fz dy dz c bx bz a Ji 0 0 (40)

Matrik komunitas diperoleh dengan mensubstitusikan titik kritis yang telah diperoleh ke dalam matrik Ji (29) yaitu:

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − = e c a J 0 0 0 0 0 0 1 (41) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − = 0 0 0 0 0 2 d gc d fc g de d bc a J (42) ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − = 0 0 0 0 0 3 b ga b fa b da c f be J (43)

3.3 Analisis kestabilan titik kritis Titik Kritis T1

Dari persamaan karakteristik diperoleh nilai eigen T1 yaitu:

1 a, 2 c, 3 e

λ = λ = λ = − (44)

Karena terdapat dua buah nilai eigen bernilai real positif, maka titik kritis T1

bersesuaian dengan bidang tak stabil dan juga terdapat satu nilai eigen bernilai real negatif yang bersesuaian dengan sebuah garis bersifat stabil. Jadi pada titik kritis T1 merupakan titik

(35)

Titik Kritis T2

ce ce d bc ad − − = − = − = 3 2 1 λ λ λ (45)

Dari nilai eigen tersebut terdapat dua buah nilai eigen imajiner murni λ1,2=± cei maka titik kritis ini membentuk sebuah bidang fokus (Center Point). Sedangkan nilai eigen

d bc ad− =

1

λ akan mevariasikan kondisi

kestabilan sebuah garis terhadap titik kritisnya. Jika ad > bc maka diperoleh nilai eigen real positif yang bersesuaian dengan titik tak stabil. Jika ad < bc maka diperoleh nilai eigen real negatif yang bersesuaian dengan titik stabil. Sedangkan jika ad = bc maka nilai eigen akan sama dengan nol sehingga sifat titik kritis T2

membentuk titik fokus (Center Point). Titik Kritis T3

ae ae b bc ad − − = − = − = 3 2 1 λ λ λ (46)

Dari nilai eigen tersebut terdapat dua buah nilai eigen imajiner murni λ1,2=± aei maka titik kritis ini membentuk sebuah bidang fokus (Center Point). Sedangkan nilai eigen

b bc ad− = 1

λ akan mevariasikan kondisi

kestabilan sebuah garis terhadap titik kritisnya. Jika ad > bc maka diperoleh nilai eigen real positif yang bersesuaian dengan titik tak stabil. Jika ad < bc maka diperoleh nilai eigen real negatif yang bersesuaian dengan titik stabil. Sedangkan jika ad = bc maka nilai eigen akan sama dengan nol sehingga sifat titik kritis T3

membentuk fokus (Center Point). kasus ad = bc

Gambar 16(a) memperlihatkan sebuah ruang fase yang bersifat titik fokus (center point) pada titik kritis T3. Hal ini terjadi karena

pada kondisi parameter ad = bc maka titik kritis T3 akan memiliki dua buah nilai eigen imajiner

murni dan semua bagian realnya akan bernilai nol. Gambar 17(a) memperlihatkan grafik laju perubahan populasi ketiga spesies. saat parameter ad = bc maka pertumbuhan dan penurunan karena pemangsaan pada spesies x akan sama besarnya dengan pertumbuhan dan penurunan karena pemangsaan pada spesies y. Sehingga spesies x dan spesies y akan mengalami laju pertumbuhan populasi yang sama. Sedangkan pemangsa z akan memiliki laju pertumbuhan terbesar karena dalam hal ini spesies yang paling diuntungkan adalah spesies pemangsa z. Laju pertumbuhan populasi ketiga spesies akan menuju kestabilan periodik. Kasus ad > bc

Gambar 16(b) memperlihatkan sebuah ruang fase yang bersifat spiral tak stabil pada titik kritis T3. Hal ini terjadi karena pada kondisi

parameter ad > bc maka titik kritis T3 akan

memiliki dua buah nilai eigen imajiner murni yang bersesuaian dengan bidang xz yang bersifat spiral stabil sehingga spesies x dan predator z akan mengalami keseimbangan populasi dan pada titik kritis T3 terdapat juga

nilai eigen real positif yang bersesuaian dengan sebuah garis sumbu y tak stabil yang artinya spesies y akan mengalami kepunahan. Gambar 17(b) memperlihatkan grafik laju perubahan ketiga spesies. saat parameter ad > bc maka spesies x akan memiliki laju pertumbuhan intrinsik yang lebih besar dari spesies y dan laju penurunan populasi karena pemangsaan oleh pemangsa pun lebih kecil dibandingkan dengan spesies y sehingga dalam kehidupannya spesies x akan mengalami kestabilan secara periodik karena laju pertumbuhan besar sedangkan pemangsaannya kecil. Sedangkan spesies y akan mengalami kepunahan karena laju pertumbuhan intrinsiknya yang kecil tidak sebanding dengan pemangsaan yang dilakukan pemangsa z. Dari gambar terlihat pemangsa z akan memiliki laju pertumbuhan terbesar karena dalam hal ini spesies yang paling diuntungkan adalah spesies pemangsa z. laju pertumbuhan spesies z akan bertambah karena pemangsaanya, dan akan distabilkan dengan adanya kematian alami dari pemangsa z.

(36)

Kasus ad < bc

Gambar 16(e) memperlihatkan sebuah ruang fase yang bersifat spiral stabil pada titik kritis T3. Hal ini terjadi karena pada kondisi

parameter ad < bc maka titik kritis T3 akan

memiliki dua buah nilai eigen imajiner murni yang bersesuaian dengan bidang yz yang bersifat spiral stabil, sehingga spesies y dan pemangsa z akan mengalami keseimbangan populasi dan pada titik kritis T3 terdapat juga

nilai eigen real positif yang bersesuaian dengan sebuah garis sumbu x tak stabil yang artinya spesies x akan mengalami kepunahan. Gambar 17(e) memperlihatkan grafik laju perubahan populasi ketiga spesies. Saat parameter ad < bc maka spesies y akan memiliki laju pertumbuhan intrinsik yang lebih besar dari spesies x dan laju penurunan populasi karena pemangsaan oleh pemangsapun lebih kecil dibandingkan dengan spesies x, sehinggga dalam kehidupannya spesies y akan mengalami kestabilan secara periodik karena laju pertumbuhan besar, sedangkan pemangsaannya kecil. Sedangkan spesies x akan mengalami kepunahan karena laju pertumbuhan intrinsiknya yang kecil tidak sebanding dengan pemangsaan yang dilakukan pemangsa z. Dari gambar terlihat pemangsa z akan memiliki laju pertumbuhan terbesar karana dalam hal ini spesies yang paling diuntungkan adalah spesies pemangsa z. laju pertumbuhan spesies z akan bertambah karena pemangsaanya dan akan distabilkan dengan adanya kematian alami dari pemangsa z.

Hasil Numerik

Secara numerik diperoleh grafik ruang fase dan laju populasi dengan memvariasikan beberapa parameter yang terkait, sebagai berikut:

Tabel 4. Nilai-nilai parameter yang digunakan dalam model dua mangsa satu pemangsa

a b c d ad = bc ad > bc ad > bc ad > bc ad < bc ad < bc 1 2 20 28 1 1 1 1 1 1 2 20 1 1 1 1 2 20 1 2 20 28 1 1 Dalam model interaksi dua spesies mangsa satu pemangsa tidak terdapat hubungan interaksi intraspesifik. dari analisis model terlihat adanya gejala bifurkasi pada ruang phasanya. Saat parameter ad = bc maka ruang fasenya pada titik kritisnya merupakan titik center, sehingga ketiga spesies dapat hidup untuk jangka waktu lama dengan stabil. Saat parameternya ad < bc maka ruang fasenya bersifat spiral tak stabil sehingga saat kondisi ini spesies x mengalami kepunahan, sedangkan spesies y dan pemangsa z memiliki laju populasi stabil periodik. Sedangkan saat ad < bc maka ruang fasenya bersifat spiral stabil.namun dalam kondisi ini spesies y mengalami kepunahan sedangkan spesies x dan pemangsa z memiliki populasi stabil