LOGARITMA
(
)
(
0
)
,
0
:
,
1
0
,
1
,
0
:
,
log
≥
∉
≠
≠
≥
∉
≠
≠
x
negatif
bilangan
x
x
maka
a
dan
a
negatif
Bilangan
a
a
a
maka
syarat
x
a( )
(
)
( )
( )
( )
( )
( )
( )
( )
( )
r
s
n
m
a
b
b
a
sehingga
b
a
a
F
x
a
F
x
F
m
n
a
sehingga
b
m
n
b
maka
x
x
x
f
Jika
b
b
b
f
a
f
b
a
f
e
e
d
c
b
b
f
a
f
b
a
f
b
n
m
b
maka
x
x
f
Jika
b
b
b
n
b
c
b
f
a
b
maka
c
b
x
f
t
dan
t
dan
b
a
b
x
x
maka
c
b
c
b
x
dan
x
akar
akar
mempunyai
c
b
c
b
c
x
b
x
a
b
a
c
b
s b m a n m r m b n a a n a a a a n a a d c b a a n m a g a a a n a g MAKS b a g g t t a a b a a a a a a c a r n r b n a a m m n⋅
=
⋅
=
⇒
=
−
=
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
⇒
=
−
=
=
+
=
⋅
=
⋅
⋅
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛ +
=
=
+
=
≠
≥
=
=
−
=
−
+
=
⋅
=
+
+
=
⇒
=
⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ −log
log
.
13
:
.
12
1
)
(
log
:
log
log
.
11
:
log
2
1
log
)
(
.
17
log
log
.
10
log
log
log
log
log
.
9
log
log
.
8
:
,
log
)
(
.
16
log
2
1
log
.
7
log
log
.
6
2
log
log
1
log
.
5
:
log
log
)
(
.
15
1
0
log
log
log
.
4
10
log
log
:
log
.
3
log
log
log
.
2
0
log
log
.
14
log
.
1
log log 2 2 1 2 1 21
EKSPONEN
( )
( )
( )
( )
a
c
x
x
c
g
b
g
a
b
x
b
a
y
x
a
a
eksponen
Persamaan
a
dengan
x
g
x
f
a
dengan
x
g
x
f
x
g
x
f
a
a
a
a
Jika
a
a
a
a
a
a
a
a
a
a
b
a
ab
a
a
a
g x x a x y x x g x f x g x f n m n m n n n m n m n m n m n n n n m n mlog
0
log
:
1
0
)
(
)
(
*
1
)
(
)
(
*
)
(
)
(
.
5
.
9
.
4
1
.
8
.
3
1
.
7
:
.
2
.
6
.
1
2 1 2 2 ) ( ) ( ) ( ) ( 0=
+
⇒
=
+
+
=
⇒
=
=
⇒
=
<
<
<
>
>
=
⇒
=
>
=
=
=
=
=
=
=
⋅
− ⋅ − +y
( )
(
)
(
x
n
)
y
kiri
ke
n
x
y
kanan
ke
a
x
y
bawah
ke
x
a
y
atas
ke
satuan
n
digeser
x
y
grafik
Jika
a a n a n a a+
=
⇒
−
−
=
⇒
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⇒
−
=
⇒
−
=
log
log
log
log
log
1
,
log
>
=
x
a
y
a(
1
,
0
)
1
,
log
<
=
x
a
y
aMAAN
PERTIDAKSA
Pertidaksa
maan
h
arg
a
mutlak
a x f a b x f x f a atau a x f a x f a x f a a x f b a < ⇔ < < < − < ⇔ > < < ⇔ < ) ( 1 ) ( log ) ( ) ( ) ( ) ( ) (
(
) (
)
y x y x y z z x y x y x y x y x y x x x memenuhi yang x a h ada tidak x R x maka x b x a x b x a x a x a x x x x untuk x x x untuk x x x + ≤ − − + − ≤ − = ⋅ + ≤ + = ⇒ ≤ ⇒ ∈ ≥ + ≤ + ⇔ + ≤ + ≤ ⇔ ≤ − = ⇒ ≤ = ⇒ ≥ = . 11 . 10 . 9 . 8 0 0 . 7 arg . 6 0 . 5 2 2 . 4 . 3 0 0 . 2 . 1 2 2 2 2 2 y a a maka a y x a a maka a b ax syarat eksponen Bentuk c b ax an penyelesai x g x f c b ax umum Bentuk maka x g x f dan a Jika c a maka c b b a x g x f b a b a maka x g x f dan a Jika b a maka b a untuk x g x f b a maka b a untuk b a maka x g x f dan a Jika R c untuk c b c a b a x g x f c untuk bc ac b a maka x g x f dan a Jika c untuk bc ac b a aritma Bentuk sifat Sifat b syarat b a negatif bilangan y f y f x negatif bilangan x x syarat y f x f syarat x f y x y x a a a a a a a a x ⇒ < < < > ⇒ > > ≥ + > + ≥ > + ≥ < < > > > ≤ > ⋅ ⇒ > ≥ < < < < ≤ > > > ≤ > ∈ + > + ⇔ > ≥ < < ⇔ > ≥ > > > ⇔ > − ≠ ∉ ≠ ≠ ∉ ≠ > : 1 0 : 1 0 : : * : ) ( ) ( : * : ) ( log ) ( log 1 0 : , ) ( ) ( 0 0 : ) ( log ) ( log 1 0 : ) ( ) ( : : ) ( log ) ( log 1 ) ( ) ( 0 : ) ( log ) ( log 1 0 : log * : * 0 ) ( , 0 ) ( 1 , , 0 ) ( log 0 ) ( ) ( 2 2 2 2 2 SNMPTN’081. Pertaksamaan mempunyai penyelesaian…….. (A) x (B) x (C) x (D) x (E) JAWAB (A):
EINSTEIN SOLUTION : (A+B)(A-B) 0 (5x + 14)(-x – 16) 0 ……… A
kuadrat
persamaan
akar
akar
Sifat
−
:
,
0
:
2 21
dan
x
akar
akar
persamaan
ax
bx
c
maka
berlaku
x
Jika
−
+
+
=
(
)
(
)
[
]
(
)
(
)(
)
(
)
(
)
(
)
(
)
( )
(
)
real akar memiliki tidak D x x sama akar memiliki D berlainan yang real akar dua memiliki D rasional akar memiliki k D real akar memiliki D D N DISKRIMINA ac b D ditulis dapat a ac b b x rumus dengan sempurna kuadrat pers membentuk an memfaktork cara dengan an diselesaik dapat R c b a dengan a dengan c bx ax a b x x syarat x x sama akarnya kedua Bila c syarat akarnya satu salah Bila c a syarat x x an berkebalik saling akar akar Bila b syarat x x berlawanan saling akar akar Bila x x x x x x a ac b x x x x x x x x ac b D dengan a D x x x x x x x x x x c b x x a D b x x a c x x a b abc x x a b x x ⇒ < = ⇒ = ⇒ > ⇒ = ⇒ ≥ − = ⇒ − ± − = ∈ ≠ = + + − = = ⇒ = = ⇒ = = ⇒ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = − = ⇒ − = − + = + − = + + − = − − = = − − − + = + = − = − = − = + − = + 0 * 0 * 0 * * 0 * : 4 : 2 4 : . 3 . . 2 . 1 : , , 0 0 2 , * 0 , 0 * , 1 * 0 , * 1 1 . 10 2 . 5 . 9 4 . 4 2 2 . 8 1 . 3 . 7 . 2 3 . 6 . 1 2 1 2 2 2 2 , 1 2 2 1 2 1 2 1 2 1 2 2 1 2 2 2 1 2 2 2 1 2 2 2 2 2 1 2 2 2 1 2 2 2 1 4 2 4 1 2 2 1 2 2 1 2 2 1 2 2 1 4 2 4 1 2 1 2 2 2 2 1 2 1 3 3 3 2 3 1 2 1(
k)
ac kb berlaku pembanding ta kons k ana kx x a h sehingga sedemikian x dan x akar memiliki c bx ax kuadrat Persamaan 2 2 2 1 2 1 2 1 : tan dim arg 0 * + = = = = + +(
n a)
dengan D b ac D akar selisih maka n x dan x akar mempunyai c bx ax kuadrat Pers 4 , 0 . * 2 2 2 1 2 − = ⋅ = + = + +(
PKB
)
Baru
Kuadrat
Persamaan
0
2+
bx
+
c
=
x
a
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
0 0 . 10 0 2 0 1 1 . 9 0 2 0 . 8 0 0 . 7 0 0 . 6 0 3 0 . 5 0 2 0 . 4 0 0 . 3 0 0 1 1 . 2 0 0 . 1 2 2 2 2 1 2 1 2 2 2 2 2 2 2 2 1 2 2 2 1 2 2 1 2 2 2 1 2 2 2 1 3 3 3 2 2 2 3 1 2 2 2 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 2 2 1 = − − + = + + ⋅ + − = + − − = + + − = + − − = + + − = + + + + = + + − − − = + − + − = + + + + − = + − − = + + − = + − − = + + − = + − = + + − − − = + + = + + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − = + + = + + − bc x c ab x a adalah c bx ax dari x x dan x x akarnya akar yang PKB a x ac b x c adalah c bx ax dari x dan x akarnya akar yang PKB ac x ac b acx adalah c bx ax dari x x dan x x akarnya akar yang PKB c k x b k x a adalah c bx ax dari dari kurangnya k k x dan k x akarnya akar yang PKB c k x b k x a adalah c bx ax dari dari lebihnya k k x dan k x akarnya akar yang PKB c x b abc x a c bx ax dari x dan x akarnya akar yang PKB c x ac b x a adalah c bx ax dari x dan x akarnya akar yang PKB c bx ax adalah c bx ax dari x dan x berlawanan akarnya akar yang PKB a bx cx adalah c bx ax dari x dan x kebalikan akarnya akar yang PKB ck kbx ax adalah c bx ax dari kx dan kx kali k akarnya akar yang PKB(
) (
)
0 2− + + ⋅ =−akarnyaα danβ adalah x α β x α β akar yang kuadrat Persamaan 2 2 2 2 1 1 2 1
:
c
x
b
x
a
c
x
b
x
a
r
ganda
Kuadrat
+
+
+
+
=
(
)
(
b
b
a
c
a
c
)
r
D
k
r
D
r
a
h
oleh
ditentukan
akarnya
a
h
ana
akar
akar
mempunyai
yang
ganda
kuadrat
Pers
=
+
+
−
−
⇒
−
1 2 2 1 1 2 1 22
4
arg
arg
dim
,
.
1. Akar-akar dari 3x2 – 2x – 5 = 0 adalah x
1 dan x2. Persamaan kuadrat baru yang akar-akarnya 4x1 dan 4x2 adalah... A. 5x2 – 10x – 4 = 0 B. 3x2 – 8x – 80 = 0 C. 3x2 + 4x – 120 = 0 D. 5x2 – 4x – 10 = 0 E. 5x2 – 4x – 12 = 0 Einstein Solution PKB : 3x2 – 2(4)x – 5(4.4) =0 Jawab : B UMPTN’99 5
GRADIEN
(
)
(
)
(
a b)
dengan gradien m y b m(
x a)
melalui garis Pers x x y y m y x dan y x melalui garis Gradien m c mx y garis suatu Gradien b a m c by ax garis suatu Gradien a m atau x y m garis suatu Gradien − = − ⇒ − − = ⇒ ⇒ + = − = ⇒ = + + = = , . . 2 , , * * 0 * tan * . 1 1 2 1 2 2 2 1 1(
)
(
)
. dim 1 tan : , . 6 0 : * : * : * : 0 0 . . 5 1 : , : , : . . 4 , , . . 3 2 1 2 1 2 1 2 1 2 2 1 1 1 2 1 1 2 1 2 2 1 1 garis kedua oleh dibentuk yang sudut adalah ana m m m m mak bebas n berpotonga garis Dua bq aq bila n berpotonga r c q p b a bila berimpit r c dan q p b a bila sejajar akan r qy px dan c by ax garis Pers m m bila l g garis m m bila l garis sejajar g garis c x m y l c x m y g garis dua Pers x x x x y y y y y x dan y x titik melalui garis Persα
α
+ − = ≠ − = = ≠ = = + + = + + − = ⋅ ⊥ = + = ⇒ + = ⇒ − − = − − ⇒ y a xx
y
4 3 Pers.Grs : 3x + 4y = 12 Einstein SolutionPers. Grs yg tegak lurus 3x + 4y = 12 mel (0,0) adalah…4x – 3y = 4.0 – 3.0 = 0 Pers. Grs yg sejajar 3x + 4y = 12 mel (0,0) adalah…3x + 4y = 3.0 + 4.0 = 0
9
GARIS
PERSAMAAN
(
,)
(
,)
:.
1 Persamaan garis melalui duatitik K x1 y1 dan L x2 y2
(
)
(
)
(
)
3 3 3 3 2 1 2 2 2 1 1 1 2 2 1 1 3 3 : _ : , , , . . 2 By Ax By Ax Hasil By Ax By Ax B y y y x A x x y x y x L titik dan y x K titik melalui yang garis dan y x M titik melalui garis Pers + = + + = + = − ⇒ = − ⊥(
)
(
)
(
)
(
)
(
)
(
)
(
) (
) (
)
(
)
(
)
(
)
(
)
0 0 0 0 0 . 10 : , , , , , . 9 : , 0 0 . 8 0 , . 7 : : : . 6 0 , , 0 . . 5 0 , . . 4 0 , . . 3 1 2 1 3 1 2 1 3 3 3 2 2 1 1 2 2 2 1 2 1 2 2 1 1 1 1 1 2 2 1 1 2 1 2 2 1 2 2 1 1 = + + + ⇒ − = + − + ⇒ − = + + + ⇒ − = + + − ⇒ − = + + − − = − − + − = = + + = + + + + + = ⇒ = + + − − = − − = + = + = = + ⇒ − = − ⇒ = + + ⊥ + = + ⇒ = + + c k y b ax bawah ke satuan k c k y b ax atas ke satuan k c by k x a kiri ke satuan k c by k x a kanan ke satuan k digeser c by ax garis Jika y y y y x x x x jika garis satu dalam terletak y x y x y x titik buah Tiga b a c c d adalah c by ax dengan c by ax antara sejajar yang garis buah dua Jarak b a c by ax d c by ax garis dengan y x A titik Jarak m m c m c m y dan m m c c x adalah c x m y h garis dan c x m y g garis potong Titik Hess Hukum ab by ax b dan a melalui garis Pers Ab Ba Ay Bx C By Ax b a melalui garis Pers Bb Aa By Ax C By Ax sejajar b a melalui garis Pers 1 y 1 x 2 x y2 Q y x2 1 = x1 y2 =P(
P Q)
Bx yA = + − Hasil pers yang aksud Ay Bx
(
P Q)
A x x B y y − + = = − = − : dim . 2 1 2 1
Persamaan garis melalui A(9,3) dan B(6,0) adalah……
A. Y = 6x – 9 B. Y = 3x + 6 C. Y = x - 6 D. Y = 9x – 6 E. Y = 6x + 3 EINSTEIN SOLUTION X y 9 3 6 0 3y = 3x + (0-18) Y= x - 6 …jawab : C Einstein Solution
Pers grs melalui (A,B)&(a,b) Ax By
ax by
(A-a)y=(B-b)x + (A.b – B.a)
7
KUADRAT
PERSAMAAN
DAN
GRAFIK
c bx ax x f fungsi Grafik ( )= 2+ + : . 1 Pengaruh faktor a⇒ putar kurva900 ke−kiri
a
>
0
a < 0 : . 2 Pengaruh faktor b y y y x x x b > 0 b < 0 b=0 y y y x x x b < 0 b > 0 b=0 0 : * 0 : * 0 : * = < > c maka koordinat pangkal melalui kurva Bila c maka x sumbu bawah di y sumbu memotong kurva Bila c maka x sumbu atas di y sumbu memotong kurva Bila(
c)
adalah y sumbu dengan potong Titik a ac b a b parabola Puncak y y maka a Jika y y maka a Jika ekstrem nilai diesbut a D a ac b y x f penyebab simetri sumbu disebut a b x a ac b a b x a x f ditulis dapat c bx ax x f f negatif selalu x f x sumbu bawah di grafik semua negatif definit disebut x f maka D dan a Jika positif selalu x f x sumbu atas di grafik semua positif definit disebut x f maka D dan a Jika ac b D maksimum ekstrem imum ekstrem ekstrem , 0 * 4 4 , 2 * 0 0 * 4 4 4 * ) ( 2 * 4 4 2 ) ( : ) ( * ) ( ) ( 0 0 * ) ( ) ( 0 0 * 4 * 2 min 2 2 2 2 2 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − ⇒ = < ⇔ = > − = − − = ⇒ − = − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = + + = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < < ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ < > − = y x y x ××
× y x 0 > c 0 = c 0 < c SNMPTN’081. Rumus fungsi untuk grafik di bawah adalah … .
-2 0 4 8 x y A. y = 8 – 2x – x2 B. y = 8 – 2x + x2 C. y = 8 + 2x – x2 D. y = 8 + 2x + x2 E. y = 8 – 3x + x2 JAWAB: C 8 2 ) 4 )( 2 ( 4 . 2 8 + − =− 2 + + − = x x x x y Einstein Solution
RI
TRIGONOMET
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
0 0)
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 tan 270 cot cot 270 tan sin 270 cos cos 270 sin cot 180 cot tan 180 tan cos 180 cos sin 180 sin : 270 180 : . 3 tan 90 cot cot 90 tan sin 90 cos cos 90 sin cot 180 cot tan 180 tan cos 180 cos sin 180 sin : 90 180 : . 2 tan 90 cot cot 90 tan sin 90 cos cos 90 sin : 90 : . 1 cos 1 cot * sec 1 tan * cos sin tan * cos 1 sin * sin 1 cos * 1 cos sin * cot sec cos * tan * cos * sin * a a a a a a a a a a a a a a a a a atau a sudut untuk Kuadran a a a a a a a a a a a a a a a a a atau a sudut untuk Kuadran a a a a a a a a a sudut untuk Kuadran a ec a a a a a a a a a a a a y x r dengan y x a x r a y r a ec x y a y x a r y a + = − + = − − = − − = − + = + + = + − = + − = + − + ΙΙΙ − = + − = + − = + + = + − = − − = − − = − + = − + − ΙΙ + = − + = − + = − + = − − Ι = + = + = − = − = = + + = = ⇒ = ⇒ = = = = a r y x 9(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
α α α α α α α α α α α α α α α α α α α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α β α α α π 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 min sin 2 1 1 cos 2 sin cos cos cos sin 2 sin : . 10 1 tan tan 2 2 tan sin 2 1 1 cos 2 sin cos 2 cos cos sin 2 2 sin : . 9 cos cos cos sin 2 cos cos cos cos 2 sin sin sin cos 2 sin sin cos sin 2 : . 8 sin sin 2 cos cos cos cos 2 cos cos sin cos 2 sin sin cos sin 2 sin sin : . 7 tan tan 1 tan tan tan tan tan 1 tan tan tan sin sin cos cos cos sin sin cos cos cos sin cos cos sin sin sin cos cos sin sin : . 6 min ) ( ) ( tan , cos ) ( sin cos ) ( . 5 : cos sin . 4 − = − = − = = − = − = − = − = = − − + = − − + + = − − + = − + + = − + − = − − + = + − + = − − + = + + − = − − + = + + = − − = + − = − + = + − + + − = ⇒ + = = + = + − = + + = + − = ⇒ + = + = + = an pengembang Rumus kembar sudut Untuk berbeda sudut dengan ri trigonomet fungsi Perkalian berbeda sudut dengan ri trigonomet Fungsi sudut dua untuk selisih dan Jumlah c k imum x f c k maksimum x f a b dan b a k dengan c x k x f ditulis dapat c x b x a x f Bentuk P Periode c A y c A y c px A y atau c px A y Bentuk imum maksimum(
) (
) (
)
: . 15 2 sin sin sin . 14 cos 2 cos 2 cos 2 : cos .13 sin sin sin : sin . 12 1 3tan tan tan 3 3 tan cos 3 cos 4 3 cos sin 4 sin 3 3 sin : 3 . 11 2 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 3 3 3 ri trigonomet fungsi Grafik c b a s dengan c s b s a s s A bc B ac C ab L C ab b a c B ac c a b A bc c b a inus Aturan C c B b A a us Aturan rangkap Sudut + + = ⇒ − − − = = = = Δ − + = − + = − + = = = − − = − = − = α α α α α α α α α α α y y sin= x 1 0 0 900 180 0 2700 3600 – 1 y 1 y cos= x 0 0 902 1800 2700 3600 x – 1 y =ytan x 00 90 0 1800 2700 3600 x A B C a b c x 11
DASAR
MATEMATIKA
FUNGSI
Bentuk linear: a b x x f b ax x f( ) = + ⇒ ′( ) = − Bentuk pecahan:d
cx
b
ax
x
f
+
+
=
)
(
a
cx
b
dx
x
f
−
+
−
=
−1(
)
Bentuk eksponen: p a px a x x x f a x F x x f a x f 1 1 1 log ) ( ) ( log ) ( ) ( = ⇒ = = ⇒ = ′ − −Bentuk logaritma: f(x) = alogx ⇒ f −1(x) =ax Bentuk akar pangkat:
a b x x f b ax x f( )= n + ⇒ −1( ) = n − Bentuk fungsi kuadrat:
a
b
a
D
x
a
x
f
c
bx
ax
x
f
2
4
1
)
(
)
(
2 1⎟
−
⎠
⎞
⎜
⎝
⎛ +
±
=
⇒
+
+
=
−(
)
( )
(
g
x
)
h
x
maka
f
x
h
(
g
( )
x
)
f
r
qx
px
b
ax
f
x
f
maka
r
qx
px
b
ax
f
a
b
r
qx
px
x
g
Maka
r
qx
px
x
fog
b
ax
x
f
Jika
a
b
q
px
x
g
Maka
q
px
x
fog
b
ax
x
f
Jika
fungsi
Komposisi
1 2 2 2 2)
(
:
)
(
)
(
:
,
)
(
)
(
:
)
(
)
(
)
(
:
)
(
)
(
:
−=
=
+
+
=
+
=
+
+
=
+
−
+
+
=
+
+
=
⇒
+
=
−
+
=
+
=
⇒
+
=
1. F(x) =3
1
,
1
3
3
2
≠
−
−
x
x
x
, rumus F-1(x) adalah … A. 2 x 3 3 x − − B. x 3 2 3 x − + C. 3 x 2 1 x 3 + − D. 1 x 2 3 x + − E. x 3 2 3 x − − Einstein Solution Jawab : A UMPTN’99DERET
DAN
BARISAN
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
baru n ke suku U baru suku banyaknya n baru n ke suku jumlah S baru beda b denngan k n n n b n U n S b n U U k b b maka aritmetika deret suku dua diantara suku k disisipkan Bila d c d atau c a b atau e a d b c a simetrisny suku rata rata tengah suku berlaku aritmetika deret membentuk e dan d c b a Jika kelipa memiliki aritmetika deret membentuk yang siku siku Segitiga n p q n p S q pn U linear n ke Suku p b p q pn U qn pn S kons pa kuadrat aritmetika deret pertama suku Jumlah m m k k b m n n k U U m n k U tersebut suku dari beda maka k adalah n dan n ke suku jumlah dan k adalah n ke suku diketahui Bila U U b geometri deret dan aritmetika deret untuk dipakai S S U U a U diketahui tidak terakhir suku jika b n a n diketahui terakhir suku jika U a n S n n a U U U U U U n a b a b a b a a umum Bentuk Aritmetika Deret A n n n n n n n n n n n n n n n n n t n n n n − = ′ = ′ − = ′ = ′ − + = ′ ′ − + = ′ ′ − = = ′ + = ′ + = + = + = + = − = − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + = ⇒ + = − = − + = ⇒ + = − − = ⇒ = + = + = = − − − = ⇒ − − = + = ⇒ − + = ⇒ + = − + = − + + + + − ; ; ; : 1 * 1 2 2 * 1 * 1 * : . 10 2 2 2 2 : , , , , , : 5 , 4 , 3 tan . 9 2 2 : . 8 2 * 2 * : tan tan . 7 2 2 : , . 6 . 5 1 . 4 2 . 3 1 2 . 2 1 . 1 , ... ... , 1 , ... ... , 3 , 2 , , : : . 1 1 2 2 2 1 2 1 2 3 2 2 1 1 1 2 3 2 1 1 1 2 1 2 1 4 3 2 1 3 2 1 13 -115
(
)
(
)
(
)
(
)
an perbanding selisih an perbanding jumlah pertama jatuh s jatuh bola asan l Panjang samasisi segitiga keliling deret rasio samasisi segitiga luas deret Rasio ar bujursangk keliling deret rasio ar bujursangk luas deret rasio sangkar bujur Deret b b b b b aritma Deret r atau r r jika divergen jumlah mempunyai Tak r r jika it memiliki konvergen jumlah Mempunyair a S ar ar ar a hingga tak geometri Deret e c d c a b e a c d b c a simetrisny suku suku kali hasil dengan sama tengah suku Kuadrat berlaku maka geometri deret adalah e dan d c b a Jika k k r k n k n ke suku diketahui Bila S S U r untuk r r a S U a U r untuk r r a S U U r ar U rasio r awal suku U a pertama suku n jumlah S tengah suku U n ke suku U Jika U U U U U ar ar ar ar a umum Bentuk b a a a a a n n n n n n n n t n n n n n n n t n n × = ⇒ = = = = = + + + + > − < ⇒ > < < − ⇒ < − = ⇒ ⋅ = ⇒ ⋅ = ⇒ ⋅ = ⇒ ⋅ = − = ⇒ = = − − = < ⇒ − − = = > ⇒ − − = = = = = = = = − = − − − − int . 10 2 1 * 4 1 * . 9 2 2 1 * 2 1 * : . 8 log ... ... log log log log : log . 7 1 1 1 : * 1 1 1 : lim / * . 6 1 ... ... , , , , . 5 : , , , , , . 4 . 3 1 1 1 1 1 1 ; ; ; ; : . 2 , ... ... , , ... ... , , , , : . 1 4 3 2 ~ 3 2 2 2 2 2 1 2 2 2 1 1 1 1 1 1 4 3 2 1 1 21. Sebuah bo la jatuh da ri k etinggian 5m , da n memantul k embali de ngan k etinggian 43kali t inggi
sebelumnya. Pemantulan semacam ini berlangsung terus hingga bola berhenti. Jarak seluruh lintasan bola adalah … . A. 16 m B. 18 m C. 20 m D. 21 m E. 35 m
Einstein Solution Jawab : E
STATISTIK
(
)
( )
sama yang bagian menjadi terurut data membagi Kuartil positif genap n untuk x x Me positif ganjil n untuk x Me diurutkan telah yang tengah data Me Median n x f x atau n x x mean rata Rata tunggal Data A n n n 4 : . 3 2 1 2 1 . 2 . 1 : . 2 2 ⎟⎠ ⇒ ⎞ ⎜ ⎝ ⎛ + + = ⇒ + = ⇒ = = ⇒ −∑
∑
● ● ● Q1 Q2 Q3Q1 =kuartil bawah;Q2 =kuartiltengah
(
median)
;Q3 =kuartil atas muncul sering yang data adalah Modus : . 4(
datatersusun)
erval Data B. int(
)
(
)
kelas erval banyaknya jangkauan kelas erval panjang kelas bawah batas kelas atas batas kelas imterval tengah titik kelas bawah tepi kelas atas tepi kelas erval panjang kelas atas batas kelas atas tepi kelas bawah batas kelas bawah tepi CATATAN data banyaknya n median kelas frekuensi me F frekuensi jumlah F median kelas erval panjang P median kelas bawah tepi Tb median Me dengan P me F F n Tb Me f d f m x simpangan m x d sementara hitungan rata rata m n d m x rata rata simpangan f x f x mean rata Rata i i i i i i i i int int * * int * 5 , 0 * 5 , 0 * : ; ; ; int ; ; : 2 . 2 ; . 1 2 1 1 = + = − = + = − = = = = = = = ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + = + = = − = − = + = ⇒ − ⇒ −∑
∑
∑
∑
∑
mula mula data banyaknya n ditambahka yang nilai q n ditambahka yang data banyaknya p baru rata rata x lama rata rata x dengan b − = = − = − = ; ; ; : 15 X _ =( )
( )
( )
( )
(
)
( )(
)
(
)
(
)
(
)
(
n p)
pq x n x data n penguranga p n pq x n x data penambahan data sekelompok dari rata Rata baru data banyaknya m lama data banyaknya n semula rata rata x sekarang rata rata x baru data nilai x m x x n x x maka x baru rata rata didapat hingga m sejumlah x baru data ditambah kemudian x rata rata dengan n ada Bila Q Q Qd kuartil semi jangkauan kuartil simpangan terkecil data terbesar data jangkauan n n S n S n S baku simpangan dari kuadrat sampel iansi S tersusun data untuk n x x f S tunggal data untuk n x x S dar s deviasi baku deviasi baku simpangan n x x Md deviasi mean rata rata deviasi simpangan rata rata Simpangan C Q kelas frekuensi Q f berada Q kelas sebelum kelas kelas frekuensi jumlah s f k ke kuartil kelas bawah tepi Tb k ke kuartil Q P Q f s f n k Tb Q Kuartil kelas erval panjang P sesudahnya kelas frekuensi dengan us kelas frekuensi selisih S sebelumnya kelas frekuensi dengan us kelas frekuensi selisih S us kelas tepi Tb us Mo P s S Tb Mo Modus b b i i gabungan i i i i k k k k k k i − − = + + = − = = − = − = = − + = − − − = ⇒ − = + + = = ⇒ − = ⇒ − = = = − = ⇒ = − = − = − = − = − = ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ − + = ⇒ = = = = = ⎟⎟ ⎠ ⎜⎜ ⎝ + + = ⇒∑
∑
∑
∑
∑
* * : . 6 ; ; ; ; : , . 5 2 1 . 4 . 3 var tan . 2 . 1 : . ; ; ; 4 . 4 int mod mod ; mod ; mod . 3 0 1 1 0 1 1 1 1 1 0 1 3 2 1 2 2 2 1 2 2 2 2 2 1 2 1(
n n n)
x x n x n x n P Q x x x x n n gabungan rata rata an Perbanding gab gab ... ... ... ... . 7 3 2 1 3 3 2 2 1 1 1 2 2 1 + + + = + + + = − − = −Soal berhub. Dgn pemilihan jabatan ketua,wakil atau juara I,II.. )! ( ! r n n
P
nr = − Permutasi siklis(melingkar)=(n-1)! Soal berhub. Dgn pengambilan bola,kartu, pelemparan mt uang atau pemilihan wanita. )! ( ! ! r n r nC
nr = −Mata Uang pelemparan n kali.Total 2n dgn r jumlah gambar. Permutasi Kombinasi
PELUANG
Peluang Kejadian P(A) = 1 - P(A’) Saling Lepas P(AUB)=P(A)+P(B) Saling Bebas P(A∩B)=P(A).P(B) Bersyarat P(A/B)= ) ( ) ( B P B A P ∩ Kejadian MajemukKOMBINASI
PERMUTASI&
(
)
(
)
(
)
(
)
(
)
! ! ! , . 2 ! 1 : * ... ! ! ! ! . , , dim sec * ! ! , tan , * . 1 3 2 1 3 2 1 k k n n C k n C Kombinasi n lingkaran sebuah pada berbeda yang objek n penyusunan cara Banyaknya n n n n P dst sama unsur n sama unsur n sama unsur n ada ana bersamaan ara semuanya diambil yang unsur n unsur dari P permutasi Banyaknya k n n P k n P berbeda yang unsur n dari diambil yang unsur k dari mungkin yang berbeda yan uru semua adalah n k untuk unsur n dari unsur k Permutasi n k n k − = = − × × × = − = = ≤ 17LIMIT
aljabar fungsi Limit[
]
[
]
[
]
[
]
r qx px r bx ax r qx px r bx ax dengan kalikan r qx px c bx ax tertinggi pangkat x dengan suku g ma g ma bagilah bx ax x f x f x g x f x g x f x g x f g f x f x g x f g f x f x g x f g f x f x f k x f k maka x g dan ada x f Jika ta kons k k k x jawaban p a jika jawaban p a jika a q b jawaban p a Jika b dan a nilai Perhatikan r qx px c bx ax akar Bentuk penyebut tertinggi pangkat adalah m pembilang tertinggi pangkat adalah n b a jawab m n jika jawab m n jika jawab m n jika bx ax pecahan Bentuk x m n x n x m x x x x x x x x x x x x x x x x x x n x x m n x + + + + + + + + + + + + − + + − ⇒ + + ⎥⎦ ⎤ ⎢⎣ ⎡ = = ⋅ = ⋅ − = − + = + = = ⇒ = = + > − < − = + + − + + = < > ⇒ + + → → → → → → → → → → → → → → → → → → → → → → → → 2 2 2 2 2 2 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ! ~ ~ 2 2 ~ ~ : sin sin ... ... ... ... ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( : , ) ( ) ( tan 0 1 ~ ). 3 ( ~ : ) 2 ( 2 : ). 1 ( : . 2 : 0 : ~ : ... ... ... ... ... ... : . 1lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
lim
(
)
(
)
n menguraika dengan selesaikan atau atau misalkan tentu tak dicari yang jawaban merupakan b atau a atau b a misalkan tertentu ya hasi jika fungsi ke a kan substitusi x g x f c b q p q p a cx q bx p ax maka q p jika m n maka q p jika maka q p jika x m x m x n x n r c r qx px c bx ax TERTENTU BILANGAN MENDEKATI LIMIT x x q p p p x m m n n x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⇒ + + − + = − − + < = = > ⇒ + + + + = + + + + + + → → + + → − − → ~ 0 ~ ~ 0 0 0 0 : ln ) ( ) ( . 3 ~ 0 ... ... ... ... . 2 ... ... ... ... . 1lim
lim
lim
lim
0 0 1 1 1 1 2 1 1 2 0 1 1 0 SNMPTN’08 1. = A. -1 B. E.1 JAWAB: E EINSTEIN SOLUTION = = 1 . 1 = 1 SNMPTN’08 2. =…… A. 8 C. D. E. 0 JAWAB: C EINSTEIN SOLUTION { = = = 19(
TURUNAN
)
L
DIFERENSIA
(
)
h
x
f
h
x
f
x
f
h)
(
)
(
lim
0−
+
=
′
→(
)
2 1 1 0 tan : . 1 V V U V U y V U y V U V U y V U y V U y V U y V U y V U y x n a y x a y x n y x y y kons c c y aljabar fungsi Turunan n n n n ′ − ′ = ′ ⇒ = ′ + ′ = ′ ⇒ ⋅ = ′ − ′ = ′ ⇒ − = ′ + ′ = ′ ⇒ + = = ′ ⇒ = = ′ ⇒ = = ′ ⇒ = = − − ax ax x x a e a y e y e y e y a n x y x y x a y ax n y x y x n y aritma dan eksponen fungsi Turunan = ′ ⇒ = = ′ ⇒ = = ′ ⇒ = = ′ ⇒ = = ′ ⇒ = 1 1 log 1 1 1 log . 2 ax ec a y ax y ax a y ax y ax a y ax y ax a y ax y x x y x y x x ec y x ec y x ec y x y x y x y x y x y x y x y ri trigonomet fungsi Turunan 2 2 2 2 cos cot sec tan sin cos cos sin tan sec sec cot cos cos cos cot sec tan sin cos cos sin . 3 − = ′ ⇒ = = ′ ⇒ = − = ′ ⇒ = = ′ ⇒ = ⋅ = ′ ⇒ = ⋅ − = ′ ⇒ = − = ′ ⇒ = = ′ ⇒ = − = ′ ⇒ = = ′ ⇒ =(
)
U ec U y U y U U y U y U U y U y U U y U y U e y e y U a n a y a y U U y U n y U U n y U y x iabel mengganti untuk U menjadi isalkan ya komposi satu salah ana fungsi beberapa dari terdiri yang komposisi merupakan mejemuk fungsi majemuk Fungsi U U U U n n 2 2 1 cos cot sec tan sin cos cos sin 1 1 var dim sin dim , : . 4 ′ − = ′ ⇒ = ′ = ′ ⇒ = ′ − = ′ ⇒ = ′ = ′ ⇒ = ′ ⋅ = ′ ⇒ = ′ = ′ ⇒ = ′ = ′ ⇒ = ′ ⋅ = ′ ⇒ = −(
)
: sin . 8 2 sin cos 2 sin cos cos . 7 2 sin sin 2 cos sin sin . 6 . 5 2 1 2 1 2 kurva ggung Garis bx bx b a n y atau bx bx b a n y bx a y bx bx b a n y atau bx bx b a n y bx a y d cx bc ad y d cx b ax y n n n n n n − − − − − = ′ = ′ ⇒ = = ′ = ′ ⇒ = + − = ′ ⇒ + + = y = f(x)g Persamaany−b =m
(
xgaris−a)
singgung kurva g:
(
a , b)
dengan gradien m= f′(x)= f′(a)(
)
(
)
⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ − = = ⇒ = = ⇒ = = ⇒ = = − ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ = = ⇒ = = ⇒ = = ⇒ = = + ′ = = ⇒ ′ = = = = = = ⎩ ⎨ ⎧ = ′′ = ′ ⎩ ⎨ ⎧ > ′′ = ′ = = ⎩ ⎨ ⎧ < ′′ = ′ = = ⇒ = < ′ ⇒ = > ′ ⇒ = = ′ 2 4 1 5 2 3 2 3 1 2 2 1 2 4 1 5 2 3 2 3 1 2 2 1 1 1 1 1 2 2 2 1 1 1 1 1 min min min min * * : min . 13 : , , , tan , tan : . 12 0 ) ( * * ) ( ) ( , : . 11 0 ) ( 0 ) ( min ) ( * 0 ) ( 0 ) ( ) ( * : . 10 ) ( , 0 ) ( * ) ( , 0 ) ( * , , 0 ) ( * : / . 9 c ab c a b a c a ab c a ab c b a c maks ab c a maks b a c a maks ab c a maks ab c b a imum dan maksimum Nilai V t d v d a S t d s d V maka waktu t jarak S kecepa V percepa a jika mekanika pada Turunan x f berubah tidak x x disekitar f bila x f fungsi belok titik merupakan x f x belok Titik x f x f bila x x di imum nilai mempunyai x f y Fungsi x f x f bila x x di maksimum nilai mempunyai x f y Fungsi fungsi suatu ekstrem Nilai turun x f y grafik maka x f Jika naik x f y grafik maka x f Jika stasioner titik y x titik maka m x f Jika fungsi suatu turun Naik( )
ab arsir di yang daerah maksimum Luas 41 . 14 ⇒( )
ab arsir di yang daerah maksimum Luas ⇒ 21 3 4 3 ab arsir di yang daerah maksimum Luas ⇒ ●(
x , y)
b a a − a b(
a ,b)
21 Einstein Solution Einstein Solution Einstein SolutionMATRIKS
(
)
(
)
q p b a r p c a y dan q p b a q r b c x maka r qy px c by ax v q s x u p r w d c c a maka MP MN s p d a r c q b maka MP MN x w v u M s r q p N d c b a A C B A sama kedua dan pertama matriks kolom banyaknya bila dilakukan dapat hanya matriks Perkalian sama ordo ber yang matriks matriks pada dilakukan dapat hanya matriks n penguranga dan n Penjumlaha sama seletaknya elemen belemen daan sama ordo memiliki bila sama dikatakan matriks Dua perkalian komutatif sifat berlaku tidak BA AB koefisien matriks q p b a r c y x q p b a ditulis dapat r qy px c by ax d b c a A a transposny matriks d c b a A an er dengan matriks invers memiliki tidak yang matriks adalah gular Matriks a c b d bc ad A A Invers bc ad A A A an er d c b a A p m p n n m t = = ⇒ = + = + ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ − − = − − = = = − − = = = ⇒ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = × ⇒ − − − ⇒ ≠ ⇒ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇒ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⇒ = + = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⇒ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − = = − = = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = × × × − , * , * ; ; . 10 : . 9 . . 8 . 7 . 6 . 5 . 4 0 min det sin . 3 1 . 2 det min det . 1 1(
D E F) (
A B C)
N f d c F g f b E i e a D i d b C h f a B g e c A dengan F E D C B A f g e d b a i h g f e d c b a N matriks i h g f e d c b a N B C A dan C A B maka C B A + + − + + = ⋅ ⋅ = ⋅ ⋅ = = ⋅ ⋅ = ⋅ ⋅ = ⋅ ⋅ = = ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ = = = = − − det ; ; , , ; ; ; det . 12 , . 11 1 1( )
( )
( )
A A A A B A AB an Deter t det det * det 1 det * det det det * : min . 13 1 = = ⋅ = −( )
( )
(
)
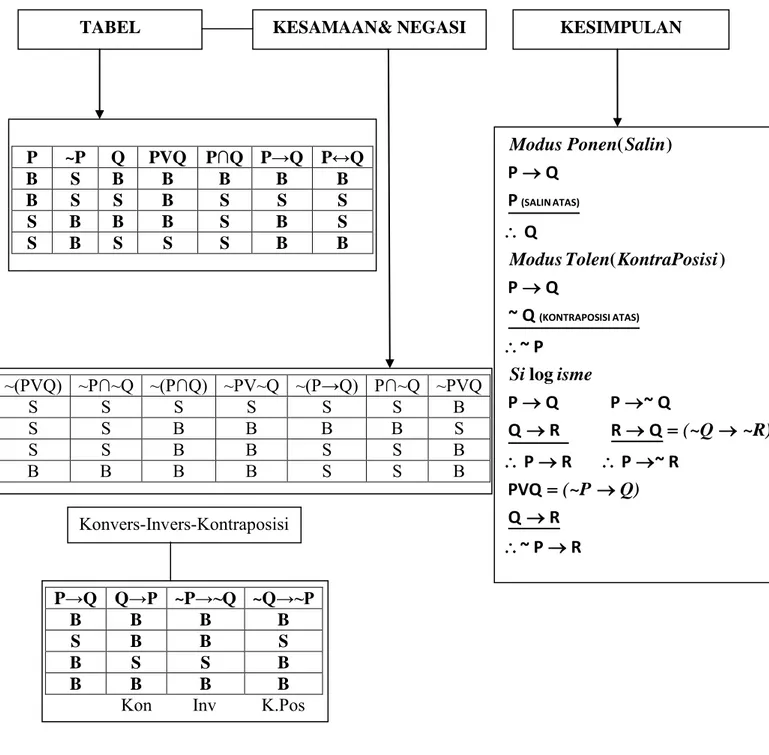
⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = = ⇒ = = = − − − − − 1 0 0 1 * * * . 14 1 1 1 1 1 I identitas matriks satuan matriks I dengan A B atau B A I AB A B AB A B ABt t t Sarrus caraLOGIKA MATEMATIKA P ~P Q PVQ P∩Q P→Q P↔Q B S B B B B B B S S B S S S S B B B S B S S B S S S B B ~(PVQ) ~P∩~Q ~(P∩Q) ~PV~Q ~(P→Q) P∩~Q ~PVQ S S S S S S B S S B B B B S S S B B S S B B B B B S S B R P ~ R Q PVQ R ~ P R P Q R R Q Q ~ P Q P P ~ Q ~ Q P Q P Q P ATAS) ISI (KONTRAPOS ATAS) (SALIN → ∴ → → = → ∴ → ∴ → = → → → → ∴ → ∴ → Q) (~P ~R) (~Q isme Si si KontraPosi Tolen Modus Salin Ponen Modus log ) ( ) (
TABEL KESAMAAN& NEGASI KESIMPULAN
P→Q Q→P ~P→~Q ~Q→~P
B B B B
S B B S
B S S B
B B B B
Kon Inv K.Pos Konvers-Invers-Kontraposisi