III. TEORI DASAR. Dasar dari metode gayaberat adalah hukum Newton tentang gayaberat dan teori

(1)

III. TEORI DASAR

3.1. Hukum Newton

Dasar dari metode gayaberat adalah hukum Newton tentang gayaberat dan teori medan potensial. Newton menyatakan bahwa besar gaya tarik menarik antara dua buah partikel yang mempunyai massa m1 dan m2 dengan jarak antara kedua titik

pusat partikel tersebut r adalah (Grant, 1965):

2 2 1 r m m G F  (1) dimana :

F = Gaya antara benda m1 dan m2

G = konstanta gayaberat = (6,672 x 10-11 m3/kg s2) r = jarak antara m1 dan m2

m1 F12 F21 m2

r

Gambar 6. Gaya tarik menarik antara dua benda m1 dan m2

Gaya persatuan massa dari m1 terhadap suatu partikel yang mempunyai jarak r

dari m1 disebut medan gayaberat dari partikel m1 yang besarnya:

r r m G r E() ₂1 ˆ (2)

(2)

Dalam kenyataannya bentuk bumi tidak bulat sempurna, tetapi berbentuk elipsoid (agak pepat pada kutubnya). Dengan demikian variasi gayaberat di setiap titik permukaan bumi dipengaruhi oleh 4 faktor yaitu:

1 Lintang 2 Topografi 3 Pasangsurut

4 Variasi rapatmassa bawah permukaan

3.2. Potensial Gayaberat

Suatu massa yang terdapat dalam sistem ruang tertentu akan menimbulkan medan potensial (skalar) disekitarnya. Medan potensial untuk gayaberat (gaya akibat tarik-menarik suatu massa) bersifat konservatif, artinya usaha yang dilakukan dalam suatu medan gayaberat tidak tergantung pada lintasan yang ditempuhnya, tetapi tergantung pada posisi awal dan akhir dan memenuhi persamaan berikut :

0 g dan g U     (3) Dimana : U = potensial skalar g= gayaberat (vektor)

Gaya yang timbul dapat diturunkan dari suatu fungsi potensial skalar U(x,y,z) berikut :









g



x y z



m z y x F r U , ,   , ,  , ,    (4)

Persamaan (3.4) dapat ditulis dalam koordinat bola menjadi :



,,





,,



g



r,,



m r F r U     (5)

Dari persamaan (3.5) dapat diperoleh bentuk persamaan potensial gayaberat :



r



Udr gdr U r r



         , , (6)

(3)

Dengan mensubstitusikan g m₂ r 

 

 _ _, maka Persamaan (6) dalam bentuk skalar menjadi : r m dr r m r U r           

_

  2 1 ) ( (7) 3.3. Pengukuran Gayaberat 1. Pengukuran absolut

Pengukuran absolut dilakukan di laboratorium-laboratorium, sukar untuk mendapatkan harga gayaberat absolut yang akurat, karena banyak kendala yang sangat mempengaruhi hasil pengukuran (Sarkowi, 2009). Oleh karena itu, pengukuran secara absolut jarang sekali dilakukan karena terlalu sukar dan melibatkan banyak faktor maupun alat. Cara pengukuran absolut yaitu pendulum, jatuh bebas, dan gravimeter.

2. Pengukuran relatif

Pengukuran relatif lebih umum dan mudah dilakukan, pada penelitian gayaberat. Pengukuran relatif dilakukan dengan membandingkan hasil pengukuran titik yang tidak diketahui nilai gayaberatnya dengan titik yang sudah diketahui yang telah diikat kepada titik-titik referensinya, misal Pastdam, IGSN, dan lainnya.

Gayaberat diukur berdasarkan adanya perbedaan sifat fisik massa yang berada diantara dua benda yang terpisah oleh jarak r. Dengan adanya rapat-massa yang berbeda menyebabkan harga gayaberat yang berbeda pada permukaan bumi.

(4)

Harga gayaberat rata-rata pada permukaan bumi dalam satuan SI adalah 9,8 m/s2. Satuan yang lebih kecil dinyatakan dalam µm/s2 atau g.u (gravity unit). Dalam satuan cgs, harga gayaberat dinyatakan dalam cm/s2 atau gal.

3. Alat-alat pengukur percepatan gayaberat a. Pendulum

√ = √ (8)

Ketelitian alat Pendulum maksimum 0.1 mGal.

b. Pengukuran gayaberat dengan benda jatuh

Dari persamaan benda jatuh bebas didapatkan persamaan berikut:

H = Vot + 1/2gt2 (9)

Dengan Vo = 0, maka:

g = 2h/t2 (10)

Ketelitian pengukuran gayaberat dengan benda jatuh ditentukan oleh h dan t dan ketelitian mencapai 10-7 Gal.

c. Pengukuran relatif menggunakan gravimeter

Gravimeter adalah alat pengukur gayaberat relatif yang prinsip kerjanya didasarkan atas memanjangnya pegas akibat perbedaan gaya tarik yang berlaku pada beban, bila sebuah gravimeter dibawa ke dua tempat yang berbeda harga gayaberatnya, perbedaan tersebut dibaca pada mistar skala. Ada dua macam alat gravimeter yaitu tipe stabil dan anstabil. Tipe yang anstabil saat ini lebih banyak digunakan karena tinggi harga ketelitian dan

(5)

akurasinya, contoh dari tipe ini adalah Worden, Scintrex Autograv dan Lacoste Romberg Gravimeter.

4. Pengukuran Di Lapangan

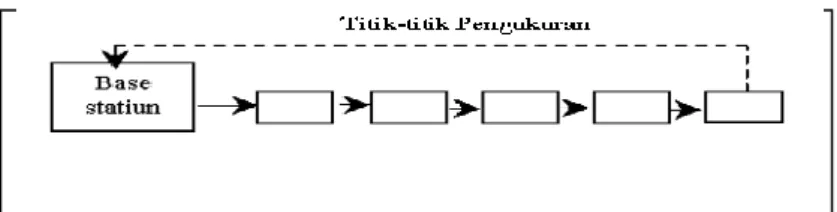
Pada pengukuran lapangan dilakukan dengan membentuk suatu loop, pengukuran dimulai dan diakhiri dititik yang sama, sehingga kesalahan penutup tiap jalur dapat dihitung. Kemudian kesalahan penutup dikoreksikan pada semua data pengamatan yang terletak di jalur yang bersangkutan, dengan pola pengukuran seperti Gambar 7 berikut:

Gambar 7. Pola pengukuran medan gayaberat

Dalam pengamatan ini terlebih dahulu dicari lokasi yang tepat untuk meletakkan stasiun utama, dimana pengukuran beda percepatan gayaberat relatif dibandingkan dengan titik lain. Setelah itu daerah yang akan dieksploitasi dibagi dalam kisi (jaringan) yang sesuai dengan tujuan penyelidikan. Hal ini dilakukan untuk memperoleh data pengamatan yang baik. Pengamatan gayaberat ini dimulai dari suatu titik pangkal di daerah penyelidikan dimana harga titik pangkal ini telah diikat terhadap titik pangkal pokok yang telah diketahui harga mutlaknya. Untuk menentukan lokasi titik pengamatan di lapangan diperlukan suatu peta yang telah diketahui kontur ketinggiannya.

(6)

Kecermatan perhitungan nilai anomali Bouguer dalam setiap penelitian sangat ditentukan oleh kecermatan data pengukuran topografi setiap stasiun, yang terdiri dari data lintang geografi sampai ketinggian 0.01 detik dan data elevasi sampai ketelitian 0.5 meter. Untuk mendapatkan harga pembacaan dalam gayaberat (milligal) dari pembacaan di lapangan, maka harga bacaan tersebut harus dikonversikan kedalam satuan milligal dengan cara tertentu sesuai dengan manual alat tersebut.

3.4. Koreksi Data Gayaberat

Harga gayaberat observasi hasil survey gayaberat akan berbeda antara satu tempat dengan tempat yang lainnya. Perbedaan tersebut disebabkan antara lain:

1. Pemempatan (flattening) dan rotasi bumi. 2. Perbedaan jarak dari pusat bumi.

3. Perbedaan ketinggian maupun kedalaman di setiap titik pengukuran terhadap bidang datum (mean sea level).

4. Adanya efek tarikan dari massa yang berada diantara bidang datum dan stasiun pengukuran.

5. Adanya suatu efek topografi permukaan yang relatif kasar dengan perbedaan elevasi yang besar.

Untuk menghilangkan perbedaan hasil pembacaan harga g, maka harus dilakukan koreksi terhadap gayaberat. Koreksi-koreksi dalam penelitian sebagai berikut

(7)

1. Koreksi tidal (pasang surut)

Percepatan gayaberat di permukaan bumi di samping dipengaruhi oleh adanya gaya tarik bumi juga dipengaruhi oleh gaya tarik matahari dan bulan, sehingga untuk mendapatkan percepatan gayaberat yang akurat harus memperhitungkan pengaruh dari gaya tarik bulan dan matahari yang sering disebut dengan koreksi pasang surut.

Besarnya koreksi pasang surut dapat di ukur langsung dengan menggunakan Gravimeter secara periodik maupun hitungan dengan menggunakan komputer berdasarkan perumusan Longman (1969).

Pasut = KS + ( TA TS) S A S B K K x T T T T _   ₍₁₁₎ Dimana :

KS = koreksi sebelum pengamatan

KTA = koreksi waktu akhir pengamatan

KTS = koreksi waktu sebelum pengamatan

TB = waktu di base

TS = waktu sebelum pengamatan

TA = waktu akhir pengamatan

2. Koreksi drift (apungan)

Pengukuran gayaberat yang dilakukan di suatu tempat, yang kemudian diulang lagi pengukuran, secara teoritis harusnya akan tetap atau konstan. Pada kenyataannya, hal ini selalu diperoleh harga pembacaan yang berbeda, mengingat adanya pengaruh pasang surut diatas. Perbedaan ini disamping

(8)

dipengaruhi oleh kondisi pasang surut juga disebabkan karena pengaruh mekanisme alat, akibat goncangan selama transportasi, yang disebut sebagai drift atau apungan.

Koreksi drift ini ditentukan dengan anggapan bahwa perubahan drift ini linier terhadap waktu, sehingga koreksi ini dapat dirumuskan sebagai berikut:

Driftstation =

x ( ) (12) dimana :

Dstation = besarnya drift pada titik pengamatan

Tstation = waktu pembacaan pada titik pengamatan

GA1 dan GA2 = pembacaan gayaberat ke-1 dan ke-2 di base station

TA1 dan TA2 = waktu pembacaan ke-1 dan ke-2 di Base Station

3. Koreksi lintang (latitude correction)

Telah diketahui bahwa bentuk bumi tidaklah bulat sempurna akan tetapi berbentuk sferoid dengan pepat pada kedua kutubnya, sehingga besarnya harga gayaberat di kutub dan di khatulistiwa tidak sama. Dengan adanya perbedaan ini maka koreksi lintang sangat mempengaruhi besar gayaberat di suatu daerah. Dalam penelitian ini digunakan koreksi lintang dari International Assosiation of Geodesy System (IAG.1967) dengan rumusan (Blakely,1955) yaitu:



1 0.0053024sin  0.0000058sin 2



846 . 978031  2  2  n g (13)

Nilai gayaberat teoritik pada lintang diberikan oleh Moritz (1980) :

)

 

 978.032,7(1 5.302410 Sin 5,810 Sin 2

(9)

Koreksi ini dilakukan karena bentuk bumi yang tidak bulat sempurna, terdapat perbedaan antara jari-jari bumi di kutub dengan di katulistiwa. Nilai gayaberat dikutub akan lebih besar dibandingkan nilai gayaberat di katulistiwa, seperti ditunjukkan pada Gambar 9.

Gambar 9. Perbedaan nilai gayaberat di kutub dengan di khatulistiwa

4. Koreksi udara bebas (free air correction)

Koreksi udara bebas adalah koreksi yang digunakan untuk menghilangkan perbedaan harga gayaberat yang disebabkan oleh pengaruh ketinggian antara pengamatan dengan titik datum referensi. Pada koreksi udara bebas hanya memperhitungkan elevasi antara titik pengamatan dengan titik datum referensi dengan mengabaikan massa diantaranya. Besar koreksi udara bebas ini adalah (Grant & West, 1965):

Equator l a b  Kutub Garis normal

(10)

KUB = 0,3086 h mgal (15) dimana : h = ketinggian titik amat

KUB = koreksi udara bebas

Gambar 10. Titik amat P pada ketinggian h terhadap permukaan acuan

Koreksi udara bebas dilakukan terhadap titik-titik pengukuran yang terletak pada ketinggian h dari permukaan air laut. Koreksi gayaberat yang dihitung dari persamaan gayaberat normal bumi dengan bentuk ellipsoid.

h

g

_h







_  , (16)







  ₂ sin 2 1 2 f m f a g h g        (17) 0.308765   h  untuk  0 (18)

5. Koreksi Bouguer (Bouguer correction)

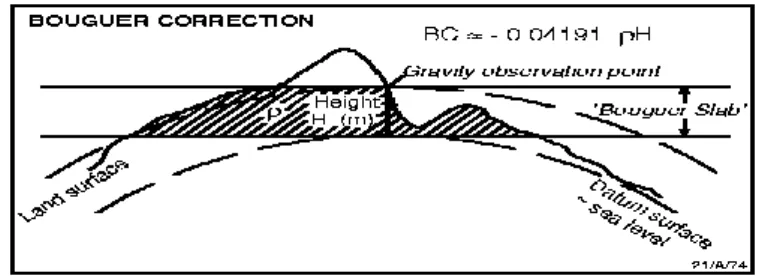
Pada koreksi udara bebas belum diperhitungkan adanya efek tarikan dari massa yang berada di antara bidang datum dan stasiun pengukuran itu sendiri, untuk itu pengukuran di darat efek tarikan dari massa tersebut menyebabkan peningkatan nilai Δg. Koreksi Bouguer berfungsi untuk mereduksi pangaruh efek tarikan dari suatu massa yang diberikan pada persamaan:

Geoid P

P0 h

(11)

(mGal) (19)

dengan h = ketinggian stasiun pengukuran (meter) ρr = densitas batuan rata-rata (gr/cc)

Gambar 11. Koreksi Bouguer terhadap data gayaberat terukur (Zhou, 1990)

6. Koreksi medan (terrain correction)

Pada koreksi medan yang diperlihatkan pada Gambar 14 nilai koreksi Bouguer diperbaiki dengan mengasumsikan terdapat suatu efek topografi permukaan yang relatif kasar dengan perbedaan elevasi yang besar, seperti permukaan atau lembah di sekitar titik pengukuran. Metode grafis yang dapat digunakan untuk menghitung koreksi medan adalah Hammer Chart.

(12)

Piringan melingkar (circular disk) pada Gambar 15 dan sebuah persamaan untuk digunakan untuk menyatakan daya tarik gayaberat yang terjadi di titik tengah piringan tersebut, yaitu:

( √ ) (20)

dengan,

R = radius piringan (cm) ρ = densitas piringan (gr/cc)

H = ketebalan piringan (cm)

Gambar 13. Piringan melingkar sebagai dasar untuk perhitungan koreksi medan (Robinson, 1988)

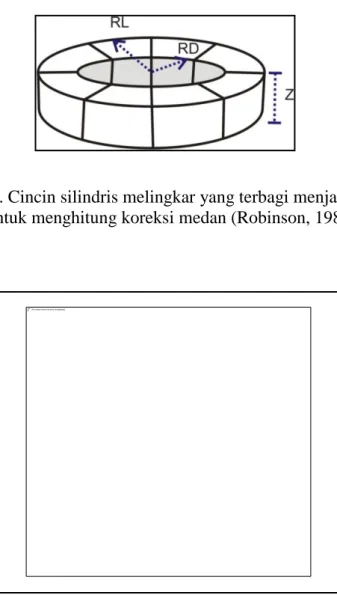
Kemudian Persamaan (20) digunakan untuk menentukan daya tarik gayaberat yang terjadi pada cincin silindris melingkar seperti yang ditunjukkan pada Gambar 16 efek gayaberat dari setiap kompartemen diperoleh dengan menggunakan persamaan (dalam meter):

( ) (√ ) (√ ) (21)

dengan,

n = jumlah kompartemen dalam zona tersebut.

z = perbedaan elevasi rata-rata kompartemen dan titik pengukuran rL dan rD = radius luar dan radius dalam kompartemen

(13)

Gambar 14. Cincin silindris melingkar yang terbagi menjadi 8 segmen untuk menghitung koreksi medan (Robinson, 1988)

Gambar 15. Hammer Chart untuk menghitung koreksi medan (Reynolds, 1997)

7. Anomali Bouguer (Bouguer anomaly)

Setelah dilakukan koreksi terhadap data percepatan gayaberat hasil pengukuran, maka akan diperoleh anomali percepatan gayaberat yaitu (Blakely, 1995):

a. Anomali udara bebas (g fa)

h

g

(14)

b. Anomali Bouguer (gbg)

1. Anomali Bouguer sederhana (Δgbgs)

h

g

_obs



_ob



_n



0 .

03086



0 .

04193





(23)

2. Anomali Bouguer lengkap (Δgbg)

TC h h g g g_bg  _ob _n     0.03086 0.04193



(24)

3.5. Estimasi Rapat Massa

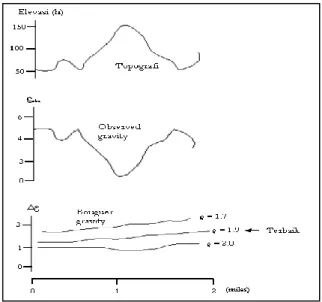
Dalam pengukuran gayaberat yang dicari adalah variasi rapat massa (densitas) untuk menggambarkan keadaan geologi bawah permukaan. Salah satu metoda untuk mengestimasi rapat massa rata-rata permukaan suatu daerah penelitian adalah metoda Nettleton.

Metoda Nettleton didasarkan pada pengertian tentang koreksi Bouguer dan koreksi medan, dimana jika rapat massa yang digunakan sesuai dengan rapat massa permukaan maka penampang anomali gayaberat menjadi ”smooth” mulus.

Contoh estimasi rapat massa metoda Nettleton pada Gambar 16.

(15)

 







    _N i i N i i i h h g k 1 2 1    (25)

dimana N = jumlah stasiun

Secara kuantitatif metoda ini menerapkan korelasi silang antara perubahan elevasi terhadap referensi tertentu dengan anomali gayaberatnya. Nilai korelasi silang yang terkecil merupakan rapat massa permukaan rata-rata yang terbaik.

3.6. Pemisahaan Anomali Regional – Residual

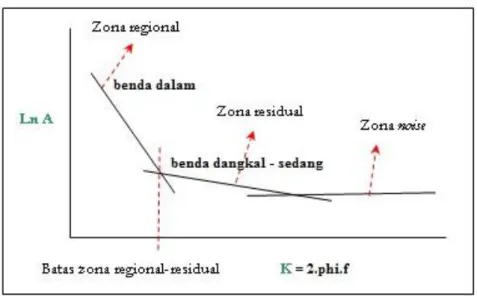
Anomali gayaberat yang terukur di permukaan pada dasarnya merupakan gabungan berbagai macam sumber dan kedalaman anomali yang berada dibawah permukaan dimana salah satunya merupakan target event dalam eksplorasi. Untuk kepentingan interpretasi, target event harus dipisahkan dari event lainya yang tidak diperlukan. Target event dapat berada di zona yang dalam (regional) atau di zona dangkal (residual).

Metoda moving average merupakan salah satu cara untuk memisahkan anomali regional-residual dengan noise. Metoda moving average dilakukan dengan cara merata-ratakan nilai anomali, proses perata-rataan dilakukan untuk tiap titik pengamatan dan bergerak dari satu titik ke titik lainnya. Hasil metoda moving average adalah anomali regional, sedangkan anomali residualnya diperoleh dengan mengurangkan anomali Bouguer lengkap terhadap anomali regional. Secara matematis pada kasus 1-D anomali regional dari moving average adalah :

 





 





N n i g i g n i g i g_r          ... ... (26)

(16)

Dimana N adalah lebar jendela yang harus bilangan ganjil, n adalah (N-1)/2. Semakin lebar jendela yang digunakan, maka nilai anomali residualnya mendekati nilai CBA, demikian juga sebaliknya semakin kecil jendela yang digunakan, maka anomali regional mendekati nilai CBA atau anomali residualnya  nol.

Penerapan moving average pada data 2-D dengan lebar jendela 5x5 dapat diilustrasikan seperti Gambar 17. Nilai g_r pada suatu titik dapat dihitung dengan

merata-ratakan semua nilai g_BOUGUER didalam sebuah kotak persegi dengan titik

pusat adalah titik yang akan dihitung harga g_r.

Gambar 17. Ilustrasi moving average dua dimensi jendela 5x5 (Robinson, 1988)

Persamaannya diberikan :



1

 

2

 

3





25



1 ... 25 R B B B B g g g g g    _        _ (27) 3.7. Analisa Spektrum

Analisa spektrum dilakukan untuk mengestimasi lebar jendela dan mengestimasi kedalaman dari anomali gayaberat. Selain itu analisa spektrum juga dapat digunakan untuk membandingkan respon spektrum dari berbagai metode filtering. Analisa spektrum dilakukan dengan men-transformasi Fourier lintasan-lintasan yang telah ditentukan.

(17)

Spektrum diturunkan dari potensial gayaberat yang teramati pada suatu bidang horisontal dimana transformasi Fouriernya sebagai berikut ( Blakely, 1996 ) :

       r F U F( )  1 dan   k e r F z z k ' 0 2 1 _        _ (28)

dimana, U = potensial gayaberat  = konstanta gayaberat

 = anomali rapat massa r = jarak

sehingga persamaannya menjadi :

  k e U F z z k ' 0 2 ) (    (29)

Berdasarkan Persamaan (29), transformasi Fourier anomali gayaberat yang diamati pada bidang horisontal diberikan oleh :

                  r F z r z F g F z 1 1 ) (     (30)  ' 0 2 ) (g_z ek z z F    (2.7-3)

dimana gz = anomali gayaberat k = bilangan gelombang

z 0 = ketinggian titik amat z = kedalaman benda anomali

Jika distribusi rapat massa bersifat random dan tidak ada korelasi antara masing-masing nilai gayaberat, maka : =1, sehingga hasil transformasi Fourier anomali gayaberat menjadi :  ' 0 z z k e C A   (31)

(18)

Estimasi lebar jendela dilakukan untuk menentukan lebar jendela yang akan digunakan untuk memisahkan data regional dan residual. Untuk mendapatkan estimasi lebar jendela yang optimal didapatkan dengan melogaritmakan spektrum amplitudo yang dihasilkan dari transformasi Fourier diatas (Persamaan 31) sehingga memberikan hasil persamaan garis lurus. Komponen k menjadi berbanding lurus dengan spektrum amplitudo.

k z z A

Ln ( ₀  ') (32)

Dari persamaan garis lurus diatas, melalui regresi linier diperoleh batas antara orde satu (regional) dengan orde dua (residual), sehingga nilai k pada batas tersebut diambil sebagai penentu lebar jendela. Hubungan panjang gelombang (λ) dengan k diperoleh dari persamaan (Blakely 1996)

2 k n x        (33)

dimana, n : lebar jendela.

Maka didapatkan didapatkan estimasi nilai lebar jendelanya

(19)

Untuk estimasi kedalaman diperoleh dari nilai gradien persamaan garis lurus diatas, Persamaan 33 (z0 –z’). Nilai gradien hasil regresi linier zona regional

menunjukkan kedalaman regional dan nilai hasil regresi linier zona residual menunjukkan kedalaman residual.

3.8. Derivatif Vertikal Orde Dua (Second Vertical Derivative)

Second Vertical Derivative (SVD) anomali Bouguer merupakan salah satu teknik filtering yang dapat memunculkan anomali residual (efek dangkal). Adanya struktur patahan disuatu daerah akan dapat diketahui dengan baik menggunakan teknik ini.

Secara teoritis, metoda ini diturunkan dari fungsi harmonik Laplace dengan mensubtitusi f dengan Δg dalam kasus gayaberat, yaitu :

2 2 2 2 2 2 2 2 0 ( ) ( ) ( ) g g g g g x y z                  (34) Sehingga, 2 2 2 2 2 2 ( g) ( g) ( g) z x y     _{ }   _     _   _ (35) atau 2 2 2 2 2 2 g g g + + = 0 x y z          (36)

sehingga second vertical derivative diberikan oleh Darby:

2 2 2 2 2 2 g g g z x y       _{ }  _    _   _ (37)

(20)

2 2 2 2 g g z x    _{ }   (38)

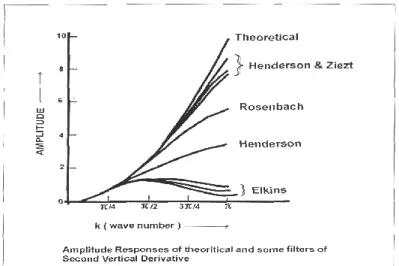
Terdapat beberapa operator filter SVD, yang dihitung oleh Henderson dan Zeits (1949), Elkins (1951) dan Rosenbach (1952). Dalam penelitian ini, penulis menggunakan operator filter SVD hasil perhitungan Elkins.

Persamaan. (38) menunjukkan bahwa second vertical derivative dari suatu anomali gayaberat permukaan adalah sama dengan negatif dari derivatif orde dua horizontal. Artinya bahwa anomali second vertical deivative dapat melalui derivatif horizontal yang secara praktis lebih mudah dikerjakan. Contoh grafis proses penurunan second vertical derivative untuk data penampang diberikan pada Gambar 21.

Untuk data anomali gayaberat dalam grid teratur, anomali second vertical derivative dapat diturunkan melalui proses filtering dimana pers. Konvolusinya diberikan oleh :





_{ }



  



             gsvd x, y g x,y F x x,v y dxdy (39) dimana F adalah filter secod vertical derivative sesuai dengan Persamaan 39) dan g adalah anomali gayaberat sebagai data input. Beberapa filter second vertical derivative mempunyai respons amplitudo seperti diberikan pada Gambar 20, sedangkan contoh operator filter 2-D diberikan pada Gambar 21.

(21)

Gambar 19. Bermacam-macam filter rentang respon amplitudo

Gambar 20. Bermacam-macam koefisien filter

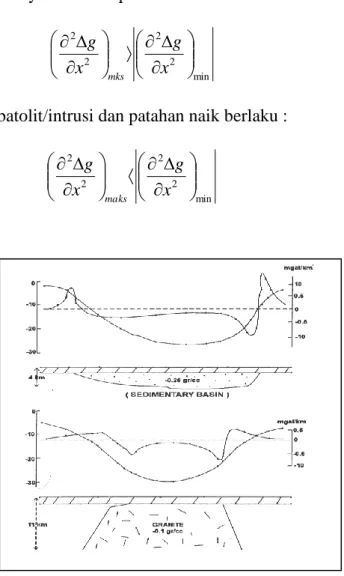
Untuk benda intrusi granit, pola second derivative untuk sedimentary basin sama dengan struktur patahan turun, sedangkan intrusi sama dengan patahan naik. Dari uraian diatas maka kriterianya adalah :

(22)

1. Untuk Sedimentary basin atau patahan turun berlaku : min 2 2 2 2                    x g x g mks (40)

2. Untuk Granit batolit/intrusi dan patahan naik berlaku :

min 2 2 2 2                    x g x g maks (41)

Gambar 21. Beberapa contoh pendugaan kedalaman

Gambar 22. Contoh penajaman prospek menggunakan second vertical derivative filter

(23)

3.9. Pemodelan Tiga Dimensi (3D)

Dalam Penelitian ini dilakukan pemodelan 3D dengan menggunakan software Grav3D versi 2.0. Hal ini dilakukan setelah data gayaberat sudah terkoreksi dan dipisahkan antara anomali lokal dan anomali regional. Pada tahap pemodelan, data gayaberat digunakan untuk menafsirkan model geologi dan struktur bawah permukaan berdasarkan distribusi densitas batuannya. Secara teknis pemodelan dilakukan menggunakan model benda 3D berbentuk prisma. Apabila suatu massa 3 dimensi bentuk sembarang terdistribusi secara kontinyu dengan rapat massa 



,,



seperti ditunjukkan pada Gambar 23, potensial gayaberat di titik P (x,y,z) di atas dan di luar distribusi rapat massa tersebut diberikan oleh (Kadir, 1996) :











 









                 d d d z y x K z y x U , , , , . . 2 1 2 2 2 (42)

Komponen gayaberat vertikal akibat distribusi rapat massa diperoleh dengan mendiferensialkan persamaan 42 terhadap z :









z z y x U z y x gz _     , , , ,









 







  

                0 2 3 2 2 2 . . , , _ _ _         d d d z y x z K (43)

Gambar 23.a. Efek potensial gayaberat di titik P Gambar 23.b. Benda prisma tegak

(24)

Pendekatan perhitungan respon gayaberat dengan menggunakan benda prisma sisi tegak dengan spasi x dan y merupakan salah satu alternatif yang dapat dilakukan, kesesuaian model benda di lapangan bergantung pada jumlah dan dimensi prisma yang disusun. Dengan mengambil lebar sisi horisontal a dan b pada arah  dan , kedalaman puncak dan dasar adalah ht

dan hb, maka komponen vertikal gayaberat pada z=0 adalah:







 

  





  