PEMECAH GELOMBANG BERUPA SERANGKAIAN BALOK

(1)

Bab 4

PEMECAH GELOMBANG

BERUPA SERANGKAIAN

BALOK

4.1 Kasus 2 buah Balok

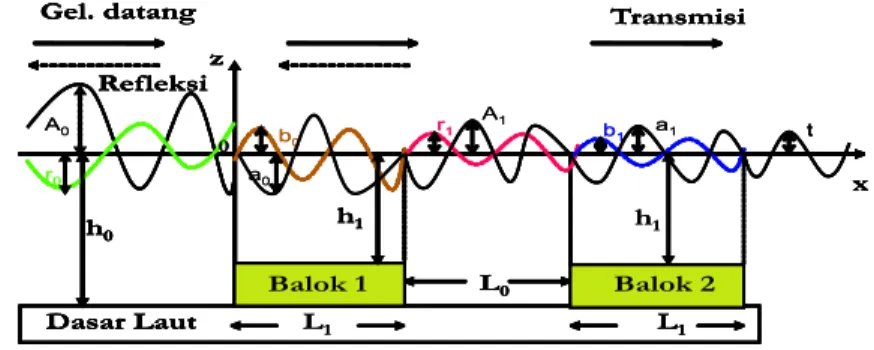
Dalam bahasan ini akan dipelajari proses transmisi dan refleksi yang terjadi untuk kasus 2 buah balok dengan bentuk geometri yang identik, yaitu dengan tinggi h0− h1, lebar L1 dan antara kedua balok terpisah pada jarak L0.

Gambar 4.1: Skema pemecah gelombang berupa 2 buah balok

(2)

Perhatikan Gambar 4.1, misalkan gelombang datang berupa gelombang monokro-matik yang menjalar dari arah kiri dinyatakan sebagai A0ei(k0x−ωt), kemudian melalui

pemecah gelombang berupa sebuah balok yang ditanam di dasar laut, maka terjadi perubahan kedalaman (discontinuous depth) di titik x = 0, x = L1, x = L0 + L1

dan x = L0 + 2L1 sehingga kedalaman h(x) dapat dinyatakan

h(x) =   

h1, berlaku untuk 0 < x < L1 atau (L0 + L1) < x < (L0+ 2L1);

h0, berlaku untuk x yang lain.

(4.1.1) dengan h1 < h0.

Ketika gelombang datang A0ei(k0x−ωt) melalui kedalaman h1, maka sebagian

ge-lombang tersebut akan ditransmisikan dan sebagian lagi akan direfleksikan berbalik arah. a0ei(k1x−ωt)menyatakan superposisi gelombang ke kanan yang menjalar di atas

kedalaman h1 dan r0e−i(k0x+ωt)menyatakan superposisi gelombang ke kiri yang

men-jalar di atas kedalaman h0. Ketika gelombang superposisi a0ei(k1x−ωt)melalui

kedala-man awal h0, maka gelombang tersebut akan ditransmisikan dan sebagian

direflek-sikan, b0e−i(k0x+ωt) menyatakan superposisi gelombang ke arah kiri, dan A1ei(k0x−ωt)

menyatakan superposisi gelombang ke arah kanan. Kemudian, gelombang super-posisi A1ei(k0x−ωt) akan melalui kedalaman h1, sehingga juga akan ditransmisikan

dan sebagian direfleksikan. a1ei(k1x−ωt) menyatakan superposisi gelombang ke kanan

dan r1e−i(k0x+ωt) menyatakan superposisi gelombang ke kiri. Hal yang serupa

ter-jadi saat gelombang superposisi a1ei(k1x−ωt) melalui kedalaman h0, maka gelombang

tersebut akan ditransmisikan dan direfleksikan. tei(k0x−ωt) menyatakan superposisi

gelombang ke kanan dan b1e−i(k1x+ωt) menyatakan superposisi gelombang ke kiri.

Sehingga profil gelombang tiap saat t dapat dinyatakan sebagai

(3)

dimana v(x) =                      A0eik0x+ r0e−ik0x, x < 0; a0eik1x+ b0e−ik1x, 0 ≤ x < L1; A1eik0(x−L1)+ r1e−ik0(x−L1), L1 ≤ x < L1+ L0; a1eik2(x−(L1+L0))+ b1e−ik2(x−(L1+L0)), L1+ L0 ≤ x < 2L1+ L0; teik0(x−(2L1+L0)), 2L 1+ L0 ≤ x. (4.1.3)

4.1.1 Ukuran Balok yang Optimal

Kemudian akan dicari nilai L0opt dan L1opt yang akan memberikan nilai

gelom-bang transmisi minimum melalui argumentasi fisis, karena jika dilakukan secara analitik akan menghasilkan banyak persamaan dan cukup sulit dalam perhitungan.

Gambar 4.2: Proses transmisi refleksi pada model 2-balok

Berikut ini adalah interpretasi fisis untuk kasus pemecah gelombang berupa 2 buah balok. Seperti terlihat pada Gambar 4.2 yaitu ketika gelombang membentur balok di x = 0, sebagian dari gelombang akan ditransmisikan ke 0 < x < L1, dan

sebagian lagi akan direfleksikan berbalik arah.

Saat gelombang transmisinya mencapai x = L1, maka akan terjadi proses yang

sama, yaitu gelombang akan terpecah menjadi dua bagian, sebagian akan ditrans-misikan menuju L1 < x < L1+ L0, dan sebagian lagi direfleksikan menuju 0 < x <

(4)

Kemudian saat gelombang transmisinya mencapai x = L1+L0, maka akan terjadi

proses yang sama, yaitu gelombang akan terpecah menjadi dua bagian, sebagian akan ditransmisikan menuju L1+ L0 < x < 2L1+ L0, dan sebagian lagi direfleksikan

menuju L1 < x < L1+ L0.

Saat gelombang transmisinya mencapai x = 2L1+ L0, maka akan terjadi proses

yang sama, yaitu gelombang akan terpecah menjadi dua bagian, sebagian akan di-transmisikan menuju x > 2L1+L0, dan sebagian lagi direfleksikan menuju L1+L0 <

x < 2L1+ L0. Proses terpecahnya gelombang menjadi gelombang transmisi dan

re-fleksi terjadi berulang kali untuk waktu yang tidak terbatas.

Seperti telah dijelaskan pada bab sebelumnya pada kasus 1 balok, maka dapat di-cari nilai amplitudo transmisi yang minimum ketika interferensi gelombang tersebut destruktif (saling melemahkan).

Maka agar |t

A| minimum haruslah memenuhi

  

L1opt = 1₄λ1

L0opt = 1₄λ0

4.1.2 Perbandingan Antara Hasil Analitik dan Numerik

Untuk melihat apakah argumentasi fisis berlaku maka akan diberikan simulasi data untuk perbandingan argumentasi fisis dan numerik.

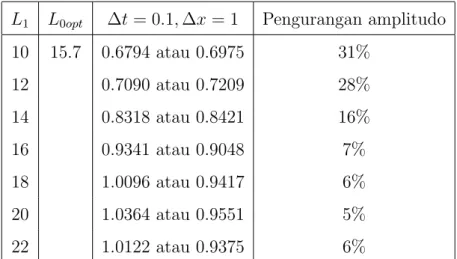
Berikut dilakukan perhitungan secara numerik dengan amplitudo gelombang datang A = 1, gravitasi g = 10, dan frekuensi ω = 1. Perhitungan numerik meng-gunakan metode Lax, dipilih selang variabel ruang [0,150] dan selang waktu [0,22]. Perhatikan Tabel 4.1, untuk kasus 2 balok dengan pemilihan lebar balok L1opt =

10 diperoleh pengurangan amplitudo yang maksimal, yaitu sebesar 31 % saat jarak antar kedua balok L0 = 15.7. Kemudian dilakukan perhitungan numerik dengan

pemilihan L0opt = 15.7, perhatikan Tabel 4.2, dapat dilihat bahwa untuk L0opt =

15.7 diperoleh pengurangan amplitudo yang maksimal sebesar 31% saat lebar balok L1 = 10.

(5)

L1opt L0 ∆t = 0.1, ∆x = 1 Pengurangan amplitudo 10 15.7 -0.6794 atau 0.6975 31% 18 0.6896 atau 0.7158 30% 20 0.7296 atau 0.7528 26% 22 0.7871 atau 0.8041 20% 24 0.8502 atau 0.8365 15% 26 0.8960 atau 0.8523 13% 28 0.9291 atau 0.8635 11% 30 0.9471 atau 0.8682 9% 31.4 0.9487 atau 0.8678 9% 34 0.9306 atau 0.8563 11%

Tabel 4.1: Hasil numerik untuk kasus 2 buah balok dengan lebar L1opt untuk

bebe-rapa nilai L0

L1 L0opt ∆t = 0.1, ∆x = 1 Pengurangan amplitudo

10 15.7 0.6794 atau 0.6975 31% 12 0.7090 atau 0.7209 28% 14 0.8318 atau 0.8421 16% 16 0.9341 atau 0.9048 7% 18 1.0096 atau 0.9417 6% 20 1.0364 atau 0.9551 5% 22 1.0122 atau 0.9375 6%

Tabel 4.2: Hasil numerik untuk kasus 2 balok yang terpisah dengan jarak L0opt untuk

beberapa nilai L1

Dari hasil yang diperoleh, dapat disimpulkan bahwa argumentasi fisis juga berlaku pada kasus 2 buah balok. Sehingga dengan pemasangan pemecah gelombang berupa 2 buah balok, diperoleh ukuran optimal balok dengan lebar balok L1opt = 10 dan

jarak antar balok L0opt = 15.7 yang dapat mengurangi amplitudo gelombang datang

(6)

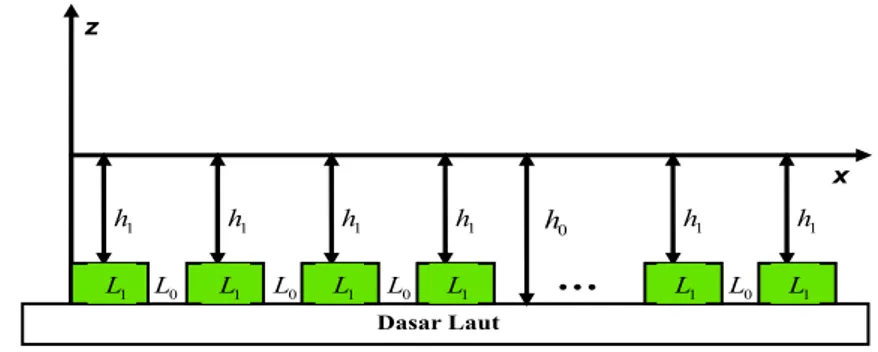
4.2 Kasus n-buah Balok

Pada kasus 2 buah balok dapat dicari ukuran optimal balok yang dapat meng-hasilkan amplitudo gelombang transmisi yang minimum. Dari kasus 2 buah balok dapat dikembangkan rumusan untuk kasus n-buah balok untuk n > 2 dengan masing-masing balok identik.

Gambar 4.3: Skema pemecah gelombang berupa n-buah balok

Perhatikan Gambar 4.3, untuk kasus n-buah balok identik maka dapat dicari uku-ran balok optimal yang akan memberikan amplitudo tuku-ransmisi yang kecil. Seperti telah dijelaskan pada kasus 2 buah balok, maka dapat dicari nilai amplitudo trans-misi yang minimum ketika interferensi gelombang tersebut destruktif atau (saling melemahkan).

Pada kasus n-buah balok, agar interferensi gelombang destruktif maka

• gelombang transmisi pada balok 1,...,n dengan kedalaman h1 berinterferensi

destruktif jika 2L1 = (m + 1₂)λ1 dengan λ1 = 2π_k₁, m = 0, 1, 2, ...

• gelombang transmisi pada jarak antar kedua balok dari balok 1,...,n dengan kedalaman h0 berinterferensi destruktif jika 2L0 = (m +1₂)λ0 dengan λ0 = 2π_k₀,

m = 0, 1, 2, ...

sehingga gelombang transmisi setelah melalui n-buah balok mempunyai amplitudo minimum.

(7)

Dari interpretasi fisis pada kasus 2 buah balok diperoleh rumusan L1opt = 1 4λ1 dan L0opt = 1 4λ0

sehingga untuk kasus n-buah balok yang identik juga berlaku hal yang sama. Maka agar |t

A| minimum haruslah memenuhi

  

L1opt = 1₄λ1

L0opt = 1₄λ0

Dari perhitungan numerik pada kasus 2 buah balok diperoleh ukuran optimal balok, yaitu L1opt = 10 dan L0opt = 15.7. Kemudian dari hasil tersebut digunakan

untuk simulasi kasus n-balok, yang memberikan hasil bahwa untuk pemasangan 3 buah balok, dari perhitungan numerik diperoleh bahwa amplitudo gelombang datang dapat dikurangi sebesar 40%, sedangkan untuk 4 buah balok amplitudo gelombang datang berkurang sebesar 51%.