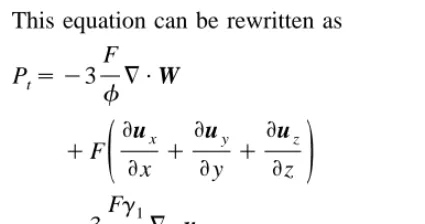www.elsevier.nlrlocaterjappgeo
Acoustic wave propagation in saturated porous media:
reformulation of the BiotrSquirt flow theory
Mamadou Sanou Diallo
), Erwin Appel
Institut fur Geologie und Palaontologie, Uni¨ ¨ Õersitat Tubingen, Sigwartstr. 10, 72076 Tubingen, Germany¨ ¨ ¨
Received 2 November 1998; accepted 16 February 2000
Abstract
A model of wave propagation in fluid-saturated porous media is developed where the principal fluidrsolid interaction mode affecting the propagation of the acoustic wave results from the conjunction of the Biot and the Squirt flow mechanism.
Ž .
The difference between the original BiotrSquirt BISQ flow theory and the new theory, which we call the reformulated BISQ, is that the average fluid pressure term appearing in the dynamic equation for a two component solidrfluid continuum is independent of squirt flow length. P-velocity and attenuation relate to measurable rock physical parameters: the Biot’s poroelastic constants, porosity, permeability, pore fluid compressibility and viscosity. Modelling shows that velocity and attenuation dispersion obtained using the reformulated BISQ theory are of the same order of magnitude as those obtained using the original BISQ theory. Investigation on permeability effect on velocity and attenuation dispersion indicate that the transition zone in velocity and attenuation peak, occurring both at the relaxation frequency, shifts toward high frequency when permeability decreases. This behaviour agrees with Biot’s theory prediction.q2000 Elsevier Science B.V. All rights
reserved.
Keywords: Acoustic waves; Dispersion; Porous media; Porosity; Permeability; Velocity
1. Introduction
The physics of acoustic wave propagation in saturated porous media has for very long cap-tured the interest of many investigators. Various
Ž
theories Biot, 1956a,b; O’Connell and
Budian-)Corresponding author. Tel.:
q49-7071-2977550; fax: q49-7071-29-5842.
E-mail addresses:
mamadou-sanou.diallo@uni-tuebin-Ž . Ž
gen.de M.S. Diallo , [email protected] E.
.
Appel .
sky, 1977; Murphy et al., 1986; Yamamoto and
.
Turgut, 1988; Dvorkin and Nur, 1993 of acous-tic wave propagation through porous media have been proposed to relate acoustic velocity and attenuation in sediments and porous rocks to physical properties of the material. Understand-ing of the whole mechanisms involved in acous-tic energy dissipation during the passage of a seismic wave in fluid-saturated porous medium is an important and challenging problem of geophysics. Important rock physical properties such as permeability, porosity and shear modu-lus are of primary importance in various fields
0926-9851r00r$ - see front matterq2000 Elsevier Science B.V. All rights reserved.
Ž .
of geoscience and could be determined if these mechanisms are fully understood.
Ž .
Biot 1956a,b predicts the existence of two kinds of dilatational waves in a homogeneous saturated porous medium loaded by an acoustic wave, the fast wave of propagational type desig-nated as the wave of the first kind and the slow wave of diffusive type, which is highly attenu-ated at low frequency designattenu-ated as wave of the second kind. He derived expressions for the velocity and attenuation of shear wave and com-pressional wave in terms of permeability, vis-cosity, and elastic constant of rocks. The experi-mental identification of the slow wave by Plona
Ž1980 and the agreement between the experi-.
mental data produced by the previous author
Ž .
with theoretical prediction by Berrymann 1980 using Biot theory served as a formal check to the validity of the theory.
Several reports of reasonably good agreement between experimental data and theoretical curves of velocity and attenuation dispersion vs. frequency predicted by the Biot model are
avail-Ž
able in the literature Keller, 1989; Yamamoto
.
et al., 1994 . Many investigators agree that this theory can be adequately used to model acoustic wave propagation in water-saturated
unconsoli-Ž
dated sand Stoll, 1980; Yamamoto and Turgut,
.
1988; Turgut and Yamamoto, 1990 or in highly
Ž .
permeable sediments Geli et al., 1987 . It is, however, important to note that the basic formu-lation of the theory explicitly assumes long-wavelength disturbances in comparison with the dimensions of the macroscopic elementary vol-ume considered in the formulation of the theory and hence very large disturbances in compari-son with the elementary pore size where micro-scopic flow occurs. As a consequence, the the-ory will be inaccurate in describing the interac-tion between acoustic waves and porous media when wavelengths are comparable to pores size, or when heterogeneity distribution is so com-plex that the requirement of statically isotropic medium cannot be guaranteed.
In Biot’s model, the hydrodynamic interac-tion between the solid frame and pore fluid is
separated into the inertia interaction and viscous interaction. Among the various loss mechanisms known in rocks, the friction losses and viscous losses resulting from relative motion between the solid frame and the fluid are known to adequately model acoustic wave attenuation in coarser sand and silt; other loss mechanisms such as local flow, thermoelasticity and scatter-ing are secondary effect for saturated coarse sediments in the frequency band of 1–30 kHz
ŽStoll, 1980; White, 1983 . The model for.
fluid-saturated porous media obtained using Biot theory indicates that attenuation has a peak. The position of this peak shifts towards low fre-quency for high permeability medium. Geertsma
Ž .
and Smit 1961 reviewed the initial Biot theory and derived approximate formula from which the relaxation frequency at which this peak occurs can be determined. This maximum peak in attenuation correspond to the maximum slope of velocity vs. log of frequency. From the
ap-Ž .
proximate formula of Geertsma and Smit 1961 ,
Ž .
Turgut and Yamamoto 1988, 1990 , and
Ya-Ž .
mamoto et al. 1994 derived analytical expres-sions relating permeability and porosity to other measurable rock physical and elastic parame-ters. For the permeability k, we have:
rh Õ0
ks 2
Ž .
12p r
Ž
myrf.
fr Õ`
where r is the bulk density of the sediment, rf
is the density of the saturant fluid, h the fluid viscosity, f is the relaxation frequency,r Õ0 and Õ are the low-frequency and high-frequency
`
limit of the velocity, respectively, m is the
Ž
inertia density of the rock grain see Appendix
.
A; Yamamoto et al., 1994 . The equation for the porosity is given by
and
(
Õss mrr.
Here, k is the bulk modulus of the saturantf
Ž
fluid, k is the bulk modulus of the grain solids
.
phase , kb the bulk modulus of the sediment framework and Õs the shear velocity. In a
satu-rated porous medium, if parameters intervening
Ž . Ž .
in Eqs. 1 and 2 are known or can be deter-mined by other methods, permeability and porosity can be calculated. The reliability of the result depend on the extent to which Biot theory can be used to model acoustic wave propagation in the considered medium.
Another loss mechanism, which is considered as a dominant source of attenuation and velocity dispersion of acoustic waves in the frequency range of 100–10 kHz for fluid-saturated
homo-Ž .
geneous porous rocks viscosity around 1 cP is
Ž .
the squirt flow Tutuncu et al., 1998 . Unlike the Biot mechanism where losses result from global relative motion between the pore fluid and solid framework, losses due to squirt flow mechanism result from the local flow of viscous fluid into and out of microcracks during the
Ž
passage of an acoustic wave O’Connell and Budiansky, 1977; Mavko and Nur, 1979;
Mur-.
phy et al., 1986; Jones, 1986 . Sams et al.
Ž1997 measured intrinsic attenuation, compres-.
sional and shear wave velocity on acoustic data from the Imperial College borehole test site. The data were obtained from VSP, crosshole surveys, sonic logging and laboratory measure-ments. Velocity and attenuation were deter-mined for both shear and compressional waves. Attenuation showed clear dependence on fre-quency with a peak in the sonic frefre-quency band. They concluded that the observed dispersion in velocity and attenuation could be well explained by the squirt flow mechanism. Bourbie et al.,
´
Ž1987 reviewed the different competing loss.
mechanisms and compared them with the results of laboratory studies. They concluded that while the squirt flow mechanism appears to partially explain the attenuation and velocity dispersion observed, it is not to be expected that a single
local or global flow model taken separately is sophisticated enough to account for the loss mechanism given the complexity of the porous medium. Experimental data from Klimentos and
Ž .
MacCann 1990 suggest that total clay content plays an important role in ultrasonic attenuation; measurements to produce experimental data were made at confining pressure of 40 MPa, which appears sufficient to suppress contribu-tion of local flow in microcracks to the total
Ž
attenuation or velocity dispersion Mavko and
.
Jizba, 1991; Winkler, 1985; Gist, 1994 . They attributed the clay-related attenuation to viscous interaction between clay particles and the pore
Ž .
fluid. Gist 1994 observed from experimental data acquired on Berea sandstone samples that the squirt flow model is not enough to account for the deviation of velocity and attenuation data from Biot theory. He filled the gap by invoking an additional loss mechanism due to the pore wall roughness. This mechanism is an extension of the theory put forward by
Klimen-Ž .
tos and MacCann 1990 on the effect of clay particles occurring between main mineral grains on attenuation.
In the squirt flow mechanism, the attenuation peak is predicted at the central relaxation
fre-Ž .
quency given by Palmer and Traviolia 1981 :
e3
frsKs
Ž .
3h
where e is the aspect ratio. In this flow model, the value of e at about 10-3 to 10-4 is
consid-ered to be causing most of the attenuation. Larger aspect ratio will not contribute much to
Ž .
the attenuation Jones, 1986 . The equations of
Ž .
Biot 1956a,b show that the frequency around which attenuation peak is predicted, is
propor-Ž .
tional to viscosity. Dvorkin et al., 1995
com-Ž .
attenuation peak due to Squirt flow mechanism shifts towards higher frequencies, whereas the one that results from the Biot’s mechanism moves in the opposite direction. It is then to be expected that for particular rock and fluid physi-cal parameters, these two peaks occur very far apart in the frequency scale that they cannot be observed simultaneously or even individually in an actual experiment due to limitations in mea-surement techniques. There is no doubt that both the loss mechanisms described above coex-ist in saturated porous media loaded by a pass-ing acoustic wave, their relative importance seems to be dependent on the nature of the
Ž .
porous medium whether consolidated or not and the frequency range of observation. Most of the cases where Biot model has been recognised as an adequate mechanism to account for atten-uation and velocity dispersion vs. frequency refer to unconsolidated sediments or highly
per-Ž
meable rocks Bourbie et al., 1987; Yamamoto
´
.
and Turgut, 1988; Yamamoto et al., 1994 , whereas reported cases where squirt flow is the most significant loss mechanism relate to exper-iments carried out on consolidated sedexper-iments
Ž
with relatively low permeability Mavko and Nur, 1979; Jones, 1986; Murphy et al., 1986;
.
Tutuncu and Sharma, 1992; Morig, 1993 .
¨
2. Theory
Ž .
Dvorkin and Nur 1993 , proposed a new theory of dynamic poroelasticity, which simul-taneously combines the Biot’s mechanism treated at macroscopic scale and the squirt flow
Ž
mechanism treated at microscopic scale at
indi-.
vidual pore level . This resulted in what is
Ž .
known as the BiotrSquirt BISQ flow theory. Model prediction of attenuation by the BISQ model seems to be more realistic for specific case than that given by Biot’s mechanism alone. The novelty in this concept with respect to that of Biot, comes mainly from the fact that in the BISQ model, the equation of fluid mass conser-vation used to describe the fluid dynamic is two
Ž
dimensional instead of one dimensional as in
.
the initial Biot’s theory , that is, not only fluid flow parallel to wave propagation direction is
Ž .
considered Biot mechanism , but also fluid flow
Ž .
in perpendicular direction squirt flow . The principal difference between the BISQ model and Biot’s model is felt through the expression of pore fluid pressure. In the Biot’s model this
Ž .
expression is given Dvorkin and Nur, 1993 by
EU g Eu
Ps yF
ž
q/
,Ž .
4Ex f Ex
Ž
whereas for the BISQ model, Dvorkin and Nur,
.
1993 it becomes:
2 J1
Ž
lR.
EU g EuPs yF 1y
ž
q/
,Ž .
5lRJ0
Ž
lR.
Ex f Exwhere u and U are respectively solid and fluid displacement in the x-direction, gsaqf and
a is a poroelastic coefficient,
kb
as1y .
ks
Ž . Ž .
The other parameters in Eqs. 4 and 5 are given as
R is the Squirt flow length, V the fluid acousticf
velocity, v the angular frequency, ra the cou-pling density and J , J represent Bessel func-0 1
tions of first and second order, respectively. vc
represents Biot’s characteristic frequency given by
vc hf
s .
The formulation of this theory like many others incorporating squirt flow mechanisms
ŽO’Connell and Budiansky, 1977; Murphy et
.
al., 1986 continues to use parameters that de-pend on micro-scale geometry of porous medium
Ž
architecture. Because local pore geometry e.g.,
.
aspect ratio is one of the parameters that affects relaxation frequency for local fluid absorption mechanism, we are confronted with the problem of having different relaxation frequencies for rocks having a variety of pore geometry. More-over, the BISQ model is based on one particular
Ž
geometrical construction a cylinder with a
con-.
stant pressure on its side while it is intended to quantify in a wide range of rocks regardless of the particular geometry or spatial distribution of the medium inhomogeneity that leads to local flow. Theoretical study by Gurevich and
Lopat-Ž . Ž
nikov 1995 shows that attenuation as well as
.
dispersion is sensitive to the spatial distribution of inhomogeneity, which may affect not only
Ž
some parameters characteristic frequency or
.
squirt flow length , but also the very form of the attenuation and dispersion curves. To circum-vent this problem, we propose a new expression for the pore fluid pressure, independent of the squirt flow length parameter R. This is achieved by reconsidering the way in which the two-di-mensional fluid flow has been incorporated by the BISQ model through the equation of fluid’s
Ž .
mass conservation. Dvorkin and Nur 1993 used the following equation:
where U is fluid displacement and u the solidx x
displacement in the wave propagation direction
Ži.e. x-direction ,. zthe fluid displacement in the
direction perpendicular to wave propagation
di-Ž .
rection radial-direction observed on a repre-sentative cylindrical volume of rock. Instead of considering a coordinate system where the fluid
flow in parallel and perpendicular directions to the wave propagation are independently treated, we will use a coordinate system where the radial fluid displacement z is replaced by U . Inr
this case, the relative fluidrsolid displacement in the direction of P-wave propagation is ex-pressed as
Wxsf
Ž
Uxyux.
.Ž .
7Ž .
Using U instead ofr z into Eq. 6 yields:
f Er Ef E2
Ž
U yu.
From now on, we will consider that U andx
U represent the axial and radial components ofr
the fluid displacement vector U, whereas ux
and ur represent the axial and radial compo-nents of the solid displacement vector u, respec-tively.
Porosity differential is related to differentials of skeleton’s deformation and of the fluid
pres-Ž .
represents the solid dilatation expressed in cartesian coordinates, which is equivalent to:
Eur ur Eux
es q q ,
Ž .
11Er r Ex
Ž .
We observe that in Dvorkin and Nur 1993 , the differential of the skeleton’s deformation in
Ž .
Eq. 9 is replaced by only the strain in the direction of the wave propagation. We will as-sume the normal strains to be equivalent in all
Ž .
directions; hence, we can rewrite Eq. 12 using
Ž . Ž .
Replacing EfrEt by this expression in Eq. Ž .8 and eliminating the fluid displacement by
Ž .
using the relation 7 gives after some algebraic
Ž .
transformations see Appendix A :
F EWr Wr EWx
The expression of pore fluid pressure from
Ž .
Biot 1962 is given by:
EWr Wr EWx
where the modulus M is given by
y1
f
Ž
ayf.
Ms q .
kf ks
It appears clearly that the effect of consider-ing radial fluid flow in the equation of fluid’s mass conservation as proposed above, results mainly in the occurrence of an additional term
Ž .
namely F EuxrEx . It can be observed that the
two expressions between parenthesis in both
Ž . Ž .
Eqs. 14 and 15 represent divergence term, hence, the new expression of pore fluid pres-sure, in what we will call as the reformulated BISQ model is given by
F Eux Fg1
Ps y =PWqF y =Pu,
Ž .
16f Ex f
The notations=PW and =Pu mean application
of the divergence operator to the relative fluidrsolid displacement and solid displace-ment, respectively.
Ž .
In the BISQ model Dvorkin and Nur, 1993 , only P-waves are considered. In a later paper,
Ž .
Dvorkin et al. 1995 devoted mainly to the squirt flow mechanism, S-waves were included. Resulting expressions of the fast P-wave and the S-wave velocities are still dependent on other parameters which are difficult to determine. We will develop a 3-D extension of our model following exactly the method adopted by Parra
Ž1997 in his extension of the BISQ model to a.
This equation can be rewritten as
We notice that the expression between paren-thesis is a divergence term, therefore, the aver-age pore fluid pressure in 3-D wave motion for an isotropic porous medium saturated with a fluid can be rewritten as
F F Fg1
This expression of pore fluid pressure has been used in the modelling of acoustic wave velocity and attenuation dispersion vs. fre-quency. Formation and saturant parameters used
Ž .
are those of Dvorkin and Nur 1993 as reported
Ž .
by Parra 1997 . We avoid the lengthy mathe-matical derivation as it has been clearly and extensively treated in the two papers cited above and give directly expressions used to determine velocity and attenuation:
1
'
Vps
'
, asvImŽ
Y.
Ž .
21Re
Ž
Y.
where for our model,
2
The notation Re and Im indicate the real and complex part of a complex number.
3. Numerical results and discussion
We analyse the effect of frequency on the attenuation and phase velocity curves, by mod-elling six cases with permeability equal to 5, 20, 50, 100, 500 and 1000 md. The formation con-sidered is a water saturated porous rock. Forma-tion and saturant parameters are given in Table 1. We first present the velocity–frequency and attenuation–frequency dispersion curves
ob-Ž .
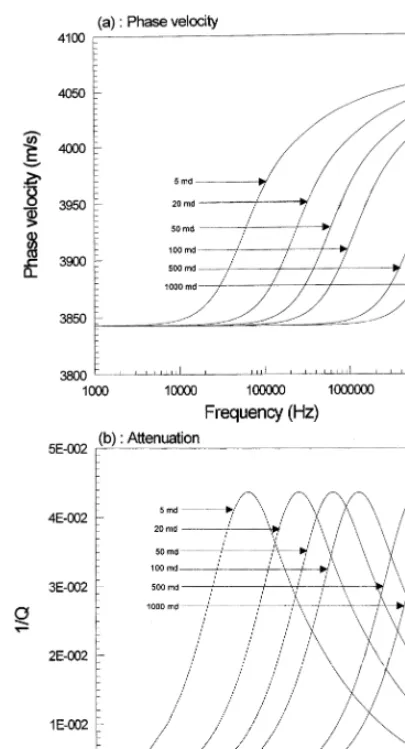
tained using the original BISQ model Fig. 1 and it is extended version to transversally
Ž . Ž
isotropic porous media after Parra 1997 Fig.
.
2 . In the latter, we considered the case of normal isotropic medium; the transversally isotropic case can be easily dealt with by find-ing wavenumber roots to the dispersion
equa-Ž .
tion given in Parra 1997 and using them to determine the velocities and attenuation of
Ž .
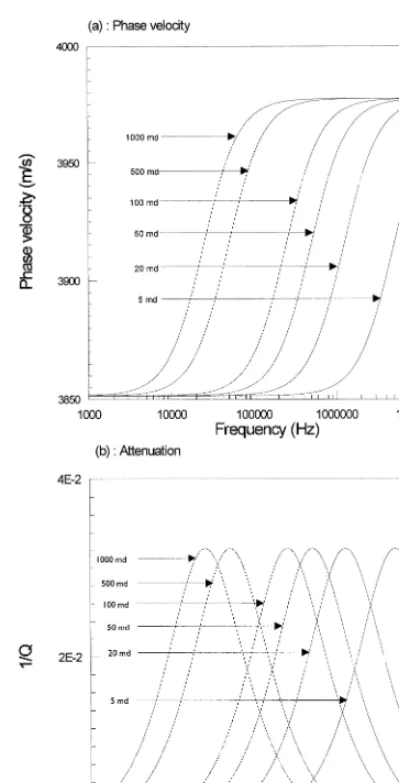
quasi-compressional waves fast and slow and quasi-SV waves. The velocity and attenuation dispersion curves obtained using our
reformu-Ž .
lated BISQ model Fig. 3 show significant dispersion of the same order as that predicted by the original BISQ theory. The main difference observed is the reversed behaviour with respect to the change in permeability. In the BISQ
Ž .
model Dvorkin and Nur, 1993; Parra, 1997 , the transition zone between the low-frequency limit and the high-frequency limit of acoustic wave velocity and attenuation peak shifts to-ward higher frequency when permeability
in-Ž .
creases Figs. 1 and 2 . In our model, the
re-Ž .
verse trend is observed Fig. 3 . The phase velocity at low frequency in the new model
ŽFig. 4a is nearly the same as that obtained.
Ž .
using Parra’s 1997 version of the BISQ-model
ŽFig. 3a , but slightly greater than that given in.
Ž .
Fig. 1. The effect of frequency for permeability 5, 20, 50,
Ž .
100, 500, and 1000 md. a Compressional velocity vs. log
Ž .
frequency and b inverse attenuation quality factor 1rQ
vs. log frequency as predicted by BISQ theory after
Ž .
Dvorkin and Nur 1993 .
Ž .
theory Parra, 1997 . The attenuation curves
ŽFig. 3b depict the same trend with respect to.
permeability as observed in the velocity
disper-Ž .
sion curves Fig. 3a . Here, again, attenuation values are of same order of magnitude as those predicted by the BISQ model of Dvorkin and
Ž .
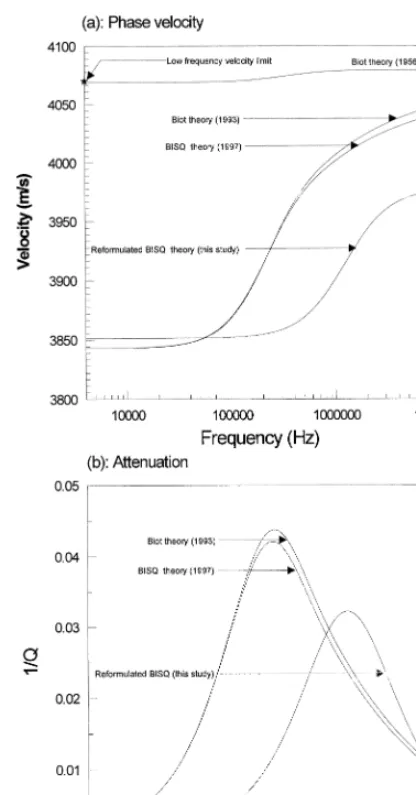
Nur 1993 in Fig. 1b. Curves of compressional velocity and attenuation dispersion predicted by
Ž .
the Biot’s 1956a,b theory are presented for
Ž .
comparison Fig. 4 . Fig. 5 displays velocity
and attenuation dispersion curves for a perme-ability of 20 md along with the velocity of the saturated rock in the limit of zero frequency
Ž .
calculated with the help of Gassman’s 1951 equations. These equations applies at low fre-quency where scattering, solid–fluid inertial ef-fect, local flow effect are negligible so that the estimated velocity reflect the effect of fluid
Ž
saturation at seismic or sonic frequency Winkler
Fig. 2. The effect of frequency for permeability 5, 20, 50,
Ž .
100, 500, and 1000 md. a Compressional velocity vs. log
Ž .
frequency and b inverse attenuation quality factor 1rQ
vs. log frequency as predicted by BISQ theory after Parra
Fig. 3. The effect of frequency for permeability 5, 20, 50,
Ž .
100, 500, and 1000 md. a Compressional velocity vs. log
Ž .
frequency and b inverse attenuation quality factor 1rQ
vs. log frequency as predicted by our reformulated BISQ theory.
.
1986, Nolen-Hoeksema et al., 1995 . As one may expect, the calculated velocity, using
Ž .
Gassman’s 1951 equations, fits very well to the low frequency velocity limit of the Biot’s
Ž1956a,b model curve because Gassmann equa-.
tions are also the low frequency limit of the
Ž .
Biot theory Biot, 1956a . The low-frequency
Ž
velocity limit from BISQ theory Dvorkin and
.
Nur, 1993; Parra, 1997 curves are identical, but
still lower than that predicted by Biot and Gassmann. The same remark applies to the re-formulated BISQ curve. The difference in low frequency velocity limit between the BISQ
the-Ž .
ory Dvorkin and Nur, 1993; Parra, 1997 and our model on the one hand, and the Biot–Gas-saman theory in the other hand can be explained by assuming that the rock may still contain some highly compressible residual gases, which have little effect on rock elastic moduli, but can
Fig. 4. The effect of frequency for permeability 5, 20, 50,
Ž .
100, 500, and 1000 md. a Compressional velocity vs. log
Ž .
frequency and b inverse attenuation quality factor 1rQ
vs. log frequency as predicted by Biot theory after Biot
Fig. 5. Comparison of the different models for a
perme-Ž .
ability of 20 md. a Compressional velocity vs. log
fre-Ž .
quency and b inverse attenuation quality factor 1rQ vs.
log frequency as predicted by the different models.
induce a noticeable change in density so that the difference in low-frequency velocity limits is
Ž
mainly due to the density effect Dvorkin et al.,
.
1995 .
4. Conclusion
We have developed a new theory of acoustic waves propagation in saturated porous media,
which combines the Biot’s and the Squirt flow mechanisms. The novelty in this theory, which we call reformulated BISQ flow theory is that the average pore fluid pressure term is indepen-dent of the characteristic squirt flow length
Ž
included in the original BISQ theory Dvorkin
.
and Nur, 1993 .
Velocity and attenuation curves obtained from our reformulated BISQ and the Biot’s theory show similar behaviour with respect to change in permeability. Attenuation peak and transition zone in velocity shift toward high frequency when permeability decreases, reversed trend is observed when permeability increases. We also notice that the relaxation frequencies predicted by the two models are very close to each other so that no significant difference should be ex-pected in permeability prediction for a given porous formation. The reformulated BISQ model, on the one hand, seems to rehabilitate the Biot’s theory in that it shows the same behaviour with respect to change in permeabil-ity characteristic, and on the other hand, agrees with the original BISQ-model in that it predicts the same order of magnitude in attenuation and velocity dispersion.
The result of the present work may be ade-quate for modelling attenuation and velocity dispersion in highly permeable homogeneous porous media and could therefore be used to extract permeability in formations where reli-able experimental data are availreli-able. The relia-bility of permearelia-bility inversion using this theory depends on the extent to which the observed acoustic energy dissipation resulting from the interaction between acoustic waves and porous medium can be handled by the Biot and Squirt flow mechanisms. In some porous rocks con-taining for example clay particles in the porous network, other acoustic energy dissipation phe-nomena may come into play so that the Biot and Squirt flow mechanism are not enough to model attenuation and velocity dispersion; in such a case, additional mechanisms have to be invoked to match theoretical models to experimental data
Acknowledgements
This work is mainly supported by the Univer-sity of Tubingen with additional funding from
¨
the Federal State Baden-Wurttemberg. Con-
¨
structive discussions with Prof. Dr. Erhard Wielandt and Prof. Dr. Rolf Schick from the Geophysics Institute of Stuttgart University at the beginning of this work are appreciated. The first author acknowledges valuable assistance from Dr. Jorge Parra at the South West
Re-Ž .
search Institute San Antonio, TX and Dr. Jack Dvorkin at the SRB group of Geophysics
De-Ž .
partment Stanford University . The first author would like to address special thanks to Dr. Manika Prasad at the SRB group of the
Geo-Ž .
physics department Stanford University for her continuous assistance throughout this project. Comments and suggestions of anonymous re-viewers for the improvement of this work are highly appreciated.
Appendix A. Derivation of the 3-D axisym-metrical equation
Ž .
Dvorkin and Nur 1993 incorporated the squirt flow mechanism in the dynamic poroelas-ticity model by combining the 2-D axisymmetri-cal equation of fluid’s mass conservation in the
x-direction with the volumetric filtration rate q
˜
in the perpendicular r-direction. The resulting equation:
where q is related to the fluid’s displacement
˜
zin the r-direction as q
˜
sfzr t.Instead of treating the perpendicular and ra-dial fluid flow independently, we will rather consider them being components of a 3-D fluid
Ž .
flow model in a cylindrical x, z, r coordinate
where the fluid displacement in the radial direc-tionÕr is replaced by U so that we can define ar
Ž .
fluid displacement as Us U ,U ,U and a solidx z r
Ž .
displacement as us u , u , u . Following thisx z r
definition, the volumetric infiltration rate in the
r-direction can be expressed as qsfU , in ther t x-direction as qsfUx t and in the z-direction as qsfU . The two subscripts in displace-z t
ment components indicate the direction and par-tial derivative with respect to time, respectively. We introduce a third vector, which describes the relative solidrfluid displacement w, which is defined as
wsf
Ž
Uyu ,.
Ž
A-2.
In what follow, all equations will be ex-pressed only in terms of the relative solidrfluid displacement w and the solid displacement u, therefore U will be replaced by
w
Us qu.
Ž
A-3.
f
Ž .
Rewriting Eq. A-1 with the above defini-tions gives
eliminating Ux t from A-4 and splitting the first term into its partial derivatives with respect to time yields
Replacing EfrEt by its expression in Eq. Ž11 ,. Ž ŽE rf.rEt by Eq. 5 in Dvorkin and Nur. Ž . Ž1995 and then adding and subtracting simulta-.
if we assume that the time dependence of fluid and solid displacement is expressed only by an
eivt term, then the partial derivatives with
re-Ž .
spect to time in A-6 are equivalent to multi-plying each term by iv, which yields, after simplification
Biot, M.A., 1941. General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164.
Biot, M.A., 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid: I. Low frequency range. J. Acoust. Soc. Am. 28, 168–178.
Biot, M.A., 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid: II. High frequency range. J. Acoust. Soc. Am. 28, 179–191.
Biot, M.A., 1962. Generalized theory of acoustic wave propagation in porous dissipative media. J. Acoust. Soc. Am. 54, 1254–1264.
Berrymann, J.G., 1980. Confirmation of Biot’s theory. Appl. Phys. Lett. 37, 382–384.
Bourbie, T., Coussy, O., Zinszner, B., 1987. Acoustics of´
Porous Media. Technip, Paris.
Dvorkin, J., Nur, A., 1993. Dynamic poroelasticity: a unified model with the squirt flow and the Biot mecha-nism. Geophysics 58, 524–533.
Dvorkin, J., Mavko, G., Nur, A., 1995. Squirt flow in fully saturated rocks. Geophysics 60, 97–107.
¨
Gassmann, F., 1951. Uber die elastizitat poroser medien.¨ ¨
Vierteljahrsschr. Naturforsch. Ges. Zuerich 96, 1–23. Geertsma, T., Smit, D.C., 1961. Some aspects of elastic
wave propagation in fluid saturated porous solids. Geo-physics 26, 169–181.
Geli, L., Bard, P.-Y., Schmitt, D.P., 1987. Seismic wave propagation in a very permeable water-saturated sur-face layer. J. Geophys. Res. 92, 7931–7944.
Gist, G.A., 1994. Fluid effects on velocity and attenuation in sandstones. J. Acoust. Am. 96, 1158–1173. Gurevich, B., Lopatnikov, S.L., 1995. Velocity and
attenu-ation of elastic waves in finely layered porous rocks. Geophys. J. Int. 121, 933–947.
Jones, T.D., 1986. Pore fluids and frequency-dependent wave propagation in rocks. Geophysics 51, 1939–1953. Keller, J.D., 1989. Acoustic wave propagation in compos-ite fluid-saturated media. Geophysics 54, 1554–1563. Klimentos, T., MacCann, C., 1990. Relationships among
compressional wave attenuation, porosity, clay content, and permeability in sandstones. Geophysics 55, 998– 1014.
Mavko, G.M., Nur, A., 1979. Wave attenuation in partially saturated rocks. Geophysics 44, 161–178.
Mavko, G.M., Jizba, D., 1991. Estimating grain-scale fluid effects on velocity dispersion in rocks. Geophysics 56, 1940–1949.
Morig, R., 1993. Untersuchungen zun Zusammenhang von¨
seismischen und lithologishen Parametern sedimentarer¨
Festgesteine, Dissertation, Technische Universitat¨ Ž .
Berlin TUB .
Murphy, W.F. III, Winkler, K.W., Kleinberg, R.B., 1986. Acoustic relaxation in sedimentary rocks: dependence on grain contacts and fluid saturation. Geophysics 51, 757–766.
Nolen-Hoeksema, Wang, Z., Harris, J.M., Langan, R.T., 1995. High-resolution crosswell imaging of west Texas carbonate reservoir: Part 5. Core analysis. Geophysics 60, 712–726.
O’Connell, R.J., Budiansky, B., 1977. Viscoelastic proper-ties of fluid-saturated cracked solids. J. Geophys. Res. 82, 5719–5736.
Palmer, I.D., Traviolia, M.L., 1981. Attenuation by squirt flow in undersaturated gas sands. Geophysics 45, 1780–1792.
Plona, T., 1980. Observation of a second bulk compres-sional wave in a porous medium at ultrasonic frequen-cies. Appl. Phys. Lett. 36, 259–261.
Parra, J., 1997. The transversely isotropic poroelastic wave equation including the Biot and the Squirt mechanisms: theory and application. Geophysics 62, 309–318. Sams, M.S., Neep, J.P., Worthington, M.H., 1997. The
measurement of velocity dispersion and frequency-de-pendent intrinsic attenuation in sedimentary rocks. Geo-physics 62, 1456–1464.
Stoll, R.D., 1980. Theoretical aspects of sound transmis-sion in sediments. J. Acoust. Soc. Am. 68, 1341–1350. Turgut, A., Yamamoto, T., 1988. Synthetic seismograms for marine sediments and determination of porosity and permeability. Geophysics 53, 1056–1067.
Turgut, A., Yamamoto, T., 1990. Measurement of acoustic wave velocities and attenuation in marine sediments. J. Acoust. Soc. Am. 87, 2376–2383.
Tutuncu, A.N., Sharma, M.M., 1992. The influence of fluids on grains contact stiffness and frame moduli in sedimentary rocks. Geophysics 57, 1571–1582. Tutuncu, A.N., Podio, A.L., Gregory, A.R., Sharma, M.M.,
rocks: Part I. Effect of frequency and strain amplitude. Geophysics 63, 184–194.
Winkler, K.W., 1985. Dispersion analysis of velocity and attenuation in Berea Sandstone. J. Geophys. Res. 90, 6793–6800.
Winkler, K.W., 1986. Estimates of velocity dispersion between seismic and ultrasonic frequencies. Geophysics 51, 183–189.
White, J.E., 1983. Underground Sound: Application of Seismic Waves. Elsevier, Amsterdam.
Yamamoto, T., Turgut, A., 1988. Acoustic wave propaga-tion through porous media with arbitrary pore size distributions. J. Acoust. Soc. Am. 83, 1744–1751. Yamamoto, T., Nye, L., Kuru, M., 1994. Porosity,