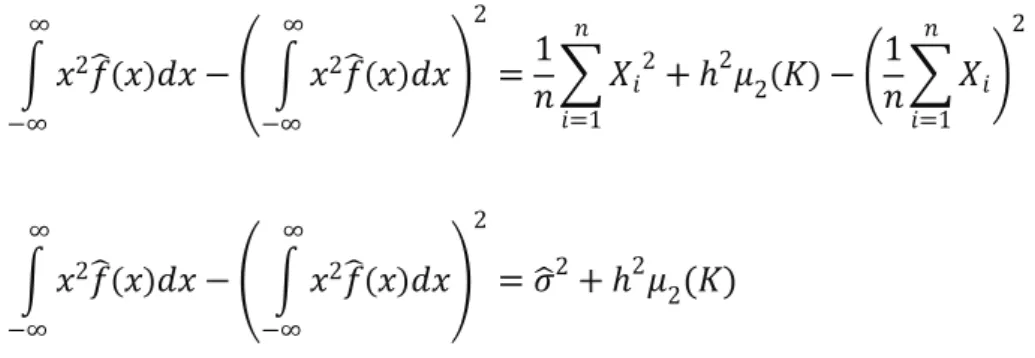40 BAB III PEMBAHASAN
A. Estimasi Nonparametrik
Tujuan dasar dalam sebuah analisa regresi adalah untuk mempelajari bagaimana respon sebuah peubah Y terhadap perubahan yang terjadi pada peubah lain yaitu X. Hubungan antara X dan Y dapat ditulis sebagai berikut:
𝑌𝑖= 𝑚(𝑋𝑖)+ 𝜀𝑖; 𝑖 = 1,2,3, … , 𝑛 (3.1) Dimana 𝑚(𝑋𝑖) adalah fungsi matematik yang disebut sebagai fungsi regresi dan 𝜀𝑖 adalah sisaan yang diasumsikan independen dengan mean nol. Pada aplikasi, terdapat sekumpulan data {(𝑋1,𝑌1), . . ,(𝑋𝑖, 𝑌𝑖)} yang berisi informasi tentang fungsi 𝑚(𝑋𝑖). Dari data-data ini diduga ataupun diestimasi fungsi 𝑚(𝑋𝑖) tersebut. Dalam beberapa penelitian, sering dijumpai permasalahan pada hubungan fungsional antara 2 variabel 𝑌 dan 𝑋 di mana bentuk –bentuk hubungan secara parametrik tidak dapat digunakan yang diakibatkan dari sedikitnya pengetahuan yang diperoleh tentang fungsi 𝑚(𝑋𝑖) ini, maka estimasi terhadap fungsi 𝑚(𝑋𝑖) ini dapat didekati secara nonparametrik. Agar pendekatan nonparametrik ini menghasilkan estimasi terhadap fungsi 𝑚(𝑋𝑖) yang masuk akal, maka hal yang harus diperhatikan adalah asumsi bahwa 𝑚(𝑋𝑖)memiliki derajat kemulusan. Biasanya kontinuitas dari 𝑚(𝑋𝑖) merupakan syarat yang cukup untuk menjamin sebuah estimator akan konvergen pada 𝑚(𝑋𝑖) yang sesungguhnya bila jumlah data bertambah tanpa batas. Estimasi nonparametrik secara umum tidaklah efektif digunakan untuk ukuran sampel yang kecil (Suyono, 1997:3). Dalam aplikasi-aplikasi yang lain, dapat digunakan
41
kemajuan fasilitas-fasilitas perhitungan dan metode-metode perhitungan untuk mengembangkan hubungan fungsional antara Y dan X. Hal inilah yang mungkin menjadi pertimbangan untuk menggunakan metode dan teknik nonparametrik.
Kelebihan statistika nonparametrik dibanding dengan statistika parametrik adalah :
1. Asumsi yang digunakan minimum sehingga mengurangi kesalahan penggunaan 2. Perhitungan dapat dilakukan dengan cepat dan mudah
3. Konsep dan metode nonparametrik mudah dipahami
4. Dapat diterapkan pada skala kualitatif (nominal dan ordinal).
Estimator-estimator nonparametrik yang banyak digunakan adalah estimator-estimator smoothing, dimana error dari observasi direduksi dari rata-rata data dengan bermacam cara.
B. Estimator Densitas Kernel
Estimator densitas kernel merupakan pengembangan dari estimator histogram. Estimator densitas kernel adalah suatu metode pendekatan terhadap fungsi densitas yang belum diketahui dengan menggunakan fungsi kernel. Estimator diperkenalkan oleh Rosenblatt (1956), Parzen (1962) sehingga disebut estimator densitas kernel Rosenblatt-Parzen (Hardle, 1994). Penghalusan dengan pendekatan kernel selanjutnya dikenal sebagai penghalusan kernel (kernel smoother) sangat tergantung pada fungsi kernel dan bandwidth.
Definisi (Hardle, 1994:32)
Didefinisikan X adalah variabel random dengan distribusi kontinu F(x) dan densitas 𝑓̂(𝑥)= 𝑑
42 𝑓 ̂(𝑥)=1 𝑛∑ 𝐾ℎ(𝑋𝑖− 𝑥) 𝑛 𝑖=1 𝑓 ̂(𝑥)=𝑛ℎ1 ∑𝑛𝑖=1𝐾(𝑋𝑖ℎ−𝑥) (3.2) dengan x adalah sebuah angka spesifik yang nilainya tetap.
Persamaan (3.2) dapat disederhanakan dengan 𝐾ℎ(𝑢) =1
ℎ( 𝑢
ℎ), dengan memisalkan
𝑢 = 𝑋𝑖 − 𝑥 sehingga dapat ditulis
𝑓̂(𝑥) = 1
𝑛∑ 𝐾ℎ(𝑋𝑖− 𝑥) 𝑛
𝑖=1 (3.3)
dengan K adalah sebuah fungsi yang merupakan fungsi kontinu, berharga real, terbatas dan memenuhi ∫𝐾(𝑥)𝑑𝑥 = 1, fungsi ini dinamakan fungsi kernel, dan h adalah bilangan positif yang disebut dengan bandwidth. Jika K(u) adalah fungsi densitas kernel, maka 𝐾ℎ(𝑢) juga.
Estimator kernel memenuhi asumsi-asumsi sebagai berikut: (Silverman, 1986)
(i) 𝐾ℎ(𝑥)≥ 0, untuk semua x
(ii) 𝐾(𝑥) bersifat simetris
𝐾(−𝑥) = 𝐾(𝑥), untuk semua x
(iii) ∫𝐾(𝑥)𝑑𝑥 = 1
(iv) ∫𝑥𝐾(𝑥)𝑑𝑥 = 0
(v) ∫𝑥2𝐾(𝑥)𝑑𝑥 = 𝜇
2(𝐾) ≠ 0, dengan 𝜇2(𝐾) momen kedua tertentu
(vi) ∫[𝐾(𝑥)]2𝑑𝑥 =∫𝐾2(𝑥) 𝑑𝑥 =‖𝐾‖
2
2= 𝑅(𝐾)
Jika fungsi kernel merupakan fungsi densitas, maka estimator fungsi dengan menggunakan fungsi kernel juga merupakan suatu fungsi densitas probabilitas. Akan dibuktikan fungsi densitas kernel memang memenuhi ∫𝑓̂(𝑥)𝑑𝑥 = 1.
43 ∫𝑓̂(𝑥)𝑑𝑥 =∫1 𝑛∑𝐾ℎ(𝑋𝑖− 𝑥)𝑑𝑥 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 = ∫ 1 𝑛 ∞ −∞ ∑1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 𝑛 𝑖=1 dengan subtitusi : −𝑢 =𝑋𝑖−𝑥
ℎ dan 𝑑𝑥 = ℎ 𝑑𝑢 maka diperoleh
∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝐾(−𝑢)𝑑𝑢 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝐾(𝑢)𝑑𝑢 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑1 𝑛 𝑖=1 ∫𝑓̂(𝑥)𝑑𝑥 =1 𝑛𝑛 ∫𝑓̂(𝑥)𝑑𝑥 = 1
Jadi, 𝑓̂(𝑥) merupakan suatu fungsi densitas.
Akan digunakan kembali subtitusi −𝑢 =𝑋𝑖−𝑥
ℎ , maka mean densitas yang di
estimasi adalah ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝑥 1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 ∞ −∞ 𝑛 𝑖=1 ∞ −∞
44 ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫ (𝑋𝑖+ 𝑢ℎ)𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 ∫𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ +1 𝑛∑ℎ ∫𝑢𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∫𝑥𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 𝑛 𝑖=1 ∞ −∞
merupakan mean sampel dari 𝑋𝑖.
Momen kedua dari 𝑥 dengan pdf merupakan densitas yang diestimasi, yaitu
∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫𝑥2 1 ℎ𝐾( 𝑋𝑖− 𝑥 ℎ )𝑑𝑥 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑ ∫ (𝑋𝑖+ 𝑢ℎ)2𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 2 ∫𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 ∞ −∞ +2 𝑛∑𝑋𝑖ℎ ∫𝑢𝐾(𝑢)𝑑𝑢 ∞ −∞ +1 𝑛∑ℎ 2 ∫𝑢2𝐾(𝑢)𝑑𝑢 ∞ −∞ 𝑛 𝑖=1 𝑛 𝑖=1 ∫𝑥2𝑓̂(𝑥)𝑑𝑥 =1 𝑛∑𝑋𝑖 2 + ℎ2𝜇2(𝐾) 𝑛 𝑖=1 ∞ −∞
dengan 𝜇2(𝐾)=∫𝑢2𝐾(𝑢)𝑑𝑢 adalah momen kedua dari u.
45 ∫𝑥2𝑓̂(𝑥)𝑑𝑥 −( ∫𝑥2𝑓̂(𝑥)𝑑𝑥 ∞ −∞ ) 2 =1 𝑛∑𝑋𝑖 2+ ℎ2𝜇 2(𝐾) 𝑛 𝑖=1 −(1 𝑛∑𝑋𝑖 𝑛 𝑖=1 ) 2 ∞ −∞ ∫𝑥2𝑓̂(𝑥)𝑑𝑥 −( ∫𝑥2𝑓̂(𝑥)𝑑𝑥 ∞ −∞ ) 2 = 𝜎̂2+ ℎ2𝜇2(𝐾) ∞ −∞
dengan 𝜎̂ adalah variansi sampel. Dengan demikian, estimasi densitas menaikkan variansi sampel sebesar ℎ2𝜇2(𝐾).
Menurut Sukarsa dan Srinadi (2012:20) menyatakan bahwa fungsi kernel ada bermacam-macam, contohnya kernel Gaussian, kernel Uniform, kernel Biweight. Tabel 3.1 menyajikan bermacam-macam fungsi kernel dan bentuknya, sebagai berikut:
Tabel 3.1 Macam-macam Fungsi Kernel
Tipe Kernel 𝐅𝐮𝐧𝐠𝐬𝐢 𝐊𝐞𝐫𝐧𝐞𝐥 Uniform 𝐾(𝑢) = 1 2𝐼(−1,1)(𝑢) Triangular 𝐾(𝑢) = (1 − |𝑢|)𝐼(−1,1)(𝑢) Biweight (Quadratik) 𝐾(𝑢) =15 16(1 − 𝑢 2)𝐼 (−1,1)(𝑢) Triweight 𝐾(𝑢) =35 32(1 − 𝑢 2)3𝐼 (−1,1)(𝑢) Gaussian 𝐾(𝑢) = 1 √2𝜋𝑒 −𝑢2 2 𝐼(−∞,∞)(𝑢) Epanechnikov 𝐾(𝑢) =3 4(1 − 𝑢 2)𝐼 (−1,1)(𝑢)
46 C. Estimasi Bias
Estimator densitas kernel 𝑓̂(𝑥) merupakan estimator tak bias asimtotik dari suatu fungsi kepadatan 𝑓(𝑥). Menurut Haeruddin (1997:27) andaikan 𝑓̂(𝑥) adalah estimator densitas kernel dari suatu fungsi kepadatan 𝑓(𝑥) pada titik 𝑥 ∈ 𝑅 dan andaikan 𝑋𝑖 berdistribusi identik dengan fungsi kepadatan 𝑓(𝑥), maka
𝐸[𝑓̂(𝑥)] = 𝐸 [1 𝑛ℎ∑ 𝐾 ( 𝑋𝑖 − 𝑥 ℎ ) 𝑛 𝑖=1 ] 𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ∑ 𝐸 [𝐾 ( 𝑋𝑖 − 𝑥 ℎ )] 𝑛 𝑖=1 𝐸[𝑓̂(𝑥)] =1 ℎ𝐸 [𝐾 ( 𝑋𝑖− 𝑥 ℎ )] 𝐸[𝑓̂(𝑥)] =1 ℎ∫ 𝐾 ( 𝑦 − 𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 misalkan 𝑠 =𝑦−𝑥 ℎ , maka 𝑑𝑦 = ℎ𝑑𝑠. Sehingga, 𝐸[𝑓̂(𝑥)] =1 ℎ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠 𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠)𝑓(𝑥 + 𝑠ℎ) 𝑑𝑠
integral tersebut tidak dapat diselesaikan kecuali menggunakan pendekatan ekspansi taylor dari 𝑓(𝑥 + 𝑠ℎ) dengan 𝑠ℎ = 0, ketika ℎ → 0. Untuk setiap kernel order ke v, maka dapat menggunakan aturan sebagai berikut
47 𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓 ′′(𝑥)ℎ2𝑠2+ 1 3!𝑓 ′′′(𝑥)ℎ3𝑠3+ ⋯ + 1 𝑣!𝑓 𝑣(𝑥)ℎ𝑣𝑠𝑣+ 𝑜(ℎ𝑣)
𝑜(ℎ𝑣) adalah sisa dari order yang lebih rendah dari ℎ𝑣 saat ℎ → 0. Maka, ekspansi taylor order dua untuk 𝑓(𝑥 + 𝑠ℎ) sebagai berikut:
𝑓(𝑥 + 𝑠ℎ) = 𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓
′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ2)
Selanjutnya, dengan aturan ∫−∞∞ 𝐾(𝑠)𝑑𝑠 = 1 dan ∫ 𝑠𝑗𝐾(𝑠)𝑑𝑠 = 𝜇 𝑗(𝐾) ∞ −∞ , maka 𝐸[𝑓̂(𝑥)] = ∫ 𝐾(𝑠) [𝑓(𝑥) + 𝑓′(𝑥)𝑠ℎ +1 2𝑓 ′′(𝑥)ℎ2𝑠2+ 𝑜(ℎ2)] 𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) ∫ 𝐾(𝑠)𝑑𝑠 + 𝑓′(𝑥)ℎ ∫ 𝑠 𝐾(𝑠)𝑑𝑠 +1 2𝑓 ′′(𝑥)ℎ2∫ 𝑠2 𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2) ∫ 𝐾(𝑠)𝑑𝑠 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥)(1) + 𝑓′(𝑥)ℎ(0) +1 2𝑓′′(𝑥)ℎ 2 ∫ 𝑠2 𝐾(𝑠)𝑑𝑠 + 𝑜(ℎ2) (1) 𝐸[𝑓̂(𝑥)] = 𝑓(𝑥) +1 2𝑓 ′′(𝑥)ℎ2𝜇 2(𝐾) + 𝑜(ℎ2) (3.4)
Akan dihitung bias, integrated squared bias, dan variansi dari 𝑓̂(𝑥) sebagai berikut (i) Bias dari 𝑓̂(𝑥)
𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝐸(𝑓̂(𝑥)) − 𝑓(𝑥)
𝐵𝑖𝑎𝑠 𝑓̂(𝑥) = 𝑓(𝑥) +1 2𝑓
′′(𝑥)ℎ2𝜇
48 𝐵𝑖𝑎𝑠 𝑓̂(𝑥) =1
2𝑓
′′(𝑥)ℎ2𝜇
2(𝐾) + 𝑜(ℎ2) (3.5)
(ii) Integrated Squared Bias dari 𝑓̂(𝑥) ∫Bias (𝑓̂(𝑥))2𝑑𝑥 =ℎ 4 4 𝜇2(𝐾) 2 ∫(𝑓′′(𝑥))2𝑑𝑥 + (𝑜(ℎ2))2 ∫Bias (𝑓̂(𝑥))2𝑑𝑥 =ℎ44𝜇2(𝐾)2𝑅(𝑓′′)+ 𝑜(ℎ4) (3.6) (iii) Variansi dari 𝑓̂(𝑥)
Selanjutnya akan dihitung variansi dari 𝑓̂(𝑥). Akan digunakan pendekatan Taylor order satu. Faktanya 𝑛−1 lebih kecil dari (𝑛ℎ)−1 jika ℎ → 0 dan 𝑛 → ∞. 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛2𝑉𝑎𝑟 (∑ 𝐾ℎ(𝑋𝑖− 𝑥) 𝑛 𝑖=1 ) 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛2∑ 𝑉𝑎𝑟(𝐾ℎ(𝑋𝑖− 𝑥)) 𝑛 𝑖=1 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛𝑉𝑎𝑟(𝐾ℎ(𝑋𝑖− 𝑥)) 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛{𝐸[𝐾ℎ 2(𝑋 𝑖 − 𝑥)] − (𝐸[𝐾ℎ(𝑋𝑖 − 𝑥)])2} 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛{ 1 ℎ2∫ 𝐾 2(𝑦 − 𝑥 ℎ ) 𝑓(𝑦)𝑑𝑦 − (𝑓(𝑥) + 𝑜(ℎ)) 2} Substitusi 𝑠 =𝑦−𝑥 ℎ dan 𝑑𝑦 = ℎ𝑑𝑠, maka 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ2∫ 𝐾2(𝑠)𝑓(𝑥 + 𝑠ℎ)ℎ𝑑𝑠 − 1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ∫ 𝐾 2(𝑠)𝑑𝑠 𝑓(𝑥 + 𝑠ℎ) −1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2
49 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ𝑅(𝐾)𝑓(𝑥) + 𝑜(ℎ) − 1 𝑛(𝑓(𝑥) + 𝑜(ℎ)) 2 𝑉𝑎𝑟(𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + 𝑜 ( 1 𝑛ℎ) 𝑉𝑎𝑟(𝑓̂(𝑥)) = ((𝑛ℎ)−1)𝑓(𝑥)𝑅(𝐾) + 𝑜((𝑛ℎ)−1), 𝑛ℎ → ∞ (3.7) dengan 𝑅(𝐾) = ∫ 𝐾2(𝑠)𝑑𝑠
D. Mean Square Error dan Mean Integrated Square Error
Menurut Suyono (1997:41) mengungkapkan bahwa suatu estimasi densitas kernel yang dibuat tergantung dari beda antara densitas yang sebenarnya 𝑓 dengan hasil estimasi 𝑓̂. Cara pengukuran beda antara densitas sebenarnya 𝑓 dengan hasil estimasi 𝑓̂ adalah dengan square error (SE) di suatu titik
𝑆𝐸𝑥(𝑓̂)={𝑓̂(𝑥)− 𝑓(𝑥)}2 (3.8)
Sehingga mean square error (MSE) dapat dirumuskan 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[{𝑓̂(𝑥)− 𝑓(𝑥)} 2 ] 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸{𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)]+ 𝐸[𝑓̂(𝑥)]− 𝑓(𝑥)}2 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[(̂(𝑓 𝑥)− 𝐸[𝑓̂(𝑥)]) 2 ]+ 𝐸[{𝐸[𝑓̂(𝑥)]− 𝑓(𝑥)}2] + 2𝐸{(𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)])(𝑓̂(𝑥)− 𝑓(𝑥))} 𝑀𝑆𝐸𝑥(𝑓̂)= 𝐸[(𝑓̂(𝑥)− 𝐸[𝑓̂(𝑥)])2]+[{𝐸[𝑓̂(𝑥)]− 𝑓̂(𝑥)}2] 𝑀𝑆𝐸𝑥(𝑓̂)= 𝑣𝑎𝑟 𝑓̂(𝑥)+(𝑏𝑖𝑎𝑠 𝑓̂(𝑥))2 (3.9)
50
Maka, berdasarkan persamaan (3.9) dapat dicari nilai MSE dari 𝑓̂(𝑥) sebagai berikut: 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 𝑣𝑎𝑟𝑓̂(𝑥) + [𝑏𝑖𝑎𝑠2𝑓̂(𝑥)]2 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + 𝑜((𝑛ℎ) −1) + [1 2𝑓 ′′(𝑥)ℎ2ì 2(𝐾) + 𝑜(ℎ2)] 2 𝑀𝑆𝐸 (𝑓̂(𝑥)) = 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + ℎ4 4 (𝑓 ′′(𝑥)ì 2(𝐾)) 2 + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) (3.10) untuk ℎ → 0, 𝑛ℎ → ∞
sedangkan pengukuran keseluruhan beda antara densitas yang sebenarnya 𝑓 dengan hasil estimasi 𝑓̂ disebut MISE yaitu mean integrated square error
(Haeruddin,1997:17). 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝑀𝑆𝐸𝑥(𝑓̂)𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝐸{𝑓̂(𝑥) − 𝑓(𝑥)}2𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝐸 [(𝑓̂(𝑥) − 𝐸[𝑓̂(𝑥)])2] 𝑑𝑥 + ∫ 𝐸 [{𝐸[𝑓̂(𝑥)] − 𝑓(𝑥)}2] 𝑑𝑥 𝑀𝐼𝑆𝐸(𝑓̂) = ∫ 𝑣𝑎𝑟𝑓̂(𝑥) 𝑑𝑥 + ∫ (𝑏𝑖𝑎𝑠 𝑓̂(𝑥))2𝑑𝑥 (3.11) Maka, 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ 𝑀𝑆𝐸[𝑓̂(𝑥)]𝑑𝑥 ∞ −∞
51 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ { 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾) + ℎ4 4 (𝑓 ′′(𝑥)𝜇 2(𝐾)) 2 + 𝑜((𝑛ℎ)−1) ∞ −∞ + 𝑜(ℎ4)} 𝑑𝑥 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = ∫ 1 𝑛ℎ𝑓(𝑥)𝑅(𝐾)𝑑𝑥 + ∫ ℎ4 4 (𝑓 ′′(𝑥)𝜇 2(𝐾)) 2 𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) ∞ −∞ + 𝑜(ℎ4) 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) ∫ 𝑓(𝑥)𝑑𝑥 ∞ −∞ +ℎ 4 4 𝜇2(𝐾) 2 ∫ (𝑓′′(𝑥))2𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) + ℎ4 4 𝜇2(𝐾) 2 ∫ (𝑓′′(𝑥))2𝑑𝑥 ∞ −∞ + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) 𝑀𝐼𝑆𝐸[𝑓̂(𝑥)] = 1 𝑛ℎ𝑅(𝐾) + ℎ4 4 𝜇2(𝐾) 2𝑅(𝑓′′) + 𝑜((𝑛ℎ)−1) + 𝑜(ℎ4) (3.12) untuk ℎ → 0, 𝑛ℎ → ∞ E. Regresi Kernel
Salah satu teknik smoothing untuk mengestimasi fungsi penghalus m pada persamaan (3.1) adalah regresi kernel. Dalam jurnal Sukarsa dan Srinadi (2012:21), Regresi kernel merupakan metode untuk memperkirakan ekspektasi bersyarat dari variabel acak dengan menggunakan fungsi kernel. Metode alternatif dalam pendekatan regresi nonparametrik ini menggunakan pemulus kernel, yang menggunakan rata-rata terbobot dari data. Tujuan analisis regresi adalah
52
menemukan hubungan antara sepasang variabel acak X dan Y, untuk mendapatkan dan menggunakan bobot yang sesuai. Menurut Hardle (1994:26), dalam setiap regresi nonparametrik, harapan bersyarat dari variabel Y relatif terhadap variabel 𝑋 dapat ditulis 𝐸(𝑌|𝑋) = 𝑚̂ (𝑥) atau 𝐸(𝑌|𝑋 = 𝑥) = ∫ 𝑦 𝑓(𝑥,𝑦)𝑑𝑦
𝑓(𝑥) . Dimana 𝑚 adalah
fungsi yang tidak diketahui untuk mendapatkan dan menggunakan bobot kernel yang sesuai.
Dalam regresi kernel terdapat berbagai estimator yang dapat digunakan untuk menduga bentuk 𝑚̂, diantaranya adalah estimator Nadaraya-Watson, estimator Polinomial Lokal, estimator Pristly-Chao dan estimator Gasser-Muller. Dalam bab ini akan dibahas mengenai estimator Nadaraya-Watson.
F. Estimator Nadaraya-Watson
Nadaraya dan Watson pada tahun 1964 mendefinisikan estimator regresi kernel sehingga disebut estimator Nadaraya-Watson (Wand dan Jones, 1995:130). Nilai dari fungsi 𝑚(𝑥) sesuai dengan nilai prediktor yang ekuivalen dengan ekspektasi dari variabel target dibawah kondisi nilai dari prediktor tetap yaitu 𝑥,
maka 𝑚̂ (𝑥)= 𝐸(𝑌|𝑋 = 𝑥) 𝑚̂ (𝑥)= ∫𝑦𝑓(𝑦|𝑥)𝑑𝑦 ∞ −∞ 𝑚̂ (𝑥) =∫ 𝑦𝑓(𝑥, 𝑦)𝑑𝑦 ∞ −∞ 𝑓(𝑥) (3.13)
53
Selanjutnya, Oryza (2013:22) menyatakan bahwa akan digunakan estimator densitas kernel sebagai metode yang sederhana untuk mengestimasi 𝑓(𝑥, 𝑦) dan 𝑓(𝑥). Estimasi dari 𝑓(𝑥, 𝑦) dan 𝑓(𝑥) dinotasikan sebagai 𝑓̂(𝑥, 𝑦) dan 𝑓̂(𝑥).
𝑓̂(𝑥, 𝑦)= 1 𝑛ℎ𝑥ℎ𝑦∑𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 ) (3.14) 𝑓̂𝑥(𝑥)= 1 𝑛ℎ𝑥∑𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 (3.15) dimana 𝐾𝑥(𝑋𝑖−𝑥 ℎ𝑥 ) dan 𝐾𝑦( 𝑌𝑖−𝑦
ℎ𝑦 ) merupakan fungsi kernel, ℎ𝑥 dan ℎ𝑦 merupakan konstan yang bernilai positif disebut dengan bandwidth. Telah disebutkan bahwa fungsi kernel memenuhi
∫−∞∞ 𝐾𝑥(𝑢)𝑑𝑢 = ∫−∞∞ 𝐾𝑦(𝑢)𝑑𝑢 = 1 (3.16) ∫−∞∞ 𝑢𝐾𝑥(𝑢)𝑑𝑢 = ∫−∞∞ 𝑢𝐾𝑦(𝑢)𝑑𝑢 = 0 (3.17) ∫ 𝑢2𝐾𝑥(𝑢)𝑑𝑢 ∞ −∞ < ∞ (3.18) ∫ 𝑢2𝐾 𝑦(𝑢)𝑑𝑢 ∞ −∞ < ∞ (3.19)
dari persamaan (3.16) dan persamaan (3.17) diperoleh menjadi persamaan di bawah ini: 1 ℎ𝑥 ∫𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) ∞ −∞ 𝑑𝑥 = 1 ℎ𝑦 ∫𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 ) ∞ −∞ 𝑑𝑦 = 1 (3.20)
54 1 (ℎ𝑥)2 ∫𝑥𝐾𝑥( 𝑥 ℎ𝑥 ) ∞ −∞ 𝑑𝑥 = 1 (ℎ𝑦)2 ∫𝑦𝐾𝑦( 𝑦 ℎ𝑦) ∞ −∞ 𝑑𝑦 = 0 (3.21)
untuk mencari perhitungan yang sederhana yaitu 𝑚̂(𝑋) dapat menggunakan subtitusi dari persamaan (3.14) dan persamaan (3.15) ke dalam persamaan (3.13) sebagai berikut: 𝑚̂ (𝑥) =∫ 𝑦𝑓̂(𝑥, 𝑦)𝑑𝑦 ∞ −∞ 𝑓̂(𝑥) 𝑚̂ (𝑥)= ∫ 𝑦 1 𝑛ℎ𝑥ℎ𝑦∑ 𝐾𝑥( 𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 𝐾𝑦(𝑌𝑖ℎ− 𝑦 𝑦 ) 𝑑𝑦 ∞ −∞ 1 𝑛ℎ𝑥∑ 𝐾𝑥(𝑋𝑖ℎ− 𝑥 𝑥 ) 𝑛 𝑖=1 𝑚̂ (𝑥)= ∑ 𝐾𝑥(𝑋𝑖ℎ− 𝑥 𝑥 ) ∫ 𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 ∞ −∞ 𝑛 𝑖=1 ℎ𝑦∑ 𝐾𝑥(𝑋𝑖− 𝑥 ℎ𝑥 ) 𝑛 𝑖=1 (3.22)
Selanjutnya, jika dimisalkan −𝑍 =𝑌𝑖−𝑦
ℎ𝑦 , maka 𝑑𝑦 = ℎ𝑦𝑑𝑍 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = ℎ𝑦 ℎ𝑦 ∫ (𝑌𝑖+ ℎ𝑦𝑍)𝐾𝑦 (𝑍)𝑑𝑍 ∞ −∞ ∞ −∞ 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = ∫𝑌𝑖𝐾𝑦(𝑍)𝑑𝑍 ∞ −∞ + ∫𝑍𝐾𝑦(𝑍)ℎ𝑦𝑑𝑍 ∞ −∞ ∞ −∞ 1 ℎ𝑦 ∫𝑦𝐾𝑦( 𝑌𝑖− 𝑦 ℎ𝑦 )𝑑𝑦 = 𝑌𝑖 (1)+ ℎ𝑦(0) ∞ −∞
55 1 ℎ𝑦∫ 𝑦𝐾𝑦( 𝑌𝑖−𝑦 ℎ𝑦 )𝑑𝑦 = 𝑌𝑖 ∞ −∞ (3.23)
Substitusi dari persamaan (3.23) ke dalam persamaan (3.22), dan penyederhanaan dari 𝐾𝑥(. ) menjadi 𝐾(. ) dan dari ℎ𝑥 menjadi ℎ menghasilkan:
𝑚̂ (𝑥)= 1 𝑛∑𝑛𝑖=1𝐾𝑥(𝑋𝑖ℎ− 𝑥)𝑌𝑖 1 𝑛∑𝑛𝑖=1𝐾𝑥(𝑋𝑖ℎ− 𝑥) 𝑚̂ (𝑥) =∑ 𝐾 ( 𝑋𝑖− 𝑥 ℎ ) 𝑌𝑖 𝑛 𝑖=1 ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥) (3.24)
dengan mensubtitusikan persamaan (3.24) terhadap model regresi pada persamaan (3.1), maka estimator Nadaraya-Watson dari model regresi (3.1) adalah
𝑚̂ (𝑥)= ∑ 𝐾 (𝑋𝑖− 𝑥 ℎ )𝑌𝑖 𝑛 𝑖=1 ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥) +𝜀𝑖, 𝑖 = 1,2,3, . . . , 𝑛 (3.25) dengan, K : fungsi kernel
h : nilai bandwidth tertentu
𝑋𝑖 : nilai amatan variabel prediktor ke-i 𝑌𝑖 : nilai amatan variabel respon ke-i
56 𝑚̂(𝑥) : estimator Nadaraya-Watson dari x
G. Estimator Nadaraya-Watson dengan Tipe Kernel Gaussian
Pada persamaan (3.25) diketahui bahwa estimator Nadaraya-Watson membutuhkan fungsi kernel, 𝐾(𝑥). Pada pembahasan ini hanya digunakan satu jenis fungsi bobot kernel, yaitu Kernel Gaussian. Alasan pemilihan kernel Gaussian, karena fungsi bobot kernel tersebut terdefinisi atau memiliki nilai pada semua bilangan riil. Jika menggunakan estimator Nadaraya-Watson dan Tipe kernel Gaussian, maka model penduga 𝑚̂ (𝑋𝑖) akan berbentuk sebagai berikut :
𝑚̂ (𝑥)= ∑ 𝐾 (𝑋𝑖− 𝑥 ℎ )𝑌𝑖 𝑛 𝑖=1 ∑𝑛𝑖=1𝐾 (𝑋𝑖ℎ− 𝑥) dengan, 𝐾(𝑥) = 1 √2𝜋𝑒𝑥𝑝 ( 1 2(−𝑥 2)) = 1 √2𝜋𝑒𝑥𝑝 (− 1 2𝑥 2) maka 𝑚̂ (𝑥) = ∑ 1 √2𝜋𝑒𝑥𝑝 (− 1 2 ( 𝑋𝑖 − 𝑥 ℎ ) 2 ) 𝑌𝑖 𝑛 𝑖=1 ∑ 1 √2𝜋𝑒𝑥𝑝 (− 1 2 ( 𝑋𝑖 − 𝑥 ℎ ) 2 ) 𝑛 𝑖=1 (3.26) H. Pemilihan Bandwidth
Menurut Silverman (1986), tingkat kemulusan 𝑓̂ ditentukan oleh fungsi kernel K dan bandwidth h, tetapi pengaruh fungsi kernel kurang signifikan dibanding pengaruh bandwidth. Bandwidth h pada estimator kernel berfungsi untuk menyeimbangkan antara bias dan variansi dari fungsi tersebut. Nilai h yang kecil akan memberikan grafik yang kurang mulus namun memiliki bias yang kecil. Sebaliknya jika bandwidth yang terlalu besar menyebabkan fungsi yang diestimasi terlalu mulus, sehingga hubungan variansinya rendah dan memiliki potensi bias
57
yang besar. Tujuan estimasi kernel adalah memperoleh kurva yang mulus namun memiliki nilai MSE yang tidak terlalu besar, maka perlu dipilih nilai h optimal untuk mendapatkan grafik optimal.
Pemilihan bandwidth h merupakan masalah utama dari estimator densitas kernel. Pemilihan bandwidth yang optimum dilakukan dengan cara memperkecil tingkat kesalahan. Semakin kecil tingkat kesalahan maka semakin baik estimasinya. Untuk mengetahui ukuran tingkat kesalahan suatu estimator dapat dilihat dari MSE (Mean Square Error) atau MISE (Mean Integrated Square Error).
1. Bandwidth “Rule of Thumb”
Menurut Wand (1995), formula-formula untuk bandwidth yang optimal yaitu dengan meminimalkan Asymptotic Integrated Mean Square Error
(AMISE) terhadap h. AMISE adalah persamaan yang dihasilkan dengan menghilangkan order tertinggi dari pendekatan formula Mean Integrated Square Error (MISE) pada persamaaan (3.12). Maka, nilai AMISE adalah sebagai berikut: 𝐴𝑀𝐼𝑆𝐸 (𝑓̂(𝑥)) ≈ 1 𝑛ℎ𝑅(𝐾) + ℎ4 4 𝜇2(𝐾) 2𝑅(𝑓′′) (3.27)
Untuk menghasilkan nilai bandwidth optimal, maka 0 = 𝜕𝐴𝑀𝐼𝑆𝐸 𝜕ℎ 0 = 𝜕 (𝑛ℎ1 𝑅(𝐾) +ℎ4 𝜇4 2(𝐾)2𝑅(𝑓′′)) 𝜕ℎ 0 = − 1 𝑛ℎ2𝑅(𝐾) + ℎ3𝜇2(𝐾)2𝑅(𝑓′′)
58 1 𝑛ℎ2𝑅(𝐾)= ℎ 3𝜇 2(𝐾)2𝑅(𝑓 ′′) 𝑅(𝐾) = 𝑛ℎ2ℎ3𝜇2(𝐾)2𝑅(𝑓′′) 𝑅(𝐾) = 𝑛ℎ5𝜇 2(𝐾)2𝑅(𝑓′′) ℎ5 = 𝑅(𝐾) 𝑛𝜇2(𝐾)2𝑅(𝑓′′) ℎ = ( 𝑅(𝐾) 𝑛𝜇2(𝐾)2𝑅(𝑓′′) ) 1 5 ⁄ sehingga, ℎ𝑜𝑝𝑡 = 𝑅(𝐾)1 5⁄ 𝑛−1 5⁄ 𝜇2(𝐾)−2 5⁄ 𝑅(𝑓")−1 5⁄ (3.28)
persamaan diatas tidak dapat langsung digunakan karena terdapat parameter yang tidak diketahui yaitu 𝑅(𝑓′′). Nilai 𝑅(𝑓′′) dapat dipermudah dengan menggunakan pendekatan kelompok distribusi standar. Sebagai contoh adalah distribusi normal dengan variansi 𝜎2, jika 𝑃 merupakan densitas normal standar, maka
𝑃(𝑥) = 1 √2𝜋𝜎𝑒 −𝑥2 2𝜎2 Sehingga, ∫𝑓′′(𝑥)2𝑑𝑥 =∫𝑃′′(𝑥)2𝑑𝑥 ∫ 𝑓′′(𝑥)2𝑑𝑥 =3 8𝜋 −12 𝜎−5 (3.29) ∫ 𝑓′′(𝑥)2𝑑𝑥 ≈ 0.212𝜎−5
59
Jika menggunakan kernel Gaussian, maka bandwidth optimal dapat diperoleh dengan mensubtitusikan persamaan (3.29) ke dalam persamaan (3.28), sehingga dapat diperoleh
ℎ𝑜𝑝𝑡=(1)− 2
5(2√𝜋)− 1
5(0.212)−15𝜎𝑛−15 = 1.06𝜎𝑛−15
pada persamaan (3.28) terdapat 𝜇2𝐾 dan ∫𝐾(𝑥)2𝑑𝑥 yang dapat disubtitusikan dengan nilai yang terangkum pada tabel (3.2)
Tabel 3.2 Nilai ∫(𝑲(𝒖))𝟐𝒅𝒖 dan ∫𝒖𝟐𝑲(𝒖)𝒅𝒖 fungsi kernel
Tipe Kernel 𝑲(𝒖) ∫(𝑲(𝒖))𝟐 𝒅𝒖 ∫𝒖𝟐𝑲(𝒖)𝒅𝒖 Uniform 𝐾(𝑢) =1 2𝐼(−1,1)(𝑢) 1 2 1 3 Triangular 𝐾(𝑢) = (1 − |𝑢|)𝐼(−1,1)(𝑢) 2 3 1 6 Biweight (Quadratik) 𝐾(𝑢) =15 16(1 − 𝑢 2)𝐼 (−1,1)(𝑢) 5 7 1 7 Triweight 𝐾(𝑢) =35 32(1 − 𝑢 2)3𝐼 (−1,1)(𝑢) 350 429 1 9 Gaussian 𝐾(𝑢) = 1 √2𝜋𝑒 −𝑢2 2 𝐼(−~,~)(𝑢) 1 2√ð 1 Epanechnikov 𝐾(𝑢) =3 4(1 − 𝑢 2)𝐼 (−1,1)(𝑢) 3 5 1 5 Sumber : Multivariat Density Estimation: Theory, Practice, and Visualization (Scott,1987)
2. Unbiased Cross Validation (UCV)
Menurut Guidoum (2015:13), metode ini pertama kali diperkenalkan oleh Rudemo (1982), kemudian dikembangkan oleh Scott (1987). Metode Unbiased Cross Validation (UCV) merupakan metode pemilihan bandwidth yang
60
bertujuan untuk mengestimasi h dengan cara meminimalkan Integrated Square Error (ISE), dengan fungsi berikut:
𝑈𝐶𝑉(ℎ, 𝑟) = ∫(𝑓̂ℎ(𝑟)(𝑥))2− 2𝑛−1(−1)𝑟∑ 𝑓̂ℎ,𝑖(2𝑟)(𝑋𝑖) 𝑛 𝑖=1 (3.30) dengan, ∫ (𝑓̂ℎ(𝑟)(𝑥)) 2 =𝑅(𝐾 (𝑟)) 𝑛ℎ2𝑟+1 + (−1)𝑟 𝑛(𝑛 − 1)ℎ2𝑟+1∑ ∑𝐾 (𝑟)∗ 𝐾(𝑟) (𝑋𝑗− 𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1 𝑓̂ℎ,𝑖(2𝑟)(𝑋𝑖)= 1 𝑛(𝑛 − 1)ℎ2𝑟+1∑𝐾 (2𝑟) (𝑋𝑗− 𝑋𝑖 ℎ ) 𝑗≠𝑖
Bandwidth yang meminimalkan fungsi ini adalah: ℎ𝑢𝑐𝑣 = 𝑎𝑟𝑔𝑚𝑖𝑛𝑈𝐶𝑉(ℎ, 𝑟) 𝑈𝐶𝑉(ℎ, 𝑟) =𝑅(𝐾(𝑟)) 𝑛ℎ2𝑟+1+ (−1)𝑟 𝑛(𝑛−1)ℎ2𝑟+1∑ ∑ (𝐾(𝑟)∗ 𝐾(𝑟)− 2𝐾(2𝑟)) ( 𝑋𝑗−𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1 (3.31)
3. Biased Cross Validation (BCV)
Menurut Guidoum (2015:11), metode ini dikembangkan oleh Scott, George, Jones dan Kappenman. Metode ini baik digunakan ketika jumlah sampel besar. Metode ini hampir sama dengan metode “Rule of Thumb”, didasarkan
pada formula yang meminimalkan Asymptotic Mean Integrated Square Error
61
mengganti 𝑅(𝑓(𝑟+2)) yang tidak diketahui nilainya dengan estimator sebagai berikut: 𝑅̂ (𝑓(𝑟+2))= (−1)𝑟+2 𝑛(𝑛−1)ℎ2𝑟+5∑ ∑ 𝐾 (𝑟+2)∗ 𝐾(𝑟+2)(𝑋𝑗−𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1 (3.32)
Maka didapatkan persamaan sebagai berikut,
𝐵𝐶𝑉(ℎ, 𝑟) =𝑅(𝐾 (𝑟)) 𝑛ℎ + 𝜇2(𝐾)2 4 (−1)𝑟+2 𝑛(𝑛 − 1)ℎ2𝑟+1∑ ∑ 𝐾(𝑟+2)∗ 𝐾(𝑟+2)( 𝑋𝑗− 𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1 (3.33)
4. Complete Cross Validation (CCV)
Menurut Guidoum (2015:13), metode ini dikembangkan oleh Jones dan Kappenman. Metode ini didasarkan pada estimasi turunan Integrated Square Density Derivative. Berikut metode CCV yang meminimalkan h:
𝐶𝐶𝑉(ℎ, 𝑟) = 𝑅(𝑓̂ℎ(𝑟)) − 𝜃̅𝑟(ℎ) + 1 2𝜇2(𝐾)ℎ 2𝜃̅ 𝑟+1(ℎ) + 1 24(𝜇2(𝐾) 2− 𝛿(𝐾))ℎ4𝜃̅ 𝑟+2(ℎ) (3.34) dengan,
h adalah nilai bandwidth r adalah order derivative
𝜇2(𝐾)=∫𝑥2𝐾(𝑥)𝑑𝑥 𝑅(𝐾(𝑟)) =∫ 𝐾𝑟(𝑥)2𝑑𝑥 𝛿(𝐾) = ∫ 𝑥4𝐾(𝑥)𝑑𝑥 𝑅(𝑓̂ℎ(𝑟)) =𝑅(𝐾 (𝑟)) 𝑛ℎ2𝑟+1 + (−1)𝑟 𝑛(𝑛 − 1)ℎ2𝑟+1∑ ∑ 𝐾(𝑟)∗ 𝐾(𝑟)( 𝑋𝑗− 𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1
62 𝜃̅𝑟(ℎ)= (−1)𝑟 𝑛(𝑛 − 1)ℎ2𝑟+1∑ ∑𝐾 (2𝑟)(𝑋𝑗− 𝑋𝑖 ℎ ) 𝑛 𝑗=1 𝑗≠1 𝑛 𝑖=1 I. Deskripsi Data
Dalam studi kasus ini, data bersumber dari http://finance.yahoo.com. Data historis diambil dari data harga saham Jakarta Islamic Index. Data yang diperlukan dalam permodelan ini adalah data harga saham Jakarta Islamic Index. Data yang digunakan data historis harian dalam rentang waktu 1 januari 2016 sampai dengan 30 april 2016 dengan jumlah data 82. Selama rentang waktu tersebut, bahwa harga saham JII berada pada kisaran 581,78 – 683,12. Nilai JII terendah tersebut terjadi pada tanggal 21 januari 2016 dan nilai JII tertinggi pada tanggal 22 april 2016. Data terdiri dalam dua variabel yaitu variabel Jakarta Islamic Index dan variabel waktu (dalam harian).
J. Uji Linearitas dan Uji Normalitas
Dengan menggunakan data tersebut dan menggunakan software SPSS versi 20 yang dapat dilihat pada lampiran 3 bagian 1 dan 2, terlebih dahulu akan dilakukan analisis data awal. Analisis regresi harus memenuhi asumsi linearitas dan normalitas. Uji linearitas dilakukan dengan membuat plot data, plot data tersebut digunakan untuk melihat apakah ada hubungan linear antara variabel X dan Y, selain itu dapat digunakan untuk menduga bentuk fungsi data yang mendekati dan melihat bagaimana perubahan pola perilaku kurva. Banyak djumpai bentuk fungsi yang dapat menggambarkan hubungan antara peubah sehingga dalam menganalisis suatu hasil penelitian haruslah ditentukan terlebih dahulu bentuk kurva yang sesuai untuk
63
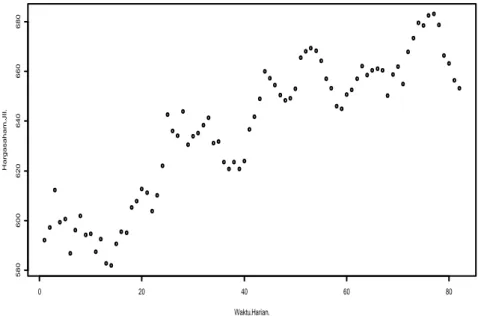
merepresentasikan data. Gambar (3.1) berikut menunjukkan pola hubungan antara harga saham JII dan waktu (dalam harian):
Gambar 3.1 Plot Harga Saham Jakarta Islamic Indeks (JII)
Plot tersebut menunjukkan bahwa variabel waktu dan variabel harga saham JII tidak berhubungan secara linear. Dari plot dapat diketahui bahwa pada waktu harian pertama, harga saham JII naik secara signifikan seiring dengan waktu demi waktu dengan kenaikan nilai harga saham. Dari output diperoleh nilai p-value sebesar 0,000 maka 𝐻0 ditolak. Jadi, dapat disimpulkan bahwa tidak terdapat hubungan linear antara waktu (harian) dan harga saham JII.
Selanjutnya perlu dilakukan uji inferensi normalitas agar diperoleh hasil yang pasti apakah asumsi kenormalan terpenuhi atau tidak. Akan dilakukan uji hipotesis asumsi normalitas terhadap data variabel respon (harga saham JII). Jumlah sampel yang dianalisis sebanyak 82 harga saham JII, maka uji normalitas dilakukan dengan menggunakan uji Kolmogorov-Smirnov. Dari statistik uji p-value, diperoleh nilai p-value adalah 0,001. Nilai ini lebih kecil dibandingkan dengan nilai
0 20 40 60 80 580 600 620 640 660 680 Waktu.Harian. H a rg a sa h a m .JI I.
64
alpha sebesar 0,05. Oleh karena itu 𝐻0 ditolak, jadi dapat disimpulkan bahwa data harga saham JII tidak berdistribusi normal.
K. Deskripsi Regresi Kernel
Setelah diketahui bahwa variabel respon tidak memenuhi asumsi linearitas, dan tidak berdistribusi normal, maka dapat digunakan solusi alternatif yaitu regresi nonparametrik dengan fungsi penduga kernel. Dalam kasus ini, fungsi kernel yang digunakan adalah kernel Gaussian. Estimator yang digunakan adalah estimator Nadaraya-Watson. Order derivatif yang digunakan adalah order nol.
L. Pemilihan Bandwidth Pada Data Harga Saham Jakarta Islamic Indeks
Dalam suatu Regresi Kernel, hal yang paling penting terletak pada besarnya nilai parameter bandwidth-nya. Oleh sebab itu, dalam pembahasan berikut ini akan dihitung nilai parameter bandwidth untuk masing-masing metode. Metode yang digunakan dalam menentukan besanya nilai parameter bandwidth pada kasus ini adalah bandwidth “Rule of Thumb”, Unbiased (Least Square) Cross Validation,
Biased Cross Validation dan Complete Cross Validation. Fungsi kernel yang digunakan untuk mencari bandwidth adalah fungsi kernel Gaussian.
Bandwidth untuk Data Harga Saham Jakarta Islamic Indeks sebagai berikut: Dengan menggunakan bantuan software R 3.2.3 dan untuk hasil output pada lampiran 3 bagian 3, dihasilkan nilai parameter bandwidth untuk data harga saham JII dengan metode bandwidth “Rule of Thumb” sebesar 22,50611, metode
Unbiased (Least Square) Cross Validation sebesar 11,79575 , metode Biased Cross Validation sebesar 15,23938 , sedangkan untuk perhitungan metode Complete Cross Validation dihasilkan bandwidth sebesar 4,770918. Nilai-nilai parameter
65
smoothing yang telah dihasilkan, maka dapat dirangkum dalam sebuah tabel berikut ini :
Tabel 3.3 Nilai parameter Bandwidth untuk Data Harga Saham JII
Metode Bandwidth
Bandwidth “Rule of Thumb” 22,50611
Unbiassed Cross Validation 11,79575
Biassed Cross Validation 15,23938
Complete Cross Validation 4,770918
Besarnya nilai parameter bandwidth tersebut, selanjutnya digunakan pada metode kernel yang akan digunakan dengan cara mensubtitusikan nilai bandwidth
tersebut pada estimator Nadaraya-Watson. Selanjutnya akan dicari model estimasi harga saham Jakarta Islamic Indeks menggunakan estimator Nadaraya Watson dengan tipe Kernel Gaussian dan parameter bandwidth yang telah dihasilkan pada tabel 3.3.
M. Estimator Nadaraya-Watson
Dalam pembahasan ini, akan dilakukan perhitungan nilai estimasi harga saham JII menggunakan software R 3.2.3. Setelah dilakukan running program, maka dihasilkan nilai estimasi yang tercantum pada lampiran 3 bagian 5.
Berikut perbandingan kurva antar metode pemilihan bandwidth (metode
Rule of Thumb, metode Unbiased (Least Square) Cross Validation, metode Biased Cross Validation dan metode Complete Cross Validation) dengan menggunakan estimator Nadaraya-Watson untuk data harga saham Jakarta Islamic Indeks :
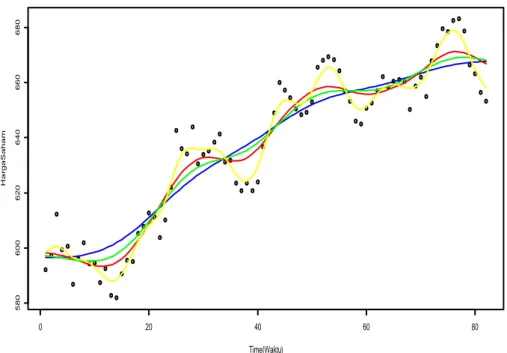
66
Gambar 3.2Kurva Hasil Estimasi Harga Saham Jakarta Islamic Indeks (JII) Keterangan: Rule of Thumb = Berwarna Biru
Unbiassed Cross Validation = Berwarna Merah
Biassed Cross Validation = Berwarna Hijau
Complete Cross Validation = Berwarna Kuning
Dari gambar 3.2 dapat dilihat bahwa kurva estimator Nadaraya-Watson dengan metode pemilihan bandwidth yaitu bandwidth “Rule of Thumb” menghasilkan kurva yang cukup mulus. Berbeda dengan metode-metode yang lain, yaitu metode Unbiased (Least Square) Cross Validation, Biased Cross Validation
maupun Complete Cross Validation menunjukkan bahwa kurva regresi tidak cukup mulus. Akan tetapi, dengan bandwidth Complete Cross Validation yang paling mendekati hasil estimasi dengan titik data actual.
0 20 40 60 80 580 600 620 640 660 680 Time(Waktu) H a r g a S a h a m
67 N. Perbandingan MSE
Pada pembahasan ini, akan dibahas perbandingan metode yang digunakan terhadap data harga saham Jakarta Islamic Indeks. Dengan perbandingan ini, maka akan diketahui metode pemilihan bandwidth yang lebih akurat dalam mengestimasi data harga saham Jakarta Islamic Indeks.
Dengan perbandingan ini, akan dilihat plot grafik metode (gambar 3.2) terhadap data harga saham JII yang ada dan menggunakan tingkat besarnya error. Dikarenakan menggunakan plot grafik akan cukup menyulitkan disaat terdapat plot yang berhimpit, maka digunakan cara melihat besarnya error yang dihasilkan dari estimator tersebut. Metode yang menghasilkan besarnya error yang paling kecil menandakan bahwa metode tersebut adalah metode yang lebih baik untuk mengestimasi data harga saham Jakarta Islamic Indeks.
Dengan estimator Nadaraya-Watson dan berbagai metode pemilihan
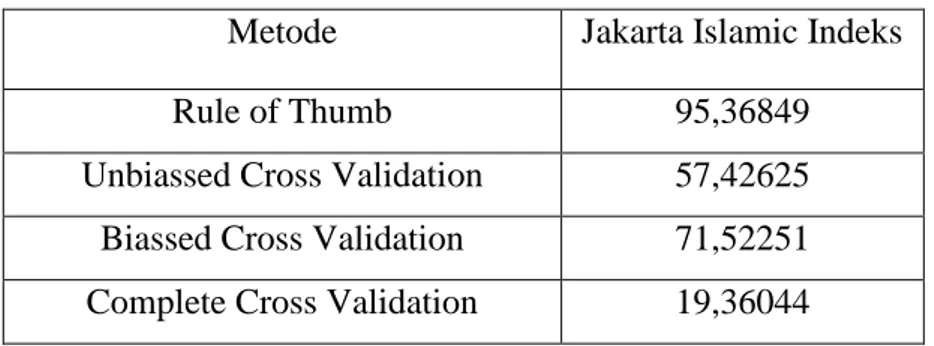
bandwidth, maka dihasilkan nilai MSE sebagai berikut : Tabel 3.4 Nilai MSE
Metode Jakarta Islamic Indeks
Rule of Thumb 95,36849
Unbiassed Cross Validation 57,42625 Biassed Cross Validation 71,52251 Complete Cross Validation 19,36044
Dari tabel 3.4 dapat dilihat bahwa pemilihan bandwidth dengan metode Rule of Thumb memiliki nilai MSE yang paling kecil untuk data harga saham JII. Nilai
68
MSE data estimasi harga saham JII yaitu sebesar 19,36044. Oleh karena itu dapat dikatakan bahwa metode pemilihan bandwidth “Complete Cross validation”
merupakan metode pemilihan bandwidth yang paling tepat digunakan untuk mengestimasi harga saham Jakarta Islamic Indeks.
O. Hasil Estimasi Harga Saham Jakarta Islamic Indeks
Berikut hasil estimasi harga saham Jakarta Islamic Indeks (JII) menggunakan metode pemilihan bandwidth “Complete Cross Validation”:
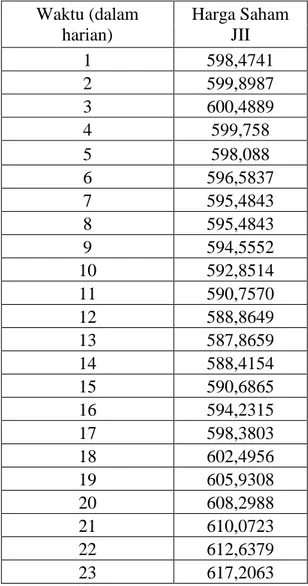
Tabel 3.5 Hasil estimasi harga saham JII Waktu (dalam harian) Harga Saham JII 1 598,4741 2 599,8987 3 600,4889 4 599,758 5 598,088 6 596,5837 7 595,4843 8 595,4843 9 594,5552 10 592,8514 11 590,7570 12 588,8649 13 587,8659 14 588,4154 15 590,6865 16 594,2315 17 598,3803 18 602,4956 19 605,9308 20 608,2988 21 610,0723 22 612,6379 23 617,2063
69 24 623,4515 25 629,5631 26 633,822 27 635,8082 28 636,157 29 635,8333 30 635,6634 31 635,8761 32 635,9126 33 634,9551 34 632,7087 35 629,6516 36 626,6908 37 624,7088 38 624,3479 39 626,0222 40 629,8538 41 635,435 42 641,7799 43 647,6047 44 651,7192 45 653,5081 46 653,3387 47 652,4385 48 652,261 49 653,7836 50 657,0184 51 660,9575 52 664,1337 53 665,4331 54 664,5066 55 661,6917 56 657,7992 57 653,9214 58 651,1712 59 650,2875 60 651,2896 61 653,5103 62 656,0047 63 658,002 64 659,1479
70 65 659,4363 66 659,0291 67 659,3043 68 657,9104 69 658,4405 70 660,1577 71 663,1219 72 667,1589 73 671,6038 74 675,4996 75 678,0866 76 678,8817 77 677,5467 78 674,1438 79 669,4772 80 664,7869 81 660,9817 82 658,2938
Dari tabel 3.5 dapat dilihat bahwa harga saham Jakarta Islamic Indeks
dengan waktu ke 36 hari yaitu 626,6908. Harga saham JII akan terus mengalami kenaikan sesuai dengan runtun waktu pada harga saham. Hingga waktu ke 82 hari, harga saham berada pada kisaran 658,2938. Dengan hasil estimasi JII menggunakan
bandwidth “Complete Cross Validation”. Harga saham JII pada setiap waktunya
yang berbeda dari hasil estimasi bandwidth unbiased cross validation, biased cross validation, Rule of Thumb.