ALGORITMA CEPAT (FAST ALGORITHM) PENDUGA
GENERALIZED-S (GS) UNTUK PENDUGAAN KEKAR
PARAMETER MODEL REGRESI LINEAR BERGANDA
DODI VIONANDA
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2010
PERNYATAAN MENGENAI TESIS DAN SUMBER INFORMASINYA
Dengan ini saya menyatakan bahwa tesis Algoritma Cepat (Fast Algorithm) Penduga Generalized-S (GS) untuk Pendugaan Kekar Parameter Model Regresi Linear Berganda adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Juli 2010
Dodi Vionanda
NRP G151070041
ABSTRACT
DODI VIONANDA. Fast Algorithm of Generalized-S (GS) Estimator for Robust Estimation Multiple Linear Regression Parameter. Under direction of ASEP SAEFUDDIN and AGUS MOHAMAD SOLEH
Generalized-S (GS) estimator is a robust estimator for regression model parameter based on robust scale estimate. GS estimates of regression model parameters are yielded by minimization of robust estimates of pairwise residual difference scales. Hence, GS estimator could be seen as a generalization of S estimator which deals with minimization of robust estimates of residual scales. By viewing GS estimator as generalization of S estimator, one could find the fact that the former has high breakdown point property as the later does. On the other hand, it has high efficiency property while the later does not. Meanwhile, several fast iterative computational methods for high breakdown robust estimators of regression parameters have been developed. The methods were called fast algorithms. There are three approaches have been proposed i.e. fast algorithm for LTS estimator, S estimator, and τ estimator. These methods have been applied for multiple linear regression model parameter estimation. This fact leads to the notion of developing a fast algorithm of GS estimator for multiple regression model parameter in this research in order to get another comprehensive method for high breakdown and high efficiency robust estimator beside fast τ approach. The algorithm is then applied to simulation data contaminated with outliers and the results yielded then will be compared with the ones produced by fast algorithm for S estimator and OLS to investigate its efficiency by looking at RMSE of the estimates resulted in various condition by considering several proportions, locations, and scales of outliers, as well as generating models. Finally, in all cases which involve outlier contamination considered, fast algorithm of GS consistently shows the better results by yielding the smallest RMSE value for each case. This fact indicates that fast algorithm of GS has higher efficiency than that of fast S. As addition, in case where the data are not contaminated with outliers, fast algorithm of GS gives the results that relatively close to OLS does, while fast S does not. Keywords: fast algorithm, GS estimates, S estimates, multiple regression model, resampling algorithm, I-step algorithm
RINGKASAN
DODI VIONANDA. Algoritma Cepat (Fast Algorithm) Penduga Generalized-S (GS) untuk Pendugaan Kekar Parameter Model Regresi Linear Berganda. Dibimbing oleh ASEP SAEFUDDIN dan AGUS MOHAMAD SOLEH
Penduga Generalized-S (GS) adalah suatu penduga kekar parameter regresi berdasarkan dugaan kekar skala. Penduga GS dapat dipandang sebagai perluasan penduga S karena penduga GS diperoleh dari minimasi dugaan M skala selisih sisaan (M estimates of residual differences scales) sedangkan penduga S didapatkan dari minimasi dugaan M skala sisaan (M estimates of residuals
scales). Hal ini menyebabkan penduga GS memiliki efisiensi yang tinggi
sementara penduga S memiliki efisiensi yang rendah. Untuk data yang tidak menyimpang begitu jauh dari asumsi normalitas, penduga GS memberikan hasil yang mendekati penduga kuadrat terkecil, namun tidak demikian halnya dengan penduga S.
Beberapa pendekatan penghitungan yang komprehensif untuk penduga kekar regresi berdasarkan dugaan kekar skala yang dinamakan dengan algoritma cepat telah dikembangkan. Dengan pendekatan ini, masalah adanya beberapa nilai minimum lokal dalam penghitungan minimasi dugaan kekar skala dapat diatasi. Sejauh ini, terdapat tiga algoritma cepat yang telah dikembangkan, yaitu algoritma cepat penduga LTS, algoritma cepat penduga S, dan algoritma cepat penduga τ. Ketiga algoritma cepat ini diterapkan dalam pendugaan parameter model regresi linear berganda.
Di sisi lain, ada juga algoritma cepat penduga GS yang diterapkan untuk pendugaan kekar parameter model regresi linear peubah ganda, namun belum ada kajian tentang algoritma cepat penduga GS untuk pendugaan kekar parameer model regresi berganda. Algoritma cepat penduga GS ini dikembangkan dengan memodifikasi algoritma cepat penduga S. Modifikasi ini dilakukan karena penduga GS dapat dipandang sebagai perluasan penduga S dan untuk mendapatkan penduga dengan efisiensi yang lebih baik. Oleh karena itu penulis tertarik untuk mengembangkan algoritma cepat penduga GS untuk pendugaan kekar parameter model regresi linear berganda dengan memodifikasi algoritma cepat penduga S.
Penelitian ini dilakukan untuk membangun algoritma cepat penduga GS dengan memodifikasi algoritma cepat penduga S dan untuk mengevaluasi hasil penghitungan yang diperoleh dari aplikasi algoritma cepat ini dengan cara membandingkannya dengan hasil yang didapatkan dari penggunaan algoritma cepat penduga S dan metoda kuadrat terkecil. Dalam hal ini pembandingan dilakukan dengan memperhatikan efisiensi yang diukur dengan ܴܯܵܧ karena secara teoritis keunggulan penduga GS dari pada penduga S terletak pada efisiensi. Pembandingan dilakukan pada beberapa kondisi yang berkenaan dengan nilai pencilan sisaan pada data yang dibangkitkan dengan memperhatikan proporsi, rataan, dan ragam pencilan, jumlah peubah penjelas, dan model pembangkit.
Penelitian ini dilaksanakan dalam dua tahap kerja, yaitu tahap pengembangan teori dan simulasi statistika. Pada tahap pengembangan teori dilakukan penurunan formula iteratif untuk penduga GS dan modifikasi algoritma cepat penduga S untuk mengembangkan algoritma cepat penduga GS. Sedangkan pada tahap simulasi statistika, yang dimaksudkan untuk mengevaluasi algoritma cepat penduga GS, dilakukan pembangkitan data, pendugaan parameter model regresi dengan menggunakan ketiga pendekatan pendugaan yang disebutkan di atas, dan pembandingan hasil yang diperoleh.
Sebagaimana halnya algoritma cepat penduga S, algoritma cepat penduga GS dibangun dengan mengkombinasikan algoritma resampling dan algoritma I step. Algoritma resampling merupakan pendekatan untuk memperoleh kandidat awal dugaan parameter regresi dan dugaan skala selisih sisaan yang didapatkan dari penghitungan dugaan parameter regresi untuk data resampel yang diambil dari data asli. Sementara algoritma I step adalah pendekatan untuk memperbaiki kandidat awal dugaan yang diperoleh dengan algoritma resampling. Perbaikan ini diperoleh dalam suatu pengerjaan iteratif dengan melakukan pendugaan kuadrat terkecil terboboti yang pada tiap iterasinya menghasilkan dugaan parameter regresi dengan skala selisih sisaan yang semakin kecil. Dengan kedua algoritma ini, pada algoritma cepat penduga GS, minimasi dugaan kekar skala selisih sisaan dilakukan hanya pada gugus berhingga resampel yang diambil dari data asli dan bukan atas tak hingga banyaknya kandidat dugaan parameter regresi.
Secara ringkas, tata kerja algoritma cepat penduga GS dapat dijabarkan sebagai berikut. Pertama, ambil resampel berukuran (sebanyak jumlah peubah penjelas) lalu hitung dugaan parameter regresi dengan menggunakan data resampel dan hitung dugaan skala selisih sisaan dengan memakai data asli. Kedua, terapkan ܭ௧௦ kali algoritma I step untuk perbaiki kandidat awal dugaan yang
diperoleh pada langkah pertama. Ketiga, terapkan kembali algoritma I step untuk
ܭ௦ kandidat dugaan yang terbaik yaitu dugaan dengan skala selisih sisaan
terkecil hingga dicapai konvergensi. Terakhir, tetapkan penduga akhir dengan mengambil dugaan parameter regresi yang menghasilkan dugaan kekar skala terkecil.
Algoritma cepat penduga GS yang diuraikan di atas, bersamaan dengan algoritma cepat penduga S dan penduga kuadrat terkecil, kemudian digunakan dalam pendugaan parameter model regresi linear berganda dengan menggunakan data simulasi. Data yang dibangkitkan pada simulasi adalah data dengan pencilan sisaan.
Berdasarkan hasil simulasi, ܴܯܵܧ dugaan yang diperoleh dengan algoritma cepat penduga GS lebih kecil dari pada yang didapatkan dengan metoda kuadrat terkecil dan algoritma cepat penduga S untuk jumlah peubah penjelas, proporsi, rataan, dan ragam pencilan yang sama. Hasil ini menunjukkan bahwa dugaan yang diperoleh dengan algoritma cepat penduga GS untuk data dengan pencilan mempunyai efisiensi yang lebih baik dari pada yang diperoleh dengan metoda metoda kuadrat terkecil dan algoritma cepat penduga S dalam semua kondisi. Hal ini sesuai dengan teori penduga GS mempunyai efisiensi yang lebih baik dari pada penduga S.
Begitu pula ܴܯܵܧ dugaaan yang diperoleh dengan algoritma cepat penduga GS maupun algoritma cepat penduga S pada suatu proporsi pencilan tertentu memiliki nilai yang sama meskipun data dibangkitkan dengan pencilan yang
mempunyai rataan dan ragam yang berbeda. Hasil ini menunjukkan perilaku kekekaran penduga GS dan penduga S. Kedua penduga resisten terhadap pencilan.
Namun tidak demikian halnya dengan dugaan yang diperoleh dengan metoda kuadrat terkecil. Dugaan kuadrat terkecil sangat sensitif terhadap pencilan. Sehingga peningkatan rataan pencilan mengakibatkan peningkatan ܴܯܵܧ dugaan secara signifikan. Akan tetapi peningkatan ragam pencilan hanya mengakibatkan sedikit menurunkan nilai ܴܯܵܧ. Penurunan nilai ܴܯܵܧ ini disebabkan oleh fakta bahwa peningkatan ragam menyebabkan nilai pencilan yang dihasilkan lebih menyebar sehingga pencilan yang diperoleh akan mendekati data yang bukan pencilan.
Di sisi lain, hasil yang didapatkan juga menunjukkan bahwa pertambahan jumlah peubah penjelas juga diikuti dengan peningkatan nilai ܴܯܵܧ dugaan yang diperoleh dari ketiga pendekatan. Peningkatan nilai ܴܯܵܧ juga seiring dengan pertambahan proporsi pencilan untuk dugaan yang dihasilkan dengan algoritma cepat penduga GS dan metoda kuadrat terkecil. Sebaliknya, nilai ܴܯܵܧ dugaan yang didapatkan dengan algoritma cepat penduga S cenderung menurun, namun bila dibandingkan dengan ܴܯܵܧ dugaan dari algoritma cepat GS maka nilai yang dihasilkan tetap lebih besar. Hal ini menunjukkan bahwa algoritma cepat penduga GS mempunyai efisiensi yang semakin baik bila digunakan pada data dengan proporsi pencilan yang semakin rendah.
Kondisi yang lebih ekstrim dapat ditemukan pada data tanpa pencilan. Pada data tanpa pencilan, ܴܯܵܧ dugaan yang diperoleh dengan algoritma cepat penduga GS mendekati nilai yang diperoleh dengan metoda kuadrat terkecil. Sementara itu, nilai yang diperoleh dengan algoritma cepat penduga S lebih besar dari apa yang diperoleh dari kedua pendekatan tersebut. Fakta ini sesuai dengan perilaku penduga S yang merupakan penduga kekar yang memiliki nilai titik breakdown yang tinggi namun mempunyai efisiensi yang rendah. Penggunaan penduga S untuk pendugaan parameter model pada data yang tidak begitu jauh menyimpang dari asumsi normalitas menghasilkan nilai dugaan yang tidak baik..
Sementara jika data dibangkitkan secara simultan dengan rataan dan ragam pencilan yang bernilai sama, maka ܴܯܵܧ dugaan yang diperoleh untuk dua model yang berbeda akan bernilai sama pula.
Kata Kunci: algoritma cepat, penduga GS, penduga S, model regresi linear berganda, algoritma resampling, algoritma I-step
© Hak Cipta milik IPB, tahun 2010 Hak Cipta dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan yang wajar IPB.
Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apa pun tanpa izin IPB.
ALGORITMA CEPAT (FAST ALGORITHM) PENDUGA
GENERALIZED-S (GS) UNTUK PENDUGAAN KEKAR
PARAMETER MODEL REGRESI LINEAR BERGANDA
DODI VIONANDA
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Program Studi Statistika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2010
Judul Tesis : Algoritma Cepat (Fast Algorithm) Penduga Generalized-S (GS) untuk Pendugaan Kekar Parameter Regresi Model Linear Berganda
Nama : Dodi Vionanda
NRP : G151070041
Program Studi : Statistika
Disetujui Komisi Pembimbing
Dr. Ir. Asep Saefuddin, M.Sc Agus Mohamad Soleh, S.Si, M.T Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Statistika
Dr. Ir. Aji Hamim Wigena, M.Sc Prof. Dr. Ir. Khairil A. Notodiputro, M.S
PRAKATA
Puji syukur penulis haturkan ke hadirat Allah SWT atas izin-Nya sehingga penulis dapat menyusun proposal penelitian yang berjudul “Algoritma Cepat (Fast Algorithm) Penduga Generalized-S (GS) untuk Pendugaan Kekar Parameter Regresi Model Linear Berganda”.
Terima kasih penulis haturkan kepada Bapak Dr. Ir. Asep Saefuddin, M.Sc, Bapak Agus Mohamad Soleh, S.Si, M.T, Bapak Dr. Ir. Aji Hamim Wigena, M.Sc dan Ibu Dr. Ir. Anik Djuraidah, MS atas bimbingan, masukan dan saran dalam penyusunan tesis ini. Di samping itu, terima kasih juga penulis sampaikan kepada segenap dosen dan karyawan Departemen Statistika FMIPA IPB serta teman-teman di Program Studi Statistika dan Statistika Terapan Sekolah Pascasarjana IPB yang telah banyak membantu dan memberi dukungan kepada penulis.
Akhirnya penulis berharap semoga penelitian ini bermanfaat.
Bogor, Juli 2010
RIWAYAT HIDUP
Penulis dilahirkan di Padang Panjang, Sumatera Barat pada tanggal 11 Juni 1979 dari ayah Suhaimi dan ibu Yusniar. Penulis adalah sulung dari tiga bersaudara.
Penulis menyelesaikan pendidikan menengah di Pondok Pesantren Modern Nurul Ikhlas, X Koto, Tanah Datar, Sumatera Barat pada tahun 1998 dan menamatkan pendidikan sarjana di Jurusan Matematika FMIPA Universitas Negeri Padang pada tahun 2002. Pada tahun 2007 penulis beroleh kesempatan untuk melanjutkan studi ke tingkat magister di Program Studi Statistika Sekolah Pascasarjana IPB.
Penulis saat ini bekerja sebagai staf pengajar di Jurusan Matematika FMIPA Universitas Negeri Padang dan di Pesantren Pramuka Alhira, X Koto, Tanah Datar, Sumatera Barat.
xi
DAFTAR ISI
Halaman
DAFTAR TABEL ... xii
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
PENDAHULUAN ... 1
Latar belakang ... 1
Tujuan penelitian ... 3
Ruang Lingkup Penelitian ... 4
TINJAUAN PUSTAKA ... 5
Pendugaan Kekar Parameter Model Regresi ... 5
Penduga S ... 6
Algoritma Cepat Penduga S ... 8
Penduga GS Parameter Regresi Linear Berganda ... 16
Paket Perangkat Lunak dalam Pendugaan Kekar Parameter Model Regresi ... 17
METODA PENELITIAN ... 19
HASIL DAN PEMBAHASAN ... 21
Algoritma Cepat Penduga GS ... 21
Pembangkitan Data ... 30
Efisiensi Relatif Algoritma Cepat Penduga S dan Algoritma Cepat Penduga GS ... 32
Perbandingan Metoda Kuadrat Terkecil,Algoritma Cepat Penduga S, dan Algoritma Cepat Penduga GS ... 34
SIMPULAN DAN SARAN ... 39
Simpulan ... 39
Saran ... 39
DAFTAR PUSTAKA ... 40
DAFTAR TABEL
Halaman
1 Perbandingan cara kerja penduga S, algoritma cepat penduga S, penduga
GS, dan algoritma cepat penduga GS ... 29
2 Perbedaan Penduga S dan Penduga GS ... 29
3 Efisiensi relatif untuk data dengan dua peubah penjelas ... 33
4 Efisiensi relatif untuk data dengan lima peubah penjelas ... 33
5 Perbandingan dugaan untuk data dengan nilai pencilan ... 35
6 Perbandingan dugaan untuk data tanpa nilai pencilan ... 37
xiii
DAFTAR GAMBAR
Halaman
1 Diagram alir algoritma resampling untuk penduga S ... 9
2 Diagram alir algoritma I-step untuk penduga S ... 12
3 Diagram alir penghitungan kandidat terbaik dalam algoritma cepat penduga S ... 15
4 Diagram alir algoritma cepat penduga S ... 16
5 Diagram tahap kerja penelitian ... 21
6 Diagram alir algoritma resampling untuk penduga GS... 22
7 Diagram alir algoritma I-step untuk penduga GS ... 23
8 Diagram alir penghitungan kandidat terbaik dalam algoritma cepat penduga GS ... 25
9 Diagram alir algoritma cepat penduga GS ... 27
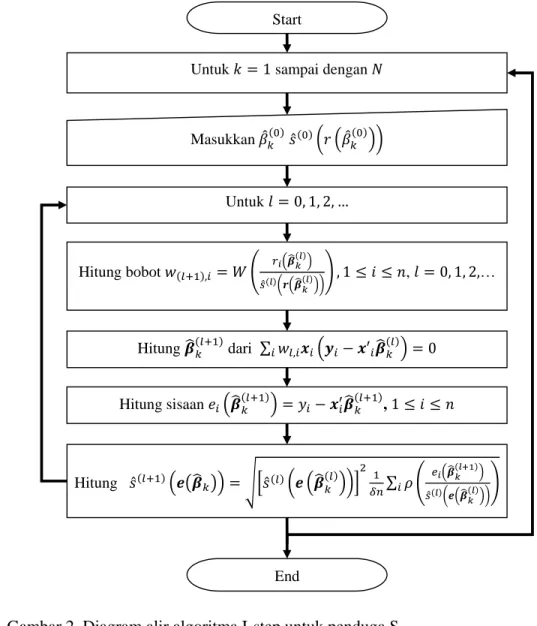
10 Diagram alir penghitungan intersep pada algoritma cepat penduga GS ... 28
11 Plot terhadap untuk data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 5% yang memiliki rataan 10 dan ragam 1 ... 30
12 Plot untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 5% yang memiliki rataan 10 dan ragam 1 ... 31
13 Plot terhadap untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 15% yang memiliki rataan 10 dan ragam 1 ... 31
14 Plot untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 15% yang memiliki rataan 10 dan ragam 1 ... 32
DAFTAR LAMPIRAN
Halaman
1 Kode R algoritma cepat penduga GS ... 43 2 Kode R simulasi dalam evaluasi kinerja algoritma cepat penduga GS ... 47 3 Seeding yang digunakan dalam pembangkitan data ... 48
PENDAHULUAN
Latar Belakang
Penduga kuadrat terkecil merupakan penduga yang umum digunakan dalam pendugaan parameter model regresi. Hal ini disebabkan oleh mudahnya penghitungan penduga ini dan sifatnya sebagai penduga tak bias terbaik untuk parameter model regresi jika data yang digunakan memenuhi asumsi klasik. (Draper & Smith 1998: 34-38). Namun asumsi yang disyaratkan ini jarang terpenuhi dengan sempurna pada data riil. Salah satu kenyataan yang kerap ditemukan adalah adanya data dengan nilai pencilan pada sisaan yang mengakibatkan gagalnya pemenuhan asumsi normalitas galat (Montgomery & Peck 1991: 382-383). Aplikasi penduga kuadrat terkecil pada kondisi ini menghasilkan dugaan yang tidak bagus. Dengan demikian diperlukan teknik pendugaan parameter regresi yang resisten terhadap pencilan yang dinamakan dengan pendugaan kekar (robust estimation).
Menurut Ryan (1997: 354-356) terdapat empat kelompok penduga kekar parameter model regresi, yaitu: penduga M, penduga pengaruh terbatas, penduga dengan titik breakdown tinggi, dan penduga prosedur dua tahap. Penduga M (Huber 1973) dan penduga pengaruh terbatas, yang dinamakan juga dengan penduga GM, merupakan penduga kekar yang memiliki titik breakdown yang rendah. Sedangkan kelompok penduga yang ketiga, sesuai dengan namanya, memiliki titik breakdown yang tinggi tetapi mempunyai efisiensi yang rendah. Penduga yang termasuk dalam kelompok ini adalah penduga LTS (Rousseeuw 1984), LMS (Hampel 1975, diacu dalam Rousseeuw & Yohai 1984), dan penduga S (Rousseeuw &Yohai 1984). Ketiga penduga ini diperoleh dengan pendekatan pendugaan kekar parameter regresi berdasarkan dugaan kekar skala. Sementara penduga prosedur dua tahap adalah kombinasi dua penduga dari kelompok yang berbeda. Penduga MM (Yohai 1987) yang dibangun dari kombinasi penduga S dan penduga M termasuk dalam kelompok ini.
Penduga MM mempunyai nilai titik breakdown yang tinggi dan efisiensi yang tinggi sehingga penduga ini memenuhi kriteria yang diharapkan untuk suatu penduga kekar. Suatu penduga kekar diharapkan menghasilkan dugaan yang tidak
2
terpengaruh oleh nilai pencilan ketika data memuat sisaan dengan nilai pencilan dan memberikan dugaan yang mendekati hasil yang didapatkan dengan metoda kuadrat terkecil ketika data tidak begitu jauh menyimpang dari asumsi normalitas. Sifat yang pertama merujuk kepada nilai titik breakdown yang tinggi sedangkan yang kedua merujuk kepada efisiensi yang tinggi.
Di samping keempat kelompok penduga kekar di atas terdapat pula dua penduga kekar yang lain, yaitu penduga ߬ (Yohai & Zamar 1988) dan penduga GS (Generalized S) (Croux et al. 1994). Kedua penduga ini memiliki kemiripan dengan penduga yang memiliki titik breakdown yang tinggi karena termasuk ke dalam penduga kekar berdasarkan dugaan kekar skala.
Penduga GS dapat dipandang sebagai perluasan penduga S. Penduga GS ialah solusi minimasi dugaan M skala selisih sisaan sedangkan penduga S adalah solusi minimasi dugaan M skala sisaan. Penduga ini dikemukakan oleh Croux et
al. (1994) untuk pendugaan parameter model regresi linear berganda. Roelant et al. (2009) kemudian mengemukakan penduga GS untuk pendugaan parameter
model regresi linear peubah ganda. Menurut Roelant et al. (2009), penduga GS parameter model regresi linear peubah ganda merupakan solusi minimasi determinan dugaan kekar matriks pencar selisih sisaan.
Komputasi pendugaan parameter model regresi berganda berdasarkan dugaan kekar skala sisaan dihadapkan kepada kendala adanya beberapa nilai minimum lokal dalam minimasi dugaan kekar skala. Permasalahan ini diatasi dengan penggunaan algoritma resampling yang diperkenalkan oleh Rousseeuw dan Leroy (1987: 197-204) yang mengaplikasikan pendekatan ini dalam penghitungan penduga LMS. Pendekatan yang sama juga digunakan oleh Rousseeuw dan Basset (1991) dalam penghitungan penduga LTS. Di samping itu mereka menambahkan bahwa aplikasi algoritma resampling pada penghitungan penduga S memerlukan waktu komputasi yang lama.
Dengan mengkombinasikan algoritma resampling dengan metoda pembobotan ulang iteratif (Huber 1981: 179-192; Huber & Ronchetti 2009: 175-186), Rousseeuw dan Driessen (2002) kemudian memperkenalkan algoritma cepat (fast algorithm) untuk penduga LTS. Gagasan yang mereka kemukakan selanjutnya dikembangkan oleh Salibian-Barrera dan Yohai (2006) untuk
3
membangun algoritma cepat penduga S dan oleh Salibian-Barrera et al. (2008) untuk membangun algoritma cepat penduga ߬. Pendekatan yang sama juga diterapkan oleh Roelant et al. (2009) pada penduga GS untuk pendugaan parameter model regresi linear peubah ganda. Roelant et al. (2009) memodifikasi algoritma cepat penduga S.
Di sisi lain, beberapa piranti lunak statistika telah memuat pendugaan kekar parameter model regresi. Sejauh ini, untuk piranti lunak SAS, STATA, dan R, pendekatan yang digunakan adalah penduga M, LTS, LMS, S, dan MM. Ketiga piranti belum menyertakan penduga ߬ dan penduga GS. Penjelasan lebih lanjut tentang hal ini dibahas pada bagian Tinjauan Pustaka.
Berdasarkan pemikiran di atas, penulis tertarik untuk mengembangkan algoritma cepat untuk penduga GS regresi berganda dengan memodifikasi metoda yang dipakai dalam pengembangan algoritma cepat penduga S dan membandingkan hasil dugaan yang diperoleh dari algoritma cepat penduga GS dengan hasil yang didapatkan dari algoritma cepat penduga S dan metoda kuadrat terkecil pada beberapa kondisi dengan memperhatikan proporsi, lokasi, dan skala pencilan dalam data, jumlah peubah penjelas, dan model.
Tujuan Penelitian Penelitian ini bertujuan untuk:
1 Memodifikasi algoritma cepat S guna mengembangkan algoritma cepat penduga GS untuk parameter model regresi linear berganda dengan memodifikasi algoritma cepat penduga S;
2 mengevaluasi efisiensi dugaan yang diperoleh dari algoritma cepat penduga GS dengan membandingkan hasil yang didapatkan terhadap nilai dugaan yang dihasilkan dari algoritma cepat penduga S dan penduga kuadrat terkecil dengan membandingkan nilai efisiensi relatif algoritma cepat GS dan algoritma cepat S dan nilai ܴܯܵܧ dugaan dari ketiga pendekatan.
4
Ruang Lingkup Penelitian Ruang lingkup penelitian ini mencakup:
1 model regresi linear berganda dengan intersep namun tidak mencakup model tanpa intersep karena penduga GS hanya bisa digunakan pada model dengan intersep;
2 penerapan algoritma cepat penduga GS untuk pendugaan paramater model tetapi tidak meliputi kajian tentang uji hipotesis dan selang kepercayaan.
TINJAUAN PUSTAKA
Pendugaan Kekar Parameter Model Regresi
Secara umum model regresi linear berganda diformulasikan dalam bentuk ′ , 1, … , , dengan adalah peubah acak (random variables) saling bebas yang dinamakan peubah respons, , … , adalah parameter regresi, , … , ′ adalah peubah tetap (fixed variables) berdimensi yang disebut peubah penjelas, dan adalah peubah acak yang dinamakan bentuk galat. Jika model memuat intersep, maka 1, , … ,
′ dan , , … , . Misalkan adalah penduga parameter regresi, vektor sisaan , … , ′ diperoleh dari ′ , 1 dan skala sisaan didapatkan dari pemetaan sisaan ke bilangan riil dengan 0, untuk 0,
| |, … , | | , … , , dan , … , , … , di mana , … , adalah sebarang permutasi 1, … , .
Dalam pendugaan kekar parameter regresi, dugaan kekar skala sisaan bisa diduga secara terpisah atau pun bersamaan dengan pendugaan parameter regresi. Dugaan kekar skala sisaan yang diperoleh secara terpisah digunakan untuk pendugaan kekar parameter regresi yang didasarkan pada pendugaan kekar lokasi. Dugaan kekar skala sisaan yang didapatkan secara bersamaan dipakai untuk pendugaan kekar parameter regresi yang dinamakan dengan pendugaan kekar parameter berdasarkan dugaan kekar skala sisaan.
Penduga kekar yang termasuk pada kelompok pertama merupakan penduga kekar dengan nilai titik breakdown yang rendah. Sejumlah kecil nilai pencilan dalam data dapat merusak dugaan yang diperoleh dengan penduga ini. Sebaliknya, penduga pada kelompok kedua merupakan penduga kekar dengan nilai titik breakdown yang tinggi. Dengan demikian kelompok penduga yang terakhir memenuhi salah satu dari dua kriteria yang diharapkan untuk suatu penduga kekar selain efisiensi yang tinggi sebagaimana yang telah dikemukakan pada bahagian pendahuluan.
6
Berkenaan dengan efisiensi, Ryan (1997: 354) mengemukakan suatu besaran yang disebut dengan efisiensi relatif. Jika data tidak memuat data dengan nilai pencilan, maka efisiensi relatif adalah rasio kuadrat tengah galat yang didapatkan dengan penduga kekar terhadap hasil yang diperoleh dari metoda kuadrat terkecil. Untuk penduga dengan efisiensi yang tinggi, nilai rasio ini diharapkan mendekati 1. Sementara itu, jika data memuat nilai pencilan, maka efisiensi relatif ialah rasio kuadrat tengah galat yang didapatkan dengan penduga kekar terhadap hasil yang diperoleh dari metoda kuadrat terkecil yang dihitung tanpa menyertakan data dengan nilai pencilan.
Penduga S
Penduga S adalah salah satu penduga dengan titik breakdown tinggi namun memiliki efisiensi yang rendah. Penduga ini diperoleh dari minimasi dugaan M skala sisaan.
Definisi 1. Misalkan penduga dan , … , ′ vektor sisaan. Penduga S didefinisikan sebagai argmin ̂ dengan ̂ diperoleh dari dugaan M skala sisaan yang merupakan solusi ∑ ̂ . (Rousseeuw & Yohai 1984)
Penduga S dapat dinyatakan dalam bentuk lain, yaitu argmin ∑ ̂ . Bentuk yang terakhir ini bisa representasikan dengan sistem persamaan yang merupakan formula penghitungan simultan pendugaan kekar parameter regresi dan pendugaan kekar skala (Maronna et al. 2006: 103; Huber & Ronchetti 2009: 174), yaitu:
1
̂
̂ 0
. 1
Besaran pada sistem persamaan di atas adalah peubah kendali dengan nilai 0.5. Sedangkan fungsi merupakan suatu fungsi simetrik yang memenuhi beberapa asumsi, yaitu untuk setiap dan 0 0, bersifat
7
differentiable (dapat diturunkan) dan turunannya bersifat kontinu, sup 1,
dan jika 1 dan 0 maka . Sementara fungsi adalah turunan fungsi yang memenuhi beberapa asumsi, yakni: untuk 0 dan fungsi terbatas, fungsi tidak turun dan lim ∞ 0, fungsi kontinu, dan | | 1 untuk .
Dalam literatur statistika kekar dikenal beberapa jenis fungsi , namun dalam tulisan ini hanya dipakai fungsi biweight Tukey atau bisquare Tukey, yaitu:
1 1 , jika | | 1 , jika | | 2 dengan turunan 1 , jika | | 0, jika | | . 3 Besaran pada Persamaan (2) dan (3) adalah tuning constant yang dihitung berdasarkan efisiensi asimtotik dugaan dan bernilai 1.547 untuk penduga S (Rousseeuw & Yohai 1984: 261).
Penduga S dihitung dengan metoda projection pursuit (Rousseeuw & Yohai 1984) atau dengan menerapkan algoritma resampling (Rousseeuw & Leroy 1987) yang dilanjutkan dengan langkah perbaikan lokal (Rupert 1992 diacu dalam Salibian-Barrera & Yohai 2006). Pada langkah perbaikan lokal ini dilakukan perbaikan lokal atas kandidat dugaan yang diperoleh dari algoritma resampling yang menurunkan nilai fungsi objektif.
Pendekatan yang lebih baik kemudian dikemukakan oleh Salibian-Barrera dan Yohai (2006) yang dinamakan dengan algoritma cepat penduga S. Berbeda dengan metoda yang diterapkan pada langkah perbaikan lokal, pada algoritma cepat penduga S kandidat dugaan dari semua resampel diperbaiki. Sehingga jumlah resampel yang diperlukan dalam algoritma cepat penduga S untuk memperoleh penduga dengan nilai titik breakdown tinggi lebih sedikit dari pada yang dibutuhkan dalam langkah perbaikan lokal.
8
Algoritma Cepat Penduga S
Algoritma cepat penduga S dikembangkan dengan mengkombinasikan konsep algoritma resampling (Rousseeuw & Leroy 1987) dan metoda pembobotan ulang iteratif (Huber 1981 179-192). Kombinasi ini membedakan pendekatan yang digunakan dalam algoritma cepat penduga S dengan yang diterapkan dalam penghitungan penduga S sebelumnya.
Algoritma resampling adalah algoritma pengambilan secara acak resampel berukuran dari data untuk mencari dan ̂ yang merupakan nilai awal kandidat dugaan kekar regresi dan kandidat dugaan kekar skala sisaan ̂ pada resampel ke- dengan 1, … , . adalah dugaan kuadrat terkecil untuk data resampel dan ̂ ialah dugaan kekar skala sisaan yang diperoleh dengan data asli dengan rumus
̂ . , 1, . . , . Gambar 1 mendeskripsikan diagram alir algoritma resampling.
Penerapan algoritma resampling mereduksi komputasi karena pendekatan ini mengurangi jumlah penghitungan yang diperlukan dalam minimasi ̂
dari minimasi atas tak hingga banyaknya kandidat menjadi minimasi atas gugus berhingga resampel (Maronna et al. 2006: 136-147).
Jumlah resampel ditentukan dari formula | | dengan proporsi data pencilan dalam subsampel dan nilai peluang dimana 1 merupakan peluang terambil paling sedikit satu subsampel dari subsampel yang tidak memuat data pencilan. Daftar nilai untuk 1 0.95 dapat dilihat pada Leroy dan Rousseeuw (1987: 198) dan untuk 1 0.99 pada Maronna et
9
Gambar 1 Diagram alir algoritma resampling untuk penduga S
Menurut Maronna et al. (2006: 138), penentuan nilai dengan formula di atas memastikan bahwa algoritma resampling mempunyai breakdown yang tinggi tetapi tidak memberikan hampiran kandidat dugaan yang baik untuk menghasilkan nilai minimal lokal dugaan kekar skala sisaan ̂ satu gugus resampel. Oleh karena itu hampiran yang diperoleh perlu diperbaiki dengan menerapkan pengerjaan iteratif yang dinamakan dengan algoritma I-step yang dikembangkan oleh Salibian-Barrera dan Yohai (2006).
Salibian-Barrera dan Yohai (2006) membangun algoritma I-step dengan memodifikasi algoritma concentration step (C-step) yang diterapkan dalam algoritma cepat penduga LTS yang dikemukakan oleh Rousseeuw dan Driesen (2006). Mereka memodifikasi C-step menjadi local improvement step (I-step).
Baik algoritma C step maupun algoritma I step dibangun berdasarkan konsep pembobotan ulang iteratif yang dikemukakan Huber (1981: 179-192). Menurut Huber, minimasi dalam penghitungan untuk pendugaan kekar parameter regresi berdasarkan dugaan kekar skala sisaan dapat dilakukan dengan menggunakan konsep titik akumulasi yang merupakan gugus titik dengan nilai
Start
Untuk 1 sampai dengan
Hitung dugaan kuadrat terkecil berdasarkan data resampel
ke-Dengan data asli, hitung sisaan Ambil resampel berukuran
Hitung dugaan kekar skala ̂
10
limit titik yang sama dengan nilai minimum lokal fungsi loss. Gugus titik ini diperoleh dengan menerapkan teknik modifikasi sisaan atau teknik modifikasi bobot dugaan dalam penyelesaian iteratif minimisasi fungsi loss.
Pada pendekatan modifikasi sisaan dilakukan penggantian sisaan dengan sisaan terwinsorisasi sedangkan pada pendekatan modifikasi bobot dugaan dilakukan perbaikan bobot dugaan pada tiap iterasi. Metoda yang terakhir inilah yang dinamakan dengan metoda pembobotan ulang iteratif. Dengan menggunakan skala yang sama untuk tiap iterasi pada metoda pembobotan ulang iteratif, nilai hampiran dugaan regresi yang didapatkan konvergen menuju ke suatu nilai yang menghasilkan skala dengan nilai minimum. Huber menambahkan bahwa, nilai hampiran yang dihasilkan dengan metoda ini lebih cepat konvergen dari pada nilai hampiran yang didapatkan dengan cara sisaan termodifikasi.
Namun, Salibian-Barrera dan Yohai (2006) mengemukakan pendapat berbeda. Menurut mereka skala yang digunakan dalam penghitungan mesti diperbaharui pada tiap iterasi. Meskipun secara teoritis kebenaran pernyataan ini belum bisa dibuktikan, tetapi secara simulasi pendekatan ini meningkatkan efisiensi komputasi. Lebih lanjut, menurut Salibian-Barrera dan Yohai (2006), untuk sebarang nilai awal , sebarang titik akumulasi dari barisan yang diperoleh dengan menerapkan kali algoritma I-step secara iteratif adalah minimum lokal ̂ .
Pembahasan yang analog dengan metoda pembobotan ulang iteratif dapat ditemukan dalam Maronna et al.(2006). Berdasarkan Maronna et al.(2006: 136), untuk penduga S, penghitungan yang dilakukan merupakan pendugaan kuadrat terkecil terboboti iteratif dengan skala yang diperbaiki pada tiap iterasi. Formula yang digunakan untuk kedua penghitungan dapat dilihat pada Maronna et
al.(2006: 41, 105). Kedua formula ini sebenarnya merupakan penghitungan
iteratif untuk Sistem Persamaan (1).
Berdasarkan formula yang dikemukakan Maronna et al.(2006) di atas, maka formula dugaan kekar skala sisaan pada iterasi ke- 1 , ̂
11 ̂ ̂ 1 ̂ , 4 untuk 0, 1, 2, … dan nilai awal dan ̂ yang didapatkan dengan algoritma resampling. Sedangkan dugaan kekar parameter regresi
pada iterasi ke- 1 diperoleh dengan menyelesaikan persamaan:
, 0 5
dengan
,
̂ , 1 6 dimana untuk fungsi pada Persamaan (3). Persamaan (5) adalah bentuk lain persamaan kedua pada Sistem Persamaan (1) dan merupakan persamaan normal terboboti, sehingga bisa dilihat sebagai dugaan kuadrat terkecil regresi , terhadap , . Misalkan hasil diperoleh di sini dilambangkan dengan dan ̃ . Diagram alir algoritma I-step diilustrasikan pada Gambar 2.
Setelah aplikasi algoritma I step dengan menggunakan nilai awal kandidat dugaan regresi dan dugaan skala pada tiap resampel yang diperoleh dengan algoritma resampling, maka diperoleh kandidat dugaan parameter regresi yang telah diperbaiki yang menghasilkan skala yang merupakan minimum lokal. Dengan demikian penghitungan dilanjutkan untuk mendapatkan dugaan parameter regresi yang memberikan skala dengan nilai minimum global.
Menurut Maronna et al. (2006: 138-139), terdapat dua pendekatan dalam pencarian nilai minimum global tersebut, yaitu dengan menjadikan kandidat dugaan kekar parameter regresi yang menghasilkan dugaan kekar skala dengan nilai terkecil sebagai nilai awal yang digunakan dalam penghitungan iteratif dengan algoritma I-step hingga diperoleh hasil yang konvergen ke suatu nilai, atau dengan menjadikan kandidat dugaan kekar regresi dan dugaan kekar skala dari semua gugus resampel sebagai nilai awal yang dipakai dalam penghitungan iteratif dengan algoritma I-step untuk mendapatkan kandidat dugaan kekar skala
12
yang konvergen ke nilai minimum lokal pada tiap gugus resampel lalu menjadikan kandidat dugaan kekar regresi yang mempunyai dugaan kekar skala terkecil sebagai hasil akhir.
Gambar 2 Diagram alir algoritma I-step untuk penduga S
Kedua alternatif di atas mempunyai kelebihan dan kekurangan. Pendekatan pertama memerlukan penghitungan yang sederhana namun memberikan hampiran dugaan kekar regresi yang kurang bagus, sedangkan yang kedua memberikan hampiran dugaan yang lebih bagus namun memerlukan penghitungan yang besar. Oleh karena itu, kedua pendekatan tersebut dikombinasikan dengan cara menerapkan I-step sebanyak kali pada tiap gugus resampel yang didapatkan dengan algoritma resampling lalu sebanyak kandidat dugaan
Start
Untuk 1 sampai dengan
Masukkan ̂ Untuk 0, 1, 2, … Hitung bobot , ̂ , 1 , 0, 1, 2,… Hitung dari ∑ , 0 Hitung sisaan , 1 Hitung ̂ ̂ ∑ ̂ End
13
terbaik untuk parameter regresi dengan skala sisaan dihitung kembali dengan algoritma I-step hingga diperoleh dugaan kekar skala yang konvergen ke nilai minimum lokal. Pendekatan ini dimaksudkan untuk memastikan bahwa pengerjaan hanya dilakukan untuk kandidat dugaan terbaik. Proses di atas dijabarkan sebagai berikut:
1 Untuk 1 , hitung dan ̃ , 0,1,2, …, hingga konvergen dengan algoritma I-step untuk nilai awal dan
̃ , bangun gugus pasangan dugaan
, ̃ , 1 dan misalkan
max ̃ ;
2 untuk , jika ∑ maka hitung
dan ̃ hingga konvergen dengan algoritma I-step, perbaharui
gugus pasangan , ̃ yang sudah ada dengan
mensubstitusi nilai dugaan dan ̃ yang baru diperoleh dan mengeluarkan pasangan yang hasilkan pada iterasi sebelumnya,
dan hitung kembali max ̃ ;
3 ulangi langkah 2 hingga .
Misalkan dugaan regresi dan dugaan kekar skala sisaan yang dihasilkan pada tahap ini adalah dan ̃ , 1 . Dalam tulisan ini diambil 5 dan 3. Diagram alir untuk pendekatan di atas diilustrasikan pada Gambar 3.
Berdasarkan uraian di atas, algoritma cepat penduga S untuk pendugaan parameter model regresi linear berganda dapat diilustrasikan dengan diagram alir pada Gambar 4 dengan tahap kerja seperti di bawah ini.
14
1 Ambil subsampel berukuran yang tidak kolinear dari data asli, hitung dugaan , 1, … , dengan metoda kuadrat terkecil berdasarkan data subsampel, dan hitung ̂ dengan menggunakan data asli;
2 terapkan kali I-step untuk memperoleh dugaan yang diperbaiki yang dilambangkan dengan dan ̃ dengan menggunakan nilai
awal dugaan regresi dan dugaan kekar skala sisaan ̂ ;
3 hitung dugaan kekar regresi dan dugaan kekar skala sisaan dengan menerapkan I-step untuk kandidat penduga yang terbaik hingga konvergen dengan nilai awal dan ̃ dan menghasilkan dan
̃ , 1 ;
4 ambil dugaan dengan dugaan kekar skala sisaan ̃ yang minimal sebagai dugaan regresi .
15
Gambar 3 Diagram alir penghitungan kandidat terbaik dalam algoritma cepat penduga S
Start Untuk 1sampai
dengan
Hitung dengan I-step
dan ̃ , hingga konvergen Bangun gugus pasangan dugaan , ̃ Hitung sebagai max ̃ Ya
Masukkan nilai dan
̃
Hitung dengan I-step hingga konvergen
dan ̃
Perbaharui gugus pasangan dugaan dengan substitusi nilai yang baru diperoleh
, ̃
Ya Tidak
Tidak
max ̃
Hitung kembali sebagai
16
Gambar 4 Diagram alir algoritma cepat penduga S
Penduga GS Parameter Regresi Linear Berganda
Penduga GS (Generalized S) adalah solusi minimasi dugaan M skala selisih sisaan. Penggunaan dugaan M skala selisih ini menyebabkan penduga GS mempunyai efisiensi yang lebih baik dari pada penduga S.
Definisi 2. Misalkan penduga , , … , ′ vektor sisaan
dengan ′ , 1 , dan ∆ ∆ , … , ∆
′
vektor selisih sisaan dengan ∆ ′ ′ , 1 ′ . Penduga GS didefinisikan sebagai argmin ̂ ∆ dengan ̂ ∆ diperoleh dari penduga M skala selisih sisaan ∆ yang merupakan solusi
∑ ∆ ′
̂ ∆
′ (Croux et al. 1994). Start
Masukkan data
ambil resampel berukuran , hitung dugaan ,
1, … , ̂
terapkan kali I-step untuk memperoleh dan
̃ dengan nilai awal dan ̂
hitung dugaan dan ̃ , 1
dengan I-step untuk kandidat penduga yang memenuhi syarat hingga konvergen dengan nilai awal dan ̃
ambil dugaan dengan dugaan kekar skala sisaan ̃ yang minimal sebagai dugaan regresi
17
Analog dengan penduga S, penduga GS dapat dinyatakan dalam bentuk lain, yaitu argmin ∑ ′ ∆̂ ∆ ′ atau dalam bentuk sistem
1 ∆ ′ ̂ ∆ ′ ∆ ′ ̂ ∆ ′ ′ 0 . 7
Besaran pada Persamaan (7) merupakan peubah kendali yang juga bernilai 0.5. Sedangkan tuning constant yang digunakan bernilai 0.9958 (Hossjer et al. 1994: 158). Penduga GS hanya digunakan untuk pendugaan model dengan intersep dan dugaan intersep diperoleh dari pendugaan kekar lokasi sisaan ′ untuk yang diperoleh dari pendugaan yang tidak menyertakan intersep karena bentuk ̂ ∆ tidak bergantung pada intersep. Penduga S dan penduga GS merupakan penduga yang konsisten dan menyebar normal asimtotik (Hossjer et
al. 1994, Salibian-Barrera & Yohai 2006).
Menurut Croux et al. (1994) komputasi penduga GS dilakukan dengan menggunakan algoritma resampling yang disertai dengan langkah peningkatan lokal seperti yang diterapkan Ruppert (1992 diacu dalam Croux et al. 1994) dalam penghitungan penduga S.
Paket Piranti Lunak dalam Pendugaan Kekar Parameter Model Regresi Terdapat dua penduga kekar parameter regresi yang diaplikasikan pada perangkat lunak SAS, yakni penduga LTS dan LMS. Keduanya terhimpun dalam SAS/IML dan SAS/STAT. Pada SAS/IML, aplikasi penduga LTS dan LMS dilakukan dengan menggunakan sintaks call lts dan call lms. Sementara pada SAS/STAT, kedua penduga kekar tersebut termasuk dalam PROC ROBUSTREG. Algoritma yang digunakan dalam penghitungan penduga LTS adalah algoritma cepat penduga LTS (Rousseeuw & Driesen 2006) (SAS Institute 2008).
Piranti lunak STATA menyertakan enam metoda untuk pendugaan kekar parameter model regresi, yaitu penduga atau penduga median regresi, penduga M, penduga LMS, penduga LTS, penduga S, dan penduga MM. Penduga median
18
regresi dalam STATA memiliki fungsi baku dengan perintah qreg, penduga M dengan rreg, penduga LMS dengan lmsregress, penduga LTS dengan ltsregress, dan penduga MM dengan MMregress, tetapi tak terdapat sintaks khusus untuk penduga S. Penduga S pada perangkat lunak ini digunakan dalam penghitungan nilai awal yang digunakan pada penduga MM. Dalam penghitungan penduga M digunakan fungsi biweight Tukey. Dalam penghitungan penduga MM, penduga S dihitung dengan menggunakan algoritma cepat penduga S (Salibian-Barrera & Yohai 2006) (Verardi & Croux 2009).
Paket pendekatan pendugaan kekar parameter regresi yang lebih lengkap dapat ditemukan pada piranti R. Beberapa pendekatan-pendekatan dimaksud terhimpun dalam library robust, robustbase, dan MASS. Pada library robust terdapat perintah lmRob. Pada library robustbase ada perintah lmrob, lmrob..M..fit, lmrob.fit.MM, lmrob.S, dan ltsReg. Pada library MASS terdapat perintah lqs dan rlm.
Perintah lmRob pada library robust digunakan untuk menghitung dugaan kekar dengan titik breakdown dan efisiensi yang tinggi. lmrob pada library robustbase dipakai untuk menghitung dugaan MM yang merupakan kombinasi penduga M dan penduga S yang dihitung dengan lmrob.M.fit dan lmrob.S. Sedangkan sintaks lmrob..M..fit digunakan untuk melakukan iterasi kuadrat terkecil terboboti guna mencari penduga M regresi dengan fungsi biweight Tukey. Perintah ini menghasilkan dugaan MM jika diawali dengan nilai awal dugaan S. Sementara ltsReg diaplikasikan untuk memperoleh dugaan LTS. Sintaks lqs pada library MASS digunakan untuk menghitung dugaan regresi dari data yang “bagus”. Pada lqs terdapat opsi ltsreg dan lmsreg untuk menghitung dugaan LTS dan LMS. Terakhir, perintah rlm dipakai untuk penghitungan penduga M regresi.
METODOLOGI PENELITIAN
Penelitian ini terdiri dari dua tahap, yaitu pengembangan teori dan simulasi statistika. Pengembangan teori meliputi:
1 Penurunan formula penghitungan iteratif penduga GS parameter model regresi berganda dengan intersep yang akan digunakan dalam membangun algoritma cepat penduga GS.
2 Modifikasi algoritma cepat penduga S untuk pengembangan algoritma cepat penduga GS.
Simulasi statistika dilakukan dengan menggunakan bahasa pemrograman (R Development Core Team, Vienna, Austria). Pada simulasi ini, kode R untuk algoritma cepat penduga S yang digunakan diunduh dari http://www.stat.ubc.ca /~matias/ fasts.txt dan kode R untuk algoritma cepat GS yang diterapkan seperti dicantumkan pada Lampiran 1. Kedua algoritma diaplikasikan dalam simulasi dengan kode R seperti pada Lampiran 2 dan pengerjaan yang dilakukan meliputi: 1 Pembangkitan data dengan ukuran contoh 60, dan jumlah peubah 2
dan 5 dengan langkah pengerjaan: a penetapan vektor parameter model ,
b pembangkitan matriks peubah penjelas ~ , , c pembangkitan vektor peubah acak galat yang terdiri:
i 1 100% titik data yang “bagus” dengan galat ~ 0, 1 , ii 100% titik data yang “tidak bagus” dengan galat ~ ,
dimana 0.05 dan 0.15 merupakan proporsi data dengan nilai pencilan, 10 dan 100 rataan pencilan, dan 1 dan 3 ragam pencilan.
d penghitungan nilai vektor peubah respons dengan persamaan . Pembangkitan data dilakukan dengan menggunakan model regresi dengan intersep dan ditujukan untuk memperoleh data yang memuat pencilan sisaan. Pembangkitan data dilaksanakan untuk dua model regresi. Di samping itu, pembangkitan juga dilaksanakan untuk memperoleh gugus data yang tidak memuat nilai pencilan. Pembangkitan ketiga kriteria data di atas dilakukan secara simultan guna memperoleh data yang memiliki bahagian data “bagus” yang sama. Sehingga pembandingan yang dilakukan sepenuhnya berkenaan
20
dengan bahagian data yang”tidak bagus”. Pembangkitan data dilakukan sebanyak 50 kali ulangan.
2 Pendugaan parameter model regresi dengan menggunakan data yang dibangkitkan dengan menerapkan pendekatan kuadrat terkecil, algoritma cepat penduga S, dan algoritma cepat penduga GS.
3 Pembandingan efisiensi relatif dugaan yang diperoleh dengan algoritma cepat penduga S dengan yang didapatkan dengan algoritma cepat penduga GS pada kasus tanpa data pencilan dan kasus dengan 5% data pencilan. Pada kondisi tanpa data pencilan, efisiensi relatif adalah rasio kuadrat tengah galat dugaan kekar terhadap kuadrat tengah galat dugaan kuadrat terkecil. Sementara pada keadaan dengan 5% data pencilan, efisiensi relatif adalah rasio kuadrat tengah galat dugaan kekar terhadap kuadrat tengah galat dugaan kuadrat terkecil untuk data yang “bagus” saja.
4 Pembandingan penduga yang diperoleh dengan ketiga pendekatan di atas yang dihitung dengan rumus ∑ dengan parameter model yang ditetapkan dan dugaan parameter regresi untuk ulangan ke . Pembandingan ini dilakukan untuk menyelidiki efisiensi dugaan algoritma cepat penduga GS dalam beberapa kondisi yang dicobakan relatif terhadap efisiensi dugaan algoritma cepat penduga S dan metoda kuadrat terkecil.
21
Gambar 5 Diagram tahap kerja penelitian
Penurunan formula penghitungan iteratif
penduga GS
Modifikasi algoritma cepat penduga S untuk pengembangan algoritma
cepat penduga GS
Pembangkitan data Pendugaan parameter model berdasarkan data
yang dibangkitkan dengan menggunakan algoritma cepat penduga
GS, algoritma cepat penduga S, dan metoda
kuadrat terkecil Pembandingan RMSE dugaan yang diperoleh dengan algoritma cepat penduga GS, algoritma cepat penduga S, dan metoda kuadrat terkecil Pengembangan Teori
Metoda Penelitian
HASIL DAN PEMBAHASAN Algoritma Cepat Penduga GS
Sebagaimana halnya dengan algoritma cepat penduga S, algoritma cepat penduga GS dikembangkan dengan mengkombinasikan algoritma resampling dan algoritma I-step. Dalam hal ini, algoritma resamping dan algoritma I-step yang digunakan dalam algoritma cepat penduga S dimodifikasi guna menyelaraskan formula yang diterapkan dengan rumusan yang dipakai dalam penghitungan penduga GS. Inti dari modifikasi ini terletak pada penggantian skala sisaan dengan skala selisih sisaan dalam semua penghitungan. Untuk algoritma resampling, hasil modifikasi dimaksud diintegrasikan dalam langkah penghitungan algoritmik yang dibahas pada paragraf di bawah ini. Sementara untuk algoritma I-step, formula iteratif yang telah dimodifikasi dapat dilihat pada Persamaan (8) dan Persamaan (9).
Algoritma resampling untuk algoritma cepat penduga GS diawali dengan pengambilan secara acak resampel berukuran dari data untuk mendapatkan dan ̂ ∆ yang merupakan nilai awal kandidat dugaan kekar parameter regresi dan kandidat dugaan kekar skala sisaan ̂ ∆ pada resampel ke- dengan 1, … , . Dalam hal ini, adalah dugaan kuadrat terkecil yang dihitung dengan data resampel dan ̂ ∆ ialah dugaan kekar skala selisih sisaan yang diperoleh dengan data asli dengan rumus
̂ ∆ ∆ ′
. , 1 ′ . Proses ini diilustrasikan dengan
diagram alir Gambar 6.
Sementara itu, untuk algoritma I-step, formula iteratif penghitungan dugaan kekar skala sisaan ke- 1 , ̂ ∆ yang dirumuskan sebagai:
̂ ∆ ̂ ∆ 1 ∆
22
Gambar 6 Diagram alir algoritma resampling untuk penduga GS dan dugaan kekar regresi dari penyelesaian persamaan:
, 0 9
dengan ,
∆ ′
̂ ∆ , 1 dimana untuk
fungsi pada Persamaan (3). Misalkan hasil yang diperoleh di sini dilambangkan dengan dan ̃ ∆ . Diagram alir algoritma I-step dalam konteks ini diilustrasikan pada Gambar 7 dan proses penghitungannya dijabarkan sebagai berikut:
Untuk 0,1, … hitung: 1 bobot , ′ ∆ ′
̂ ∆ , 1
′ ; Start
Untuk 1 sampai dengan
Hitung dugaan kuadrat terkecil berdasarkan data resampel ke-
Dengan data asli, hitung sisaan Ambil subsampel berukuran
Hitung dugaan kekar skala ̂ ∆
End
23
2 dengan menyelesaikan persamaan ∑ ′ , ′ ′ ′
′ ′′ 0;
3 sisaan ′ , 1 ;
4 selisih sisaan ∆ ′ ′ , 1 ′ ;
5 skala selisih sisaan yang diperbaiki
̂ ∆ ̂ ∆ ∑ ∆ ′
̂ ∆
′ .
Gambar 7 Diagram alir algoritma I-step untuk penduga GS Start
Untuk 1 sampai dengan
Masukkan ̂ Untuk 0, 1, 2, … Hitung bobot , ′ ∆ ′ ̂ ∆ , 1 ′ , 0, 1, 2,… Hitung dari ∑ ′ , ′ ′ ′ ′ ′′ 0 Hitung sisaan ′ , 1 Hitung ̂ ∆ ̂ ∆ ∑ ∆ ′ ̂ ∆ ′ End
Hitung selisih sisaan
24
Seperti yang diterapkan pada penduga S, hasil yang diperoleh dengan algoritma resampling dan algoritma I-step, yang diterapkan sebanyak 3 ulangan, dalam membangun algoritma cepat penduga GS merupakan kandidat dugaan yang mesti diperbaiki dengan penghitungan lebih lanjut hingga hasil yang dapat bersifat konvergen. Dalam hal ini, penghitungan juga dilakukan hanya untuk 5 kandidat dugaan terbaik dan proses dilalui dijabarkan sebagai berikut:
1 Untuk 1 , hitung dan ̃ ∆ , 0,1,2, …,
hingga konvergen dengan algoritma I-step untuk nilai awal dan
̃ ∆ , bangun gugus pasangan dugaan
, ̃ ∆ , 1 dan misalkan
max ̃ ∆ ;
2 untuk , jika ∑ ∆ maka hitung
dan ̃ ∆ hingga konvergen dengan algoritma I-step,
perbaharui gugus pasangan , ̃ ∆ yang sudah ada
dengan mensubstitusi nilai dugaan dan ̃ ∆ yang baru diperoleh dan mengeluarkan pasangan yang hasilkan pada iterasi
sebelumnya, dan hitung kembali
max ̃ ∆ ;
3 ulangi langkah 2 hingga .
Misalkan dugaan regresi dan dugaan kekar skala sisaan yang dihasilkan pada tahap ini adalah dan ̃ , 1 . Diagram alir untuk pendekatan di atas diilustrasikan pada Gambar 8.
25
Gambar 8 Diagram alir penghitungan kandidat terbaik dalam algoritma
cepat penduga GS Start
Untuk 1sampai
dengan
Hitung dengan I-step
dan ̃ ∆ , hingga konvergen Bangun gugus pasangan dugaan , ̃ ∆ Hitung sebagai max ̃ ∆ Ya ∆
Masukkan nilai dan
̃ ∆
Hitung dengan I-step hingga konvergen
dan ̃ ∆
Perbaharui gugus pasangan dugaan dengan substitusi nilai yang baru diperoleh
, ̃ ∆
Ya Tidak
Tidak
max ̃ ∆
Hitung kembali sebagai
26
Berdasarkan pembahasan di atas, algoritma cepat penduga GS untuk pendugaan parameter model regresi linear berganda dapat disarikan seperti berikut:
1 ambil resampel berukuran yang tidak kolinear dari data asli, hitung dugaan , 1, … , dengan metoda kuadrat terkecil dengan menggunakan data resampel, dan hitung ̂ ∆ dengan data asli; 2 terapkan kali I-step dengan nilai awal dan ̂ ∆ untuk
memperoleh dugaan regresi dan dugaan kekar skala selisih sisaan yang diperbaiki yang dilambangkan dengan dan ̃ ∆ ;
3 hitung dugaan regresi dan dugaan kekar skala selisih sisaan menerapkan I-step untuk kandidat penduga yang memenuhi syarat hingga konvergen dengan nilai awal dan ̃ ∆ dan menghasilkan ′ dan ̃ ′ ∆ ′ ,
1 ′ ;
4 ambil dugaan ′ dengan dugaan kekar skala selisih sisaan ̃ ′ ∆ ′
yang minimal sebagai dugaan regresi .
Diagram alir untuk langkah di atas diilustrasikan dengan Gambar 9.
Dugaan parameter ′ yang dihasilkan pada langkah di atas kemudian
digunakan dalam pendugaan intersep yang dipandang sebagai sisaan ′ ′ ′. Dugaan intersep didapatkan dengan menggunakan pendugaan M
lokasi dengan dugaan skala diketahui. Formula yang dipakai dalam penghitungan ini didasarkan pada pendekatan yang dikemukakan Maronna et al. (2006, 39). Berikut ini proses yang dimaksud.
1 Masukkan nilai ′.
2 Hitung sisaan ′ ′ ′, dugaan awal intersep
med ′ , skala ̂ ′
. med ′ , dan bobot
awal , ′
27
Persamaan (3) namun tuning constant yang digunakan pada fungsi adalah 4.68. 3 Untuk 0, 1, 2, … a hitung ∑ ∑ , ′ , ; b hitung , ′ ̂ ′ ; c berhenti jika 10 ̂ ′ .
Diagram alir untuk langkah penghitungan ini diilustrasikan dengan Gambar 10 dan kode R untuk semua langkah di atas dilampirkan pada Lampiran 1.
Gambar 9 Diagram alir algoritma cepat penduga GS Start
Masukkan data
ambil resampel berukuran , hitung dugaan , 1, … , ̂ ∆
terapkan kali I-step untuk memperoleh dan ̃ ∆ dengan nilai awal dan ̂ ∆
hitung dugaan dan ̃ ∆ , 1
dengan I-step untuk kandidat penduga yang memenuhi syarat hingga konvergen dengan nilai awal dan ̃ ∆
ambil dugaan dengan dugaan kekar skala sisaan ̃ ∆ yang minimal sebagai dugaan regresi
28
Gambar 10 Diagram alir penghitungan intersep pada algoritma cepat penduga GS
Start
Masukkan ′
Hitung sisaan ′ ′ ′
Hitung dugaan awal intersep
med ′
Hitung skala ̂ ′
. med ′
Hitung bobot awal ,
′
̂ ′
End
Misalkan eps = 1e-20, error = 1, dan 0 error > eps? Hitung ∑ ∑ , ′ , Hitung , ′ ̂ ′ Hitung ̂ ′ Hitung 1 Ya Tidak
29
Dengan merangkum ulasan tentang penduga S, algoritma cepat penduga S, penduga GS, dan algoritma cepat penduga GS yang telah dikemukakan sebelumnya, perbandingan proses penghitungan keempat pendekatan tersebut dapat ditunjukkan dengan Tabel 1.
Tabel 1 Perbandingan cara kerja penduga S, algoritma cepat penduga S, penduga GS, dan algoritma cepat penduga GS
Metoda Komputasi Keterangan
Penduga S
Metoda projection pursuit Dikemukakan oleh Rousseeuw dan Yohai (1984) Kombinasi algoritma resampling
dan langkah perbaikan lokal
Dikemukakan oleh Ruppert (1992 diacu dalam Salibian-Barrera dan Yohai 2006)
Algoritma cepat Penduga S
Kombinasi algoritma resampling dan algoritma I-step
Dikemukakan oleh Salibian-Barrera dan Yohai (2006) Penduga GS Kombinasi algoritma resampling
dan langkah perbaikan lokal
Dikemukakan oleh Croux et al. (1994) Algoritma cepat
Penduga GS
Kombinasi algoritma resampling dan algoritma I-step
Selanjutnya, perbedaan spesifik antara penduga S dan penduga GS dapat disarikan seperti Tabel 2.
Tabel 2 Perbedaan Penduga S dan Penduga GS
Kriteria Penduga S Penduga GS
Besaran skala yang digunakan
Skala sisaan Skala selisih sisaan Tuning constant dalam
fungsi biweight Tukey
1.547 0.9958
Aplikasi pada model dengan atau tanpa intersep
Bisa digunakan untuk pendugaan model dengan atau tanpa intersep
Hanya bisa digunakan untuk model dengan intersep
Dugaan intersep Diperoleh bersamaan dengan parameter yang lain
Tidak bisa dihitung secara langsung dalam pendugaan parameter melainkan diduga secara terpisah dengan dugaan kekar lokasi
30
Pembangkitan Data
Data dibangkitkan dengan menggunakan model regresi 1 untuk jumlah peubah penjelas 2 dan 1
untuk 5. Pada kedua kondisi, data yang dibangkitkan berukuran contoh 60 untuk kasus tanpa nilai pencilan dan dengan nilai pencilan, yakni dengan proporsi 0.05, dan 0.15. Pencilan yang dibangkitkan adalah pencilan sisaan dengan rataan 10 dan 100 dan ragam 1 dan 3.
Di samping itu, data juga dibangkitkan dengan mengunakan model 0.5 3 2 untuk jumlah peubah penjelas 2 dan 1 2 1.5 0.5 0.5 1.5 untuk 5. Data yang dibangkitkan yang berukuran contoh 60 untuk kasus tanpa nilai pencilan dan dengan nilai pencilan dengan proporsi 0.05, dan 0.15, namun data hanya memuat pencilan sisaan dengan rataan 10 dan ragam 1.
Berdasarkan salah satu gugus data yang dibangkitkan untuk data dengan model 1 untuk nilai seeding 1, diperoleh plot terhadap dan plot seperti Gambar 11 s.d. 14.
Gambar 11 Plot terhadap untuk data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 5% yang memiliki rataan 10 dan ragam
1 -1 0 1 2 3 05 1 0 Fitted values R es idual s lm(y1 ~ x) Residuals vs Fitted 58 60 59
31
Gambar 12 Plot untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 5% yang memiliki rataan 10 dan ragam
1
Gambar 13 Plot terhadap untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 15% yang memiliki rataan 10 dan ragam 1 -2 -1 0 1 2 -1 0123 45 Theoretical Quantiles S tanda rd iz ed r es idua ls lm(y1 ~ x) Normal Q-Q 58 60 59 0 1 2 3 4 -5 0 5 1 0 Fitted values R es idual s lm(y2 ~ x) Residuals vs Fitted 53 58 56
32
Gambar 14 Plot untuk satu data yang dibangkitkan dengan ukuran contoh 60, jumlah peubah 2, model 1 , dan proporsi pencilan 15% yang memiliki rataan 10 dan ragam 1
Plot yang diperoleh pada Gambar 11 dan 12 menunjukkan bahwa pembangkitan data dengan 5% nilai pencilan sisaan menghasilkan tepat 5% (tiga data) pencilan sisaaan. Sedangkan Gambar 13 dan 14 memperlihatkan bahwa pembangkitan data dengan 15% nilai pencilan sisaan tidak tepat menghasilkan 15% (sembilan data) yang juga nilai pencilan sisaaan. Akan tetapi, secara visual sembilan data tersebut tidak mengikuti pencaran 51 data yang lain. Kondisi yang serupa juga ditemukan pada pembangkitan data dengan ukuran contoh 60
dan jumlah peubah 5, model 1 , dan
proporsi pencilan 5%, 15%.
Efisiensi Relatif Algoritma Cepat Penduga S dan Algoritma Cepat Penduga GS
Berdasarkan simulasi di atas, kinerja algoritma cepat penduga GS dibandingkan dengan algoritma cepat S dengan memperhatikan nilai efisiensi relatif dugaan yang diperoleh yang dihitung untuk data tanpa pencilan dan pada data dengan 5% pencilan. Dalam hal ini pembandingan dilakukan pada dua kondisi, yakni kasus dengan jumlah peubah penjelas 2 dan 5.
-2 -1 0 1 2 -1 01 23 Theoretical Quantiles S tanda rd iz ed r es idua ls lm(y2 ~ x) Normal Q-Q 53 58 56
33
Pembandingan pada kasus pertama dilakukan dengan menggunakan data yang dibangkitkan dengan model 1 untuk nilai pencilan dengan rataan 10 dan 100 dan ragam 1 dan 3. Hal yang sama juga dilakukan pada kasus dengan jumlah peubah penjelas 5 yang menggunakan model pembangkit
1 . Hasil penghitungan untuk 2
ditampilkan pada Tabel 3 dan untuk 5 pada Tabel 4.
Tabel 3 Efisiensi relatif untuk data dengan dua peubah penjelas
Proporsi Pencilan Rataan Pencilan Ragam Pencilan Efisiensi Relatif FAST S FAST GS Rataan Simp Baku Rataan Simp Baku 5% 10 1 2.542 0.260 2.525 0.256 3 2.639 0.411 2.621 0.412 100 1 23.130 2.321 23.129 2.318 3 23.174 2.369 23.174 2.370 tanpa pencilan 1.068 0.050 1.012 0.013
Tabel 4 Efisiensi relatif untuk data dengan lima peubah penjelas
Proporsi Pencilan Rataan Pencilan Ragam Pencilan Efisiensi Relatif FAST S FAST GS Rataan Simp Baku Rataan Simp Baku 5% 10 1 2.576 0.263 2.514 0.241 3 2.629 0.448 2.571 0.436 100 1 23.312 2.259 23.291 2.250 3 23.307 2.234 23.286 2.224 tanpa pencilan 1.179 0.164 1.020 0.108
Berdasarkan Tabel 3 dan Tabel 4, algoritma cepat penduga GS memiliki rataan efisiensi relatif yang lebih kecil dari pada algoritma cepat penduga S dalam semua kondisi. Hasil ini menunjukkan bahwa algoritma cepat penduga GS memiliki efisiensi yang lebih baik dari pada algoritma cepat penduga S. Sehingga aplikasi algoritma cepat penduga GS pada data yang tidak begitu jauh menyimpang dari asumsi normalitas galat memberikan hasil yang lebih mendekati hasil yang diperoleh dengan metoda kuadrat terkecil dari pada aplikasi algoritma cepat penduga S. Bahkan untuk data tanpa pencilan algoritma cepat penduga GS
34
memiliki kinerja yang baik yang ditandai dengan efisiensi relatif yang mendekati 1.
Berbeda dengan hasil yang diperoleh untuk dugaan yang akan diulas pada bagian berikut, nilai efisiensi relatif dipengaruhi oleh nilai rataan dan ragam pencilan yang ditunjukkan oleh perbedaan rataan nilai efisiensi relatif yang signifikan antara data tanpa pencilan, data dengan pencilan yang mempunyai rataan 10, dan data dengan pencilan yang memiliki rataan 100 untuk kedua kasus pada Tabel 3 dan Tabel 4. Perbedaan ini terjadi karena kekekaran penduga S dan penduga GS hanya untuk dugaan bukan untuk nilai fitted.
Namun demikian, kondisi ini tidak menjadi masalah karena aspek yang diperhatikan pada tinjauan tentang efisiensi relatif hanya pada perilaku hasil penghitungan untuk data yang tidak begitu menyimpang dari asumsi normalitas atau bahkan dengan sempurna memenuhi asumsi normalitas. Proporsi, rataan, dan ragam pencilan bukanlah aspek yang dipertimbangkan dalam melihat efisiensi relatif.
Perbandingan Metoda Kuadrat Terkecil, Algoritma Cepat Penduga S, dan Algoritma Cepat Penduga GS
Data simulasi di atas, kinerja algoritma cepat penduga GS juga dapat dibandingkan dengan algoritma cepat S dan metoda kuadrat terkecil dengan memperhatikan nilai dugaan yang diperoleh dari ketiga pendekatan. Dalam hal ini pembandingan dilakukan pada dua kondisi, yakni kasus dengan model yang sama dan model yang berbeda.
Pembandingan pada kasus model yang sama dilakukan dengan menggunakan data yang dibangkitkan dengan model 1 untuk jumlah peubah penjelas 2 dan dengan model 1
untuk 5. Hasil dimaksud ditampilkan pada Tabel 5 dan Tabel 6. Sedangkan pembandingan pada kasus dua model yang berbeda dilaksanakan dengan menggunakan data yang dibangkitkan dengan model 1
dan 0.5 3 2 untuk jumlah peubah penjelas 2 dan dengan
model 1 dan 1 2 1.5
35
dengan nilai pencilan yang memiliki rataan 10 dan ragam 1. Hasil pembandingan yang kedua ini ditampilkan pada Tabel 7.
Tabel 5 Perbandingan dugaan untuk data dengan nilai pencilan Rataan
Pencilan
Ragam
Pencilan OLS Fast S Fast GS 2 peubah penjelas dengan 5% data pencilan
10 1 0.671 0.459 0.294
3 0.672 0.459 0.296
100 1 6.549 0.459 0.294
3 6.539 0.459 0.294
2 peubah penjelas dengan 15% data pencilan
10 1 1.664 0.441 0.353
3 1.675 0.446 0.356
100 1 16.651 0.441 0.354
3 16.649 0.441 0.355
5 peubah penjelas dengan 5% data pencilan
10 1 0.873 0.661 0.403
3 0.921 0.670 0.392
100 1 8.092 0.669 0.392
3 8.120 0.669 0.392
5 peubah penjelas dengan 15% data pencilan
10 1 1.883 0.646 0.446
3 1.951 0.642 0.449
100 1 18.826 0.640 0.437
3 18.839 0.640 0.444
Berdasarkan Tabel 5, dugaan yang diperoleh dengan algoritma cepat penduga GS lebih kecil dari pada yang didapatkan dengan metoda kuadrat terkecil dan algoritma cepat penduga S untuk jumlah peubah penjelas, proporsi, rataan, dan ragam pencilan yang sama. Hasil ini menunjukkan bahwa dugaan yang diperoleh dengan algoritma cepat penduga GS untuk data dengan pencilan mempunyai efisiensi yang lebih baik dari pada yang diperoleh dengan metoda metoda kuadrat terkecil dan algoritma cepat penduga S dalam semua kondisi. Hal ini sesuai dengan teori penduga GS mempunyai efisiensi yang lebih baik dari pada penduga S.
36
Tabel di atas juga memperlihatkan bahwa dugaaan yang diperoleh dengan algoritma cepat penduga GS maupun algoritma cepat penduga S pada suatu proporsi pencilan tertentu memiliki nilai yang sama meskipun data dibangkitkan dengan pencilan yang mempunyai rataan dan ragam yang berbeda. Hasil ini menunjukkan perilaku kekekaran penduga GS dan penduga S. Kedua penduga resisten terhadap pencilan.
Namun tidak demikian halnya dengan dugaan yang diperoleh dengan metoda kuadrat terkecil. Dugaan kuadrat terkecil sangat sensitif terhadap pencilan. Sehingga peningkatan rataan pencilan mengakibatkan peningkatan dugaan secara signifikan. Akan tetapi peningkatan ragam pencilan hanya mengakibatkan sedikit menurunkan nilai . Penurunan nilai ini disebabkan oleh fakta bahwa peningkatan ragam menyebabkan nilai pencilan yang dihasilkan lebih menyebar sehingga pencilan yang diperoleh akan mendekati data yang bukan pencilan.
Di sisi lain, Tabel 5 juga menunjukkan bahwa pertambahan jumlah peubah penjelas juga diikuti dengan peningkatan nilai dugaan yang diperoleh dari ketiga pendekatan. Peningkatan ini lebih dipengaruhi oleh bertambahnya suku positif pada penjumlahan yang digunakan dalam penghitungan karena
merupakan jumlah kuadrat. Sehingga penambahan jumlah peubah penjelas mengakibatkan peningkatan suku positif yang dijumlahkan.
Peningkatan nilai juga seiring dengan pertambahan proporsi pencilan untuk dugaan yang dihasilkan dengan algoritma cepat penduga GS dan metoda kuadrat terkecil. Sebaliknya, nilai dugaan yang didapatkan dengan algoritma cepat penduga S cenderung menurun, namun bila dibandingkan dengan
dugaan dari algoritma cepat GS maka nilai yang dihasilkan tetap lebih besar. Hal ini menunjukkan bahwa algoritma cepat penduga GS mempunyai efisiensi yang semakin baik bila digunakan pada data dengan proporsi pencilan yang semakin rendah. Kondisi yang lebih ekstrim dapat ditemukan pada data tanpa pencilan.
Pada data tanpa pencilan, dugaan yang diperoleh dengan algoritma cepat penduga GS mendekati nilai yang diperoleh dengan metoda kuadrat terkecil. Sementara itu, nilai yang diperoleh dengan algoritma cepat penduga S lebih besar