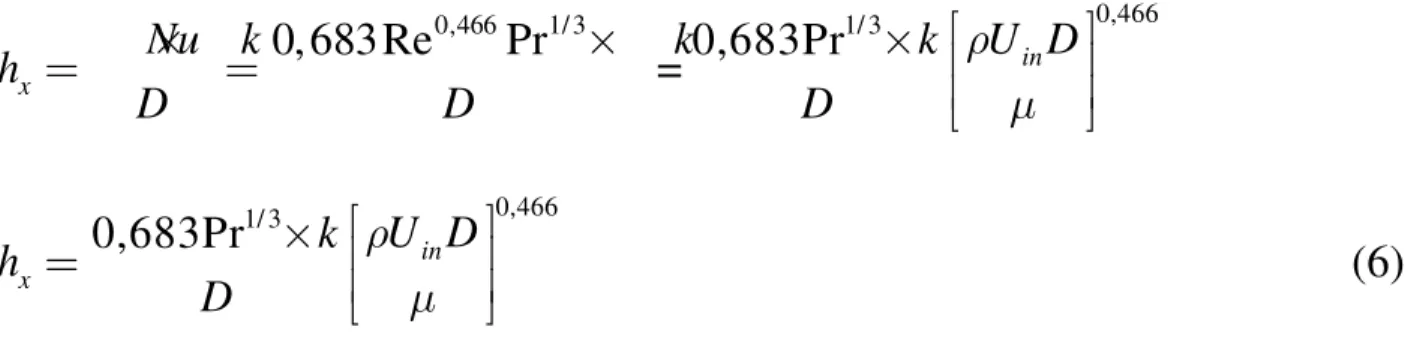Analisis Perpindahan Panas Konveksi Alamiah pada Ruang Tertutup ( Cavity ) Analisis Perpindahan Panas Konveksi Alamiah pada Ruang Tertutup ( Cavity )
dengan Menggunakan CFD dengan Menggunakan CFD
Nama
Nama :Janter :Janter NaibahoNaibaho NIM
NIM : : 07 07 0401 0401 014014
Departemen Teknik Mesin, Fakultas Teknik Universitas Sumatera Utara, Medan Indonesia Departemen Teknik Mesin, Fakultas Teknik Universitas Sumatera Utara, Medan Indonesia Abstrak
Abstrak
Tugas ini adalah analisis perpindahan panas pada ruang tertutup (cavity) misalkan sebuah Tugas ini adalah analisis perpindahan panas pada ruang tertutup (cavity) misalkan sebuah rumah atau kamar (room) dengan menggunakan perangkat lunak CFD. Analisa dilakukan rumah atau kamar (room) dengan menggunakan perangkat lunak CFD. Analisa dilakukan untuk aliran steadi, incompressible, laminar, dan dua dimensi. Sebuah rumah dinding persegi untuk aliran steadi, incompressible, laminar, dan dua dimensi. Sebuah rumah dinding persegi dengan dimensi 4m
dengan dimensi 4m
×
×
4m, dengan tinggi atap 2 m. Pada bagian atap kanan mengalir fluks4m, dengan tinggi atap 2 m. Pada bagian atap kanan mengalir fluks panas I = 800 W/mpanas I = 800 W/m22.Dinding kanan, bawah, kiri, dan atap kiri mempunyai temperatur 303 K,.Dinding kanan, bawah, kiri, dan atap kiri mempunyai temperatur 303 K, 293
293 K, K, 298 298 K K dan dan 313K 313K secara secara berurutan. berurutan. Koefisien Koefisien perpindahan perpindahan panas panas rata-rata rata-rata daridari rumah dibandingkan dengan koefisien perpindahan panas yang terdapat pada literatur. rumah dibandingkan dengan koefisien perpindahan panas yang terdapat pada literatur. Hasil analisa dengan CFD dan hasil dengan perhitungan dari literatur menunjukkan Hasil analisa dengan CFD dan hasil dengan perhitungan dari literatur menunjukkan hasil
hasil yang yang sama. sama. Medan Medan temperatur temperatur dan dan vektor vektor kecepatan kecepatan juga juga ditampilkan. ditampilkan. VariasiVariasi bilangan Reynolds yang diuji pada analisis ini adalah 40
bilangan Reynolds yang diuji pada analisis ini adalah 40 ≤≤ ReRe ≤≤ 40000. Koefisien40000. Koefisien perpindahan panas rata-rata dari rumah dibandingkan dengan koefisien perpindahan panas perpindahan panas rata-rata dari rumah dibandingkan dengan koefisien perpindahan panas yang terdapat pada literatur. Hasil analisis dengan CFD dan hasil dengan perhitungan dari yang terdapat pada literatur. Hasil analisis dengan CFD dan hasil dengan perhitungan dari literatur menunjukkan hasil yang sama. Medan temperatur dan vector kecepatan juga literatur menunjukkan hasil yang sama. Medan temperatur dan vector kecepatan juga ditampilkan. Persamaan menghitung bilangan Nu yang sesuai untuk kasus ini dirumuskan ditampilkan. Persamaan menghitung bilangan Nu yang sesuai untuk kasus ini dirumuskan dengan
dengan persamaan persamaan NNu u C
=
=
C aRR a L Lmm . Hasil analisa . Hasil analisa CFD digunakan untuk menghitung konstantaCFD digunakan untuk menghitung konstanta C dan nC dan n yang sesuai dengan teknik regresi. Konstanta yang sesuai adalah C=0,607937718 danyang sesuai dengan teknik regresi. Konstanta yang sesuai adalah C=0,607937718 dan n=0,920059852.
n=0,920059852. Keywords: konveksi
Keywords: konveksi alamiah, ruang tertutup (Cavity) alamiah, ruang tertutup (Cavity) atau rumah, CFDatau rumah, CFD
I. Pendahuluan I. Pendahuluan
Perpindahan panas pada rumah dapat dijumpai pada analisa perpindahan panas konveksi Perpindahan panas pada rumah dapat dijumpai pada analisa perpindahan panas konveksi melalui pipa pada komponen sistem pendingin seperti kondensor dan evaporator, tabung dan melalui pipa pada komponen sistem pendingin seperti kondensor dan evaporator, tabung dan bentuk rumah lainnya. Persamaan menghitung koefisien perpindahan panas pada rumah ini bentuk rumah lainnya. Persamaan menghitung koefisien perpindahan panas pada rumah ini dapat dijumpai buku literatur perpindahan, seperti pada [1] dan [2]. persamaan-persamaan dapat dijumpai buku literatur perpindahan, seperti pada [1] dan [2]. persamaan-persamaan yang dirumuskan secara analitik akan diuji dengan menggunakan perangkat lunak komersial yang dirumuskan secara analitik akan diuji dengan menggunakan perangkat lunak komersial CFD. Perangkat lunak
CFD. Perangkat lunak yang akan digunakan adalah FLUENT.yang akan digunakan adalah FLUENT. Tujuan tugas ini antara lain:
(1) Mengulang kembali (review) pelajaran perpindahan panas konveksi bebas atau
alamiah (natural flow), khususnya aliran yang melalui ruang tertutup misalkan rumah. (2) Mengetahui cara mengaplikasikan CFD untuk analisis perpindahan panas konveksi
alamiah.
(3) Memberikan pemahaman dasar untuk melakukan analisis CFD yang lebih rumit.
II. Perumusan Masalah
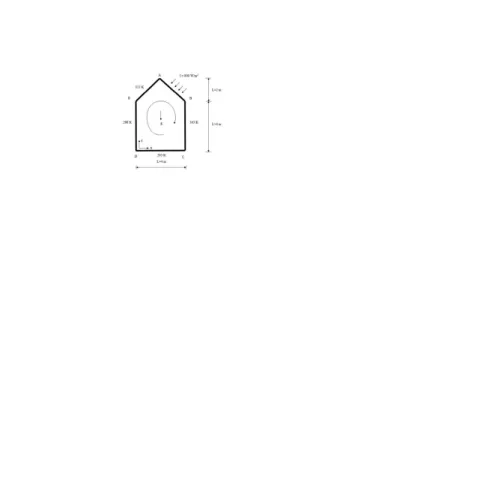
Untuk mendapatkan tujuan-tujuan itu pada tugas ini dilakukan analisis pada masalah yang sangat sederhana. Pada suatu rumah yang mempunyai diameter 0,1 m dan temperatur permukaan dijaga konstan pada 350K dialirkan udara lingkungan yang bertemperatur 300K. Skema dari rumah dan aliran udara ditampikan pada gambar berikut ini.
Gambar 1 Daerah perhitungan
Udara yang mengalir di atas rumah adalah diasumsikan sebagai gas ideal dan incompressible. Asumsi-asumsi lain yang digunakan adalah aliran laminar, steadi, dua dimensi, efek difusivitas dan gravitasi diabaikan. Dengan mengunakan asumsi - asumsi ini, maka persamaan pembentuk aliran (governing equations) yang akan dianalisis adalah:
a. Persamaan kontinuitas ( u v) 0 x y
∂
∂
+
=
∂
∂
(1) b. Persamaan momentumMomentum arah -x : 2 2 2 2 (u u v v) p ( u u) x y x x y ρ ρ µ
∂
∂
∂
∂
∂
+
=− +
+
∂
∂
∂ ∂ ∂
(2)Momentum arah –y:
2 2 2 2 (u v v v) p ( v v) g x y y x y ρ ρ µ ρ
∂ ∂
+
= − +
∂ ∂ ∂
+ −
∂
∂
∂ ∂ ∂
(3) c. Persamaan energi 2 2 2 2 ( ) ( ) p T T k T T u v x y ρC x y∂
+
∂
= −
∂
+
∂
∂
∂
∂
∂
(4)Persamaan-persamaan di atas, masih dapat disederhanakan lagi. Misalnya tekanan searah sumbu-x dapat dianggap konstan, sehingga
∂ ∂ =
ρ / x 0. Selanjutnya turunan tekanan searah sumbu-y dapat dianggap sama dengan turunan tekanan hidrostatis fluida diam diluar lapisan batas. Atau dalam bentuk persamaan menjadi:h dp y y ρ
∂
=
∂
∂
Dengan menggunakan defenisi tekanan hidrostatis h p
= −
ρr gy,dimana ρr adalah massa jenis fluida yang diam diluar lapisan batas (biasa disebut fluida referensi), maka:r g y ρ ρ
∂
=
∂
Jika persamaan (6) dan (5) disubstitusi pada persamaan (3), maka akan di dapat:
(
)
2 2 2 2 r v v v v u v g x y x y ρ ρ µ
ρ ρ∂
+
∂
=
∂
+ + −
∂
∂
∂
∂ ∂
Perbedaan massa jenis pada persamaan (7) biasa dikenal sebagai perbedaan massa jenis semu, pseudo-density difference. Pendekatan Boussinesq dapat digunakan untuk mengubah perubahan rapat massa ini menjadi perbedaan temperatur. Dengan menganggap udara
bertindak sebagai gas ideal, maka massa jenis udara dapat dinyatakan dengan persamaan:
(
)
1
r T T r ρ
=
ρ
−
β−
pada suhu referensi, yaitu suhu dilua lapisan batas. Jika persamaan ini disubstitusi ke persamaan (7), dan massa jenis dapat dianggap konstan, maka persamaan menjadi:
(
)
2 2 2 2 r v v v v u v g T T x y x y µ β ρ
∂ ∂
+ =
∂ ∂
+ + −
∂ ∂
∂ ∂
Persamaan (9) ini untuk selanjutnya akan digunakan sebagai pengganti persamaan (3). Perbedaan utama persamaan (9) dan persamaan (3) ada dua. Pertama, rapat massa dapat dianggap konstan (tidak perlu dihitung lagi). Kedua,gaya yang bekerja pada partikel udara, sekarang sudah bukan lagi fungsi rapat massa tetapi telah berubah menjadi fungsi temperatur. Dengan kata lain, seandainya distribusi temperatur diketahui, maka distribusi kecepatan akan dapat dihitung. Metode inilah yang telah diikuti selama puluhan tahun untuk menyelesaikan permasalah konveksi alamiah.
Bilangan tanpa dimensi
Pada kasus-kasus konveksi paksa persamaan empirik yang digunakan untuk mencari bilangan Nusselt dinyatakan dengan bilangan tanpa dimensi yaitu bilangan Reynolds. Sementara pada konveksi alamiah digunakan bilangan tanpa dimensi yang lain. Untuk mengetahui bilangan tanpa dimensi yang digunakan, maka persamaan pembentuk aliran harus diubah ke dalam bentuk tanpa dimensi. Parameter-parameter tanpa dimensi yang digunakan adalah:
, , , , r s r T T x y u v X Y U V dan L L V V θ T T
−
= = = =
=
−
Pada persamaan (10) huruf besar menyatakan bilangan tanpa dimensi. L adalah panjang plat datar dan V adalah kecepatan rata-rata fluida. Jika persaman (10) didifferensialkan, akan didapat: 1 1 1 1 1 , , , , s r X x Y y U y V y dan T L L V V θ T T
∂ = ∂ ∂ = ∂ ∂ = ∂ ∂ = ∂
∂ =
∂
−
Substitusi persamaan (11) ke dalam persamaan (9) dan dilakukan sedikit manipulasi akan didapat persamaan:
(
)
2 3 2 2 2 2 2 2 2 2 2 s r g T T L V V V V U V X Y V L VL Y X ρ β µ µ θ µ ρ ρ
−
∂
∂
∂
∂
+
=
×
+
∂
∂
∂
∂
Bagian yang di dalam kurung adalah bilangan-bilangan tanpa dimensi. Dengan
mengelompokkan semua bilangan tanpa dimensi menjadi satu group, maka persamaan (12) dapat ditulis menjadi:
2 2 2 2 2 2 1 Re Re L Gr V V V V U V X Y θ Y X
∂
+
∂
=
+
∂
+
∂
∂
∂
∂
∂
Dimana: Bilangan Grashof:
(
)
2 3 2 s r L g T T L Gr ρ β µ−
=
Dan bilangan Reynolds, Re ρVL
µ
=
Sebagai catatan, bilangan tanpa dimensi yang lebih sering digunakan untuk menuliskan rumus empirik pada kasus-kasus konveksi alamiah adalah bilangan Rayleigh biasa disebut sebagai Rayleigh number yang didefenisikan sebagai:
(
)
3 s r L g T T L Ra β να−
=
Dimana ν
=
µ ρ/ adalah viskositas kinematik, dan α=
k / ρC padalah difusivitas termal. Dengan menggunakan parameter-parameter tanpa dimensi pada persamaan (10) danturunannya pada persamaan (11), persamaan energi pada persamaan (4) dapat diubah dalam bentuk tanpa dimensi menjadi:
2 2 2 2 1 RePr U V X Y X Y θ θ
θ θ
∂
+
∂
=
∂
+
∂
∂
∂
∂
∂
Kondisi batas yang digunakan pada daerah perhitungan adalah wall yang dibagi atas AB, BC, CD, DE dan EA. Pada batas AB dimasukkan fluks panas I= 800 W/m2. Pada bagian BC,CD,DE dan EA mempunyai temperature 303 K, 293 K, ,298 K, dan 313 K berturut-turut. Pada seluruh bagian bagian kondisi batas yang digunakan tekanannya sama dengan tekanan atmosfer atau p = pa= 0 dengan gravitasi sebesar = 9,81 m/s2.
Koefisien perpindahan panas konveksi lokal pada rumah dapat dihitung dengan menggunakan persamaan: 0 ( / ) y x s in k T y h T T =
− ∂ ∂
=
−
(5)persamaan bilangan nusselt lokal adalah:
4/ 5 5/ 8 1/ 2 1/ 3 1/ 4 2/ 3 0, 62 Re Pr Re 0, 3 1 282000 1 (0, 4/ Pr) Nu
=
+
+
+
Bilangan Reynold Re=
vD = 0,1 0,1×
= 524,284875429914Karena 40 ≤Re ≤4000 maka Nu
=
0, 683Re0,466Pr1/ 3Dengan menggunakan teknik similaritas persamaan temperatur dapat dipecahkan dan persamaan koefisien konveksi lokal menjadi:
0,466 1/ 3 0, 683Re Pr x Nu k k h D D
×
×
=
=
= 0,466 1/ 3 0,683Pr k U Din D ρ µ
×
0,466 1/ 3 0,683Pr in x U D k h D ρ µ
×
=
(6)Koefisien perpindahan panas rata-rata di sepanjang rumah dapat dihitung dengan persamaan: 1
x
h h dx
D
=
∫
(7)Sifat fisik fluida dievaluasi pada T=300K sebagai berikut: density 1,1614 kg/m3,konduktifitas panas k= 0,0263 W/m.K , kapasitas panas cp= 1,007 J/kgK, viskositas = 158,9 × 10-7 Ns/m2
= 1,589× 10-5kg/m.s dan bilangan Prandtl Pr=0,707. β= 10 -51/K, RaL=5 x 105 Pl = 0,02
III. Metode Numerik
Persamaan pembentuk aliran (governing equations) akan didiskritisasi dengan menggunakan teknik volume atur (disebut grid). Pada proses diskritisasi persamaan momentum dan persamaan energi, digunakan orde pertama upwind scheme. Untuk mengkopling medan kecepatan dan medan tekanan digunakan algoritma SIMPLE.
Bentuk grid yang digunakan adalah segiempat dengan segitiga di bagian atasnya.
III.1 Pengujian Jumlah Grid yang Sesuai
Pada penyelesaian numerik jawaban yang didapatkan adalah merupakan jawaban pendekatan dan akan semakin dekat dengan jawaban sebenarnya jika ukuran grid semakin kecil atau jumlah grid makin besar. Sementara, jumlah grid yang banyak membuat perhitungan semakin
lambat. Maka untuk memastikan bahwa ukuran grid yang digunakan tidak berpengaruh besar pada jawaban akhir, maka dilakukan pengujian jumlah grid yang sesuai (grid independency test ).
Lima jumlah grid yang berbeda Nx × Ny yaitu: 100× 10=1000, 100× 20=2000, 100× 25=2500, 100× 32=3200, dan 120× 30=3600 telah diuji pada kecepatan udara di sisi masuk 0,1 m/s. Sebagai parameter pengujian koefisien konveksi ratarata pada permukaan rumah sebagai fungsi dari jumlah grid ditampilkan pada Gambar 3.
Pada gambar dapat dilihat semakin besar jumlah grid maka koefisien konveksi rata-rata akan semakin mengerucut. Koefisien konveksi rata-rata yangdihasilkan oleh grid 2500 dan 3200 masing-masing 4,546607 W/m2K dan 4,468907 W/m2K. Perbedaan kedua angka ini hanya 0,0777. Dari grafik juga dapat dilihat bahwa perbedaan koefisien konveksi untuk jumlah grid >2500 tidak terlalu besar selisihnya dengan grid 2500. Maka dapat diambil kesimpulan bahwa perhitungan dengan grid 2500 akan memberikan hasil yang hampir sama dengan 3200. Maka untuk menghemat waktu perhitungan dan juga mendapatkan hasil yang baik maka jumlah grid yang akan digunakan pada perhitungan ini adalah Nx= 100 dan Ny = 25
dengan jumlah total grid 2500.
Gambar 3 Koefisien konveksi rata-rata fungsi grid III. 2 Validasi Metode Numerik
Sebelum hasil dari sebuah metode numerik dianalisis, maka perlu dilakukan validasi. Pada laporan ini koefisien konveksi lokal yang dihitung dengan menggunakan persamaan (6) yang telah diyakini benar akan dibandingkan dengan koefisien konveksi lokal yang merupakan hasil perhitungan CFD. Perhitungan dilakukan pada kecepatan udara masuk 0,1 m/s. Hasilnya dalam bentuk grafik ditampilkan pada Gambar 4. Grafik ini menunjukkan bahwa hasil dengan CFD hampir sesuai dengan hasil dengan persamaan (6). Maka dapat diambil kesimpulan bahwa metode numerik yang digunakan ini dapat digunakan untuk melakukan analisa.
Gambar 4 Perbandingan hasil CFD dan teori
IV. Hasil dan Diskusi
Dengan menggunakan metode ini perhitungan untuk menganalisis koefisien perpindahan panas pada plat datar dilakukan dengan variasi kecepatan V =0,1m/s, 0,25 m/s, 0,5m/s, 0,75m/s, dan 1 m/s.
Bilangan Reynolds dihitung dengan menggunakan persamaan :
Re ρVD
µ
=
(8)Dengan menggunakan persamaan ini maka didapat variasi untuk bilangan Reynolds adalah 40 ≤ Re ≤ 40000. Nilai bilangan Re ini masih berada di bawah bilangan Re kritis 5×105 sebagai batas aliran turbulent. Maka asumsi yang digunakan pada persamaan pembentuk aliran yaitu aliran laminar dapat diterima.
Hasil pertama yang akan ditampilkan adalah bilangan Nusselt sebagai fungsi dari bilangan Reynolds dan ditampilkan pada Gambar 5. Bilangan Nusselt rata-rata dirumuskan dengan persamaan berikut:
hD Nu
k
=
(9)Dimana D adalah diameter rumah dan h adalah koefisien konveksi rata-rata yang dihitung dengan menggunakan persamaan (7).
Gambar 5 Bilangan Nu sebagai fungsi dari bilangan Re
Grafik Nu pada Gambar 5 menunjukkan bahwa semakin besar bilangan Re (kecepatan juga semakin besar) maka bilangan Nu akan semakin besar. Hal ini juga dapat dibuktikan dengan melakukan experiment. Secara teori, telah ada diusulkan persamaan yang dapat digunakan untuk menghitung bilangan Nusselt pada rumah. Pada tugas ini akan diusulkan suatu persamaan baru yaitu:
R Lm
Nu C a
=
(10)Dengan menggunakan regresi pangkat, maka nilai C dan n yang sesuai adalah 0,607937718 dan 0,920059852. Persamaan ini memang sebaiknya harus diuji dengan menggunakan experiment dan jika tervalidasi dengan baik dapat digunakan untuk menghitung bilangan Nu rata-rata pada plat datar yang sesuai dengan batasan Re yang ada.
Gambar 7 Vektor kecepatan pada
Distribusi temperatur dan vektor kecepatan pada daerah perhitungan pada kecepatan udara masuk ditampilkan pada Gambar 6 dan Gambar 7. Kedua gambar ini menunjukkan kecenderungan yang sama dengan beberapa literatur.
V. Kesimpulan
Pada tugas ini telah dilakukan analisis perpindahan panas secara konveksi alamiah melalui sebuah rumah dengan mengunakan perangkat lunak CFD. Asumsi aliran yang dianalisis adalah dua dimensi, incompressible, laminar, dan steady. Hasil yang didapatkan dengan CFD menujukkan trend yang sama dengan hasil teory yang dirumuskan dari referensi untuk distribusi temperatur dan vektor kecepatan, tetapi sedikit berfluktuasi untuk Perbandingan koefisien perpindahan panas lokal h (W/m2K) hasil CFD dan teori (yang ada di literatur). Kemungkinan disebabkan oleh ketidaktelitian dalam memasukkan input sehingga mendapatkan hasil yang berbeda dengan literatur. Pada tugas ini juga telah diajukan persamaan yang dapat digunakan untuk menghitung bilangan Nu, yaitu
0,920059852 R 0,607937718 R m L L Nu C a Nu a
=
=
Daftar Pustaka[1]. Fundamentals of Heat and Mass Transfer, Incropera/ DeWitt/ Bergman/ Lavine, Sixth Edition