TUGAS AKHIR - SM141501
KARAKTERISKTIK ALIRAN TAK TUNAK DAN
PERPINDAHAN PANAS FLUIDA SISKO PADA
PIPA ANNULUS VERTIKAL
SESTIKA WIJININGUTAMI NRP 1211 100 038 Dosen Pembimbing:
Prof. Dr. Basuki Widodo, M.Sc Drs. Kamiran, M.Si
JURUSAN MATEMATIKA
Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Teknologi Sepuluh Nopember
FINAL PROJECT - SM141501
CHARACTERISTIC OF UNSTEADY FLOW AND
HEAT TRANSFER OF THE SISKO FLUID IN A
VERTICAL ANNULUS
SESTIKA WIJININGUTAMI NRP 1211100038
Supervisor:
Prof. Dr. Basuki Widodo, M.Sc Drs. Kamiran, M.Si
MATHEMATICS DEPARTMENT
Faculty of Mathematics and Science Sepuluh Nopember Institute of Technology Surabaya 2015
vii
ANNULUS VERTIKAL Nama : Sestika Wijiningutami NRP : 1211 100 038
Jurusan : Matematika ITS
Pembimbing : 1. Prof. Dr. Basuki Widodo, M.Sc 2. Drs. Kamiran, M.Si
Abstrak
Fluida sisko merupakan salah satu fluida non-Newtonian yang mempunyai karakteristik bingham plastik. Permasalahannya adalah fluida ini tidak dapat mengalir tanpa adanya energi panas yang diberikan sebelum dialirkan dalam pipa. Pada penelitian ini, dikaji bagaimana karakteristik aliran tak tunak dan perpindahan panas fluida sisko pada pipa annulus vertikal. Model matematis dari aliran fluida sisko dikembangkan dari persamaan kontinuitas, momentum, dan persamaan panas. Model yang diperoleh berupa Persamaan Differensial Parsial (PDP). Kemudian, persamaan tersebut diselesaikan dengan menggunakan metode beda hingga implisit Crank-Nicholson. Dari simulasi diperoleh bahwa kecepatan fluida sisko lebih kecil daripada fluida Newtonian. Tetapi temperatur fluida sisko lebih besar daripada fluida Newtonian. Selain itu, semakin besar waktu yang diberikan kepada kedua fluida, kecepatannya semakin besar dan temperaturnya semakin kecil. Dengan demikian terlihat bahwa profil kecepatan dan temperatur fluida sisko dipengaruhi oleh besarnya waktu yang diberikan dan nilai parameter material, selain itu distribusi temperatur juga dipengaruhi oleh bilangan Brinkman.
Kata kunci — Fluida sisko, Bingham Plastic, Pipa
ix
TRANSFER OF THE SISKO FLUID IN A VERTICAL ANNULUS
Name : Sestika Wijiningutami
NRP : 1211 100 038
Department : Mathematics
Supervisor : 1. Prof. Dr. Basuki Widodo, M.Sc
2. Drs. Kamiran, M.Si
Abstract
Sisko fluid is one of the non-Newtonian fluid that has the characteristics of Bingham Plastic. The problem is that this fluid can’t flow without heat energy given before flowed in the pipeline. In this research, examined how the characteristics of unsteady flow and heat transfer sisko fluid in the pipe vertical annulus. Mathematical model of sisko fluid flow developed from the equation of continuity, momentum, and heat equation. The model obtained in the form of Partial Differential Equations (PDE). Then, the equation is solved using an implicit finite difference method of Crank-Nicholson. From the simulation shows that, the velocity of sisko fluid smaller than Newtonian fluid, but temperature of sisko fluid higher than Newtonian fluid. Beside that, in greater time, the velocity of sisko and Newtonian fluid getting higher, but the temperature getting smaller. Thus it appears that velocity and temperature of the sisko fluid profile affected by the amount of time given and the value of material parameters, in addition to the temperature distribution is also affected by the number Brinkman.
Keyword — Sisko Fluid, Bingham Plastic, Vertical Annulus Pipe, Crank-Nicholson, Brinkman Number.
xi
Puji dan Syukur kehadirat Allah SWT, karena berkat limpahan Rahmat dan Karunia-nya sehingga penulis dapat menyusun Tugas Akhir yang berjudul :
“Karakterisktik Aliran Tak Tunak Dan Perpindahan Panas Fluida Sisko Pada Pipa Annulus Vertikal”
dengan baik dan tepat pada waktunya.
Selama proses pembuatan Tugas Akhir, penulis tak lupa menyampaikan ucapan terima kasih kepada seluruh pihak yang telah mendukung dan membantu sehingga Tugas Akhir ini bisa terselesaikan, adapun pihak-pihak yang terlibat antara lain: 1. Ibu Prof. Dr. Erna Apriliani, M.Si sebagai Ketua Jurusan
Matematika FMIPA ITS.
2. Bapak Prof. Dr. Basuki Widodo, M.Sc sebagai dosen pembimbing utama, dan Bapak Drs. Kamiran, M.Si sebagai dosen pembimbing II, atas kesabaran, waktu, dan segala bimbingan yang telah diberikan kepada penulis.
3. Bapak Drs. Chairul Imron, MI.Komp, Ibu Prof. Dr. Erna Apriliani, M.Si dan Ibu Dra. Wahyu Fistia Doctorina, M.Si sebagai dosen penguji.
4. Bapak Drs. Chairul Imron, MI.Komp, sebagai Koordinator Tugas Akhir Jurusan Matematika FMIPA ITS.
5. Bapak Drs. Daryono Budi Utomo, M.Si selaku dosen wali, atas segala nasehatnya kepada penulis.
6. Bapak Ibu dosen beserta seluruh staf Tata Usaha jurusan Matematika ITS.
7. Teman-teman mahasiswa jurusan Matematika ITS.
Penulis menyadari bahwa Tugas Akhir ini masih jauh dari sempurna, sehingga penulis mengharapkan kritik dan saran yang sangat diharapkan dari semua pihak demi kesempurnaan Tugas Akhir ini. Semoga Tugas Akhir ini dapat bermanfaat bagi penulis dan bagi pembaca penelitian ini pada umumnya.
Surabaya, 13 Juli 2015 Penulis
xii
Dalam pelaksanaan Tugas Akhir ini, penulis memperoleh dukungan dan motivasi dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih secara khusus kepada:
1. Kedua orang tua, terima kasih atas segala do’a dan dukungannya kepada penulis.
2. Saudara-saudara kandung yang selalu mendoakan, memberikan motivasi dan kasih sayang yang berlimpah. 3. Teman – teman Christin, Ita, Mashurriyah, Ainur, Ilmi, dan
Wardatus yang selalu menghibur dan memberi semangat dalam pembuatan Tugas Akhir ini.
4. Teman-teman satu atap Veda, Mila, Chaca, Eva, Renna, mbak via, dan Teh Gita atas segala bantuannya.
5. Sahabat-sahabat dekat, Khabib, Indra yang selalu ada dan membantu, serta men-support penulis disaat-saat sedih. 6. Teman – teman Matematika angkatan 2011 terimakasih atas
segala dukungan dan kebersamaannya selama kurang lebih 4 tahun ini.
7. Mas Muji, mas Gede, Yahya, Agus, yang selalu memberi pencerahan dalam proses pelaksanaan Tugas Akhir ini. Dan masih banyak lagi pihak lain yang terlibat dalam penyelesaian Tugas Akhir ini yang tidak bisa penulis sebutkan satu-satu. Semoga Allah membalas dengan balasan yang berlebih bagi pihak-pihak yang membantu penulis. Amin ya rabbal
xiii HALAMAN JUDUL ... i LEMBAR PENGESAHAN ... v ABSTRAK ... vii ABSTRACT ... ix KATA PENGANTAR ... xi
DAFTAR ISI ... xiii
DAFTAR GAMBAR ... xv
DAFTAR SIMBOL ... xvii
DAFTAR LAMPIRAN ... xix
BAB I. PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Rumusan Masalah ... 3 1.3 Batasan Masalah ... 3 1.4 Tujuan ... 3 1.5 Manfaat ... 4 1.6 Sistematika Penulisan ... 4
BAB II. TINJAUAN PUSTAKA 2.1 Penelitian Terdahulu ... 7
2.1.1 Analisis Aliran dan Perpindahan Panas Fluida Sisko dalam Keadaan Stedi... 7
2.1.2 Application of Optimal Homotopy Asymptotic Method for Non-Newtonian Fluid Flow In A Vertical Annulus ... 8
2.2 Dasar Teori ... 8
2.2.1 Fluida ... 8
2.2.2 Aliran Fluida pada Pipa Annulus ... 9
2.2.3 Koordinat Polar Silinder ... 10
2.2.4 Teorema Divergensi Gauss ... 13
2.2.5 Persamaan Aliran Fluida ... 14
2.2.5.1 Persamaan Kontinuitas ... 14
2.2.5.2 Persamaan Momentum ... 14
xiv
2.2.7 Metode Beda Hingga ... 17
2.2.8 Metode Crank-Nicholson ... 18
BAB III. METODOLOGI PENELITIAN 3.1 Tahapan Penelitian ... 21
3.2 Diagram Alur Metode Penelitian ... 22
BAB IV. ANALISIS DAN PEMBAHASAN 4.1 Pemodelan Matematika Kecepatan Aliran dan Distribusi Temperatur Fluida Sisko Dalam Pipa ... 25
4.1.1 Pemodelan Matematika Kecepatan Aliran .... 25
4.1.2 Pemodelan Matematika Distribusi Temperatur ... 29
4.2 Model Kecepatan Aliran dan Distribusi Temperatur Non-Dimensional ... 30
4.2.1 Model Kecepatan Aliran Non-Dimensional .. 30
4.2.2 Model Distribusi Temperatur Non-Dimensional ... 32
4.3 Penyelesaian Numerik ... 33
4.3.1 Kondisi Awal dan Kondisi Batas ... 33
4.3.2 Penyelesaian Numerik Kecepatan Aliran ... 34
4.3.3 Penyelesaian Numerik Distribusi Temperatur ... 37
4.4 Algoritma Program ... 40
4.5 Simulasi Kecepatan Aliran dan Distribusi Temperatur Fluida Sisko pada Pipa ... 41
4.5.1 Simulasi Kecepatan Aliran ... 41
4.5.2 Simulasi Distribusi Temperatur ... 47
4.6 Validasi Model ... 54 BAB V. PENUTUP 5.1 Kesimpulan ... 57 5.2 Saran ... 57 DAFTAR PUSTAKA ... 59 LAMPIRAN ... 61 BIODATA PENULIS ... 75
xv
Halaman
Gambar 2.1 Bentuk Pipa Annulus 10
Gambar 2.2 Koordinat Silinder 11
Gambar 2.3 Sebuah Elemen Luasan pada permukaan 13 Gambar 2.4 Control Volume pada daerah aliran Temperatur 15
Gambar 4.1 Penampang Horizontal Pipa Annulus 34
Gambar 4.2 Distribusi Kecepatan Aliran dengan power 42
index
Gambar 4.3 Distribusi Kecepatan Aliran dengan power 43
index
Gambar 4.4 Distribusi Kecepatan Aliran dengan power 44
index
Gambar 4.5 Distribusi Kecepatan Aliran dengan power 45
index
Gambar 4.6 Distribusi Kecepatan Aliran dengan power 46
index
Gambar 4.7 Distribusi Kecepatan Aliran dengan power 46
index
Gambar 4.8 Distribusi Temperatur Aliran dengan power 47
index
Gambar 4.9 Distribusi Temperatur Aliran dengan power 48
index
Gambar 4.10 Distribusi Temperatur aliran dengan power 49
index
Gambar 4.11 Distribusi Temperatur aliran dengan power 50
index
Gambar 4.12 Distribusi Temperatur aliran dengan power 51
index
Gambar 4.13 Distribusi Temperatur aliran dengan power 52
xvi
index
Gambar 4.15 Distribusi temperatur aliran dengan power 54
index
Gambar 4.16 Distribusi Kecepatan aliran dengan power 55
index
Gambar 4.17 Distribusi Kecepatan aliran dengan power 56
xvii : Nilai parameter material : Tensor Rivlin-Erickson : Nilai parameter material
: Bilangan Brinkman
: Kapasitas panas pada tekanan konstan : Jari-jari silinder dalam
: Bilangan Eckert : Tensor identitas : konstanta panas : Gradien kecepatan : Banyaknya pendiskritan : Power index : Tekanan : Bilangan Prandtl : Fluks panas
: Body Force
(Gaya yang bekerja pada benda): Waktu
: Jari-jari silinder : Jari-jari silinder dalam : Jari-jari silinder luar ̿ : Tensor tegangan
:
Temperatur fluida:
Kecepatan:
Kecepatan radial:
Kecepatan tangensial:
Kecepatan aksial : Kerapatan fluida: gravitasi
xviii
1
Pada bab ini, dibahas latar belakang dari permasalahan yang mendasari penulisan serta uraian singkat apa saja yang dilakukan untuk penyelesaian Tugas Akhir. Permasalahan tersebut kemudian dituangkan dalam suatu rumusan masalah, tujuan dan manfaat yang dapat diambil dengan membatasi ruang lingkupnya.
1.1
Latar Belakang Masalah
Aliran fluida pada pipa telah banyak dijumpai baik dalam kehidupan sehari-hari maupun dalam proses industri. Dalam industri, fluida menjadi bagian yang sangat penting. Perannya dalam proses produksi tidak dapat diganti dengan bahan lain. Seperti contohnya dalam industri perminyakan. Dari proses pengeboran dalam tanah, pengolahan, sampai menjadi bahan yang siap untuk didistribusikan, hampir semua proses produksi berbentuk fluida. Sebagian besar fluida mengalir pada pipa–pipa saluran tertutup.
Fluida tersebut berbentuk dua jenis, yaitu fluida gas dan fluida cair. Sedangkan, Fluida cair sendiri dibagi menjadi fluida Newtonian dan fluida non-Newtonian. Dikatakan fluida Newtonian, karena karakteristik jenis fluida ini menganut hukum-hukum Newton. Seperti contohnya adalah air. Sebaliknya, fluida non-Newtonian mempunyai karakteristik yang menyimpang dari hukum-hukum Newton. Fluida sisko merupakan salah satu jenis fluida non-Newtonian. Dikatakan menyimpang karena fluida tersebut tidak dapat mengalir dalam pipa tanpa adanya energi panas yang diberikan pada fluida sisko sebelum dialirkan dalam pipa (Nirmalasari N.A, 2011). Sehingga, jenis fluida ini mempunyai karakteristik yang sulit untuk diprediksi. Dengan demikian, karakteristik fluida seperti ini akan menjadi masalah tersendiri bagi kegiatan industri.
Fluida dialirkan dalam berbagai jenis pipa. Baik itu pipa vertikal maupun horisontal. Tentu saja, setiap bentuk pipa ini juga mempunyai laju aliran yang berbeda. Perbedaan ini terletak pada gaya gravitasi yang bekerja pada pipa vertikal. Apapun bentuk pipa, laju aliran tersebut dipengaruhi oleh beberapa hal. Kerapatan fluida, tekanan, temperatur, sampai sudut kemiringan pada pipa adalah hal-hal yang perlu diperhatikan untuk mengetahui perubahan laju aliran fluida tersebut. Pada penelitian sebelumnya telah dibahas analisis aliran dan perpindahan panas fluida sisko pada keadaaan stedi dengan kondisi pipa berbentuk horisontal. Metode numerik yang digunakan adalah metode beda hingga eksplisit pusat. Dari model yang sudah didapat, kemudian disimulasikan untuk mengetahui karakteristik dari fluida. Berdasarkan hasil keluarannya, profil kecepatan dan temperatur pada fluida sisko dipengaruhi oleh besarnya tekanan yang diberikan dan nilai parameter material, selain itu distribusi panas juga dipengaruhi oleh bilangan Brinkman (Nirmalasari N.A, 2011). Namun secara nyata aliran fluida ini adalah aliran tak tunak yang kecepatannya berubah terhadap waktu. Untuk beberapa industri seperti industri perminyakan, penyulingan minyak, pengawetan makanan dan juga sistem perpipaan pada pembangkit listrik tenaga panas bumi menggunakan pipa jenis pipa annulus vertikal (Radhika, 2012).
Berdasarkan uraian dari permasalahan diatas, maka pada Tugas Akhir ini akan membahas model aliran tak tunak dan perpindahan panas fluida sisko pada pipa anulus vertikal. Model matematika dari aliran fluida sisko dikembangkan dari persamaan kontinuitas, persamaan momentum, dan Persamaan distribusi panas. Selanjutnya, dari model tersebut akan diselesaikan secara numerik dengan menggunakan metode beda hingga implisit
Crank-Nicholson. Karena metode ini mempunyai nilai akurasi
yang lebih baik dari metode beda hingga eksplisit. Penyelesaian numerik yang diperoleh kemudian disimulasi menggunakan software Matlab.
1.2
Rumusan Masalah
Permasalahan yang dibahas dalam Tugas Akhir ini adalah:
Bagaimana karakteristik dari aliran tak tunak dan perpindahan panas fluida sisko pada pipa Annulus vertikal dengan menggunakan metode beda hingga implisit Crank-Nicholson?
1.3
Batasan Masalah
Dalam Tugas Akhir ini, permasalahan yang dibahas akan dibatasi ruang lingkup pembahasannya antara lain :
a. Kajian yang digunakan adalah model tiga dimensi pada koordinat silinder.
b. Jenis alirannya adalah aliran laminar.
c. Model aliran yang digunakan adalah model aliran tak tunak fluida sisko pipa dengan panjang dan diameter D.
d. Power index yang digunakan adalah dan .
e. Metode numerik yang dipakai adalah metode beda hingga implisit Crank-Nicholson.
f. Laju aliran dan perpindahan panas fluida sisko pada pipa akan disimulasikan dengan menggunakan software Matlab ITS.
1.4
Tujuan
Berdasarkan rumusan masalah diatas, tujuan dalam Tugas Akhir ini adalah :
Mengetahui karakteristik dari aliran tak tunak dan perpindahan panas fluida sisko pada pipa Annulus vertical dengan menggunakan metode beda hingga implisit Crank-Nicholson.
1.5
Manfaat
Manfaat dari Tugas Akhir ini adalah :
1. Mengetahui tentang aplikasi matematika pada industri khususnya di bidang fluida.
2. Mengetahui tentang aplikasi numerik pada permasalahan laju aliran tak tunak dan perpindahan panas fluida sisko pada pipa menggunakan metode beda hingga.
1.6
Sistematika Penulisan
Sistematika penulisan dari Tugas Akhir ini adalah sebagai berikut :
1. BAB I PENDAHULUAN
Bab ini berisi tentang uraian secara umum dari Tugas Akhir yang berupa latar belakang, rumusan masalah, batasan masalah, tujuan, manfaat dan sistematika dari penulisan. 2. BAB II TINJAUAN PUSTAKA
Bab ini berisi landasan teori dari penelitian. Yang berisi pembahasan penelitian terdahulu secara singkat, pengertian fluida dan fluida sisko secara umum, Persamaan differensial parsial, aliran fluida pada pipa Annulus, koordinat polar silinder, persamaan-persamaan pada aliran fluida, metode beda hingga, dan metode Crank-Nicholson.
3. BAB III METODOLOGI PENELITIAN
Bab ini berisi langkah-langkah dan metode dalam menyelesaikan Tugas Akhir.
4. BAB IV ANALISIS DAN PEMBAHASAN
Bab ini berisi pemodelan matematika kecepatan aliran dan perpindahan panas fluida sisko pada pipa, model kecepatan aliran dan perpindahan panas fluida sisko pada pipa
program, dan hasil simulasi kecepatan aliran dan perpindahan panas fluida sisko pada pipa.
5. BAB V KESIMPULAN DAN SARAN
Bab ini berisi kesimpulan yang diperoleh dari pembahasan masalah pada bab sebelumnya serta saran yang diberikan untuk pengembangan penelitian selanjutnya.
7
Pada bab ini, dibahas mengenai dua penelitian sebelumnya yang berkaitan dengan fluida sisko, dasar teori dari fluida sisko dan persamaan-persamaan yang digunakan untuk memperoleh model kecepatan aliran dan perpindahan panas fluida sisko pada pipa Annulus vertikal. Serta dipaparkan secara umum metode numerik Crank-Nicholson.
2.1
Penelitian Terdahulu
Terdapat dua penelitian sebelumnya yang akan menjadi referensi utama dalam mengembangkan model persamaan kecepatan aliran dan peripndahan panas fluida sisko pada pipa Annulus vertikal.
2.1.1 “Analisis Aliran dan Perpindahan Panas Fluida
Sisko dalam Keadaan Stedi”
Pada Tugas Akhir ini dikaji tentang model kecepatan aliran dan perpindahan panas fluida sisko yang mengalir pada pipa dalam keadaan stedi untuk mengetahui bagaimana profil kecepatan dan perpindahan panasnya. Untuk itu dibuat asumsi dan batasan masalah serta digunakan persamaan kontinuitas, persamaan momentum linier, persamaan tekanan pada fluida bergerak dan persamaan distribusi panas. Model tersebut selanjutnya diselesaikan secara numerik menggunakan metode beda hingga dengan skema pusat dan divisualisasikan dengan bantuan program Matlab ITS. Berdasarkan simulasi dan visualisasi, dihasilkan kecepatan fluida Newtonian lebih besar daripada fuida sisko saat , dan sebaliknya untuk . Temperatur fluida sisko selalu lebih besar daripada fluida Newtonian. Dengan demikian terlihat bahwa profil kecepatan dan temperatur fluida sisko dipengaruhi oleh besarnya tekanan yang diberikan dan nilai parameter material, selain itu distribusi panas
juga dipengaruhi oleh bilangan Brinkman. Tetapi dalam kenyataanya, beberapa industri menggunakan aliran unsteady pada pipa annulus vertikal.
2.1.2 “Application of Optimal Homotopy Asymptotic
Method for Non-Newtonian Fluid Flow In A
Vertical Annulus”
Pada penelitian ini, aliran yang digunakan adalah aliran fluida sisko pada pipa annulus vertikal. Aliran diasumsikan mengalir keatas yang dipengaruhi oleh gradien tekanan dan gaya gravitasi. Persamaan momentum tak linier diselesaikan dengan menggunakan optimal Homotopy asymptotic method (OHAM). Dapat diketahui bahwa untuk gradien tekanan yang bernilai negatif, gaya gravitasi lebih berpengaruh pada fluida
shear-thinning daripada fluida Newtonian dan shear-thickening.
Penyelesaian dari Persamaan diferensial derajat dua ditunjukkan dengan menggunakan OHAM untuk menentukan solusi analitis dari permasalahan. Karena alirannya juga diasumsikan dalam keadaan steady, maka hasil ini belum tentu berlaku jika alirannya adalah aliran unsteady.
2.2
Dasar Teori
2.2.1 Fluida
Fluida merupakan bagian dari perubahan bentuk benda, termasuk benda cair, gas, dan padat. Fluida memiliki kemampuan untuk mengalir. Sifat ini disebabkan karena adanya tegangan
geser (shear stress) atau tidak mampu
mempertahankan/mengembalikan bentuknya.
Fluida dibagi menjadi 2, yaitu fluida newtonian dan fluida non newtonian. Fluida sisko merupakan salah satu fluida yang termasuk kedalam fluida non newtonian serta masuk kedalam karakterikstik bingham plastic. Fluida ini akan mengalir seperti air pada saat mencapai regangan geser tertentu. Uniknya fluida ini biasa digunakan untuk melapisi pipa annulus. Dengan
demikian persamaan tensor tegangan fluida sisko pada pipa annulus didefinisikan sebagai (M. Khan, 2014) :
̿ dengan [ |√ ( ( )) |
] (2.1)
Berdasarkan alirannya, fluida terdiri dari (Anggriani, 2014): 1. Aliran Tunak : merupakan suatu aliran fluida dimana
kecepatannya tidak terpengaruh oleh perubahan waktu, sehingga kecepatan konstan pada setiap titik pada aliran tersebut .
2. Aliran Tak Tunak : aliran yang pada kondisi aliran yang kedalamannya berubah menurut waktu dan kecepatannya juga berubah menurut waktu. Pada aliran tak tunak berlaku.
.
Berdasarkan pergerakan alirannya, fluida terdiri dari :
1. Aliran laminar: fluida yang bergerak dalam lapisan – lapisan dengan satu lapisan meluncur secara lancar.
2. Aliran turbulen : Aliran dimana pergerakan dari partikel – partikel fluida sangat tidak menentu karena mengalami percampuran serta putaran partikel antar lapisan.
3. Aliran transisi : Aliran transisi merupakan aliran peralihan dari aliran laminar ke aliran turbulen.
2.2.2 Aliran Fluida pada Pipa Annulus
Pipa anulus adalah pipa luar pembatas fluida. Atau dengan kata lain pipa ini adalah pipa yang terdiri dari dua silinder tetap yang sepusat. Koordinat yang digunakan adalah koordinat silinder. Diasumsikan bahwa dua pipa ini dalam keadaan diam, sehingga tidak ada gesekan yang ditimbulkan antar kedua pipa. Aliran fluida yang dibahas adalah aliran fluida yang mengalir antara pipa dalam dan pipa luar, sehingga ada atau tidaknya
aliran pipa bagian dalam diabaikan. Aliran tersebut mengalir sejajar dengan dinding sehingga dan .
Gambar 2.1. Bentuk pipa Annulus
Temperatur pada permukaan dinding pipa diasumsikan konstan. Sehingga temperatur dinding pipa luar maupun pipa dalam tidak berubah sepanjang waktu.
2.2.3 Koordinat Polar Silinder
Dalam beberapa persoalan hubungan diferensial dapat dijelaskan dalam koordinat polar silinder. Dengan koordinat silinder, tempat kedudukan sebuah titik ditunjukkan oleh koordinat-koordinat dan . Koordinat adalah jarak radial dari sumbu , adalah sudut yang diukur dari sebuah garis sejajar dengan sumbu- (dengan arah yang berlawanan perputaran jarum jam dianggap positif), dan adalah koordinat sepanjang sumbu- . Komponen-komponen kecepatan adalah kecepatan radial ( ), kecepatan tangensial ( ), dan kecepatan aksial ( ). Jadi, kecepatan pada sebuah titik sembarang dapat dinyatakan sebagai (Nirmalasari, 2011):
̂ ̂ ̂ (2.2) 𝒓 𝒍 𝒛 𝒓𝟎 𝑹 𝒓𝟏 𝒅𝑹 𝒈
Gambar 2.2. Koordinat silinder
Dari gambar (2.2), hubungan koordinat kartesian dengan koordinat silinder adalah:
Dengan ̂, ̂, dan ̂ vektor-vektor satuan dalam arah dan , ̂ ̂ ̂ ̂ ̂ ̂ ̂ ̂ Sehingga diperoleh, ̂ ̂ ̂ ̂ ̂ ̂ ̂ ̂ ̂̂ ̂̂ ̂
Operator nabla ( ) jika dikenakan pada fungsi skalar disebut gradient. Jika diberikan,
Didefinisikan bahwa ⃗⃗ ⃗⃗ Dengan demikian,
⃗⃗ ⃗⃗
Atau dalam koordinat silinder,
( ⃗⃗ ) ( ⃗⃗ ) ( ⃗⃗ ) Maka, ( ⃗⃗ ) , ( ⃗⃗ ) , ( ⃗⃗ )
Jadi, didapat gradient pada fungsi skalar :
̂ ̂ ̂ (2.3)
Namun jika dikenakan pada fungsi vektor disebut divergensi, dalam koordinat silinder dinyatakan sebagai berikut. ⃗⃗ ⃗ ( ̂ ̂ ̂) ( ̂ ̂ ̂) ̂ ( ̂ ̂ ̂ ̂ ̂ ̂ ) ̂ ( ̂ ̂ ̂ ̂ ̂ ̂ ) ̂ ( ̂ ̂ ̂ ̂ ̂ ̂ ) Dengan substitusi derivative parsial yang sudah didapat, maka ⃗⃗ ⃗ ̂ ( ̂ ̂ ̂ ) ̂ ( ̂ ̂ ̂ ̂ ̂ ) ̂ ( ̂ ̂ ̂ ) ( ) ( ) ( ) ( )
Sehingga, didapat divergensi pada fungsi vektor :
⃗⃗ ⃗ ( ) (2.4)
Curl vektor ⃗⃗ ⃗ juga dapat dicari: ⃗⃗ ⃗ ( ̂ ̂ ̂) ⃗ ̂ ⃗⃗ ̂ ⃗⃗ ̂ ⃗⃗ dengan ⃗ ̂ ̂ ̂
maka, ⃗⃗ ⃗ ( ̂ ̂) ( ̂ ̂ ̂) ( ̂ ̂)
Sehingga, didapat Curl vektor ⃗⃗ ⃗ :
⃗⃗ ⃗ ̂ ( ) ̂ ( ) ̂ ( ( ) ) (2.5)
Persamaan Laplace dari fungsi skalar adalah:
⃗⃗ ( ⃗⃗ ) ( ̂ ̂ ̂) ( ̂ ̂ ̂) ̂ ( ̂ ̂ ̂) ̂ ( ̂ ̂ ̂) ̂ ( ̂ ̂ ̂)
Dengan substitusi derivative parsial yang sudah didapat, maka
( )
Sehingga, didapat Persamaan Laplace:
( ) (2.6)
2.2.4 Teorema Divergensi Gauss
Teorema divergensi biasa digunakan dalam dinamika fluida terutama pada dimensi tiga. Teorema ini menghubungkan integral luasan suatu vektor dengan integral volum vektor tersebut. Misalkan suatu vector dengan tegak lurus dengan permukaan elemen .
Gambar 2.3 sebuah elemen luasan pada permukaan 𝐴
𝑑𝑠
Maka,
∬ ∭
2.2.5 Persamaan Aliran Fluida
Untuk mendapatkan model kecepatan aliran dan perpindahan panas fluida sisko pada pipa Annulus vertikal, dibutuhkan Persamaan aliran fluida secara umum.
2.2.5.1 Persamaan Kontinuitas
Massa fluida yang bergerak tidak berubah ketika mengalir. Dengan demikian persamaan kontinuitas adalah pernyataan bahwa massa adalah kekal. (Nirmalasari, 2011)
Massa m dari fluida yang mengalir konstan pada volume yang bergantung waktu dengan permukaan tertutup ( ). (Egon Krause, 2005) ∫ ( ) (2.7) Dengan, ∫ ( ) ∫ ( ) ∫ ( ) ( )
Integral permukaan ( ) ditransformasikan kedalam integral volume dengan menggunakan teorema Divergensi Gauss
∫ ( ) ∫
( ) ∫ ( ) ( )
Substitusikan dengan Persamaan (2.9), sehingga ∫ (
( ))
( )
Persamaan kontinuitas fluida secara umum:
( ) (2.8)
2.2.5.2 Persamaan Momentum
Keseimbangan unsur gaya yang bekerja pada volume cairan digambarkan dengan teorema momentum. Laju perubahan
momentum dari volume tertutup sama dengan jumlah dari gaya yang bekerja pada volume tersebut (Egon Krause, 2005).
∫ ( ) ∑
Dengan gaya-gaya yang bekerja adalah gaya pada benda ( ) dan
gaya permukaan. Didefinisikan gaya permukaan:
∫ ( )( ̿) ∫ ( ̿) ( ) Sehingga Persamaan momentumnya menjadi
∫ (
( ) )
( ) ∫ ( ̿) ( )
Persamaan momentum fluida yang digunakan adalah (T.S.L Radhika, 2012):
(
( ) ) ( ̿) (2.9)
2.2.5.3 Persamaan Distribusi Panas
Untuk memperoleh profil distribusi panas pada fluida sisko, digunakan persamaan distribusi panas secara umum pada benda tiga dimensi (Lienhard, 2005):
Gambar 2.4. Control Volume pada daerah aliran panas Berdasarkan gambar 2.4, konduksi panas yang keluar dari , adalah
( ) ( ⃗ )
Sehingga laju keseluruhan pada daerah , diperoleh dari panas pada daerah ditambahkan dengan jumlah aliran panas yang masuk ke daerah . Atau
∫ ( ) ( ⃗ ) ∫ ̇ (2.10) Laju dari penambahan energi daerah
∫ (
) (2.11)
Jika Persamaan (2.12) dan (2.13) di substitusi pada , maka ∫ ( ) ( ⃗ ) ∫ ̇ ∫ ( )
atau
∫ ( ̇) ∫ ( ) ( ⃗ ) Dengan menggunakan divergensi Gauss, ∫ ( ̇) ∫ ( ) dapat ditulis,
∫ ( ̇ ( ))
Jadi, Persamaan distribusi panas pada fluida secara umum pada benda tiga dimensi adalah
( ) ̇ (2.12)
Atau pada fluida sisko persamaan distribusi panas didefinisikan dalam bentuk (M.Khan, 2010):
̿ (2.13)
2.2.6 Persamaan Differensial Parsial
Persamaan diferensial parsial (PDP) adalah suatu persamaan yang mengandung satu atau lebih turunan parsial dari suatu fungsi dari dua atau lebih variabel bebas (Soehardjo, 2004). Turunan parsial dinotasikan sebagai berikut :
, ,
Contoh dari persamaan differensial parsial adalah sebagai berikut:
(2.15)
Dengan ( ) adalah suatu fungsi sebarang dengan variabel bebas dan , dan adalah kontanta. Persamaan diferensial parsial diatas merupakan persamaan diferensial parsial tingkat dua derajat satu. Pangkat tertinggi dari derivatif parsial tertinggi dalam persamaan adalah derajat dari persamaan diferensial parsial tersebut.
2.2.7 Metode Beda Hingga
Metode beda hingga adalah metode numerik yang umum digunakan untuk menyelesaikan masalah matematis dari suatu gejala fisis. Pada umumnya metode ini sering digunakan untuk mencari penyelesaian dari persamaan diferensial parsial (PDP). Dengan cara membawanya menjadi suatu grid yang selanjutnya dinotasikan sebagai indeks. Indeks subscript pertama sebagai variabel ruang dan subscript kedua sebagai variabel waktu.
( ) ( )
Misalkan diberikan suatu persamaan distribusi panas:
(2.16)
dengan adalah suatu konstanta. Dengan syarat awal :
( ) , jika adalah jari-jari silinder dalam dan adalah jari-jari silinder luar
dan syarat batas :
( ) , jika adalah konstanta
Untuk menyelesaikan sistem persamaan diatas dengan skema beda hingga akan dihitung nilai pendekatan pada jaringan titik ( ) dengan domain komputasi didiskritkan baik pada arah maupun arah sebagai berikut :
,
dimana adalah banyaknya grid.
2.2.8 Metode Crank-Nicholson
Metode Crank-Nicholson merupakan metode pengembangan pada metode beda hingga dari skema eksplisit dan implisit. Pada skema Crank-Nicholson, diferensial terhadap waktu ditulis dengan . Bentuk umum persamaan beda hingga pada titik ke dan sebagai berikut (S. E Fadugba, 2013):
( ) ( ( ) )
( ) ( ( ) ) (2.17) Jika maka diperoleh skema eksplisit seperti Persamaan (2.18) dan akan diperoleh skema implisit seperti Persamaan (2.19) berikut: ( ) ( ( ) ) (2.18) ( ) ( ( ) ) (2.19)
Jika bernilai antara 0 dan 1 ( ) atau dengan kata lain rata-rata dari skema eksplisit dan implisit, maka akan menghasilkan beda tengah seperti Persamaan (2.20) berikut:
( ) ( ( ) ) ( ( ) ) (2.20)
Dengan mengaplikasikan Persamaan (2.20) untuk semua titik, maka diperoleh sistem dengan koefisien matriks tridiagonal sebagai berikut: ( ) ( ) ( ) ( ) ( ) ( )
Misalkan ( ) , maka akan diperoleh Persamaan (2.21) yang merupakan pendekatan skema Crank-Nicolson:
( )
( )
( ) ( ) ( ) ( ) (2.21) Untuk
21
Bab ini menjelaskan langkah-langkah dan proses pelaksanaan tiap langkah yang digunakan dalam penyelesaian masalah pada Tugas Akhir ini.
3.1 Tahapan Penelitian
Secara singkat, tahapan penelitian ini dapat diuraikan sebagai berikut:
1. Mengkaji model aliran fluida
Pada tahap ini dikaji model matematika aliran fluida secara umum yang terdiri dari persamaan kontinuitas, persamaan momentum, dan distribusi panas. Selain itu dikumpulkan beberapa referensi untuk mendukung penelitian.
2. Mengkaji model matematika dari fluida sisko pada pipa Pada tahap ini dikaji beberapa model matematika fluida sisko pada pipa yang telah dihasilkan dari penelitian sebelumya dan model tersebut diusulkan dalam penelitian ini.
3. Mengembangkan model matematika
Mengembangkan model aliran dan distribusi panas fluida sisko pada pipa Annulus vertikal dengan menggunakan persamaan fluida umum dan referensi model pada penelitian sebelumnya. Setelah model kecepatan didapat, maka selanjutnya adalah mengembangkan model distribusi panasnya. Kemudian kedua model yang sudah diperoleh, dibentuk dalam persamaan
non-Dimensional.
4. Pendiskritan metode beda hingga Crank-Nicholson
Pada tahap ini, dilakukan pendiskritan model aliran dan perpindahan panas fluida sisko pada pipa annulus vertikal non
menggunakan metode beda hingga Crank-Nicholson. Kemudian dari persamaan diskrit tersebut dibentuk menjadi matriks penyelesaian.
5. Membuat algoritma program
Pada tahapan ini, dibuat algoritma penyelesaian dari persamaan diskrit pada metode beda hingga implisit Crank-Nicholson.
6. Membuat program
Algoritma yang telah dibuat kemudian diimplementasi dalam bentuk program komputer dengan menggunakan software Matlab.
7. Simulasi
Dengan menggunakan program yang telah dibuat, dilakukan simulasi dengan menggunakan beberapa nilai pada parameter atau variabel masukan.
8. Analisis Karakteristik
Hasil yang diperoleh dari beberapa simulasi akan dianalisis, untuk kemudian dicari karakteristik aliran fluida dan perpindahan panas pada pipa Annulus vertikal dan membuat kesimpulan. 9. Pembuatan laporan
Pada tahap ini dilakukan penulisan laporan Tugas Akhir. 10. Publikasi hasil penelitian
3.2 Diagram Alur Metode Penelitian
Secara umum tahapan-tahapan yang dilakukan dalam menyelesaikan Tugas Akhir ini ditampilkan dalam bentuk diagram alur metode penelitian sebagai berikut :
Publikasi hasil penelitian Pembuatan Laporan Analisis karakteristik
Simulasi Membuat program Membuat algoritma program
Pendiskritan metode beda hingga Crank-Nicholson Mengembangkan model kecepatan aliran dan perpindahan
panas
Mengkaji model matematika dari fluida sisko pada pipa Mengkaji model aliran fluida
Mulai
25
ANALISIS DAN PEMBAHASAN
Pada bab ini dibahas mengenai model persamaan kecepatan aliran dan distribusi temperatur, bagaimana mengubahnya menjadi model persamaan non-Dimensional, dan menyelesaikan kedua model persamaan secara numerik. Selain itu, dari proses diskritisasi model juga dapat diperoleh grafik simulasi yang kemudian akan dicari karakteristik dari kecepatan aliran dan distribusi temperatur.
4.1 Pemodelan Matematika Kecepatan Aliran dan
Distribusi Temperatur Fluida Sisko pada Pipa
Langkah pertama untuk mencari karakteristik kecepatan aliran dan distribusi temperatur adalah mendapatkan model persamaan kecepatan aliran dan distribusi temperatur fluida sisko pada pipa. Dengan bentuk pipa yang diteliti adalah bentuk pipa pada gambar (2.1). Kedua model persamaan ini masih dalam kondisi dimensional.
4.1.1 Pemodelan Matematika Kecepatan Aliran Fluida
Sisko pada Pipa
Persamaan kecepatan aliran diturunkan dari persamaan kontinuitas yang dibentuk ke dalam koordinat polar silinder dan tegangan tensor yang disubstitusikan ke dalam persamaan momentum fluida. Pada Tugas Akhir ini didasarkan pada model kecepatan aliran fluida tak tunak dan tak mampu mampat dengan asumsi-asumsi sebagai berikut :
1. Pipa lurus vertikal. Dengan aliran bergerak dari bawah ke atas secara laminar.
2. Luas penampang pipa konstan.
3. Pipa berbentuk annulus dengan pusat yang sama.
4. Variabel bebas yang berpengaruh adalah jari-jari pipa dan waktu.
5. Kecepatan dan temperatur merupakan fungsi jari-jari dan waktu.
Pada Tugas Akhir ini fluida yang digunakan adalah fluida sisko. Dimana fluida ini akan mengalir seperti air jika mencapai regangan geser tertentu. Dengan demikian, berdasarkan asumsi-asumsi yang telah dibuat, model matematika yang dikembangkan untuk menjelaskan profil kecepatan aliran fluida sisko pada pipa annulus terdiri dari persamaan kontinuitas dan momentum pada fluida bergerak dalam koordinat silinder.
Aliran fluida sisko merupakan aliran tak mampu-mampat, maka kerapatan fluida konstan atau
(4.1)
kemudian substitusi Persamaan (4.1) ke dalam Persamaan (2.8), sehingga didapat persamaan kontinuitas fluida Sisko menjadi :
( )
atau dapat dinyatakan dengan
(4.2)
Jika dinyatakan dalam koordinat silinder : ( )
(4.3)
Substitusikan Persamaan (4.2) ke dalam Persamaan momentum fluida (2.9) :
( ( ) ) ( ̿) dengan demikian,
(
) ( ̿)
maka persamaan fluida yang digunakan menjadi
( ̿) (4.4)
Nilai
̿ merupakan divergensi dari tegangan tensor fluida sisko yang didefinisikan pada Persamaan (2.1)̿ dengan [ |√ ( ( )) |
]
Dalam hal ini adalah gradient kecepatan pada sumbu-z yang berupa fungsi skalar dengan variabel bebas jari-jari dan waktu. Sehingga,
atau dalam bentuk matriks :
Karena adalah vektor , sehingga didapat transpos dari :
Dengan demikian,
(4.5) Dari Persamaan (4.5), maka :
|√ ( )| |√ ( ) | |√ | ( ) Sehingga tegangan geser pada fluida sisko menjadi [ ( ) ]
maka ( ) (4.6)
Pada persamaan (4.6) terdapat power index yang digunakan untuk menentukan jenis fluida. Jika maka
, sehingga fluida untuk adalah fluida dengan
karakteristik bingham plastic. Kemudian untuk maka ( )
, sehingga fluida untuk adalah fluida
Newtonian. Untuk , yang mempunyai (
) .
Jika , maka fluida tersebut adalah fluida dengan karakteristik shear-thickening. Sedangkan, jika , maka fluida tersebut adalah fluida dengan karakteristik shear-thinning.
Sesuai dengan batasan masalah pada bab I, Pada Tugas Akhir ini digunakan power index dan power index . Kemudian selanjutnya dapat dihitung nilai dari ̿ pada Persamaan (4.4) : ̿ ( ̿ ) ̿ ̿ diperoleh, ̿ ( ) ( ) ( )
Karena tegangan geser pada fluida adalah fungsi dengan variabel bebas jari-jari dan waktu ( ) maka,
Pada aliran laminar, aliran hanya bergerak pada sumbu-z, maka percepatan radial dan tangensialnya adalah nol. Begitu juga tekanan pada arah radial dan tangensialnya juga nol. Atau,
(4.7) Sehingga ̿ (4.8)
Substitusikan Persamaan (4.6) ke dalam Persamaan (4.8). maka,
̿ ( ( ) ) ( ( ) ) (4.9) Karena tekanan hanya terjadi pada sumbu-z, dengan menggunakan aturan rantai, differensial tekanan menjadi :
(4.10) Substitusikan Persamaan (4.7) ke dalam Persamaan (4.10). Sehingga,
Jika kedua ruas dikalikan , diperoleh :
Maka Persamaan (4.9) menjadi :
Kemudian dapat dirumuskan Persamaan Momentum pada fluida sisko sebagai berikut :
( ( ( ) ) ( ) ) atau, ( ( ) ) ( )
Tekanan pada fluida didefinisikan sebagai (T.S.L Radhika, 2012)
dengan P adalah tekanan dan adalah grafitasi.
Maka ( ( ) ) ( )
Misalkan bahwa (konstanta)
Sehingga didapat Persamaan kecepatan aliran fluida sisko: ( ( ) ) ( ) (4.12) Dapat disimpulkan bahwa kecepatan aliran fluida sisko dipengaruhi oleh kerapatan, grafitasi, jari-jari pipa, tegangan geser, dan juga parameter material fluida dan yang mana tiap-tiap fluida memiliki parameter yang berbeda.
4.1.2 Pemodelan Matematika Distribusi Temperatur
Aliran Fluida Sisko pada Pipa
Persamaan distribusi temperatur yang sudah didefinisikan pada (2.13) yaitu:
̿
dengan :
adalah kerapatan fluida dan kapasitas temperatur pada tekanan konstan.
Berdasarkan substitusi tensor tegangan ̿ dan Persamaan Laplace, Persamaan (4.13) menjadi:
* (( ( ) ) )+ * ( ) + (4.13)
Pada distribusi temperatur, tekanan pada fluida dapat diabaikan. Sehingga . Kemudian, karena temperatur adalah fungsi
dan , maka .
Selanjutnya didapat Persamaan distribusi temperatur fluida sisko: [( ( ) ) ] ( ) (4.14)
4.2 Model Kecepatan Aliran dan Distribusi
Temperatur Non-Dimensional
Model kecepatan aliran dan distribusi temperatur yang telah didapat masih tergantung pada satuan, sehingga belum bisa diterapkan pada berbagai kasus, supaya model matematika kecepatan aliran dan distribusi temperatur tersebut dapat diterapkan pada berbagai kondisi dengan satuan yang bervariasi, maka Persamaan (4.12) dan (4.14) akan dibentuk kedalam persamaan non-dimensional. Berikut variabel non-dimensional yang akan disubtitusikan pada Persamaan (4.12) dan (4.14) :
( ) ( ) ( ) ( ) ( ) ( )
4.2.1 Model Kecepatan Aliran Non-Dimensional
Model kecepatan aliran dimensional pada Persamaan (4.12) yang sudah didapat :
( ( ) ) ( ) dengan
Mensubstitusikan variabel-variabel non-dimensional pada pada persamaan kecepatan: ( ) (( ) ) (4.15) (4.16) ( ( ) ) ( ( ( )) ( ) ( ( ( ))) ) ( ( ) ( ) ( ) ) ( ( ) ( ) ( ) ) ( ( ) ) ( ( ) ) ( ( ) ) (4.17) (4.18) ( ) ( ) ( ( ) ( )) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (4.19)
Kemudian substitusikan Persamaan (4.15) sampai (4.19) kedalam model kecepatan aliran dimensional :
( ( ) ) ( ) Kalikan kedua ruas dengan ,
( ) ( ( ) ) ( )
atau
( )
( ( ) ) ( ) Sehingga model kecepatan aliran non-dimensional : ( ) ( ( ) ) ( ) (4.20)
4.2.2 Model Distribusi Temperatur Non-Dimensional
Model distribusi temperatur fluida sisko dimensional pada Persamaan (4.14) yang sudah didapat :
(( ( ) ) ) ( )
Mensubstitusikan variabel-variabel non-dimensional pada persamaan distribusi temperatur:
(( ) ) (( ) ) ( ) ( ) ( ) (4.21) ([ ( ) ] ) ([ ( ) ] ( ) ( ) ) (4.22) ( ) ( ) ( )(( ) (( ) ) ( ) ) ( ) ( ) (4.23)
dengan mensubstitusi Persamaan (4.21) sampai (4.23) ke dalam Persamaan (4.14): ( ) [ ( ) ] ( ) ( ) ( ) ( )
Kalikan kedua ruas dengan ( ) sehingga didapat:
[ ( ) ] ( )( ) ( ) Karena ( ) ( ). Maka model
persamaan distribusi temperatur fluida sisko menjadi:
[ ( ) ] ( ) ( ) (4.24)
4.3 Penyelesaian Numerik
Model kecepatan aliran dan distribusi temperatur fluida sisko pada pipa annulus yang sudah didapat pada Persamaan (4.20) dan (4.24) akan diselesaikan secara numerik dengan metode beda hingga Crank-Nicholson.
4.3.1 Kondisi Awal dan Kondisi Batas
Dalam Tugas Akhir ini, pipa yang digunakan adalah pipa annulus dengan pusat jari-jari sama antara silinder dalam dan silinder luar, maka
Kondisi batas pada kecepatan aliran: ( ) , ( ) , dengan kondisi awal :
( ) ,
Sedangkan kondisi batas pada distribusi temperatur. ( ) ,
( ) , dengan kondisi awal :
( ) ,
Kondisi batas dan kondisi awal di atas merupakan kondisi batas dan kondisi awal pada Persamaan Dimensional. Sehingga perlu disubstitusikan variabel Non-Dimensional, agar didapat kondisi batas dan kondisi awal yang nantinya akan digunakan untuk Persamaan Non-Dimensional.
Kondisi batas pada kecepatan aliran : ( )
( ) , dengan kondisi awal :
( ) , kondisi batas pada Distribusi temperatur : ( ) ,
dengan kondisi awal :
( ) ,
4.3.2 Penyelesaian Numerik Kecepatan Aliran
Model kecepatan aliran pada Persamaan (4.20) terdapat parameter material b. Apabila nilai parameter material bernilai 0, maka fluida tersebut adalah fluida Newtonian. Fluida sisko adalah fluida dengan nilai parameter material b tidak sama dengan 0. Pada Tugas Akhir ini akan digunakan parameter material untuk fluida sisko pada power index 0 dan pada power index 1.
Untuk Persamaan (4.20) menjadi :
( )
(4.25)
Selanjutnya, Persamaan (4.25) didiskritkan dengan menggunakan metode beda hingga implisit Crank-Nicholson.
( ) * ( )+ ( ( ) ( ) )
Fluida sisko hanya mengalir antara fluida dalam dan fluida luar. Maka , dimana , untuk pendiskritan sebanyak .
Gambar 4.1 Penampang horizontal pipa Annulus Misalkan dan ( ).
Maka selanjutnya didapatkan skema numerik untuk adalah
𝑟 𝑑 𝑟
( ) ( ) ( ) ( ( ) ) ( ) ( ) ( ) (4.26)
Kemudian didapat matriks tridiagonal dari Persamaan (4.26) sebagai berikut: [ ][ ] [ ] [ ][ ] dengan ( )
Untuk Persamaan (4.20) menjadi :
( ) (
)
( ) (4.27)
Selanjutnya, Persamaan (4.27) didiskritkan dengan menggunakan metode beda hingga implisit Crank-Nicholson.
( ) ( ) ( ) ( ) ( ( ) ( ) )
Dengan definisi dan cara yang sama pada Persamaan (4.25) maka didapat skema numerik untuk Persamaan (4.27) sebagai berikut:
( ) ( ( ) ( ) ) ( ) ( ) ( ) ( )
Misalkan dan ( ),
maka selanjutnya didapatkan skema numerik untuk adalah ( ( )) ( ( ) ( )) ( ( ) ( )) ( ) ( ( )) ( ( ) ( )) ( ( ) ( )) (4.28)
Kemudian didapat matriks tridiagonal dari Persamaan (4.28) sebagai berikut: [ ][ ] [ ] [ ][ ] dengan ( ) ( ) ( ) ( )
( )
( )
( )
(( ) )
4.3.3 Penyelesaian Numerik Distribusi Temperatur
Sama halnya dengan model kecepatan aliran. Model Distribusi temperatur juga dipengaruhi oleh power index . Sehingga diperoleh model Distribusi temperatur untuk fluida non-Newtonian: ( ) ( ) atau ( ) (4.29)
Selanjutnya, Persamaan (4.29) didiskritkan dengan menggunakan metode beda hingga implisit Crank-Nicholson.
( ) ( ) ( ) ( ) ( ) ( ) ( ) Misalkan dan ( )
Maka didapatkan skema numerik untuk adalah ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (4.30)
Kemudian didapat matriks tridiagonal dari Persamaan (4.30) sebagai berikut: [ ][ ] [ ] [ ][ ] dengan ( ) ( ) ( ) ( )
Setelah itu, distribusi temperatur untuk fluida Newtonian:
[ ] ( ) (4.31)
Persamaan (4.31) didiskritkan dengan menggunakan metode beda hingga implisit Crank-Nicholson.
[ ] ( ) ( ) ( ) ( ) ( ) ( )
Misalkan dan ( ) [ ] ( ) ( ) ( )
Maka didapatkan skema numerik untuk adalah ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) (4.32)
Kemudian didapat matriks tridiagonal dari Persamaan (4.32) sebagai berikut: [ ][ ] [ ] [ ][ ] dengan ( ) ( )
[ ]
( )
4.4 Algoritma Program
Dalam Tugas Akhir ini, penyelesaian numerik dari model kecepatan aliran mempengaruhi penyelesaian numerik distribusi temperatur. Dengan menggunakan nilai parameter material dan parameter lain yang sama, maka algoritma penyelesaiannya sebagai berikut:
1. Mendefinisikan parameter-parameter yang dibutuhkan dengan input , , , dan . 2. Membentuk matriks tridiagonal sisi kiri dan kanan pada
kecepatan aliran.
3. Mendefinisikan syarat awal dan syarat batas pada kecepatan aliran.
4. Membentuk konstanta yang berupa vektor pada sisi kanan persamaan matriks kecepatan aliran.
5. Menyelesaikan skema numerik dengan mengoperasikan matriks-matriks yang sudah terbentuk, sehingga didapat nilai kecepatan pada titik-titik sepanjang jari-jari pipa.
6. Menampilkan grafik kecepatan dengan perbedaan parameter material.
7. Mendefinisikan parameter-parameter yang dibutuhkan dengan input , , , dan .
8. Membentuk matriks tridiagonal sisi kiri dan kanan pada distribusi temperatur aliran.
9. Mendefinisikan syarat awal dan syarat batas pada distribusi temperatur aliran.
10. Membentuk konstanta yang berupa vektor pada sisi kanan dengan memasukkan hasil dari kecepatan aliran yang sudah didapat pada persamaan matriks distribusi temperatur aliran.
11. Menyelesaikan skema numerik dengan mengoperasikan matriks-matriks yang sudah terbentuk, sehingga didapat nilai temperatur pada titik-titik sepanjang jari-jari pipa.
12. Menampilkan grafik temperatur dengan perbedaan parameter material.
13. Kemudian ditampilkan juga distribusi temperatur aliran dengan perbedaan nilai bilangan Brinkman.
Algoritma progam kecepatan aliran dan distribusi temperatur di atas berlaku untuk power index dan .
4.5 Simulasi Kecepatan Aliran dan Distribusi
Temperatur Fluida Sisko pada Pipa
Pada subbab ini akan ditampilkan grafik simulasi kecepatan aliran dan distribusi temperatur fluida sisko pada ketinggian pipa . Berdasarkan persamaan yang sudah didapat, fluida Newtonian mempunyai nilai power index dan . Sedangkan fluida sisko mempunyai nilai power index dan .
4.5.1 Simulasi Kecepatan Aliran Fluida Sisko Pada
Pipa
Dengan mendifinisikan parameter . Selanjutnya, akan dibandingkan besar kecepatan fluida sisko dengan dan fluida Newtonian dengan pada
power index , serta fluida sisko dengan dan fluida
Newtonian dengan untuk power index . Perbandingan tersebut juga ditunjukkan pada variasi waktu, dan jari-jari pipa bagian dalam yang dinotasikan dengan .
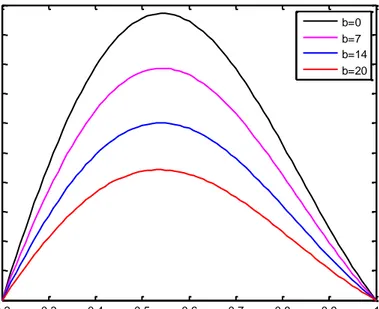
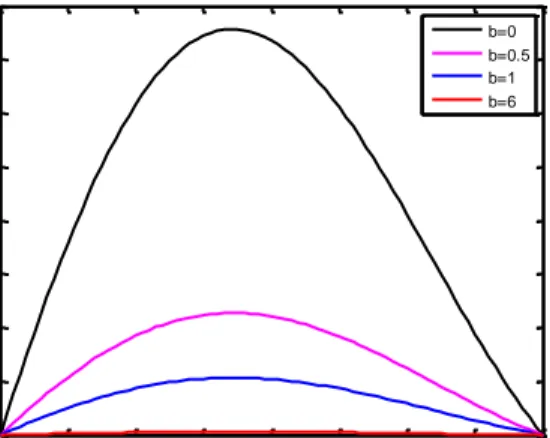
Gambar 4.2 Distribusi kecepatan aliran dengan power index
Pada Gambar (4.2) terlihat bahwa semakin besar nilai b, besar kecepatan akan semakin kecil. Hal ini disebabkan karena besar parameter material b sebanding dengan besar tegangan geser fluida. Sehingga semakin besar nilai parameter yang diberikan, tegangan geser pada fluida akan semakin besar, dan pada akhirnya, kecepatan fluida tersebut semakin kecil. Dengan demikian, pada power index , kecepatan fluida sisko lebih kecil daripada fluida Newtonian.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 12 14 16 18 20
Kecepatan Fluida dengan Power index 0
Jari-Jari K e c e p a ta n b=0 b=7 b=14 b=20
Gambar 4.3 Distribusi kecepatan aliran dengan power index
Berdasarkan Gambar (4.2) dan (4.3), semakin besar nilai
t, maka kecepatan fluida semakin besar. Artinya, semakin lama
fluida akan mengalir semakin cepat. Hal ini disebabkan karena semakin besar nilai t, tegangan geser fluida semakin kecil.
Pada Gambar (4.2) dan (4.3), juga terlihat bahwa semakin dekat aliran fluida dengan dinding pipa, aliran fluida akan semakin menurun. Kondisi ini disebabkan karena semakin dekat jarak fluida yang mengalir dengan dinding pipa, maka gesekan antar fluida semakin besar. Sehingga kecepatan pada dinding pipa sama dengan 0.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 5 10 15 20 25 30
Kecepatan Fluida dengan Power index 0
Jari-Jari K e c e p a ta n b=0 b=7 b=14 b=20
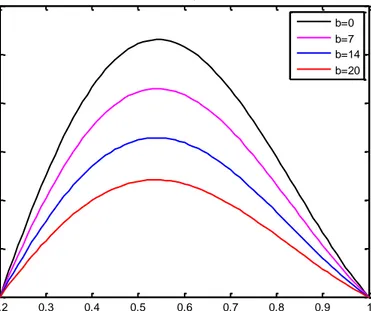
Gambar 4.4 Distribusi kecepatan aliran dengan power index
Gambar (4.3) dan (4.4), menunjukkan bahwa kecepatan aliran juga dipengaruhi oleh panjangnya jari-jari antara pipa dalam dan pipa luar. Semakin kecil jarak kedua pipa, kecepatan aliran akan semakin kecil. Kondisi ini dikarenakan jarak antara bagian tengah jari-jari pipa dengan dinding semakin kecil. Seperti yang sudah dijelaskan sebelumnya bahwa semakin aliran mendekati dinding, kecepatan aliran semakin kecil. Menyebabkan kesempatan aliran untuk mengalir lebih cepat semakin berkurang.
Jadi, disimpulkan, kecepatan aliran fluida sisko dengan
power index dipengaruhi waktu yang ditentukan,
parameter material dan jarak jari-jari antara kedua pipa.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 12 14
Kecepatan Fluida dengan Power index 0
Jari-Jari K e c e p a ta n b=0 b=7 b=14 b=20
Tegangan geser pada suatu fluida mempunyai nilai yang sebanding dengan gaya yang bekerja pada fluida tersebut. Tetapi, keduanya mempunyai arah yang berlawanan.
Selanjutnya, ditampilkan distribusi kecepatan aliran fluida dengan power index adalah sebagai berikut:
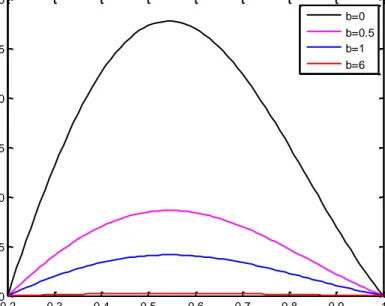
Gambar 4.5 Distribusi kecepatan aliran dengan power index
Pada Gambar (4.5), menunjukkan hasil yang tidak jauh berbeda dengan Gambar (4.2). Pada power index kecepatan fluida sisko juga lebih kecil daripada fluida Newtonian. Atau dengan kata lain, semakin besar nilai b, kecepatan fluida semakin kecil. Tidak menutup kemungkinan untuk nilai b yang besar, kecepatan fluida akan sama dengan 0. Hal ini dikarenakan untuk nilai b yang besar, tegangan geser pada fluida juga akan bernilai besar.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 5 10 15 20 25 30
Kecepatan Fluida dengan Power index 1
Jari-Jari K e c e p a ta n b=0 b=0.5 b=1 b=6
Gambar 4.6 Distribusi kecepatan aliran dengan power index
Perbedaan nilai t yang ditunjukkan pada Gambar (4.6). Semakin besar nilai t, kecepatan fluida juga semakin besar.
Gambar 4.7 Distribusi kecepatan aliran dengan power index 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 5 10 15 20 25 30 35 40
Kecepatan Fluida dengan Power index 1
Jari-Jari K e c e p a ta n b=0 b=0.5 b=1 b=6 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 2 4 6 8 10 12 14 16 18 20
Kecepatan Fluida dengan Power index 1
Jari-Jari K e c e p a ta n b=0 b=0.5 b=1 b=6
Seperti pada Gambar (4.4), Gambar (4.7) menunjukkan semakin kecil jarak kedua pipa, kecepatan aliran akan semakin kecil. Dengan penyebab yang sama dengan power index yaitu dikarenakan jarak antara bagian tengah jari-jari pipa dengan dinding semakin kecil. Sehingga kesempatan aliran untuk mengalir lebih cepat semakin berkurang.
. Sehingga dapat disimpulkan kecepatan fluida sisko lebih kecil daripada fluida Newtonian pada power index dan .
4.5.2 Simulasi Distribusi Temperatur Aliran Fluida
Sisko Pada Pipa
Dengan mendifinisikan parameter , dan . Selanjutnya, akan dibandingkan besar distribusi temperatur antara fluida sisko dengan dan fluida Newtonian dengan untuk power index , serta fluida sisko dengan dan fluida Newtonian dengan
untuk power index . Perbandingkan tersebut juga ditunjukkan pada variasi waktu, dan Bilangan Brinkman.
Gambar 4.8 Distribusi temperatur aliran dengan power index 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 200 220 240 260 280 300 320 340 360 380
Distribusi Temperatur Fluida dengan Power index 0
Jari-Jari T e m p e ra tu r b=0 b=7 b=14 b=20
Pada Gambar (4.8) menunjukkan bahwa besarnya gesekan pada fluida mempunyai pengaruh lebih besar dari pada besarnya kecepatan aliran tersebut. Gesekan terbesar terjadi pada dinding pipa menyebabkan temperatur fluida mengalami titik tertinggi. Semakin aliran menjauhi dinding, temperaturnya menurun sampai kemudian temperaturnya kembali naik.
Gambar 4.9 Distribusi temperatur aliran dengan power index
Pada Gambar (4.8) dan (4.9), terlihat semakin besar nilai
t, distribusi temperatur semakin kecil. Kondisi ini disebabkan
adanya pengaruh tegangan geser fluida yang semakin lama semakin kecil. Dari kedua gambar tersebut juga terlihat untuk nilai b yang lebih besar, distribusi temperatur pada fluida akan lebih tinggi dari pada nilai b yang lebih kecil. Seperti yang sudah dibahas pada kecepatan, semakin besar parameter material b, menyebabkan tegangan fluida semakin besar. Dengan demikian,
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 150 200 250 300 350 400
Distribusi Temperatur Fluida dengan Power index 0
Jari-Jari T e m p e ra tu r b=0 b=7 b=14 b=20
temperatur fluida juga semakin besar. Sehingga dapat disimpulkan temperatur fluida sisko lebih besar dari pada fluida Newtonian.
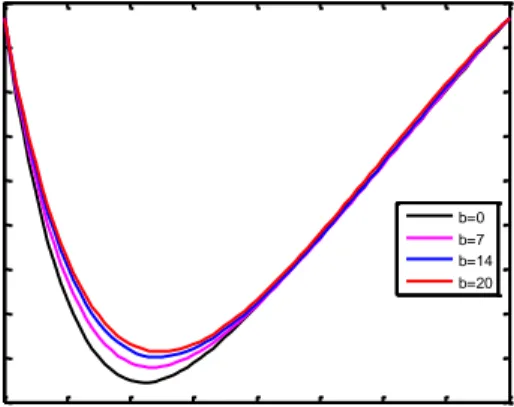
Gambar (4.10), diberikan nilai bilangan Brinkman yang berbeda. Hasilnya menunjukkan bahwa semakin besar bilang Brinkman, distribusi temperatur fluida semakin kecil.
Gambar 4.10 Distribusi temperatur aliran dengan power index
Bilangan Brinkman adalah perbandingan antara perubahan viskositas dengan distribusi temperature (Nirmalasari. N.A, 2011). Bilangan Brinkmann merupakan salah satu dari parameter Non-Dimensional, yang mana nilainya berbanding terbalik dengan temperatur fluida.
Jadi, disimpulkan bahwa distribusi temperatur aliran fluida dengan power index dipengaruhi oleh waktu yang ditentukan, parameter material dan bilangan Brinkman.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 100 150 200 250 300 350 400
Distribusi Temperatur Fluida dengan Power index 0
Jari-Jari T e m p e ra tu r Br=0.5 Br=2 Br=5 Br=7.5
Selanjutnya akan ditampilkan distribusi temperatur aliran fluida dengan power index sebagai berikut:
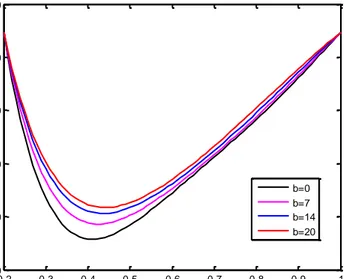
Gambar 4.11 Distribusi temperatur aliran dengan power index
Seperti pada kecepatan, temperature fluida juga mempunyai karakter yang sama. Pada Gambar (4.11), menunjukkan hasil yang tidak jauh berbeda dengan Gambar (4.8). Pada power index temperatur fluida sisko juga lebih besar daripada fluida Newtonian. Atau semakin besar nilai b, temperatur fluida semakin besar.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 180 200 220 240 260 280 300 320 340 360 380
Distribusi Temperatur Fluida dengan Power index 1
Jari-Jari T e m p e ra tu r b=0 b=0.5 b=1 b=6
Gambar 4.12 Distribusi temperatur aliran dengan power index
Demikian juga dengan perbedaan nilai t. Semakin besar nilai t, tegangan geser pada fluida semakin kecil, sehingga hal tersebut menyebabkan temperatur fluida juga semakin kecil. Seperti yang sudah dijelaskan, fluida sisko tidak dapat mengalir tanpa adanya energi panas. Jadi, fluida sisko yang mula-mula diam mempunyai tegangan geser yang besar. Setelah diberikan suatu energi panas dengan temperatur tertentu, tegangan gesernya akan semakin kecil.
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 100 150 200 250 300 350 400
Distribusi Temperatur Fluida dengan Power index 1
Jari-Jari T e m p e ra tu r b=0 b=0.5 b=1 b=6