Interpolasi Definisi dan Macam macamnya

I . PENGERTIAN DAN TUJUAN INTERPOLASI A. Pengertian

Interpolasi adalah proses pencarian dan penghitungan nilai suatu fungsi yang

grafiknya melewati sekumpulan titk yang diberikan. Titik-titik tersebut mungkin merupakan hasil eksperimen dalam sebuah percobaan, atau diperoleh dari suatu fungsi yang diketahui. B. Tujuan

Y

X (x0,y0)

(x1,y1)

Y

X (x0,y0)

(x1,y1) II. MACAM-MACAM INTERPOLASI

PEMBAHASAN A. Interpolasi Linier

Interpolasi linear atau interpolasi lanjar adalah interpolasi dua buah titik dengan sebuah garis lurus. Misal diberikan dua buah titik, (x0,y0) dan (x1,y1). Polinom yang

menginterpolasi kedua titik itu adalah persamaan garis lurus yang berbentuk: P(x)=a₀+a₁x

Gambar dibawah ini memperlihatkan garis lurus yang menginterpolasi titik-titik (x0,y0) dan

(x1,y1).

Gambar 1.1 Interpolasi Linier

Koefisien a₀ dan a₁ dicari dengan proses substitusi dan eliminasi. Dengan mensubstitusikan (x0, y0) dan (x1, y1) ke dalam persamaan p1(x)=a0+a1x diperoleh dua persamaan linear:

y₀=a₀+a₁x₀ . . . (1) y₁=a₀+a₁x₁ . . . (2)

Dari dua persamaan diatas, dengan eliminasi diperoleh:

a (¿¿0+a1x1) y0−y1=

(

a0+a1x0

)

−¿

y₀−y₁=a₁x₀−a₁x₁

x (¿¿0−x1) ⇔y0−y1=a1¿

⇔a₁=y0−y1

x0−x1

Substitusikan nilai a₁ ke dalam persamaan (1), diperoleh:

y₀=a₀+a₁x₀ ⇔y0=a0+

(

y₀−y₁ x₀−x₁

)

x0

⇔y₀=a₀+x0y0−x0y1 x0−x1

⇔y₀=a₀+x0y0−x0y1

x0−x1 ⇔a₀=y₀−x0y0−x0y1

x0−x1

⇔a₀=y0(x0−x1)−x0 y0+x0y1 x₀−x₁

⇔a₀=x0y0−x1y0−x0y0+x0y1

x0−x1 ⇔a₀=x0y1−x1y0

x0−x1

Dengan melakukan manipulasi aljabar untuk menentukan nilai p₁(x) dapat dilakukan sebagai berikut:

Y

X P1(x0,y0)

P2 (x1,y1)

(x,y) p₁(x)=x1y0−x0y1

x1−x0

+ y1– y0 x1−x0

x

p₁(x)=x1y0−x0y1+xy1– x y0

x1−x0

p1(x)=

x1y0−x0y1+xy1– x y0+(x0y0−x0y0) x₁−x₀

p₁(x)=x1y0−x0y0−x0y1+xy1– x y0+x0y0 x1−x0

x−x₀ ¿ ¿ ¿– y₀(x−x₀) y₀

(

x₁−x₀

)

+y₁¿

p₁(x)=¿

y x−x0

¿ ¿ ¿ (¿¿1−y₀)¿ y₀

(

x₁−x₀

)

+¿

p1(x)=¿

y x−x0

¿ ¿ ¿ (¿¿1−y₀)¿

¿ p₁(x)=y₀+¿

Dalam menentukan persamaan dari interpolasi linear juga dapat dilakukan melalui cara berikut:

Gambar 1.3 Interpolasi Linier

Persamaan garis lurus yang melalui 2 titik P1 (x0,y0) dan P2 (x1,y1) dapat dituliskan dengan:

y−y₀ y1−y0

= x−x0 x1−x0

Sehingga diperoleh persamaan dari interpolasi linear sebagai berikut:

y=y1−y0

x1−x0

(

x−x₀

)

+y₀

Algoritma Interpolasi Linear

1. Tentukan nilai x₀, y₀, x₁,dany₁.

2. Periksa apakah x₀=x₁ . Jika ya, maka kembali ke langkah 1 sebab nilai fungsinya tidak terdefinisi dalam kondisi ini. Jika tidak, maka dilanjutkan ke langkah 3. 3. Masukkan nilai x .

4. Periksa apakah min

{

x₀, x₁

}

≤ x ≤ max

{

x₀, x₁

}

. Jika tidak, maka masukkan nilai x yang lain. Jika ya, maka dilanjutkan langkah 5.

5. Hitung P=y0+(x−x0)

y₁−y₀ x1−x0

.

6. Periksa apakah y₀=y₁ . Karena jika sama, maka akan diperoleh P=y₀ . 7. Tulis hasil y=P .

Contoh

1. Perkirakan atau prediksi jumlah penduduk Purworejo pada tahun 2005 berdasarkan data tabulasi berikut:

Tahun 1990 2000

Penyelesaian:

Dipunyai: x0 = 1990, x1 = 2000, y0 = 187.900, y1 = 205.700.

Ditanya: Prediksi jumlah penduduk Gunungpati pada tahun 1995. Ingat :

y x−x0

¿ ¿ ¿ (¿¿1−y0)¿

¿ p₁(x)=y₀+¿

Misalkan x=1995 1995−1990

¿ ¿ ¿

(205.700−187.900)¿ p₁(2005)=187.900+¿

p₁(2005)=196.800

Jadi, diperkirakan jumlah penduduk Purworejo pada tahun 1995 adalah 196.800 orang.

2. Dari data ln(9.0) = 2.1972, ln(9.5) = 2.2513, tentukan ln(9.2) dengan interpolasi linier sampai 4 desimal. Bandingkan hasil yang diperoleh dengan nilai sejati ln(9.2)=2.2192.

Penyelesaian: Dipunyai:

x₀=9.0,y₀=2.1972 . x₁=9.5,y₁=2.2513.

Ditanya : tentukan nilai ln(9.2) sampai 5 angka bena kemudian dibandingkan dengan nilai sejati ln(9.2) = 2.2192.

Ingat: y x−x0

¿ ¿ ¿ (¿¿1−y₀)¿

Y

X x0,y0

x1,y1

x2,y2

x2 x1

x0 y0

y1

y2

Y

X x0,y0

x1,y1

x2,y2

x2 x1

x0 y0

y1

y2 9.2−9.0

¿ ¿ ¿

(2.2513−2.1972)¿ p₁(9.2)=2.1972+¿

p₁(9.2)=2.21884

Galat = nilai sejati ln(9.2) – nilai ln(9.2) hasil perhitungan dengan metode interpolasi linear

Galat = 2.2192 – 2.21884 = 3,6 x 10-4 _.

B. Interpolasi Kuadratik

Misal diberi tiga buah titik data,

(

x₀, y₀

)

,

(

x₁, y₁

)

, dan(x₂, y₂) . Polinom yang menginterpolasi ketiga buah titik itu adalah polinom kuadrat yang berbentuk:

p2(x)=a0+a1x+a2x 2

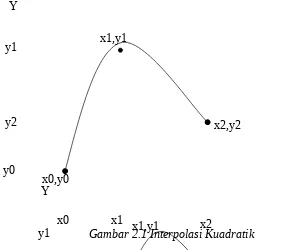
Bila digambar, kurva polinom kuadrat berbentu parabola, seperti ditunjukkan dalam Gambar 2.4 dan Gambar 2.5

Gambar 2.1 Interpolasi Kuadratik

Masih terdapat grafik berbentuk parabola yang lain, selain yang ditunjukkan pada

Gambar 2.1 Bukan Interpolasai Kuadratik

Menyelesaikan Polinom p2(x) ditentukan dengan cara berikut:

1. Substitusikan (xi, yi) ke dalam persamaan p2(x)=a0+a1xi+a2xi

2

dengan i = 0,

1, 2. Diperoleh tiga persamaan dengan tiga buah parameter yang tidak diketahui

yaitu: a₀, a₁, dan a₂: a0+a1x0+a2x02=y0

a0+a1x1+a2x12=y1 a0+a1x2+a2x22=y2

2. Hitung a₀, a₁, dan a₂ dari sistem persamaan tersebut dengan metode eliminasi Gauss.

Selain menggunakan metode eliminasi Gauss, menentukan a₀, a₁, dan a₂ dapat ditentukan dengan cara sebagai berikut:

a) Hitung F₀₁=yi+1−yi

xi+1−xi

, F₁₂=yi+2−yi+1

yi+2−yi+1

, dan F₀₁₂=F12−F01

xi+2−xi

b) Hitung P=y1+

(

x−xi

)

F01+(x−xi)(x−xi+1)F012

Algoritma Interpolasi Kuadratik

2. Periksa apakah x₀<x₁<x₂ . Jika tidak, maka kembali ke langkah 1 sebab nilai fungsinya tidak terdefinisi dalam kondisi ini. Jika tidak, maka dilanjutkan ke langkah 3.

3. Masukkan nilai x .

4. Periksa apakah min

{

x₀, x₁, x₂

}

≤ x ≤max

{

x₀, x₁, x₂

}

. Jika tidak, maka masukkan nilai x yang lain. Jika ya, maka dilanjutkan langkah 5.

5. Hitung F₀₁=y1−y0 x1−x0

, F₁₂=y2−y1 x2−x1

,danF₀₁₂=F12−F01 x2−x0 6. Hitung P=y1+

(

x−xi

)

F01+

(

x−xi

)

(x−xi)F012

7. Periksa apakah F₀₁₂=_{0. Jika ya, maka persamaan yang dihasilkan linear. Jika tidak} maka persamaan yang dihasilkan merupakan persamaan kuadrat.

8. Tulis hasil y=P . Contoh :

1. Diberikan titik ln(8.0) = 2.0794, ln(9.0) = 2.1972, dan ln(9.5) = 2.2513. Tentukan nilai ln(9.2) dengan interpolasi kuadratik.

Penyelesaian:

Diketahui: x0=8.0,y0=2.0794 x₁=9.0,y₁=2.1972 x₂=9.5,y₂=2.2513 Ditanya : Tentukan nilai ln (9.2).

Sistem persamaan yang terbentuk adalah:

a₀+8.0a₁+64.00a₂=2.0794

a₀+9.0a₁+81.00a₂=2.1972 a0+9.5a1+90.25a2=2.2513

Untuk perhitungan secara manual, sistem persamaan diselesaikan dengan metode eliminasi Gauss dengan langkah sebagai berikut:

Matriks yang terbentuk dari persamaan

a₀+8.0a₁+64.00a₂=2.0794 a0+9.0a1+81.00a2=2.1972

adalah:

[

1 1 1 8 9 9.5 64 81 90.25 2.0794 2.1972 2.2513

]

R21(−1) R31(−1)

[

1 0 0 8 1 1.5 64 17 26.25 2.0794 0.1178 0.1719

]

R12(−8)

R32(−1.5)

[

1 0 0 0 1 0 −72 17 0.75 1.137 0.1178

−0.0048

]

R31( 1

0.75)

[

1 0 0 0 1 0 −72 17 1 1.137 0.1178

−0.0064

]

R13(72) R23(−17)

[

1 0 0 0 1 0 0 0 1 0.6762 0.2266 −0.0064

]

Menggunakan metode Eliminasi gauss menghasilkan

a₀=0.6762,a₁=0.2266,a₂=−0.0064 .

Polinom kuadratnya adalah: p2(x)=a0+a1x+a2x2

p2(9.2)=0.6762+0.2266.(9.2)+−0.0064.(9.2) 2

p₂(9.2)=2.2192

2. Dalam suatu eksperimen fisika pergerakan sebuah benda pedat berbentuk parabola. Dengan data sebagai berikut :

t (detik) Y (m)

5 2,01

6,5 2,443

8 2,897

Dengan menggunakan interpolasi kuadratik perkirakan ketinggian bola pada saat t=7 detik.

Penyelesaian:

Dipunyai data pergerakan suatu benda padat:

t (detik) Y (m)

5 2,01

6,5 2,443

Dengan menggunakan interpolasi kuadratik akan diprediksi ketinggian bola saat t=7 detik.

Sistem persamaan lanjar yang terbentuk adalah:

a₀+5,0a₁+25,00a₂=2,01

a₀+6,5a₁+42,25a₂=2,443 a₀+8,0a₁+64,00a₂=2,897

Penyelesaian sistem persamaan dengan menggunakan metode eliminasi Gauss

¿

[

1 5 25

1 6,5 42,25 1 8 64

2,01 2,443 2,897

]

R2,R1(−1) R3,R1(−1)

[

1 5 25 0 1,5 17,25 0 3 39

2,01 0,443 0,887

]

R2

(

1 1,5

)

¿

[

1 5 25

0 1 11,5 0 3 39

2,01 0,28867

0,887

]

R1,R2(−5) R3,R2(−3)

[

1 0 −32,5 0 1 11,5

1 0 4,5

0,56667 0,28867 0,021

]

¿R3

(

1 4,5

)

[

1 0 −32,5

0 1 11,5 1 0 1

0,56667 0,28867 0,00467

]

R1,R3(32,5)

R2,R3(11,5)

[

1 0 0 0 1 0 1 0 1

0,71733 0,235 0,00467

]

Diperoleh : a₀=0,71733,a₁=0,235,a₂=0,00467

Sehingga Polinom Kuadratnya adalah:

p2(x)=0,71733+0,235x+0,00467x2 Sehingga p₂(7) = 2,588

Jadi,diprediksi, pada t = 7 detik tinggi bola 2,588 m.

Definisi : Suatu fungsi f (x) dinamakan suatu spline berderajat k jika 1. Domain dari S adalah suatu interval [a; b].

2. S; S0; :::; S(k�1) kontinu pada [a; b].

3. Terdapat titik-titik xi sedemikian sehingga a = x0 < x1 < ::: < xn = b dan juga S adalah suatu polinomial berderajat k pada setiap [xi; xi+1].

Dengan kata lain, spline adalah potongan-potongan fungsi polinomial dengan turunan-turunan memenuhi kendala-kendala kekontinuan tertentu. Ketika k=1, spline

dina-makan spline linear. Ketika k=2 , spline dinamakan spline kuadratik. Ketika k=3, spline dinamakan spline kubik.

C.1 Spline Linear

akan dicari suatu fungsi spline linear S(x) sedemikian sehingga S

(

x_i

)

=(y_i)

untuk 0≤i ≤ n . Diambil

S_x=

{

S0(x); xϵ[x1, x2] S₁(x); xϵ

[

x₁, x_2]

⋮ ⋮

Sn−1(x); xϵ[xn−1, xn]

Dengan setiap Si(x) adalah linier

Diperhatikan fungsi linear S_i(x) . Garis ini melalui titik (xi, yi) dan (xi+1, yi+1) , se-hingga kemiringan dari Si(x) yaitu

m_i=yi+1−yi xi+1−xi

Kita dapat juga mengatakan bahwa garis tersebut melalui titik (xi, yi) dan x ,(S(x))

¿ untuk sembarang x∈[x_i, x_+1i] , sehingga

m_i=Si(x)−yi x−xi

yang memberikan

S_i(x)=y_i+m_i

(

x−x_i

)

¿y_i+ yi+1−yi

xi+1−xi

(

x−x_i

)

(C.1 .1)

Contoh C.2

Buatlah interpolasi spline linier untuk data berikut:

y 1,3 4,5 2,0 2,1 5,0 3,0

Penyelesaian :

[

0,0;0,1]S₀(x)=1,3+4,5−1,3

0,1−0 (x−0)=1,3+32x

[

0,1;0,4]S1(x)=4,5+

2,0−4,5

0,4−0,1(x−0,1)= 16

3 − 25

3 x

[

0,4;0,5

]

S₂(x)=2+2,1−2,0

0,5−0,4(x−0,4)=1,6+x

[

0,5;0,75]S₃(x)=2,1+ 5,0−2,1

0,75−0,5(x−0,5)=−3,7−11,6x

[

0,75;1

]

S4(x)=5+ 3−5

1−0,75(x−0,75)=11−8x

Jadi spline adalah potongan linear, yaitu linear di antara setiap titik data. Persamaan (C.1.1) dapat dituliskan kembali sebagai

S_i(x)=a_ix+b_i,i=0,1,… , n−1 dengan

a_i=yi+1−yi xi+1−xi

dan b_i=y_i−a_ix_i

kekurangan utama spline linear adalah pada titik-titik data di mana dua spline bertemu, kemiringannya berubah secara mendadak. Secara formal ini berarti bahwa turunan pertama dari fungsi tidak kontinyu pada titik-titik tersebut. Kelemahan ini diatasi oleh penggunaan polinomial spline orde yang lebih tinggi.

C.2 Spline Kuadratik

Tidak seperti spline linear, spline kuadratik tidak dide.nisikan sepenuhnya oleh nilai-nilai di x_i . Berikut ini kita perhatikan alasannya. Spline kuadratik didefnisikan oleh

Si(x)=aix2+bix+ci

Jadi terdapat 3n parameter untuk mende.nisikan S(x) . Diperhatikan titik-titik data:

x₀ x₁ x_{2 ⋯} x_n

y_y y₁ y₂ ⋯ y_n

Syarat-syarat untuk menentukan 3n parameter dijelaskan seperti berikut ini.

S_i

(

x_i

)

=y_idan S_i

(

x_i+1

)

=y_i+1

jadi, disini didapatkan 2n persamaan

2. Syarat pada kontinuitas dari S'(x) memberikan suatu persamaan tunggal untuk setiap titik dalam x_i, i=0,1,2,… , n−1 yaitu:

S'

i−1

(

xi

)

=S'i(xi)

Jadi dari sini dipunyai n−1 persamaan. Sekarang totalnya terdapat 3n−1 persamaan, tetapi karena terdapat 3n parameter yang tidak diketahui maka sistem mempunyai kekurangan ketentuan.

3. Pilihan-pilihan yang mungkin untuk melengkapi kekurangan ketentuan yaitu S'

(

x0

)

=0atau S( {x} rsub {0} )=

Sekarang dimisalkan zi=S '

i

(

xi

)

. karena Si

(

xi

)

=yi , S'i

(

xi

)

=zi , dan

S'

i

(

xi+1

)

=zi+1 , maka kita dapat mendefinisikan : S_i(x)= zi+1−zi

2

(

xi+1−xi

)

(

x−x_i

)

2+z_i

(

x−x_i

)

+y_iC.2 .1

Selanjutnya, dengan pengambilan x=x_i+1 diperoleh y_i+1=S_i(x)= zi+1−zi

2

(

xi+1−xi

)

(

x−x_i

)

2+z_i

(

x−x_i

)

+y_{i yi+1−yi=}zi+1−zi

2

(

x−xi

)

+zi

(

x−xi

)

y_i+1−y_i=zi+1−zi

2

(

x−xi

)

Jadi, kita dapat menentukan z_i+1dari z_i : z_i+1=2 yi+1−yi

xi+1−xi

−z_i

Contoh C.2

Buatlah interpolasi spline kuadratik untuk data berikut ini

x 0,0 0,1 0,4 0,5

y 1,3 4,5 2,0 2,1

dengan ketetapan zo=0

Penyelesaian :

pertama-tama hitung nilai z_i z₁=2 y1−y0

x1−x0

−z₀=24,5−1,3

0,1−0 −0=64 z2=2

y₂−y₁ x2−x1

−z₁=2 2−4,5

0,4−0,1−64=

−242

3

z₃=2 y3−y2 x3−x2

−z₂=2 2,1−2

0,5−0,4+ 242

3 = 248

S₀(x)= z1−z0 2

(

x1−x0

)

(

x−x₀

)

2+z₀

(

x−x₀

)

+y_{0 ¿320x}2

+1.3untuk0≤ x ≤0,1

S₁(x)= z2−z1 2

(

x2−x1

)

(

x−x₁

)

2+z₁

(

x−x₁

)

+y₁ ¿−2170

9 (x−0,1) 2

+64(x−0,1)+4,5

¿−2170 9 x

2

+1010 9 x+

194

45 , untuk0,1≤ x ≤0,4

S₂(x)= z3−z2 2

(

x3−x2

)

(

x−x₂

)

2+z₂

(

x−x₂

)

+y₂ ¿2450

3 (x−0,4) 2

−242

3 (x−0,4)+2

¿2450 3 x

2

−2202 3 x+

4948

30 ,untuk0,4≤ x ≤0,5 persamaan C.2.1 dapat ditulis kembali sebagai

Si(x)=aix

2

+bix+ci,i=0,1,2,… , n−1

dengan

a_i= zi+1−zi 2

(

xi+1−xi

)

,b_i=z_i−2a_ix_i, c_i=a_ix_i2−z_ix_i+y_i

C.3 Spline Kubik

Diketahui suatu fungsi f(x) yang dibatasi oleh interval a dan b, dan memiliki sejumlah titik data a=x₀<x₁<…<x_n=b . Interpolasi spline kubik S(x) adalah

suatu potongan fungsi polinomial berderajat tiga (kubik) yang menghubungkan dua titik yang bersebelahan, dengan ketentuan, untuk i=0,1,2,… , n−1

(S0) Potongan fungsi pada subinterval

[

x_i, x_i+1

]

,i=0,1,2,… , n−1 S_i(x)=a_i

(

x−x_i

)

3

+b_i

(

x−x_i

)

2

+c_i

(

x−x_i

)

+d_i (S1) Pada setiap titik data x=x_{i ,}i=0,1,…, n

S

(

xi

)

=f(xi)

(S2) Nilai-nilai fungsi harus sama pada titik-titik dalam: S_i

(

x_i+1

)

=S_i+1

(

x_i+1

)

, i=0,1,2,… , n−2

(S3) Turunan-turunan pertama pada titik dalam harus sama: S '_i

(

x_i+1

)

=S '_i+1

(

x_i+1

)

, i=0,1,2,… , n−2

(S4) Turunan-turunan kedua pada titik dalam harus sama:

S} rsub {i} left ({x} rsub {i+1} right ) = {S_i+1

(

x_i+1

)

, i=0,1,2,… , n−2

(S5) Salah satu syarat batas di antara dua syarat batas x₀ dan x_n berikut ini harus dipenuhi:

 S(x₀)=S left ({x} rsub {n} right ) = (disebut batas alamiah/ natural boundary)  S'

(

x0

)

=f

'

(x0) dan S

'

(

xn

)

=f '

(xn) (disebut batas apitan/ clamped boundary)

d_i=y_i, c_i=di+1−di

hi

−hi

3

(

2bi+bi

)

, ai=

1 3hi

(

b_i+1−b_i

)

C.3.1

Buatlah interpolasi spline kubik untuk data berikut ini

x 0 1 2 3

y 0 1 4 5

terhadap syarat batas : S'

(

x0

)

=S'(0)=c0=2dan S'

(

xn

)

=S'(3)=cn=2

Penyelesaian:

Lebar subinterval pada sumbu x: h₁=h₂=h₃=h₄=1

dan beda terbagi pertama, dengan mengingat bahwa di=f

(

xi

)

=yi , yaitu :

d₁−d₀ h0

=1,d2−d1

h1

=3,d3−d2

h2

=1

Persamaan matriks dapat dituliskan sebagai

[

2 1

1 4 0 0 1 0 0 1 0 0 4 1 1 2

]

[

b₀ b₁ b₂ b3

]

=3

[

1 3 1 −2 −1 −3 2 −1

]

[

−3 6 −6

3

]

yang mempunyai penyelesaian

b₀=−3,b₁=6,b₂=−6,b₃=−3

Disubstitusikan penyelesaian tersebut ke persamaan C.3.1 untuk memperoleh koefisien-koefisien lain dari spline kubik:

d₀=0,d₁=1,d₂=4 c0=1−

1

3

(

3+2(−3)

)

=2,c1=3− 1

3

(

−3+2(3)

)

=2,c2=3− 1

3

(

−3+2(3)

)

=2, a₀=3−(−3)

3 =2,a1= −3−3

3 =−2,a2=

3−(−3)

3 =2

Terakhir, kita dapat menuliskan persamaan spline kubik seperti:

S0=2x 3

+3x2+2x , untuk x∈

[

0,1

]

x−1 ¿ ¿ S1=−2(x−1)

3 +3¿

x−2 ¿ ¿ S2=2(x−2)

3 +3¿

D. Interpolasi Newton

 Persamaan Polinom Linier

p₁(x)=y₀+

(

y1−y0

)

(

x₁−x₀

)

(x−x0)  Bentuk pers ini dapat ditulis :

 Yang dalam hal ini a₀=y₀=f

(

x₀

)

D.1.1

x₁ ¿ x0 −f(¿)

f¿ a₁=

(

y1−y0

)

(

x₁−x₀

)

=¿

 Persamaan ini merupakan bentuk selish terbagi (divided-difference) a₁=f[x₁, x₀]

 Polinom kuadratik

p₂(x)=a₀+a₁

(

x−x₀

)

+a₂

(

x−x₀

) (

x−x₁

)

atau

p₂(x)=p₁(x)+a₂

(

x−x₀

) (

x−x₁

)

Dari persamaan ini menunjukkan bahwa p₂(x) _{dapat dibentuk dari persamaan sebelumnya} p₁(x) . Nilai a₂ dapat ditemukan dengan mengganti x=x₂ untuk mendapatkan a₂=f

(

x2

)

−a0−a1

(

x2−x0

)

(

x₂−x₀

) (

x₂−x₁

)

D.1.3

jika nilai a₀ dan a₁ pada persamaan D.1.1 dan D.1.2 dimasukkan ke persamaan D.1.3 maka akan didapatkan:

x2 ¿ x0 −f(¿)

¿ x1 ¿ x₀ −f(¿)

¿ f¿

¿ a₂=¿

jadi, tahapan pembentukan polinom newton: p₁(x)=p₀(x)+a₁(x−x₀)

p₁(x)=a₀+a₁

(

x−x₀

)

p₂(x)=p₁(x)+a₂

(

x−x₀

) (

x−x₁

)

p₃(x)=p₂(x)+a₃

(

x−x₀

) (

x−x₁

)(

x−x₂

)

 Nilai konstanta a₀, a₁, … , a_n , merupakan nilai selisih terbagi , dengan nilai a₀=f

(

x₀

)

a₁=f[x₁, x₀] ⋮=⋮ a_n=f[x_n, x_n−1, … , x₁, x₀]

x_i ¿ xj

−f(¿) f¿ f

[

xi, xj

]

=¿

f

[

xi, xj ,xk

]

=

f

[

x_i, x_j

]

−f

[

x_j, x_k

]

xi−xk

f

[

x_n, x_n−1, … , x₁, x0]=f

[

xn, xn−1, … , x1, x0]−f[xn−1, xn−2, … , x1, x0] xn−x0

Karena a₀, a₁, … , a_n , merupakan nilai selisih terbagi, maka polinom Newton dinamakan polinom interpolasi selisih terbagi Newton. Nilai selisih terbagi dapat dihitung dengan menggunakan tabel yng disebut tabel selisih terbagi.

Dengan demikian polinom Newton dapat ditulis dalam hub rekursif sebagai :  Rekurens

p_n(x)=p_n−1(x)+

(

x−x₀

) (

x−x₁

)

…

(

x−x_n−1

)

f

[

x_n−1, x_n−2, … , x₁, x₀

]

 Basis

p₀(x)=f

(

x₀

)

Contoh :

Bentuklah polinom Newton derajat satu, dua, tiga dan empat yang menghampiri f(x)=cosx dalam range [0.0, 4] dan jarak antar titik adalah 1.0. Lalu taksirlah f(x) dengan x=2.5 dengan Polinom Newton derajat 3

x_i y_i ST-1 ST-2 ST-3 ST-4

0 1 -0.4597 -0.2484 0.1466 -0.147

1 0.5403 -0.9654 0.1913 0.088

2 -0.4161 -0.5739 0.4551

3 -0.99 0.3363

4 -0.6536

E. Interpolasi Kubik

Misal diberikan empat buah titik data , x0,y0

¿ )(, x1 , y1 ), x₂

¿ , y2 ), dan ( x₃ , y₃ ).Polinom yang mengiterpolasi keempat buah titik itu ialah polinom kubik yang berbentuk :

p₃(x) = a0 + a1 x+ a2x2 + a3x3 Polinom p3(x) ditentukan dengan cara berikut:

1.Sulihkan ( x_i , y_i ) kedalam persamaan (p.5.9), i=0,1,2,3. Sehingga diperoleh empat buah persamaan dengan empat buah parameter yang tidak diketahui yaitu a_0,a₁, a₂dan a₃:

a0+a1xo+a2x02+a3x03=y0 a0+a1x1a2x12+a3x13=y1 a0+a1x2+a2x22+a3x23=y2 a0+a1x3+a2x3

2 +a3x3

3 =y3

 Jarak yang dibutuhkan sebuah kendaraan untuk berhenti adalah fungsi kecepatan. data percobaan berikut ini menunjukkan hubungan antara kecepatan dan jarak yang

dibutuhkan untuk menghentikan kecepatan.

 Perkiraan jarak henti yang dibutuhkan bagi sebuah kendaraan yang melaju dengan