SELEKSI FITUR DATASET MENGGUNAKAN PRINCIPAL COMPONENT ANALYSIS (PCA) UNTUK MENINGKATKAN AKURASI
KLASIFIKASI DECISION TREE C4.5
TESIS
MUHAMMAD ZUL FAHMI NASUTION 157038067
PROGRAM STUDI S2 TEKNIK INFORMATIKA
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
MEDAN 2018
SELEKSI FITUR DATASET MENGGUNAKAN PRINCIPAL COMPONENT ANALYSIS (PCA) UNTUK MENINGKATKAN AKURASI
KLASIFIKASI DECISION TREE C4.5
TESIS
Diajukan untuk melengkapi tugas dan memenuhi syarat memperoleh ijazah Magister Teknik Informatika
MUHAMMAD ZUL FAHMI NASUTION 157038067
PROGRAM STUDI S2 TEKNIK INFORMATIKA
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
MEDAN 2018
PERSETUJUAN
Judul : SELEKSI FITUR DATASET MENGGUNAKAN
PRINCIPAL COMPONENT ANALYSIS (PCA) UNTUK MENINGKATKAN AKURASI
KLASIFIKASI DECISION TREE C4.5
Kategori : TESIS
Nama : MUHAMMAD ZUL FAHMI NASUTION
Nomor Induk Mahasiswa : 157038067
Program Studi : TEKNIK INFORMATIKA
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI
INFORMASI UNIVERSITAS SUMATERA UTARA
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Prof. Dr. Marwan Ramli Prof. Dr. Opim Salim Sitompul
Diketahui/Disetujui oleh Magister Teknik Informatika Ketua,
Prof. Dr. Muhammad Zarlis NIP. 19570701 198601 003
PERNYATAAN
SELEKSI FITUR DATASET MENGGUNAKAN PRINCIPAL COMPONENT ANALYSIS (PCA) UNTUK MENINGKATKAN AKURASI
KLASIFIKASI DECISION TREE C4.5
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringaksan yang masing-masing telah disebutkan sumbernya.
Medan, 30 Januari 2018
Muhammad Zul Fahmi Nasution 157038067
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN
AKADEMIS
Sebagai sivitas akademika Universitas Sumatera Utara, saya yang bertanda tangan dibawah ini:
Nama : Muhammad Zul Fahmi Nasution
NIM : 157038067
Program Studi : Magister Teknik Informatika Jenis Karya Ilmiah : Tesis
Demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada Universitas Sumatera Utara Hak Bebas Royalti Non-Ekslusif (Non-Exclusive Royalty Free Right) atas tesis saya yang berjudul:
SELEKSI FITUR DATASET MENGGUNAKAN PRINCIPAL COMPONENT ANALYSIS (PCA) UNTUK MENINGKATKAN AKURASI
KLASIFIKASI DECISION TREE C4.5
Beserta perangkat yang ada (jika diperlukan). Dengan Hak Bebas Royalti Non- Eksklusif ini, Universitas Sumatera Utara berhak menyimpan, mengalih media, meformat, mengelola dalam bentuk database, merawat dan mempublikasikan tesis saya tanpa meminta izin dari saya selama tetap mencantumkan nama saya sebagai penulis dan sebagai pemegang dan/atau sebagai pemilik hak cipta.
Demikian peryataan ini dibuat dengan sebenarnya.
Medan, 30 Januari 2018
Muhammad Zul Fahmi Nasution 157038067
Telah diuji pada
Tanggal: 23 Januari 2018
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Opim Salim Sitompul Anggota : 1. Prof. Dr. Marwan Ramli
2. Dr. Syahril Efendi, S.Si, M.IT 3. Dr. Erna Budhiarti Nababan
RIWAYAT HIDUP
DATA PRIBADI
Nama Lengkap : Muhammad Zul Fahmi Nasution Tempat dan Tanggal Lahir : Medan, 18 Agustus 1986
Alamat Rumah : Jl. HM Yamin Gang Pisang No. 21, Kota Medan Telepon/Faks/HP : 081397781873
E-mail : [email protected]
DATA PENDIDIKAN
SD : SDN 060877 Medan TAMAT : 1998 SLTP : SLTP Negeri 14 Medan TAMAT : 2001 SLTA : SMK Negeri 8 Medan TAMAT : 2004 S1 : STMIK Mikroskil Medan TAMAT : 2010 S2 : Teknik Informatika USU TAMAT : 2018
KATA PENGANTAR
Alhamdulillah, puji syukur penulis panjatkan kehadirat Allah SWT yang telah memberikan rahmat dan hidayah-Nya serta segala sesuatunya dalam hidup, sehingga penulis dapat menyelesaikan penyusunan tesis ini. Tidak lupa penulis mengucapkan terimakasih sebesar – besarnya kepada :
1. Prof. Dr. Runtung Sitepu, S.H., M.Hum selaku rektor Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti dan menyelesaikan pendidikan program magister
2. Prof. Dr. Opim Salim Sitompul selaku Dekan Fasilkom-TI Universitas Sumatera Utara
3. Prof. Dr. Muhammad Zarlis selaku Ketua Program Studi Magister Teknik Informatika Universitas Sumatera Utara
4. Dr. Syahril Efendi, S.Si, M.IT selaku Sekretaris Program Studi Magister Teknik Informatika
5. Prof. Dr. Opim Salim Sitompul selaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis
6. Prof. Dr. Marwan Ramli selaku Pembimbing Kedua yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis
7. Dr. Syahril Efendi, S.Si, M.IT selaku Pembanding Pertama yang telah banyak memberikan kritik dan saran kepada penulis
8. Dr. Erna Budhiarti Nababan selaku Pembanding Kedua yang telah banyak memberikan kritik dan saran kepada penulis
9. Seluruh Staf pengajar dan pegawai di Program Studi Magister Teknik Informatika Universitas Sumatera Utara
10. Sahabat-sahabat angkatan 2015 KOM-C yang telah memberikan semangat dan dukungan moril kepada penulis selama penyelesaian tesis ini
Penulis menyadari bahwa tesis ini masih jauh dari kesempurnaan, karena kesempurnaan hanya milik Allah SWT. Oleh karena itu penulis menerima saran dan kritik yang bersifat membangun demi kesempurnaan tesis ini. Sehingga dapat bermanfaat bagi kita semuanya.
Medan, 30 Januari 2018
Muhammad Zul Fahmi Nasution
ABSTRAK
Split atribut merupakan proses utama dalam pembentukan decision tree C4.5. Proses split atribut di C4.5 masih belum meng-optimalkan akurasi prediksi pada pembentukan decision tree untuk memindahkan fitur yang tidak diperlukan. Fitur yang tidak diperlukan dapat menimbulkan noisy-data dan fitur yang kurang relevan.
Hal ini menyebabkan ukuran decision tree menjadi sangat besar (over-fitting).
Akibatnya terjadi ketidakseimbangan data sehingga tingkat akurasi menjadi rendah pada pengklasifikasian model decision tree C4.5. Seleksi fitur merupakan salah satu isu yang penting dalam pemodelan klasifikasi dimana hal ini bertujuan untuk menyederhanakan data yang kurang relevan sehingga meningkatkan akurasi. Model seleksi fitur digunakan untuk menyederhanakan data yang berdimensi tinggi menjadi data yang berdimensi rendah dengan atribut-atribut yang tidak saling berkorelasi.
Pada penelitian ini, metode yang diusulkan digunakan untuk memilih fitur yang relevan dan tidak saling berkorelasi dari sebuah dataset. Sehingga penelitian ini mengusulkan Principal Component Analysis (PCA) untuk melakukan seleksi fitur sehingga menghasilkan fitur yang tidak saling berkorelasi dan kemudian diklasifikasikan menggunakan model decision tree C4.5. Untuk melakukan pengujian terhadap model yang diusulkan, maka penelitian ini menggunakan dataset dari UCI Cervical cancer yang terdiri dari 858 data rekam medis pasien dengan 32 atribut observasi. Evaluasi kinerja klasikasi dari model yang diusulkan berdasarkan Accuracy, Particularity dan tingkat kesalahan pengklasifikasian. Hasil pengujian diperoleh bahwa metode usulan ini mampu meningkatkan akurasi model klasifikasi dengan tingkat akurasi sebesar 86.75%
Kata kunci: Decision Tree C4.5, Over-fitting, Feature Selection, Classification, Principal Component Analysis
PCA Based Feature Selection to Improve the Accuracy of Decision Tree C4.5 Classification
Abstract
Splitting attribute is a major process in decision tree C4.5 classification. However, this process does not give a significant impact on the establishment of the decision tree in terms of removing irrelevant features. It is a major problem in decision tree classification process called over-fitting resulting from noisy data and irrelevant features. In turns, over-fitting creates misclassification and data imbalance. Many algorithms have been proposed to overcome misclassification and overfitting on classifications decision tree C4.5. Feature selection is one of important issues in classification model which is intended to remove irrelevant data in order to improve accuracy. The feature selection framework is used to simplify high dimensional data to low dimensional data with non-correlated attributes. In this research, we proposed a framework for selecting relevant and non-correlated feature subsets. We consider principal component analysis (PCA) for feature selection to perform non-correlated feature selection and decision tree C4.5 algorithm for the classification. From the experiments conducted using available data sets from UCI Cervical cancer data set repository with 858 instances and 32 attributes, we evaluated the performance of our framework based on accuracy, particularity and classification error. Experimental results show that our proposed framework is robust to enhance classification accuracy with 86.75% accuracy rates.
Keywords: Decision Tree C4.5, Over-fitting, Feature Selection, Classification, Principal Component Analysis
DAFTAR ISI
Hal.
PENGESAHAN ii
PERYATAAN ORISINALITAS iii
PERSETUJUAN PUBLIKASI iv
PANITIA PENGUJI v
RIWAYAT HIDUP vi
UCAPAN TERIMA KASIH vii
ABSTRAK viii
ABSTRACK ix
DAFTAR ISI x
DAFTAR GAMBAR xii
DAFTAR TABEL xiii
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Rumusan Masalah 3
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 4
BAB 2 LANDASAN TEORI 5
2.1 Model Pohon Keputusan (Decision Tree) 5
2.2 Model Decision Tree C4.5 8
2.3 Teknik Klasifikasi 10
2.4 Analisis Komponen Utama (PCA) 12
2.5 Penelitian Terdahulu 17
2.6 Kontribusi Penelitian 18
BAB 3 METODOLOGI PENELITIAN 19
3.1 Data yang digunakan 19
3.2 Software yang digunakan 21
3.3 Metodologi Penelitian 21
3.3.1 Data preprocessing 22
3.3.2 Menghitung korelasi antar data observasi 23 3.3.3 Menentukan eigenvalue dari matrik kovarian 24 3.3.4 Memilih sejumlah principal component (PC) 24 3.3.5 Menghitung Bobot atribut menggunakan eigenvektor 24 3.3.6 Memilih atribut dengan bobot nilai eigenvektor tertinggi 25 3.3.7 Membentuk model prediksi klasifikasi decision tree C4.5 25 3.3.8 Pengujian akurasi menggunakan Confusion Matrix 26 3.3.9 Hasil akurasi model klasifikasi decision tree C4.5 27
BAB 4 HASIL DAN KESIMPULAN PENGUJIAN 28
4.1 Hasil Pengujian 28
4.1.1 Persiapan Data Awal (Data Preprocessing) 28
4.1.2 Proses Seleksi Atribut 28
4.1.2.1 Proses Perhitungan Korelasi 28
4.1.2.2 Dekomposisi Nilai Eigen dari Matrik Kovarian 30 4.1.2.3 Hasil Orthogonal Principal Component (PC)
terhadap varians kovarian dataset Cervical cancer 33 4.1.2.4 Menghitung Bobot Atribut menggunakan Eigenvektor
dari dataset Cervical cancer 34
4.1.2.5 Hasil Seleksi Atribut dataset Cervical cancer 35
4.1.3 Pembentukan Model Klasifikasi 37
4.1.3.1 Pembentukan Model Klasifikasi C4.5-Non-PCA
dataset Cervical cancer 38
4.1.3.1.1 Hasil Perolehan Nilai Entropy (C4.5-Non-PCA) 38 4.1.3.1.2 Hasil Perolehan Nilai Information Gain
(C4.5-Non-PCA) 39
4.1.3.1.3 Hasil Perolehan Nilai Gain Ratio C4.5-Non-PCA 40 4.1.3.1.4 Pengujian Model Klasifikasi C4.5-Non-PCA 42 4.1.3.2 Pembentukan Model Klasifikasi PCA+C4.5
dataset Cervical cancer 44
4.1.3.2.1 Hasil Perolehan Nilai Entropy (PCA+C4.5) 44 4.1.3.2.2 Hasil Perolehan Nilai Information Gain
(PCA+C4.5) 45
4.1.3.2.3 Hasil Perolehan Nilai Gain Ratio (PCA+C4.5) 46 4.1.3.2.4 Pengujian Model Klasifikasi PCA+C4.5 47 4.1.3.3 Evaluasi Hasil Pengujian Model Klasifikasi 49 4.1.3.3.1 Hasil Evaluasi Klasifikasi C4.5-Non-PCA
dengan PCA+C4.5 49
4.1.3.3.2 Hasil Evaluasi Model Klasifikasi PCA+C4.5
menggunakan Data Uji Rekam Medis 49
4.2 Kesimpulan Pengujian 53
BAB 5 KESIMPULAN DAN SARAN 55
5.1 Kesimpulan 55
5.2 Saran 56
DAFTAR PUSTAKA 57
LAMPIRAN 59
DAFTAR GAMBAR
Hal.
Gambar 2.1 Skematis Decision Tree 6
Gambar 2.2 Pemetaan Atribut dan corresponding Decision Tree 7
Gambar 2.3 Proses Klasifikasi 11
Gambar 2.4 Model Konseptual untuk Efektifitas menggunakan PCA 13
Gambar 3.1 Arsitektur Umum Penelitian 21
DAFTAR TABEL
Hal.
Tabel 2.1 Penelitian Terdahulu 17
Tabel 3.1 Data Rekam Medis Pasien Kanker Servik 20 Tabel 3.2 Confusion Matrix (two-class prediction) 26 Tabel 4.1 Hasil Persiapan Data Awal (Data Preprocessing) 28 Tabel 4.2 Hasil Matrik Kovarian dataset Cervical Cancer 30
Tabel 4.3 Hasil Dekomposisi Nilai Eigen 32
Tabel 4.4 Hasil Orthogonal Principal Component (PC) terhadap
Varians Dataset Cervical Cancer 34 Tabel 4.5 Bobot Atribut menggunakan Eigenvector dataset
Cervical Cancer 35
Tabel 4.6 Hasil Seleksi Atribut Dataset Cervical cancer 36 Tabel 4.7 Data Uji dataset Cervical Cancer 37 Tabel 4.8 Hasil Diskritisasi dataset Cervical cancer
(C4.5-Non-PCA) 38
Tabel 4.9 Nilai Entropy Atribut X1 per Partisi 38 Tabel 4.10 Hasil Perolehan Information Gain dataset Cervical cancer
(C4.5-Non-PCA) 39
Tabel 4.11 Hasil Perolehan Gain Ratio dataset Cervical cancer
(C4.5-Non-PCA) 40
Tabel 4.12 Rules Model Klasifikasi C4.5-Non-PCA dataset
Cervical Cancer 41
Tabel 4.13 Hasil Pengujian Model Klasifikasi C4.5-Non-PCA
untuk Data Uji dataset Cervical Cancer 42 Tabel 4.14 Confusion Matrix Model Klasifikasi C4.5-Non-PCA
menggunakan Data Uji dataset Cervical Cancer 43 Tabel 4.15 Hasil Diskritisasi dataset Cervical cancer (PCA+C4.5) 44 Tabel 4.16 Hasil Information Gain dataset Cervical Cancer (PCA+C4.5) 45 Tabel 4.17 Hasil Perolehan Gain Ratio Cervical Cancer (PCA+C4.5) 46 Tabel 4.18 Rules Model Klasifikasi PCA+C4.5 dataset Cervical Cancer 46 Tabel 4.19 Hasil Pengujian Model Klasifikasi PCA+C4.5 menggunakan Data Uji dataset Cervical Cancer 47 Tabel 4.20 Confusion Matrix Model Klasifikasi PCA+C4.5
dataset Cervical Cancer 48
Tabel 4.21 Performance metrics Model Klasifikasi C4.5-Non-PCA
dan Model Klasifikasi PCA+C4.5 (dataset Cervical Cancer) 49 Tabel 4.22 Hasil Observasi dan Diskritisasi Data Rekam Medis 50 Tabel 4.23 Hasil Pengujian Model Klasifikasi PCA+C4.5
(Data Rekam Medis) 51
Tabel 4.24 Confusion Matrix Model Klasifikasi PCA+C4.5
(Data Rekam Medis) 52
Tabel 4.25 Performance metrics Model Klasifikasi C4.5-Non-PCA dan PCA+C4.5 (dataset Cervical Cancer) serta Model PCA+C4.5
(Data Rekam Medis) 54
BAB 1 PENDAHULUAN
1.1. Latar Belakang
Algoritma C4.5 adalah sebuah decision tree yang digunakan untuk klasifikasi dengan konsep information entropy. Algoritma C4.5 menggunakan kriteria split dari ID3 yang telah dimodifikasi yang dinamakan Gain Ratio (Mitchell, 1997).
Algoritma ID3 menggunakan Information Gain (IG) untuk kriteria split atribut, sedangkan Algoritma C4.5 menggunakan Gain Ratio (GR), dimana atribut yang memiliki gain tertinggi dipilih sebagai akar (root).
Dalam pendekatan decision tree, pruning merupakan proses untuk memotong atau menghilangkan beberapa cabang (node) yang tidak diperlukan.
Node yang tidak diperlukan dapat menimbulkan noisy-data dan fitur yang kurang relevan (Zhang, 2012). Hal ini menyebabkan ukuran decision tree menjadi sangat besar yang disebut over-fitting. Akibatnya terjadi ketidakseimbangan data sehingga tingkat akurasi menjadi rendah (Wang, et al. 2012).
Zhang (2012) mengusulkan dua metode pruning. Metode pertama disebut heterogeneous-cost sensitive learning (HCSL) dengan memodifikasi average- gain split atribut (Mitchell, 1997) yang dikalikan dengan selisih misklasifikasi (misclassification cost dari atribut sebelum di-split dan setelah di-split). Metode pruning kedua adalah menggunakan nilai ambang (threshold pruning). Kedua metode pruning tersebut diuji menggunakan model pengklasifikasian Decision Tree dengan kriteria split dari algoritma ID3 dan C4.5 (heterogenenous cost) terhadap enam dataset dan menyimpulkan bahwa kedua metode pruning yang diusulkan tersebut dapat digunakan untuk model pengklasifikasian decision tree.
Sivapriya & Nadira (2013) mengusulkan reduksi fitur Principal Component Analysis (PCA) dan seleksi fitur gain-ratio algoritma decision tree C4.5 untuk meningkatkan klasifikasi Support Vector Machine (SVM). Data yang digunakan adalah citra MRI (Magnetic Resonance Images) dari jaringan saraf manusia untuk diklasifikasikan melalui pengujian neuropsychological. Metode ini memiliki performa klasifikasi SVM dengan tingkat akurasi sebesar 97%.
Hussain et al. (2015) menggunakan pendekatan Principal Component Analysis (PCA) sebagai metode seleksi fitur untuk mereduksi indikator-indikator yang berhubungan dengan prediksi tingkat ketahanan hidup pasien terinfeksi kanker payudara. Data yang digunakan berasal dari SEER dataset sebanyak 684.394 rekam medis pasien. Dengan pendekatan yang diusulkan memperoleh akurasi sebesar 92%.
Dang et al. (2016) mengusulkan model prediksi penyakit tumor menggunakan Principal Component Analysis sebagai ekstraksi fitur dan algoritma ID3 untuk seleksi fitur. Hasil seleksi fitur diklasifikasikan menggunakan metode Multi Layer Perceptron (MLP). Dataset yang digunakan adalah dataset DNA dari Leukemia, Prostate dan Diffuse large B-cell lymphoma (DLBCL). Hasil pengujian dari sistematis reduksi fitur dengan mengkombinasikan ekstraksi dan seleksi fitur serta MLP sebagai metode klasifikasi dapat meningkatkan performa akurasi dari dataset DNA.
Kavitha & Kannan (2016) mengusulkan reduksi fitur Principal Component Analysis dan seleksi fitur menggunakan algoritma Wrapper filter serta kriteria split dari algoritma C4.5 untuk digunakan sebagai metode untuk menghasilkan fitur-fitur yang relevan dari dataset UCI Heart dataset. Metode yang diusulkan dapat digunakan untuk menghasilkan fitur-fitur yang relevan sehingga meningkatkan efisiensi dan akurasi.
Berdasarkan latar belakang diatas, Metode seleksi fitur dataset menggunakan Principal Component Analysis (PCA) diusulkan untuk menyederhanakan dan menghilangkan fitur-fitur yang kurang relevan tanpa mengurangi maksud dan tujuan informasi dari data aslinya. Hasil seleksi fitur oleh PCA akan dibangun klasifikasinya dengan model decision tree C4.5 untuk memperoleh fitur terbaik dan paling penting agar diharapkan meningkatkan akurasi pengklasifikasian decision tree C4.5.
1.2. Rumusan Masalah
Split atribut merupakan proses utama dalam pembentukan decision tree C4.5.
Proses split atribut di C4.5 masih belum meng-optimalkan akurasi prediksi pada pembentukan decision tree untuk memindahkan fitur yang tidak diperlukan. fitur yang tidak diperlukan dapat menimbulkan noisy-data dan fitur yang kurang relevan. Hal ini menyebabkan ukuran decision tree menjadi sangat besar (over- fitting). Akibatnya terjadi ketidakseimbangan data sehingga tingkat akurasi menjadi rendah pada pengklasifikasian model decision tree C4.5.
1.3. Batasan Masalah
Penelitian ini mempertimbangkan beberapa batasan masalah sebagai berikut:
1. Penelitian ini membahas pengaruh metode seleksi fitur dataset menggunakan Principal Component Analysis (PCA) untuk meningkatkan akurasi pengklasifikasian Decision Tree C4.5.
2. Metode klasifikasi yang digunakan dalam penelitian ini adalah decision tree dengan induksi gain ratio sebagai splitting-attribute.
3. Analisis kinerja dari metode klasifikasi Decision Tree C4.5 berdasarkan pengukuran akurasi menggunakan Confusion Matrix.
4. Penelitian ini menggunakan 2 dataset. Dataset pertama diperoleh dari UCI repository of machine learning dataset yaitu: Cervical Cancer dataset yang beralamat (http://archive.ics.uci.edu/ml). Data ini berkaitan dengan serangkaian prediksi pengujian medis terhadap pasien yang terinfeksi kanker servik. Dataset kedua berasal dari Rumah Sakit Umum H. Adam Malik Medan merupakan data rekam medis pasien sebanyak 20 pasien rawat jalan yang dicurigai terinfeksi kanker servik dan diklasifikasikan berdasarkan prediksi pengujian medis yang akan diberikan.
1.4. Tujuan Penelitian
Penelitian ini dilakukan dengan tujuan untuk menyederhanakan dan menghilangkan atribut atau fitur yang kurang relevan tanpa mengurangi maksud dan tujuan dari data aslinya menggunakan Principal Component Analysis (PCA) untuk meningkatkan akurasi metode klasifikasi decision tree C4.5.
1.5. Manfaat Penelitian
Manfaat penelitian ini diharapkan dapat digunakan sebagai berikut:
1. Dapat menjadi acuan pembentukan Decision Tree sebagai metode pengklasifikasian data dan Principal Component Analysis (PCA) sebagai metode seleksi fitur dataset untuk meningkatkan akurasi klasifikasi decision tree C4.5.
2. Dapat memberikan informasi mendalam terhadap metode seleksi fitur dataset menggunakan Principal Component Analysis (PCA) untuk meningkatkan akurasi metode klasifikasi decision tree C4.5.
LANDASAN TEORI
2.1. Model Pohon Keputusan (Decision Tree)
Decision tree merupakan struktur data yang bersifat hirarkikal yang diimplementasikan dari divide-and-conquer strategy dan efficient nonparametric method serta dapat digunakan pada metode klasifikasi dan metode regresi (Alpaydin, 2010). Decision tree merupakan algoritma machine learning dalam teknik klasifikasi yang bersifat supervised learning untuk membentuk pohon keputusan dari data. Pohon yang terbentuk menyerupai pohon terbalik, dimana akar (root) berada di bagian paling atas dan daun (leaf) berada di bagian paling bawah (Abellan & Castellano 2016).
Data dalam pohon keputusan biasanya dinyatakan dalam bentuk tabel dengan field dan record. Atribut menyatakan suatu parameter yang dibuat sebagai kriteria dalam pembentukan tree. Manfaat utama dari penggunaan pohon keputusan adalah kemampuannya untuk menyederhanakan proses pengambilan keputusan yang kompleks menjadi lebih sederhana sehingga pengambilan keputusan lebih menginterpretasikan solusi permasalahan. Pohon keputusan juga berguna untuk mengeksplorasi data, yaitu menemukan hubungan tersembunyi antara sejumlah calon variabel input dengan sebuah variabel target. Pohon keputusan merupakan himpunan aturan IF...THEN. Setiap path dalam tree dihubungkan dengan sebuah aturan, dimana premis terdiri atas sekumpulan node yang ditemui dan kesimpulan aturan terdiri atas kelas yang terhubung dengan leaf dari path. Decision tree terdiri dari sekumpulan aturan untuk membagi sejumlah populasi yang heterogen menjadi lebih kecil, lebih homogen dengan memperhatikan variabel tujuannya. Variabel tujuan biasanya dikelompokkan dengan pasti dan model pohon keputusannya lebih mengarah kepada perhitungan
probabilitas dari masing-masing record terhadap kategori atau untuk mengklasifikasikan record dengan mengelompokkannya dalam kelas yang sama.
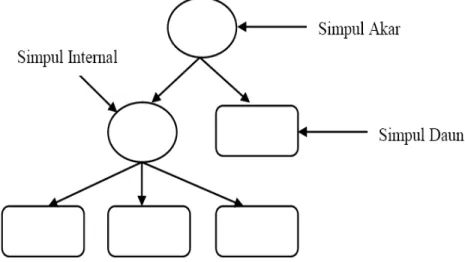
Pohon keputusan merupakan salah satu metode klasifikasi yang menggunakan representasi struktur pohon (tree) dimana setiap simpul internal (internal node) merupakan sebuah atribut, setiap cabang merupakan nilai atribut, dan setiap simpul daun (leaf node) atau simpul terminal merupakan label class, serta simpul yang paling atas adalah simpul akar (root node).
Elemen - elemen pada decision tree terdiri dari satu atau lebih variabel atribut (predictive attributes or features) dan satu atribut kelas (single class variable). Classification tree dapat digunakan untuk memprediksi nilai pada atribut kelas dengan mempertimbangkan nilai pada setiap variabel atribut yang diuji (Abellan & Castellano 2016).
Gambar 2.1. Skematis Decision Tree
Berikut penjelasan mengenai 3 jenis simpul yang terdapat pada pohon keputusan diatas:
a. Simpul akar merupakan simpul yang paling atas. Simpul ini tidak mempunyai input dan mempunyai output lebih dari satu.
b. Simpul internal merupakan simpul percabangan dari simpul akar. Simpul ini hanya ada satu input dan mempunyai minimal dua output.
c. Simpul daun merupakan simpul terakhir. Simpul ini hanya terdapat satu input dan tidak ada keluaran (output), simpul ini sering disebut juga simpul terminal.
Metode pohon keputusan mengubah fakta yang sangat besar menjadi pohon keputusan yang merepresentasikan aturan. Aturan dapat dengan mudah dipahami
dengan bahasa alami. Dan juga dapat diekspresikan dalam bentuk bahasa terstruktur yang disebut Structured Query Language untuk mencari record pada kategori tertentu. Decision tree berguna untuk mengeksplorasi data, menemukan hubungan tersembunyi antara sejumlah calon variabel input dengan sebuah variabel target. Karena decision tree memadukan antara eksplorasi data dan pemodelan, decision tree juga sangat bagus sebagai langkah awal dalam pembentukan model bahkan ketika dijadikan sebagai model akhir dari beberapa teknik lain.
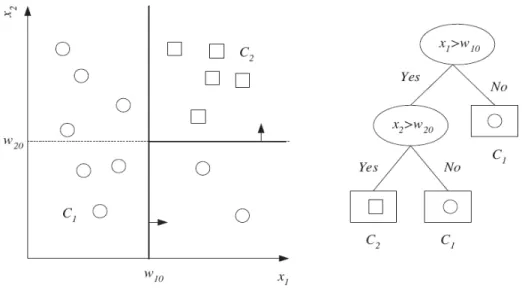
Gambar 2.2. Pemetaan atribut dari dataset dan model klasifikasi decision tree.
(Sumber: Alpaydin, 2010)
Gambar 2.2 menjelaskan tentang pemetaan atribut sebuah dataset untuk dimodelkan pada pengklasifikasian decision tree. Node yang berbentuk oval adalah simpul akar (root/internal node) dan node berbentuk persegi adalah simpul daun/subset (leaf node). Hasil perhitungan probabilitas dari record pada atribut x1 lebih besar dari record pada atribut w10 sehingga dipilih sebagai simpul akar dan memiliki 2 simpul percabangan dengan kondisi nilai Yes dan No. Simpul cabang yang bernilai No diklasifikasikan kedalam subset C1 sedangkan simpul cabang yang bernilai Yes diklasifikasikan kedalam subset C2 namun belum termasuk ke dalam kelas yang sama sehingga dilakukan kembali perhitungan probabilitas secara rekursif untuk membentuk pohon subset dan menghasilkan kembali 2 simpul percabangan yang memiliki nilai Yes dan No, semua subset C1 dan C2 masuk ke dalam kelas yang sama, maka setelah dilakukan split pertumbuhan tree dihentikan.
2.2. Model Decision Tree C4.5
C4.5 adalah algoritma klasifikasi supervised learning untuk membentuk decision tree dari data yang dikembangkan oleh J. Ross Quinlan sebagai pengembangan dari algoritma ID3. Jika ID3 (Iterative Dichotomiser 3) menggunakan entropy untuk kriteria split, sedangkan C4.5 decision tree menggunakan kriteria split yang telah dimodifikasi yang dinamakan Gain Ratio (Mitchael, 1997) dalam proses pemilihan split atribut. Split atribut merupakan proses utama dalam pembentukan pohon keputusan (decision tree). Algoritma C4.5 dapat bekerja pada variabel kontinyu dan missing value (Quinlan, 1986). Atribut yang memiliki Gain Ratio tertinggi yang dipilih (Zhang, 2012).
C4.5 menggunakan dua pendekatan heuristic untuk dilakukan uji peringkat probabilitas yaitu: (1) Information gain, meminimalkan total entropy dari subset {Si} dimana terjadi bias saat diuji dengan data numerik. (2) Gain ratio, pembagian Information gain dengan informasi entropy dari tiap atribut.
Agoritma C4.5 merupakan salah satu varian decision tree yang mirip dengan struktur flowchart, yang masing-masing internal node dinyatakan sebagai atribut pengujian. Setiap cabang mewakili output dari pengujian dan tiap node (leaf node) menentukan label class. Node paling atas dari sebuah pohon adalah node root. Algoritma C4.5 menggunakan information gain sebagai penentu simpul akar, internal dan daun. Tahapan algoritma C4.5 adalah sebagai berikut:
(Mitchell, 1997)
(1) menghitung nilai Entropy pada masing – masing atribut :
(2.1)
Dimana:
• S = Himpunan Kasus
• n = Jumlah Partisi S
• pi = Proporsi Subset dari S pada partisi ke-i
(2) menghitung nilai Information Gain pada masing-masing atribut:
(2.2)
∑
=
−
=
n
i
pi pi
S Entropy
1
log2
* )
(
) (
| *
|
| ) |
( )
, (
1
i n
i
i Entropy S S
S S Entropy A
S
Gain
∑
=
−
=
Dimana:
• S = Keseluruhan Dataset
• A = Atribut Subset
• n = Jumlah Partisi Atribut A
• | Si | = Ukuran Subset dari Dataset yang dimiliki atribut A pada partisi ke-i
• | S | = Ukuran Jumlah Kasus dalam Dataset
(3) menghitung nilai Split Information untuk masing-masing atribut :
(2.3)
Dimana:
• D = Keseluruhan Dataset
• A = Atribut Subset
• v = Jumlah Partisi Atribut A
• | Dj | = Ukuran Subset dari Dataset yang dimiliki atribut A partisi ke-j
• | D | = Ukuran Jumlah Kasus dalam Dataset
(4) menghitung nilai Gain Ratio untuk masing – masing atribut : Gain Ratio (A) = ( )
( ) (2.4)
(5) atribut yang memiliki Gain Ratio tertinggi dipilih menjadi akar (splitting- attribute) dan atribut yang memiliki nilai Gain Ratio lebih rendah dari akar (root) dipilih menjadi cabang (branches),
(6) menghitung lagi nilai Gain Ratio tiap-tiap atribut dengan tidak mengikutsertakan atribut yang terpilih menjadi akar (root) di tahap sebelumnya,
(7) atribut yang memiliki Gain Ratio tertinggi dipilih menjadi cabang (branches).
(8) mengulangi langkah ke-4 dan ke-5 sampai dengan dihasilkan nilai Gain = 0 untuk semua atribut yang tersisa
| )
|
| (|
| log
|
| ) |
( 2
1 D
D D
D D
SplitInfo j
v
j j
A = −
∑
×=
2.3. Teknik Klasifikasi
Klasifikasi merupakan proses analisis data untuk menemukan model yang menguraikan atau membedakan data kelas yang penting agar dapat digunakan untuk memprediksi kelas dari objek yang label kelasnya tidak diketahui. Model ditemukan berdasarkan analisis data training atau objek data yang kelasnya diketahui (Han, et al. 2012). Model itu sendiri dapat berupa algoritma klasifikasi yang sering digunakan, diantaranya: k-nearest neighbor, rough set, algoritma genetika, metode rule based, C4.5, naive bayes, analisis statistik, memory based reasoning, dan support vector machines (SVM).
Teknik klasifikasi didasarkan pada empat komponen utama yaitu:
(1) Class label attribute.
Variabel predictor yang berupa kategori untuk merepresentasikan “label” yang terdapat pada objek. Contohnya: risiko penyakit jantung, risiko kredit, jenis pinjaman dan sebagainya.
(2) Predictor
Variabel categorical-label yang direpresentasikan oleh karakteristik (atribut) data. Contohnya: merokok atau tidak, minum alkohol atau tidak dan lain sebagainya.
(3) Training dataset
Merupakan satu set data yang berisi nilai dari komponen class dan predictor yang digunakan untuk menentukan kelas yang cocok berdasarkan predictor.
(4) Testing dataset
Merupakan data baru yang akan diklasifikasikan oleh model predictor yang telah dibuat dan pengukuran akurasi dari pengklasifikasi dengan metode evaluasi.
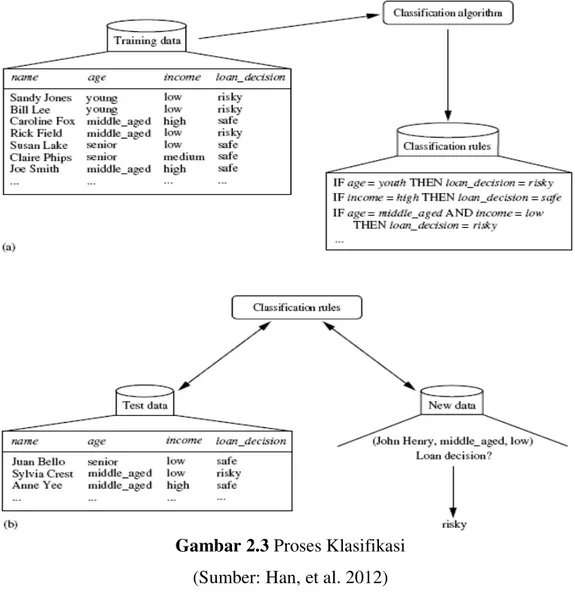
Proses klasifikasi dapat dicontohkan seperti yang ditunjukkan pada Gambar 2.4
Gambar 2.3 Proses Klasifikasi (Sumber: Han, et al. 2012)
Gambar 2.3. (a) adalah proses pembelajaran dimana data training dianalisis menggunakan algoritma klasifikasi. Atribut keputusan kredit sebagai label kelas dan model pembelajaran atau pengklasifikasian dipresentasikan dalam bentuk aturan klasifikasi (classification rule). (b) adalah proses klasifikasi digunakan untuk mengestimasi keakurasian dari classification rule yang dihasilkan. Apabila akurasi dapat diterima maka aturan yang diperoleh dapat digunakan pada klasifikasi data baru (Han, et al. 2012).
2.4. Analisis Komponen Utama (Principal Component Analysis)
PCA adalah kombinasi linear dari variabel awal yang secara geometris kombinasi linear ini merupakan sistem koordinat baru yang diperoleh dari rotasi sistem semula. Metoda PCA sangat berguna digunakan jika data yang ada memiliki jumlah variabel yang besar dan memiliki korelasi antar variabelnya. Perhitungan dari principal component analysis didasarkan pada perhitungan nilai eigen dan vektor eigen yang menyatakan penyebaran data dari suatu dataset.
Tujuan dari analisa PCA adalah untuk melakukan seleksi variabel yang ada tanpa harus kehilangan informasi yang termuat dalam data asli. Dengan menggunakan PCA, variabel yang tadinya sebanyak n variabel akan diseleksi menjadi k variabel baru yang disebut principal component, dengan jumlah k lebih sedikit dari n. Dengan hanya menggunakan k principal component akan menghasilkan nilai yang sama dengan menggunakan n variabel. Variabel hasil dari seleksi disebut principal component. Sifat dari variabel baru yang terbentuk dengan analisa PCA nantinya selain memiliki jumlah variabel yang berjumlah lebih sedikit tetapi juga menghilangkan korelasi antar variabel yang terbentuk.
Secara teknis, PCA merupakan suatu teknik seleksi data multivariat (multivariable) yang mengubah atau mentranformasi suatu matriks data asli menjadi suatu set kombinasi linier yang lebih sedikit namun menyerap sebagian besar jumlah varian dari data awal. Tujuan utamanya ialah menjelaskan sebanyak mungkin jumlah varian data asli dengan sedikit mungkin principal component.
Principal component adalah himpunan variabel baru yang merupakan kombinasi linier dari variabel-variabel yang diamati. Principal component memiliki sifat varians yang semakin mengecil, sebagian besar variasi/keragaman informasi dalam himpunan variabel yang diamati cenderung berkumpul pada beberapa principal component pertama dan semakin sedikit informasi dari variabel asal yang terkumpul pada principal component terakhir. Hal ini berarti bahwa principal component pada urutan terakhir dapat diabaikan tanpa kehilangan banyak informasi. PCA dapat digunakan untuk melakukan seleksi variabel-variabel yang sedang dilakukan pengamatan. Principal component bersifat ortogonal yang artinya bahwa setiap principal component merupakan wakil dari seluruh variabel asal sehingga principal component tersebut dapat dijadikan pengganti variabel asal (Van der Maaten, et al. 2009). Skema
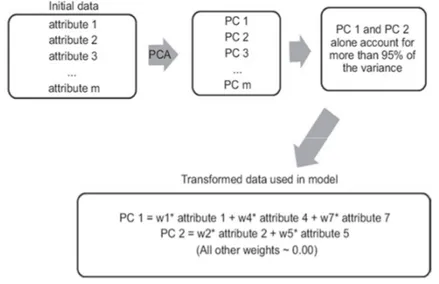
mereduksi dimensi dari data melalui hipotesa dataset berjumlah m variabel dapat ditunjukkan pada Gambar 2.4
Gambar 2.4. Model konseptual untuk efektifitas menggunakan PCA untuk tahap seleksi fitur. Dataset akhir hanya terdiri dari PC1 dan PC2.
(Sumber: Kotu & Deshpande, 2015)
PCA digunakan untuk menjelaskan struktur matriks varians-kovarians dari suatu set variabel melalui kombinasi linier dari variabel-variabel tersebut. Secara umum principal component dapat berguna untuk seleksi fitur dan interpretasi variabel-variabel. Principal Component Analysis biasanya digunakan untuk:
1. Identifikasi nilai peubah baru yang mendasari data peubah ganda
2. Mengurangi banyaknya dimensi himpunan nilai peubah yang biasanya terdiri atas nilai peubah yang banyak dan saling berkolerasi dengan mempertahankan sebanyak mungkin keragaman dalam himpunan data tersebut
3. Menghilangkan nilai peubah asal yang mempunyai sumbangan informasi yang relatif kecil.
Ambil p buah variabel yang terdiri atas n buah objek. Bahwa dari p buah variabel tersebut dibuat sebanyak k buah principal component (dengan k <= p) yang merupakan kombinasi linier atas p buah variabel tersebut. k principal component tersebut dapat menggantikan p buah variabel yang membentuknya tanpa kehilangan banyak informasi mengenai keseluruhan variabel. Umumnya
Principal Component Analysis merupakan analisis perantara yang berarti hasil principal component dapat digunakan untuk analisis selanjutnya.
Bentuk matematis bahwa Y merupakan kombinasi linier dari variabel- variabel x1, x2,..,xp dapat dinyatakan sebagai berikut: (Kotu & Deshpande 2015)
Zm=∑ ( ∗ ) (2.5)
Dimana:
wi : bobot atau koefisien untuk variabel ke - i xi : variabel ke - i
Zm : kombinasi linier dari variabel x
Dalam Principal Component Analysis metode untuk mendapatkan nilai-nilai koefisien atau bobot dari kombinasi linier variabel-variabel pembentuknya adalah sebagai berikut: (Kotu & Deshpande 2015)
a. Ada sebanyak p principal component, yaitu sebanyak variabel yang diamati dan setiap principal component adalah kombinasi linier dari variabel-variabel tersebut
b. Setiap p principal component saling ortogonal (tegak lurus) dan saling bebas.
c. Principal component dibentuk berdasarkan urutan varians dari yang terbesar hingga yang terkecil.
Menurut (Jhonson & Wichern 2007), Jika diperoleh vector x‘= [x1, x2,..,xp] yang memiliki matrik kovarian dengan sejumlah eigenvalue: λ1 ≥ λ2 ≥…≥ λp ≥ 0, maka diperoleh kombinasi linear sebagai berikut :
Y1 = a’1 x = a11x1 + a12x2 +…..+ a1pxp
Y2 = a’2 x = a21x1 + a22x2 +…..+ a2pxp
. .
. .
Yp = a’p x = ap1x1 + ap2x2 +…..+ appxp
dimana :
Yp= komponen ke – i a = nilai eigenvektor x = nilai standar variabel
Komponen yang ke-i yaitu Yp merupakan kombinasi linear dari x1, x2,..,xp dengan weight yaitu: ap1x1,…ap2x2…,apixi, pemilihannya harus sedemikian rupa, sehingga memaksimumkan rasio dari varian component pertama (Y1) dengan jumlah varian (total variance) data asli. Komponen berikutnya yaitu Y2, juga kombinasi linear yang dibobot dari seluruh variabel asli, tidak berkorelasi dengan component pertama (Y1) dan harus menyerap secara maksimum sisa varian yang ada.
Untuk mendapatkan koefisien principal component secara bersamaan dapat menggunakan salah satu model sebagai berikut:
a. Dekomposisi eigenvalue dan eigenvector dari matrik korelasi atau kovarian dari variabel-variabel yang diamati. Dalam hal ini eigenvalue merupakan varians setiap principal component dan eigenvector merupakan koefisien dari principal component.
b. Dekomposisi nilai singular dari matrik data yang berukuran n x n.
Menurut (Jolliffe, 2002), Prosedur pengerjaan Principal Component Analysis untuk reduksi dimensi dari variabel acak x (matrik berukuran n x n, dimana baris-baris yang berisi observasi sebanyak n dari variabel acak x) adalah sebagai berikut:
1. Menghitung matrik kovarian dari data observasi
Matrik kovarian ialah matriks yang nilai-nilai kovariansi pada tiap cell-nya diperoleh dari sampel. Misalkan x dan y adalah variabel acak. (Jolliffe, 2002)
Cov (x,y) = ∑ ( − μ ) ( − μ ) (2.6)
Dengan µx dan µy merupakan rata – rata (mean) sampel dari variabel x dan y, dimana xi dan y merupakan nilai observasi ke-i dari variabel x dan y. Dari data nilai yang digunakan, diperoleh matrik kovarian berukuran n x n.
2. Mencari eigenvalues dan eigenvector dari matrik kovarian yang telah diperoleh yaitu: (Jhonson & Wichern 2007)
Eigenvalues (λ) adalah bilangan skalar dan A adalah matrik dengan ukuran n x n untuk memperoleh nilai n eigenvalues (λ1, λ2……..λn) maka memenuhi persamaan berikut:
Determinan (A – λI) = 0 (2.7) A = matrik nxn
λ = nilai eigenvalue
I = matriks identitas merupakan matriks persegi dengan elemen diagonal utama bernilai 1, sedangkan elemen lain bernilai nol
Eigenvalues dan Eigenvector keduanya dapat mendifinisikan matriks A.
Persamaan untuk menghitung Eigenvector adalah:
Ax = λx (2.8)
Ax – λx = 0 (A – λ) x = 0
(A – λI) x = 0, x ≠ 0
A = matrik nxn yang memiliki n eigenvalue (λn) λ = nilai eigenvalue
x = matrik non-zero I = matrik identitas
Sehingga diperoleh kombinasi linear yaitu:
a. λ1, λ2, λ3… λn adalah eigenvalue matrik A
b. x1, x2, x3… xn adalah eigenvector sesuai eigenvalue-nya (λn)
Persamaan eigenvalue & eigenvector merupakan Eigen Value Decomposition (EVD), dengan persamaan sebagai berikut:
AX = XD (2.9)
A= X D X-1
A = matrik nxn yang memiliki n eigenvalue (λn) D = eigenvalue dari eigenvector-nya
X = eigenvector dari matrik A X-1 = invers dari eigenvector X
3. Menentukan variabel baru (principal component) dengan mengalikan variabel asli dengan matrik eigenvector melalui persamaan: (Jolliffe, 2002) Zki = U1k X1i + U2k X2i + …+ Upk Xpi (2.10)
Zki = matriks n x n dari principal component dengan koordinat objek ke-i pada posisi ke-k pada principal component
U = matriks p x k (matrik eigenvector) X = matriks n x n (variabel asli)
2.5. Penelitian Terdahulu
Penelitian yang pernah dilakukan sebelumnya dapat dilihat pada tabel 2.1 Tabel 2.1 Penelitian Terdahulu
No. Nama Peneliti dan Tahun
Metode Hasil Penelitian
1. Zhang (2012) Optimasi Algoritma C4.5 melalui metode split atribut dan pruning yang disebut: heterogeneous cost sensitive learning (HCSL) dan Theshold pruning untuk mereduksi permasalahan misklasifikasi dan over-fitting.
Kombinasi metode splitting atribut dan pruning menjadikan performa parameter missing rate sebesar 20% dari dataset dan misklasifikasi antara 100 sampai 600.
2. Sivapriya &
Nadira (2013)
Penelitian silang (hybrid) yaitu:
reduksi fitur PCA dan seleksi fitur gain-ratio Decision Tree C4.5 untuk meningkatkan klasifikasi Support Vector Machine (SVM) bagi data medis. Data yang digunakan adalah citra MRI (Magnetic Resonance Images) untuk diklasifikasikan melalui neuropsychological test.
Metode silang ini memiliki nilai kontribusi untuk performa akurasi klasifikasi SVM sebesar 97%.
3. Hussain et al.
(2015)
Pendekatan Principal Component Analysis (PCA) sebagai metode seleksi fitur untuk mereduksi indikator-indikator yang berhubungan dengan prediksi tingkat ketahanan hidup pasien terinfeksi kanker payudara. Data yang digunakan berasal dari SEER dataset sebanyak 684.394 rekam medis pasien.
Metode seleksi fitur PCA yang diusulkan memperoleh akurasi sebesar 92%.
Tabel 2.1. Penelitian Terdahulu (Lanjutan)
2.6. Kontribusi Penelitian
Dari penelitian ini diharapkan hasil analisis pengaruh metode seleksi fitur Principal Component Analysis (PCA) pada akurasi metode klasifikasi Decision Tree C4.5
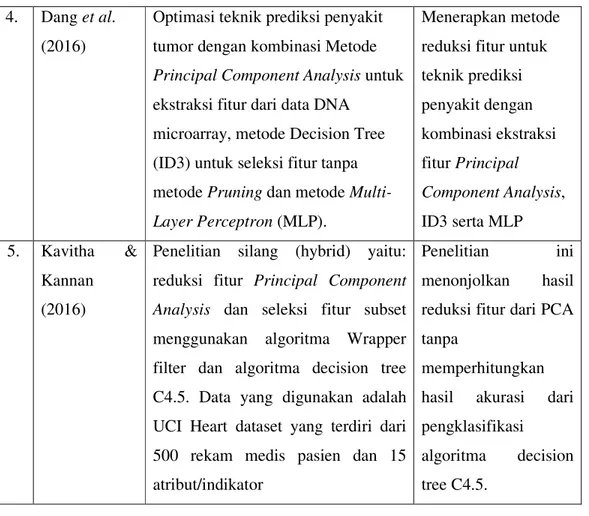
4. Dang et al.
(2016)
Optimasi teknik prediksi penyakit tumor dengan kombinasi Metode Principal Component Analysis untuk ekstraksi fitur dari data DNA
microarray, metode Decision Tree (ID3) untuk seleksi fitur tanpa metode Pruning dan metode Multi- Layer Perceptron (MLP).
Menerapkan metode reduksi fitur untuk teknik prediksi penyakit dengan kombinasi ekstraksi fitur Principal
Component Analysis, ID3 serta MLP 5. Kavitha &
Kannan (2016)
Penelitian silang (hybrid) yaitu:
reduksi fitur Principal Component Analysis dan seleksi fitur subset menggunakan algoritma Wrapper filter dan algoritma decision tree C4.5. Data yang digunakan adalah UCI Heart dataset yang terdiri dari 500 rekam medis pasien dan 15 atribut/indikator
Penelitian ini menonjolkan hasil reduksi fitur dari PCA tanpa
memperhitungkan hasil akurasi dari pengklasifikasi
algoritma decision tree C4.5.
BAB 3
METODOLOGI PENELITIAN
3.1. Data yang digunakan
Data yang digunakan dalam penelitian ini terdiri atas 2 dataset. Dataset pertama adalah dataset Cervical Cancer (http://archive.ics.uci.edu/ml). Dataset ini memiliki sejumlah atribut yang proporsional serta mempunyai missing value.
Dataset ini dibagi menjadi 90% sebagai data training dan 10% sebagai data testing. Data ini berkaitan dengan serangkaian prediksi pengujian medis yang akan diberikan bagi pasien yang dicurigai terinfeksi kanker servik. Dataset ini terdiri atas faktor demografi, kebiasaan dan data historis rekam medis pasien yang dicurigai terinfeksi kanker servik.
Dataset kedua adalah data rekam medis dari Rumah Sakit Umum H. Adam Malik Medan sebanyak 20 pasien rawat jalan yang dicurigai terinfeksi kanker servik dan diklasifikasikan berdasarkan prediksi pengujian medis yang akan diberikan. Data rekam medis yang diperoleh dari Rumah Sakit Umum H. Adam Malik Medan tersebut dilakukan pengujian model klasifikasi decision tree C4.5 menggunakan dataset Cervical cancer hasil dari seleksi fitur menggunakan PCA.
Pengujian dilakukan dengan menyesuaikan atribut dari data rekam medis dengan atribut hasil seleksi PCA dari dataset Cervical Cancer sehingga membentuk atribut yang paling sesuai untuk dimodelkan pada klasifikasi decision tree C4.5.
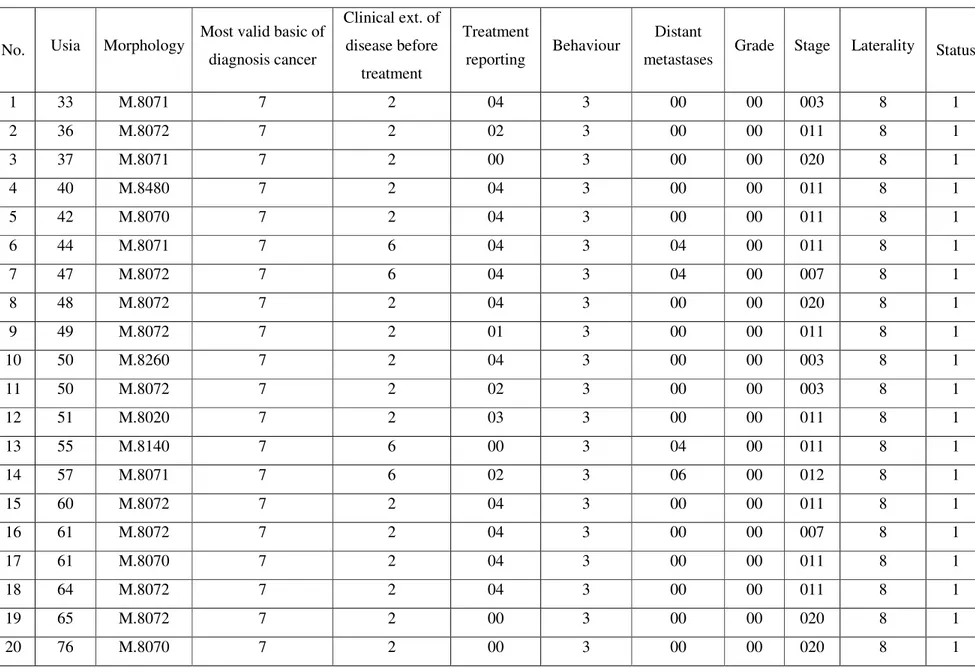
Berikut adalah data rekam medis pasien terinfeksi kanker servik yang digunakan tertera pada tabel 3.1.
Tabel 3.1 Data Rekam Medis Pasien Kanker Servik (Sumber: R.S. Adam Malik Medan, data diolah)
No. Usia Morphology Most valid basic of diagnosis cancer
Clinical ext. of disease before
treatment
Treatment
reporting Behaviour Distant
metastases Grade Stage Laterality Status
1 33 M.8071 7 2 04 3 00 00 003 8 1
2 36 M.8072 7 2 02 3 00 00 011 8 1
3 37 M.8071 7 2 00 3 00 00 020 8 1
4 40 M.8480 7 2 04 3 00 00 011 8 1
5 42 M.8070 7 2 04 3 00 00 011 8 1
6 44 M.8071 7 6 04 3 04 00 011 8 1
7 47 M.8072 7 6 04 3 04 00 007 8 1
8 48 M.8072 7 2 04 3 00 00 020 8 1
9 49 M.8072 7 2 01 3 00 00 011 8 1
10 50 M.8260 7 2 04 3 00 00 003 8 1
11 50 M.8072 7 2 02 3 00 00 003 8 1
12 51 M.8020 7 2 03 3 00 00 011 8 1
13 55 M.8140 7 6 00 3 04 00 011 8 1
14 57 M.8071 7 6 02 3 06 00 012 8 1
15 60 M.8072 7 2 04 3 00 00 011 8 1
16 61 M.8072 7 2 04 3 00 00 007 8 1
17 61 M.8070 7 2 04 3 00 00 011 8 1
18 64 M.8072 7 2 04 3 00 00 011 8 1
19 65 M.8072 7 2 00 3 00 00 020 8 1
20 76 M.8070 7 2 00 3 00 00 020 8 1
3.2. Software yang digunakan
Penelitian ini dibangun dengan dukungan perangkat lunak Rapid Miner®
versi 5.3 dan menggunakan spesifikasi processor Intel Celeron 1.60GHz dengan kapasitas memory 2 GB. Untuk memudahkan perhitungan nilai-nilai dalam proses seleksi fitur menggunakan PCA, pengujian dan evaluasi model klasifikasi decision tree C4.5, maka penelitian ini menggunakan dua dukungan perangkat lunak yaitu: Matlab versi 2013 dan Rapid Miner® versi 5.3.
3.3. Metodologi Penelitian
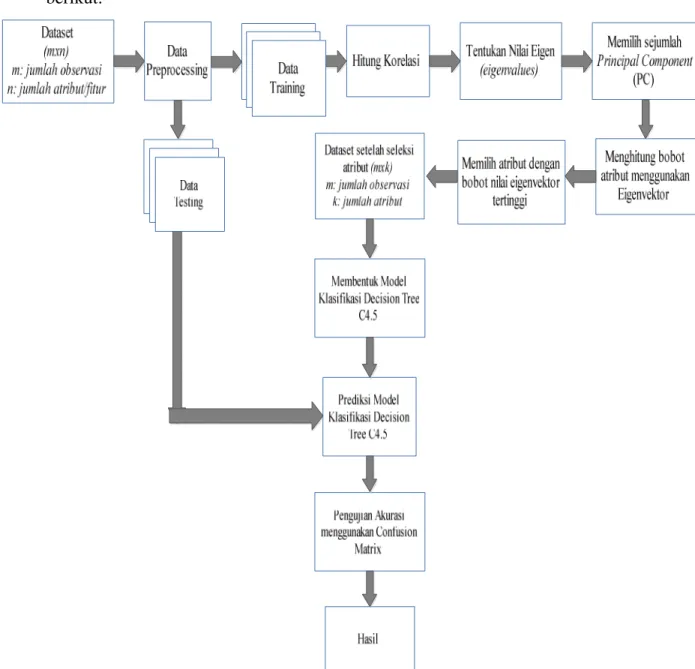
Arsitektur umum secara keseluruhan pada penelitian ini digambarkan sebagai berikut:
Gambar 3.1 Arsitektur Umum Penelitian
Berikut penjelasan gambar 3.1 yang dapat dijabarkan:
3.3.1 Data Preprocessing
Pada penelitian ini, hanya melakukan dua proses preprocessing. Pertama adalah penanganan missing value. Missing value pada atribut yang bernilai numerik digantikan dengan nilai rata-rata (mean) dari atribut pada kolom yang sama.
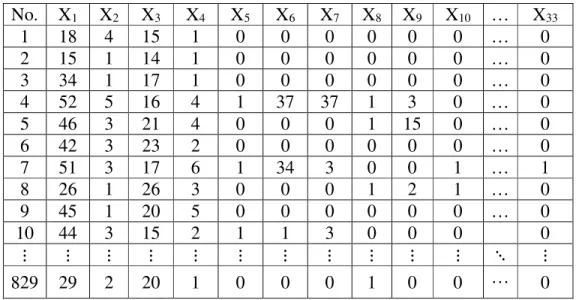
Sedangkan missing value pada atribut yang bernilai nominal digantikan dengan nilai kemungkinan terbanyak dari atribut pada kolom yang sama. Selanjutnya adalah proses cleaning dilakukan dengan membuang duplikasi data sehingga jumlah data observasi yang semula sebanyak 858 record menjadi 829 record.
Proses selanjutnya adalah mengganti empat variabel class dari dataset Cervical Cancer yaitu: Hinselmann, Schiller, Biopsy dan Citology dengan satu class baru dengan nama pengujian. Sehingga dataset Cervical Cancer yang awalnya sebanyak 32 atribut dengan 4 variabel class menjadi 32 atribut dengan 1 variabel class. Dengan demikian, jika nilai observasi salah satu dari 4 variabel class dari dataset Cervical Cancer tersebut menunjukkan bernilai 1 maka nilai observasi pada variabel class pengujian yang baru diklasifikasikan sebagai pasien dengan pengujian medis (bernilai 1). Sebaliknya, jika nilai observasi dari keempat variabel class dari dataset Cervical Cancer tersebut menunjukkan bernilai 0 maka nilai observasi pada variabel class pengujian yang baru akan diklasifikasikan sebagai pasien tanpa pengujian medis (bernilai 0). Dalam penelitian ini, atribut hasil preprocessing direpresentasikan kedalam bentuk label (x1, x2, x3…x33) yang mewakili urutan data yang sesuai dengan dataset yang diuji. Berikut hasil representasi atribut dalam bentuk label:
X1: Age X11: IUD (years)
X2: Number of sexual partners X12: STDs
X3: First sexual intercourse X13: STDs (number)
X4: Number of pregnancies X14: STDs: condylomatosis
X5: Smoke X15: STDs: cervical condylomatosis
X6: Smoke (years) X16: STDs: vaginal condylomatosis X7: Smoke (packs/year) X17: vulvo-perineal condylomatosis X8: Hormonal contraceptives X18: STDs: syphilis
X9: Hormonal contraceptives (years) X19: pelvic inflammatory disease
X10: IUD X20: genital herpes
X21: STDs: molluscum contagiosum X28: STDs: Time since last diagnosis
X22: STDs:AIDS X29: Dx:Cancer
X23: STDs:HIV X30: Dx:CIN
X24: STDs:Hepatitis B X31: Dx:HPV
X25: STDs:HPV X32: Dx
X26: STDs: Number of diagnosis X33: Pengujian (Class) X27: STDs: Time since first diagnosis
3.3.2 Menghitung korelasi antar data observasi
Kovarian (Covariance) digunakan untuk mengukur besarnya hubungan antara dua atribut. Jenis hubungan yang dapat terjadi antara dua buah atribut berdasarkan nilai covariance-nya adalah:
a. Positif : bila nilai covariance-nya positif atau > 0 b. Negatif : nilai covariance-nya negatif atau < 0 c. Zero : bila nilai covariance-nya nol atau = 0
Sehingga untuk memperoleh nilai kovarian maka digunakan persamaan 2.6.
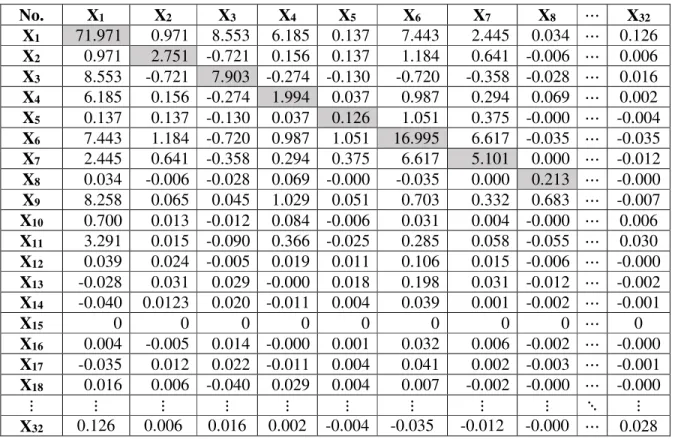
Selanjutnya adalah matrik kovarian (covariance matrix) diperoleh dengan menghitung pasangan 2 buah atribut dari total n atribut.
Misalkan: Atribut x, y dan z, dengan jumlah atribut = 3, x y z
− − −
− − −
− − − Maka matrik kovariannya berukuran 3x3 = nxn, yaitu:
( , ) ( , ) ( , )
( , ) ( , ) ( , )
( , ) ( , ) ( , )
Dimana cov(x,x), cov(y,y) dan cov(z,z) nilainya sama dengan perhitungan nilai variansi (variance) dari atribut x, y dan z. sehingga matrik kovariannya:
( ) ( , ) ( , )
( , ) ( ) ( , )
( , ) ( , ) ( )
Jika nilai komponen diagonalnya (var(x), var(y) dan var(z)) adalah 1, maka matrik kovariannya sama dengan matrik korelasi sebab hasil korelasi dari data yang tidak distandarisasi adalah sama dengan hasil kovarian dari data yang
distandarisasi. Berarti bahwa matrik kovarian merupakan matrik simetris. Bila didekomposisikan dengan Eigenvalue, maka nilai pada diagonal eigenvalue ≥ 0.
Dengan demikian nilai:
cov(y,x) = cov(x,y) cov(z,x) = cov(x,z) cov(z,y) = cov(y,z)
3.3.3 Menentukan eigenvalue dari matrik kovarian
Nilai eigen (λ ) merupakan bilangan skalar yang mendefinisikan matrik kovarian.
Dimana matrik kovarian tersebut adalah matriks bujur sangkar (square matrix) berukuran m x m, maka untuk nilai eigen (λ) yang sesuai dengan matrik kovarian tersebut diperoleh melalui persamaan 2.8, sehingga setiap skalar (λ1, λ2……..λm) memenuhi persamaan 2.9 untuk membentuk matrik eigenvektor.
3.3.4 Memilih sejumlah principal component (PC)
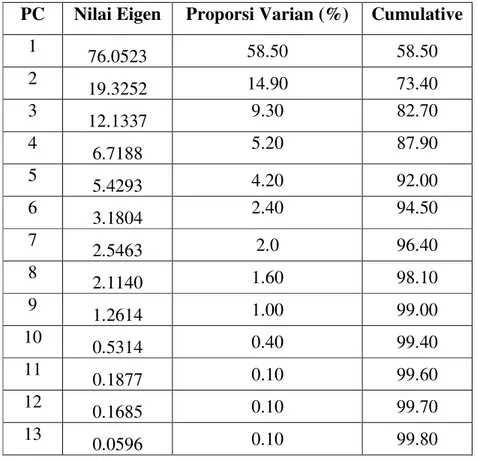
Principal Component Analysis (PCA) merupakan teknik analisis untuk mentransformasi atribut - atribut asli yang masih saling berkorelasi satu dengan yang lain menjadi satu himpunan atribut baru yang tidak saling berkorelasi. Pada penelitian ini, komponen utama yang dipilih memiliki jumlah kontribusi maksimum dengan nilai sebesar 99% (variance threshold) berdasarkan proporsi varians dari masing-masing principal component yang terpilih karena nilai tersebut mencukupi untuk menjelaskan total varians kovarians dari atribut asal, maka terlebih dahulu dihitung nilai proporsi varians dari masing-masing principal component yang diperoleh melalui persamaan:
Nilai Proporsi Principal Component (%) = x 100% (3.1) Dimana, varians kovarians diperoleh dari penjumlahan total nilai diagonal matrik kovarian.
3.3.5 Menghitung bobot atribut menggunakan persamaan eigenvektor
Untuk menentukan atribut mana yang termasuk kedalam principal component (atribut yang sangat mempengaruhi varians kovarians data observasi) dengan jumlah kontribusi maksimum sebesar 99%, maka dilakukan perhitungan bobot
nilai eigenvektor melalui persamaan 2.9, dimana setiap nilai vektor x yang terbentuk bersesuaian dengan satu nilai eigen (λ) untuk masing-masing atribut.
3.3.6 Memilih atribut asli berdasarkan bobot nilai eigenvektor tertinggi
Pada penelitian ini, Interpretasi hasil seleksi fitur menggunakan PCA diperoleh dengan memilih atribut yang memiliki bobot nilai eigenvektor tertinggi dari sejumlah principal component yang memiliki korelasi cukup besar terhadap pembentukaan atribut asli dengan jumlah proporsi varians kovarians sebesar 99%. Sehingga diperoleh sejumlah atribut hasil seleksi atribut dari dataset Cervical Cancer. Atribut lain yang memiliki bobot nilai yang rendah belum cukup memberikan pengaruh terhadap pembentukan atribut asli dari masing- masing data observasi. Dapat disimpulkan bahwa atribut terpilih inilah yang dimodelkan kedalam klasifikasi decision tree C4.5.
3.3.7 Membentuk model prediksi klasifikasi decision tree C4.5
Atribut hasil seleksi menggunakan PCA, kemudian dibentuk kedalam model prediksi klasifikasi decision tree C4.5 untuk menghasilkan atribut terbaik dan paling penting sehingga membantu prediksi permasalahan pengujian medis yang akan diberikan terhadap pasien yang dicurigai memiliki resiko terinfeksi kanker servik.
Algoritma C4.5 menggunakan dua pendekatan heuristic untuk dilakukan uji peringkat probabilitas dan membagi data secara rekursif hingga tiap bagian terdiri dari data yang berasal dari kelas yang sama yaitu:
(1) Information gain merupakan selisih perolehan nilai informasi output dan subset dalam satuan bits per atribut. Dapat dihitung menggunakan persamaan 2.2 (2) Gain ratio merupakan rasio perolehan nilai Information Gain dengan informasi entropy dari masing – masing atribut. Dapat dihitung menggunakan persamaan 2.4. Proses selanjutnya pada pembentukan model klasifikasi Algoritma C4.5 adalah menghitung kembali nilai Gain Ratio masing - masing atribut dengan tidak meng-ikutsertakan atribut yang terpilih menjadi akar (root- node) di tahap sebelumnya. Atribut berikutnya yang memiliki Gain Ratio tertinggi dipilih kembali menjadi node cabang (internal-node) dan mengulangi langkah demi langkah pada sub bab diatas hingga semua tupel terpartisi,
mendapatkan kelas yang sama (homogenitas) dan menghasilkan nilai Gain Ratio
= 0 untuk semua atribut yang tersisa.
3.3.8 Pengujian akurasi menggunakan Confusion Matrix
Untuk melakukan pengujian model prediksi klasifikasi C4.5-Non-PCA dan PCA+C4.5 dari dataset Cervical Cancer serta pengujian model prediksi klasifikasi PCA+C4.5 dengan data uji rekam medis, maka perhitungan pengujian tersebut ditabulasikan kedalam tabel yang disebut confusion matrix (Witten &
Frank, 2005). Confusion Matrix merupakan parameter baik atau buruknya sebuah pengklasifikasian atas data pengujian dalam kelas yang berbeda yakni kelas positif dan kelas negatif (two-class prediction). Berikut tabel 3.2 menjelaskan Confusion Matrix (two-class prediction):
Tabel 3.2. Confusion Matrix (two-class prediction)
(Sumber: Witten, et al. 2005)
Tabel 3.2 menjelaskan parameter model pengklasifikasian 2 kelas yaitu kelas yes dan no. True Positives (TP) and True Negatives (TN) merupakan jumlah klasifikasi yang bernilai benar. Parameter False Positive (FP) akan disimpulkan saat prediksi yang dihasilkan tidak tepat atau bernilai yes (positive) ketika prediksi yang diharapkan adalah no (negative). Sebaliknya, Parameter False Negative (FN) akan disimpulkan saat prediksi yang dihasilkan tidak tepat atau bernilai no (negative) ketika prediksi yang diharapkan adalah yes (positive).
Hasil dari parameter Confusion Matrix adalah akurasi.
Persamaan Confusion Matrix untuk menghitung nilai akurasi adalah: (Witten, et al. 2005)
!" #
!" #"$!"$# (3.2) Two-Class
Prediction
Predicted Class
Yes No
Actual Class
Yes True Positive False Negative No False Positive True Negative
TP (True Positive) adalah jumlah data dalam kelas yes yang hasil kelas prediksinya memang benar diklasifikasikan kedalam kelas aktual yang bernilai yes
TN (True Negative) adalah jumlah data dalam kelas no yang hasil kelas prediksinya memang benar diklasifikasikan kedalam kelas aktual yang bernilai no
FP (False Positive) adalah jumlah data yang sebenarnya termasuk kedalam kelas aktual yang bernilai no namun hasil kelas prediksinya diklasifikasikan ke dalam kelas yang bernilai yes.
FN (False Negative) adalah jumlah data yang sebenarnya termasuk kedalam kelas aktual yang bernilai yes namun hasil kelas prediksinya diklasifikasikan ke dalam kelas yang bernilai no.
3.3.9 Hasil akurasi model klasifikasi decision tree C4.5
Tahap akhir dari penelitian ini adalah mengukur hasil akurasi model klasifikasi decision tree C4.5 setelah melalui proses seleksi fitur dataset menggunakan Principal Component Analysis (PCA) yang diharapkan memperoleh hasil akurasi model klasifikasi decision tree C4.5 yang lebih signifikan sehingga model penelitian ini mampu menjawab tujuan penelitian yang telah dijabarkan pada bab sebelumnya.