Theory and Problems of
ADVANCED
CALCULUS
Second Edition
ROBERT WREDE, Ph.D.
MURRAY R. SPIEGEL, Ph.D.
Former Professor and Chairman of Mathematics
Rensselaer Polytechnic Institute
Hartford Graduate Center
distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher.
0-07-139834-1
The material in this eBook also appears in the print version of this title: 0-07-137567-8
All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in cor-porate training programs. For more information, please contact George Hoare, Special Sales, at [email protected] or (212) 904-4069.
TERMS OF USE
This is a copyrighted work and The McGraw-Hill Companies, Inc. (“McGraw-Hill”) and its licensors reserve all rights in and to the work. Use of this work is subject to these terms. Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work, you may not decompile, disassemble, reverse engineer, reproduce, modify, create derivative works based upon, transmit, distribute, disseminate, sell, publish or sublicense the work or any part of it without McGraw-Hill’s prior consent. You may use the work for your own noncommercial and personal use; any other use of the work is strictly prohibited. Your right to use the work may be terminated if you fail to comply with these terms. THE WORK IS PROVIDED “AS IS”. McGRAW-HILL AND ITS LICENSORS MAKE NO GUARANTEES OR WAR-RANTIES AS TO THE ACCURACY, ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE, AND EXPRESSLY DISCLAIM ANY WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PAR-TICULAR PURPOSE. McGraw-Hill and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free. Neither McGraw-Hill nor its licensors shall be liable to you or anyone else for any inaccuracy, error or omission, regardless of cause, in the work or for any dam-ages resulting therefrom. McGraw-Hill has no responsibility for the content of any information accessed through the work. Under no circumstances shall McGraw-Hill and/or its licensors be liable for any indirect, incidental, special, punitive, con-sequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.
iii
and unsolved problems remains a part of this second edition.
Advanced calculus is not a single theory. However, the various sub-theories, including
vector analysis, infinite series, and special functions, have in common a dependency on the
fundamental notions of the calculus. An important objective of this second edition has been to
modernize terminology and concepts, so that the interrelationships become clearer. For
exam-ple, in keeping with present usage fuctions of a real variable are automatically single valued;
differentials are defined as linear functions, and the universal character of vector notation and
theory are given greater emphasis. Further explanations have been included and, on occasion,
the appropriate terminology to support them.
The order of chapters is modestly rearranged to provide what may be a more logical
structure.
A brief introduction is provided for most chapters. Occasionally, a historical note is
included; however, for the most part the purpose of the introductions is to orient the reader
to the content of the chapters.
I thank the staff of McGraw-Hill. Former editor, Glenn Mott, suggested that I take on the
project. Peter McCurdy guided me in the process. Barbara Gilson, Jennifer Chong, and
Elizabeth Shannon made valuable contributions to the finished product. Joanne Slike and
Maureen Walker accomplished the very difficult task of combining the old with the new
and, in the process, corrected my errors. The reviewer, Glenn Ledder, was especially helpful
in the choice of material and with comments on various topics.
ROBERTC. WREDE
v
CHAPTER 1
NUMBERS
1
Sets. Real numbers. Decimal representation of real numbers. Geometric
representation of real numbers. Operations with real numbers.
Inequal-ities. Absolute value of real numbers. Exponents and roots. Logarithms.
Axiomatic foundations of the real number system. Point sets, intervals.
Countability.
Neighborhoods.
Limit
points.
Bounds.
Bolzano-Weierstrass theorem. Algebraic and transcendental numbers. The
com-plex number system. Polar form of comcom-plex numbers. Mathematical
induction.
CHAPTER 2
SEQUENCES
23
Definition of a sequence. Limit of a sequence. Theorems on limits of
sequences. Infinity. Bounded, monotonic sequences. Least upper bound
and greatest lower bound of a sequence. Limit superior, limit inferior.
Nested intervals. Cauchy’s convergence criterion. Infinite series.
CHAPTER 3
FUNCTIONS, LIMITS, AND CONTINUITY
39
Functions. Graph of a function. Bounded functions. Montonic
func-tions. Inverse funcfunc-tions. Principal values. Maxima and minima. Types
of functions. Transcendental functions. Limits of functions. Right- and
left-hand limits. Theorems on limits. Infinity. Special limits. Continuity.
Right- and left-hand continuity. Continuity in an interval. Theorems on
continuity. Piecewise continuity. Uniform continuity.
CHAPTER 4
DERIVATIVES
65
The concept and definition of a derivative. Right- and left-hand
deriva-tives. Differentiability in an interval. Piecewise differentiability.
Differ-entials.
The
differentiation
of
composite
functions.
Implicit
differentiation. Rules for differentiation. Derivatives of elementary
func-tions. Higher order derivatives. Mean value theorems. L’Hospital’s
rules. Applications.
CHAPTER 5
INTEGRALS
90
Introduction of the definite integral. Measure zero. Properties of definite
integrals. Mean value theorems for integrals. Connecting integral and
differential calculus. The fundamental theorem of the calculus.
General-ization of the limits of integration. Change of variable of integration.
Integrals of elementary functions. Special methods of integration.
Improper integrals. Numerical methods for evaluating definite integrals.
Applications. Arc length. Area. Volumes of revolution.
CHAPTER 6
PARTIAL DERIVATIVES
116
Functions of two or more variables. Three-dimensional rectangular
coordinate systems. Neighborhoods. Regions. Limits. Iterated limits.
Continuity. Uniform continuity. Partial derivatives. Higher order
par-tial derivatives. Differenpar-tials. Theorems on differenpar-tials. Differentiation
of composite functions. Euler’s theorem on homogeneous functions.
Implicit functions. Jacobians. Partial derivatives using Jacobians.
The-orems on Jacobians. Transformation. Curvilinear coordinates. Mean
value theorems.
CHAPTER 7
VECTORS
150
Vectors. Geometric properties. Algebraic properties of vectors. Linear
independence and linear dependence of a set of vectors. Unit vectors.
Rectangular (orthogonal unit) vectors. Components of a vector. Dot or
scalar product. Cross or vector product. Triple products. Axiomatic
approach to vector analysis. Vector functions. Limits, continuity, and
derivatives of vector functions. Geometric interpretation of a vector
derivative. Gradient, divergence, and curl. Formulas involving
r
.
Vec-tor interpretation of Jacobians, Orthogonal curvilinear coordinates.
Gradient, divergence, curl, and Laplacian in orthogonal curvilinear
coordinates. Special curvilinear coordinates.
CHAPTER 8
APPLICATIONS OF PARTIAL DERIVATIVES
183
Applications to geometry. Directional derivatives. Differentiation under
the integral sign. Integration under the integral sign. Maxima and
minima. Method of Lagrange multipliers for maxima and minima.
Applications to errors.
CHAPTER 9
MULTIPLE INTEGRALS
207
CHAPTER 10
LINE INTEGRALS, SURFACE INTEGRALS, AND
INTEGRAL THEOREMS
229
Line integrals. Evaluation of line integrals for plane curves. Properties
of line integrals expressed for plane curves. Simple closed curves, simply
and multiply connected regions. Green’s theorem in the plane.
Condi-tions for a line integral to be independent of the path. Surface integrals.
The divergence theorem. Stoke’s theorem.
CHAPTER 11
INFINITE SERIES
265
Definitions of infinite series and their convergence and divergence.
Fun-damental facts concerning infinite series. Special series. Tests for
con-vergence and dicon-vergence of series of constants. Theorems on absolutely
convergent series. Infinite sequences and series of functions, uniform
convergence. Special tests for uniform convergence of series. Theorems
on uniformly convergent series. Power series. Theorems on power series.
Operations with power series. Expansion of functions in power series.
Taylor’s theorem. Some important power series. Special topics. Taylor’s
theorem (for two variables).
CHAPTER 12
IMPROPER INTEGRALS
306
Definition of an improper integral. Improper integrals of the first kind
(unbounded intervals). Convergence or divergence of improper
integrals of the first kind. Special improper integers of the first kind.
Convergence tests for improper integrals of the first kind. Improper
integrals of the second kind. Cauchy principal value. Special improper
integrals of the second kind. Convergence tests for improper integrals
of the second kind. Improper integrals of the third kind. Improper
integrals containing a parameter, uniform convergence. Special tests
for uniform convergence of integrals. Theorems on uniformly
conver-gent integrals. Evaluation of definite integrals. Laplace transforms.
Linearity. Convergence. Application. Improper multiple integrals.
CHAPTER 13
FOURIER SERIES
336
CHAPTER 14
FOURIER INTEGRALS
363
The Fourier integral. Equivalent forms of Fourier’s integral theorem.
Fourier transforms.
CHAPTER 15
GAMMA AND BETA FUNCTIONS
375
The gamma function. Table of values and graph of the gamma function.
The beta function. Dirichlet integrals.
CHAPTER 16
FUNCTIONS OF A COMPLEX VARIABLE
392
Functions. Limits and continuity. Derivatives. Cauchy-Riemann
equa-tions. Integrals. Cauchy’s theorem. Cauchy’s integral formulas. Taylor’s
series. Singular points. Poles. Laurent’s series. Branches and branch
points. Residues. Residue theorem. Evaluation of definite integrals.
1
Numbers
Mathematics has its own language with numbers as the alphabet. The language is given structure with the aid of connective symbols, rules of operation, and a rigorous mode of thought (logic). These concepts, which previously were explored in elementary mathematics courses such as geometry, algebra, and calculus, are reviewed in the following paragraphs.
SETS
Fundamental in mathematics is the concept of aset,class, or collectionof objects having specified characteristics. For example, we speak of the set of all university professors, the set of all letters
A;B;C;D;. . .;Z of the English alphabet, and so on. The individual objects of the set are called membersorelements. Any part of a set is called asubsetof the given set, e.g.,A,B,Cis a subset of
A;B;C;D;. . .;Z. The set consisting of no elements is called theempty setornull set.
REAL NUMBERS
The following types of numbers are already familiar to the student:
1. Natural numbers1;2;3;4;. . .; also calledpositive integers, are used in counting members of a set. The symbols varied with the times, e.g., the Romans used I, II, III, IV, . . . Thesumaþb
andproductaborabof any two natural numbersaandbis also a natural number. This is often expressed by saying that the set of natural numbers is closed under the operations of additionandmultiplication, or satisfies theclosure propertywith respect to these operations. 2. Negative integers and zerodenoted by1;2;3;. . .and 0, respectively, arose to permit
solu-tions of equasolu-tions such asxþb¼a, whereaandbare any natural numbers. This leads to the operation ofsubtraction, or inverse of addition, and we writex¼ab.
The set of positive and negative integers and zero is called the set ofintegers. 3. Rational numbersorfractionssuch as2
3, 5
4, . . . arose to permit solutions of equations such as
bx¼afor all integersaandb, whereb6¼0. This leads to the operation ofdivision, orinverse of multiplication, and we writex¼a=borabwhereais thenumeratorandbthedenominator. The set of integers is a subset of the rational numbers, since integers correspond to rational numbers whereb¼1.
4. Irrational numberssuch aspffiffiffi2andare numbers which are not rational, i.e., they cannot be expressed asa=b(called thequotientofaandb), whereaandbare integers andb6¼0.
The set of rational and irrational numbers is called the set ofreal numbers.
DECIMAL REPRESENTATION OF REAL NUMBERS
Any real number can be expressed in decimal form, e.g., 17=10¼1:7, 9=100¼0:09, 1=6¼0:16666. . .. In the case of a rational number the decimal exapnsion either terminates, or if it does not terminate, one or a group of digits in the expansion will ultimately repeat, as for example, in 1
7¼0:142857 142857 142. . .. In the case of an irrational number such as ffiffiffi 2
p
¼1:41423. . . or ¼3:14159. . .no such repetition can occur. We can always consider a decimal expansion as unending, e.g., 1.375 is the same as 1.37500000 . . . or 1.3749999 . . . . To indicate recurring decimals we some-times place dots over the repeating cycle of digits, e.g.,1
7¼0:11_44_22_88_55_77,_ 19
6 ¼3:166._
The decimal system uses the ten digits 0;1;2;. . .;9. (These symbols were the gift of the Hindus. They were in use in India by 600A.D.and then in ensuing centuries were transmitted to the western world by Arab traders.) It is possible to design number systems with fewer or more digits, e.g. thebinary systemuses only two digits 0 and 1 (see Problems 32 and 33).
GEOMETRIC REPRESENTATION OF REAL NUMBERS
The geometric representation of real numbers as points on a line called thereal axis, as in the figure below, is also well known to the student. For each real number there corresponds one and only one point on the line and conversely, i.e., there is aone-to-one(see Fig. 1-1)correspondencebetween the set of real numbers and the set of points on the line. Because of this we often use point and number interchangeably.
(The interchangeability of point and number is by no means self-evident; in fact, axioms supporting the relation of geometry and numbers are necessary. The Cantor–Dedekind Theorem is fundamental.) The set of real numbers to the right of 0 is called the set ofpositive numbers; the set to the left of 0 is the set ofnegative numbers, while 0 itself is neither positive nor negative.
(Both the horizontal position of the line and the placement of positive and negative numbers to the right and left, respectively, are conventions.)
Between any two rational numbers (or irrational numbers) on the line there are infinitely many rational (and irrational) numbers. This leads us to call the set of rational (or irrational) numbers an everywhere denseset.
OPERATIONS WITH REAL NUMBERS
Ifa,b,cbelong to the setRof real numbers, then:
1. aþbandabbelong toR Closure law
2. aþb¼bþa Commutative law of addition 3. aþ ðbþcÞ ¼ ðaþbÞ þc Associative law of addition
4. ab¼ba Commutative law of multiplication
5. aðbcÞ ¼ ðabÞc Associative law of multiplication 6. aðbþcÞ ¼abþac Distributive law
7. aþ0¼0þa¼a, 1a¼a1¼a
0 is called theidentity with respect to addition, 1 is called theidentity with respect to multi-plication.
_ 5 _ 4 _ 3 _ 2 _ 1 0 1 2 3 4 5 1
2 4
3
_
_p √2 e p
8. For anyathere is a numberxinRsuch thatxþa¼0.
xis called theinverse of a with respect to additionand is denoted bya. 9. For anya6¼0 there is a numberxinRsuch that ax¼1.
xis called theinverse of a with respect to multiplicationand is denoted bya1or 1=a.
Convention: For convenience, operations called subtraction and division are defined by
ab¼aþ ðbÞandab¼ab1, respectively.
These enable us to operate according to the usual rules of algebra. In general any set, such asR, whose members satisfy the above is called afield.
INEQUALITIES
Ifabis a nonnegative number, we say thataisgreater than or equal to borbisless than or equal to a, and write, respectively,aAborb%a. If there is no possibility thata¼b, we writea>borb<a.
Geometrically, a>b if the point on the real axis corresponding to a lies to the right of the point corresponding tob.
EXAMPLES. 3<5 or 5>3;2<1 or1>2;x@3 means thatxis a real number which may be 3 or less than 3.
Ifa,b;andcare any given real numbers, then:
1. Eithera>b,a¼bora<b Law of trichotomy 2. Ifa>bandb>c, thena>c Law of transitivity 3. Ifa>b, then aþc>bþc
4. Ifa>bandc>0, thenac>bc
5. Ifa>bandc<0, thenac<bc
ABSOLUTE VALUE OF REAL NUMBERS
The absolute value of a real numbera, denoted byjaj, is defined asaifa>0,aifa<0, and 0 if
a¼0.
EXAMPLES. j 5j ¼5,j þ2j ¼2,j 3 4j ¼
3 4,j
ffiffiffi
2
p
j ¼pffiffiffi2,j0j ¼0.
1. jabj ¼ jajjbj orjabc. . .mj ¼ jajjbjjcj. . .jmj
2. jaþbj@jaj þ jbj orjaþbþcþ þmj@jaj þ jbj þ jcj þ jmj
3. jabjAjaj jbj
The distance between any two points (real numbers)aandbon the real axis isjabj ¼ jbaj.
EXPONENTS AND ROOTS
The productaa. . .aof a real numberaby itself ptimes is denoted byap, wherepis called the exponentandais called thebase. The following rules hold:
1. apaq¼apþq 3. ðapÞr¼apr
2. a p
aq¼a
pq 4. a
b
p
¼a
p
These and extensions to any real numbers are possible so long as division by zero is excluded. In particular, by using 2, with p¼q and p¼0, respectively, we are lead to the definitions a0¼1,
aq¼1=aq.
Ifap¼N, wherepis a positive integer, we callaapthrootofNwrittenppffiffiffiffiN
. There may be more than one realpth root ofN. For example, since 22¼4 andð2Þ2¼4, there are two real square roots of 4, namely 2 and2. For square roots it is customary to definepffiffiffiffiNas positive, thuspffiffiffi4¼2 and then
pffiffiffi4¼ 2.
Ifpandqare positive integers, we defineap=q¼pqffiffiffiffiffiap .
LOGARITHMS
Ifap¼N,pis called thelogarithmofNto the basea, writtenp¼logaN. IfaandNare positive anda6¼1, there is only one real value forp. The following rules hold:
1. logaMN¼logaMþlogaN 2. logaM
N ¼logaMlogaN
3. logaMr¼rlogaM
In practice, two bases are used, basea¼10, and thenatural basea¼e¼2:71828. . .. The logarithmic systems associated with these bases are called commonand natural, respectively. The common loga-rithm system is signified by logN, i.e., the subscript 10 is not used. For natural logarithms the usual notation is lnN.
Common logarithms (base 10) traditionally have been used for computation. Their application replaces multiplication with addition and powers with multiplication. In the age of calculators and computers, this process is outmoded; however, common logarithms remain useful in theory and application. For example, the Richter scale used to measure the intensity of earthquakes is a logarith-mic scale. Natural logarithms were introduced to simplify formulas in calculus, and they remain effective for this purpose.
AXIOMATIC FOUNDATIONS OF THE REAL NUMBER SYSTEM
The number system can be built up logically, starting from a basic set ofaxiomsor ‘‘self-evident’’ truths, usually taken from experience, such as statements 1–9, Page 2.
If we assume as given the natural numbers and the operations of addition and multiplication (although it is possible to start even further back with the concept of sets), we find that statements 1 through 6, Page 2, withRas the set of natural numbers, hold, while 7 through 9 do not hold.
Taking 7 and 8 as additional requirements, we introduce the numbers1;2;3;. . .and 0. Then by taking 9 we introduce the rational numbers.
Operations with these newly obtained numbers can be defined by adopting axioms 1 through 6, whereRis now the set of integers. These lead toproofsof statements such asð2Þð3Þ ¼6,ð4Þ ¼4,
ð0Þð5Þ ¼0, and so on, which are usually taken for granted in elementary mathematics.
We can also introduce the concept of order or inequality for integers, and from these inequalities for rational numbers. For example, ifa,b,c,d are positive integers, we definea=b>c=d if and only if
ad>bc, with similar extensions to negative integers.
POINT SETS, INTERVALS
A set of points (real numbers) located on the real axis is called aone-dimensional point set. The set of pointsxsuch thata@x@bis called aclosed intervaland is denoted by½a;b. The set
a<x<bis called anopen interval, denoted byða;bÞ. The setsa<x@banda@x<b, denoted by
ða;band½a;bÞ, respectively, are calledhalf openorhalf closedintervals.
The symbolx, which can represent any number or point of a set, is called avariable. The given numbersaorbare calledconstants.
Letters were introduced to construct algebraic formulas around 1600. Not long thereafter, the philosopher-mathematician Rene Descartes suggested that the letters at the end of the alphabet be used to represent variables and those at the beginning to represent constants. This was such a good idea that it remains the custom.
EXAMPLE. The set of allxsuch thatjxj<4, i.e.,4<x<4, is represented byð4;4Þ, an open interval.
The setx>acan also be represented bya<x<1. Such a set is called aninfiniteorunbounded interval. Similarly,1<x<1represents all real numbersx.
COUNTABILITY
A set is calledcountableordenumerableif its elements can be placed in 1-1 correspondence with the natural numbers.
EXAMPLE. The even natural numbers 2;4;6;8;. . .is a countable set because of the 1-1 correspondence shown. Given set
Natural numbers
2 4 6 8 . . .
l l l l
1 2 3 4 . . .
A set isinfiniteif it can be placed in 1-1 correspondence with a subset of itself. An infinite set which is countable is calledcountable infinite.
The set of rational numbers is countable infinite, while the set of irrational numbers or all real numbers is non-countably infinite (see Problems 1.17 through 1.20).
The number of elements in a set is called itscardinal number. A set which is countably infinite is assigned the cardinal numberFo(the Hebrew letteraleph-null). The set of real numbers (or any sets
which can be placed into 1-1 correspondence with this set) is given the cardinal numberC, called the cardinality of the continuuum.
NEIGHBORHOODS
The set of all pointsxsuch thatjxaj< where >0, is called aneighborhoodof the pointa. The set of all points x such that 0<jxaj< in which x¼a is excluded, is called a deleted neighborhoodofaor an open ball of radiusabouta.
LIMIT POINTS
A set containing all its limit points is called aclosed set. The set of rational numbers is not a closed set since, for example, the limit pointpffiffiffi2is not a member of the set (Problem 1.5). However, the set of all real numbersxsuch that 0@x@1 is a closed set.
BOUNDS
If for all numbersxof a set there is a numberMsuch thatx@M, the set isbounded aboveandMis called anupper bound. Similarly ifxAm, the set isbounded belowandmis called alower bound. If for allxwe havem@x@M, the set is calledbounded.
IfMis a number such that no member of the set is greater thanMbut there is at least one member which exceedsMfor every >0, thenMis called theleast upper bound(l.u.b.) of the set. Similarly if no member of the set is smaller thanmm but at least one member is smaller thanmm þfor every >0, thenmm is called thegreatest lower bound(g.l.b.) of the set.
BOLZANO–WEIERSTRASS THEOREM
The Bolzano–Weierstrass theorem states that every bounded infinite set has at least one limit point. A proof of this is given in Problem 2.23, Chapter 2.
ALGEBRAIC AND TRANSCENDENTAL NUMBERS A numberxwhich is a solution to thepolynomial equation
a0xnþa1xn1þa2xn2þ þan1xþan¼0 ð1Þ wherea06¼0,a1;a2;. . .;anare integers andnis a positive integer, called thedegreeof the equation, is called an algebraic number. A number which cannot be expressed as a solution of any polynomial equation with integer coefficients is called atranscendental number.
EXAMPLES. 2
3and
ffiffiffi
2
p
which are solutions of 3x2¼0 andx22¼0, respectively, are algebraic numbers.
The numbers and ecan be shown to be transcendental numbers. Mathematicians have yet to determine whether some numbers such aseoreþare algebraic or not.
The set of algebraic numbers is a countably infinite set (see Problem 1.23), but the set of transcen-dental numbers is non-countably infinite.
THE COMPLEX NUMBER SYSTEM
Equations such as x2þ1¼0 have no solution within the real number system. Because these equations were found to have a meaningful place in the mathematical structures being built, various mathematicians of the late nineteenth and early twentieth centuries developed an extended system of numbers in which there were solutions. The new system became known as thecomplex number system. It includes the real number system as a subset.
We can consider a complex number as having the formaþbi, whereaandbare real numbers called therealandimaginary parts, andi¼pffiffiffiffiffiffiffi1is called theimaginary unit. Two complex numbersaþbi
andcþdiareequalif and only ifa¼candb¼d. We can consider real numbers as a subset of the set of complex numbers withb¼0. The complex number 0þ0icorresponds to the real number 0.
Theabsolute valueormodulusofaþbiis defined asjaþbij ¼pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffia2þb2. Thecomplex conjugateof
From the point of view of an axiomatic foundation of complex numbers, it is desirable to treat a complex number as an ordered pairða;bÞof real numbersaandbsubject to certain operational rules which turn out to be equivalent to those above. For example, we defineða;bÞ þ ðc;dÞ ¼ ðaþc;bþdÞ,
ða;bÞðc;dÞ ¼ ðacbd;adþbcÞ, mða;bÞ ¼ ðma;mbÞ, and so on. We then find that ða;bÞ ¼að1;0Þ þ bð0;1Þand we associate this withaþbi, whereiis the symbol forð0;1Þ.
POLAR FORM OF COMPLEX NUMBERS
If real scales are chosen on two mutually perpendicular axesX0OXandY0OY(thexandyaxes) as in Fig. 1-2 below, we can locate any point in the plane determined by these lines by the ordered pair of numbersðx;yÞcalledrectangular coordinatesof the point. Examples of the location of such points are indicated byP,Q,R,S, andT in Fig. 1-2.
Since a complex numberxþiycan be considered as an ordered pairðx;yÞ, we can represent such numbers by points in anxyplane called thecomplex planeorArgand diagram. Referring to Fig. 1-3 above we see thatx¼cos,y¼sinwhere¼pxffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2þy2¼ jxþiyjand, called theamplitudeor argument, is the angle which lineOPmakes with the positivexaxisOX. It follows that
z¼xþiy¼ðcosþisinÞ ð2Þ
called thepolar formof the complex number, whereandare calledpolar coordintes. It is sometimes convenient to write cisinstead of cosþisin.
If z1¼x1þiyi¼1ðcos1þisin1Þ and z2¼x2þiy2¼2ðcos2þisin2Þ and by using the addition formulas for sine and cosine, we can show that
z1z2¼12fcosð1þ2Þ þisinð1þ2Þg ð3Þ
z1
z2¼ 1 2f
cosð12Þ þisinð12Þg ð4Þ
zn¼ fðcosþisinÞgn
¼n
ðcosnþisinnÞ ð5Þ
wherenis any real number. Equation (5) is sometimes calledDe Moivre’s theorem. We can use this to determine roots of complex numbers. For example, ifnis a positive integer,
z1=n¼ fðcosþisinÞg1=n ð6Þ
¼1=n cos þ2k
n
þisin þ2k
n
k¼0;1;2;3;. . .;n1
_ 4
X¢ _ 3 _ 2 _ 1 1 2 3 4 X 4
Y
Y¢ 3
2
1
_ 1
_ 2
_ 3 O Q(_ 3, 3)
S(2, _ 2)
P(3, 4)
T(2.5, 0)
R(_ 2.5, _ 1.5)
Fig. 1-2
X′ O X
Y
Y′ ρ
φ
y
x
P(x, y)
from which it follows that there are in generalndifferent values ofz1=n. Later (Chap. 11) we will show thatei¼cosþisinwheree¼2:71828. . .. This is calledEuler’s formula.
MATHEMATICAL INDUCTION
The principle of mathematical induction is an important property of the positive integers. It is especially useful in proving statements involving all positive integers when it is known for example that the statements are valid forn¼1;2;3 but it issuspectedorconjecturedthat they hold for all positive integers. The method of proof consists of the following steps:
1. Prove the statement forn¼1 (or some other positive integer). 2. Assume the statement true forn¼k; wherek is any positive integer.
3. From the assumption in 2 prove that the statement must be true forn¼kþ1. This is part of the proof establishing the induction and may be difficult or impossible.
4. Since the statement is true forn¼1 [from step 1] it must [from step 3] be true forn¼1þ1¼2 and from this forn¼2þ1¼3, and so on, and so must be true for all positive integers. (This assumption, which provides the link for the truth of a statement for a finite number of cases to the truth of that statement for the infinite set, is called ‘‘The Axiom of Mathematical Induc-tion.’’)
Solved Problems
OPERATIONS WITH NUMBERS 1.1. Ifx¼4,y¼15,z¼ 3,p¼2
3,q¼ 1
6, andr¼ 3
4, evaluate (a) xþ ðyþzÞ, (b) ðxþyÞ þz, (c) pðqrÞ, (d) ðpqÞr, (e) xðpþqÞ
(a) xþ ðyþzÞ ¼4þ ½15þ ð3Þ ¼4þ12¼16 (b) ðxþyÞ þz¼ ð4þ15Þ þ ð3Þ ¼193¼16
The fact that (a) and (b) are equal illustrates theassociative law of addition. (c) pðqrÞ ¼2
3fð 1 6Þð
3 4Þg ¼ ð
2 3Þð
3 24Þ ¼ ð
2 3Þð
1 8Þ ¼
2 24¼
1 12
(d) ðpqÞr¼ fð2 3Þð
1 6Þgð
3 4Þ ¼ ð
2 18Þð
3 4Þ ¼ ð
1 9Þð
3 4Þ ¼
3 36¼
1 12
The fact that (c) and (d) are equal illustrates theassociative law of multiplication. (e) xðpþqÞ ¼4ð2
316Þ ¼4ð4661Þ ¼4ð36Þ ¼126 ¼2
Another method: xðpþqÞ ¼xpþxq¼ ð4Þð2 3Þ þ ð4Þð
1 6Þ ¼
8 3
4 6¼
8 3
2 3¼
6
3¼2 using the distributive
law.
1.2. Explain why we do not consider (a) 0 0 (b)
1
0as numbers.
(a) If we definea=bas that number (if it exists) such thatbx¼a, then 0=0 is that number xsuch that 0x¼0. However, this is true for all numbers. Since there is no unique number which 0/0 can represent, we consider it undefined.
(b) As in (a), if we define 1/0 as that numberx(if it exists) such that 0x¼1, we conclude that there is no such number.
1.3. Simplifyx 2
5xþ6
x22x3.
x25xþ6
x22x3¼
ðx3Þðx2Þ ðx3Þðxþ1Þ¼
x2
xþ1provided that the cancelled factorðx3Þis not zero, i.e.,x6¼3. Forx¼3 the given fraction is undefined.
RATIONAL AND IRRATIONAL NUMBERS 1.4. Prove that the square of any odd integer is odd.
Any odd integer has the form 2mþ1. Sinceð2mþ1Þ2
¼4m2þ4mþ1 is 1 more than the even integer 4m2þ4m¼2ð2m2þ2mÞ, the result follows.
1.5. Prove that there is no rational number whose square is 2.
Letp=qbe a rational number whose square is 2, where we assume thatp=qis in lowest terms, i.e.,pandq have no common integer factors except1 (we sometimes call such integersrelatively prime).
Thenðp=qÞ2¼2,p2¼2q2andp2is even. From Problem 1.4,pis even since ifpwere odd,p2would be odd. Thusp¼2m:
Substitutingp¼2minp2¼2q2 yieldsq2¼2m2, so thatq2 is even andqis even.
Thus p and q have the common factor 2, contradicting the original assumption that they had no common factors other than1. By virtue of this contradiction there can be no rational number whose square is 2.
1.6. Show how to find rational numbers whose squares can be arbitrarily close to 2.
We restrict ourselves to positive rational numbers. Sinceð1Þ2¼1 andð2Þ2¼4, we are led to choose rational numbers between 1 and 2, e.g., 1:1;1:2;1:3;. . .;1:9.
Since ð1:4Þ2
¼1:96 and ð1:5Þ2
¼2:25, we consider rational numbers between 1.4 and 1.5, e.g., 1:41;1:42;. . .;1:49:
Continuing in this manner we can obtain closer and closer rational approximations, e.g.ð1:414213562Þ2
is less than 2 whileð1:414213563Þ2is greater than 2.
1.7. Given the equation a0xnþa1xn1þ þan¼0, where a0;a1;. . .;an are integers and a0 and
an6¼0. Show that if the equation is to have a rational rootp=q, thenpmust divide anand q must dividea0exactly.
Sincep=qis a root we have, on substituting in the given equation and multiplying byqn, the result
a0pnþa1pn1qþa2pn2q2þ þan1pqn1þanqn¼0 ð1Þ or dividing byp,
a0pn1þa1pn2qþ þan1qn1¼
anqn
p ð2Þ
Since the left side of (2) is an integer, the right side must also be an integer. Then sincepandqare relatively prime,pdoes not divideqnexactly and so must dividean.
In a similar manner, by transposing the first term of (1) and dividing byq, we can show thatqmust dividea0.
1.8. Prove thatpffiffiffi2þpffiffiffi3cannot be a rational number.
Ifx¼pffiffiffi2þpffiffiffi3, thenx2¼5þ2pffiffiffi6,x25¼2pffiffiffi6and squaring,x410x2þ1¼0. The only possible rational roots of this equation are1 by Problem 1.7, and these do not satisfy the equation. It follows that
ffiffiffi
2
p
1.9. Prove that between any two rational numbers there is another rational number.
The set of rational numbers is closed under the operations of addition and division (non-zero
denominator). Therefore,aþb
2 is rational. The next step is to guarantee that this value is betweena andb. To this purpose, assumea<b. (The proof would proceed similarly under the assumptionb<a.)
Then 2a<aþb, thusa<aþb
2 andaþb<2b, therefore
aþb
2 <b.
INEQUALITIES
1.10. For what values ofxisxþ3ð2xÞA4x?
xþ3ð2xÞA4xwhenxþ63xA4x, 62xA4x, 64A2xx, 2Ax, i.e.x@2.
1.11. For what values ofxisx23x2<102x?
The required inequality holds when
x23x210þ2x<0; x2x12<0 or ðx4Þðxþ3Þ<0
This last inequality holds only in the following cases.
Case 1:x4>0andxþ3<0, i.e.,x>4 andx<3. This isimpossible, sincexcannot be both greater than 4 and less than3.
Case 2:x4<0 andxþ3>0, i.e. x<4 and x>3. This is possible when3<x<4. Thus the inequality holds for the set of allxsuch that3<x<4.
1.12. IfaA0 andbA0, prove that1
2ðaþbÞA ffiffiffiffiffi
ab p
.
The statement is self-evident in the following cases (1) a¼b, and (2) either or both ofaandbzero. For bothaandbpositive anda6¼b, the proof is by contradiction.
Assume to the contrary of the supposition that1
2ðaþbÞ<
ffiffiffiffiffi
ab
p
then1 4ða
2
þ2abþb2Þ<ab.
That is,a22abþb2¼ ðabÞ2<0. Since the left member of this equation is a square, it cannot be less than zero, as is indicated. Having reached this contradiction, we may conclude that our assumption is incorrect and that the original assertion is true.
1.13. Ifa1;a2;. . .;an andb1;b2;. . .;bn are any real numbers, proveSchwarz’s inequality
ða1b1þa2b2þ þanbnÞ2@ða12þa22þ þa2nÞðb21þb22þ þb2nÞ
For all real numbers, we have
ða1þb1Þ2þ ða2þb2Þ2þ þ ðanþbnÞ2A0 Expanding and collecting terms yields
A22
þ2CþB2A0 ð1Þ
where
A2¼a21þa22þ þa2n; B2¼b21þb22þ þb2n; C¼a1b1þa2b2þ þanbn ð2Þ The left member of (1) is a quadratic form in . Since it never is negative, its discriminant, 4C24A2B2, cannot be positive. Thus
C2A2B20 or C2A2B2
This is the inequality that was to be proved.
1.14. Prove that1 2þ
1 4þ
1 8þ þ
1
Sn¼ 1 2þ
1 4þ
1 8þ þ
1 2n1
Let
1 2Sn¼
1 4þ
1 8þ þ
1 2n1þ
1 2n Then
1 2Sn¼
1 2
1
2n: ThusSn¼1 1
2n1<1 for alln:
Subtracting,
EXPONENTS, ROOTS, AND LOGARITHMS 1.15. Evaluate each of the following:
ðaÞ 3
4
38 314 ¼
34þ8 314 ¼3
4þ814
¼32¼ 1
32¼
1 9
ðbÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð5106
Þð4102
Þ
8105
s
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
54
8
106
102
105
s
¼pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi2:5109
¼pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi251010
¼5105or 0:00005
ðcÞ log2=3 278
¼x: Then 2 3
x
¼27 8 ¼
3 2
3
¼ 2 3
3
or x¼ 3
ðdÞ ðlogabÞðlogbaÞ ¼u: Then logab¼x;logba¼yassuminga;b>0 anda;b6¼1: Thenax¼b,by¼aandu¼xy.
SinceðaxÞy¼axy¼by¼awe haveaxy¼a1orxy¼1 the required value.
1.16. IfM>0,N>0; anda>0 buta6¼1, prove that loga
M
N ¼logaMlogaN.
Let logaM¼x, logaN¼y. Thena x
¼M,ay¼Nand so M
N¼
ax
ay¼a
xy
or loga M
N¼xy¼logaMlogaN
COUNTABILITY
1.17. Prove that the set of all rational numbers between 0 and 1 inclusive is countable.
Write all fractions with denominator 2, then 3;. . .considering equivalent fractions such as1
2;24;36;. . .no
more than once. Then the 1-1 correspondence with the natural numbers can be accomplished as follows:
Rational numbers
Natural numbers
0 1 1
2 1 3
2 3
1 4
3 4
1 5
2 5 . . .
l l l l l l l l l
1 2 3 4 5 6 7 8 9 . . .
Thus the set of all rational numbers between 0 and 1 inclusive is countable and has cardinal numberF o (see Page 5).
1.18. IfAandBare two countable sets, prove that the set consisting of all elements fromAorB(or both) is also countable.
SinceAis countable, there is a 1-1 correspondence between elements ofAand the natural numbers so that we can denote these elements bya1;a2;a3;. . ..
Similarly, we can denote the elements ofBbyb1;b2;b3;. . ..
AorB
Natural numbers
a1 b1 a2 b2 a3 b3 . . .
l l l l l l
1 2 3 4 5 6 . . .
Case 2: If some elements ofAandBare the same, we count them only once as in Problem 1.17. Then the set of elements belonging toAorB(or both) is countable.
The set consisting of all elements which belong toAorB(or both) is often called theunionofAandB, denoted byA[BorAþB.
The set consisting of all elements which are contained in bothAand Bis called theintersectionofAand B, denoted byA\BorAB. IfAandBare countable, so isA\B.
The set consisting of all elements inAbutnotinBis writtenAB. If we letBBbe the set of elements which are not inB, we can also writeAB¼ABB. IfAandBare countable, so isAB.
1.19. Prove that the set of all positive rational numbers is countable.
Consider all rational numbersx>1. With each such rational number we can associate one and only one rational number 1=xinð0;1Þ, i.e., there is aone-to-one correspondencebetween all rational numbers>1 and all rational numbers inð0;1Þ. Since these last are countable by Problem 1.17, it follows that the set of all rational numbers>1 is also countable.
From Problem 1.18 it then follows that the set consisting of all positive rational numbers is countable, since this is composed of the two countable sets of rationals between 0 and 1 and those greater than or equal to 1.
From this we can show that the set of all rational numbers is countable (see Problem 1.59).
1.20. Prove that the set of all real numbers in½0;1is non-countable.
Every real number in½0;1has a decimal expansion:a1a2a3. . .wherea1;a2;. . .are any of the digits
0;1;2;. . .;9.
We assume that numbers whose decimal expansions terminate such as 0.7324 are written 0:73240000. . . and that this is the same as 0:73239999. . ..
If all real numbers in½0;1 are countable we can place them in 1-1 correspondence with the natural numbers as in the following list:
1 2 3 .. .
$ $ $
0:a11a12a13a14. . .
0:a21a22a23a24. . .
0:a31a32a33a34. . . .. .
We now form a number
0:b1b2b3b4. . .
whereb16¼a11;b26¼a22;b36¼a33;b46¼a44;. . .and where allb’s beyond some position are not all 9’s.
This number, which is in½0;1is different from all numbers in the above list and is thus not in the list, contradicting the assumption that all numbers in½0;1were included.
Because of this contradiction it follows that the real numbers in½0;1cannot be placed in 1-1 corre-spondence with the natural numbers, i.e., the set of real numbers in½0;1is non-countable.
LIMIT POINTS, BOUNDS, BOLZANO–WEIERSTRASS THEOREM 1.21. (a) Prove that the infinite sets of numbers 1;1
2; 1 3;
1
4;. . . is bounded. (b) Determine the least upper bound (l.u.b.) and greatest lower bound (g.l.b.) of the set. (c) Prove that 0 is a limit point of the set. (d) Is the set a closed set? (e) How does this set illustrate the Bolzano–Weierstrass theorem?
(a) Since all members of the set are less than 2 and greater than1 (for example), the set is bounded; 2 is an upper bound,1 is a lower bound.
We can find smaller upper bounds (e.g.,3
(b) Since no member of the set is greater than 1 and since there is at least one member of the set (namely 1) which exceeds 1for every positive number, we see that 1 is the l.u.b. of the set.
Since no member of the set is less than 0 and since there is at least one member of the set which is less than 0þfor every positive(we can always choose for this purpose the number 1=nwherenis a positive integer greater than 1=), we see that 0 is the g.l.b. of the set.
(c) Letxbe any member of the set. Since we can always find a numberxsuch that 0<jxj< for any positive number(e.g. we can always pickxto be the number 1=nwherenis a positive integer greater than 1=), we see that 0 is a limit point of the set. To put this another way, we see that any deleted
neighborhood of 0 always includes members of the set, no matter how small we take >0. (d) The set is not a closed set since the limit point 0 does not belong to the given set.
(e) Since the set is bounded and infinite it must, by the Bolzano–Weierstrass theorem, have at least one limit point. We have found this to be the case, so that the theorem is illustrated.
ALGEBRAIC AND TRANSCENDENTAL NUMBERS 1.22. Prove thatp3ffiffiffi2
þpffiffiffi3is an algebraic number.
Letx¼p3ffiffiffi2
þpffiffiffi3. Thenxpffiffiffi3¼p3ffiffiffi2
. Cubing both sides and simplifying, we findx3þ9x2¼
3pffiffiffi3ðx2þ1Þ. Then squaring both sides and simplifying we findx69x44x3þ27x2þ36x23¼0. Since this is a polynomial equation with integral coefficients it follows that p3ffiffiffi2
þpffiffiffi3, which is a solution, is an algebraic number.
1.23. Prove that the set of all algebraic numbers is a countable set.
Algebraic numbers are solutions to polynomial equations of the form a0x
n
þa1x
n1
þ þan¼0 wherea0;a1;. . .;anare integers.
LetP¼ ja0j þ ja1j þ þ janj þn. For any given value ofPthere are only a finite number of possible polynomial equations and thus only a finite number of possible algebraic numbers.
Write all algebraic numbers corresponding toP¼1;2;3;4;. . .avoiding repetitions. Thus, all algebraic numbers can be placed into 1-1 correspondence with the natural numbers and so are countable.
COMPLEX NUMBERS
1.24. Perform the indicated operations.
(a) ð42iÞ þ ð6þ5iÞ ¼42i6þ5i¼46þ ð2þ5Þi¼ 2þ3i (b) ð7þ3iÞ ð24iÞ ¼ 7þ3i2þ4i¼ 9þ7i
(c) ð32iÞð1þ3iÞ ¼3ð1þ3iÞ 2ið1þ3iÞ ¼3þ9i2i6i2¼3þ9i2iþ6¼9þ7i
ðdÞ 45þ5i 3i ¼
5þ5i 43i
4þ3i 4þ3i¼
ð5þ5iÞð4þ3iÞ
169i2 ¼
2015iþ20iþ15i2 16þ9
¼3525þ5i¼5ð257þiÞ¼57þ15i
ðeÞ iþi
2
þi3þi4þi5
1þi ¼
i1þ ði2ÞðiÞ þ ði2Þ2þ ði2Þ2i
1þi ¼
i1iþ1þi
1þi
¼1i þi
1i 1i¼
ii2 1i2¼
iþ1
2 ¼
1 2þ
1 2i
ðfÞ j34ijj4þ3ij ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð3Þ2
þ ð4Þ2
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð4Þ2
þ ð3Þ2
q
ðgÞ 1 1 þ3i
1 13i
¼
13i 19i2
1þ3i 19i2
¼
6i 10
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð0Þ2þ 106
2
s
¼35
1.25. Ifz1andz2are two complex numbers, prove thatjz1z2j ¼ jz1jjz2j.
Letz1¼x1þiy1,z2¼x2þiy2. Then
jz1z2j ¼ jðx1þiy1Þðx2þiy2Þj ¼ jx1x2y1y2þiðx1y2þx2y1Þj
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx1x2y1y2Þ2þ ðx1y2þx2y1Þ2
q
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2
1x22þy21y22þx21y22þx22y21
q
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx2
1þy21Þðx22þy22Þ
q
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 1þy2
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 2þy22
q
¼ jx1þiy1jjx2þiy2j ¼ jz1jjz2j:
1.26. Solvex32x4¼0.
The possible rational roots using Problem 1.7 are1,2,4. By trial we findx¼2 is a root. Then the given equation can be written ðx2Þðx2þ2xþ2Þ ¼0. The solutions to the quadratic equation
ax2þbxþc¼0 are x¼b
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
b2
4ac
p
2a . For a¼1, b¼2, c¼2 this gives x¼
2pffiffiffiffiffiffiffiffiffiffiffi48
2 ¼
2pffiffiffiffiffiffiffi4
2 ¼
22i
2 ¼ 1i.
The set of solutions is 2,1þi,1i.
POLAR FORM OF COMPLEX NUMBERS
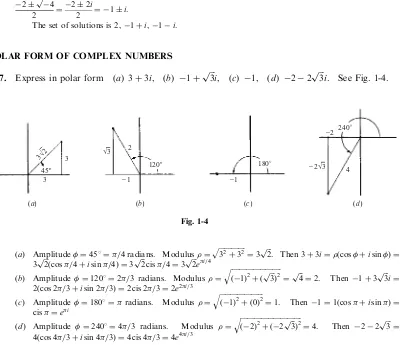
1.27. Express in polar form (a) 3þ3i, (b) 1þpffiffiffi3i, (c) 1, (d) 22pffiffiffi3i. See Fig. 1-4.
(a) Amplitude¼458¼=4 radians. Modulus¼ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi32
þ32
p
¼3pffiffiffi2. Then 3þ3i¼ðcosþisinÞ ¼
3p2ffiffiffiðcos=4þisin=4Þ ¼3pffiffiffi2cis=4¼3pffiffiffi2ei=4 (b) Amplitude¼1208¼2=3 radians. Modulus¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð1Þ2þ ðpffiffiffi3Þ2
q
¼pffiffiffi4¼2. Then1þ3pffiffiffi3i¼
2ðcos 2=3þisin 2=3Þ ¼2 cis 2=3¼2e2i=3 (c) Amplitude¼1808¼radians. Modulus¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð1Þ2þ ð0Þ2
q
¼1. Then1¼1ðcosþisinÞ ¼
cis¼ei
(d) Amplitude ¼2408¼4=3 radians. Modulus ¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð2Þ2þ ð2pffiffiffi3Þ2
q
¼4. Then 22pffiffiffi3¼
4ðcos 4=3þisin 4=3Þ ¼4 cis 4=3¼4e4i=3
45° 120° 180°
240°
3 3 3√2
_ 2√3 √3
(a) (b) (c) (d)
2
_ 1 _ 1
_ 2
4
1.28. Evaluate (a) ð1þpffiffiffi3iÞ10, (b) ð1þiÞ1=3.
(a) By Problem 1.27(b) and De Moivre’s theorem,
ð1þpffiffiffi3iÞ10¼ ½2ðcos 2=3þisin 2=3Þ10¼210ðcos 20=3þisin 20=3Þ
¼1024½cosð2=3þ6Þ þisinð2=3þ6Þ ¼1024ðcos 2=3þisin 2=3Þ ¼10241
2þ 1 2
ffiffiffi
3
p
i
¼ 512þ512pffiffiffi3i
(b) 1þi¼pffiffiffi2ðcos 1358þisin 1358Þ ¼pffiffiffi2½cosð1358þk3608Þ þisinð1358þk3608Þ. Then
ð1þiÞ1=3¼ ðpffiffiffi2Þ1=3 cos 1358þk3608 3
þisin 1358þk3608 3
The results fork¼0;1;2 are
ffiffiffi
2
6
p
ðcos 458þisin 458Þ;
ffiffiffi
2
6
p
ðcos 1658þisin 1658Þ;
ffiffiffi
2
6
p
ðcos 2858þisin 2858Þ
The results fork¼3;4;5;6;7;. . .give repetitions of these. These complex roots are represented geometrically in the complex plane by pointsP1;P2;P3on the circle of Fig. 1-5.
MATHEMATICAL INDUCTION
1.29. Prove that 12þ22þ33þ42þ þn2¼1
6nðnþ1Þð2nþ1Þ.
The statement is true forn¼1 since 12¼1
6ð1Þð1þ1Þð21þ1Þ ¼1.
Assumethe statement true forn¼k. Then 12þ22þ32þ þk2¼1
6kðkþ1Þð2kþ1Þ
Addingðkþ1Þ2to both sides, 12þ22þ32þ þk2þ ðkþ1Þ2¼1
6kðkþ1Þð2kþ1Þ þ ðkþ1Þ 2
¼ ðkþ1Þ½1
6kð2kþ1Þ þkþ1
¼1
6ðkþ1Þð2k 2
þ7kþ6Þ ¼1
6ðkþ1Þðkþ2Þð2kþ3Þ
which shows that the statement is true forn¼kþ1ifit is true forn¼k. But since it is true forn¼1, it follows that it is true forn¼1þ1¼2 and forn¼2þ1¼3;. . .;i.e., it is true for all positive integersn.
1.30. Prove thatxnyn hasxyas a factor for all positive integersn.
The statement is true forn¼1 sincex1y1¼xy.
Assumethe statement true forn¼k, i.e., assume thatxkykhasxyas a factor. Consider xkþ1ykþ1¼xkþ1xkyþxkyykþ1
¼xkðxyÞ þyðxkykÞ
The first term on the right hasxyas a factor, and the second term on the right also hasxyas a factor because of the above assumption.
Thusxkþ1ykþ1hasxyas a factorifxkykdoes.
Then sincex1y1hasxyas factor, it follows thatx2y2hasxyas a factor,x3y3hasxyas a factor, etc.
P2
P3 P1
165°
285°
45°
√26
1.31. ProveBernoulli’s inequalityð1þxÞn>1þnxforn¼2;3;. . .ifx>1,x6¼0.
The statement is true forn¼2 sinceð1þxÞ2¼1þ2xþx2>1þ2x. Assume the statement true forn¼k, i.e.,ð1þxÞk>1þkx.
Multiply both sides by 1þx(which is positive sincex>1). Then we have
ð1þxÞkþ1>ð1þxÞð1þkxÞ ¼1þ ðkþ1Þxþkx2>1þ ðkþ1Þx Thus the statement is true forn¼kþ1 if it is true forn¼k.
But since the statement is true forn¼2, it must be true forn¼2þ1¼3;. . .and is thus true for all integers greater than or equal to 2.
Note that the result is not true forn¼1. However, the modified resultð1þxÞnA1þnxis true for n¼1;2;3;. . ..
MISCELLANEOUS PROBLEMS
1.32. Prove that every positive integer Pcan be expressed uniquely in the form P¼a02nþa12n1þ
a22n2þ þan where thea’s are 0’s or 1’s.
DividingPby 2, we haveP=2¼a02n1þa12n2þ þan1þan=2.
Thenanis the remainder, 0 or 1, obtained whenPis divided by 2 and is unique. LetP1 be the integer part ofP=2. ThenP1¼a02n1þa12n2þ þan1.
DividingP1 by 2 we see thatan1is the remainder, 0 or 1, obtained whenP1is divided by 2 and is
unique.
By continuing in this manner, all thea’s can be determined as 0’s or 1’s and are unique.
1.33. Express the number 23 in the form of Problem 1.32.
The determination of the coefficients can be arranged as follows:
2Þ23
2Þ11 Remainder 1 2Þ5 Remainder 1 2Þ2 Remainder 1 2Þ1 Remainder 0 0 Remainder 1
The coefficients are 1 0 1 1 1. Check: 23¼124þ023þ122þ12þ1. The number 10111 is said to represent 23 in thescale of twoorbinary scale.
1.34. Dedekind defined acut,section, orpartitionin the rational number system as a separation ofall rational numbers into two classes or sets calledL(the left-hand class) andR(the right-hand class) having the following properties:
I. The classes are non-empty (i.e. at least one number belongs to each class).
II. Every rational number is in one class or the other.
III. Every number inLis less than every number inR.
Prove each of the following statements:
(a) There cannot be a largest number inLand a smallest number inR.
(b) It is possible forLto have a largest number and forRto have no smallest number. What type of number does the cut define in this case?
(d) It is possible forLto have no largest number and forRto have no smallest number. What type of number does the cut define in this case?
(a) Letabe the largest rational number inL, andbthe smallest rational number inR. Then eithera¼bor a<b.
We cannot havea¼bsince by definition of the cut every number inLislessthan every number inR.
We cannot havea<bsince by Problem 1.9,1
2ðaþbÞis a rational number which would be greater
thana(and so would have to be inR) but less thanb(and so would have to be inL), and by definition a rational number cannot belong tobothLandR.
(b) As an indication of the possibility, letLcontain the number2
3and all rational numbers less than 2 3, while
Rcontains all rational numbers greater than2
3. In this case the cut defines the rational number 2 3. A
similar argument replacing2
3by any other rational number shows that in such case the cut defines a
rational number.
(c) As an indication of the possibility, letLcontain all rational numbers less than2
3, whileRcontains all
rational numbers greaters than2
3. This cut also defines the rational number 2
3. A similar argument
shows that this cut always defines a rational number.
(d) As an indication of the possibility letLconsist of all negative rational numbers and all positive rational numbers whose squares are less than 2, whileRconsists of all positive numbers whose squares are greater than 2. We can show that ifais any number of theLclass, there is always a larger number of theLclass, while ifbis any number of theRclass, there is always a smaller number of theRclass (see Problem 1.106). A cut of this type defines an irrational number.
From (b), (c), (d) it follows that every cut in the rational number system, called aDedekind cut, defines either a rational or an irrational number. By use of Dedekind cuts we can define operations (such as addition, multiplication, etc.) with irrational numbers.
Supplementary Problems
OPERATIONS WITH NUMBERS
1.35. Givenx¼ 3,y¼2,z¼5,a¼3
2, andb¼ 1
4, evaluate:
ðaÞ ð2xyÞð3yþzÞð5x2zÞ; ðbÞ xy2z
2
2ab1; ðcÞ
3a2bþab2 2a22b2
þ1; ðdÞ
ðaxþbyÞ2þ ðaybxÞ2 ðayþbxÞ2þ ðaxbyÞ2:
Ans. (a) 2200, (b) 32, (c) 51=41, (d) 1
1.36. Find the set of values ofxfor which the following equations are true. Justify all steps in each case.
ðaÞ 4fðx2Þ þ3ð2x1Þg þ2ð2xþ1Þ ¼12ðxþ2Þ 2 ðcÞ ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffix2
þ8xþ7
p
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi2xþ2¼xþ1
ðbÞ 81 x
1
x2¼
1
4 ðdÞ
1x
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2
2xþ5
p ¼
3 5
Ans. (a) 2, (b) 6;4 (c) 1;1 (d) 1 2
1.37. Prove that x
ðzxÞðxyÞþ
y
ðxyÞðyzÞþ
z
ðyzÞðzxÞ¼0 giving restrictions if any.
RATIONAL AND IRRATIONAL NUMBERS
1.38. Find decimal expansions for (a) 3 7, (b)
ffiffiffi
5
p
.
1.39. Show that a fraction with denominator 17 and with numerator 1;2;3;. . .;16 has 16 digits in the repeating portion of its decimal expansion. Is there any relation between the orders of the digits in these expansions?
1.40. Prove that (a) pffiffiffi3, (b) p3ffiffiffi2
are irrational numbers.
1.41. Prove that (a) p3ffiffiffi5
p4ffiffiffi3
, (b) pffiffiffi2þpffiffiffi3þpffiffiffi5are irrational numbers.
1.42. Determine a positive rational number whose square differs from 7 by less than .000001.
1.43. Prove that every rational number can be expressed as a repeating decimal.
1.44. Find the values ofxfor which
(a) 2x35x29xþ18¼0, (b) 3x3þ4x235xþ8¼0, (c) x421x2þ4¼0.
Ans. (a) 3;2;3=2 (b) 8=3;2pffiffiffi5 (c) 1 2ð5
ffiffiffiffiffi
17
p Þ;1
2ð5
ffiffiffiffiffi
17
p Þ
1.45. Ifa,b,c,dare rational andmis not a perfect square, prove thataþbpffiffiffiffim¼cþdpffiffiffiffimif and only ifa¼c andb¼d.
1.46. Prove that1þ
ffiffiffi
3
p þpffiffiffi5 1pffiffiffi3þp ¼ffiffiffi5
12pffiffiffi52pffiffiffiffiffi15þ14pffiffiffi37
11 :
INEQUALITIES
1.47. Find the set of values ofxfor which each of the following inequalities holds:
ðaÞ 1
xþ
3
2x A5; ðbÞ xðxþ2Þ@24; ðcÞ jxþ2j<jx5j; ðdÞ x xþ2>
xþ3
3xþ1:
Ans. (a) 0<x@12, (b) 6@x@4, (c) x<3=2, (d) x>3;1<x<1
3, orx<2
1.48. Prove (a) jxþyj@jxj þ jyj, (b) jxþyþzj@jxj þ jyj þ jzj, (c) jxyjAjxj jyj. 1.49. Prove that for all realx;y;z,x2þy2þz2Axyþyzþzx:
1.50. Ifa2þb2¼1 andc2þd2¼1, prove thatacþbd@1. 1.51. Ifx>0, prove thatxnþ1þ 1
xnþ1>x
n
þ1
xn wherenis any positive integer.
1.52. Prove that for all reala6¼0,jaþ1=ajA2:
1.53. Show that in Schwarz’s inequality (Problem 13) the equality holds if and only ifap¼kbp,p¼1;2;3;. . .;n wherekis any constant.
1.54. Ifa1;a2;a3are positive, prove that13ða1þa2þa3ÞAp3ffiffiffiffiffiffiffiffiffiffiffiffiffiffia1a2a3.
EXPONENTS, ROOTS, AND LOGARITHMS
1.55. Evaluate (a) 4log28, (b) 3
4log1=8ð1281Þ, (c)
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð0:00004Þð25,000Þ ð0:02Þ5ð0:125Þ
s
, (d) 32 log35, (e) ð1
8Þ 4=3
ð27Þ2=3
Ans. (a) 64, (b) 7/4, (c) 50,000, (d) 1/25, (e) 7=144 1.56. Prove (a) logaMN¼logaMþlogaN, (b) logaM
r
COUNTABILITY
1.58. (a) Prove that there is a one to one correspondence between the points of the interval 0@x@1 and
5@x@ 3. (b) What is the cardinal number of the sets in (a)?
Ans. (b) C, the cardinal number of the continuum.
1.59. (a) Prove that the set of all rational numbers is countable. (b) What is the cardinal number of the set in (a)?
Ans. (b) F o
1.60. Prove that the set of (a) all real numbers, (b) all irrational numbers is non-countable.
1.61. Theintersectionof two setsAandB, denoted byA\BorAB, is the set consisting of all elements belonging to bothAandB. Prove that ifAandBare countable, so is their intersection.
1.62. Prove that a countable set of countable sets is countable.
1.63. Prove that the cardinal number of the set of points inside a square is equal to the cardinal number of the sets of points on (a) one side, (b) all four sides. (c) What is the cardinal number in this case? (d) Does a corresponding result hold for a cube?
Ans. (c) C
LIMIT POINTS, BOUNDS, BOLZANO–WEIERSTRASS THEOREM
1.64. Given the set of numbers 1;1:1; :9;1:01; :99;1:001; :999;. . .. (a) Is the set bounded? (b) Does the set have a l.u.b. and g.l.b.? If so, determine them. (c) Does the set have any limit points? If so, determine them. (d) Is the set a closed set?
Ans. (a) Yes (b) l:u:b:¼1:1;g:l:b:¼:9 (c) 1 (d) Yes
1.65. Give the set:9; :9;:99; :99;:999; :999 answer the questions of Problem 64.
Ans. (a) Yes (b) l:u:b:¼1;g:l:b:¼ 1 (c) 1;1 (d) No
1.66. Give an example of a set which has (a) 3 limit points, (b) no limit points.
1.67. (a) Prove that every point of the interval 0<x<1 is a limit point.
(b) Are there are limit points which do not belong to the set in (a)? Justify your answer.
1.68. LetSbe the set of all rational numbers inð0;1Þhaving denominator 2n,n¼1;2;3;. . .. (a) DoesShave any limit points? (b) IsSclosed?
1.69. (a) Give an example of a set which has limit points but which is not bounded. (b) Does this contradict the Bolzano–Weierstrass theorem? Explain.
ALGEBRAIC AND TRANSCENDENTAL NUMBERS
1.70. Prove that (a)
ffiffiffi
3
p pffiffiffi2
ffiffiffi
3
p
þpffiffiffi2, (b)
ffiffiffi
2
p
þpffiffiffi3þpffiffiffi5are algebraic numbers. 1.71. Prove that the set of transcendental numbers inð0;1Þis not countable.
1.72. Prove that every rational number is algebraic but every irrational number is not necessarily algebraic.
COMPLEX NUMBERS, POLAR FORM
1.73. Perform each of the indicated operations: (a) 2ð53iÞ 3ð2þiÞ þ5ði3Þ, (b) ð32iÞ3 ðcÞ 3 5
4iþ 10
4þ3i; ðdÞ 1i 1þi
10
; ðeÞ 254i þ7i
2
; ðfÞ ð1þiÞð2þ3iÞð42iÞ ð1þ2iÞ2ð1iÞ :
Ans. (a) 14i, (b) 946i, (c) 11 5
2
5i, (d) 1, (e) 10 37, (f)
16 5
1.74. Ifz1andz2are complex numbers, prove (a)
z1
z2
¼
jz1j
jz2j
, (b) jz21j ¼ jz1j2giving any restrictions.
1.75. Prove (a) jz1þz2j@jz1j þ jz2j, (b) jz1þz2þz3j@jz1j þ jz2j þ jz3j, (c) jz1z2jAjz1j jz2j.
1.76. Find all solutions of 2x43x37x28xþ6¼0.
Ans. 3,1 2,1i
1.77. Letz1andz2be represented by pointsP1andP2in the Argand diagram. Construct linesOP1andOP2,
whereOis the origin. Show thatz1þz2can be represented by the pointP3, whereOP3is the diagonal of a
parallelogram having sides OP1 andOP2. This is called the parallelogram lawof addition of complex
numbers. Because of this and other properties, complex numbers can be considered asvectors in two dimensions.
1.78. Interpret geometrically the inequalities of Problem 1.75.
1.79. Express in polar form (a) 3pffiffiffi3þ3i, (b) 22i, (c) 1pffiffiffi3i, (d) 5, (e) 5i.
Ans. (a) 6 cis=6 ðbÞ 2pffiffiffi2cis 5=4 ðcÞ 2 cis 5=3 ðdÞ 5 cis 0 ðeÞ 5 cis 3=2 1.80. Evaluate (a) ½2ðcos 258þisin 258Þ½5ðcos 1108þisin 1108Þ, (b) 12 cis 168
ð3 cis 448Þð2 cis 628Þ:
Ans. (a) 5pffiffiffi2þ5pffiffiffi2i; ðbÞ 2i
1.81. Determine all the indicated roots and represent them graphically: (a) ð4pffiffiffi2þ4p2ffiffiffiiÞ1=3; ðbÞ ð1Þ1=5; ðcÞ ðpffiffiffi3iÞ1=3; ðdÞ i1=4.
Ans. (a) 2 cis 158;2 cis 1358;2 cis 2558
(b) cis 368;cis 1088;cis 1808¼ 1;cis 2528;cis 3248
(c) p3ffiffiffi2
cis 1108;p3ffiffiffi2
cis 2308;p3ffiffiffi2 cis 3508
(d) cis 22:58;cis 112:58;cis 202:58;cis 292:58
1.82. Prove that1þpffiffiffi3iis an algebraic number.
1.83. If z1¼1cis1 and z2¼2cis2, prove (a) z1z2¼12cisð1þ2Þ, (b) z1=z2¼ ð1=2Þcisð12Þ.
Interpret geometrically.
MATHEMATICAL INDUCTION Prove each of the following.
1.84. 1þ3þ5þ þ ð2n1Þ ¼n2
1.85. 1
13þ 1 35þ
1 57þ þ
1
ð2n1Þð2nþ1Þ¼ n 2nþ1 1.86. aþ ðaþdÞ þ ðaþ2dÞ þ þ ½aþ ðn1Þd ¼1
2n½2aþ ðn1Þd
1.87. 1
123þ 1 234þ
1
345þ þ 1 nðnþ1Þðnþ2Þ¼
nðnþ3Þ
4ðnþ1Þðnþ2Þ
1.88. aþarþar2þ þarn1¼aðr
n
1Þ
r1 ;r6¼1
1.89. 13þ23þ33þ þn3¼1 4n
2
ðnþ1Þ2
1.90. 1ð5Þ þ2ð5Þ2þ3ð5Þ3þ þnð5Þn1¼5þ ð4n1Þ5
nþ1
16
1.92. ðcosþisinÞn¼cosnþisinn. Can this be proved ifnis a rational number? 1.93. 1
2þcosxþcos 2xþ þcosnx¼
sinðnþ1 2Þx
2 sin1 2x
,x6¼0;2;4;. . .
1.94. sinxþsin 2xþ þsinnx¼cos
1
2xcosðnþ 1 2Þx
2 sin1 2x
; x6¼0;2;4;. . .
1.95. ðaþbÞn¼anþnC1a
n1
bþnC2a
n2
b2þ þnCn1ab
n1
þbn wherenCr¼
nðn1Þðn2Þ. . .ðnrþ1Þ
r! ¼
n!
r!ðnrÞ!¼nCnr. Herep!¼pðp1Þ. . .1 and 0!is defined as 1. This is called thebinomial theorem. The coefficientsnC0¼1,nC1¼n,nC2¼
nðn1Þ
2! ;. . .;nCn¼1 are called thebinomial coefficients. nCr is also written
n
r .
MISCELLANEOUS PROBLEMS
1.96. Express each of the following integers (scale of 10) in the scale of notation indicated: (a) 87 (two), (b) 64 (three), (c) 1736 (nine). Check each answer.
Ans. (a) 1010111, (b) 2101, (c) 2338
1.97. If a number is 144 in the scale of 5, what is the number in the scale of (a) 2, (b) 8?
1.98. Prove that every rational numberp=qbetween 0 and 1 can be expressed in the form p
q¼
a1
2þ a2
22þ þ
an 2nþ
where thea’s can be determined uniquely as 0’s or 1’s and where the process may or may not terminate. The representation 0:a1a2. . .an. . .is then called thebinary formof the rational number. [Hint: Multiply both sides successively by 2 and consider remainders.}
1.99. Express2
3in the scale of (a) 2, (b) 3, (c) 8, (d) 10.
Ans. (a) 0:1010101. . .; (b) 0.2 or 0:2000. . .; (c) 0:5252. . .; (d) 0:6666. . .
1.100. A number in the scale of 2 is 11.01001. What is the number in the scale of 10.
Ans. 3.28125
1.101. In what scale of notation is 3þ4¼12?
Ans. 5
1.102. In the scale of 12, two additional symbols t and e must be used to designate the ‘‘digits’’ 10 and 11, respectively. Using these symbols, represent the integer 5110 (scale of 10) in the scale of 12.
Ans. 2e5t
1.103. Find a rational number whose decimal expansion is 1:636363. . ..
Ans. 18/11
1.104. A number in the scale of 10 consists of six digits. If the last digit is removed and placed before the first digit, the new number is one-third as large. Find the original number.
Ans. 428571
1.105. Show that the rational numbers form a field.
1.107. (a) Ifxis a rational number whose square is less than 2, show thatxþ ð2x2Þ=10 is a larger such number. (b) Ifxis a rational number whose square is greater than 2, find in terms ofxa smaller rational number whose square is greater than 2.
23
Sequences
DEFINITION OF A SEQUENCE
A sequence is a set of numbersu1;u2;u3;. . .in a definite order of arrangement (i.e., acorrespondence with the natural numbers) and formed according to a definite rule. Each number in the sequence is called aterm;unis called thenthterm. The sequence is calledfiniteorinfiniteaccording as there are or are not a finite number of terms. The sequenceu1;u2;u3;. . .is also designated briefly byfung.
EXAMPLES. 1. The set of numbers 2;7;12;17;. . .;32 is a finite sequence; the nth term is given by
un¼2þ5ðn1Þ ¼5n3,n¼1;2;. . .;7.
2. The set of numbers 1;1=3;1=5;1=7;. . .is an infinite sequence with nth term un¼1=ð2n1Þ, n¼1;2;3;. . ..
Unless otherwise specified, we shall consider infinite sequences only.
LIMIT OF A SEQUENCE
A numberlis called thelimitof an infinite sequenceu1;u2;u3;. . .if for any positive numberwe can find a positive numberNdepending onsuch thatjunlj< for all integersn>N. In such case we write lim
n!1un¼l.
EXAMPLE . Ifun¼3þ1=n¼ ð3nþ1Þ=n, the sequence is 4;7=2;10=3;. . .and we can show that lim n!1un¼3.
If the limit of a sequence exists, the sequence is calledconvergent; otherwise, it is calleddivergent. A sequence can converge to only one limit, i.e., if a limit exists, it is unique. See Problem 2.8.
A more intuitive but unrigorous way of expressing this concept of limit is to say that a sequence
u1;u2;u3;. . .has a limit l if the successive terms get ‘‘closer and closer’’ to l. This is often used to provide a ‘‘guess’’ as to the value of the limit, after which the definition is applied to see if the guess is really correct.
THEOREMS ON LIMITS OF SEQUENCES If lim
n!1an¼Aand limn!1bn¼B, then
1. lim
n!1ðanþbnÞ ¼nlim!1anþnlim!1bn¼AþB
2. lim
n!1ðanbnÞ ¼nlim!1annlim!1bn¼AB
3. lim
n!1ðanbnÞ ¼ ðnlim!1anÞðnlim!1bnÞ ¼AB
4. lim n!1
an
bn¼ lim n!1an
lim n!1bn
¼AB