PENERAPAN MODEL REGRESI LINEAR ROBUST DENGAN ESTIMASI M PADA DATA NILAI KALKULUS II MAHASISWA UNIVERSITAS WIDYA DHARMA KLATEN

Abstrak:Model persamaan regresi linear dapat dinyatakan dalam bentuk matriks sebagaiy  X



u, dengan dengan



_j 



₁,



₂,,



_p adalah parameter yang belum diketahui dari n pengamatan

y

_i



y

₁

,

y

₂

,



,

y

_n, dengan x_ij adalah koefisien yang diketahui dan u adalah variabel random_i independen dan berdistribusi identik. Dalam pengamatan seringkali ditemukan observasi yang nilainya jauh berbeda dengan observasi lainnya. Observasi ini disebut sebagai outlier yang mengakibatkan asumsi kenormalan pada regresi linear dilanggar. Regresi linear robust dengan estimasi M tidak peka terhadap suatu data yang mengandung pengamatan outlier. Dengan estimasi ini, pengamatan outlier ini tidak perlu dibuang dari observasi karena seringkali justru pengamatan outlier sangat berarti dalam observasi.

Penelitian ini bertujuan untuk menunjukkan bahwa regresi linear robust dengan estimasi M dapat mengatasi suatu data yang mengandung pengamatan outlier. Setelah itu, peneliti menerapkannya pada data nilai kalkulus II pada mahasiswa Universitas Widya Dharma Klaten. Dari data ini, peneliti mendapatkan persamaan model regresi linear robust: Y 0,177X₁0, 655X₂0, 947, dengan Y menunjukkan nilai kalkukulus II, X₁ menunjukkan nilai kalkulus I, dan X₂ menunjukkan nilai trigonometri.

Kata kunci : Model regresi linear, Pengamatan outlier, Regresi linear robust estimasi M.

ESTIMASI M PADA DATA NILAI KALKULUS II MAHASISWA

UNIVERSITAS WIDYA DHARMA KLATEN

Yuliana*

Model regresi linear merupakan suatu persamaan yang menyatakan adanya hubungan antara variabel tak bebas (dependen) dengan variabel bebas (independen) secara linear. Model persamaan regresi linear dapat dinyatakan dalam bentuk matriks sebagai

u X y 



 .

Variabel y adalah vektor respon,X  (x_ij) adalah matriks desain berordo n p (pn) full rank dan nilainya diketahui,



merupakan parameter yang belum diketahui berordo p 1 dan

u

adalah suatu vektor random sesatan atau selisih nilai yang diharapkan dengan nilai observasi dengan ordo n 1. Distribusisesatan

u

adalah

N

(

0

,



2

)

, identik dan saling independen antara respon satu dengan respon

yang lainnya. Asumsi ini menghasilkan model regresi linear normal sederhana. Dalam sejumlah data hubungan sebenarnya jarang dapat diketahui akan tetapi hubungan tersebut dapat diestimasi berdasarkan data pengamatan. Metode yang populer digunakan adalah estimasi kuadrat terkecil. Hal ini didasarkan pada kenyataan bahwa ia meminimumkan jumlah kuadrat perbedaan nilai yang diharapkan dengan nilai observasinya.

Dalam pengamatan seringkali ditemukan observasi yang nilainya jauh berbeda dengan observasi lainnya. Observasi ini disebut sebagai outlier yang mengakibatkan asumsi kenormalan pada regresi linear dilanggar. Nilai observasi ini bisa

terlalu besar bahkan bisa terlalu kecil dibandingkan dengan lainnya. Menurut Sembiring (1995: 72) kategori suatu observasi dikatakan outlier jika observasi tersebut tidak mengikuti pola umum model atau nilai sesatannya berjarak tiga kali standar deviasinya atau lebih dari rata­ratanya (yaitu nol). Observasi outlier dapat menyebabkan estimasi parameter regresi linear tidak tepat sehingga regresi yang memiliki observasi outlier harus diambil langkah tepat dalam mengatasinya. Penangganan yang mudah dilakukan adalah dengan membuang observasi outlier tersebut dari sekumpulan data, kemudian membandingkan estimasi data tersebut dengan data penuh. Tindakan ini belum tentu bijaksana dikarenakan observasi outlier seringkali justru memberikan informasi sangat berarti dalam estimasi. Oleh karena itu sangat disayangkan jika observasi outlier tersebut dibuang dari pengamatan.

Dengan melihat data mahasiswa Universitas Widya Dharma Klaten semester I jurusan Pendidikan Matematika tahun 2012/2013, sebagian besar mereka berasal dari lulusan SMA IPS dan SMK. Hanya sebagian kecil, mereka yang berasal dari SMA IPA. Padahal mata kuliah kalkulus II yang didalamnya dipelajari materi integral harus sudah dipahami sejak di SMA IPA. Adapun sebagai prasyarat dalam mengambil mata kuliah kalkulus II, yaitu kalkulus I dan trigonometri yang dipelajari di semester I. Melihat kondisi semacam ini, sangat dimungkinkan data nilai kalkulus II yang dipelajari pada semester II akan memuat suatu data outlier sehingga untuk menemukan model regresi linear perlu penanganan khusus.

Metode estimasi regresi robust adalah salah satu alternatif dalam mengatasi permasalahan regresi linear, jika diyakini data mengandung suatu outlier. Estimasi regresi robust tidak sensitif terhadap observasi outlier sehingga asumsi kenormalan pada

regresi linear masih tetap dipenuhi. Metode regresi robust menurut Huber (1981: 43) mempunyai tiga estimasi, yaitu estimasi L (kombinasi linear dari statistik order/terurut), estimasi M (estimasi dengan maksimum likelihood) dan estimasi R (estimasi yang berasal dari uji rank). Estimasi M lebih fleksibel dan dapat digunakan untuk menyelesaikan masalah estimasi multiparameter. Dalam menentukkan estimasi parameter, pada aplikasinya estimasi M lebih mudah digunakan dibandingkan dengan estimasi R maupun estimasi L.

METODE

Penelitian yang dilakukan oleh peneliti dilaksanakan di Universitas Widya Dharma Klaten yang beralamat di Jalan Ki Hajar Dewantoro, Klaten, kotak pos 57401. Dalam penelitian ini, yang dimaksudkan subjek penelitiannya, yaitu mahasiswa angkatan 2012/2013. Dari subjek penelitian, diambil data nilai kalkulus I dan nilai trigonometri sewaktu subjek kuliah berada pada semester 1, sedangkan nilai kalkulus II diambil saat subjek kuliah berada pada semester 2.

Metode penelitian yang digunakan penulis dalam penelitian ini meliputi studi pustaka dan studi kasus. Data yang digunakan pada penelitian ini merupakan data nilai ujian akhir semester II mata kuliah kalkulus II sebagai variabel dependen dan nilai ujian akhir semester I mata kuliah kalkulus I dan trigonometri sebagai variabel independen. Semua data diperoleh dari pengamatan yang sudah dilakukan oleh peneliti pada mahasiswa jurusan pendidikan matematika 2012/2013. Adapun langkah­langkah yang dilakukan oleh, yaitu (1) menunjukkkan sifat­ sifat dari estimasi M, (2) mengumpulkan data hasil pengamatan nilai ujian akhir semester mata kuliah

kalkulus I, trigonometri, dan kalkulus II, (3) melakukan estimasi parameter model regresi linear menggunakan metode kuadrat terkecil (MKT), (4) melakukan identifikasi bahwa dari data pengamatan yang telah terkumpul tersebut mengandung suatu pengamatan outlier, (5) melakukan estimasi parameter model regresi linear dengan estimasi M secari iterasi, (6) memperoleh estimasi parameter pada masing­ masing iterasinya, peneliti menggunakan metode kuadrat terboboti, (7) langkah 5 dan 6 di atas diulang secara terus menerus hingga diperoleh estimasi parameter model yang konvergen. Untuk memudahkan dalam perhitungan, perhitungan estimasi dilakukan menggunakan program komputer, yaitu SPSS Statistics 17 dan perhitungan secara manual.

Dalam penelitian ini menggunakan uji hipotesis t untuk menunjukkan bahwa secara individu variabel X₁ dan X₂ berpengaruh atau berarti terhadap variabel Y. Adapun langkah­langkah uji statistiknya seperti dalam Budiyono (2004 : 124). Selain menggunakan uji t, peneliti melakukan analisis menggunakan uji F. Dengan uji F ini, peneliti hendak menunjukkan bahwa variabel independen berpengaruh terhadap variabel dependennya seperti dalam Budiyono (2004 : 129).

HASIL PENELITIAN DAN PEMBAHASAN

Sebelum memperoleh suatu model regresi linear dengan estimasi M, pada pembahasan ini akan dibahas dahulu mengenai estimasi M, kemudian mengidentifikasi outlier dari data yang telah dikumpulkan. Selanjutnya, dari studi kasus diperoleh suatu data yang digunakan untuk mendapatkan model regresi yang tepat. Studi kasus yang digunakan adalah hubungan nilai kalkulus I dan nilai trigonometri terhadap nilai kalkulus II pada mahasiswa Universitas Widya Dharma Klaten.

Pada umumnya, metode kuadrat terkecil (MKT) digunakan untuk estimasi parameter regressi linear. Akan tetapi, estimasi parameter menggunakan metode kuadrat terkecil menjadi kurang baik apabila distribusi residualnya tidak normal dan mengandung outlier. Salah satu solusi untuk mengatasi permasalahan ini, yaitu menggunakan regresi robust. Regresi robust ini tidak sensitif terhadap data yang menganding pengamatan outlier. Metode regresi robust yang paling sering digunakan adalah estimasi M, yang diperkenalkan oleh Huber pada tahun 1973 (Chen, 2002). Secara umum, persamaan model regresi llinear yaitu

0 1 1 2 2 ... X

       

i p p i i

Y





X



X



X







,

untuk data ke­i dan n pengamatan. Taksiran model regresi linear berganda, yaitu

0 1 1 2 2 ... X b

       

i p p i i

Y b b X b X b X





.

Menurut Fox (2002), estimasi M meminimalisasi fungsi objektif dengan persa maan

1

( )

(

Xb).





_



n i i i

e

y





_{Kemudian, dari persamaan}

ini dicari turunan pertama parsial terhadap para meternya



_jdengan j = 0,1,2,…,k dan disamadengankan nol. Hal ini menghasilkan p = k + 1 dengan persamaan (1) : T 1

(

Xb) X

0









n i i

Y



_,

dengandengan







'

dan



merupakan fungsi influence yang digunakan untuk memproleh fungsi bobot. Lalu, residualnya distandarisasi sehingga persamaan (1) menjadi per samaan (2)

: T 1 ( Xb) X 0         



n i i Y





. Menurut Fox (2002),

nilai­nilai yang harus ditentukan dahulu untuk estimasi parameternya,yaitu

_

_

_MAR

_{/ 0, 6745}

, dengan MAR merupakan Median Absolute Residual, yang dapat dicari menggunakan rumus

1 1  

_

 n i i i MAR Y Y n . Kemudian menggunakan

fungsi pembobot w_i 



( ) /e_i* e_i*, dengan e_i* merupakan nilai residual yang telah distandardisasi, sehingga *

/

i i

e e



.

Dengan memasukkan nilai­nilai ini, maka persamaan (2) dapat ditulis menjadi persamaan (3):

T 1

(

Xb)

X

0





















n i i i

Y

w



atau T T 1 1

X

X

Xb

0

 









n n i i i i i

w Y

w

_.

Persamaan (3) agar lebih mudah dalam penyelesainnya dapat ditulis dalam bentuk matriks menjadi persamaan (4) : T T

X WXb



X WY

, dengan

W merupakan matriks diagonal berukuran , dengan w_i sebagai elemen diagonalnya. Persamaan (4) dikalikan dengan T 1

(X WX)

 pada kedua ruasnya,

sehingga menjadi persamaan (5) :

T 1 T

b



(X WX) X WY

 . Bentuk ini merupakan

penyelesaian estimasi parameter regresi linear kuadrat terkecil yang terboboti. Dengan persamaan ini, parameter regresi robust ini dapat diestimasi dengan tepat. Agar lebih efisien, peneliti menggunakan program SPSS Statistics 17 untuk mendapatkan hasil seperti pada persamaan (5) di atas.

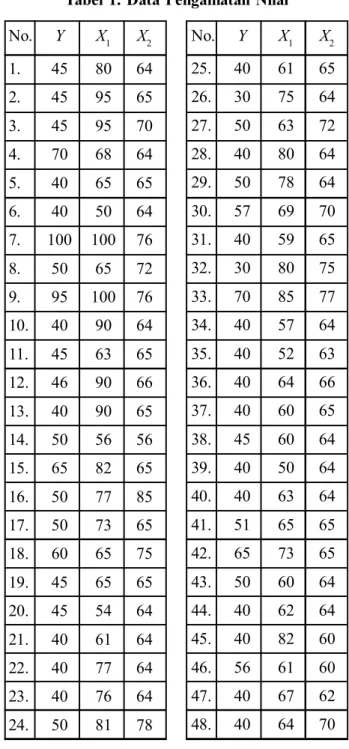
Peneliti ingin mengetahui hubungan nilai kalkulus I (X₁) dan nilai trigonometri (X₂), terhadap nilai kalkulus II (Y) dengan melihat model regresi linearnya. Dari penelitian yang telah dilakukan oleh peneliti diperoleh data sebagai berikut.

Tabel 1. Data Pengamatan Nilai

No. Y X₁ X₂ 1. 45 80 64 2. 45 95 65 3. 45 95 70 4. 70 68 64 5. 40 65 65 6. 40 50 64 7. 100 100 76 8. 50 65 72 9. 95 100 76 10. 40 90 64 11. 45 63 65 12. 46 90 66 13. 40 90 65 14. 50 56 56 15. 65 82 65 16. 50 77 85 17. 50 73 65 18. 60 65 75 19. 45 65 65 20. 45 54 64 21. 40 61 64 22. 40 77 64 23. 40 76 64 24. 50 81 78 No. Y X₁ X₂ 25. 40 61 65 26. 30 75 64 27. 50 63 72 28. 40 80 64 29. 50 78 64 30. 57 69 70 31. 40 59 65 32. 30 80 75 33. 70 85 77 34. 40 57 64 35. 40 52 63 36. 40 64 66 37. 40 60 65 38. 45 60 64 39. 40 50 64 40. 40 63 64 41. 51 65 65 42. 65 73 65 43. 50 60 64 44. 40 62 64 45. 40 82 60 46. 56 61 60 47. 40 67 62 48. 40 64 70

Dari data yang telah terkumpulkan seperti pada Tabel 1 di atas diestimasi menggunakan MKT untuk mendapatkan estimasi parameter model regresi linear berganda. Rumus yang digunakan adalah

T 1 T

(X X) X Y







. Agar lebih efisien, peneliti menerapkan program SPSS Statistics 17. Hasil estimasi parameter yang diperoleh, yaitu b₀ = ­25,029, b₁ = 0,304, dan b₂ = 0,774 sehingga taksiran model regresi linear, yaitu

Y

_i



0,304

X

₁



0, 774

X

₂



25, 029

.

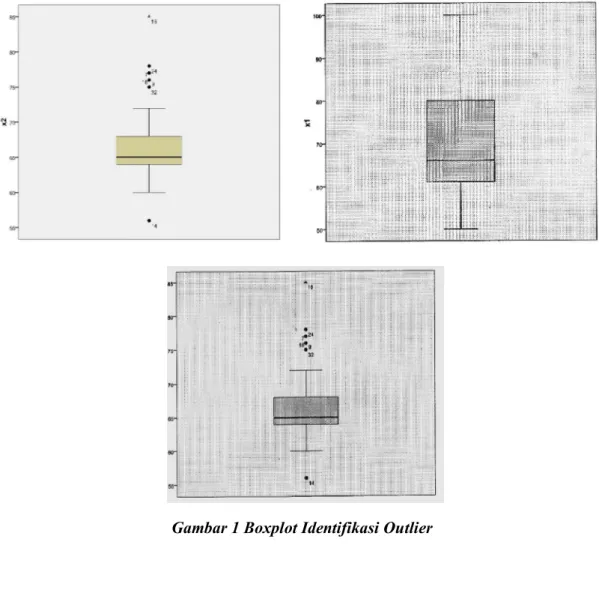
Dalam penelitian ini, outlier dari suatu pengamatan dapat diidentifikasi dengan metode grafis, dengan melihat boxplot, dan nilai DfFITS. Identifikasi outlier melalui metode grafis dapat menggunakan boxplot. Hasil yang diperoleh menggunakan SPSS Statistics 17 dapat dilihat melalui gambar sebagai berikut.

Suatu data dikatakan outlier apabila data tersebut bernilai kurang dari 1,5



IQR terhadap kuartil 1, atau bernilai lebih dari 1,5



IQR terhadap kuartil 3. Oleh karena itu, diperlukan perhitungan nilai kuartil 1, kuartil 3, dan IQR agar dapat mengidentifikasi outlier menggunakan boxplot. Adapun perhitungan IQR terlihat pada Tabel 2 berikut.

Tabel 2. Perhitungan IQR

Variabel Nilai Q₁ Nilai Q₃ Nilai IQR

Y 40 50 10 X₁ 61 80 19 X₂ 64 67 3 1 ­0.18091 0.18091 17 0.06309 0.06309 33 1.08841 1.08841 2 ­1.21537 1.21537 18 0.80986 0.80986 34 ­0.08686 0.08686 3 ­1.30987 1.30987 19 ­0.00153 0.00153 35 0.03089 0.03089 4 0.65757 0.65757 20 0.24119 0.24119 36 ­0.15364 0.15364 5 ­0.13275 0.13275 21 ­0.10755 0.10755 37 ­0.13058 0.13058 6 0.02256 0.02256 22 ­0.29845 0.29845 38 0.08395 0.08395 7 5.95372 5.95372 23 ­0.26806 0.26806 39 0.02256 0.02256 8 ­0.03060 0.03060 24 ­1.31000 1.31000 40 ­0.11420 0.11420 9 5.12176 5.12176 25 ­0.13117 0.13117 41 0.15593 0.15593 10 ­1.21276 1.21276 26 ­0.57121 0.57121 42 0.44034 0.44034 11 0.01626 0.01626 27 0.00946 0.00946 43 0.27162 0.27162 12 ­0.61533 0.61533 28 ­0.41609 0.41609 44 ­0.11095 0.11095 13 ­1.15562 1.15562 29 0.07123 0.07123 45 ­0.67754 0.67754 14 1.74256 1.74256 30 0.23603 0.23603 46 0.92605 0.92605 15 0.70308 0.70308 31 ­0.12937 0.12937 47 ­0.12620 0.12620 16 ­5.74808 5.74808 32 ­2.13862 2.13862 48 ­0.40180 0.40180

Berdasarkan data pada Tabel 2, diketahui bahwa tidak terdapat data yang nilainya kurang dari 1,5 kali IQR terhadap Q₁, atau nilainya kurang dari 1,5 kali IQR terhadap Q₁, namun terdapat data yang nilainya lebih dari 1,5 kali IQR terhadap Q₃. Oleh karena itu, dapat disimpulkan bahwa titik yang terdapat di luar kotak boxplot merupakan suatu pengamatan outlier. Selanjutnya data keberapa saja yang merupakan outlier dapat diketahui menggunakan metode DfFITS.

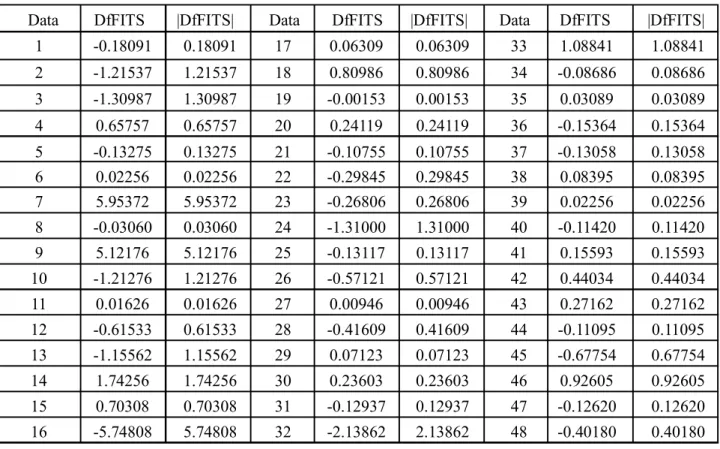
Selain menggunakan metode grafis, peneliti melakukan identifikasi outlier dengan metode DfFITS. Data yang merupakan pengamatan outlier, yaitu data yang nilai mutlak DfFITS­nya lebih besar dari

2

p n 

/

2 2 / 48



0, 408

. Adapun, nilai DfFITS dari data pada Tabel 1 terlihat pada Tabel 3 berikut.

Tabel 3. Nilai DfFITS

No. X₁ X₂ Y Y_i,0



_i,0 1. 80 64 45 48.827 ­3.827 2. 95 65 45 54.161 ­9.161 3. 95 70 45 58.031 ­13.031 4. 68 64 70 45.179 24.821 5. 65 65 40 45.041 ­5.041 6. 50 64 40 39.707 0.293 7. 100 76 100 64.195 35.805 8. 65 72 50 50.459 ­0.459 9. 100 76 95 64.195 30.805 10. 90 64 40 51.867 ­11.867 11. 63 65 45 44.433 0.567 12. 90 66 46 53.415 ­7.415 13. 90 65 40 52.641 ­12.641 14. 56 56 50 35.339 14.661 15. 82 65 65 50.209 14.791 16. 77 85 50 64.169 ­14.169 17. 73 65 50 47.473 2.527 18. 65 75 60 52.781 7.219 19. 65 65 45 45.041 ­0.041 20. 54 64 45 40.923 4.077 21. 61 64 40 43.051 ­3.051 22. 77 64 40 47.915 ­7.915 23. 76 64 40 47.611 ­7.611 24. 81 78 50 59.967 ­9.967

Berdasarkan nilai DfFITS pada Tabel 3 di atas, terlihat bahwa terdapat data yang nilainya lebih besar dari 0,408 (data yang dicetak tebal). Data tersebut menunjukkan pengamatan outlier. Adapun yang termasuk ke dalam pengamatan outlier adalah pada data ke­2, ke­3, ke­4, ke­7, ke­15, data ke­9, data ke­ 10, data ke­12, data ke­13, data ke­14, data ke­15, data ke­16, data ke­18, data ke­24, data ke­26, data ke­28, data ke­32, data ke­33, data ke­42, data ke­45, dan data ke­46.

Selanjutnya, untuk mengatasi pengamatan outlier tersebut sehingga diperoleh regresi linear yang tepat digunakan suatu regresi robust estimasi M.

Peneliti melakukan estimasi pa rameter model regresi menggunakan metode kuadrat terkecil, sehingga didapatkan yˆ_i,0, dan menghitung

,0   ˆ,0

i yi yi



, yang diperlakukan sebagai nilai awal. Berdasarkan hasil estimasi regresi linear berganda dengan MKT, diperoleh b₀ = ­25,029, b₁ = 0,304, dan b₂ = 0,774. Untuk efisiensi perhitungan, peneliti menggunakan program SPSS Statitistics 17. Dari data ini dicari, kemudian dicari nilai estimasi model dan nilai residual, yang hasil selengkapnya dapat dilihat pada data Tabel 4 berikut.

Tabel 4.

Nilai Estimasi Model dan Nilai Residual

No. X₁ X₂ Y Y_i,0



_i,0 25. 61 65 40 43.825 ­3.825 26. 75 64 30 47.307 ­17.307 27. 63 72 50 49.851 0.149 28. 80 64 40 48.827 ­8.827 29. 78 64 50 48.219 1.781 30. 69 70 57 50.127 6.873 31. 59 65 40 43.217 ­3.217 32. 80 75 30 57.341 ­27.341 33. 85 77 70 60.409 9.591 34. 57 64 40 41.835 ­1.835 35. 52 63 40 39.541 0.459 36. 64 66 40 45.511 ­5.511 37. 60 65 40 43.521 ­3.521 38. 60 64 45 42.747 2.253 39. 50 64 40 39.707 0.293 40. 63 64 40 43.659 ­3.659 41. 65 65 51 45.041 5.959 42. 73 65 65 47.473 17.527 43. 60 64 50 42.747 7.253 44. 62 64 40 43.355 ­3.355 45. 82 60 40 46.339 ­6.339 46. 61 60 56 39.955 16.045 47. 67 62 40 43.327 ­3.327 48. 64 70 40 48.607 ­8.607

Langkah berikutnya menentukan nilai



ˆ

₀ dan pembobot awal * ,0 ,0 * ,0

(

)



i i i

w

 



dengan ,0 * ,0 0 ˆ  i i







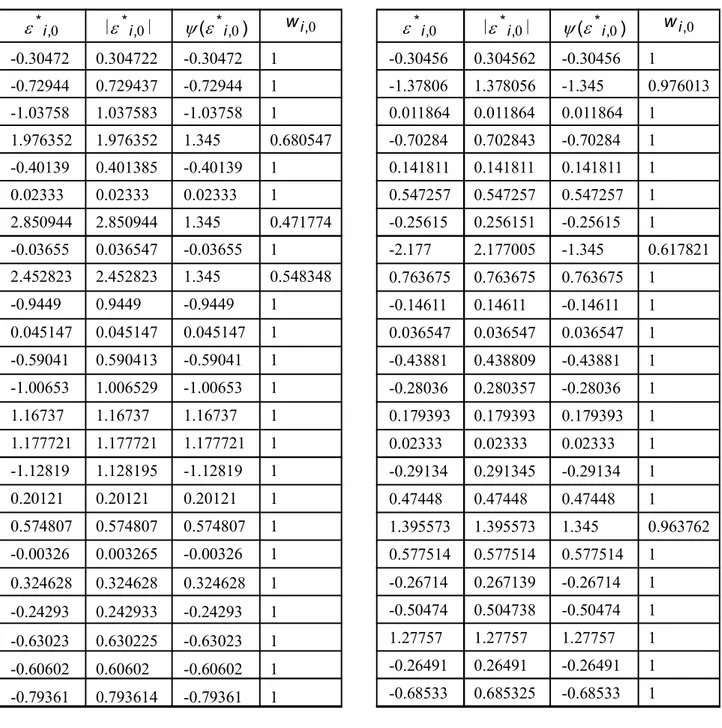
. Nilai

dicari dengan . Metode yang digunakan untuk memperoleh fungsi pembobot, yaitu metode Huber, dengan nilai koefisien c = 1,345. Apabila menggunakan nilai seperti pada Tabel 4 diperoleh . Hasil perhitungan pembobot dapat dilihat pada Tabel 5 berikut.

Tabel 5. Perhitungan Pembobot Awal

­0.30472 0.304722 ­0.30472 1 ­0.72944 0.729437 ­0.72944 1 ­1.03758 1.037583 ­1.03758 1 1.976352 1.976352 1.345 0.680547 ­0.40139 0.401385 ­0.40139 1 0.02333 0.02333 0.02333 1 2.850944 2.850944 1.345 0.471774 ­0.03655 0.036547 ­0.03655 1 2.452823 2.452823 1.345 0.548348 ­0.9449 0.9449 ­0.9449 1 0.045147 0.045147 0.045147 1 ­0.59041 0.590413 ­0.59041 1 ­1.00653 1.006529 ­1.00653 1 1.16737 1.16737 1.16737 1 1.177721 1.177721 1.177721 1 ­1.12819 1.128195 ­1.12819 1 0.20121 0.20121 0.20121 1 0.574807 0.574807 0.574807 1 ­0.00326 0.003265 ­0.00326 1 0.324628 0.324628 0.324628 1 ­0.24293 0.242933 ­0.24293 1 ­0.63023 0.630225 ­0.63023 1 ­0.60602 0.60602 ­0.60602 1 ­0.79361 0.793614 ­0.79361 1 0 , * i



|

_

*_i,0|

_

₍

_

*_i,0) wi,0 ­0.30456 0.304562 ­0.30456 1 ­1.37806 1.378056 ­1.345 0.976013 0.011864 0.011864 0.011864 1 ­0.70284 0.702843 ­0.70284 1 0.141811 0.141811 0.141811 1 0.547257 0.547257 0.547257 1 ­0.25615 0.256151 ­0.25615 1 ­2.177 2.177005 ­1.345 0.617821 0.763675 0.763675 0.763675 1 ­0.14611 0.14611 ­0.14611 1 0.036547 0.036547 0.036547 1 ­0.43881 0.438809 ­0.43881 1 ­0.28036 0.280357 ­0.28036 1 0.179393 0.179393 0.179393 1 0.02333 0.02333 0.02333 1 ­0.29134 0.291345 ­0.29134 1 0.47448 0.47448 0.47448 1 1.395573 1.395573 1.345 0.963762 0.577514 0.577514 0.577514 1 ­0.26714 0.267139 ­0.26714 1 ­0.50474 0.504738 ­0.50474 1 1.27757 1.27757 1.27757 1 ­0.26491 0.26491 ­0.26491 1 ­0.68533 0.685325 ­0.68533 1 0 , * i



|

_

*_i,0|

_

₍

_

*_i,0) wi,0

Dari data di atas disusun matriks pembobot berupa matriks diagonal dengan elemen diagonalnya adalah w_i,0. Kemudian, peneliti menghitung penaksir koefisien regresi menggunakan rumus tersebut sehingga diperoleh nilai estimasi parameter yaitu :

1

­12,943

0,199

0,694











 











robust ke

b

. Agar lebih efisien dalam

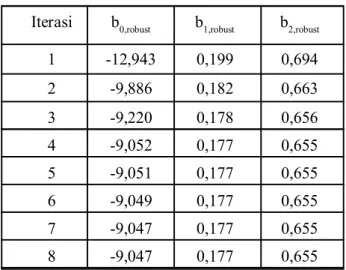
perhitungan, peneliti menggunakan program SPSS Statistics 17. Estimasi penaksir koefisien regresi dengan iterasi dilakukan secara terus menerus, hingga diperoleh penaksir yang konvergen. Hasilnya seperti pada Tabel 6 berikut.

Iterasi b_0,robust b_1,robust b_2,robust 1 ­12,943 0,199 0,694 2 ­9,886 0,182 0,663 3 ­9,220 0,178 0,656 4 ­9,052 0,177 0,655 5 ­9,051 0,177 0,655 6 ­9,049 0,177 0,655 7 ­9,047 0,177 0,655 8 ­9,047 0,177 0,655

Tabel 6. Hasil Iterasi Estimasi Parameter

Berdasarkan data pada Tabel 6, terlihat bahwa selisih estimasi parameter pada iterasi ke­8 dan ke­7 sudah sama dengan nol sehingga peneliti tidak perlu melakukan perhitungan pada iterasi berikutnya. Hal ini menunjukkan bahwa estimasi parameter telah konvergen, sehingga diperoleh model regresi robust dengan estimasi M, yaitu:

1 2

0,177 0, 655 0, 947

  

Y X X .

Agar persamaan regresi robust dengan estimasi M yang diperoleh dapat dipakai untuk melakukan prediksi secara cermat, koefisien regresi pada model regresi linear robust dengan estimasi M perlu diuji signifikansinya terlebih dahulu. Dalam penelitian ini, koefisien regresi linear pada model regresi robust perlu dilakukan uji secara individu dan uji serentak. Pada uji individu ini, peneliti menguji variabel X₁ dan X₂ secara terpisah. Hipotesis yang digunakan, yaitu: H₀ : Koefisien model regresi robust tidak signifikan dan H₁ : Koefisien model regresi robust signifikan. Taraf signifikansi yang digunakan, yaitu ± = 0,05. Statistik uji yang digunakan, yaitu nilai t

hitung untuk mengambil suatu kesimpulan yang dapat

dicari menggunakan rumus

i i b b t s  _{. Nilai t} hitung yang

diperoleh terlihat pada Tabel 7 berikut.

Tabel 7.

Nilai t _hitung Model Regresi Linear Robust

Variabel Nilai t_hitung

X₁ 2,023

X₂ 2,142

Dengan mengambil taraf signifikasnsi ± = 0,05 dan n = 48 maka diperoleh nilai t_tabel = 2,0106. Dari data pada Tabel 7 di atas diketahui bahwa nilai t_hitung untuk variabel X₁ = 2,023 sedangkan nilai t_hitung untuk variabel X₂ = 2,142. Nilai t_hitung pada model regresi robust ini, keduanya masing­masing mempunyai yang nilai lebih besar dari nilai t­­­­_{t ab el}, sehingga keputusanya menolak H₀. Hal ini berarti bahwa koefisien model regresi linear robust X₁ dan X₂, keduanya signifikan.

Pada uji serentak ini, peneliti menguji variabel X₁ dan X₂ secara bersamaan. Hipotesis yang digunakan pada uji serentak yaitu: H₀ : Variabel bebas pada model regresi linear robust tidak berpengaruh terhadap variabel tak bebasnya, dan H₁ : Variabel bebas pada model regresi linear robust berpengaruh terhadap variabel tak bebas. Taraf signifikansi yang digunakan, yaitu ± = 0,05. Uji statistik yang digunakan merupakan Uji F, dengan mencari nilai F_obs sehingga dapat digunakan untuk mengambil suatu kesimpulan. Setelah dihitung, nilai F_obs untuk model regresi linear robust diperoleh sebesar 4,757. Berdasarkan tabel statistik dengan mengambil ± = 0,05, dk RKR = 2, dan dk RKG = 45 diperoleh nilai F_tabel = 3,204. Karena nilai F_obs pada model regresi robust lebih besar daripada nilai F_tabel maka peneliti menolak H₀. Keputusan ini menunjukkan bahwa variabel bebas pada model regresi linear robust berpengaruh terhadap variabel tak bebasnya.

Dari kedua uji hipotesis di atas menunjukkan bahwa koefisien parameter model regresi robust signifikan dan variabel independennya berpengaruh terhadap variabel dependennya. Hal ini berarti bahwa model regresi robust dengan estimasi M pada nilai kalkulus II sebagai variabel dependen dan nilai kalkulus I dan nilai trigonometri sudah tepat.

SIMPULAN DAN SARAN Simpulan

Berdasarkan hasil penelitian dan pembahasan yang telah diuraikan di atas dapat disimpulkan bahwa : (1) melalui regresi linear robust dengan estimasi M diperoleh suatu estimasi parameter regresi yang konvergen tanpa harus membuang pengamatan outliernya. Hal ini berarti regresi linear robust dengan Estimasi M dapat digunakan untuk mengatasi suatu data yang mengandung pengamatan outlier. (2) Dari model regresi robust yang telah didapat tersebut diperoleh suatu model regresi robust dengan persamaan : . Dari model regresi linear robust ini dapat digunakan untuk memprediksikan suatu nilai kalkulus II secara tepat.

Saran

Pada penelitian ini peneliti hanya menggunakan estimasi M untuk mengatasi outlier, sehingga untuk penelitian selanjutnya disarankan dapat menggunakan metode estimasi robust yang lain, seperti estimasi S, LTS, LMS, dan MM. Disamping itu, peneliti hanya menggunakan data sekunder yang sudah ada. Dari data itu, peneliti tidak melakukan analisis butir soal dan tidak memeriksa validitas maupun realibilitas butir soal. Oleh karena itu, peneliti menyarankan kepada penelitian berikutnya untuk melakukan analisis validitas dan realibilitas yang menjamin bahwa soal yang diujikan benar­benar valid.

DAFTAR PUSTAKA

Bain, L.J. and M. Engelhardt. 1992. Introduction to Prabability and Mathematical Statistics. Second Edition. Duxbury Press, California.

Bartle, R. G. 1992. Introduction to Real Analysis. John Willey and sons Inc., Singapore.

Budiyono. 2004. Statistik untuk Penelitian. Surakarta: UNS Press.

Chen, Colin.2002. Robust Regression and Outlier Detection with the RobustREG Procedure. SUGI Paper : 265­267, SAS Institute, Cary, NC.

Dudewicz, E. J. and S. Mishra.1988. Modern Mathematical Statistics. John Wiley and Sons Inc., New York.

Huber, P. J. 1980. Robust Statistics. John Wiley and Sons Inc., New York.

Sembiring, R. K. 1995. Analisis Regresi. ITB, Bandung.SPSS Statistics 17.