BAB 4
HASIL DAN PEMBAHASAN
4.1
Solusi Schwarzchild
4.1.1
Metrik Schwarzchild
Salah satu solusi persamaan medan Einstein diberikan oleh Karl Schwarzchild
bagi medan statik dan bersimetri bola. Kondisi statik berarti gµν bergantung
x0
, dands2
invarian terhadap perubahan koordinatx0
→ −x0
, maka tidak ada
suku yang bersangkutan dengan dxjdx0
pada bentuk ds2
. Ini berarti bahwa
gj0 =g0j = 0.
Didekat obyek masif M ruang-waktu yang melengkung, garis duniadsdari partikel dan berkas cahaya adalah geodesik, untuk mendapatkannya perlu
dike-tahui tensor metrikgµν di dalam koordinat yang dipilih. dalam koordinat bola
x0
=t, x1
=r, x2
=θ, x3
=φ
dengan M sebagai titik pusatnya. jika M nol maka rumus jarak
ds2
=−c2
dt2 +dr2
+ (r2
dθ2 +r2
sin2
θdφ2
) (4.1)
Jika massa M dinyalakan maka akan terjadi dua hal, ruang posisi akan me-lengkung sehingga lingkaran r tidak secara tepat berada pada jarak r dari pusat lingkaran, dan jam pada setiap permukaan r tidak teramati dari per-mukaan r yang lain. Efek ini dapat dituliskan dalam elemen jarak
ds2
=−e2νc2
dt2
+e2λdr2 + (r2
dθ2 +r2
sin2
θdφ2
dengan ν=ν(r), λ=λ(r).
Persamaan 26 memberi elemen tensor metrik
g00=−e
atau dapat ditulis
gµν =
Selanjutnya untuk semua komponen simbol Cristoffelnya akan berlaku
Γρµν = 1 2g
ρτ(∂
µgντ +∂νgρµ−∂τgµν) (4.6)
dari simbol Cristoffel tersebut akan didapatkan 64 komponen, dan dari
komponen-komponen tersebut yang tidak nol adalah
Γ1
Lalu untuk tensor Riccinya
Rµν = ∂τΓτµν −∂µΓττ ν + ΓτµνΓρρτ −ΓτµρΓρτ µ.
dari komponen-komponen simbol Cristoffel, maka komponen-komponen tensor
Ricci yang tidak nol adalah
R00 =
Pada area yang sangat jauh dari sumber medan gravitasi atau di
per.(4.7),(4.8),(4.8),(4.10) memberikan
−ν′′+ν′λ′−ν′2−2ν
r = 0 (4.11)
ν′′ +ν′2
−λ′
ν′
− 2λ
′
r = 0 (4.12)
(1−λ′
r+ν′
r)e−2λ
−1 = 0 (4.13)
Selisihkan pers.(4.11) dengan pers. (4.12) memberikan
λ′+ν′ = 0
Sehingga
λ′+ν′ = konstan (4.14)
Dengan syarat batas r → ∞, maka ν, µ → 0. Didalam limit ini elemen garis akan menjadi Minkowskian. Akan didapat
λ′+ν′ = 0 →ν=−λ (4.15)
Kondisi ini membuat pers. (4.13) menjadi
(1 + 2rν′)e2ν = d
dr[re
2ν] = 1
dengan mengintegralkannya
Z
d[re2ν] =
Z dr re2ν = r
dengan −2m adalah konstanta integrasi.
Dengan demikian, elemen garis (26) menjadi
ds2
Pers.(4.19) dikenal sebagai solusi Schwarzschild atau elemen garis
Schwarzschild. Elemen garis atau metrik ini menggambarkan medan gravitasi
di luar sumber yang bersimetri bola serta tidak bergantung pada distribusi
ma-teri di dalam sumber. Metrik tersebut akan bernilai takhingga saat r = 2m, jarak r= 2m ini disebut sebagai jari-jari Schwarzschild.
Untuk menginterpretasi metrik tersebut, kita perhatikan kasus medan
lemah
g00 = η00+h00
= −1 + 2
c2φ (4.20)
dengan φ adalah potensial Newton. Untuk sumber terpusat dengan massa
total M, maka dari gravitasi newton didapat
φ = −GM
sehingga
g00 = −
1−2GM
c2r
(4.22)
Dari pers.(4.95) dan pers. (4.96) memberikan
m= GM
c2 (4.23)
Karena itu konstanta m merupakan massa gravitasional sumber.(Turunan
dalam subbab ini dapat dilihat di lampiran 5)
4.1.2
Implikasi Solusi Schwarzchild
Sebuah partikel jatuh secara radial menuju jari-jari Schwarzchild, partikel ini
mulai jatuh saat r = R dengan drdt = 0 seperti di gambar(4.1). Pergerakan partikel dideskripsikan oleh persamaan geodesik
d2
xν
ds2 + Γ ν αβ
dxα
ds dxβ
ds = 0 (4.24)
Dari hasil simbol Cristoffel pada solusi Schwarzchild, dan danganx0
=−ct,
˙
t= dτdt, persamaan geodesik dengan ν = 0 adalah
¨
t+ 2m
r(r−2m)t˙r˙ = 0
atau
d ds
1− 2m
r
˙
t
= 0, (4.25)
Gambar 4.1: Partikel Jatuh Menuju Lubang Hitam
dengan K adalah konstanta integrasi.
Selanjutnya, metrik Schwarzchild untuk benda jatuh secara radial akan
menjadi
dengands2
sehingga untuk pers. (4.26) didapat
dengan memasukkan pers.(4.30) ke pers.(4.28) dan menata ulangnya akan
di-dapat
tanda minus dipilih karena benda jatuh ke pusat medan gravitasi, maka r
berkurang seiring t bertambah. Akhirnya dengan menata ulang persamaan tersebut kemudian mengintegralkannya akan didapat
t = −1
Ini adalah waktu yang dibutuhkan oleh paartikel yang melintas dari r = R
hingga sembarang r yang diukur dalam koordinat Schwarzchild, yaitu waktu yang diukur oleh pengamat yang berada sangat jauh dari medan gravitasi.
ini diambil ρ= 2m+ε, dengan ε sangat kecil, maka
ct = −
R−2m
2m
1/2Z r−2m
R−2m
(2m+ε)3/2
ε(R−2m)1/2dε = −2mln
r−2m R−2m
,
atau
r−2m = (R−2m)e−ct/2m. (4.33)
Maka t → ∞ saat r → 2m, atau menurut pengamat yang sangat jauh dari jari-jari Schwarzschild partikel yang jatuh ke jari-jari Schwarzschild akan
se-makin melambat saat menuju jari-jari Schwarzschild dan akhirnya akan
ter-lihat berhenti sebelum masuk dalam jari-jari Schwarzschild walaupun
sebe-narnya partikel tersebut masuk kedalamnya, cahaya yang tersedot oleh lubang
hitam akan mengalami pergeseran merah karena melawat tarikan gaya
grav-itasi. Karena itulah benda yang mempunyai sifat seperti ini disebut lubang
hitam. Jari-jari Schwarzschild disebut pula sebagi horison peristiwa, karena
semua pengamatan yang terjadi didalamnya tersembunyi dari pengamatan
luar. Area r = 2m disebut horison peristiwa karena merupakan batas peris-tiwa yang dapat diamati serta dapat disebut pula permukaan infinite red-shift
karena dipermukaan ini cahaya akan mengalami pergeseran merah secara terus
menerus.
4.2
Solusi Kerr
Secara astrofisika benda langit haruslah berotasi, sedangkan metrik
Schwarzschild menggambarkan medan gravitasi diluar sumber yang simetri
bola, tidak bergantung pada distribusi materi didalam sumber serta tidak
haruslah berotasi juga, oleh karena itu perlu dibentuk persamaan metrik yang
menyempurnakan lubang hitam Schwarzschild tersebut. Pada tahun 1963 Kerr
menemukan bentuk metrik ruang waktu untuk lubang hitam yang berotasi
se-bagai penyempurnaan metrik Schwarzschild.
4.2.1
Bentuk Edington dari Metrik Schwarzchild
Metrik Scharzschild akan menjadi singular saatr= 2m. Untuk menghilangkan kesingularan ini Edington pada tahun 1924 menggunakan transformasi
koor-dinat dengan memakai bentuk koorkoor-dinat waktu baru
c¯t = ct+ 2mln
dengan memasukkan koordinat baru tersebut kedalam metrik Schwarzschild
akan didapat
metrik Schwarzschild dengan bentuk Edington tersebut bila diubah ke
koordi-nat Cartesian menjadi
lalu bentuk metrik dari koordinat kartesian adalah
gµν =ηµν+ℓµℓν, ℓµ= ( 2m
r )
1/2 (1,x
r) (4.37)
dengan ηµν adalah matrik Minkowski dengan diagonal (-1,1,1,1) dan
ℓµℓνηµν = 0.
4.2.2
Metrik Kerr
Dari bentuk metrik gµν =ηµν+ℓµℓν dan ℓµℓνηµν = 0, selanjutnya invers dari
ℓµ yaitu ℓµ dituliskan sebagai
ℓµ =ηµνℓ
ν (4.38)
maka akan didapt invers dari gµν
gµν =ηµν −ℓµℓν (4.39)
yang merupakan tensor metrik kontravarian. Dari persamaan tersebut akan
bisa didapatkan
ℓµ = gµνℓ
ν (4.40)
yang menunjukkan bahwa ℓµ adalah vektor-empat kontravarian yang
berhubungan denganℓν. Selama vektorℓµ adalahnull, ℓµ mempunyai hubun-gan yang penting yaitu:
Determinan dari g akan bernilai −1, maka
Γννµ =
∂ ∂xµln
√ −g
= ∂
∂xµln
√
1
= 0 (4.42)
maka tensor Riccinya hanya akan bernilai
Rµν = Γσµν,σ−ΓσντΓτσµ. (4.43)
Setiap persamaan harus sesuai jika kita membentuk ulang ℓµ dan dapat kita tuliskan
gµν =ηµν+αℓµℓν, gµν =ηµν −αℓµℓν, (4.44)
setiap persamaan harus sesuai untuk sembarang konstanta α, sehingga
Γµνσ =
1
2α[(ℓµℓν),σ+ (ℓµℓσ),ν−(ℓνℓσ),µ] Γµνσ = 1
2α(η µτ
−αℓµℓν)[(ℓτℓν),σ+ (ℓτℓσ),ν−(ℓνℓσ),τ]
= 1
2α[(ℓ µℓ
ν),σ+ (ℓµℓσ),ν−ηµτ(ℓνℓσ),τ] +1
2α 2
sehingga untuk tensor Riccinya
gµν adalah polinomial dalam α maka gµν berorde satu sedangkan Rµν berorde empat. Karena α adalah konstanta sembarang maka gµν harus men-jadi solusi dari setiap nilai α. Pada ruang-waktu kosong atau Rµν = 0, karena
Rµν sebagai polinomial dari α maka Rµν harus lenyap secara terpisah. Dari
Rµν akan kita dapat 10 persamaan yang harus diselesaikan.Dari pers. (4.46) terlihat bahwa untuk suku ke-4 sudah lenyap. Jika ℓµ 6= 0, maka untuk suku ketiga akan mengimplikasikan
a2 = 0,
dengan
akan didapatkan juga a· l = 0,maka dapat dituliskan untuk sebuah fungsi skalar A
aµ = Aℓµ (4.48)
lalu untuk aµ
aµ = gµνaν = ηµνℓβℓν,β
= ℓβℓµ,β. (4.49)
Bila didefinisikan B =ℓµ
,µ, maka suku pertama
ηστ(ℓµℓν),στ = (ℓσℓµ),σν + (ℓσℓν),σµ
= (ℓσ,σℓµ+ℓσℓµ,σ),ν+ (ℓσ,σℓν+ℓσℓν,σ),µ = (Bℓµ+Aℓµ),ν + (Bℓν+Aℓν),µ
(ℓµℓν) = [(A+B)ℓµ],ν + [(A+B)ℓν],µ (4.50)
dengan
≡ηµν ∂
2
∂xµ∂xν (Persamaan D’Alembert) (4.51)
kemudian dengan mengkontraksikan persamaan (61) dengan ηµν dan
mem-baginya dengan 2
ηµν(ℓµℓν) = ηµν{(Bℓµ+Aℓµ),ν+ (Bℓν +Aℓν),µ} (ℓνℓν) = [(A+B)ℓν],ν + [(A+B)ℓµ],µ
lalu untuk bagian suku keduanya akan bernilai nol jika pada suku pertama
dan ketiga berlaku
(ℓσℓτ)
,σ(ℓµℓν),τ = (ℓσ,σℓτ +ℓσℓτ,σ)(ℓµ,τℓν +ℓµℓν,τ) = (Bℓτ +Aℓτ)(ℓµ,τℓν +ℓµℓν,τ)
= (A+B)2Aℓµℓν (4.53)
ℓσℓτ(ℓµℓν),στ = ℓσℓτ(ℓµℓν,στ +ℓνℓµ,στ +ℓµ,σℓν,τ +ℓµ,τℓν,σ) = ℓσ[A(ℓµℓν)],σ−Aℓτ(ℓµℓν),τ
+ℓσ[A(ℓνℓµ)],σ−Aℓτ(ℓνℓµ),τ + 2A2(ℓµℓν) = 2(ℓσA,σ+A
2
)ℓµℓν (4.54)
(ℓσℓµ),τ(ℓτℓν),σ = (ℓµℓσ,τ +ℓσℓµ,τ)(ℓνℓτ,σ+ℓτℓν,σ) = ℓµℓσ,τℓνℓ,στ +ℓµℓσ,τℓτℓν,σ
+ℓσℓµ,τℓνℓ,στ +ℓσℓµ,τℓτℓν,σ
= ℓµℓν[(Aℓσ),σ−B,τℓτ + 3A2] (4.55)
kembali mengambil persamaan (61)
(ℓµℓν) = [(A+B)ℓµ],ν+ [(A+B)ℓν],µ ℓµℓν +ℓνℓµ+ 2ηστℓµ,σℓν,τ = ℓµ(A+B),ν+ℓν(A+B),µ
+(A+B)(ℓµ,ν +ℓν,µ)
dengan ℓν akan didapat
dengan menghapus faktor α2
/2 dari suku kedua akan didapat
= 2(Aℓσ),σ−(Aℓσ),σ+ (Bℓσ),σ
0 = [(A+B)ℓσ],σ (4.59)
seperti halnya diawal bahwa setiap kompenen dari Rµν akan lenyap secara terpisah. Semua isi persamaan medan diwujudkan dalam pers. (61).
Pada keadaan stasioner atau tak bergantung waktu,dimungkan untuk
mereduksi persamaan medan kedalam 2 bentuk persamaan diferensial untuk
satu fungsi kompleks. Penyederhanaan ini dapat dicapai dengan manipulasi
aljabar pada pers. (61).
Pertama-tama dengan mengenalkan sebuah vektor tiga λj melalui per-samaan
ℓµ = ℓ(1, λ1, λ2, λ3) (4.60)
Selama ℓµ adalah ruang datar dan vektor null (ℓµℓνηµν = 0), λj adalah unit vektor ruang datar, λ2 = 1. Maka pers. (61) dapat diuraikan mejadi
∇2 (ℓ2
) = 0, (4.61)
∇2 (ℓ2
λi) = [(A+B)ℓ],i, (4.62)
∇2 (ℓ2
λiλj) = [(A+B)ℓλi],j+ [(A+B)ℓλj],i (4.63)
Persamaan-persamaan tersebut dapat kita manipulasi dengan mengganti pers.
(4.63) menggunakan pers. (4.61) untuk menghilangkan suku pada pers. (4.62)
sehingga akan kita dapatkan
λi,kλj,k =
(A+B)
jika kita definisikan
(A+B)
2ℓ =p (4.65)
λi,k =M
maka dapat kita tulis untuk pers. (77)
M+MT − 1 pM M
T = 0. (4.66)
Selama λ2 = 1, akan didapat bentuk persamaan matriks yang penting
λjλj,i = 1
2(λjλj),i = 0, M
Tλ= 0 (4.67)
Ini menunjukkan bahwa λ berada dalam ruang null dari MT. Dari bentuk
Aℓµ=ℓνℓµ,ν, akan didapat pula
Aℓλi =ℓν(ℓλi),ν =Aℓλi+ℓ2λjλi,j
atau
Mλ = 0 (4.68)
maka λjuga berada dalam ruang null dariM. Dengan memakai suatu matrik orthogonal baru R yang bila dioperasikan pada λ akan menghasilkan
Rλ = λ′ (4.69)
λ′ =
1
0
jika λ berada dalam ruang null dari M dan MT, maka λ′ juga berada dalam
Dari bentuk λ′ dan karena ia merupakan ruang null dari M dan MT maka
bentuk M′
haruslah
M′
= diag(0, N) (4.73)
dimanaN adalah matrik 2×2. Selama matrik tersebut tidak berubah terhadap perotasian, maka bentuk metrikN′
danM′
juga memenuhi bentuk persamaan
(79)
yang mengimplikasikan bahwaI−N′
atau
untuk sembarang θ. Dengan memilih kemungkinan pertama akan didapat
N′
maka kita dapatkan untuk nilai M′
M′
Merotasikan kembali ke koordinat semula untuk mendapatkan M =
RTM′
Karena R adalah matrik rotasi orthogonal kolom dan baris, maka matrik R
akan memenuhi
R1iR1k+R2iR2k+R3iR3k =δik
jika R1i ≡Ri maka pers.(4.78) akan menjadi
Mik =p(1−cosθ)(δik−RiRk) +P sinθǫiklRl (4.79)
dengan kembali melihat bentuk λ′ dari pers.(4.69) dan (4.70) maka akan kita
dapatkan
R·λ= 1 (4.80)
denganRdisini menunjukkan vektor R1i =Ri. Akan didapat bahwaRi =λi. Maka akan kita dapatkan bentuk
Mik =λi,k = p(1−cosθ)(δik−λiλk) +psinθǫiklλl
= α(δik−λiλk) +βǫiklλl (4.81)
dengan
α=p(1−cosθ), β=psinθ.
Dengan memakaii=kpada pers.(94) dan menjumlahkannya akan didapatkan
∇ ·λ = 2α. (4.82)
Mengalikan pers.(94)dengan ǫjki lalu menjumlakannya di idan k
∇ ×λ=−2βλ. (4.83)
menu-runkan persamaan (94) terhadap xk
λi,kk = [α(δik−λiλk)],k+ (βǫiklλl),k
= α,k(δik−λiλk)−αλi,kλk−αλiλk,k+ǫikl(βλl),k
∇2λ
= ∇α−λ(∇α·λ)−2(α2+β2)λ+∇β×λ. (4.84)
Dan cara kedua dengan identitas vektor
∇ ×(∇ ×λ) = ∇(∇ ·λ)− ∇2λ
∇2λ
= 2λα−2λ× ∇β−4β2λ (4.85)
dengan menjumlahkan persamaan (97) dengan persamaan (98) akan didapat
∇α = λ× ∇β−λ(λ· ∇α)−2(α2−β2)λ (4.86)
dari bentuk tersebut akan didapat
∇α·λ = β2−α2 (4.87)
∇α = λ(β2−α2)− ∇β×λ. (4.88)
Dari persamaan (96), dapat dilihat bahwa divergensi dari βλ adalah nol, maka
∇ ·βλ = β(∇ ·λ) +∇β·λ
dan lalu dengan pers. (4.82) bisa didapatkan
pers.(4.89) akan didapat nilai ∇β
∇β = −2αβλ+ (∇α×λ). (4.90)
Persamaan (4.87),(100),(4.90), dan (4.89) dapat dibentuk dengan cara yang
lebih ringkas dengan mengenalkan suatu fungsi kompleks baru γ =α+iβ
∇γ·λ = −γ2 (4.91)
∇γ = −γ2λ
−iλ× ∇γ. (4.92)
Pengenalan fungsiγ ini untuk menyederhakan persamaan medan einstein dan akan membuat hubungan solusi Kerr dan Schwarzschild semakin jelas.
Disini akan didapatkan pasangan persamaan diferensial biasa yang akan
menentukanγdan akan menunjukkan bahwa γ yang akan menentukan metrik, sepertihalnya fungsi ℓ dan λj. Persamaan diferensial pertama didapatkan de-ngan cara membentuk laplasianγ dari pers. (4.92) serta menyederhanakannya dengan pers. (4.82) dan pers. (96)
∇2
γ = −γ2
∇ ·λ−2γ∇γ·λ+i∇ ·(∇γ×λ) = −2αγ2
+ 2γ3
−i∇γ·(∇ ×λ) = −2γ2
(α+iβ−γ)
= 0 (4.93)
Maka γ adalah fungsi komplek harmonik. Persamaan diferensial yang ke-dua adalah dengan menguadratkan pers.(4.92) dan memakai pers. (4.91) untuk
(∇γ)2
= γ4
−(λ×γ)2 = γ4
−(∇γ)2
−(λ· ∇γ)2 = γ4
(4.94)
Kedua persamaan diferensial terakhir menunjukkan fungsi γ. Selanjutnya dipilih ω= 1/γ
∇ω =λ−iλ× ∇ω, (4.95)
λ· ∇ω=λ· ∇ω∗ = 1, (4.96)
(∇ω)2
= 1, (4.97)
lalu
∇ω· ∇ω∗
=−i(∇ω+∇ω∗
) +Hλ (4.98)
dengan H representasi dari fungsi λ dan ω yang takperlu dituliskan.
Pers.(4.98) dapat diselesaikan dengan mengalikan dot dengan∇ωuntuk meda-patkan H serta menggunakan pers.(4.95) dan (4.96) untuk menyederhanakan
H =i(1 +∇ω· ∇ω∗
) (4.99)
sehingga akan didapatkan nilai λ
λ = ∇ω+∇ω
∗
−i∇ω× ∇ω∗
1 +∇ω· ∇ω∗ (4.100)
dapatkan
ℓ2
=ℜ(γ) = α. (4.101)
Dari pers. (4.93) kita tahu bahwa α adalah harmionik. Jadi pers. (4.61) bisa langsung lenyap. Untuk menunnjukkan ℓ2
= α adalah solusi dari pers.(4.62) kita menghitung sisi sebelah kiri dengan ℓ2
=α sebagai solusi coba denganα
harmonik.
∇2
(αλj) = α∇2λj+ 2α,kλ,k (4.102)
Dengan memakai pers.(94),(98),(100), dan pers.(4.90) maka persamaan
terse-but akan menjadi
∇2
(αλj) = 4α∇α+ 2β∇β = ∇(α2
+β2
). (4.103)
. Selanjutnya dihitung sisi sebelah kanan dari pers.(4.62). Dari definisi α =
p(1−cos∴) dan β=psinθ yang sebelumnya dijelaskan pers.(94)akan didapat
α2 +β2
= 2p2
(1−cosθ) = 2αp (4.104)
dari definisi pers.(4.65) akan kita dapatkan
A+B = ℓ
α(α
2 +β2
) (4.105)
lalu dengan ℓ2
=α bagian sisi kanan dari pers.(4.62) menjadi
Persamaan tersebut akan sesuai dengan pers.(4.103), dan terbkti bahwaℓ2
=α
Penyederhanaan panjang yang telah dibuat berguna untuk
menyeder-hanakan persamaan medan menjadi dua persamaan yang sederhana yang
diberikan oleh pers.(4.93) dan pers.(4.97), dengan fungsi metrik yang diberikan
oleh pers.(4.100) dan pes.(4.101), bentuk-bentuk ini akan digunakan untuk
menyelesaikan persamaan medan Einstein. Fungsi kompleks γ memegang
peranan sebagi potensial Newton yang tergeneralisasi karena mematuhi
per-samaan Laplace, dan dalam limit medan lemahℜ(γ) adalah potensial Newton. Dalam kesseuaian dengan Newtonian, pertama-tama mempertimbangkan
so-lusi sederhana simetri bola ke persamaan Laplace
γ = 1
Maka disini ω=r. Selanjutnya fungsi metrikℓ2
yang sesuai dengan potensial
Newton, dan vektor λi dapat diperoleh dari pers.(4.100) dan (4.101)
ℓ2
Dari definisi pers.(4.60) dan pers.(4.37) akan didapatkan elemen garis
ds2
Bentuk ini sesuai dengan bentuk Edington dari metrik Schwarzschild pada
pers.(4.36)
Penyederhanaan dari solusi Schwarzschild terhadap masalah ini akan
men-garahkan pada suatu keumuman pergeseran dari titik awal
atau
γ = (x+a)−1/2 (4.111)
dengan ai =konstanta sembarang. Karena pesamaan tersebut memenuhi
pers.(4.93) dan pers.(4.97) untuk setian sembarang konstanta ai. Jika kon-stanta ai real maka solusi ini sesuai dengan pergerseran dari titik awal dan tidak ada hal fisis yang menarik. Disisi lain, saat kita pilihai adalah imajiner maka akan ada keadaan fisis yang baru. tanpa harus kehilangan keumuman ,
kita dapat menuliskan pergerseran fungsi γ imaginer sebagai berikut
γ =p(x+ia)2 (4.112)
persamaan ini mewakili solusi Kerr.
Dari fungsi γ baru ini, bisa didpatkan fungsi metrik ℓ2
dan λi dari pers.(4.100) dan pes.(4.101), seperti kasus Schwarszchild tapi dengan sedikit
tambahan aljabar. Pertama-tama dengan membagi ωmenjadi bagian real dan imajiner agar lebih mudah
ω = ρ+iσ ω2
= x2
−a2
+ 2ia·x (4.113)
dengan
r=√x2, a=√a2 (4.114)
dengan menguadartkat pers.(4.113) lalu memisahkan bagian imajiner dan
re-alnya akan didapat
ρ2
−σ2 =r2
−a2
selanjutnya akan dapat diperoleh hubungan kuadrat antaraρ2
Untuk mendapatkan nilaiλdari pers. (4.100) pertama-tama dihitung nilai
∇ω
sehingga akan didapatkan untuk nilai λ
λ= ρ
Hal ini dapat dapat dibandigkan dengan bentuk edington dalam solusi
Akhirnya akan bisa didapatkan
ini adalah bentuk yang ditemukan Kerr pada tahun 1963.
Dengan pemilihan koordinat alternatif t, ρ, θ, φ yaitu
cosθ= z
ρ, (ρ+ia)e
iφsinθ =x+iy.
akan didapatkan suatu bentuk elemen garis baru
ds2
dengan mengenalkan suatu bentuk variabel baru
x0
sehingga pers.(4.120) dapat menjadi
atau
Persamaan tersebut merupakan solusi Kerr dalam koordinat
Boyer-Linquist(1967), metrik Kerr ini akan kembali menjadi bentuk metrik
Schwarzschild bilaa= 0, adanya suku silangdφ′
dt′
membuatnya tampak sama
dengan metrik dari ruang datar yang berotasi. (Penurunan untuk subbab ini
secara lengkap dapat dilihat di lampiran 6 dan analisis vektor yang terkait
dapat dilihat di lampiran 4).
4.2.3
Implikasi Solusi Kerr
Pada tahun 1918, Lense dan Thirring mempelajari tentang medan gravitasi
dari suatu benda berbentuk bola yang berotasi. Dengan menggunakan
per-samaan medan ralativistik terhadap ruang massa-energi, mereka mendapatkan
pendekatan solusi untuk putaran rendah dan medan yang lemah didalam atau
diluar bola. Solusi dari bagian luar bola mempunyai bentuk
ds2 = −
suku pertama dalam a/ρ
dimana suku pertama ρ=r. Persamaan ini sama dengan solusi Schwarzchild dengan tambahan suku silang yang proposinal dengan a. Untuk membanding-kan persamaan ini dengan pers.(4.123), persamaan ini harus diuraimembanding-kan kedalam
bentuk isotropik. Perubahan dapat dilakukan dengan perubahan koordinat
ra-dial untuk menguraikan elemen garis Schwarzschild kedalam bentuk isotropik,
ρ= ˆρ(1 +m/2ˆρ)2
, dengan ˆρ adalah penanda radial isotropik.
ds2
lalu melebarkan suku pertama dalam m/ρˆ
ds2
yang sesuai dengan pers.(4.123) jika kita ambil
ma=−κJ
c3 (4.126)
menjadi
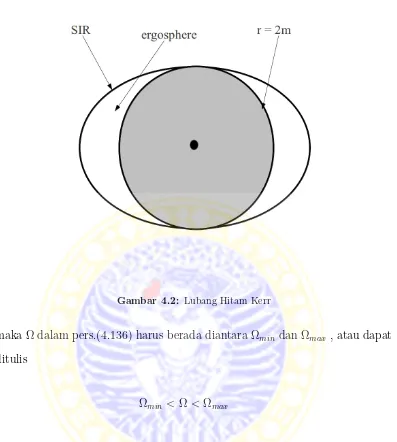
Pada solusi Schwarzschild permukaan r = 2m adalah even horizon (EH) dan juga permukaan dariinfinite red-shift (SIR) sebagaimana yang telah
dike-tahui, tetapi pada solusi Kerr, SIR dan EH adalah dua permukaan yang
berbeda. Area diantara keduanya disebutergosphere.
Untuk menyelidiki solusi Kerr ini pertama-tama, sebuah permukaan hiper
(hyppersurface) dinyatakan dalam bentuk
f(x0
, x1
, x2
, x3 ) = 0
Dalam solusi Schwarzschild EH diberikan oleh r −2m = 0, maka fungsi f
dapat ditulis
f =r−2m =x1
−2m
dan ℓµ = (0,1,0,0). Permukaan hiper null jika ℓµℓµ = 0. Dari bentuk Ed-ington diketahui bahwa g11
= 1−2m/r, maka terlihat bahwa ℓµℓ
Dalam solusi Kerr, permukaan hiper menuntut ∆ = 0, maka
r =r± =m±
√ m2
−a2 (4.128)
yang setara dengan
r2 + =a
2
= 2mr+ (4.129)
maka fungsi f dapat ditulis
f =r−r+ =r−m−
√ m2
−c2 (4.130)
dan ℓµ= (0,1,0,0) serta g11= ∆/ρ2. Karena ∆ = 0 saat r=r+ maka
ℓµℓµ= 0 di r=r+ (4.131)
maka dapat disimpulkan bahwa r = r+ adalah null dari permukaan hiper. cahaya takkan mampu yang masuk takkan mampu keluar dari lubang hitan
Kerr. Horizon peristiwa dari lubang hitam Kerr adalah
r =r+ =m+
√ m2
−c2 (4.132)
yang mana EH ini akan menjadi EH Schwarzchild saat a= 0.
Kembali memperhatikan properti dari r = 2m dalam solusi Schwarzchild, yaitu SIR. Faktor pergeseran merah adalah
z = νem
νrec − 1,
ca-haya diemisikan saat r2 dan diterima di r1 maka
z =
s
g00(r1)
g00(r2) − 1
dengan g00(r) = 1−2m/r. Maka untuk cahaya yang diemisikan saat r dan diterima di suatu jarak yang jauh, g00(r1) = 1 maka
z = p 1 g00(r)
−1 =
r r
r−2m −1,
dan sebagaimana r → 2m, z → ∞. Permukaan r = 2m adalah SIR yang
didefinisikan g00= 0.
Dalam kasus solusi Kerr, kondisi g00 = 0 memberikan
ρ2
= 2mr ⇒r2
−2mr+a2 cos2
θ= 0
dengan solusi
r1,2 =m±
√ m2
−a2cos2θ,
saat r =r1
r=r1 ==m+
√
m2−a2cos2θ (4.133)
persamaan tersebut merupakan SIR dari solusi Kerr yang akan kembali
men-jadi SIR dalam solusi Schwarzschild saat a= 0.
Diantara permukaan EH dan SIR ada sebuah area yang disebut sebagai
ergosphere yang disefinisikan sebagai
m+√m2
−a2 =r
+< r < r1 ==m+
√ m2
Sebuah partikel denganr, θ yang tetap tapi bergerak dengan bertambahnya
φ, maka kecepatan-4nya adalah
dxµ
kondisi u0
haruslah timelike
atau dengan menakai pers.(4.135)
Ω2
bila pers.(4.136) bernilai nol maka
Ω
Komponen-komponen metrik g00, g03 dan g33 dapat ditulis ulang dari bentuk pers.(4.127)
−gg03
33
= ω
c (4.138)
maka dua solusi pers.(4.137) dapat dituliskan
Gambar 4.2: Lubang Hitam Kerr
maka Ω dalam pers.(4.136) harus berada diantara Ωmin dan Ωmax , atau dapat
ditulis
Ωmin <Ω<Ωmax
dengan Ω adalah kecepatan sudut dari partikel di dalam ruang-waktu Kerr
yang dilihat pengamat yang jauh dari lubang hitam. Secara umum, g00 < 0, Ωmin < 0, maka pengamat yang jauh masih bisa melihat partikel bergerak berlawanan arah dengan rotasi lubang hitam. Saat g00 → 0, maka Ωmin = 0 dan Ωmax = 2ω, dan partikel tidak mampu bergerak barlawanan dengan rotasi lubang hitam, tapi masih bisa diam. Untuk hal ini, SIR disebut sebagai batas
diam. Dan saat berada di ergosphere atau Ω > 0 partikel takkan mampu menahan untuk mengikuti putaran lubang hitam. Adanya ergoshere inilah