X tot N. JK antar RJK

111 BAB VIII

ANALISIS VARIAN (ANAVA) A. Analisis Varian Satu Jalur

Langkah-langkah pengujian hipotesis dengan anava satu jalur (1) Menghitung Jumlah Kuadrad Total (JKtot):

JKtot = ∑ Xtot2

(2) Menghitung Jumlah Kuadrad Antar Kelompok (JKantar):

JKantar =



 



N X n X _tot A A 2 2



 



(3) Menghitunng Jumlah Kuadrad Dalam Kelompok (JKdal):

JKdal = JKtot─ JKantar

(1) Menghitung Mean Kuadrad (Rerata Jumlah Kuadrat atau RJK) antar Kelompok (RJKantar): RJKantar =

1



a

JK

_antar  a = jumlah kelompok

(5) Menghitung Rerata Jumlah Kuadrat dalam Kelompok (RJKdal)

RJKdal =

a

N

JK

_dal



 N = jumlah seluruh sampel

(6) Menghitung harga Fhitung dengan rumus:

dalam antar

RJK RJK

(7) Konsultasikan pada table F dengan db pembilang (a-1) dan db penyebut (N-a)

(8) Aturan keputusan : Jika F hitung lebih besar daripada F table pada taraf





N X_tot 2





112

signifikansi tertentu (Misalnya: ts 5% atau 1%), maka Ha diterima dan H0 ditolak.

(9) Membuat kesimpulan, apakah terdapat perbedaan yang signifikan atau tidak

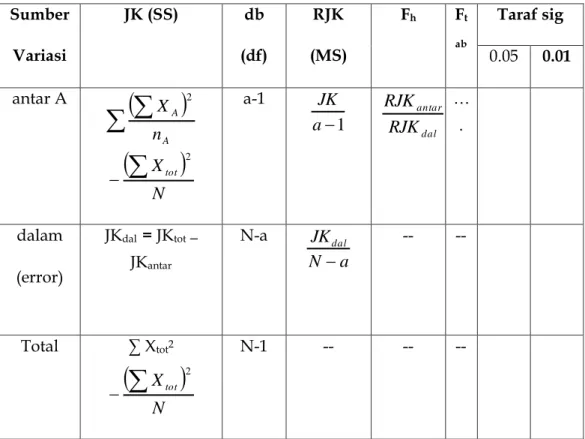
(10) Membuat Tabel Ringkasan Analisis Varians untuk Menguji Hipotesis k Sampel

Tabel 7.1. Tabel Ringkasan Analisis Varians untuk Menguji Hipotesis k Sampel Sumber Variasi JK (SS) db (df) RJK (MS) Fh Ft ab Taraf sig 0.05 0.01 antar A





 

A A n X 2 a-1 1  a JK dal antar

RJK

RJK

… . dalam (error) JKdal = JKtot─ JKantar N-a a N JKdal  -- -- Total ∑ Xtot2 N-1 -- -- -- Contoh aplikasinya.

Seorang peneliti ingin mengetahui pengaruh metode mengajar terhadap prestasi belajar IPA. Metode mengajar digolongkan menjadi 4,





N Xtot 2









N X_tot 2





113

yaitu : Metode ceramah (A1), Metode Diskusi (A2), Metode Pemberian

Tugas (A3), dan Metode campuran (A4).

Hipotesis Penelitian:

H0: Tidak terdapat perbedaan yang signifikan prestasi belajar IPA antara siswa yang mengikuti pembelajaran metode ceramah, metode diskusi, metodepemberian tugas, dan metode campuran

H1: Terdapat perbedaan yang signifikan prestasi belajar IPA antara siswa yang mengikuti pembelajaran metode ceramah, metode diskusi, metodepemberian tugas, dan metode campuran

Hipotesis Statistik: H0: µ1 = µ2 = µ3 = µ4

H1 : µ1 ≠ µ2 ≠ µ3 ≠ µ4 (salah satu tanda ≠)

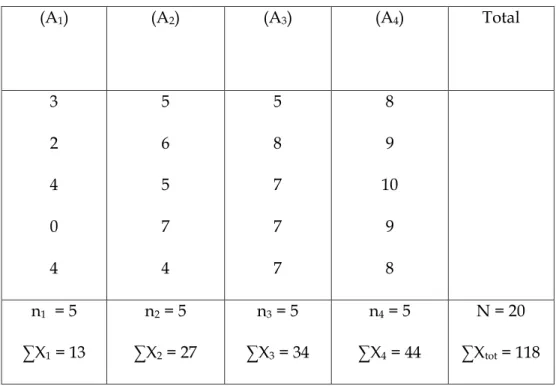
Tabel 8.2. Data Hasil Belajar IPA Siswa SMA Klas II di Singaraja

(A1) (A2) (A3) (A4) Total 3 2 4 0 4 5 6 5 7 4 5 8 7 7 7 8 9 10 9 8 n1 = 5 ∑X1 = 13 n2 = 5 ∑X2 = 27 n3 = 5 ∑X3 = 34 n4 = 5 ∑X4 = 44 N = 20 ∑Xtot = 118

114

∑X12 = 45 ∑X22 = 151 ∑X32 = 236 ∑ X42 = 390 ∑Xtot2 = 822

X 1 = 2,6 X 2 = 5,4 X 3 = 6,8 X 4 = 8,8 X tot = 5,9

Masukkan ke dalam rumus berikut.

Perhitungan: JKtot = ∑ Xtot2 = 822

20

118

2



= 125,8 JKantarA =



 



N X n X _tot A A 2 2



 

 =



 

 

 

 



N X n X n X n X n X tot A A A A A A A A 2 4 2 4 3 2 3 2 2 2 1 2 1











_{   } =

5

44

5

34

5

27

5

13

2 2 2 2







-

101

,

8

20

118

2



JKdal = JKtot─ JKantar = 125,8 – 101,8 = 24

Atau JK dal:

 

24

5

44

5

34

5

27

5

13

822

2 2 2 2 2 2































A A tot

n

X

X

dbA = a-1 = 4-1 = 3

RJKantar = JKantar : dbantar = 101,8 : 3 = 33,93.

db dalam = N – a = 20-4 = 16 RJKdal = JKdal : dbdal = 24:16 = 1,5

Fhitung = RJKantar : RJKdal = 33,93 : 1,5 = 22,66  lihat table F





N Xtot 2





115

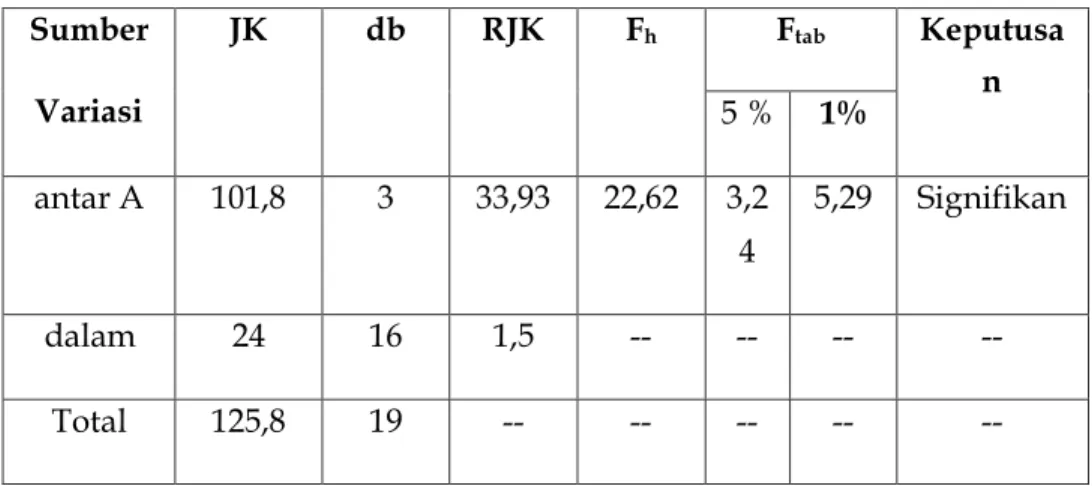
Tabel 8.3. Tabel Ringkasan Analisis Varians untuk Menguji Hipotesis 4 Kelompok Sumber Variasi JK db RJK Fh Ftab Keputusa n 5 % 1% antar A 101,8 3 33,93 22,62 3,2 4 5,29 Signifikan dalam 24 16 1,5 -- -- -- -- Total 125,8 19 -- -- -- -- --

Jika harga F signifikan, dilanjutkan dengan uji simple effect antar sel dengan rumus t-Sceffe berikut. Untuk n1 = n2 :

n

RJK

X

X

t

dal

*

2

2 1





, dimana db t = db dalam Untuk n1 ≠ n2:          2 1 2 1 1 1 n n RJK X X t dal , dimana db t = db dalam

116

Uji t Scheffe: db t sama dengan db dalam = 16

t1-2 :

3

,

615

5

5

,

1

2

0

,

4

6

,

2



_

_



x

t

 signifikan t1-3:







5

5

,

1

2

8

,

6

6

,

2

x

t

5,422 signifikan t1-4:







5

5

,

1

2

8

,

8

6

,

2

x

t

-8,004  signifikan t2-3:







5

5

,

1

2

8

,

6

4

x

t

-1,807  non signifikan t2-4:







5

5

,

1

2

8

,

8

4

x

t

- 4,389  signifikan t3-4:







5

5

,

1

2

8

,

8

8

,

6

x

t

- 2,582  signifikan Menarik kesimpulan

1. Metode mengajar berpengaruh terhadap hasil belajar siswa

2. Metode mengajar IV lebih berpengaruh terhadap hasil belajar siswa dari pada metode mengajar III, II, dan I

3. Metode mengajar III lebih berpengaruh terhadap prestasi belajar siswa daripada metode mengajar II dan I

4. Metode mengajar II lebih berpengaruh terhadap prestasi belajar siswa dibandingkan dengan metode mengajar I.

117 B. Anava Dua Jalur

Anava dua jalur dapat berbentuk 2 x 2; 3 x 2; 3 x 3; dan sebagainya Misalnya, seorang peneliti ingin mengetahui pengaruh insentif dan motivasi kerja terhadap peningkatan produktivitas kerja pada suatu perusahaan.

1). Hipotesis Penelitian:

H0: (1) Tidak terdapat perbedaan produktivitas kerja antara karyawan yang diberi insentif dengan karyawan yang tidak diberi insentif

(2) Tidak terdapat perbedaan produktivitas kerja antara karyawan yang memiliki motivasi tinggi dan karyawan yang memiliki motivasi kerja rendah

(3) Tidak ada pengaruh interaksi antara insentif dan motivasi kerja terhadap produktivitas kerja

H1: (1) Terdapat perbedaan produktivitas kerja antara karyawan yang diberi insentif dengan karyawan yang tidak diberi insentif (2) Terdapat perbedaan produktivitas kerja antara karyawan yang memiliki motivasi tinggi dan karyawan yang memiliki motivasi kerja rendah

(3) Terdapat pengaruh interaksi yang signifikan antara insentif dan motivasi kerja terhadap produktivitas kerja

118 2). Hipotesis Statistik: (1) H0: µ1 = µ2 H1: µ1 ≠ µ2 (2) H0: µ1 = µ2 H1: µ1 ≠ µ2 (3) H0: Inter AB = 0 H1: Inter AB ≠ 0 3). Rancangan Analisis

Tabel 3.4. Rancangan Anava 2 Jalur (Faktorial 2x2) Insentif (A) Motivasi Kerja (B) A1 (dapat insentif) A2

(tidak dapat insentif)

Motivasi Tinggi (B1) A1 B1 A2 B1 Motivasi Rendah (B2) A1 B2 A2 B2 Keterangan:

A = Insentif (A1=dapat insentif dan A2= tidak dapat insentif)

119 Y = Produktivitas Kerja

4). Contoh aplikasi

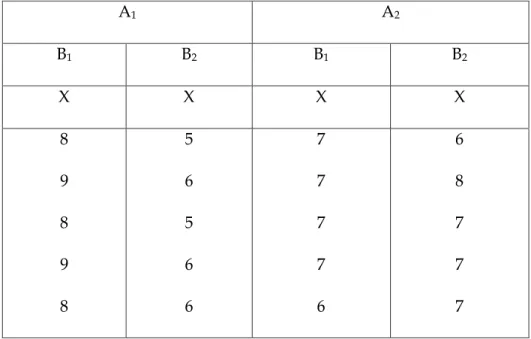
Tabel 8.5. Data Hasil Penelitian

A1 A2 B1 B2 B1 B2 X X X X 8 9 8 9 8 5 6 5 6 6 7 7 7 7 6 6 8 7 7 7

Tabel 8.6. Tabel Statistik Induk (untuk menolong perhitungan)

Stat A1 A2 Total A1 A2 B1 B2 B1 B2 B1 B2 n 5 5 5 5 20 10 10 10 10 ∑X 42 28 34 35 139 70 69 76 63 ∑X2 _{354 158 232 247 991 512 479 586 405} X 8,4 5,6 6,8 7 6,95 7 6,9 7,6 6,3

120 Tabel 8.7. Statistik Induk

(A) (B) A1 A2 Total B1 n = 5 ∑ X = 42 ∑ X2 _{= 354} X = 8,4 n = 5 ∑ X = 34 ∑ X2 _{= 232} X = 6,8 n = 10 ∑ X = 76 ∑ X2 _{= 586} X = 7,6 B2 n = 5 ∑ X = 28 ∑ X2 _{= 158} X = 5,6 n = 5 ∑ X = 35 ∑ X2 _{= 247} X = 7 n = 10 ∑ X = 63 ∑ X2 _{= 405} X = 6,3 Total n = 10 ∑ X = 70 ∑ X2 _{= 512} X = 7 n = 10 ∑ X = 69 ∑ X2 _{= 479} X = 6,9 N = 20 ∑ Xtot = 139 ∑ X2tot = 991 X = 6,95 5). Langkah-langkah perhitungan a. JKtot = ∑ Xtot2





= 991 – (1392 : 20) = 991 – 966,05 = 24,95 N X_tot 2





121 b. JKantar A = =



 

 



N X n X n X tot A A A A 2 2 2 2 1 2 1







_{ } = (702 : 10) + (692 _{: 10) - (139}2 _{: 20) = (490 + 476,1) – 966,05} = 966,1 – 966,05 = 0,05 c. JK antarB = =





 





 







 N X n X n X tot B B B B 2 2 2 2 1 2 = (762 : 10) + (632 _{: 10) - (139}2 _{: 20) = (577,6 + 396,9) – 966,05} = 974,5 – 966,05 = 8,45 d. JKinter AB =



 



A B TOT AB AB

JK

JK

N

X

n

X









 

2 2 = (422_{:5) +(28}2_{:5)+ (34}2_{:5)+ (35}2_{:5) - (139}2 _{: 20) – 0,05 – 8,45} = (352,8 + 156,8 + 231,2 + 245 ) – 966,05 – 0,05 – 8,45 = 985,8 – 966,05 – 0,05 – 8,45 = 11,25 e. JK dal = = 991 – 985,8 = 5,2

atau JK dal = JKtot – JKantarA – JKantarB – JKinterAB



 



N X n X _tot A A 2 2



 





 



N X n X _tot B B 2 2



 







 

 



AB AB tot n X X 2 2

122 = 24,95 – 0,05 – 8,45 – 11,25 = 5,2 f. JKtot = JKA+ JKB+ JKAB+JKdal = 0,05 + 8,45 + 11,25 + 5,2 = 24,95 db A = a-1 = 2 – 1 = 1 db B = b-1 = 2 – 1 = 1 db inter AB = db A x db B = 1x1 = 1 db dalam = N – ab = 20 – (2x2) = 20 -4 = 16 RJKA = JKA : dbA = 0,05 : 1 = 0,05 RJKKB = JKB : dbB = 8,45 : 1 = 8,45 RJKKAB = JKAB dbAB = 11,25 : 1 = 11,25

RJKKdalam = JKdal : dbdal = 5,2 : 16 = 0,325

FA = RJKA : RJKdalam = 0,05 : 0,325 = 0,154 FB = RJKKB : RJKdalam = 8,45 : 0,325 = 26

FAB = RJKAB : RJKdalam = 11,25 : 0,325 = 34,61 Tabel 8.8. Tabel Ringkasan Analisis ANAVA AB Sumber Variasi JK db RJK Fh Ftab 5% 1% A B Inter AB dalam 0,05 8,45 11,25 5,2 1 1 1 16 0,05 8,45 11,25 0,325 0,154*) 26,00**) 34,61**) -- 4,49 4,49 4,49 -- 8,53 8,53 8,53 --

123 Total _24,95 19 -- -- -- -- *) non signifikan **) signifikan Kesimpulan

FA = 0,154*)  non signifikan, artinya? Tidak tedapat perbedaan yang

signifikan produktivitas kerja karyawan antara yang mendapat insentif dan tidak mendapat insentif. Pemberian insentif tidak berpengaruh terhadap peningkatan produktivitas kerja karyawan

FB = 26,00**)  signifikan, artinya ? Terdapat perbedaan yang signifikan

produktivitas kerja karyawan antara karyawan yang memiliki motivasi kerja tinggi dan rendah. Motivasi kerja berpengaruh terhadap peningkatan produktivitas kerja.

FAB = 34,61**)  signifikan, artinya ? Dilanjutkan pada uji simple effect,

untuk mengetahui pengaruh antara insentif dan motivasi kerja terhadap produktivitas kerja.

Karena pengaruh interaksi signifikan, dilanjutkan dengan uji t-Scheffe atau uji Tukey, dengan rumus sebagai berikut.

Rumus Tukey:

n

RJKdal

X

X

Q



1



2 _{ db Q = n dan m}

(n = sampel, dan m = jumlah kelompok)

atau Untuk n1 = n2 : t = n xRJKdal X X 2 2 1 _{, dimana db t = db dalam}

124

db t sama dengan db dalam = 16. Nilai t tabel untuk db = 16 pada taraf signifikansi 5% = 2,120. Uji t1-2:

n

xRJKdal

X

X

t

2

2 1





=

10

325

.

0

2

8

.

6

4

.

8

x

t





= 6.276 (signifikan) Uji t1-3: n xRJKdal X X t 2 3 1  =

5

.

49

10

325

.

0

2

0

.

7

4

.

8



_

x

(signifikan) Uji t1-4: n xRJKdal X X t 2 4 1  =

10

.

98

10

325

.

0

2

6

.

5

4

.

8





x

(signifikan) Uji t2-3: n xRJKdal X X t 2 3 2   =

0

.

78

10

325

.

0

2

0

.

7

8

.

6





x

(non signifikan) Uji t2-4: n xRJKdal X X t 2 4 2   =

4

.

707

10

325

.

0

2

6

.

5

8

.

6





x

(signifikan) Uji t3-4: n xRJKdal X X t 2 4 3   =

5

.

49

10

325

.

0

2

6

.

5

0

.

7



_

x

(signifikan)

125

C. Analisis Varians Dua Jalur (Anava AB) = Faktorial (3x3) 1). Rancangan analisis

Tabel 3.9. Rancangan Anava 2 Jalur (Faktorial 3x3) Metode (A) Inteligensi (B) A1 A2 A3 Inteligensi Tinggi (B1) A1 B1 A2 B1 A3 B1 Inteligensi Sedang (B2) A1 B2 A2 B2 A3 B2 Inteligensi Rendah (B3) A1 B3 A2 B3 A3 B3 Keterangan : A = Metode Mengajar

A1 = Metode Mengajar I (ceramah)

A2 = Metode Mengajar II (diskusi)

126 B = Inteligensi

B1 = Inteligensi Tinggi

B2 = Inteligensi Sedang

B3 = Inteligensi Rendah

Y = Hasil Belajar Matematika

Misalnya, seorang peneliti ingin mengetahui pengaruh metode mengajar terhadap hasil belajar matematika.

2). Hipotesis Penelitian

H0: (1) Tidak ada perbedaan hasil belajar matematika antara siswa yang dalam

pembelajaranya menggunakan metode I, metode II, dan Metode III. (2) Tidak ada perbedaan hasil belajar matematika antara siswa yang

memiliki inteligensi tinggi, sedang, dan rendah.

(3) Tidak ada pengaruh interaksi antara metode mengajar dan inteligensi terhadap hasil belajar matematika

H1: (1) Ada perbedaan hasil belajar matematika antara siswa yang dalam pembelajaranya menggunakan metode I, metode II, dan Metode III.

(1) Ada perbedaan hasil belajar matematika antara siswa yang memiliki inteligensi tinggi, sedang, dan rendah.

(2) Ada pengaruh interaksi antara metode mengajar dan inteligensi terhadap hasil

belajar matematika

127 H0: (1) µ1 = µ2 = µ3

(2) µ1 = µ2 = µ3

(3) AB = 0

H1: (1) µ1 ≠ µ2≠ µ3 (salah satu tanda tidak sama)

(2) µ1 ≠ µ2≠ µ3 (salah satu tanda tidak sama)

(3) AB ≠ 0

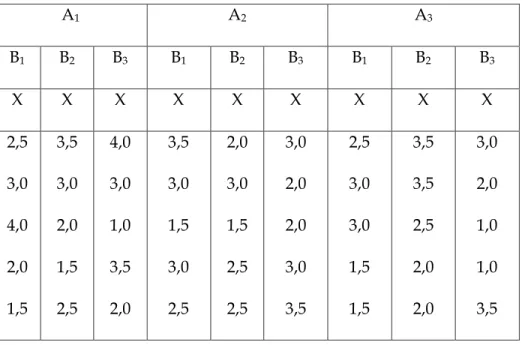
Tabel 8.10. Data Hasil Penelitian

A1 A2 A3 B1 B2 B3 B1 B2 B3 B1 B2 B3 X X X X X X X X X 2,5 3,0 4,0 2,0 1,5 3,5 3,0 2,0 1,5 2,5 4,0 3,0 1,0 3,5 2,0 3,5 3,0 1,5 3,0 2,5 2,0 3,0 1,5 2,5 2,5 3,0 2,0 2,0 3,0 3,5 2,5 3,0 3,0 1,5 1,5 3,5 3,5 2,5 2,0 2,0 3,0 2,0 1,0 1,0 3,5 Keterangan: A = Metode Mgajar

A1 = Metode Mengajar I (ceramah)

A2 = Metode Mengajar II (diskusi)

128 B = Inteligensi

B1 = Inteligensi Tinggi

B2 = Inteligensi Sedang

B3 = Inteligensi Rendah

X = Hasil Belajar Matematika (IPK) 5). Langkah-langkah analisis

Tabel 8.11. Tabel Kerja Statistik Induk (A) (B) A1 A2 A3 Total B1 n = 5 ∑ X = 13,0 ∑ X2 _{= 37,5} X = 2,6 n = 5 ∑ X = 13,5 ∑ X2 _{= 38,75} X = 2,7 n = 5 ∑ X = 11,5 ∑ X2 _{= 28,75} X = 2,3 n = 15 ∑ X = 38,0 ∑ X2 _{= 105} X = 2,53 B2 n = 5 ∑ X = 12,5 ∑ X2 ₌ 33,75 n = 5 ∑ X = 11,5 ∑ X2 _{= 27,75} X = 2,3 n = 5 ∑ X = 13,5 ∑ X2 _{= 38,75} X = 2,7 n = 15 ∑ X = 39,0 ∑ X2 ₌ 100,25

129 X = 2,5 X = 2,6 B3 n = 5 ∑ X = 13,5 ∑ X2 ₌ 38,75 X = 2,7 n = 5 ∑ X = 13,5 ∑ X2 _{= 38,75} X = 2,7 n = 5 ∑ X = 10,5 ∑ X2 _{= 27,25} X = 2,1 n = 15 ∑ X = 37,0 ∑ X2 ₌ 107,75 X = 2,47 Total n = 15 ∑ X = 39,0 ∑ X2 ₌ 113,5 X = 2,6 n = 15 ∑ X = 38,5 ∑ X2 _{= 104,75} X = 2,56 n = 15 ∑ X = 35,5 ∑ X2 _{= 94,75} X = 2,36 N = 45 ∑ X = 113 ∑ X2 _{= 313} X = 2,51 2) Perhitungan: a. JKtot = ∑ Xtot2 =

313

283

,

76

29

,

24

45

113

313

2









b. JKantar =



 



N X n X _tot A A 2 2



 

 =



 

 

 



N X n X n X n X _tot A A A A A A 2 3 2 3 2 2 2 1 2 1









_{  }





N X_tot 2





130 =

  

 

  

284,23 283,76 0,47 45 113 15 5 , 35 15 5 , 38 15 39 2 2 2 2       c. JK antarB =





 





 





 







 N X n X n X n X tot B B B B B B 2 3 2 3 2 2 2 1 2 =

  

 

  

283,77 283,76 0,01. 45 113 15 5 , 37 15 5 , 37 15 38 2 _ 2 _ 2 _ 2 _{  } d. JKinter AB =





A B tot AB AB JK JK N X n X           



 

2 2 = 01 , 0 47 , 0 45 113 5 5 , 10 5 5 , 13 5 5 , 11 5 5 , 13 5 5 , 11 5 5 , 13 5 5 , 13 5 5 , 12 5 132 2 2 2 2 2 2 2 2 2 _{ }                      = (33,8+31,25+36,45+36,45+26,45+36,45+26,45+36,45+22,05) -283,76 – 0,47 – 0,01 = 285,8 -283,76 -0,47 – 0,01 = 1,56. e. JK dal =





313 285,8 27,20 2 2 _

 

_{  }



AB AB tot n X X

atau JK dal = JKtot – JKantarA – JKantarB – JKinter = 29,24 – 0,47 – 0,01 -1,56

= 27,20 f. JKtot = JKA+ JKB+ JKAB+JKdal = 0,47+0,01+1,56+27,2 = 29,24 db A = a-1 = 3-1 = 2 db B = b-1 = 3-1 = 2 db inter AB = db A x db B = 2 x 2 = 4 db dalam = N – ab = 45 – (3x3) = 36 RJKKA = JKA : dbA = 0,47 : 2 = 0,24 RJKKB = JKB : dbB = 0,01 : 2 = 0,005

131 RJKAB = JKAB dbAB = 1,56 : 4 = 0,39

RJKdalam = JKdal : dbdal = 27,2 : 36 = 0,76

FA = RJKA : RJKdalam = 0,24 : 0,76 = 0,32

FB = RJKB : RJKdalam = 0,005 : 0,76 = 0,006

FAB = RJKAB : RJKdalam = 0,39 : 0,76 = 0,51

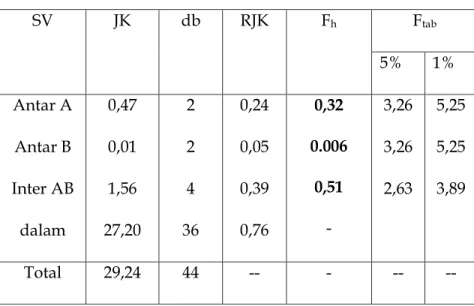
Tabel 3.12. Tabel Ringkasan Analisis ANAVA AB

SV JK db RJK Fh Ftab 5% 1% Antar A Antar B Inter AB dalam 0,47 0,01 1,56 27,20 2 2 4 36 0,24 0,05 0,39 0,76 0,32 0.006 0,51 - 3,26 3,26 2,63 5,25 5,25 3,89 Total 29,24 44 -- - -- -- Kesimpulan: FA = 0,32  non signifikan FB = 0,006  non signifikan FAB = 0,51  non signifikan Catatan:

Jika hasil uji hipotesis terdapat pengaruh interaksi yang signifikan (F inter AB adalah signifikan), maka dilanjutkan dengan uji simple effect dengan

132

uji Tukey (jika n tiap kelompok sama) atau uji t- Scheffe (jika n sama atau tidak sama), dengan rumus sebagai berikut.

Rumus Tukey:

n

RJKdal

X

X

Q



1



2 Uji t-Scheffe: n xRJKdal X X t 2 2 1  Tugas Latihan

Seorang peneliti bermaksud untuk mengetahui pengaruh metode pembelajaran kooperatif dan motivasi belajar terhadap hasil belajar matematika pada siswa SMA. Untuk itu, dilakukan eksperimen selama satu semester terhadap dua kelas sebagai kelompok eksperimen dan dua kelas sebagai kelompok kontrol. Kelompok eksperimen diajar dengan metode pembelajaran kooperatif, sedangkan kelompok kontrol diajar dengan metode pembelajaran konvensional. Motivasi belajar siswa diklasifikasikan menjadi motivasi tinggi dan rendah. Jumlah sampel penelitian sebanyak 100 orang.

1. Buatlah rancangan analisisnya 2. Rumuskan hipotesis statistiknya 3. Hitunglah harga F masing-masing

4. Jika terjadi pengaruh interaksi yang signifikan, lakukan uji lanjut Catatan: datanya dikarang sendiri (angka puluhan, n = 100)

133 D. Analisis Varians Tiga Jalur

Analisis varians tiga jalur (rancangan analisis varians ABC), digunakan untuk menganalisis data pada sampel yang variabel bebasnya terdiri atas tiga variabel. Misalnya, kita bermaksud menguji pengaruh jenis kelamin, tempat tinggal, dan sikap sosial terhadap prestasi belajar IPS. Dalam hal ini variabel penelitiannya adalah sebagai berikut.

Variabel bebasnya:

A = jenis kelamin (A1 = laki-laki; dan A2 = perempuan)

B = tempat tinggal (B1 = kota; B2 = pinggiran kota; B3 = desa; B4 = desa terpencil)

C = sikap sosial (C1 = sikap tinggi; C2 = sikap sosial sedang; C3 = sikap sosial rendah)

Variabel terikatnya: adalah prestasi belajar IPS.

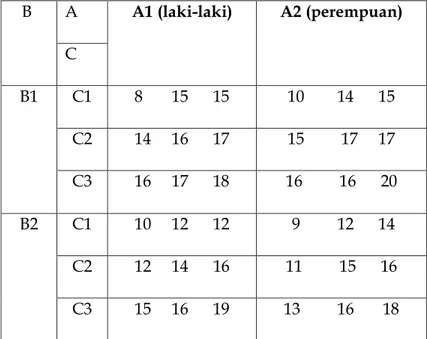
Misalnya, data hasil penelitian seperti tabel berikut. Tabel 8.13. Tabel Data (Fiktif)

B A A1 (laki-laki) A2 (perempuan) C B1 C1 8 15 15 10 14 15 C2 14 16 17 15 17 17 C3 16 17 18 16 16 20 B2 C1 10 12 12 9 12 14 C2 12 14 16 11 15 16 C3 15 16 19 13 16 18

134 B3 C1 11 11 15 11 11 13 C2 16 16 18 13 13 18 C3 16 20 20 14 15 18 B4 C1 9 11 14 12 12 12 C2 14 15 19 15 16 18 C3 14 18 20 17 19 20

Untuk menganalisis data tersebut, terlebih dahulu perlu dibuatkan tabel data statistik induk yang diperlukan untuk menguji hipotesis penelitian. Statistik yang diperlukan untuk menghitung jumlah kuadrat adalah seperti tabel berikut.

Tabel 8.14. Tabel Statistik Induk Temp at Tingg al (B) Sikap Sosial (C)

A1 (laki-laki) A2 (perempuan) Total ∑X Total ∑X2 n ∑X ∑X2 _{n ∑X ∑X}2 Kota (B1) Tingg i (C1) Sedan g (C2) Renda h (C3) 3 3 3 38 47 51 514 741 869 3 3 3 39 49 52 521 803 912 77 96 103 Jumla h 9 136 2124 9 140 2236 276 4360

135 Pingg iran (B2) Tingg i (C1) Sedan g (C2) Renda h (C3) 3 3 3 34 42 50 388 596 842 3 3 3 35 42 47 421 602 749 69 84 97 Jumla h 9 126 1826 9 124 1772 250 3598 Desa (B3) Tingg i (C1) Sedan g (C2) Renda h (C3) 3 3 3 37 50 56 467 836 1056 3 3 3 35 44 47 411 662 745 72 94 103 Jumla h 9 143 2359 9 126 1818 269 4177 Desa Terpe ncil (B4) Tingg i (C1) Sedan g (C2) Renda h (C3) 3 3 3 34 48 52 398 782 920 3 3 3 36 49 56 432 805 1050 70 97 108 Jumla h 9 134 2100 9 141 2287 275 4387 Total 36 539 8409 36 531 8113 1070 16522

136 Semu a Langkah-langkah perhitungan: 1).

620

,

611

72

1070

16522

2







Tot

JK

2).

0

,

889

72

1070

36

531

36

539

2 2 2









A

JK

3).

24

,

278

72

1070

18

275

18

269

18

250

18

276

2 2 2 2 2













B

JK

4).

.

028

,

328

72

1070

6

108

6

103

6

97

6

103

6

97

6

94

6

84

6

96

6

70

6

72

6

69

6

77

2 2 2 2 2 2 2 2 2 2 2 2 2

































































C

JK

FK (Faktor Koreksi) adalah

 

15901,389 72 10702 2   N Xtot 5).

00

,

19

999555

,

18

278

,

24

889

,

0

389

,

15901

55556

,

15945

9

141

9

126

9

124

9

140

9

134

9

143

9

126

9

136

2 2 2 2 2 2 2 2



































_{A B} AB

FK

JK

JK

JK

137 6).



 

 





 

 



694 , 1 028 , 328 889 , 0 389 , 15901 333333 , 3400 083333 , 3640 333333 , 2821 083333 , 2914 083333 , 1752 083333 , 1704 12 56 47 47 52 12 52 56 50 51 12 49 44 42 49 12 48 50 42 47 12 36 35 35 39 12 34 37 34 38 2 2 2 2 2 2                                      C A AC JK JK FK JK 7).

972

,

9

278

,

24

028

,

328

389

,

15901

66667

,

16263

6

108

6

103

6

97

6

103

6

97

6

94

6

84

6

96

6

70

6

72

6

69

6

77

2 2 2 2 2 2 2 2 2 2 2 2









































C B BC

JK

JK

FK

JK

8).

75

,

4

972

,

9

694

,

1

00

,

19

028

,

328

278

,

24

889

,

0

389

,

15901

99996

,

1628

3

56

3

49

3

36

3

47

3

44

3

35

3

47

3

42

3

35

3

52

3

49

3

39

3

52

3

48

3

34

3

56

3

50

3

37

3

50

3

42

3

34

3

51

3

47

3

38

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

















































































BC AC AB C B A ABC

JK

JK

JK

JK

JK

JK

FK

JK

9). 334 , 232 972 , 9 694 , 1 75 , 4 0 , 19 028 , 328 278 , 24 889 . 0 611 , 620                  tot A B C AB AC BC ABC dal JK JK JK JK JK JK JK JK JK

138 10). Menghitung Derajat Kebebebasan

71

1

72

1

48

23

1

72

1

6

2

*

3

*

1

*

*

6

2

*

3

*

2

2

*

1

*

3

3

*

1

*

2

1

3

1

3

1

4

1

1

1

2

1



























































































N

db

db

db

db

db

db

db

db

N

db

db

db

db

db

db

db

db

db

db

db

db

db

db

c

db

b

db

a

db

total ABC BC AC AB C B A dal C B A ABC C B BC C A AC B A AB C B A

11). Menghitung Rerata Jumlah Kuadrat (RJK) RJKA = JKA/dbA = 0,889/1 = 0.889 RJKB = JKB/dbB = 24,278/3 =8,093 RJKC = JKC/dbC =328,028/2 = 164,014 RJKAB = JKAB/dbAB = 19/3 = 6,333 RJKBC = JKBC/dbBC = 9,972/6 = 1,662 RJKAC = JKAC/dbAC = 1,694/2 = 0,847

RJKABC = JKABC/dbABC = 4,75/6= 0,792

RJKdal = RJKdal/dbdal = 232,00/48 = 4,833 (varians terkecil/pembagi)

12). Menghitung harga F

FA = RJKA/RJKdal = 0,889/ 4,833 = 0,184

FB = RJKB/RJKdal = 8,093/4,833 = 1,674

139 FAB= RJKAB/RJKdal = 6,333/4,833 =1,310

FAC = RJKAC/RJKdal =0,847/4,833 =0,175

FBC = RJKBC/RJKdal =1,1662/4,833 = 0,344

FABC = RJKABC/RJKdal= 0,792/4,833 = 0,164

Tabel 8.15. Tabel Ringkasan Anava ABC

SV JK Db RJK F h F tab A B C AB AC BC ABC dalam 0,889 24,278 328,028 19,00 1,694 9,972 4,75 232,00 1 3 2 3 2 6 6 48 0,889 8,093 164,014 6,333 0.847 1,662 0,792 4,833 0,184ns 1,674ns 33,934*) 1,310ns 0,175ns 0,344ns 0,164ns -- 4,08 2,84 3,23 2,84 3,23 2,17 2,17 -- Total 620,611 71 -- --

Memperhatikan tabel di atas, ternyata hanya FC (F antar C atau F

antar sikap sosial yang signifikan). Ini berarti terdapat perbedaan yang signifikan prestasi belajar IPS antara siswa yang memiliki sikap sosial tinggi, sedang, dan rendah. Prestasi belajar IPS yang tertinggi diperoleh oleh siswa yang memiliki sikap sosial rendah.

140

Uji lanjut antar C dengan t – Scheffe, t tabel = 2,021 t1-2 = 5,449 (sig)

t1-3 = 8,071 (sig)

t2-3 = 2,620 (sig)

E. Anava Rancangan AS (Rancangan Pengukuran Berulang)

Rancangana analisis varians ini disebut juga Treatment by Subject. Rancangan ini hanya terdiri atas satu kelompok sampel dan digunakan untuk menganalisis suatu perkembangan dari suatu periode ke periode berikutnya. Misalnya, ingin diteliti tentang pengaruh penggunaan metode inovatif terhadap prestasi belajar IPA. Misalnya, diperoleh data seperti tabel berikut.

Tabel 8.16. Data Perkembangan Prestasi Belajar IPA

Kasus A1 A2 A3 A4 XTot X1 X2 X3 X4 1 2 3 4 5 6 4 2 6 5 5 7 3 6 6 7 4 5 5 6 8 7 7 7 8 6 9 7 8 9 20 20 29 26 24 28

141

Berdasarkan data pada tabel di atas, kemudian dihitung statistik induk yang diperlukan untuk menganalisis data tersebut, seperti tabel berikut.

Tabel 8.17. Tabel Kerja Statistik Induk

Statistik A1 A2 A3 A4 Total XS n ∑X ∑X2 6 29 155 6 31 171 6 40 272 6 47 375 24 147 973 6 147 3677 X 4,83 5,16 6,6 7,83 6,125 6,125 Langkah mengerjakan: 1)

72

,

625

24

147

973

2







Tot

JK

2).

34

,

792

24

147

6

47

40

31

29

2



2



2



2

_

2

_



A

JK

3).

18

,

875

24

147

4

3677

2







S

JK

4). JKAS JKTOT JKAJKS 72,62534,79218,87518,958. 5). dbA= a-1 = 4-1 = 3 6). dbS = s-1 = 6-1 = 5 7). dbAS = dbA * dbS = 3 * 5 = 15

142 8). 11,597 3 792 , 34 _   A A A db JK RJK 9). 3,775 5 875 , 18 _   S S S db JK RJK 10). 1,264 15 958 , 18 _   AS AS AS db JK RJK

Tabel 8.18. Tabel Ringkasan Anava AS

SV JK db RJK Fhitung F tabel S A AS (dalam) 18,875 34,792 18,958 5 3 15 3,775 11,597 1,264 2,987 9,175*) - - 5.42 - Total 72,625 23 - - -

*) = signifikan pada taraf signifikansi 5%

Dalam hal ini yang menjadi sasaran uji hipotesisnya adalah F antar A. FA hitung diperoleh 9,175 lebih besar dari Ftabel (ts. 1%) = 5,42, sehingga H0 ditolak dan H1 diterima.Dengan demikian ada perbedaan yang signifikan prestasi belajar IPA antara periode pengukuran pertama sampai dengan pengukuran terakhir. Oleh karena harga F hitung signifikan, maka harus dilanjutkan dengan uji simple effect antar periode pengukuran dengan menggunakan rumus t-Scheffe. Yang diuji adalah antar periode, yaitu: (1) t (A1-A2); t (A1-A3); t (A1-A4); t (A2-A3), t (A2-A4); dan t (A3-A4). Untuk hasil uji FS tidak dibahas karena asumsi dalam Psikologi menyatakan bahwa

143

dugunakan untuk menguji homogenitas varians. Db t = db dalam = 15. Harga t tabel untuk ts 5% = 2,132

t (A1-A2) =   n RJK X X dal * 2 2 1

₀

_.

₅₀₈

649

.

0

33

.

0

4213333

.

0

33

.

0

6

264

.

1

*

2

16

.

5

83

.

4



_

_

_

(ns) t (A1-A3) = 4.83 – 6,6 = 1,77/0,0.649 = 2,727 ( signifikan) t (A1-A4) = 4,83 – 7,83 = 3/0,649 = 4,622 (sig) t (A2-A3) = 5,16 – 6,6 = 1,44/0.649 = 2,219 (sig) t (A2-A4) = 5,16 – 7,83 = 2,67/0,649 = 4,114 (sig) t (A3-A4) = 6,6 – 7,83 = 1,23/0,649 = 1,895 (ns) Simpulan

Penggunaan metode inovatif berpengaruh terhadap peningkatan prestasi belajar IPA antara pengukuran periode 1 dan 3; 1 dan 4; 2 dan 3; dan 2 dengan pengukuran ke empat.

144

DAFTAR PUSTAKA

Anas Sudijono. 2000. Statistik Pendidikan. Raja Grafindo, Jakarta Budiyono, 2004. Statistika untuk penelitian, UNS Press, Surakarta. Cochran WG. 1977. Sampling Techniques. John Wiley & Sons, Inc.

Fleiss JL, 1981. Statistical Methods for Rates and Proportions. Second Edition. John Wiley & Sons.

Furqon. 2009. Statistika Terapan untuk Penelitian. Cetakan ketujuh. ALFABETA: Bandung.

Hanafiah KA, 2003. Rancangan Percobaan, Teori & Aplikasi. Fakultas Pertanian Universitas Sriwijaya, Palembang. Penerbit PT RajaGrafindo Persada, Jakarta.

Riduwan. 2008. Dasar-dasar Statistika. Bandung:Alfabeta Sudjana, 1996, Metode Statistika, Tarsito, Bandung

_______, 1996, Analisis Korelasi & Regresi, Tarsito, Bandung.

Sugiarto, D. Siagian, LT Sunaryanto, DS Oetomo, 2003. Teknik Sampling. Penerbit PT Gramedia Pustaka Utama, Jakarta.

Sugiyono. 2003. Statistik untuk Penelitian. Alfabeta, Bandung.

Supranto J, 2000. Teknik Sampling untuk Survei dan Eksperimen. Penerbit PT Rineka Cipta, Jakarta.

Sutrisno Hadi. 1989. Statistik I, Andi Offset, Yogyakarta _______, 1988. Statistik II, Andi Offset, Yogyakarta

Usman,Husaini. 2006. Pengantar Statistika. Jakarta: PT Bumi Aksara

Tulus Winarsunu. 2002. Statistik Dalam Penelitian. Psikologi & Pendidikan, UMM Press, Malang.

145