TUJUAN PEMBELAJARAN OUTCOME PEMBELAJARAN

(1)

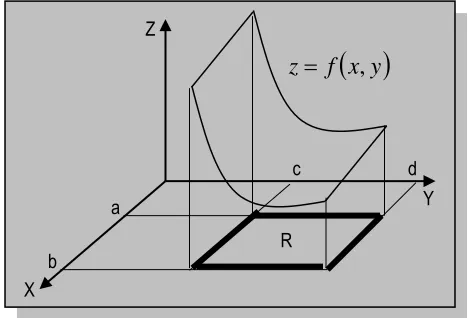
Agar pembaca memahami apa yang disebut dengan Integral Lipat Dua atas Persegipanjang dan bukan Persegipanjang, selanjutnya dapat memahami penggunaan Integral Lipat Dua untuk menghitung Volume Bidang Empat, Massa suatu Benda dan Pusat Massa suatu Benda

Setelah mempelajari bab ini diharapkan mahasiswa dapat :

1. Memahami dan mampu menyelesaikan Integral Lipat Dua atas Persegipanjang dan Bukan Persegipanjang

2. Memahami dan mampu menggunakan Integral Lipat Dua untuk menentukan Volume Bidang Empat, Massa Suatu Benda, Pusat massa suatu benda

TUJUAN PEMBELAJARAN

▸ Baca selengkapnya: tujuan pembelajaran isbd adalah

(2)

Integral dalam Ruang Dimensi 3 170

5.1. Integral Lipat Dua atas Persegipanjang

Adalah Henry Lebesque yang menyumbang tentang pengintegralan dalam dimensi satu dan dimensi n yang dikenal dengan Integral Lebesque yaitu yang memberikan sumbangan pada integral Riemann. Integral Riemann untuk fungsi satu peubah yang telah kita pelajari adalah dalam interval

 

a

,

b

dibagi menjadi n buah partisi

P

yang panjangnya



x

_k, dimana

k



1 ,

2 ,

3 ...

n

, jika kita mengambil suatu titik

k

c

dari sub interval ke-

k

, maka menurut Riemann didefinisikan :

Diketahui

R

suatu persegipanjang dengan sisi-sisi sejajar dengan sumbu-sumbu koordinat, misalkan

R





 

x

,

y

:

a



x



b

,

c



y



d



jika dibuat partisi

P

dari

R

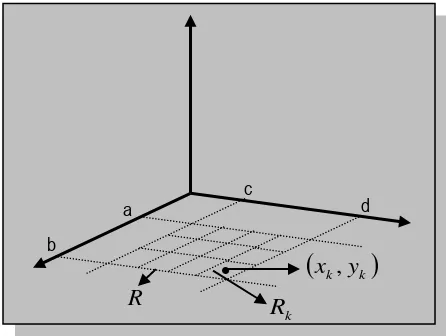
dengan cara membuat garis-garis yang sejajar dengan sumbu x dan sumbu y seperti Gambar 6.1.

Gambar 5.1. Pembagian Daerah R c

a b

d



x

k

,

y

k





R

k

R

 













n

k

k k P

b

a

x

c

f

Lim

dx

x

f

1 0

)

(

)

(3)

Terlihat daerah

R

dengan batas

R





 

x

,

y

:

a



x



b

,

c



y



d



dibagi menjadi n buah partisi yang berbentuk persegipanjang kecil yaitu

R

_k dimana

k



1 ,

2 ,

3 ,...

n

, jika kita mengambil satu buah partisi yaitu

R

_kyang panjang sisinya



x

_k dan



y

_k, maka luas partisi

R

_k adalah



A

_k





x

_k

.



y

_k, jika didalam



A

_kkita mengambil sebuah titik yaitu



x

_k

,

y

_k



kemudian kita substitusikan kedalam fungsinya yaitu

 

x

y

f

z



,

, maka diperoleh tinggi satu buah partisi yaitu



x

k

y

k



f

z



,

, sehingga volume satu buah partisi diperoleh



x

k

y

k



A

k

f

,



karena semuanya terdapat

n

buah partisi, maka menurut penjumlahan Riemann diperoleh :











n k

k k k

y

A

x

f

1

,

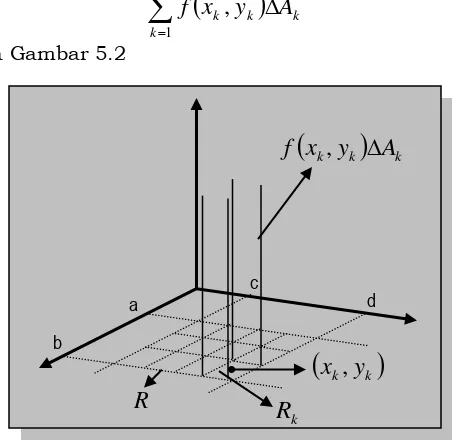
Seperti pada Gambar 5.2

Definisi Integral Lipat Dua :

Andaikan

f

(

x

,

y

)

suatu fungsi dua variable bebas yang terdefinisi pada suatu persegi panjang tertutup

R

, jika :













n k

k k k

P

f

x

y

A

Lim

1 0

,

Gambar 5.2. Volume satu partisi c

a b

d



x

k

,

y

k





R

k

R



x

k

y

k



A

k

(4)

Ada, kita katakana

f

(

x

,

y

)

dapat diintegralkan pada

R

, lebih

lanjut integral yang dituliskan



 

R

dA

y

x

f

,

yang disebut

Integral Lipat Dua

f

(

x

,

y

)

pada

R

diberikan :

 

_















n

k

k k k P

R

A

y

x

f

Lim

dA

y

x

f

1

0

,

Seperti halnya integral lipat satu, yaitu jika

f

 

x



0

, maka



 

b a

dx

x

f

menyatakan luas daerah dibawah kurva

y



f

 

x

dalam interval

 

a

,

b

, dalam integral lipat dua juga menyatakan hal yang sama, jika

 

x

,

y



0 f

maka



 

R

dA

y

x

f

,

menyatakan Volume benda pejal di

bawah permukaan

z



f

 

x

,

y

dan di atas persegi panjang

R

.

Sifat-Sifat Integral Lipat Dua :

1. Integral lipat dua adalah linier a.



 





 

R R

dA

y

x

f

k

dA

y

x

kf

,

b.





   









 





 

R R R

dA

y

x

g

dA

y

x

f

dA

y

x

g

y

x

f

,

2. Integral lipat dua adalah aditif pada persegi panjang yang saling melengkapi hanya pada suatu ruas garis

a.



 





 





 

R R R

dA

y

x

f

dA

y

x

f

dA

y

x

f

1 2

,

3. Sifat pembandingan berlaku, jika

f

   

x

,

y



g

x

,

y

untuk semua

 

x

,

y

di

R

, maka

a.



 





 

R R

dA

y

x

g

dA

y

x

f

,

4. jika

f

 

x

,

y



1

pada

R

, maka integral lipat dua merupakan luas daerah

R

a.









 

R R

R

kA

dA

k

kdA

1

(5)

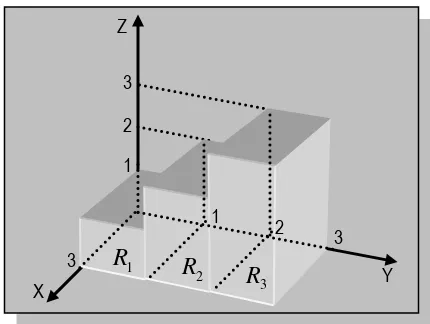
Andaikan

f

 

x

,

y

berupa fungsi tangga yaitu :

 

3

2

1 ,

y



x

f

3

2 ,

3

0

2

1 ,

3

0

1

0 ,

3

0 











y

x

y

x

y

x

Hitung



 

R

dA

y

x

f

,

dengan

R



 

x

,

y

:

0 

x



3 ,

0 

y



3

Jika fungsi

f

 

x

,

y

kita gambar, maka seperti Gambar 5.3

Diketahui ada tiga daerah persegi panjang, yaitu : .

R

₁





 

x

,

y

:

0 

x



3 ,

0 

y



1 

.

R

₂





 

x

,

y

:

0 

x



3 ,

1 

y



2 

.

R

3





 

x

,

y

:

0 

x



3 ,

2 

y



3 

 

_

 

_

 

_

 







1 2 3

,

R R R

R

dA

y

x

f

dA

y

x

f

dA

y

x

f

dA

y

x

f

 

1

2 .

 

2

3 .

 

3

.

1 A

R



A

R



A

R



     

3

1

2 .

3

1

3 .

3

1 .

1 











3

1 2

3 Y X

Z

2 1 3

Gambar 5.3. Fungsi Tangga

1

R

2

R

3

R

(6)

     

3

2 .

3

3 .

1 





18 

Tentukan



 

R

dA

y

x

f

,

jika diketahui

 

16

8

64 ,

2

y

x

y

x

f







dimana

 



,

:

0 



4 ,

0 



8 



x

y

x

y

R

Jika daerah

R

kita bagi menjadi delapan buah bujur sangkar yang sama, dengan sebuah titik tengah



x

_k

,

y

_k



yaitu :

1.

R

₁





 

x

,

y

:

0 

x



2 ,

0 

y



2 

, dengan titik tengah



x

₁

,

y

₁

  



1 ,

1

2.

R

2





 

x

,

y

:

0 

x



2 ,

2 

y



4 



x

2

,

y

2

  



1 ,

3

3.

R

3





 

x

,

y

:

0 

x



2 ,

4 

y



6 



x

3

,

y

3

  



1 ,

5

4.

R

₄





 

x

,

y

:

0 

x



2 ,

6 

y



8 



x

₄

,

y

₄

  



1 ,

7

5.

R

₅





 

x

,

y

:

2 

x



4 ,

0 

y



2 



x

₅

,

y

₅

  



3 ,

1

6.

R

₆





 

x

,

y

:

2 

x



4 ,

2 

y



4 



x

₆

,

y

₆

  



3 ,

3

7.

R

₇





 

x

,

y

:

2 

x



4 ,

4 

y



6 



x

₇

,

y

₇

  



3 ,

5

8.

R

₈





 

x

,

y

:

2 

x



4 ,

6 

y



8 



x

₈

,

y

₈

  



3 ,

7

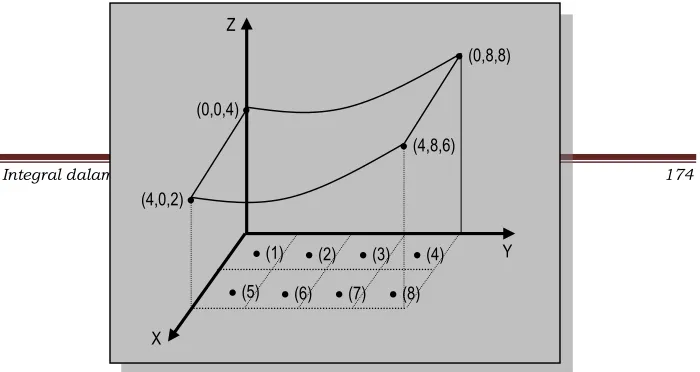
Jika ke delapan daerah bujur sangkar kita gambar, maka seperti Gambar 5.4

Contoh 5.2 :

Penyelesaian 5.2

:

(4,0,2) 

 (1)  (2)  (3)  (4)

 (5)  (6)  (7)  (8)

 (4,8,6)

 (0,8,8)

(0,0,4)  Z

X

(7)

Untuk melakukan penjumlahan Riemann, maka titik tengah



x

_k

,

y

_k



kita substitusikan ke dalam fungsi

 

16

memperoleh tinggi masing-masing balok yang alasnya berbentuk bujur sangkar, diperoelh :

1.



x

₁

,

y

₁

  



1 ,

1







Sehingga menurut Sifat penjumlahan diperoleh :

(8)

Karena

 

R

1



A

 

R

2



A

 

R

3



A

 

R

4



A

 

R

5



A

 

R

6



A

 

R

7



A

 

R

8



4 A

Maka integral di atas dapat ditulis menjadi :

(9)

5.1.1. Soal-Soal Latihan

(10)



x

k

,

y

k



sebagai titik tengah bujur sangkar, jika

f

 

x

,

y

sebagai

berikut :

1.

f

 

x

,

y



12 

x



y

2.

f

 

x

,

y



10 

y

2 3.

f

 

x

,

y



x

2



2 y

2 4.

f

 

x

,

y



2 

x



2 y

5.2. Integral Lipat

Untuk menghitung masalah



 

R

dA

y

x

f

,

dengan

R

berupa

persegipanjang yaitu :

 



x

y

a

x

b

c

y

d



R



,

:



,



Jika kita asumsikan bahwa

f

 

x

,

y



0

pada

R

sehingga kita dapat menafsirkan integral lipat dua sebagai Volume dari benda pejal di bawah permukaan, seperti pada Gambar 6.3

Volume benda pejal di bawah permukaan didefinisikan sebagai berikut :

 





R

dA

y

x

f

V

,

a b X

Y d c

Z

 

x

y

f

z



,

R

(11)

Dengan kata lain bahwa volume benda pejal seperti Gambar 5.5 dapat ditentukan dengan integral lipat dua yaitu :

Atau dapat kita tulis :

Tentukan integral berikut











3

0 2

1

3

2 x

y

dxdy

Pada integral di atas, cara pengintegralan yang pertama (di dalam kurung) dengan menganggap variable

y

sebagai konstanta, sehingga integral lipat di atas dapat diselesaikan sebagai berikut :









3

0 2

1

3

2 x

y

dxdy

 





_















3

0 2

1

3

2 x

y

dx

dy











3

0

2 1 2

3 yx

dy

x



 













3

0

2 2

)

1 (

3

1 )

2 (

3

2 y

y

dy



 













3

0

3

1

6

4 y

y

dy











3

0

3

3 y

dy

Contoh 5.3 :

Penyelesaian 5.3

:

 



 















R

d c

b a

dy

dx

y

x

f

dA

y

x

f

,

 



 















R

b a

d c

dx

dy

y

x

f

dA

y

x

(12)

Integral dalam Ruang Dimensi 3 180 kurung) dengan menganggap variable

y

sebagai konstanta, sehingga integral lipat di atas dapat diselesaikan sebagai berikut

(13)





Volume benda pejal tersebut adalah :

(14)

5.2.1. Soal-Soal Latihan

A. Hitung Integral di bawah ini :

1.



B. Hitung Integral Lipat Dua yang ditunjukan atas R di bawah ini

(15)

3.





R

dA

x

xy

1

2 ,

R





(

x

,

y

);

0 

x



3 ,

1 

y



2 

4.









R

dA

y

x

2

,

R





(

x

,

y

);

0 

x



1 ,

0 

y



1 

5.









R

dA

y

2

4

,

R





(

x

,

y

);

0 

x



2 ,

0 

y



2 

C. Tentukan Volume benda pejal dibawah bidang :

1.

z



x



y



1

atas

R





(

x

,

y

);

0 

x



1 ,

1 

y



3 

2.

z



2 x



3 y

atas

R





(

x

,

y

);

1 

x



2 ,

0 

y



4 

5.3. Integral Lipat Dua atas Daerah Bukan

Persegipanjang

Misalkan ada suatu himpunan tertutup

S

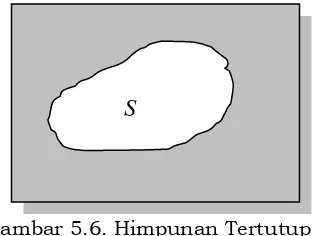
dan terbatas di bidang seperti Gambar 5.6 berikut :

Himpunan tertutup

S

dikelilingi oleh persegi panjang

R

dengan sisi-sisinya sejajar dengan sumbu-sumbu koordinat seperti Gambar 5.7

S

Gambar 5.6. Himpunan Tertutup S

S

(16)

Andaikan

f

 

x

,

y

terdefinisi pada

S

dan didefinisikan

f

 

x

,

y



0

pada bagian

R

diluar

S

kita katakan

f

dapat diintegralkan pada

S

jika ia dapat diintegralkan pada

R

dan berlaku :

 

_

 





R S

dA

y

x

f

dA

y

x

f

,

Misalkan terdapat himpunan

S

sederhana dimana



₁

 

x

dan



₂

 

x

adalah fungsi-fungsi yang kontinu pada interval

 

a

,

b

yang didefinisikan sebagai berikut :

   

 



x

y

x

y

x

a

x

b



S



,

:



₁





₂

,



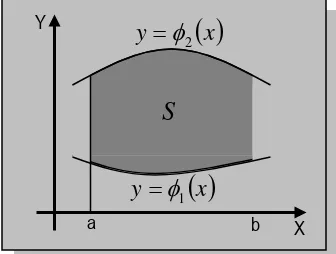
Jika kita gambar himpunan

S

tersebut seperti Gambar 5.8

Jika kita ingin menghitung integral lipat dua dari suatu fungsi

f

 

x

,

y

atau suatu himpunan

S

yang

y

sederhana, maka kita lakukan melingkungi

S

dalam suatu persegi panjang

R

dan membuat

 

x

,

y



0 f

diluar

S

seperti Gambar 5.9

Gambar 5.8. Himpunan S dibatasi oleh y sederhana

 

x

y





₁

 

x

y





₂

S

b _X Y

a

S

b _X Y

a

 

x

y





₁

 

x

y





₂ d

c

(17)

Dengan demikian integral lipat dua dapat didefinisikan sebagai

Secara singkat integral lipat dua untuk himpunan

S

adalah :

(18)





 





1

0

2

10

4

x x

dydx

y

x

3

5 

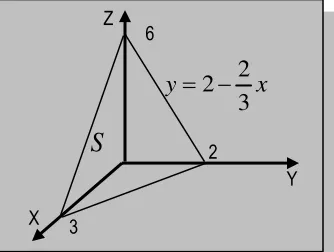
Gunakan integral lipat dua untuk menentukan volume bidang empat yang dibatasi oleh bidang-bidang koordinat dan bidang

0

12

4

6

3 x



y



z





Daerah segitiga di bidang yang membentuk alas bidang empat sebagai

S

, kita akan mencari Volume benda pejal di bawah permukaan



x

y



z

12

3

6

4

1 





dan di atas daerah

S

, bidang yang diberikan

memotong bidang

xy

pada garis

y



12

3 x



6

1 



dan garis



y



x

12

6

3

1 



, jika kita gambar maka bidang empat tersebut seperti

pada Gambar 5.10

Diketahui batas

S

meliputi batas

x

yaitu

 

0 ,

4

, batas

y

adalah









_

2

2 ,

0 x

sedangkan fungsinya adalah

z



12

3 x

6 y



4

1 





sehingga

volume benda pejal tersebut adalah :

Contoh 5.7 :

Penyelesaian 5.7

:

S

3

Y Z

X

2

4

2

2 x

y





(19)



V

Z

dA

(20)

(21)

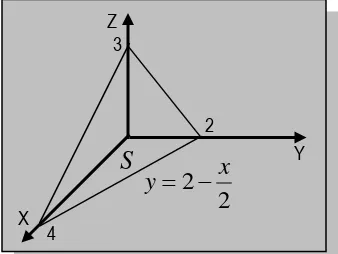
Tentukan Volume benda pejal yang dibatasi oleh bidang-bidang koordinat dan bidang yang mempunyai persamaan

z



6 

2 x



3 y

Diketahui batas

S

_{meliputi batas}

x

_yaitu

0 

x



3

, yang didapat jika

0 

y

dan

z



0

, sedangkan batas

y

adalah

y

x

3

2

0 





yang

diperoleh jika

z



0

, sedangkan fungsinya adalah

z



6 

2 x



3 y

jika kita gambar pada sistem koordinat, maka benda pejal tersebut seperti pada Gambar 5.11 dan volumenya sebagai berikut :



V

Z

dA

S









 





3

0 3 2 2

0

3

2

6

x

dydx

y

x

















_



3

0

3 2 2

0 2

2

3

2

6 y

xy

y

dx

x

 

















_



3

0

2

0 )

3

2

2 (

2

3 )

3

2

2 (

2 )

3

2

2 (

6 x

x

dx















_

_

_

_



3

0

2 2

)

9

4

3

8

4 (

2

3

4

12 x

x

dx

Penyelesaian 5.8

:

S

x

y

3

2

2 



6

Y Z

X

2

3

(22)

5.3.1. Soal-Soal Latihan

A. Hitung Integral Lipat Berikut Ini

1.

 

B. Hitung Integral Lipat Dua yang diberikan berikut ini

1.



x

,

S

adalah daerah segitiga dengan titik-titik

(23)

5.









S

dA

y

x

3

,

S

adalah daerah segitiga dengan titik-titik

   

0 ,

2 ,

0

dan

 

2 ,

2

C. Tentukan Volume Benda Pejal dengan Integral Lipat Dua yang dibatasi oleh :

1. Bidang empat yang dibatasi oleh bidang-bidang koordinat dan bidang

z



8 

2 x



4 y

3 x



4 y



z



12 

0 x



y



z



8

5.4. Penerapan Integral Lipat Dua

Penerapan Integral Lipat dua yang paling jelas adalah untuk menentukan volume benda pejal seperti yang telah dibahas, penerapan lainnya adalah untuk menentukan massa suatu benda yang tak homogeny serta letak pusat massa sebuah benda yang tidak homogen.

Benda yang tak homogen adalah benda yang mempunyai kerapanya berubah-ubah atau tidak konstan, dimana kerapatan di setiap titik berbeda, artinya kerapatan di titik A berbeda dengan kerapatan di titik B, secara matematis maka kerapatan yang berubah-ubah itu dirumuskan sebagai fungsi yang mempunyai variable

5.4.1. Massa

Andaikan suatu benda yang mencakup daerah

S

di bidang

xy

dan andaikan kerapatan (massa per satuan luas) di

 

x

,

y

dinyatakan oleh

 

x

,

y



seperti pada Gambar 5.12

Z

(24)

Untuk mempermudah, maka benda tak homogen dalam Gambar 5.12 dibagi-bagi atau dibuat partisi-partisi berupa persegipanjang kecil-kecil misalnya

R

1

,

R

2

,

R

3

,...

R

_k seperti pada Gambar 5.13

Kemudian kita ambil satu titik yaitu



x

_k

,

y

_k



yang terletak di dalam salah satu partisi yaitu partisi

R

_k, maka massa dari

R

_k adalah



x

k

,

y

k

  

A

R

k



yaitu kerapatan di titik



x

_k

,

y

_k



dalam partisi

R

_k dikali luas partisi

R

_k, sehingga massa total benda tersebut didekati oleh



  







n

k

k k k

y

A

R

x

m

1

,



, dimana massa sebenarnya,

m

_diperoleh

dengan mengambil limit dari rumus di atas untuk norma partisi mendekati nol, sehingga menurut teorema diperoleh integral lipat dua yaitu :

Gambar 5.13. Partisi atas Daerah S Y

Z

S



x

k

,

y

k





k

R









S

k

y

dA

x

(25)

Sebuah benda tak homogen (lamina) mempunyai kerapatan sehingga massa total lamina tersebut adalah :

 

Sebuah benda tak homogen (lamina) mempunyai kerapatan

 

x

,

y



x



y



, lamina tersebut dibatasi oleh sumbu

x

, garis

x



0

dan garis

x



1

serta kurva

y



x

2, tentukan massa totalnya.

Contoh 5.10 :

Penyelesaian 5.10

:

(26)

Dari soal di atas, berarti lamina tersebut di batasi oleh batas

x

dari

0 

x

sampai

x



1

, serta batas

y

dari

y



0

sampai

y



x

2sehingga massa total lamina tersebut adalah :

 





5.4.2. Pusat Massa

Titik pusat massa yaitu suatu titik yang menyebabkan benda dalam keadaan setimbang, titik pusat massa ini dituliskan sebagai koordinat

titik yaitu :



oleh rumus berikut

Penyelesaian 5.11

:

(27)

Secara rinci jika suatu benda tak homogen (lamina) yang dibatasi oleh

x

ditentukan oleh rumus :

 

pusat massa





x

ditentukan oleh rumus :

 

Sebuah benda tak homogen (lamina) mempunyai kerapatan

 

x

,

y



x



y



, lamina tersebut dibatasi oleh sumbu

x

, garis

x



0

dan garis

x



1

serta kurva

y



x

, koordinat titik pusat massa.

(28)

Dari soal di atas, berarti lamina tersebut di batasi oleh batas

x

dari

0 

x

sampai

x



1

, serta batas

y

dari

y



0

sampai

y



x

sehingga koordinat titik pusat massa adalah :

(29)

Sehingga diperoleh koordinat titik pusat massa benda tidak homogen tersebut adalah

(30)

5.4.3. Soal-Soal Latihan

Tentukan massa dan titik pusat massa dari lamina yang dibatasi oleh kurva dan kerapatan yang diberikan berikut ini