ANALISIS DATA SURVIVAL MENGGUNAKAN MODEL HAZARD PROPORSIONAL YUDA SUSANTI G

ANALISIS DATA SURVIVAL MENGGUNAKAN

MODEL HAZARD PROPORSIONAL

YUDA SUSANTI

G54103014

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

ABSTRACT

YUDA SUSANTI. Survival Data Analysis Using Proportional Hazard Model. Supervised by HADI SUMARNO and KUTHA ARDANA.

A lot of events occured in daily life are connected with time, for example a salesman who needs time to sell an amount certain item, time duration which is needed to recover from disease, etc. Data about time duration of an event is called survival data. Commonly, survival data can not be observed completely. Therefore, an accurate method is needed to analyze the survival data.

Proportional hazard model is employed to analyze and determine the survival rate from censored data affected one or more explanatory variables. This model assumed that the hazard rate of group is proportional to the hazard rate of another group. The model would be applied to determine the survival rate of the Multiple Myeloma patients.

ABSTRAK

YUDA SUSANTI. Analisis Data Survival Menggunakan Model Hazard Proporsional. Dibimbing oleh HADI SUMARNO dan KUTHA ARDANA.

Banyak peristiwa yang terjadi dalam kehidupan sehari-hari terkait dengan waktu, seperti seorang sales yang membutuhkan waktu untuk menjual sejumlah barang tertentu, lamanya waktu yang diperlukan oleh seseorang untuk memperoleh kesembuhan dari penyakit yang dideritanya, dan lain-lain. Data tentang lamanya waktu dari suatu peristiwa disebut dengan data survival. Data survival pada umumnya tidak dapat diamati secara utuh. Karenanya diperlukan suatu metode analisis yang tepat untuk menentukan tingkat survival dari data tersebut.

Model hazard proporsional digunakan untuk menganalisis dan menentukan tingkat survival dari data tersensor yang dipengaruhi satu atau lebih peubah penjelas. Model ini mengasumsikan bahwa fungsi resiko untuk individu pada suatu grup proporsional dengan fungsi resiko pada grup lain. Model ini diaplikasikan untuk menentukan tingkat bertahan pasien Multiple Myeloma.

ANALISIS DATA SURVIVAL MENGGUNAKAN

MODEL HAZARD PROPOSIONAL

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

YUDA SUSANTI

G54103014

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

Judul Skripsi

: Analisis Data Survival Menggunakan

Model Hazard Proporsional

Nama

: Yuda Susanti

NRP

: G54103014

Menyetujui:

Pembimbing I,

Pembimbing II,

Dr. Ir. Hadi Sumarno, M.S.

Ir. N. K. Kutha Ardana, M.Sc.

NIP. 131 430 804

NIP. 131 842 412

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP. 131 578 806

PRAKATA

Alhamdulillaahi Rabbil ’Aalamiin, segala puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam semoga selalu tercurah kepada Nabi Muhammad SAW beserta keluarga, sahabat, dan pengikutnya hingga akhir jaman.

Karya ilmiah ini berjudul “Analisis Data Survival Menggunakan Model Hazard Proporsional”. Karya ilmiah ini disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Departemen Matematika.

Penulis mengucapkan terima kasih kepada Bapak Hadi Sumarno dan Bapak Kutha Ardana selaku dosen pembimbing atas waktu yang diberikan, bimbingan dan saran yang telah diberikan, serta Bapak Putu Purnaba atas kesediaannya menjadi penguji yang juga telah memberikan saran dan masukan yang dibutuhkan penulis. Ungkapan terima kasih juga disampaikan kepada:

1. Mimi dan Bapak tercinta, adik-adikku: Lia, Fajar, Aldi yag tersayang, serta seluruh keluarga atas segala doa, kasih sayang, serta dukungan yang telah diberikan kepada penulis.

2. Seluruh dosen Departemen Matematika FMIPA IPB atas ilmu dan nasihat yang bermanfaat sehingga membantu penulis dalam menyelesaikan karya ilmiah ini, serta kepada seluruh staf Departemen Matematika yang telah membantu penulis selama belajar di Departemen Matematika IPB.

3. Niken, Nidia, dan Lia M atas kesediaannya menjadi pembahas dalam seminar tugas akhir penulis.

4. Teman-teman Wisma Ayu Depan yang telah memberikan semangat, motivasi dan membantu dalam pelaksanaan seminar.

5. Semua teman seperjuangan, senasib, dan sepenanggungan, Matematika 40. Terima kasih atas kenangan dan kebersamaan dalam segala suasana hati. Biar jauh di mata, namun tetap di hati.

6. Biru Muda, kakak-kakak kelas Matematika 39, serta adik-adik Matematika angkatan 41, 42 dan 43.

7. Semua pihak yang telah memberikan dukungan kepada penulis yang tidak dapat disebut satu per satu sehingga karya ilmiah ini dapat diselesaikan.

Penulis menyadari bahwa penulisan karya ilmiah ini masih jauh dari sempurna. Oleh karena itu kritik dan saran yang membangun sangat penulis harapkan sebagi pemicu untuk bisa berkarya lebih baik di masa mendatang. Semoga karya ilmiah ini dapat bermanfaat bagi pihak yang membutuhkan.

Bogor, Februari 2008

RIWAYAT HIDUP

Penulis dilahirkan di Cirebon pada tanggal 9 November 1985 sebagai anak pertama dari empat bersaudara dari pasangan Bapak Sujana dan Ibu Susilowati.

Pada tahun 1997 penulis menyelesaikan pendidikan dasar di SDN 06 PAGI Jakarta Timur, kemudian melanjutkan studi ke sekolah menengah pertama di SLTPN 139 Jakarta Timur hingga tahun 2000. Pada tahun 2003 penulis menyelesaikan pendidikan menengah atas di SMUN 44 Jakarta Timur dan pada tahun yang sama diterima di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI).

Semasa menjadi mahasiswa, penulis aktif di organisasi kemahasiswaan tingkat fakultas dan tingkat departemen. Pada periode tahun 2004-2005 penulis menjadi Bendahara Dua Serambi Ruhiyah Mahasiswa FMIPA (SERUM-G), dan pada periode waktu yang sama menjadi staf Departemen Kerohanian Matematika di Gugus Mahasiswa Matematika (GUMATIKA). Pada periode tahun 2005-2006 penulis menjadi Bendahara Umum SERUM-G. Pada periode tahun 2005-2007 penulis menjadi Asisten Praktikum Pendidikan Agama Islam untuk tingkat TPB, serta kepanitiaan yang diselenggarakan oleh Badan Eksekutif Mahasiswa FMIPA pada periode 2004/2005 dan periode 2005/2006.

vii

vii

DAFTAR ISI

Halaman

DAFTAR ISI ... vii

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I. PENDAHULUAN I.1 Latar Belakang ... 1

I.2 Permasalahan ... 1

I.3 Tujuan ... 1

II. LANDASAN TEORI ... 1

III. MODEL III.1 Contoh Data Survival ... 4

III.2 Model Hazard Proporsional untuk Dua Populasi ... 4

III.3 Bentuk Umum Model Hazard Proporsional ... 5

III.4 Fitting Model Hazard Proporsional ... 5

III.5 Fungsi Survivor Model Hazard Proporsional ... 7

III.6 Penduga Fungsi Hazard dan Fungsi Survivor ... 8

III.7 Algoritma Penentuan Rasio Hazard ... 9

III.8 Standar Error dan Selang Kepercayaan untuk Rasio Hazard ... 9

IV. CONTOH KASUS ... 10

V. SIMPULAN ... 15

DAFTAR PUSTAKA ... 15

DAFTAR TABEL

Halaman

1 Contoh Data Tidak Tersensor ... 4

2 Contoh Data Tersensor ... 4

3 Hasil Analisis Survival Model Hazard Proporsional ... 10

DAFTAR GAMBAR

Halaman 1 Fungsi Hazard Usia Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 11

2 Fungsi Hazard Jenis Kelamin Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 11

3 Fungsi Hazard Nitrogen Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 12

4 Fungsi Hazard Kalsium Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 12

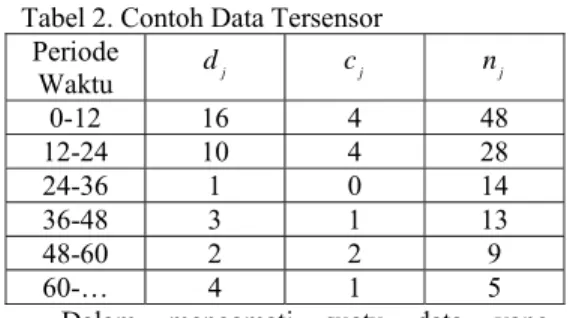
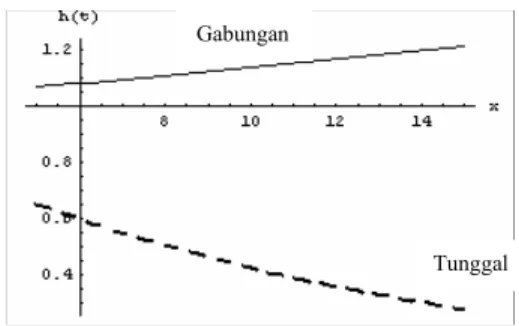
5 Fungsi Hazard Hemoglobin Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 13

6 Fungsi Hazard %Plasma Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 13

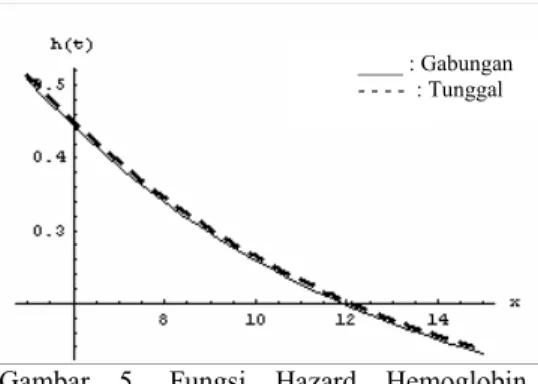
7 Fungsi Hazard Protein Bence-Jones Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan ... 14

DAFTAR LAMPIRAN

Halaman 1 Kode Program Analisis Survival dengan Peubah Gabungan ... 17

2 Kode Program Analisis Survival dengan Peubah Interaksi (NHB) ... 17

3 Kode Program Analisis Survival dengan Peubah Interaksi (N&HB) ... 18

4 Kode Program Analisis Survival dengan Peubah Tunggal ... 18

5 Output Analisis Survival dengan Peubah Gabungan ... 19

6 Output Analisis Survival dengan Peubah Interaksi (N&HB) ... 20

7 Output Analisis Survival dengan Peubah Interaksi (NHB) ... 20

8 Output Analisis Survival untuk tiap-tiap Peubah Tunggal a. Usia ... 21 b. Jenis Kelamin ... 22 c. Nitrogen ... 23 d. Kalsium ... 23 e. Hemoglobin ... 24 f. % Plasma ... 25 g. Protein Bence-Jones ... 26

9 Data Survival Times dari 48 pasien Multiple Myeloma ... 27

I.

PENDAHULUAN

I.1 Latar Belakang

Banyak peristiwa terjadi dalam kehidupan sehari-hari yang terkait dengan waktu, misalnya waktu yang diperlukan oleh seorang sales untuk menjual sejumlah barang tertentu, lamanya waktu yang diperlukan oleh seseorang untuk memperoleh kesembuhan dari penyakit yang dideritanya dan lain-lain.

Data pengamatan di atas disebut data survival. Data survival adalah data tentang pengamatan jangka waktu dari awal pengamatan sampai terjadinya suatu peristiwa (survival time). Data survival pada umumnya tidak dapat diamati secara utuh (tersensor), sehingga diperlukan suatu analisis survival untuk menganalisis dengan tepat.

Seringkali terjadinya peristiwa tersebut ditentukan oleh faktor lain. Ketahanan pasien penderita suatu penyakit misalnya dipengaruhi oleh jenis kelamin, kondisi psikologi, denyut jantung, kadar serum hemoglobin, merokok atau tidak dan kebiasaan diet. Faktor-faktor tersebut dimungkinkan mempunyai pengaruh

yang kuat pada saat pasien bertahan hidup yang dipandang sebagai peubah penjelas. I.2 Permasalahan

Untuk melakukan analisis data tersensor, dapat digunakan metode Life Table atau Kaplan-Meier. Kedua metode tersebut masih sesuai digunakan pada saat ingin membandingkan karakteristik dua populasi. Namun apabila yang ingin dibandingkan adalah lebih dari dua populasi, misalnya ingin melihat perbedaan karakteristik tingkat pendidikan, jenis pekerjaan dan lain-lain, maka metode Life Table atau Kaplan-Meier menjadi tidak praktis, sehingga diperlukan metode lain yang lebih tepat dan sesuai. I.3 Tujuan

Berdasarkan masalah di atas penulisan ini bertujuan untuk memodelkan dan melakukan analisis data survival pada kasus pasien Multiple Myeloma dengan melihat peubah penjelas, menggunakan model hazard proporsional.

II. LANDASAN TEORI

Definisi 1. Data Survival

Data survival adalah data tentang pengamatan jangka waktu dari awal pengamatan sampai terjadinya suatu peristiwa (survival time). Peristiwa itu dapat berupa kegagalan, kematian, respon, timbulnya gejala

dan lain-lain.

( Lee, 1992 ) Definisi 2. Waktu Awal

Waktu awal yaitu waktu pada saat terjadinya kejadian awal, seperti waktu seseorang divonis menderita kanker, waktu pemberian perlakuan dan lain-lain.

( Lee, 1992 ) Definisi 3. Waktu Akhir

Waktu akhir yaitu waktu pada saat terjadinya kejadian akhir seperti kematian, respon dari perlakuan dan lain-lain.

( Lee, 1992 ) Definisi 4. Data Tersensor dan Data Tidak

Tersensor

Data tersensor adalah data yang tidak bisa diamati secara utuh, karena adanya individu yang hilang ataupun dengan alasan lain,

sehingga tidak dapat diambil datanya atau sampai akhir pengamatan individu tersebut belum mengalami peristiwa (resiko). Jika berada dalam kondisi sebaliknya maka disebut data tidak tersensor.

( Lee, 1992 ) Definisi 5. Fungsi Survivor

Misalkan T peubah acak dengan fungsi kepekatan peluang ( )f t . Fungsi sebaran untuk T yaitu

0

( ) ( ) ( )

t

F t =P T < =t

∫

f u du

Fungsi survivor adalah fungsi yang menyatakan peluang seseorang dapat bertahan hingga atau lebih dari waktu t ( mengalami kejadian sesudah waktu t ) yang didefinisikan sebagai berikut :

( ) ( )

S t =P T≥ . t

Teorema 1. Fungsi Survivor

Fungsi survivor ( )S t dengan ( )S t =P T( ≥ t) memiliki fungsi kepekatan peluang dari T , yaitu : f t( ) dS t( )

dt = −

2 Bukti : ( ) 1 ( ) 1 ( ) P T t P T t F t ≥ = − < = − , dengan ( )F t =P T( < t) karena ( )S t =P T( ≥ , maka t) ( ) ( ) ( ) 1 ( ) 0 ( ) 0 ( ) ( ) ( ) ( ) ( ) dS t dF t S t F t dt dt dS t f t dt dS t f t dt dS t f t dt = − ⇔ = − ⇔ = − ⇔ = − ⇔ = − ▪ Terbukti ( Collett, 1994 ) Definisi 6. Peluang Bersyarat

Jika P B( ) 0> maka peluang bersyarat dari kejadian A setelah diketahui kejadian B ialah ( | ) ( ) ( ) P A B P A B P B ∩ = .

( Hogg and Craig, 1995 ) Definisi 7. Fungsi Hazard

Fungsi hazard yaitu fungsi yang menyatakan peluang seseorang mengalami resiko atau suatu kejadian seperti kegagalan atau meninggal pada waktu t dengan syarat bahwa seseorang itu telah bertahan hingga waktu t, fungsinya diberikan:

0 ( | ) ( ) lim t P t T t t T t h t t δ δ δ → ≤ ≤ + ≥ =

Dari definisi di atas diperoleh hubungan antara fungsi survivor dengan fungsi hazard. Dengan menggunakan definisi peluang bersyarat, diperoleh: ( ) ( ) 1 ( ) lim ( ) t F t t F t h t t S t δ δ δ →∞ + − ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠ ( ) ( ) ( ) f t h t S t = Karena f t( ) dS t( ) dt = −

(

)

(

)

0 ln ( ) maka ( ) ln ( ) ( ) ln ( ) ( ) ( ) exp ( ) t d S t h t dt S t h u du S t H t S t H t = − = − = − = −

∫

( Collett, 1994 ) Definisi 8. Metode Parametrik

Metode parametrik adalah metode analisis yang memiliki asumsi sebaran. Misalnya data yang diamati menyebar normal, menyebar binom dan lain-lain.

( Lee, 1992 ) Definisi 9. Metode Non-Parametrik

Metode non-parametrik adalah metode analisis yang tidak berdasarkan asumsi sebaran tertentu.

( Lee, 1992 ) Definisi 10. Metode Maximum Likelihood Misalkan X₁,X₂,...,X masing-masing n peubah acak yang saling bebas dari sebaran yang memiliki fungsi kepekatan peluang

( , )

f xθ dengan parameter θ dimana θ ∈ Ω , Ω adalah ruang parameter. Fungsi kepekatan peluang bersama dariX₁,X₂,...,X adalah n

1 2

( , ) ( , )... ( , )n

f x θ f x θ f x θ merupakan fungsi dari θ dinotasikan dengan ( )Lθ yang kemudian disebut fungsi Likelihood dan dituliskan sebagai :

1 2 1 2

( , , ,..., )n ( ; ) ( ; )... ( ; )n

Lθ x x x = f x θ f x θ f x θ dimana θ ∈ Ω .

Andaikan dicari fungsi sederhana dari

1, ,...,2 n

x x x yaitu u x x( , ,..., )1 2 xn

sehingga θ =u x x( , ,..., )1 2 xn membuat fungsi Likelihood maksimum untuk semua θ ∈ Ω . Statistik U X( 1,X2,...,Xn) disebut penduga kemungkinan maksimum dari θ dinotasikan dengan θ =U X( 1,X2,...,Xn).

( Hogg and Craig, 1995 ) Teorema 2. Deret Taylor

Jika diberikan fungsi f, n 1[ , ]

f ∈ ^ + a b , f kontinu dan terturunkan sampai turunan ke

1

n+ . Misalkan x0∈[ , ]a b untuk setiap

[ , ]

x∈ a b terdapat c=c x( ) yang terletak antara x danx maka 0

( + ) ( | ) ( ) ( ) ( ) ( )

P t T t t P t T t t T t P T t F t t F t S t δ δ δ ≤ < ≤ ≤ + ≥ = _≥ + − =

3 2 0 0 0 0 0 ( ) ( 1) 1 0 0 0 0 ''( ) ( ) ( ) '( )( ) ( ) 2! ( ) ( ) ... ( ) ( ) ! ( 1)! n n n n f x f x f x f x x x x x f x f x x x x x n n + + = + − + − + + − + − + ( Stewart, 2003) Definisi 11. Ragam

Ragam dari peubah acak X adalah nilai harapan dari kuadrat selisih antara X dengannilai harapannya, dinotasikan dengan

2

X

σ . Secara matematis dapat dinyatakan sebagai 2 _{var( ) ( [ ])}2

X X E X E X

σ = = ⎡_⎣ − ⎤_{⎦ .}

Cara lain menetukan ragam, yaitu

2 2 2 2 ( [ ]) 2 [ ] ( [ ]) X E X E X E X X E X E X σ = ⎡_⎣ − ⎤_⎦ ⎡ ⎤ = _⎣ − + _⎦

Karena E adalah operator linier maka

[ ] [ ] (

)

(

) (

)

(

)

2 2 2 2 2 2 2 2 2 [ ] 2 [ ] [ ] [ ] X E X E X E X E X E X E X E X E X E X σ = ⎡_⎣ ⎤_⎦− + ⎡ ⎤ = _{⎣ ⎦}− + ⎡ ⎤ = _{⎣ ⎦}− Akar kuadrat dari 2

X

σ yaitu σ disebut X simpangan baku dari X .

( Hogg and Craig, 1995 ) Sifat Ragam

Bila X suatu peubah acak dan a konstanta, maka: 2 2 2 2 2

aX a X a

σ = σ = σ . (Walpole,1992) Ragam bagi Penduga Parameter

Ragam bagi penduga parameter θ yang memaksimumkan fungsi Likelihood didefinisikan sebagai berikut

1 2 2 ln ( ) ˆ var( ) E d L d θ θ θ − ⎛ ⎛ ⎞⎞ = −⎜_⎜ ⎜ ⎟⎟_⎟ ⎝ ⎠ ⎝ ⎠

Ketika nilai harapan dari turunan persamaan sulit diperoleh, selanjutnya ragam dari ˆθ diperoleh dari pendekatan

1 2 2 ln ( ) ˆ var( ) d L d θ θ θ − ⎛ ⎞ ≈ −⎜ ⎟ ⎝ ⎠

Dan standar error ˆθ merupakan akar dari ragam ˆθ yaitu

ˆ ˆ

. .( ) var( )

s e θ = θ

( Collett, 1994) Definisi 12. Uji Hipotesis

Uji hipotesis adalah suatu aturan yang digunakan untuk menerima atau menolak

suatu hipotesis dari hasil amatan yang diperoleh. Hipotesis mengenai populasi yang akan diterima kebenarannya sampai ada bukti untuk menolaknya dinamakan hipotesis nol (H ). Apabila hipotesis ini ditolak ₀ kebenarannya maka ada hipotesis lain yang kita anggap benar, yaitu hipotesis tandingan (H1) .

Dalam perumusan hipotesis dikenal dua macam hipotesis yaitu

a. Hipotesis satu arah . 0 0 1 0 1. : : H H μ μ μ μ ≤ > 0 0 1 0 2. : : H H μ μ μ μ ≥ < b. Hipotesis dua arah

0 0 1 0 : : H H μ μ μ μ = ≠

( Hogg and Craig, 1995) Definisi 13. Selang Kepercayaan

Selang kepercayaan adalah selang yang dapat dipercaya pada tingkat kepercayaan tertentu. Contoh μ σ diketahui: Bila X , adalah nilai tengah contoh acak berukuran n, yang diambil dari suatu populasi dengan ragam diketahui, maka selang kepercayaan

(1−α)100% bagi μ adalah / 2 / 2 X Z X Z n n α α σ _μ σ − < < +

Besaran Zα/ 2 adalah nilai yang luas daerah

disebelah kanan di bawah kurva normal baku adalah

2 α

. ( Wallpole, 1992 )

Definisi 14. Statistik Uji Wald

Uji Wald digunakan untuk menguji parameter β . Berdasarkan hipotesis

0 1 : 0 : 0 i i H H β β = ≠

dengan statistik uji-nya adalah: ˆ ˆ . .( ) i i i W s e β β = dimana: i ˆ _penduga i β = β i ˆ ˆ . .( ) standar error _i s e β = β 1, 2,..., i= p

Statistik uji Wald akan megikuti sebaran normal baku Ζ. Kaidah pengambilan keputusan yaitu tolak hipotesis nol jika nilai

4

( )

hit

Z Z memenuhi Zhit >Zα/ 2 untuk taraf nyata uji α .

(Collett, 1994) Definisi 15. Statistik 2 ln L−

Statistik 2 ln L− digunakan untuk menguji peranan peubah secara bersama-sama. Bila model memiliki p peubah penjelas,maka model reduksi akan memiliki

q< peubah bebas. Pengurangan ini p berdasarkan hasil uji Wald untuk setiap peubah yang tidak nyata. Statistik uji-nya yaitu: 0 1 2lnL 2 ln L L ⎛ ⎞ − = − ⎜ ⎟ ⎝ ⎠ dimana: 0

L = nilai likelihood peubah penjelas tereduksi

1

L = nilai likelihood dengan semua peubah penjelas

Berdasarkan hipotesis:

0 1 2 1

: ... 0

: minimal ada satu nilai 0, 1, 2,..., , 1,..., p p p q i H H i p p p q β β β β + = + = = + = ≠ = + +

Statistik 2 ln L− akan mengikuti sebaran Chi-Square dengan derajat bebas p− . q Kaidah keputusan yang diambil adalah jika

( ) 2lnL χp q− α

− > , maka hipotesis nol ditolak. (Collett, 1994)

III. MODEL

III. 1 Contoh Data Survival

Data yang termasuk dalam data survival memenuhi empat kriteria, yaitu:

1. Waktu kejadian, t . j

2. Banyaknya objek yang diamati, n . j 3. Banyaknya objek yang meninggal, d . j 4. Banyaknya objek yang tersensor, c . j Jika

∑

cj=0 maka pengamatan tersebut dilakukan secara utuh, sebaliknya jika

0 j c ≠

∑

disebut dengan data survival tersensor.

Tabel 1. Contoh Data Tidak Tersensor j Waktu j n d j S t ˆ( ) 0 11 11 1 1.000 1 13 10 5 0.909 2 14 5 2 0.455 3 15 3 2 0.2732 4 17 1 1 0.091 Dimana 0 ˆ _{ˆ( )} j j j n S S t n = = (3.1.1) dengan

0 banyaknya individu dalam satu

himpunan data

n =

ˆ _{ˆ( ) penduga fungsi survivor}

banyaknya individu dengan waktu kelangsungan hidup j j j S S t n t = = = ≥

Tabel 2. Contoh Data Tersensor Periode Waktu d j c j n j 0-12 16 4 48 12-24 10 4 28 24-36 1 0 14 36-48 3 1 13 48-60 2 2 9 60-… 4 1 5

Dalam mengamati suatu data yang dibutuhkan adalah populasi atau contoh yang akan dijadikan objek.

( Sanella , 2006 ) III. 2 Model Hazard Proporsional untuk Dua Populasi

Misalkan tersedia data survival untuk individu suatu populasi, maka dapat dihitung fungsi hazard untuk individu dalam populasi tersebut yaitu 1 1 1 ( ) ( ) ( ) f t h t S t = .

Apabila ada populasi lain dengan fungsi hazard h t , dan ₂( ) h t dapat dinyatakan ₂( ) proporsional terhadap h t , maka 1( )

2( ) . ( )1

h t =ψ h t , dengan ψ merupakan konstan ψ > . Karena 0 ψ > maka dapat 0 dilakukan transformasi dengan menggunakan fungsi eksponen, yaitu ψ =exp( )β ,

1 , 0 , 1 , 0 1 , 0 β β ψ β β > > ⎧ ⎪ −∞ < < ∞ ⎨= = ⎪< < ⎩ .

5

Misal X adalah peubah indikator dengan

1, jika individu mendapat perlakuan baru 0, jika individu mendapat perlakuan standar

X =⎧⎨

⎩

Jika x adalah nilai dari i X untuk individu ke- i , i=1, 2,...,n maka fungsi hazard untuk individu itu dapat ditulis

0

( ) xi ( )

i

h t =e h tβ (3.2.1) Persamaan (3.2.1) adalah model hazard proporsional untuk membandingkan dua populasi.

III. 3 Bentuk Umum Model Hazard

Proporsional

Model hazard proporsional pada persamaan (3.2.1) dapat dibuat lebih umum yaitu resiko kematian individu ke-i bergantung pada nilai x₁i,x₂i,...,x dari p pi peubah penjelas X₁,X₂,...,X . Himpunan p nilai peubah penjelas pada model hazard proporsional direpresentasikan oleh vektor

i x , sehingga x = (x xi 1, ,...,2 x ) . p

Misalkan h t adalah fungsi hazard dari 0( ) individu yang nilai peubah penjelasnya membuat vektor

i

x sama dengan nol, h t 0( ) disebut baseline fungsi hazard . Maka hazard untuk individu ke-i dapat ditulis sebagai berikut

( )

( ) i ( )

i o

h t =ψ x h t

dengan , ψ

( )

xi adalah nilai fungsi dari vektor

peubah penjelas untuk individu ke-i.

( )

i

ψ x dapat diartikan sebagai hazard pada

waktu t untuk individu yang vektor peubah penjelasnya adalah

i

x , yang relatif terhadap hazard individu yang peubah penjelasnya

0 =

x . ψ

( )

xi tidak mungkin negatif maka

dapat ditulis ψ

( )

xi =exp( )ηi dimana η i

adalah kombinasi linier p peubah penjelas pada xi ,yaitu 1 1 2 2 ... i xi xi pxpi η =β +β + +β 1 p j ji j= β x = ∑

dengan β = koefisien dari peubah penjelas i

1, 2,... p

x x x . Maka bentuk umum hazard proporsional menjadi 1 1 2 2 0 0 1 1 0 1 1 2 2 0 ( ) exp( ... ) ( ) exp ( ) (3.3.1) ( ) exp ( ) ( ) log ... ( ) i i i j ji p j ji j p i j ji j i i i j ji h t x x x h t x h t h t x h t h t x x x h t β β β β β β β β = = = + + + ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝ ⎠ ⎛ ⎞ ⇔ = ⎜_⎜ ⎟_⎟ ⎝ ⎠ ⎛ ⎞ ⇔ ⎜ ⎟= + + + ⎝ ⎠

∑

∑

(3.3.2)

Persamaan (3.3.2) di atas menunjukkan bahwa model hazard proporsional juga dapat dilihat sebagai model linier logaritma dari rasio hazard.

III. 4 Fitting Model Hazard Proporsional Fitting model hazard proporsional (persamaan 3.3.1) dalam pengamatan survival data memerlukan pendugaan koefisien yang belum diketahui dari peubah penjelas

P

X X

X₁, ₂,..., pada komponen linier

1, ...,2 p

β β β , j=1, 2,...,p. Ada dua komponen dari model yaitu

β

j dan h t yang akan o( )

diduga secara terpisah.

β

j akan diduga terlebih dahulu yang kemudian akan dipergunakan untuk mengkonstruksi pendugaan baseline fungsi hazard h t_o( ).

Penduga

β

j

Parameter

β

j pada model hazard proporsional merupakan parameter yang belum diketahui dan akan diduga dengan menggunakan metode maximum likelihood. Fungsi likelihood adalah peluang bersama dari data pengamatan yang dianggap sebagai fungsi dari parameter yang tidak diketahui dalam asumsi model. Pendugaan

β

j dengan metode maximum likelihood adalah nilai ketika fungsi likelihood maximum.

Misal data disediakan untuk n individu yang terdiri dari r waktu kematian yang tidak tersensor dan n-r individu tersensor kanan, diurutkan menjadi t1< < < . t2 ... tr

Diasumsikan hanya ada satu orang yang meninggal pada tiap waktu kematian, jadi tidak ada data yang saling terkait. Hal lain yang perlu dipertimbangkan adalah peluang kematian individu ke-i yang meninggal pada waktu kematian

j

t , dengan syarat t_j menjadi satu-satunya waktu pengamatan dari r waktu

6

kematian t₁,t₂,...,t_r, sehingga dinotasikan menjadi ( | )P A B .

Misalkan kejadian A adalah individu dengan nilai peubah penjelas xji meninggal

pada saat

j

t dan kejadian B adalah kematian tunggal pada saat

j t , makaP A

(

∩B

)

=P A

( )

sehingga

(

)

(

)

( )

( )

( )

| P A A B P B P A B P P B = ∩ =

[individu dengan nilai peubah penjelas meninggal pada saat ] [kematian tunggal pada saat ]

ji j j P x t P t = (3.4.1)

Pembilang pada ekspresi di atas adalah bentuk sederhana dari resiko kematian pada waktu

j

t untuk individu yang nilai peubah penjelasnya xji. Jika pembilang itu adalah

individu ke-i yang meninggal pada saat

j

t , fungsi hazard ini dapat ditulis menjadi ( )h t_{i j} . Penyebutnya adalah jumlah dari resiko kematian pada waktu

j

t (dinotasikan h tl( )j )

untuk semua individu yang mempunyai resiko kematian pada waktu

j

t . Ini adalah

penjumlahan nilai h tl( )j didalam himpunan

resiko

j

t ,

(

R t( )_j

)

. Dengan R t( )j adalah

himpunan resiko pada waktu

j

t yang terdiri dari individu-individu yang bertahan hidup hingga

j

t . Sehingga peluang dalam ekspresi (3.4.1) menjadi ( ) ( ) ( ) j i j l j l R t h t h t ∈

∑

,

dengan menggunakan persamaan (3.3.1), maka baseline fungsi hazard adalah

0 1 0 ( ) 1 1 ( ) 1 exp ( ) ( | ) exp ( ) exp exp j j p j ji j p j jl l R t j p j ji j p j jl l R t j x h t P A B x h t x x β β β β = ∈ = = ∈ = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

∑

∑

∑

∑

∑

∑

, sehingga dengan mengambil hasil peluang bersyarat di atas, memberikan fungsi likelihood 1 1 ( ) 1 exp ( ) (3.4.2) exp j p j ji r j p j j jl l R t j x L x β β β = = ∈ = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

∑

∏

∑

∑

Misal data terdiri dari n pengamatan survival time, dinotasikan t₁,t₂,...,t_n.

i

δ adalah indikator sensor yaitu

0 , jika individu ke- mengalami sensor kanan 1 , selainnya

i

i

δ = ⎨⎧

⎩

maka persamaan (3.6) dapat ditulis

1 1 ( ) 1 exp ( ) exp i j p j ji r j p j j jl l R t j x L x δ β β β = = ∈ = ⎡ ⎛ ⎞ ⎤ ⎢ ⎜_⎜ ⎟_⎟ ⎥ ⎢ _{⎝ ⎠} ⎥ = _{⎢ ⎥} ⎛ ⎞ ⎢ _{⎜ ⎟}⎥ ⎢ ⎜_⎝ ⎟_⎠⎥ ⎣ ⎦

∑

∏

∑

∑

Jika persamaan di atas di ln-kan maka diperoleh 1 1 ( ) 1 1 1 ( ) 1 1 exp ln ( ) ln exp exp ln exp i j j p j ji n j p i j jl l R t j p j ji n j i _p i j jl l R t j n i j i x L x x x δ β β β β δ β δ β = = ∈ = = = ∈ = = ⎛ _{⎡ ⎛ ⎞ ⎤} ⎞ ⎜ _{⎢ ⎜ ⎟ ⎥} ⎟ ⎜ ⎟ ⎜ _{⎢ ⎝ ⎠ ⎥} ⎟ ⎜ ⎟ = _{⎢ ⎥} ⎛ ⎞ ⎜ _{⎢ ⎥} ⎟ ⎜ ⎟ ⎜ _{⎢ ⎜ ⎟⎥} ⎟ ⎜ _{⎣ ⎝ ⎠⎦} ⎟ ⎝ ⎠ ⎡ ⎛ ⎞ ⎤ ⎢ ⎜_⎜ ⎟_⎟ ⎥ ⎢ ⎝ ⎠ ⎥ = _{⎢ ⎥} ⎛ ⎞ ⎢ _{⎜ ⎟}⎥ ⎢ ⎜ ⎟⎥ ⎝ ⎠ ⎣ ⎦ =

∑

∑

∑

∑

∑

∑

∑

∑

∑

1 ( ) 1 ln exp (3.4.3) j p p ji j jl j l R t j x β x = ∈ = ⎡ ⎛ ⎛ ⎞⎞⎤ ⎢ − ⎜_⎜ ⎜_⎜ ⎟_⎟⎟_⎟⎥ ⎢ _{⎝ ⎝ ⎠⎠}⎥ ⎣

∑

∑

∑

⎦

Penduga

β

j dapat diperoleh dengan

memaximumkan fungsi ln-likelihood yaitu dengan mencari solusi dari

ln ( ) 0 j j d L d β β =

Turunan pertama ln (L β terhadap _j)

β

j,

dinotasikan u

( )

β , sehingga j ln ( ) ( ) j j j d L u d β β β = ,

Jadi ˆβ dapat diperoleh dari persamaan _j ˆ ( ) 0 ˆ ln ( ) 0 ˆ j j j u d L d β β β = =

7 1 1 ( ) 1 ln exp 0 ˆ j p p n i j ji j jl i j l R t j j x x δ β β β = = ∈ = ⎛ ⎡ ⎛ ⎛ ⎞⎞⎤⎞ ⎜ ⎢ ⎜ ⎟⎥⎟ ∂ − _⎜ ⎜_⎜ ⎟_⎟⎟ ⎜ ⎢_{⎣ ⎝ ⎝ ⎠⎠}⎥_⎦⎟ ⎝ ⎠ ⇔ = ∂

∑ ∑

∑

∑

( ) 1 1 1 1 ( ) 1 exp 0 exp j j p p j jl jl p n l R t j j i ji p i j j jl l R t j x x x x β δ β ∈ = = = = ∈ = ⎡ ⎛ ⎞ ⎤ ⎢ ⎜_⎜ ⎟_⎟ ⎥ ⎢ _{⎝ ⎠} ⎥ ⇔ _⎢ − _⎥= ⎛ ⎞ ⎢ _{⎜ ⎟} ⎥ ⎢ ⎜_⎝ ⎟_⎠ ⎥ ⎣ ⎦

∑

∑

∑

∑ ∑

∑

∑

Penduga parameter

β

j di atas sulit dicari

secara analitis tapi lebih mudah diselesaikan secara numerik, namun dalam karya ilmiah ini hal tersebut tidak dibahas lebih mendalam.

Standar Error dan Selang Kepercayaan ˆβ j

Ragam dari ˆβ dapat didefinisikan j

sebagai berikut

( )

( )

1 2 2 ln ˆ var j j j L β β

β

− ⎛ ⎞ ⎜∂ ⎟ ≈ −⎜ ⎟ ∂ ⎜ ⎟ ⎝ _⎠ 2 2 ( ) 1 1 ( ) 1 1 2 1 ( ) 1 _{( ) 1} exp exp ˆ var( ) exp _exp j j j j p p p p j jl jl j jl jl n _{l R t j j} l R t j j j i _p p i j jl _{j jl} l R t j l R t j x x x x x _x β β β δ β _β ∈ = = ∈ = = = ∈ = _{∈ =} ⎛ ⎡ _{⎛ ⎞⎛ ⎞ ⎛ ⎛ ⎞ ⎞} ⎤ ⎜ ⎢ _{⎜ ⎟⎜ ⎟ ⎜ ⎜ ⎟ ⎟} ⎥ ⎜ ⎢ _⎝⎜ ⎟⎜_⎠⎝ ⎟_⎠ ⎜_⎝ ⎜_⎝ ⎟_⎠ ⎟_⎠ ⎥ ⎜ ⎢ ⎥ ≈ −_⎜ − + ⎢ ⎛ ⎞ _{⎛ ⎛ ⎞⎞} ⎥ ⎜ ⎟ ⎢ _{⎜ ⎟ ⎜ ⎜ ⎟⎟} ⎥ ⎜ ⎟ ⎜ ⎟ ⎢ ⎝ ⎠ _{⎝ ⎝ ⎠⎠} ⎥ ⎣ ⎦ ⎝

∑

∑

∑

∑

∑

∑

∑

∑

∑

_∑

_∑

1 2 2 ( ) 1 1 ( ) 1 1 2 1 ( ) 1 _{( ) 1} exp exp exp _exp j j j j p p p p j jl jl j jl jl n l R t j j l R t j j i _p p i j jl j jl l R t j _{l R t j} x x x x x _x β β δ β _β − ∈ = = ∈ = = = ∈ = _{∈ =} ⎞ ⎟ ⎟ ⎟ ⎟ ⎜ ⎟ ⎜ ⎟ ⎠ ⎡ _{⎛ ⎞⎛ ⎞ ⎛ ⎛ ⎞ ⎞} ⎤ ⎢ _{⎜ ⎟⎜ ⎟ ⎜ ⎜ ⎟ ⎟} ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎢ _{⎝ ⎠⎝ ⎠ ⎝ ⎝ ⎠ ⎠} ⎢ ≈ − ⎢ ⎛ ⎞ _{⎛ ⎛ ⎞⎞} ⎜ ⎟ ⎢ ⎜ ⎟ ⎜_⎜ ⎜_⎜ ⎟_⎟⎟_⎟ ⎢ ⎝ ⎠ _{⎝ ⎝ ⎠⎠} ⎣

∑

∑

∑

∑

∑

∑

∑

∑

∑

_∑

_∑

1 (3.4.4) − ⎛ ⎞ ⎜ ⎥⎟ ⎜ _⎥⎟ ⎜ ⎥⎟ ⎜ ⎥⎟ ⎜ ⎥⎟ ⎜ ⎥_⎦⎟ ⎝ ⎠

Standar error dari ˆβ adalah akar dari ragam ˆj β , yaitu j

2 2 ( ) 1 1 ( ) 1 1 2 1 ( ) 1 _{( ) 1} ˆ ˆ . .( ) var( ) exp exp exp _exp j j j j j j p p p p j jl jl j jl jl n _{l R t j j} l R t j j i _p p i j jl j jl l R t j _{l R t j} s e x x x x x _x β β β β δ β _β ∈ = = ∈ = = = ∈ = _{∈ =} = ⎡ _{⎛ ⎞⎛ ⎞ ⎛ ⎛ ⎞ ⎞} ⎤ ⎢ _{⎜ ⎟⎜ ⎟ ⎜ ⎜ ⎟ ⎟} ⎥ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎢ _{⎝ ⎠⎝ ⎠ ⎝ ⎝ ⎠ ⎠} ⎥ ⎢ ⎥ = − ⎢ ⎛ ⎞ _{⎛ ⎛ ⎞⎞} ⎥ ⎜ ⎟ ⎢ _{⎜ ⎟ ⎜ ⎜ ⎟⎟} ⎜ ⎟ ⎜ ⎟ ⎢ ⎝ ⎠ _{⎝ ⎝ ⎠⎠} ⎣ ⎦

∑

∑

∑

∑

∑

∑

∑

∑

∑

_∑

_∑

1 (3.4.5) − ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎥⎟ ⎜ ⎥⎟ ⎝ ⎠

Standar error di atas dapat digunakan untuk mencari selang kepercayaan untuk ˆβ , j

yaitu

(

1−α

)

100% selang kepercayaan untuk ˆ j β adalah ˆ _{/ 2. . .}

(

ˆ

)

j Zα s e j β ± β .

III. 5 . Fungsi Survivor Model Hazard Proporsional

Fungsi hazard kumulatif untuk individu ke- i adalah diperoleh dengan cara mengintegralkan kedua sisi pada persamaan (3.3.1)

8 0 1 0 0 ( ) exp ( ) (3.5.1) t p t i j ji j h u du β x h u du = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

∫

∫

sehingga fungsi hazard kumulatif untuk individu ke- i adalah

0 1 ( ) exp ( ) (3.5.2) p i j ji j H t β x H t = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

Dengan mengalikan tiap sisi dari persamaan (3.5.2) dengan −1 dan mengeksponenkannya, serta menggunakan persamaan S t( )=exp

{

−H t( )

}

,

akan diperoleh fungsi survivor untuk individu ke- i yaitu 0 1 0 1 ( ) exp ( ) ( ) ( ) exp p i j ji j p i j ji j H t x H t H t H t x β β = = ⎛ ⎞ − = − ⎜_⎜ ⎟_⎟ ⎝ ⎠ ⎛ ⎞ − = − ⎜_⎜ ⎟_⎟ ⎝ ⎠

∑

∑

(

)

(

)

(

)

exp 1 exp 1 0 1 0 0

exp ( ) exp ( ) exp

exp ( ) exp ( ) ( ) ( ) (3.5.3) p x jji j p x j ji j p i j ji j i i H t H t x H t H t S t S t β β β ⎛ ⎞ ⎜∑ ⎟ ⎜₌ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜∑ ⎟ ⎜₌ ⎟ ⎝ ⎠ = ⎡ ⎛ ⎞⎤ − = ⎢− ⎜_⎜ ⎟_⎟⎥ ⎢ _{⎝ ⎠}⎥ ⎣ ⎦ ⎡ ⎤ − =_⎣ − _⎦ = ⎡_⎣ ⎤_⎦

∑

III. 6 Penduga Fungsi Hazard dan Fungsi

Survivor

Misal komponen linier dari model hazard proporsional terdiri dari p peubah penjelas

1, 2,..., p

X X X dan koefisien penduga dari peubah ini adalah β βˆ ˆ1, 2,...,β . Penduga ˆP

fungsi hazard untuk individu ke- i adalah

0 1 ˆ_{( ) exp} p ˆ ˆ_{( ) (3.6.1)} i j ji j h t β x h t = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

dimana xji adalah nilai peubah penjelas ke-j

untuk individu ke- i , i=1, 2,...,n, dan 0

ˆ ( )

h t adalah penduga baseline fungsi hazardh t0( ) .

Penduga baseline fungsi hazard telah diturunkan oleh (Kalbfleisch dan Prentice, 1973) menggunakan pendekatan metode maximum likelihood. Misal ada r waktu kematian yang diurutkan meningkat yaitu

1 2 ... r

t < < < , dan ada t t d kematian, serta j j

n individu yang mempunyai resiko kematian pada waktu tj. Penduga baseline fungsi

hazard pada waktu t yaitu _j

0

ˆ_{( ) 1} ˆ _(3.6.2)

j j

h t = −ξ

dimana ˆξ adalah solusi dari persamaan j

1 1 ˆ exp ( ) ( ) 1 ˆ exp ˆ exp 1 p j jl j j j p j jl _p j j jl x l D t l R t j x x β β β ξ = = ⎛ ⎞ ⎜ ⎟ ∈ _{⎜ ⎟} ∈ = ⎝ ⎠ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ _{⎛ ⎞} ⎝ _{⎠ = ⎜ ⎟} ⎜ ⎟ ⎝ ⎠ ∑ −

∑

∑

∑

∑

(3.6.3) untuk j=1, 2,...,r ( )j

D t = kumpulan semua dj kematian

individu pada waktu t . _j ( )j

R t = kumpulan semua individu yang mempunyai resiko kematian (n_j) pada waktu

j

t

Pada kasus tidak adanya keterkaitan waktu kematian, yaitu dimana

1 , untuk 1, 2,...,

j

d = j= r, maka sisi kiri persamaan (3.6.3) akan mempunyai bentuk tunggal, sehingga persamaan tersebut dapat diselesaikan untuk mendapatkan

1 ˆ exp 1 ( ) 1 ˆ exp ˆ ₁ ˆ exp p j jl j j x p j jl j j _p j jl l R t j x x β β ξ β = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = ∈ = ∑ ⎛ ⎛ ⎞ ⎞ ⎜ ⎜ ⎟ ⎟ ⎜ ⎝ ⎠ ⎟ = −_{⎜ ⎟} ⎛ ⎞ ⎜ _{⎜ ⎟}⎟ ⎜ _{⎝ ⎠}⎟ ⎝ ⎠

∑

∑

∑

dimana xji adalah nilai peubah penjelas ke-j

untuk individu ke- i .

Diasumsikan bahwa resiko kematian adalah konstan untuk waktu kematian yang berdekatan. Lalu, ˆξ dapat dianggap sebagai j

penduga dari peluang individu yang bertahan hidup dari t sampai j t( 1)j+ . Maka penduga

baseline fungsi survivor yaitu 0 1 ˆ_{( )} k ˆ _(3.6.4) j j S t ξ = =

∏

untuk tk ≤ <t t( 1)k+ , k=1, 2,...,r− , 1

nilai penduga baseline fungsi survivor sama dengan nol untuk t≥ . Kumulatif baseline t_r fungsi hazard yaituH t0( )= −lnS t0( ), maka penduganya adalah 0 0 1 ˆ ˆ ˆ ( ) ln ( ) k ln j (3.6.5) j H t S t ξ = = − = −

∑

untuk tk ≤ <t t( 1)k+ ,k=1, 2,...,r− 1

Penduga baseline fungsi hazard, fungsi survivor, dan kumulatif fungsi hazard pada persamaan (3..6.2), (3.6.4), dan (3.6.5) dapat digunakan untuk mencari hubungan penduga untuk individu dengan nilai peubah penjelas

9

ji

x . Dengan mengintegralkan kedua sisi dari persamaan (3.6.1) , akan diperoleh

0 1 0 0 ˆ_{( ) exp} ˆ ˆ_{( ) (3.6.6)} t p t i j ji j h u du β x h u du = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

∫

∫

Sehingga penduga fungsi hazard kumulatif untuk individu ke- i adalah

0 1 ˆ ˆ _{( ) exp} p ˆ _{( ) (3.6.7)} i j ji j H t β x H t = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

dengan mengalikan tiap sisi dari persamaan (3.6.7) dengan 1− dan mengeksponenkannya, serta menggunakan persamaan

(

)

ˆ_{( ) exp} ˆ_{( )}

S t = −H t , akan diperoleh penduga fungsi survivor untuk individu ke- i yaitu

0 1 ˆ ˆ _{( ) exp} p ˆ _{( )} i j ji j H t β x H t = ⎛ ⎞ − = − ⎜_⎜ ⎟_⎟ ⎝

∑

⎠ 0 1 ˆ ˆ ˆ ( ) ( ) exp p i j ji j H t H t β x = ⎛ ⎞ − = − ⎜_⎜ ⎟_⎟ ⎝

∑

⎠

(

)

(

)

(

)

exp ˆ 1 ˆ exp 1 0 1 0 0 ˆ ˆ ˆ

exp ( ) exp ( ) exp

ˆ ˆ exp ( ) exp ( ) ˆ ˆ ( ) ( ) (3.6.8) p x j ji j p x jji j p i j ji j i i H t H t x H t H t S t S t β β β ⎛ ⎞ ⎜∑ ⎟ ⎜₌ ⎟ ⎝ ⎠ ⎛ ⎞ ⎜∑ ⎟ ⎜₌ ⎟ ⎝ ⎠ = ⎡ ⎛ ⎞⎤ − = ⎢− ⎜_⎜ ⎟_⎟⎥ ⎢ ⎝ ⎠⎥ ⎣ ⎦ ⎡ ⎤ − =_⎢⎣ − _⎥⎦ ⎡ ⎤ = ⎣ ⎦

∑

untukt_{( )k} ≤ <t t_{( )k+1},k=1, 2,...,r− . 1

III. 7 Algoritma Penentuan Rasio Hazard 1. Misalkan ada p populasi, yaitu populasi

1, 2,..., p .

2. Fungsi hazard untuk populasi ke-i yaitu 0

( ) xi ( )

i

h t =eβ h t , i=1, 2,...,p.

3. Fungsi hazard untuk populasi ke-i+1

yaitu 1 1( ) 0( ) i x i h t eβ +h t + = , i=1, 2,...,p. 4. Maka rasio hazard populasi ke-i+ 1

terhadap populasi ke-i yaitu 1 1 ( ) 1 0 0 ( ) ( ) ( ) ( )

=

i i i i x x x i x i h t e h t h t e h t

e

β β β ψ + +− + = =

III. 8 Standar Error dan Selang Kepercayaan untuk Rasio Hazard

Parameter β adalah logaritma dari rasio resiko kematian pada waktu t untuk individu pada populasi satu yang relatif terhadap populasi yang berbeda. Rasio hazard itu sendiri adalah ψ =exp( )β dan hubungan penduga rasio hazard dengan rasio hazard adalah ψˆ=exp( )βˆ .

Dengan menggunakan sifat ragam dan pendekatan deret Taylor, maka ragam dari suatu fungsi ( )g x dengan x adalah peubah acak, diberikan

(

)

(

)

(

)

(

)

(

)

(

)

0 0 2 2 0 0 0 0 0 0 0 0 0 0 ( ) var ( ) var ! var ( ) '( ) ''( ) ... 2! var 0 '( ) var ''( ) ... 2! n _k k k g x g x x x k x x g x g x x x g x x x g x x x g x = ⎡ ⎤ = _⎢ − _⎥ ⎣ ⎦ ⎡ − ⎤ ≈ ⎢ + − + + ⎥ ⎢ ⎥ ⎣ ⎦ − ≈ +⎡_⎣ ⎤_⎦ − +⎡_⎣ ⎤_⎦ +

∑

(

)

( ) 2 var g x( ) dg x var( )x dx ⎛ ⎞ ≈ ⎜_⎝ ⎟_⎠ (3.8.1) Standar error dari ψ dapat diperoleh dari ˆ standar error ˆβ dengan menggunakan j

persamaan (3.21), dari hasil tersebut diperoleh pendekatan ragam untuk ˆψ dalam ˆβ , yaitu j

( )

(

)

2

2

ˆ ˆ

ˆ

var exp( ) var( ) ˆ ˆ ( ) var( ) (3.8.2) j j j ψ β β ψ β ≈ ≈

sehingga standar error untuk ˆψ dapat didefinisikan sebagai berikut

ˆ

ˆ ˆ

. .( ) . .( ) (3.8.3)j

s e ψ =ψs e β

(

1−α

)

100% selang kepercayaan untuk rasio hazard adalah

/ 2

ˆ Z_α ( . .( )) (3.8.4)s e ˆ

9

IV. CONTOH KASUS

Multiple myeloma adalah penyakit yang berbahaya yang ditandai dengan penimbunan plasma sel yang tidak normal dan sel darah putih dalam sumsum tulang.

Perkembangbiakan plasma sel yang tidak normal dalam tulang menyebabkan rasa sakit dan merusak jaringan tulang. Pasien yang mengidap multiple myeloma selalu mengalami kekurangan darah sehingga menyebabkan kambuhnya infeksi dan lemah. Salah satu universitas di USA telah memeriksa hubungan antara peubah penjelas yang mempengaruhi dan waktu ketahanan (survival times dalam satuan bulan) dari pasien.

Dalam pengamatan peubah respon utama adalah waktu dari diagnosa waktu awal sampai pasien meninggal. Pada data lampiran 9 terdapat 48 pasien multiple myeloma, 48 pasien tersebut berusia antara 50 sampai dengan 80 tahun. Beberapa dari mereka belum meninggal pada saat pengamatan berakhir, pasien tersebut termasuk jenis sensor kanan.

Untuk pasien dengan status meninggal pada saat pengamatan dengan survival times tertentu ditandai dengan angka 1, sedangkan 0 menjelaskan bahwa pasien mengalami sensor kanan.

Pada waktu diagnosis nilai dari peubah-peubah yang mempengaruhi tingkat survival pasien kemudian dicatat, meliputi :

a. Usia pasien (tahun)

b. Jenis kelamin pasien (0=pria, 1=wanita)

c. Kandungan nitrogen dalam darah d. Kandungan kalsium dalam darah e. Kandungan hemoglobin dalam darah f. Persentase sel plasma

g. Kandungan protein Bence-Jones dalam urine (0=tidak ada, 1=ada) Diantara 48 pasien tersebut ada 60,4% pasien laki-laki, sisanya wanita dan 31,25% pasien yang mengandung protein Bence-Jones pada urine sisanya tidak mengandung protein Bence-Jones. Banyaknya pasien yang meninggal pada tiap waktu kematian dan banyaknya pasien yang beresiko meninggal pada tiap waktu kematian tersebut akan dihitung. Diberikan data 48 pasien Multiple Myeloma (lihat lampiran 9). Semua hasil analisis data 48 pasien Multiple Myeloma menggunakan SAS 9.1 for Windows (Statistics Aplication Software) menggunakan model hazard proporsional.

Dilakukan analisis survival dengan peubah-peubah penjelas untuk melihat pengaruh peubah penjelas terhadap tingkat bertahan hidup pasien :

a. Fungsi hazard untuk tiap peubah tunggal adalah

0

( ) exp( ) ( ) h t = βX h t

b. Fungsi hazard untuk peubah gabungan adalah

1 1 2 2 3 3 4 4 5 5 6 6 7 7 0

( ) exp( i i i i i i i) ( )

i

h t = βX +β X +βX +β X +β X +β X +β X h t

1

X = usia, X2= jenis kelamin, X = nitrogen, 3 X4= kalsium 5

X = hemoglobin, X = % plasma, ₆ X = protein Bence-Jones ₇ Tabel 3. Hasil Analisis Survival Model Hazard Proporsional

Peubah Tunggal Peubah Gabungan

Peubah penjelas _{β ˆ ˆ} . . s e β Nilai p ψ ˆ β ˆ s e. . β ˆ Nilai p ψ ˆ Usia 0.00973 0.02783 0.7267 1.010 -0.01936 0.02792 0.4882 0.981 Jenis kelamin 0.06583 0.35449 0.8527 1.068 -0.25090 0.40229 0.5328 0.778 Nitrogen 0.01868 0.00559 0.0008 1.019 0.02083 0.00593 0.0004 1.021 Kalsium -0.08570 0.13173 0.5153 0.918 0.01312 0.13244 0.9211 1.013 Hemoglobin -0.13291 0.05939 0.0252 0.876 -0.13524 0.06889 0.0496 0.874 % Plasma 0.00145 0.00570 0.7986 1.001 -0.00159 0.00658 0.8085 0.998 Protein -0.53939 0.38823 0.1647 0.583 -0.64044 0.42669 0.1334 0.527

11

Peubah Tunggal Peubah Gabungan Peubah penjelas

Selang kepercayaan Selang kepercayaan

Usia 0.956 - 1.066 0.929 - 1.036 Jenis kelamin 0.533 - 2.140 0.354-1.712 Nitrogen 1.008 - 1.030 1.009-1.033 Kalsium 0.709 - 1.188 0.782-1.314 Hemoglobin 0.779 - 0.984 0.763-1.000 % Plasma 0.990 - 1.013 0.986-1.011 Protein 0.272 - 1.248 0.228-1.216 a. Pengaruh Usia

Secara teori kondisi seorang pasien multiple myeloma dipengaruhi oleh faktor usia yaitu banyak diderita oleh seseorang yang berusia >50 tahun terutama seseorang yang berusia sekitar 70 tahun, hanya sedikit sekali kasus multiple myeloma yang diderita oleh seseorang yang berusia < 40 tahun (www.mayoclinic.com). Semakin tua usia seseorang maka kondisi tubuhnya akan semakin lemah sehingga dapat dikatakan tingkat bertahan hidupnya rendah.

Gambar 1. Fungsi Hazard Usia Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

Dari Gambar 1 dapat dilihat bahwa untuk analisis survival peubah tunggal semakin bertambah usia seorang pasien maka resiko kematiannya semakin tinggi, sedangkan untuk analisis survival peubah gabungan semakin bertambah usia pasien maka resiko kematiannya semakin rendah, dan hasil analisis pada Tabel 3 menunjukkan bahwa untuk analisis survival peubah tunggal dengan nilai ψ =1.010, artinya pasien yang berusia satu tahun lebih tua maka resiko kematiannya 1.010 kali lebih tinggi dibandingkan pasien yang berusia satu tahun lebih muda, sedangkan untuk analisis survival peubah gabungan nilai ψ =0.981, artinya pasien yang berusia satu tahun lebih tua mempunyai resiko kematian 0.981 kali lebih rendah dibandingkan pasien yang berusia satu tahun lebih muda.

Namun dilihat dari nilai p > α =0.05 untuk analisis survival peubah tunggal maupun analisis survival peubah gabungan yang menunjukkan bahwa peubah penjelas usia tidak berpengaruh nyata terhadap tingkat bertahan hidup pasien. Dengan demikian tidak terdapat perbedaan tingkat bertahan hidup antara pasien yang berusia lebih muda dengan pasien yang berusia lebih tua.

b. Pengaruh Jenis Kelamin

Seorang pria yang terkena penyakit

multiple myeloma akan lebih beresiko berkembang penyakitnya dibandingkan seorang pasien wanita.

(www.mayoclinic.com) Dari Tabel 3 hasil analisis survival peubah tunggal nilai ψ =1.068, hal tersebut menunjukkan bahwa pasien wanita lebih tinggi resiko kematiannya 1.068 kali dibandingkan dengan pasien pria. . Tapi hasil analisis survival peubah gabungan diperoleh nilai ψ =0.778 yang berarti pasien wanita memiliki resiko kematian lebih rendah 0.778 kali dibandingkan pasien pria.

Namun dilihat dari nilai p > α =0.05 untuk analisis survival peubah tunggal maupun analisis survival peubah gabungan yang menunjukkan bahwa peubah penjelas jenis kelamin tidak berpengaruh nyata terhadap tingkat bertahan hidup pasien. Dengan demikian tidak terdapat perbedaan tingkat bertahan hidup antara pasien wanita dengan pasien pria.

Jenis Kelamin 0,000 0,200 0,400 0,600 0,800 1,000 1,200 1 2 x h(t) Tunggal Gabungan

Gambar 2. Fungsi Hazard Jenis Kelamin Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

Tunggal

Gabungan

12

c. Pengaruh Nitrogen

Gambar 3. Fungsi Hazard Nitrogen Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

Dari Gambar 3 dapat dilihat bahwa analisis peubah gabungan memiliki resiko kematian yang lebih tinggi dibandingkan analisis peubah tunggal.

Pada Tabel 3 hasil analisis survival peubah tunggal maupun analisis survival peubah gabungan menunjukkan bahwa nitrogen berpengaruh nyata terhadap tingkat bertahan hidup pasien. Hal ini menunjukkan bahwa terdapat perbedaan tingkat bertahan hidup antara pasien yang kandungan nitrogennya tinggi dengan pasien yang kandungan nitrogennya rendah.

Nilai rasio hazard nitrogen hasil analisis survival peubah tunggal dan analisis survival peubah gabungan sebesar 1.019 dan 1.021, hal ini berarti untuk setiap kenaikan nitrogen sebesar satu satuan pada seorang pasien, maka mempunyai resiko kematian lebih tinggi 1.019 kali untuk analisis survival peubah tunggal dan 1.021 kali untuk analisis survival peubah gabungan dibandingkan pasien yang kandungan nitrogennya turun satu satuan. Dengan kata lain seorang pasien yang kandungan nitrogennya naik satu satuan peluang bertahan hidupnya akan lebih kecil dibandingkan pasien yang kandungan nitrogennya turun satu satuan.

d. Pengaruh Kalsium

Kandungan kalsium yang lebih tinggi dalam darah pada seorang pasien multiple myeloma akan lebih beresiko untuk berkembang penyakitnya dibandingkan pasien yang kandungan kalsiumnya normal, hal tersebut dapat terjadi ketika kalsium terlarut ke dalam darah.

(www.mayoclinic.com)

Gambar 4. Fungsi Hazard Kalsium Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

Gambar 4 menunjukkan untuk analisis survival peubah tunggal semakin banyak kandungan kalsium dalam darah maka resiko kematiannya semakin rendah, sedangkan analisis survival peubah gabungan semakin banyak kandungan kalsium dalam darah maka resiko kematiannya semakin tinggi.

Pada Tabel 3 hasil analisis survival peubah tunggal nilai ψ =0.918, hal tersebut menunjukkan bahwa pasien yang kandungan kalsiumnya lebih tinggi mempunyai resiko kematian yang lebih rendah 0.918 kali dibandingkan dengan pasien yang kandungan kalsiumnya lebih rendah. Tapi hasil analisis survival peubah gabungan diperoleh nilai

1.013

ψ = yang berarti pasien yang kandungan kalsiumnya lebih tinggi mempunyai resiko kematian yang lebih tinggi 1.013 kali dibandingkan dengan pasien yang kandungan kalsiumnya lebih rendah.

Namun dilihat dari nilai p > α =0.05 untuk analisis survival peubah tunggal maupun analisis survival peubah gabungan yang menunjukkan bahwa peubah penjelas kalsium tidak berpengaruh nyata terhadap tingkat bertahan hidup pasien. Dengan demikian tidak terdapat perbedaan tingkat bertahan hidup antara pasien yang kalsium dalam daranhnya tinggi dengan pasien kalsium dalam darahnya rendah.

e. Pengaruh Hemoglobin

Hemoglobin sangat diperlukan oleh seseorang, apalagi seorang pasien yang mengidap multiple myeloma yang selalu mengalami kekurangan darah, sehingga semakin banyak hemoglobin dalam darah maka akan semakin baik untuk kondisi pasien yang mengidap multiple myeloma.

Pada Tabel 3 hasil analisis survival peubah tunggal dan peubah gabungan, hemoglobin berpengaruh nyata terhadap tingkat bertahan hidup pasien, artinya tingkat bertahan hidup

Tunggal Gabungan

Gabungan

14

pasien yang kandungan hemoglobinnya tinggi berbeda dengan tingkat bertahan hidup pasien yang kandungan hemoglobinnya rendah.

Nilai rasio hazard hemoglobin hasil analisis survival peubah tunggal dan analisis survival peubah gabungan sebesar sebesar 0.876 dan 0.874, artinya untuk setiap kenaikan hemoglobin sebesar satu satuan pada seorang pasien, maka mempunyai resiko kematian lebih kecil 0.876 kali untuk analisis survival peubah tunggal dan 0.874 kali untuk analisis survival peubah gabungan dibandingkan pasien yang kandungan hemoglobin nya turun satu satuan. Dengan kata lain seorang pasien yang kandungan hemoglobin nya naik satu satuan peluang bertahan hidupnya akan lebih besar dibandingkan pasien yang kandungan hemoglobin nya turun satu satuan.

Gambar 5. Fungsi Hazard Hemoglobin Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

f. Pengaruh Sel Plasma (%)

Persentase sel plasma yang nomal adalah <5%, tapi pada pasien multiple myeloma persentase sel plasma meningkat hingga >10%, maka seorang pasien multiple myeloma yang persentase sel plasmanya di atas normal akan lebih beresiko berkembang penyakitnya.

(www.mayoclinic.com)

Gambar 6. Fungsi Hazard % Sel Plasma Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan

Dari Gambar 6 dapat dilihat untuk analisis peubah tunggal semakin banyak persentase sel

plasma dalam darah maka resiko kematiannya semakin tinggi, sedangkan analisis peubah gabungan semakin banyak persentase sel plasma dalam darah maka resiko kematiannya semakin rendah.

Pada Tabel 3 hasil analisis survival peubah tunggal nilai ψ =1.001, hal tersebut menunjukkan bahwa pasien yang persentase sel plasmanya lebih tinggi mempunyai resiko kematian yang lebih tinggi 1.001 kali dibandingkan dengan pasien yang persentase sel plasmanya lebih rendah. Tapi hasil analisis survival peubah gabungan diperoleh nilai

0.998

ψ = yang berarti pasien yang persentase sel plasmanya lebih tinggi mempunyai resiko kematian yang lebih rendah 0.998 kali dibandingkan dengan pasien yang persentase sel plasmanya lebih rendah.

Namun dilihat dari nilai p > α =0.05 untuk analisis survival peubah tunggal maupun analisis survival peubah gabungan yang menunjukkan bahwa peubah penjelas persentase sel plasma tidak berpengaruh nyata terhadap tingkat bertahan hidup pasien. Dengan demikian tidak terdapat perbedaan tingkat bertahan hidup antara pasien yang persentase sel plasma dalam daranhnya tinggi dengan pasien persentase sel plasma dalam daranhnya rendah.

g. Pengaruh Protein Bence-Jones

Multiple myeloma adalah kanker yang menyerang sumsum tulang yang mengakibatkan produksi protein yang berlebihan dan membuat saluran ginjal tersumbat. Maka seorang pasien multiple myeloma yang kandungan proteinnya lebih banyak akan lebih beresiko berkembang penyakitnya dibandingkan yang kandungan

proteinnya sedikit. (http://kiamat.info)

Pada Tabel 3 nilai rasio hazard protein Bence-Jones hasil analisis survival peubah tunggal dan analisis survival peubah gabungan sebesar sebesar 0.583 dan 0.527, artinya pasien yang mengandung protein Bence-Jones maka mempunyai resiko kematian lebih kecil 0.583 kali untuk survival analisis peubah tunggal dan 0.527 kali untuk analisis survival peubah gabungan dibandingkan pasien yang tidak mengandung protein Bence-Jones.

Namun dilihat dari nilai p > α =0.05 untuk analisis survival peubah tunggal maupun analisis survival peubah gabungan yang menunjukkan bahwa peubah penjelas protein Bence-Jones tidak berpengaruh nyata terhadap tingkat bertahan hidup pasien.

____ : Gabungan - - - - : Tunggal

Tunggal

Gabungan

14

Dengan demikian tingkat bertahan hidup pasien yang mengandung protein Bence-Jones sama dengan tingkat bertahan hidup pasien yang tidak ada kandungan protein Bence-Jones. Protein 0,000 0,500 1,000 1,500 1 2 x h(t) T unggal Gabungan

Gambar 7. Fungsi Hazard Protein Bence-Jones Analisis Survival dengan Peubah Tunggal dan Peubah Gabungan.

Melihat hasil analisis di atas, ternyata peubah penjelas yang berpengaruh nyata terhadap tingkat bertahan hidup pasien adalah nitrogen dan hemoglobin. Akan dilihat apakah ada interaksi antara kedua peubah penjelas tersebut. Pertama, dilakukan analisis survival dengan dua peubah penjelas yaitu nitrogen dan hemoglobin. Kedua, dilakukan analisis survival dengan tiga peubah penjelas yaitu nitrogen, hemoglobin, dan interaksi nitrogen-hemoglobin (NHB). Kemudian dengan statistik −2ln L dapat ditentukan adakah interaksi antara nitrogen dan hemoglobin. Bentuk interaksinya adalah perkalian antara

nilai nitrogen dan nilai hemoglobin, yaitu

1 2 1

.

2 X X

=

X X , dimana 1 2 X X =nitrogen-hemoglobin(

NHB

) 1 X = nitrogen ( N ), 2 X = hemoglobin ( HB )

Maka model hazard proporsional untuk pasien ke- i setelah ada interaksi yaitu

1 1 2 2 12 1 2 0

( ) ( ) ( )

i

h t =expβX +β X +β X X h t

Hasil analisis survival dengan peubah penjelas nitrogen dan hemoglobin

Analysis of Maximum Likelihood Estimates

Parameter Standard Hazard 95% Hazard Ratio

Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits nitrogen 1 0.01857 0.00567 10.7121 0.0011 1.019 1.007 1.030 hemoglobin 1 -0.13364 0.06205 4.6384 0.0313 0.875 0.775 0.988 1 2 0 ( ) exp( 0.01857 - 0.13364 ) ( ) i h t = X X h t 2lnL 202.938 − =

Hasil analisis survival dengan peubah penjelas nitrogen, hemoglobin, dan NHB

Analysis of Maximum Likelihood Estimates

Parameter Standard Hazard 95% Hazard Ratio Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits nitrogen 1 0.02339 0.04456 0.2756 0.5996 1.024 0.938 1.117 HB 1 -0.12164 0.12643 0.9257 0.3360 0.885 0.691 1.134 NHB 1 -0.0004803 0.00440 0.0119 0.9132 1.000 0.991 1.008 1 2 1 2 0 ( ) exp( 0.65551 - 0.38293 - 0.05201 ) ( ) i h t = X X X X h t 2lnL 202.926 − = , 5%;1 2 _3.84 χ =

Dari hasil analisis survival dengan peubah penjelas nitrogen dan hemoglobin terlihat bahwa nilai-p nitrogen dan hemoglobin < α =0.05, artinya nitrogen dan hemoglobin berpengaruh terhadap tingkat bertahan hidup pasien. Sedangkan hasil

0 1