Metode Numerik Stepest Descent Dengan Arah Pencarian Negatif Sigma Gradien

Metode Numerik Stepest Descent Dengan Arah Pencarian

Negatif Sigma Gradien

Rukmono Budi Utomo

Universitas Muhammadiyah Tangerang

rukmono.budi.u@mail.ugm.ac.id

Abstrak—Penelitian ini mengkaji tentang metode numerik stepest descent dengan

arah pencarian negatif sigma gradien. Penelitian dilakukan dengan memahami terlebih dahulu mengenai metode numerik Stepest Descent dengan arah pencarian negatif gradien beserta algoritmanya. Setelah itu dikonstruksi metode numerik Stepest Descent dengan arah pencarian negatif sigma gradien beserta algoritmanya. Dalam penilitian ini juga diberikan contoh penggunaan kedua metode numerik dalam menyelesaikan masalah optimisasi satu fungsi tujuan tanpa kendala beserta analisis hasilnya.

Kata kunci:stepest descent, arah pencarian negatif sigma gradien I. PENDAHULUAN

Dalam menyelesaikan suatu masalah dunia nyata (real problem), langkah awal yang dilakukan para matematikawan adalah menyatakan masalah dunia nyata tersebut kedalam pengertian matematis. Langkah ini meliputi identifikasi variabel-variabel yang terjadi pada masalah, dan membentuk hubungan antar variabel-variabel tersebut[1]. Langkah selanjutnya adalah menjabarkan variabel-variabel, merumuskan asumsi-asumsi yang diperlukan dan membuat kerangka model sebelum akhirnya merumuskan model matematis yang dimaksud. Model matematis merupakan suatu formula matematika yang menjelaskan atau merepresentasikan sistem fisik atau masalah dalam dunia nyata dalam pernyataan matematik. Model matematik dapat berbentuk model statistik, stokastik, persamaan diferensial tergantung bidang yang digunakan dalam menyusun model matematis tersebut.

Setelah memperoleh model matematis, langkah selanjutnya yang dilakukan matematikawan adalah berusaha memperoleh solusi penyelesaian dari model matematis yang telah dihasilkan. Solusi penyelesaian ini dapat berupa solusi sejati (analytic) maupun hampiran (numeric). Solusi analitik merupakan solusi sejati dari suatu model matematis sedangkan solusi numerik merupakan solusi hampiran atau pendekatan (approximate) dari solusi sejati [2]. Karena merupakan solusi hampiran, maka terdapat besarnya kesalahan atau galat dari solusi numerik terhadap solusi sejati. Besarnya kesalahan atau galat ini disimbolkan dengan konstanta positif epsilon



. Konstanta positif epsilon



yang menyatakan galat tidak boleh terlalu besar karena akan mengakibatkan solusi numerik yang dihasilkan akan jauh dari solusi sejati, untuk hal demikian besarnya epsilon



diharapkan sedekat mungkin dengan nol.

Kesalahan atau galat yang dimiliki oleh solusi numerik umumnya disebabkan oleh dua faktor yakni karena pemotongan (cutting) ekspansi suku yang terlalu panjang, dan pembulatan (rounding) digit angka desimal. Meskipun memiliki galat, bukan berarti metode numerik (solusi numerik) tidak menjadi pilihan, atau hanya sekadar menjadi pilihan kedua dalam menyelesaikan model matematis. Dalam beberapa kasus, metode numerik sering menjadi pilihan utama tatkala model matematis yang dihasilkan sangat sulit ditemukan solusi sejatinya.

Dalam kehidupan sehari-hari, salah satu masalah dunia nyata yang sering ditemukan adalah pengoptimalan atau masalah optimisasi. Beberapa contoh masalah optimisasi yang sering dijumpai adalah masalah pergudangan (inventory) untuk menentukan seberapa besar barang yang harus dipesan dari produsen, masalah meminimalkan biaya produksi suatu perusahaan, sampai kepada aspek yang lebih jauh dari pada itu seperti optimisasi pada jaringan listrik, kabel, dan rute perjalanan. Masalah optimisasi seperti ini jelas memerlukan model matematis yang tepat untuk memperoleh solusi yang optimal.

Secara umum masalah optimisasi berdasarkan fungsi tujuan yang ingin dioptimalkan dibagi atas dua jenis yakni masalah optimisasi single objektif dan masalah optimisasi multi objektif. Masalah optimisasi single objektif hanya memiliki satu fungsi tujuan yang dioptimalkan, sedangkan masalah optimisasi multi objektif memiliki sekurangnya dua fungsi objektif yang dioptimalkan. Menurut kendala (constrain), masalah optimisasi juga dibagi atas dua, yakni masalah optmisasi dengan dan tanpa kendala. Berdasarkan variabel bebas (independent) masalah optimisasi terbagi atas dua jenis yakni masalah optimiasasi dengan satu dan banyak variabel bebas.

Berbagai metode penyelesaian dapat digunakan untuk menyelesaikan berbagai jenis masalah optmisasi. Contohnya untuk menyelesaikan masalah optimisasi single objektif dengan satu variabel bebas dapat digunakan metode rasio emas (golden rato), Fibonacci, dan biseksi, sedangkan untuk menyelesaikan masalah optimiasi single objektif dengan beberapa (multi) variabel bebas dapat digunakan metode numerik Aksial, Newton, Hook and Jeeves, Roosenberg dan Stepest Descent [3]. Untuk menyelesaikan masalah optimisasi multi objektif dapat menggunakan Pengali Lagrange dan Kuhn-Tucker .Pada Masalah optimiasi multi objectif tidak dibahas dan peneliti lebih memfokuskan kajian pada masalah optimisasi single objektif tanpa kendala.

Metode numerik Stepest Descent merupakan salah satu metode yang dapat digunakan dalam menyelesaikan masalah optmisasi single objektif tanpa kendala dengan banyak variabel bebas. Metode numerik Stepest Descent bekerja dengan mengambil sembarang titik awal

X



R

ndengan menggunakan arah pencarian (direction) negatif gradient

d

_k

 

Z X

 

_k [4]. Metode numerik Stepest Descent sering digunakan karena solusi numerik yang dihasilkan cenderung akurat dengan solusi sejati, bahkan dalam beberapa kasus, solusi numerik yang dihasilkan dapat identik dengan solusi sejati atau dengan kata lain solusi numerik tanpa galat. Meskipun demikian, penelitian lebih lanjut pada metode numerik ini terus dikembangkan, salah satunya dengan mementuk arah pencarian (direction) yang lain. Sebagaimana diketahui perbedaaan yang mendasar dari metode-metode numerik untuk menyelesaikan masalah optimisasi single tanpa kendala ada pada arah pencariannya. Metode numerik Aksial, misalnya memiliki arah pencarian verktor normal, sedangkan metode numerik arah konjugasi melibatkan matriks Hessian dalam arah pencariannya .

Penelitian ini mengkaji dan membahas mengenai metode numerik Steepest Descent dengan arah pencarian (direction) berupa negatif sigma gradien

 

1 n k k k

d

Z X



  



. Penelitian ini bertujuan untuk melihat proses iterasi dalam memperoleh solusi numerik dengan menggunakan metode Stepest Descent dengan arah pencarian yang lain dalam hal ini negatif sigma gradien. Penelitian dilakukan dengan memahami terlebih dahulu mengenai metode numerik Steepest Descent dengan arah pencarian negatif gradien biasa kemudian menyusun algoritma untuk metode Steepest Descent dengan arah pencarian negatif sigma gradient.Buku-buku yang digunakan dalam menunjang penelitian antara lain An

Introduction to Optimization karya Edwin K.P.Chong dan Stanislaw H Zak, Theory of Multiobjective Optimization karya Yoshikazu Sawaragi, Hirotaka Nakayama dan Tetsuzo Tanino, Nonlinear Programming Theory and Algorithm karya Mochtar S Bazaraa, Hanif D Sherali dan C.M Shetty, An Introduction to Model Building karya Wayne L Winston, Metode Numerik karya Rinaldi Munir , Diktat

kuliah Optimisasi karya Salmah dan buku-buku lainnya yang dapat dilihat pada daftar pustaka. Dalam penelitian ini pulaakan diberikan contoh perhitungan numerik untuk metode Steepest Descent dengan kedua arah pencarian tersebut beserta analisis dan perbandingan keakuratan solusi antara keduanya.

II. HASIL DAN PEMBAHASAN Definisi Norm

Diberikan

X Y

,

sembarang dua vektor. Sembarang bilangan riil

||

X

||

dinamakan norm dari

X

apabila memenuhi aksioma-aksioma sebagai berikut

i.

|

X

|| 0



ii.

||

aX

|| 0

 

X



0

iii.

||

aX

|| | |||



a

X

||,

a



R

iv.

|

X



Y

|| ||



X

||



||

Y

||

Definisi Kombinasi Linear [5]

Misalkan

X

_i ,

1 i

 

m

vektor-vektor di

V

maka

X

disebut kombinasi linear dari vektor-vektor

X

_i

jika 1 m i i i

X

a X







Definisi Bentuk Kuadratik [6]

2 2 2

11 1 2 2 12 1 2 1,3 1 3 23 2 3

( )

2

...

_{nn n}

...

...

F X



c x



c

x

 

c x



c x x



c x x

 

c x x



dengan

c

_ij



R

,

Definisi Fungsi Positif

Bentuk kuadratik

X AX

T disebut positif (negatif) definit jika

X AX

T

 

( )0

untuk semua

X



0

dan terdapat sekurangnya satu vektor tak nol sedemikian hingga

X AX

T



0

. Apabila tidak memenuhi keduanya, maka bentuk kuadratik tersebut dikatakan Tidak definite.

Teorema Fungsi Definit

Suatu matriks

A

dikatakan

i. Positif definit jika dan hanya jika



_i



0

ii. Negatif definit jika dan hanya jika



_i



0

iii. Positif semi definit jika dan hanya jika



_i



0

iv. Negatif semi definit jika dan hanya jika



_i



0

dengan



_i merupakan nilai-nilai eigen dari matriks

A

dan ketidaksamaan dicapai untuk sekurang-kurangnya satu

j

. Apabila



_itidak memenuhi butir i,ii,iii, dan iv maka matriks

A

disebut Tidak definite.

Definisi Minimum Global [7]

Fungsi

F x

( )

dikatakan memiliki minimum global di

x

₀ dalam

S

jika

f x

( )



f x

( )

₀

Definisi Minimum Lokal Relatif

Fungsi

F x

( )

dikatakan memiliki minimum lokal di

x

₀ dalam

S

jika terdapat sekitar



dari

x

₀

sedemikian hingga

f x

( )



f x

( )

₀ untuk setiap

x

di dalam persekitaran tersebut.

Algoritma Stepest Descent denganNegatif Gradien dan Negatif Sigma Gradien[8],[9],[10]

Diberikan suatu fungsi objektif

Z



F X

( )



F x x

( ,

_{2 2}

,.,

x

_n

)

dan akan ditentukan nilai 1 2

{ ,

,.,

_n

}

X



x x

x

yang meminimalkanatau memaksimalkan fungsi

Z



F X

( )

tersebut

i. Ambil

X

₁



{ ,

x x

_{1 2}

,.,

x

n

}



R

n sembarang titik awal dan





0

suatu konstanta positif yang

menyatakan besarnya kesalahan atau galat yang ditoleransi. ii. Dibentuk fungsi gradient

 

1 2

,

,

,

n

Z

Z

Z

Z X

x

x

x













_{ }

_











dan tentukan



Z X

 

k dengan

1, 2,

,

k



n

yang menyatakan posisi iterasi

iii. Apabila



Z X

 

k





,

k



1, 2,

,

n

maka iterasi berhenti, sebaliknya iterasi dilanjutkan

iv. Tentukan



_k dengan cara mencari titik ekstrim

Z X



_k





_k

d

_k



yakni dengan cara menderivatifkan fungsi

Z X



_k





_k

d

_k



dan menyamadengankan nol dengan arah pencarian negative gradien

d

_k

 

Z X

 

_k

,

k



1, 2,

,

n

v. Nilai

X

_k ditentukan dengan

X

_k



X

_k1





_k1

d

_k1

Berdasarkan algoritma Stepest Descent dengan arah pencarian negatifgradien

d

_k

 

Z X

 

_k ,

1, 2,

,

k



n

akan dikembangkan suatu metode Stepest Descent dengan arah pencarian negatif sigma gradient. Algoritma Stepest Descet dengan arah pencarian negative sigma gradien memiliki langkah yang sama dengan metode numerik steepest descent dengan arah pencarian negatifgradien, namun dalam hal ini arah pencarian didefinisikan sebagai

 

1 n k k k

d

Z X



  



dan iterasi berhenti ketika nilai norm

 

1 n k k

Z X











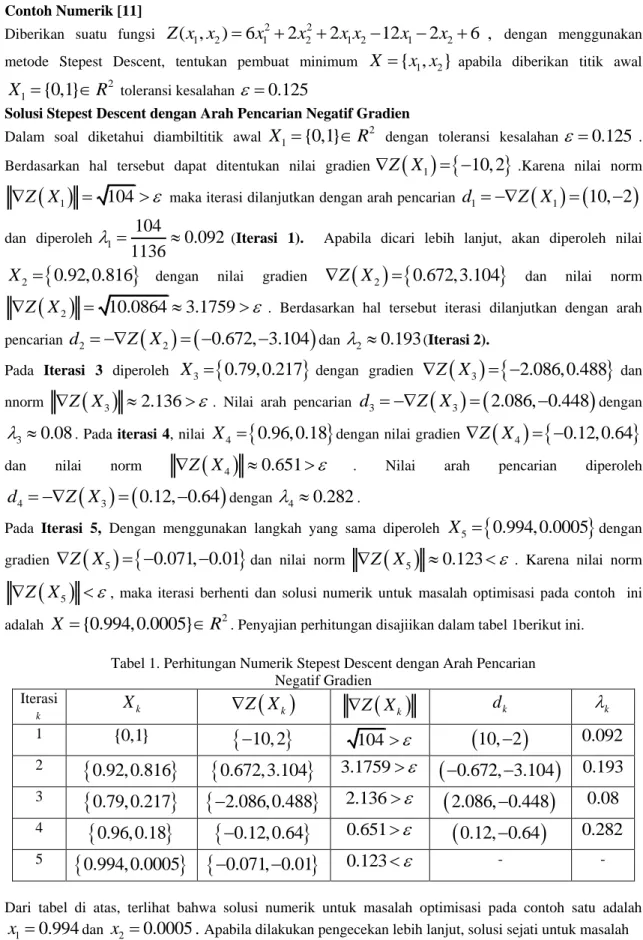
Contoh Numerik [11]

Diberikan suatu fungsi

Z x x

( ,

_{1 2}

)



6

x

₁2



2

x

₂2



2

x

_{1 2}

x



12

x

₁



2

x

₂



6

,

dengan menggunakan metode Stepest Descent, tentukan pembuat minimum

X



{ ,

x x

_{1 2}

}

apabila diberikan titik awal

2 1

{0,1}

X





R

toleransi kesalahan





0.125

Solusi Stepest Descent dengan Arah Pencarian Negatif Gradien

Dalam soal diketahui diambiltitik awal

X

₁



{0,1}



R

2 dengan toleransi kesalahan





0.125

. Berdasarkan hal tersebut dapat ditentukan nilai gradien



Z X

  

₁

 

10, 2



.Karena nilai norm

 

1

104

Z X









maka iterasi dilanjutkan dengan arah pencarian

d

₁

 

Z X

  

₁



10, 2





dan diperoleh 1

104

0.092

1136







(Iterasi 1). Apabila dicari lebih lanjut, akan diperoleh nilai





2

0.92, 0.816

X



dengan nilai gradien



Z X

  

₂



0.672,3.104



dan nilai norm

 

2

10.0864

3.1759

Z X











. Berdasarkan hal tersebut iterasi dilanjutkan dengan arah pencarian

d

₂

 

Z X

  

₂

 

0.672, 3.104





dan



₂



0.193

(Iterasi 2).

Pada Iterasi 3 diperoleh

X

₃





0.79, 0.217



dengan gradien



Z X

  

₃

 

2.086, 0.488



dan nnorm



Z X

 

3



2.136





. Nilai arah pencarian

d

3

 

Z X

  

3



2.086, 0.448





dengan

3

0.08





. Pada iterasi 4, nilai

X

₄





0.96, 0.18



dengan nilai gradien



Z X

  

₄

 

0.12, 0.64



dan nilai norm



Z X

 

₄



0.651





. Nilai arah pencarian diperoleh

  



4 3

0.12, 0.64

d

 

Z X





dengan



₄



0.282

.

Pada Iterasi 5, Dengan menggunakan langkah yang sama diperoleh

X

₅





0.994, 0.0005



dengan gradien



Z X

  

₅

 

0.071, 0.01





dan nilai norm



Z X

 

5



0.123





. Karena nilai norm

 

5

Z X







, maka iterasi berhenti dan solusi numerik untuk masalah optimisasi pada contoh ini adalah

X



{0.994, 0.0005}



R

2. Penyajian perhitungan disajiikan dalam tabel 1berikut ini.

Tabel 1. Perhitungan Numerik Stepest Descent dengan Arah Pencarian Negatif Gradien Iterasi k

X

k



Z X

 

k



Z X

 

k

d

k



k 1

{0,1}





_{10, 2}



₁₀₄

_

_



_{10, 2}





0.092

2



_{0.92, 0.816}





_0.672,3.104



_3.1759







_

_{0.672, 3.104}

_



_0.193

3



_{0.79, 0.217}





_

_{2.086, 0.488}



_2.136







_{2.086, 0.448}

_



_0.08

4



_{0.96, 0.18}







_{0.12, 0.64}



0.651







_{0.12, 0.64}





0.282

5



_{0.994, 0.0005}





_

_{0.071, 0.01}

_



_0.123





- -

Dari tabel di atas, terlihat bahwa solusi numerik untuk masalah optimisasi pada contoh satu adalah

1

0.994

x



dan

x

₂



0.0005

.

Apabila dilakukan pengecekan lebih lanjut, solusi sejati untuk masalah optimisasi pada contoh ini adalah

x

1



1

dan

x

2



0

, berdasarkan hal tersebut galat dari solusi numerik yang dihasilkan untuk

x

₁ adalah 0.006 dan

x

₂ adalah 0.005.

Solusi Stepest Descent dengan Arah Pencarian Negatif Gradien

Pada bagian ini akan dicoba pencarian solusi numerik masalah optimisasi ini dengan cara Stepest Descent dengan arah pencarian negatif sigma gradien.

Pada iterasi 1, tetap dilakukan pengambilan titik awal

X

₁



{0,1}



R

2dengan





0.125

, selanjutnya diperoleh



Z X

  

₁

 

10, 2



dengan



Z X

 

₁



104





. Lebih lanjut arah pencarian

  



1 1

10, 2

d

 

Z X





dan ₁

104

0.092

1136







. Apabila dicari lebih lanjut, akan diperoleh nilai





2

0.92, 0.816

X



dengan nilai gradien



Z X

  

₂



0.672,3.104



dan nilai norm

 

2 1

10.633

k k

Z X













. Berdasarkan hal tersebut iterasi dilanjutkan dengan arah pencarian

  



2 2 1

9.328, 5.104

k k

d

Z X



  







dan



₂



0.0099

(Iterasi 2).

Pada Iterasi 3 diperoleh

X

₃





1.0123, 0.7654



dengan gradien



Z X

  

₃



1.6784,3.0862



dan

nilai normdiperoleh

 

3 1

11.2069

k k

Z X













. Nilai arah pencarian

d

3 diperoleh

  



3 3 1

7.6496, 8.1902

k k

d

Z X



  







dengan



3



0.017

.

Pada Iterasi 4 diperoleh

X

₄





1.1423, 0.6261



dengan gradien



Z X

  

₄



2.9598, 2.7890



dan nilai norm diperoleh

 

4 1

11.9388

k k

Z X













. Nilai arah pencarian

d

₄ diperoleh

  



3 4 1

4.6898, 10.9792

k k

d

Z X



  







dengan



₄



0.03

.

Pada Iterasi 5, dengan menggunakan langkah yang sama diperoleh

X

₅





1.2876, 0.2858



dengan gradien



Z X

  

₅



4.0248,1.7224



dan nilai norm



Z X

 

₅



12.7016





.Nilai arah

pencarian

d

₅ diperoleh

  



5 5 1

0.6650, 12.7016

k k

d

Z X



  







dengan



₅



0.031

dan nilai





6

1.3082, 0.1085

X





. Hasil perhitungan disajikan dalam tabel 2 di bawah ini. Tabel 2. Perhitungan Numerik Stepest Descent dengan Arah Pencarian

negatif sigma gradien. Iterasi k k

X



Z X

 

_k

_{ }

1 n k k

Z X







d

k



k 1

_{0,1}



_

_{10, 2}



₁₀₄

_

_



_{10, 2}

_



_0.092

2



_{0.92, 0.816}





_0.672,3.104



10.633







_{9.328, 5.104}

_



0.0099

3



_{1.0123,0.7654}





_{1,6784,3.0862}



11.2069







_{7.6496, 8.1902}

_



0.017

4



_{1.1423, 0.6261}





_{2.9598, 2,7890}



_11.9388







_{4.6898, 10.9792}

_



_0.03

5



_{1.2876, 0.2858}





_{4.0248,1.7224}



_12.7016







_{0.6650, 12.7016}

_



_0.031

6



_{1.3082, 0.1085}

_



- - - -

Pada tabel 2 di atas, terlihat bahwa iterasi tidak mungkin berhenti dikarenakan nilai norm

 

1 n k k

Z X







selalu lebih besar dari epsilon. Hal ini ditandai dengan nilai gradien



Z X

 

_k yang semakin membesar dan nilai



_k,

k



1, 2,

,5

yang semakin membesar. Hasil perhitungan nilai

X

_k

terlihat bahwa nilai

x

₁semakin menjaui dari nilai aslinya yakni

x

₁



1

, begitupun pada

x

₂ yang juga menjauh dari nilai aslinya yakni

x

₂



0

meskipun sampai iterasi ke 5, terlihat nilai

x

₂ seolah menuju nilai aslinya, namun hal demikian tidak benar dengan melihat pada iterasi selanjutnya dimana nilai

x

₂

justru menjauhi nilai nol.

III. SIMPULAN DAN SARAN Simpulan

Terdapat beberapa hal yang menjadi kesimpulan dalam penelitian ini, diantarnya:

1. Masalah optimisasi berdasarkan fungsi onjektifnya dibagi atas 2 jenis yakni masalah optimisasi

single objektif dan masalah optimisasi multi objektif.

2. Menurut variabel bebasnya masalah optimisasi dibagi atas 2 jenis yakni masalah optimisasi dengan satu variabel bebas dan multi variabel bebas. Lebih lanjut, menurut kendalanya masalah optimisasi juga dibagi atas 2 jenis yakni masalah optimisasi dengan dan tanpa kendala

3. Masalah optimisasi single objektif tanpa kendala dengan satu variabel bebas dapat diselesaikan dengan metode numerik golden rasio, Fibonacci, biseksi dl, sedangkan masalah optimisasi single objektif tanpa kendala dengan multi variable bebas dapat diselesaikan salah satunya dengan metode numerik Stepest Descent

4. Metode numerik Stepest Descent dimulai dengan mengambil sembarang

X



{ ,

x x

1 2

,.,

x

n

}

dengan arah pencarian negatif gradien

d

_k

 

Z X

 

_k . Iterasi berhenti ketika norm

 

k

Z X







,

k



1, 2,

,

n

5. Metode numerik Stepset Descent dengan arah pencarian negatif sigma gradient juga dimulai dengan mengambil

X



{ ,

x x

_{1 2}

,.,

x

_n

}

, namun menggunakan arah pencarian

 

1 n k k k

d

Z X



  



. Iterasi berhenti ketika nilai norm

 

1 n k k

Z X











,

k



1, 2,

,

n

6. Pada contoh dalam penelitian ini, terlihat bahwa untuk masalah optimisasi single objektif tanpa kendala meminimalkan

Z x x

( ,

_{1 2}

)



6

x

₁2



2

x

₂2



2

x

_{1 2}

x



12

x

₁



2

x

₂



6

dengan toleransi kesalahan





0.125

, solusi numerik yang dihasilkan melalui Stepest Descent dengan arah negatif gradient akan berhenti pada iterasi ke 5 yakni dengan nilai

x

1



0.994

dan

2

0.0005

x



dengan nilai norm



Z X

 

₅



0.123





. Galata atau kesalahan yang dihasilkan untuk

x

₁ adalah 0.006 dan

x

₂ adalah 0.005.

7. Berbeda dengan solusi numerik yang dihasilkan oleh Stepest Descent dengan arah pencarian negatif gradient, solusi numerk yang dihasilkan dengan metode numerik negaif sigma gradient justru tidak akan berhenti untuk nilai iterasi berapapun. Hal ini dapat disebabkan nilai gradien

 

k

Z X



dan



_k ,

k



1, 2,

,

n

akan semakin membesar seiring bertambahnya iterasi. Hal demikan terlihat contoh di atas dengan nilai

X

_kyang semakin menjaui dari nilai aslinya.

Saran

Terdapat beberapa hal yang menjadi saran dalam penelitian ini, diantarnya:

1. Umumnya metode numerik Stepest Descent dengan arah pencarian negatif gradien sudah cukup baik dalam menyelesaikan masalah optimisasi single objektif tanpa kendala, namun penelitian untuk mengembangkan arah pencarian yang lain tetap diperlukan agar langkah iterasi untuk mencari solusi numerik menjadi lebih singkat dan menjadi semakin akurat.

2. Berkaca pada hasil Stepest Descent dengan arah pencarian negatif sigma gradien yang justu menghasilkan solusi yang tidak optimal, maka perlu dikembangkan lagi arah pencarian yang lain agar solusi numerik dari masalah optmiasi menjadi lebih akurat dan dengan langkah yang lebih sedikit.

UCAPAN TERIMA KASIH

Ucapan terimakasih penulis ucapkan kepada Rektorat Universitas Muhammadiyah Tangerang dan Departemen S3 Matematika ITB atas bantuan finansial sehingga penulis dapat menyelesaikan paper dan mengikuti seminar nasional matematika dan pembelajaran matematika UNY pada tanggal 5 November 2016

Daftar Pustaka

[1]Widowati, Sutimin, “ Pemodelan Matematika: Analisis danAplikasinya”, Semarang, Penerbit Undip Press: 2013 [2]Munir, Rinaldi. “Metode Numerik”, Bandung, Informatika: 2008

[3]Epperson, James,”An Introduction to Numerical Methods and Analysis”, New York: John Willey and Sons. Inc: 2013 [4]Otto, S.R. and Denier, J.P,”An introduction to Programming and Numerical Methods in Matlab “, London, Springer-Verlag:

2005

[5]Anton, Howard,“Aljabar Linier Elementer: Penerjemah Pantur Silaban, Jakarta, Erlangga: 1991

[6]Bazaraa, S. Mochtar,Nonlinear Programming Theory and Algorithms”, London, John-Willey Inter Science: 2006 [7]Salmah, “Diktat Optimisasi”, Yogyakarya, FMIPA UGM: 2011

[8]Bober, William,“An Introduction to Numerical and Analytical Methods with Matlab for Engineers and Scientist”, London: Taylor and Francis Group: 2014

[9]K.P.Chong,Edwin,“An Introduction to Optimization”, New York, John Wiley & Sons: 2001 Inc.

[10]Corless, Robert, M, and Fillion, Nicholas.“A Graduate Introduction to Numerical Methods”,London, Springer-Verlag:2013 [11]Linna, “ Metode Numerik Stepest Descent: Soal UAS FKIP UMT”, 2016