INTERPOLASI DATA SPASIAL DENGAN PENCILAN
MENGGUNAKAN METODE MEDIAN POLISH KRIGING
(Studi Kasus: Kandungan Fluorida Air Tanah di DKI Jakarta)
Elly Nurmaidah
PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
JAKARTA 2018 M / 1439 H
i
INTERPOLASI DATA SPASIAL DENGAN PENCILAN
MENGGUNAKAN METODE MEDIAN POLISH KRIGING
(Studi Kasus: Kandungan Fluorida Air Tanah di DKI Jakarta)
Skripsi
Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Sarjana Matematika (S.Mat)
Fakultas Sains dan Teknologi
Universitas Islam Negeri Syarif Hidayatullah Jakarta
Oleh:
Elly Nurmaidah 1113094000003
PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
JAKARTA 2018 M/ 1439 H
iv PERSEMBAHAN
ا الله مــسـب
ل
حرلا نمحر
ـ
مي
Syukurku kepada-Mu wahai Dzat Yang Maha Agung, yang telah menitipkan diriku kepada malaikat yang Engkau turunkan ke bumi,
Ibu Arnah dan Bapak Endang Soleh.
Yaa Rabb, malaikat yang menjagaku ini amat sangat menyayangiku. Hasil karyaku ini saja takkan mampu membalas kasih sayang yang mereka berikan.
Wahai Dzat Penguasa langit dan bumi, muliakanlah malaikatku ini. Tempatkanlah mereka di Surga-Mu kelak dan pertemukanku
kembali dengan malaikatku.
نيــما نيــما نيــما
v
MOTTO
“Maka sesungguhnya bersama kesulitan ada kemudahan, sesungguhnya bersama kesulitan ada kemudahan”.
(QS. Al-Insyirah : 5-6)
Bukankah dengan mengingat Allah hati menjadi tenang?
“Jadikanlah sabar dan sholat sebagai penolongmu. Dan sesungguhnya yang demikian itu sungguh berat kecuali bagi orang-orang yang khusyu’, (yaitu)
orang-orang yang meyakini bahwa mereka akan kembali kepada-Nya.” (QS. Al-Baqarah : 45-46)
Di antara kita terdapat bukit yang sangat tinggi dan hanya ketakutan kepada Allah lah yang membuat kita bertemu – Uwais Al Qarni
vi
KATA PENGANTAR
Alhamdulillah,segala puji bagi Allah Subhanahu wa Ta’ala yang senantiasa melimpahkan rahmat dan karunia-Nya kepada kita semua tidak terkecuali kepada penulis, sehingga penulis dapat menyelesaikan skripsi ini yang berjudul “Interpolasi Data Spasial Dengan Pencilan Menggunakan Metode Median Polish Kriging (Studi Kasus: Kandungan Fluorida Air Tanah di DKI Jakarta)”. Shalawat serta salam senantiasa tercurah kepada junjungan baginda besar Nabi Muhammad Shalallahu ‘Alayhi wa Sallam, keluarga, para sahabatnya dan para pengikutnya sampai akhir zaman.
Dalam penyusunan skripsi ini, penulis banyak mendapatkan dorongan, semangat, motivasi, dan bimbingan serta kritikan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis ingin mengucapkan terima kasih kepada:
1. Bapak Dr. Agus Salim, M.Si, selaku Dekan Fakultas Sains dan Teknologi, Universitas Islam Negeri Syarif Hidayatullah Jakarta,
2. Ibu Dr. Nina Fitriyati, M.Kom, selaku Ketua Program Studi Matematika Fakultas Sains dan Teknologi UIN Syarif Hidayatullah Jakarta, sekaligus sebagai Dosen Pembimbing I,
3. Ibu Irma Fauziah, M.Sc, selaku Sekretaris Program Studi Matematika Fakultas Sains dan Teknologi UIN Syarif Hidayatullah Jakarta, sekaligus sebagai Pembimbing Akademik,
4. Bapak Mahmudi, M.Si selaku Dosen Pembimbing II yang telah banyak sekali membantu penulis memberikan pengarahan, saran, semangat, dan motivasi dalam menyelesaikan skripsi ini,
5. Ibu Yanne Irene, M.Si selaku Dosen Penguji I dan Bapak Muhammad Manaqib, M.Sc selaku Dosen Penguji II yang telah memberi pengarahan dan saran untuk perbaikan isi serta penulisan pada skripsi ini
6. Seluruh Ibu dan Bapak Dosen Program Studi Matematika Fakultas Sains dan Teknologi UIN Syarif Hidayatullah Jakarta yang selama perkuliahan telah memberikan ilmu-ilmunya dan pengalaman yang bermanfaat,
vii Jakarta, Januari 2018
Penulis 7. Kedua orang tua penulis, IbuArnah dan Bapak Endang Soleh tercinta yang tiada henti-hentinya memberikan kasih sayang, motivasi, semangat dan doa, serta dukungan baik berupa moral maupun materil kepada penulis,
8. Busainah Hasibah, adik penulis yang selalu membawa keceriaan,seluruh keluarga besar penulis yang selalu memberikan doa dan dukungannya kepada penulis,
9. Akhi fillah yang semoga selalu dalam lindungan Allah, yang selalu membantu, memberi semangat, motivasi, dan dukungan dalam penulisan skripsi ini,
10. Cypress Family yaitu Ilva, Inul, Lisna, Mput, Mul, Pika, Ady, Faiz, Nadya, Nda, Imas, Ndi, Angga, Uta, Icyn, Ayu, Khoe, Yuyun, Alfi, Irfi, Emin, Kopong, Panjul, Bagus, Ainun, Sofi, Oot, Ara, Day, Aul, dan Dikey. Terima kasih sudah memberi dukungan dan semangat untuk penulis,
11. Keluarga Besar Himatika FST UIN Syarif Hidayatullah Jakarta, Keluarga Besar DEMA FST periode 2015 dan 2016, matematika angkatan 2011, angkatan 2012, angkatan 2014, angkatan 2015,. Terima kasih atas dukungannya,
12. Seluruh pihak-pihak yang sangat membantu dan tidak dapat disebutkan namanya satu persatu. Jazaakumullahu Khairan Katsiran.
Penulis menyadari bahwa penulisan skripsi ini masih banyak kekurangan dan jauh dari kesempurnaan, oleh karena itu penulis memohon maaf jika terdapat kesalahan yang kurang berkenan.Semoga skripsi ini dapat bermanfaat dan memberikan kontribusi yang berarti. Aamiin aamiin aamiin yaa Robbal ‘Alaamiin.
viii DAFTAR ISI LEMBAR PENGESAHAN ... ii PERNYATAAN ... iii PERSEMBAHAN ... iv MOTTO ... v ABSTRAK ... v ABSTRACT ... xiv KATA PENGANTAR ... vi
DAFTAR ISI ... viii
DAFTAR TABEL ... x
DAFTAR GAMBAR ... xi
DAFTAR LAMPIRAN ... xii
BAB I PENDAHULUAN ... xiii
1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 3
1.3 Batasan Masalah ... 3
1.4 Tujuan Penelitian ... 4
1.5 Manfaat Penelitian ... 4
BAB II TINJAUAN PUSTAKA ... 5
2.1 Air Tanah dan Fluorida pada Air Tanah ... 5
2.1.1 Air Tanah ... 5
2.1.2 Fluorida pada Air Tanah ... 6
2.2 Data Spasial ... 7
2.3 Asumsi Stasioner Orde Dua ... 8
2.4 Semivariogram ... 9
2.4.1 Semivariogram Eksperimental ... 10
2.4.2 Semivariogram Teoritis ... 10
2.5 Metode Ordinary Kriging ... 12
2.6 Sifat Estimator Metode Kriging ... 12
ix
2.6.2 Estimator Tak Bias ... 13
2.6.3 Variansi Minimum ... 14
2.6.4 Penghitungan Variansi Kriging ... 19
2.7 Median Polish Kriging ... 20
BAB III METODE PENELITIAN ... 23
3.1 Sumber Data ... 23
3.2 Metode Pengolahan Data ... 23
3.3 Alur Penelitian ... 29
BAB IV HASIL DAN PEMBAHASAN ... 31
4.1 Statistika Deskriptif ... 31
4.2 Uji Stasioneritas ... 32
4.3 Uji Box-Plot ... 35
4.4 Semivariogram Eksperimental ... 36
4.5 Model Semivariogram Teoritis ... 38
4.5.1 Model Spherical ... 38
4.5.2 Model Exponential ... 39
4.5.3 Model Gaussian ... 39
4.5.4 Hasil Uji Validasi Silang dan Pemilihan Model Terbaik ... 41
4.6 Hasil Interpolasi Data Kandungan Fluorida pada Air Tanah ... 42
BAB V PENUTUP ... 50
5.1 Kesimpulan ... 50
5.2 Saran ... 50
x
DAFTAR TABEL
Tabel 2.1 Kadar Fluorida Air Tanah ... 7
Tabel 4.1 Statistika Deskriptif Kandungan Fluorida Air Tanah... 31
Tabel 4.2 Klasifikasi Kadar Fluorida Air Tanah ... 31
Tabel 4.3 Pasangan Hasil Pengamatan Uji Cox-Stuart ... 33
Tabel 4.4 Hasil Z Score ... 36
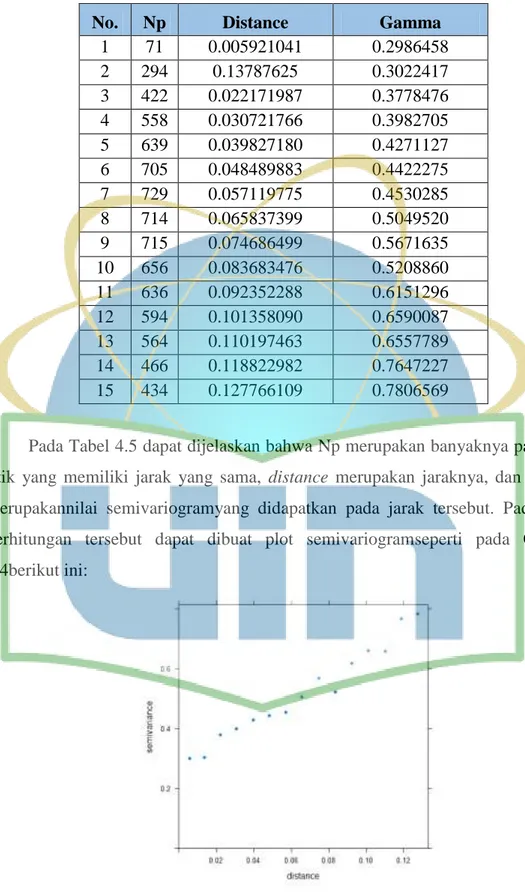
Tabel 4.5 Hasil Semivariogram Eksperimental ... 37
Tabel 4.6 Nilai Uji Validasi Silang 𝑄1 ... 41
Tabel 4.7 Median Baris dan Kolom Grid 5 × 3 ... 45
Tabel 4.8 Hasil Baris ... 45
Tabel 4.9 Hasil Kolom ... 45
Tabel 4.10 Nilai Residual ... 46
Tabel 4.11 Median Baris dan Kolom Grid 3 × 2 ... 48
Tabel 4.12 Hasil Baris ... 48
Tabel 4.13 Hasil Kolom ... 48
Tabel 4.14 Nilai Residual ... 48
xi
DAFTAR GAMBAR
Gambar 2.1 Semivariogram Eksperimental... 9
Gambar 2.2 Model Semivariogram Teoritis ... 11
Gambar 3.1 Contoh Boxplot Berpencilan ... 25
Gambar 3.2 Alur Penelitian ... 30
Gambar 4.1 Plot X Terhadap Fluorida dan Y Terhadap Fluorida ... 32
Gambar 4.2 Scatterplot Tiga Dimensi X dan Y terhadap Indeks Kandungan Fluorida Air Tanah ... 33
Gambar 4.3 Box Plot Kandungan Fluorida Air Tanah ... 35
Gambar 4.4 Semivariogram Eksperimental... 37
Gambar 4.5 Semivariogram Model Spherical ... 39
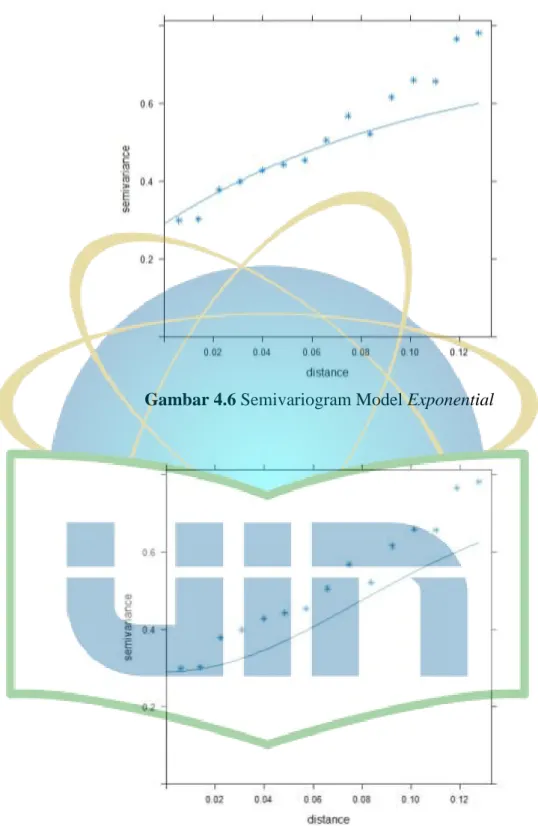
Gambar 4.6 Semivariogram Model Exponential ... 40
Gambar 4.7 Semivariogram Model Gaussian... 40
Gambar 4.8Scatterplot Persebaran Fluorida Grid 10 × 6 ... 42
Gambar 4.9Scatterplot Persebaran Fluorida Grid10 × 3 ... 43
Gambar 4.10 Scatterplot Persebaran Fluorida Grid 5 × 3 ... 44
Gambar 4.11 Diagram Lingkaran Hasil Estimasi Median Polish Kriging ... 46
Gambar 4.12 Scatterplot Persebaran Fluorida Grid 4 × 3 ... 47
xii
DAFTAR LAMPIRAN
Lampiran I Data Kandungan Fluorida Air Tanah di DKI Jakarta Tahun 2015 ... 55
Lampiran II Uji Z Score Data Berpencilan ... 61
Lampiran III Hzil Uji Validasi Silang 𝑄1 Model Terbaik ... 63
Lampiran IV Data Fluorida Berdasarkan Grid 5 × 3 ... 68
Lampiran V Peta Persebaran Kandungan Fluorida Air Tanah di DKI Jakarta ... 73
Lampiran VI Hasil Estimasi Menggunakan Metode Median Polish Kriging ... 74
Lampiran VII Peta Hasil Estimasi Median Polish Kriging ... 76
Lampiran VIII Hasil Estimasi Metode Robust Kriging ... 77
xiii
ABSTRAK
Elly Nurmaidah, Interpolasi Data Spasial Dengan Pencilan Menggunakan Metode
Median Polish Kriging (Studi Kasus: Kandungan Fluorida Air Tanah Di DKI Jakarta). Di bawah bimbingan Dr. Nina Fitriyati, M.Kom dan Mahmudi, M.Si.
Pada penelitian ini akan diinterpolasi kandungan fluorida air tanah di DKI Jakarta. Berdasarkan data kandungan fluorida di DKI Jakarta tahun 2015, terdapat data pencilan kandungan fluorida. Oleh karena itu, metode yang digunakan adalah Median Polish Kriging. Beberapa grid yang diuji untuk menginterpolasi kandungan fluorida adalah berukuran 10 × 6, 10 × 3, 5 × 3, 4 × 3, dan 3 × 2. Namun, hanya grid berukuran5 × 3yang berhasil menginterpolasi kadar fluorida pada daerah yang tidak tersampel. Hasil interpolasi menunjukkan bahwa 81% daerah di Jakarta memiliki kadar kandungan fluorida rendah yaitu 0-0,5 mg/l, sebanyak 8% memiliki kadar kandungan fluorida sedang yaitu 0,5-1 mg/l, dan sebanyak 11% memiliki kadar yang tidak baik yakni di atas 1,5 mg/l. Daerah dengan kadar fluorida air tanah yang tidak aman dikonsumsi (di atas 1,5 mg/l), antara lain Kelurahan Joglo dan Kelurahan Duri Kosambi yang terletak di Jakarta Barat.
xiv
ABSTRACT
Elly Nurmaidah, Interpolation of Spatial Data with Outliers Using Median Polish
Kriging Method (Case Study: Fluoride Content of Groundwater in DKI Jakarta). Supervice by Dr. Nina Fitriyati, M.Kom dan Mahmudi, M.Si.
In this research we will interpolate the fluoride content of ground water in DKI Jakarta. Based on the fluoride data in DKI Jakarta on 2015, there are outliers in the fluoride content. Therefore, we use the Median Polish Kriging method. We use some grids to interpolate the fluoride content i.e. 10 × 6.10 × 3.5 × 3.4 × 3, and 3 × 2. However, only 5 × 3 grid that interpolates fluoride levels successfully in an unsampled areas. Interpolation results indicate that 81% areas in Jakarta have a low content of fluoride (0-0.5 mg / l), 8% areas have a moderate fluoride content (0.5-1 mg / l), and 11% areas have the highest fluoride content (above 1.5 mg / l). The areas with the highest fluoride content have unsafe level water to consume i.e. Kelurahan Joglo and Kelurahan Duri Kosambi located in West Jakarta.
1
BAB I
PENDAHULUAN
1.1 Latar Belakang
Artinya :
“Dan Dialah yang menurunkan air hujan dari langit, lalu kami tumbuhkan dengan air itu segala macam tumbuhan, maka Kami keluarkan dari tumbuh-tumbuhan itu tanaman yang menghijau, Kami keluarkan dari tanaman yang menghijau itu butir yang banyak; dan dari mayang kurma mengurai tangkai-tangkai yang menjulai, dan kebun-kebun anggur, dan (Kami keluarkan pula) zaitun dan delima yang serupa dan yang tidak serupa. Perhatikanlah buahnya di waktu pohonnya berbuah, dan (perhatikan pulalah) kematangannya. Sesungguhnya pada yang demikian itu ada tanda-tanda (kekuasaan Allah) bagi orang-orang yang beriman.” (QS. Al-An’aam:99). Dari ayat di atas dapat kita ketahui air sangat bermanfaat bagi kelangsungan hidup.
Air merupakan salah satu komponen lingkungan yang memiliki peranan penting dalam kehidupan. Air yang digunakan sebagai sumber air minum harus memiliki kualitas yang baik, sesuai dengan Peraturan Menteri Kesehatan Republik Indonesia No. 492/MENKES/PER/IV/2010 tentang persyaratan kualitas air minum
2 dimana air minum tersebut dikatakan aman apabila memenuhi persyaratan fisika, mikrobiologis, kimiawi, dan radioaktif [2].
Berdasarkan data dari Badan Pusat Statistik (BPS) DKI Jakarta tahun 2007 sekitar 34,26% rumah tangga menggunakan air PAM atau air ledeng, 32,16% air tanah dengan menggunakan pompa, 1,35% sumur gali, 31,26% air kemasan, dan 0,95% sumber lainnya. Terlihat bahwa sumber air minum yang banyak digunakan dimasyarakat di antaranya adalah air tanah dan air PAM. Air baku sebagai sumber air yang digunakan PAM dapat berasal dari air tanah dalam, mata air, dan sungai. Air tanah dalam dan mata air biasanya berkualitas baik dan hanya memerlukan pengolahan sederhana untuk dapat digunakan sebagai air minum yang memenuhi syarat. Hampir semua sumber atau persediaan air dalam tanah mengandung ion fluorida, meskipun dengan kadar yang berbeda-beda.
Fluorida adalah salah satu senyawa kimia yang terbukti dapat menyebabkan efek terhadap kesehatan melalui air minum. Fluorida memiliki efek yang bermanfaat terhadap pencegahan karies gigi pada konsentrasi tertentu, namun pada keterpaparan yang berlebihan dapat meningkatkan terjadinya efek yang tidak diinginkan. Efek buruk tersebut dapat bervariasi dari fluorosis gigi ringan yaitu keadaan gigi menjadi kekuningan atau kecoklatan dan terdapat bintik-bintik pada enamel gigi hingga fluorosis skeletal seiring dengan meningkatnya kadar dan lamanya paparan. Oleh karena itu, asupan fluorida haruslah dibatasi agar dapat mencegah karies namun tidak menimbulkan terjadinya fluorosis. Fluorida terdapat luas di alam, baik di udara maupun di berbagai sumber lainnya seperti makanan dan minuman yang dikonsumsi sehari-hari. Adanya asupan fluorida dari berbagai sumber pangan diantaranya seperti air, daging, dan ikan menyebabkan asupan fluorida meningkat [9].
Penelitian tentang kandungan Fluorida di DKI Jakarta tahun 2015 telah dilakukan oleh Khaddafi[13]. Pada penelitian tersebut, telah dibahas mengenai interpolasi data spasial yang berpencilan menggunakan metode Robust Kriging pada data kandungan fluorida air tanah di DKI Jakarta untuk daerah yang tidak tersampel. Metode Robust Kriging merupakan metode yang tepat (outlier-resistant) untuk
3 mengestimasi data spasial yang terdapat pencilan (outlier) di dalamnya. Dari metode tersebut didapatkan interpolasi 29 daerah yang tidak tersampel. Interpolasi tersebut menunjukkan bahwa 3,44% daerah di DKI Jakarta memiliki kadar kandungan fluorida pada air tanah cukup rendah yaitu kelurahan Kemayoran Jakarta Pusat dan daerah lainnya di DKI Jakarta yaitu 96,54% memiliki kadar kandungan fluorida yang tidak baik pada air tanah. Estimasi dengan metode Robust Kriging menghasilkan nilai taksiran yang cukup tinggi dari nilai titik tersampel dan menghasilkan rata-rata error yang cukup besar yaitu sebesar 679,58. Oleh karena itu, pada penelitian ini penulis akan mengestimasi kandungan fluorida air tanah di wilayah DKI Jakarta menggunakan metode Median Polish Kriging [5]. Median Polish Kriging menghasilkan hasil analisis yang baik, zona yang ditargetkan dalam penelitian penyebaran data menggunakan pendekatan median dengan bantuan grid. Pada metode ini dilakukan pendekatan median kolom dan baris secara iterasi [20] dan diharapkan menghasilkan rata-rata error yang lebih kecil dibanding dengan metode sebelumnya yakni metode Robust Kriging. Oleh karena itu, interpolasi dengan metode Median Polish Kriging ini diharapkan dapat memberikan perkiraan yang baik dalam memprediksi air tanah di wilayah DKI Jakarta yang mengandung fluorida dan masih aman dikonsumsi.
1.2 Rumusan Masalah
Rumusan masalah pada penelitian ini sebagai berikut:
1. Apa sajakah informasi yang diperoleh dari hasil interpolasi menggunakan metode Median Polish Kriging?
2. Bagaimanakah keadaan kandungan fluorida air tanah di DKI Jakarta?
1.3 Batasan Masalah
Batasan masalah dalam penelitian ini mencakup:
1. Metode yang digunakan adalah metode Interpolasi Median Polish Kriging.
4 3. Peneliti mencoba beberapa grid, yaitu grid 10 x 6, 10 x 3, 5 x 3, 4 x 3, dan
3 x 2.
1.4 Tujuan Penelitian
Adapun tujuan dari penelitian ini yaitu:
1. Memberikan informasi yang diperoleh dari hasil interpolasi menggunakan metode Median Polish Kriging.
2. Mengetahui keadaan.kandungan fluorida air tanah di DKI Jakarta.
1.5 Manfaat Penelitian
Manfaat dari penelitian ini yaitu:
1. Dapat lebih mempelajari geostatistik dalam perhitungan spasial kandungan fluoride air tanah di DKI Jakarta menggunakan metode Median Polish Kriging.
2. Memberikan informasi mengenai manfaat dan bahaya dari kandungan
5
BAB II
LANDASAN TEORI
2.1 Air Tanah dan Fluorida pada Air Tanah
Air yang layak dikomsumsi adalah air yang memenuhi standar mutu dan tidak mengandung kandungan yang dapat membahayakan tubuh. Berikut ini adalah pembahasan tentang teori air tanah dan fluorida pada air tanah:
2.1.1 Air Tanah
Berdasarkan Undang-Undang Nomor 7 Tahun 2004 tentang Sumber Daya Air mendefinisikan air tanah sebagai air yang terdapat dalam lapisan tanah atau batuan di bawah permukaan tanah [18]. Air tanah adalah segala bentuk aliran air hujan yang mengalir di bawah permukaan tanah sebagai akibat struktur perlapisan geologi, beda potensi kelembaban tanah, dan gaya gravitasi bumi. Air bawah permukaan tersebut biasa dikenal dengan air tanah [17].
Air hujan yang meresap ke bawah permukaan tanah dalam bentuk penelusan maupun peresapan membawa unsur-unsur kimia. Komposisi zat terlarut dalam air tanah dapat dikelompokkan menjadi 4 kelompok [17], yaitu:
1. Unsur utama (major constituents) dengan kandungan 1,0-1000 mg/l, yakni: natrium, kalsium, magnesium, bikarbonat, sulfat, klorida, dan silika.
2. Unsur sekunder (secondary constituents) dengan kandungan 0,01-10 mg/l, yakni besi, strountium, kalium, kabornat, nitrat, fluorida, dan boron.
3. Unsur minor (minor constituents) dengan kandungan 0,0001-0,1 mg/l, yakni atimon, aluminium, arsen, barium, brom, cadmium, krom, kobalt, tembaga, germanium, jodium, timbal, litium, mangan, molibdiunum, nikel, fosfat, rubidium, selenium, titanium, uranium, vanadium, dan seng.
6 4. Unsur langka (trace constituents) dengan kandungan biasanya kurang dari 0,001 mg/l, yakni berilium, bismut, cerium, cesium, galium, emas, indium, lanthanum, niobium, platina, radium, ruthenium, scandium, perak, thalium, tharium, timah, tungsten, ytrium, dan zirkon.
2.1.2 Fluorida pada Air Tanah
Fluorida merupakan suatu anion anorganik, monoatomic dari fluorin dengan rumus kimia F− dan merupakan anion fluorin paling sederhana. Fluorida merupakan sebuah senyawa yang sering dimanfaatkan karena garam fluorida yang kerap dijumpai di dalam alam berupa sodium fluoroide, magnesium fluoride, ammonium fluorofosfat, ammonium fluoride, calcium fluoride, hexadesil ammonium fluoride, ammonium fluorosilikat, dan aluminium fluoride serta garam lainnya.
Kadar ion fluorida dalam air tanah bergantung pada sifat geologis, kimia, dan fisika, serta iklim dari suatu area. Umumnya mata air dan air sumur mengandung konsentrasi ion fluorida yang lebih tinggi dibanding air permukaan seperti danau dan sungai. Kandungan ion fluorida dalam air dapat meningkat oleh adanya kegiatan manusia seperti fluoridasi pada air, pembuangan limbah, dan pengaruh dari kegiatan industri. Kontaminasi dalam limbah dan pembuangan industri juga dapat meningkatkan konsentrasi ion fluorida dalam air [22].
Selain manfaat fluorida untuk kesehatan gigi, fluorida pada kandungan air pun berguna untuk kesehatan tulang. Manfaat dari fluorida ini dapat kita rasakan jika penggunaannya masih dalam batas aman. Peraturan menteri kesehatan nomor 492 tahun 2010 tentang persyaratan air minum menetapkan bahwa kandungan fluorida yang aman dikonsumsi adalah 1,5 mg/L [4]. Hal tersebut menunjukkan bahwa kandungan fluorida pada air tersebut masih dalam batas aman.
Dari pernyataan di atas dapat diketahui bahwa kandungan maksimal fluorida pada air minum ialah 1,5 mg/l. Kemudian diklasifikasikan menjadi tiga kelompok
7 yaitu kadar rendah, sedang dan tinggi [6]. Hal ini untuk mempermudah mengetahui klasifikasi kadar fluorida pada air tanah.
Tabel 2.1 Kadar Fluorida Air Tanah
Rumus Parameter Kelas
𝑥𝑚𝑖𝑛− (𝑥𝑚𝑖𝑛+ 𝑇) 0 − 0,5 Rendah (𝑥𝑚𝑖𝑛+ 𝑇) − (𝑥𝑚𝑖𝑛+ 2𝑇) 0,5 − 1 Sedang (𝑥𝑚𝑖𝑛+ 2𝑇) − 𝑥𝑚𝑎𝑥 1 − 1,5 Tinggi dengan: 𝑇 =𝑥𝑚𝑎𝑥−𝑥𝑚𝑖𝑛 𝑛 (2.1) Keterangan :
𝑥𝑚𝑎𝑥 = nilai pengkelasan terbesar 𝑥𝑚𝑖𝑛 = nilai pengkelasan terkecil 𝑛 = banyaknya pengkelasan
Kadar fluorida yang tinggi memiliki kaitan dengan terjadinya dental fluorosis yaitu suatu keadan gigi menjadi kekuningan atau kecoklatan dan terdapat bintik-bintik hitan pada enamel gigi. Sementara kadar yang rendah yaitu kurang dari 0,5 mg/l memiliki kaitan dengan tingginya terjadi kerusakan gigi, meskipun status nutrisi juga merupakan faktor yang berpengaruh [9]. Kadar fluorida sekitar 1 mg/l dapat mencegah keroposnya gigi secara efektif tanpa pengaruh berbahaya pada kesehatan. Jika kadar fluoride melebihi batas yakni 1,5 mg/l maka dapat menyebabkan fluorosis [8].
2.2 Data Spasial
Data spasial mempunyai pengertian sebagai suatu data yang mengacu pada posisi, objek, dan hubungan di antaranya dalam ruang bumi. Di dalam data spasial terdapat informasi mengenai bumi termasuk permukaan bumi, di bawah permukaan bumi, perairan, kelautan, dan bawah atmosfer [22]. Data spasial merupakan data
8 dependen, karena dikumpulkan dari lokasi berbeda yang mengindikasikan adanya ketergantungan antara pengukuran dengan lokasi. Nilai pengukuran data di lokasi 𝑠 biasa dinotasikan dengan 𝑍(𝑠) dimana 𝑍(𝑠) merupakan variabel teregional, yaitu variabel yang berdistribusi dalam ruang. Himpunan dari variabel teregional 𝑍(𝑠) disebut proses spasial {𝑍(𝑠), 𝑠 ∈ 𝐷}, dimana 𝐷 adalah himpunan acak di ruang berdimensi D, ℝ𝑑[7]. Data spasial ini didapatkan dari beberapa sumber, di antaranya adalah citra satelit, peta analog, foto udara (Aerial Photograps), data tabular, dan data survei.
2.3 Asumsi Stasioner Orde Dua
Himpunan variabel acak {𝑍(𝑠), 𝑠 ∈ 𝐷} diasumsikan memenuhi asumsi stasioner bila distribusi dari variabel teregional di lokasi tertentu sama untuk setiap penambahan jarak sebesar h, distribusi variabel teregional 𝑍(𝑠1), 𝑍(𝑠2), … , 𝑍(𝑠𝑛) sama dengan 𝑍(𝑠1+ ℎ), 𝑍(𝑠2+ ℎ), … , 𝑍(𝑠𝑛 + ℎ). Apabila mean dan variansinya konstan, maka kondisi ini disebut stasioner orde dua. Menurut Cressie, suatu fungsi dikatakan memenuhi kondisi stasioner orde dua jika memenuhi kedua syarat berikut:
1. Ekspektasi atau mean variabel acak ada dan konstan untuk semua titik. 𝐸[𝑍(𝑠)] = 𝜇(𝑠) = 𝜇, ∀ 𝑠 ∈ 𝐷
Dengan kata lain, ekspektasi dari variabel teregional di titik s atau mean ada dan konstan untuk setiap 𝑠 ∈ 𝐷.
2. Selisih variabel acak yang berjarak h, [𝑍(𝑠 + ℎ) − 𝑍(𝑠)] memiliki variansi dan kovariansi yang hanya bergantung pada jarak, tidak bergantung pada lokasi atau dapat dinotasikan:
𝑉𝑎𝑟[𝑍(𝑠 + ℎ) − 𝑍(𝑠)]
= 𝐸([𝑍(𝑠 + ℎ) − 𝑍(𝑠)]2) − (𝐸[𝑍(𝑠 + ℎ) − 𝑍(𝑠)])2 Karena 𝐸[𝑍(𝑠 + ℎ) − 𝑍(𝑠)] = 0, maka
9
Gambar 2.1 Semivariogram Eksperimental
(1
2) 𝑉𝑎𝑟[𝑍(𝑠 + ℎ) − 𝑍(𝑠)] = ( 1
2) 𝐸([𝑍(𝑠 + ℎ) − 𝑍(𝑠)]
2) = 𝛾(ℎ) Fungsi 𝛾(ℎ) disebut juga semivariogram. Jika data spasial memenuhi stasioner orde dua, syarat estimasi dapat dilakukan dengan metode Ordinary Kriging.
2.4 Semivariogram
Pada geostatistik terdapat suatu perangkat dasar dari geostatistika untuk visualisasi, memodelkan dan menjelaskan korelasi spasial antar data, serta eksploitasi korelasi spasial dari variabel teregional yang biasa dikenal sebagai variogram. Semivariogram adalah setengah dari variogram. Variabel teregional yang memenuhi asumsi stasioner orde dua menjadi dasar penggunaan semivariogram. Bagian-bagian dari semivariogram disajikan pada Gambar 2.1 di bawah ini,
1. Nugget Effect(𝐶0), yaitu nilai semivariogram pada jarak interval mendekati nol. 2. Sill (𝐶0+ 𝐶𝑖), yaitu nilai semivariogram yang konstan untuk jarak tertentu
sampai dengan jarak yang tidak terhingga sehingga antara dua variabel teregional yang berjarak ℎ tidak berkorelasi. Nilai sill umumnya akan mendekati nilai variansi dari populasi.
3. Range(𝑎), yaitu jarak pada saat nilai semivariogram mencapai sill, atau jarak maksimum dimana masih terdapat korelasi antar variabel teregional.
10
2.4.1 Semivariogram Eksperimental
Semivariogram eksperimental adalah semivariogram yang diperoleh dari data yang diamati atau data hasil pengukuran. Semivariogram didefinisikan sebagai berikut: 𝛾(ℎ) =1 2[𝑉𝑎𝑟(𝑍(𝑠) − 𝑍(𝑠 + ℎ))] =1 2(𝐸([𝑍(𝑠) − 𝑍(𝑠 + ℎ)] 2) − (𝐸[𝑍(𝑠) − 𝑍(𝑠 + ℎ)])2)
Karena pada data stasioneritas terdapat sifat 𝐸[𝑍(𝑠)] = 𝐸[𝑍(𝑠 + ℎ)], sehingga 2𝛾(ℎ) = 𝐸[𝑍(𝑠) − 𝑍(𝑠 + ℎ)]2
Dari rumus di atas diperoleh rumus praktis dari semivariogram eksperimental ditaksir sebagai berikut
𝛾(ℎ) = 1 2𝑁(ℎ)∑ (𝑍(𝑠𝑖) − 𝑍(𝑠𝑖+ ℎ)) 2 𝑁(ℎ) 𝑖=1 dengan
𝛾(ℎ) = nilai semivariogram dengan jarak ℎ 𝑍(𝑠𝑖) = nilai pengamatan di titik 𝑠
𝑍(𝑠𝑖+ ℎ) = nilai pengamatan di titik 𝑠𝑖+ ℎ
𝑁(ℎ) = banyaknya pasangan titik yang mempunyai jarak ℎ
2.4.2 Semivariogram Teoritis
Dalam mengakomodir pencilan harus dicari model semivariogram teoritis mana yang cocok dengan semivariogram eksperimental. Melakukan penaksiran parameter yang cocok dengan semivariogram eksperimental merupakan suatu hal yang sulit dilakukan, karena tidak ada aturan yang jelas. Dalam praktiknya, penaksiran parameter dilakukan dengan cara trial and error, yaitu dengan mencocokkan model semivariogram yang dipilih dengan grafik semivariogram eksperimentalnya. Grafik semivariogram teoritis disajikan pada Gambar 2.2 di bawah ini,
11
Gambar 2.2 Model Semivariogram Teoritis
Adapun model semivariogram teoritis yang digunakan sebagai pembanding semivariogram eksperimental yang telah diperoleh sebagai berikut:
1. Model Spherical 𝛾(ℎ) = {𝐶0+ 𝐶𝑖[( 3ℎ 2𝑎) − 1 2( ℎ 𝑎) 3 ] , untuk ℎ ≤ 𝑎 𝐶0+ 𝐶𝑖 , untuk ℎ > 𝑎 2. Model Exponential 𝛾(ℎ) = {𝐶0+ 𝐶𝑖[1 − 𝑒𝑥𝑝 (− ℎ 𝑎)] , untuk ℎ ≤ 𝑎 𝐶0+ 𝐶𝑖 , untuk ℎ > 𝑎 3. Model Gaussian 𝛾(ℎ) = { 𝐶0 + 𝐶𝑖[1 − 𝑒𝑥𝑝 (− ( ℎ 𝑎) 2 ) ] , untuk ℎ ≤ 𝑎 𝐶0+ 𝐶𝑖 , untuk ℎ > 𝑎 dengan
ℎ = Jarak lokasi antar sampel 𝐶0 = Nugget effect
𝐶0+ 𝐶𝑖 = Sill
12
2.5 Metode Ordinary Kriging
Metode Ordinary Kriging merupakan metode kriging yang datanya memiliki asumsi rata-rata (mean) tidak diketahui dan bernilai konstan. Metode kriging digunakan untuk mengestimasi besarnya karakteristik dari estimator, yaitu 𝑍̂ pada titik yang tidak tersampel berdasarkan informasi dari titik-titik tersampel yang berada disekitarnya. Misalkan akan diestimasi karakteristik 𝑍̂ pada suatu lokasi 𝑠0. Hal ini dapat dilakukan dengan membentuk kombinasi linear dari titik-titik yang telah diketahui yaitu dengan membentuk persamaan [7]:
𝑍̂(𝑠0) = ∑ 𝜆𝑖𝑍(𝑠𝑖) 𝑛 𝑖=1 𝑑𝑒𝑛𝑔𝑎𝑛 ∑ 𝜆𝑖 = 1 𝑛 𝑖=1
di mana 𝜆𝑖 adalah bobot dari 𝑍(𝑠𝑖) dengan 𝑖 = 1, 2, … , 𝑛 dan 𝑍̂(𝑠0) merupakan nilai estimasi pada variabel 𝑠0, sedangkan 𝑍(𝑠𝑖) adalah nilai dari variabel 𝑠𝑖.
2.6 Sifat Estimator Metode Kriging
Dalam metode Kriging, untuk mendapatkan taksiran yang akurat maka harus memenuhi kriteria B.L.U.E (Best Linier Unbiased Estimator) [7]. Sebelum menjelaskan mengenai kondisi yang harus dipenuhi untuk taksiran yang dapat dikatakan best dan unbiased, akan dijelaskan terlebih dahulu mengenai taksiran yang linier.
2.6.1 Estimator Linier
Misalkan 𝑍(𝑠1), 𝑍(𝑠2), … , 𝑍(𝑠𝑛) adalah pengukuran 𝑍 pada lokasi 𝑠1, 𝑠2, … , 𝑠𝑛. Taksiran dari 𝑍 di titik 𝑠0 yaitu 𝑍̂(𝑠0) dapat dinyatakan sebagai kombinasi linier dari 𝑍(𝑠1), 𝑍(𝑠2), … , 𝑍(𝑠𝑛). Dapat ditulis sebagai berikut:
𝑍̂(𝑠0) = ∑ 𝜆𝑖𝑍(𝑠𝑖) 𝑛
𝑖=1
dimana 𝜆𝑖 adalah bobot dari 𝑍(𝑠𝑖) dengan 𝑖 = 1,2, … , 𝑛 dan 𝜆𝑖 disebut bobot kriging. Dari persamaan diatas, taksiran dinyatakan sebagai kombinasi linier. Hal ini menunjukkan sifat linier dari taksiran, dimana taksiran yang dinotasikan dengan 𝑍̂(𝑠) merupakan kombinasi linier dari variabel teregional 𝑍(𝑠).
13 Selanjutnya akan ditaksir nilai dari 𝜆𝑖, bobot dari 𝑍(𝑠𝑖) untuk 𝑖 = 1,2, … , 𝑛. nilai taksiran 𝜆𝑖 kemudian akan digunakan untuk menghitung 𝑍̂(𝑠0). Karena taksiran dari metode Kriging memenuhi kriteria B.L.U.E (Best Linier Unbiased Estimator), pada pembahasan selanjutnya akan dijelaskan kondisi yang harus dipenuhi agar taksiran menjadi tak bias.
2.6.2 Estimator Tak Bias
Taksiran dalam metode kriging ini diupayakan memenuhi sifat tak bias. Taksiran Z di lokasi 𝑠0, 𝑍̂(𝑠0), dikatakan tak bias jika 𝐸 (𝑍̂(𝑠0)) = 𝜇. Syarat agar hal tersebut terpenuhi dapat dilihat pada penjabaran berikut ini:
𝐸 (𝑍̂(𝑠0)) = 𝐸 (∑ 𝜆𝑖 𝑛 𝑖=1 𝑍(𝑠𝑖)) = ∑ 𝜆𝑖 𝑛 𝑖=1 𝐸{𝑍(𝑠𝑖)} 𝐸 (𝑍̂(𝑠0)) = ∑ 𝜆𝑖 𝑛 𝑖=1 𝜇
Agar taksiran menjadi tak bias, 𝐸 (𝑍̂(𝑠0)) = 𝜇, maka:
𝐸 (𝑍̂(𝑠0)) = ∑ 𝜆𝑖 𝑛 𝑖=1 𝜇 𝜇 = ∑ 𝜆𝑖 𝑛 𝑖=1 𝜇 𝜇 (∑(𝜆𝑖) − 1 𝑛 𝑖=1 ) = 0 Karena 𝜇 ≠ 0 maka
14 ∑(𝜆𝑖) − 1 𝑛 𝑖=1 = 0 ∑(𝜆𝑖) = 1 𝑛 𝑖=1
Jadi syarat agar 𝑍̂(𝑠0) tak bias adalah ∑𝑛𝑖=1𝜆𝑖 = 1 atau dengan kata lain, jumlah dari semua bobot kriging sama dengan 1. Selanjutnya akan dibahas mengenai variansi minimum.
2.6.3 Variansi Minimum
𝑍̂ (𝑠𝑂) disebut taksiran yang terbaik (best) jika memiliki variansi residual yang minimum. Bobot kriging 𝜆 = (𝜆1, 𝜆2, … , 𝜆𝑛)didapatkan dengan cara meminimumkan mean square predicted error terhadap kendala ∑𝑛𝑖=1𝜆𝑖 = 1, dengan menggunakan metode pengali Lagrange. Mean square predicted error dapat dinyatakan sebagai berikut:
𝑀𝑆𝑃𝐸 = 𝐸 [𝑍̂(𝑠𝑂) − 𝑍(𝑠𝑜)] 2
Misalkan 𝑅 adalah residual dari penaksiran di lokasi 𝑠𝑂, maka 𝑅 dapat dinyatakan sebagai berikut:
𝑅(𝑠𝑜) = 𝑍̂(𝑠𝑜) − 𝑍(𝑠𝑜)
Sehingga variansi dari residual pada lokasi So dapat dinyatakan sebagai berikut: 𝑉𝑎𝑟 (𝑅(𝑠𝑜)) = 𝑉𝑎𝑟 (𝑍̂(𝑠𝑜) − 𝑍(𝑠𝑜)) = 𝑐𝑜𝑣 (𝑍̂(𝑠𝑜), 𝑍̂(𝑠𝑜)) − 𝑐𝑜𝑣 (𝑍̂(𝑠𝑜), 𝑍(𝑠𝑜)) − 𝑐𝑜𝑣 (𝑍(𝑠𝑜), 𝑍̂(𝑠𝑜)) + 𝑐𝑜𝑣(𝑍(𝑠𝑜), 𝑍(𝑠𝑜)) = 𝐶𝑜𝑣 (𝑍̂(𝑠𝑜), 𝑍̂(𝑠𝑜)) − 2 𝑐𝑜𝑣(𝑍̂(𝑠0), 𝑍(𝑠0)) + 𝑐𝑜𝑣(𝑍(𝑠0), 𝑍(𝑠0)) (2.2) Karena 𝑍̂(𝑠𝑜) = ∑𝑛 𝜆𝑖 𝑍(𝑠𝑖 𝑖=1 ), maka : Cov (𝑍̂(𝑠𝑜), 𝑍̂(𝑠𝑜)) = 𝑣𝑎𝑟 (𝑍̂(𝑠𝑜))
15 = 𝑣𝑎𝑟 (∑ 𝜆𝑖 𝑍(𝑠𝑖 𝑛 𝑖=1 )) = ∑𝑛𝑖=1∑𝑛𝑗=1𝜆𝑖 𝜆𝑗 𝐶𝑖𝑗 (2.3)
𝐶𝑜𝑣 (𝑍(𝑠0)𝑍(𝑠0)) adalah kovariansi dari variabel teregional 𝑍(𝑠0). Jika diasumsikan bahwa setiap variabel teregional mempunyai variansi yang sama, 𝜎̂2, maka : a. 𝐶𝑜𝑣 (𝑍(𝑠0), 𝑍(𝑠0)) = 𝑉𝑎𝑟 (𝑍(𝑠0)) 𝐶𝑜𝑣 (𝑍(𝑠0), 𝑍(𝑠0)) = 𝜎̂2 (2.4) b. 2𝐶𝑜𝑣 (𝑍̂(𝑠0), 𝑍(𝑠0)) = 2𝐶𝑜𝑣 (∑𝑛𝑖=1𝜆𝑖𝑍(𝑠𝑖), 𝑍(𝑠0)) = 2𝐸 (∑ 𝜆𝑖𝑍(𝑠𝑖)𝑍(𝑠0) 𝑛 𝑖=1 ) − 2𝐸 (∑ 𝜆𝑖𝑍(𝑠𝑖) 𝑛 𝑖=1 ) 𝐸(𝑍(𝑠0)) = 2 ∑ 𝜆𝑖𝐸(𝑍(𝑠𝑖)𝑍(𝑠0)) 𝑛 𝑖=1 − 2 ∑ 𝜆𝑖𝐸(𝑍(𝑠𝑖) 𝑛 𝑖=1 )𝐸(𝑍(𝑠0)) = 2 ∑ 𝜆𝑖(𝐸(𝑍(𝑠𝑖)𝑍(𝑠0)) 𝑛 𝑖=1 − 𝐸(𝑍(𝑠𝑖))𝐸(𝑍(𝑠0))) = 2 ∑𝑛𝑖=1𝜆𝑖𝐶𝑖0 (2.5)
Substitusikan ketiga bentuk persamaan (2.3), (2.4), (2.5) pada persamaan variansi dari residual penaksiran :
𝑉𝑎𝑟(𝑅(𝑠0)) = 𝑐𝑜𝑣 (𝑍̂(𝑠0)𝑍̂(𝑠0)) − 2𝑐𝑜𝑣 (𝑍̂(𝑠0)𝑍(𝑠0)) + 𝑐𝑜𝑣 (𝑍(𝑠0)𝑍(𝑠0)) 𝜎̂𝑅2 = 𝜎̂2+ ∑ ∑ 𝜆 𝑖𝜆𝑗𝐶𝑖𝑗 − 2 ∑ 𝜆𝑖𝐶𝑖0 𝑛 𝑖=1 𝑛 𝑗=1 𝑛 𝑖=1
Karena tujuannya adalah ingin didapatkan variansi dari kesalahan yang minimum, yang harus dilakukan adalah melakukan peminimalan fungsi dengan n
16 variabel (karena variansi dari residual merupakan sistem persamaan dengan n variabel yang tidak diketahui).
Membuat turunan parsial pertama dari 𝜎̂𝑅2 = 0 akan menghasilkan 𝑛 persamaan dengan 𝑛 variabel yang tidak diketahui. Dengan adanya kondisi ketidakbiasaan, perlu ditambahkan satu persamaan lain tanpa perlu menambah variabel yang tidak diketahui. Hal ini mengarah kepada sistem persamaan dengan 𝑛 + 1 persamaan dengan 𝑛 variabel yang tidak diketahui. Untuk menyelesaikan persamaan tersebut, akan digunakan metode pengali Lagrange, yaitu metode yang digunakan untuk meminimumkan fungsi dengan kendala. Akan dikenalkan variabel yang tidak diketahui lainnya pada persamaan 𝜎̂𝑅2, variabel baru ini, misalkan 𝑚, disebut parameter Lagrange, dengan menambahkan 𝑚, dan mengikut sertakan syarat ketidakbiasaan, sistem persamaannya dapat dibuat sebagai berikut:
𝜎̂𝑅2 = 𝜎̂2+ ∑ ∑ 𝜆𝑖𝜆𝑗𝐶𝑖𝑗− 2 ∑ 𝜆𝑖𝐶𝑖0 𝑛 𝑖=1 𝑛 𝑗=1 𝑛 𝑖=1 + 2𝑚(∑ 𝜆𝑖 − 1) 𝑛 𝑖=1 dengan, ∑ 𝜆𝑖 = 1 𝑛 𝑖=1
Variansi dari kesalahan akan diminimalkan dengan menghitung turunan parsial pertama terhadap 𝜆1, . . . , 𝜆𝑘 dan 𝑚 dan membuat setiap turunan tersebut sama dengan nol. Di bawah ini akan dicontohkan untuk 𝜆1. Untuk yang lainnya dapat dilakukan dengan cara yang sama.
a) 𝜕(∑ ∑ 𝜆𝑖 𝜆𝑗 𝐶𝑖𝑗 𝑛 𝑗=1 𝑛 𝑖=1 ) 𝜕(𝜆1) = 𝜕(𝜆12𝐶11+ 2𝜆1 ∑𝑛𝑗=2𝜆𝑗 𝐶1𝑗) 𝜕(𝜆1) = 2𝜆1𝐶11+ 2 ∑𝑛𝑗=2𝜆𝑗 𝐶1𝑗 (2.6) = 2 ∑ 𝜆𝑗 𝐶𝑖𝑗 𝑛 𝑗=1
17 b) 𝜕(2 ∑ 𝜆𝑖 𝐶𝑖0 𝑛 𝑖=1 ) 𝜕(𝜆1) = 𝜕(2𝜆1 𝐶10) 𝜕(𝜆1) = 2𝐶10 (2.7) c) 𝜕(2𝑚 (∑ 𝜆𝑖 𝑛 𝑖=1 −1)) 𝜕(𝜆1) = 2𝑚 (2.8)
Dengan menggabungkan ketiga persamaan (2.6), (2.7) dan (2.8), maka diperoleh persamaan di bawah ini :
𝜕(𝜎̂𝑅2) 𝜕(𝜆1) = 2 ∑ 𝜆𝑗𝐶𝑖𝑗 𝑛 𝑗=1 − 2𝐶10+ 2𝑚 = 0 2 ∑ 𝜆𝑗 𝑛 𝑗=1 𝐶1𝑗+ 2𝑚 = 2𝐶10 ∑ 𝜆𝑗 𝑛 𝑗=1 𝐶1𝑗+ 𝑚 = 𝐶10
Jika penurunan yang sama dilakukan terhadap 𝜆1, . . . , 𝜆𝑘, maka akan diperoleh sistem persamaan sebagai berikut:
𝜕(𝜎̂𝑅2) 𝜕(𝜆1)= 2 ∑ 𝜆𝑗 𝐶1𝑗 −2𝐶10 +2𝑚 𝑛 𝑗=1 = 0 → ∑ 𝜆𝑗 𝐶1𝑗 +𝑚 𝑛 𝑗=1 = 𝐶10 𝜕(𝜎̂𝑅2) 𝜕(𝜆2) = 2 ∑ 𝜆𝑗 𝐶2𝑗 −2𝐶20 +2𝑚 𝑛 𝑗=1 = 0 → ∑ 𝜆𝑗 𝐶2𝑗 +𝑚 𝑛 𝑗=1 = 𝐶20 ⋮ 𝜕(𝜎̂𝑅2) 𝜕(𝜆𝑛) = 2 ∑ 𝜆𝑗 𝐶𝑛𝑗 −2𝐶𝑛0 +2𝑚 𝑛 𝑗=1 = 0 → ∑ 𝜆𝑗 𝐶𝑛𝑗 +𝑚 𝑛 𝑗=1 = 𝐶𝑛0
Turunan parsial terhadap 𝜆1, . . . , 𝜆𝑘 yang meminimalkan variansi kesalahan dan memenuhi kendala ∑𝑛𝑖=1𝜆𝑖 = 1 dapat dinyatakan dalam sistem persamaan dengan n+1 persamaan dibawah ini:
∑𝑛𝑗=1𝜆𝑗 𝐶𝑖𝑗 +𝑚 = 𝐶𝑚∀ 𝑖 = 1, 2, … , 𝑛 ; dan 𝑗 = 1,2, … , 𝑛
18 [ 𝐶(0) 𝐶(𝑠2− 𝑠1) ⋮ 𝐶(𝑠𝑛− 𝑠1) 1 𝐶(𝑠1− 𝑠2) 𝐶(0) ⋮ 𝐶(𝑠𝑛 − 𝑠2) 1 ⋯ ⋯ ⋱ ⋯ ⋯ 𝐶(𝑠1− 𝑠𝑛) 𝐶(𝑠2− 𝑠𝑛) ⋮ 𝐶(0) 1 1 1 ⋮ 1 0][ 𝜆1 𝜆2 ⋮ 𝜆𝑛 𝑚 ] = [ 𝐶(𝑠0− 𝑠1) 𝐶(𝑠0− 𝑠2) ⋮ 𝐶(𝑠0− 𝑠𝑛) 1 ] (2.9)
Misalkan 𝛴 disebut matriks kovariogram dan dinyatakan sebagai berikut:
𝛴 = [ 𝐶(0) 𝐶(𝑠2− 𝑠1) ⋮ 𝐶(𝑠𝑛− 𝑠1) 𝐶(𝑠1− 𝑠2) 𝐶(0) ⋮ 𝐶(𝑠𝑛− 𝑠2) ⋯ ⋯ ⋱ … 𝐶(𝑠1− 𝑠𝑛) 𝐶(𝑠2− 𝑠𝑛) ⋮ 𝐶(0) ]
Matriks kovariogram merupakan matriks semi definit positif. Sistem persamaan (2.9) disebut juga sistem persamaan Kriging. Karena adanya hubungan antara kovariogram dan semivariogram, yaitu
𝛾(ℎ) = 𝐶(0) − 𝐶(ℎ)
Maka persamaan Kriging dapat dinyatakan dalam bentuk semivariogram. Sistem persamaan Kriging dalam bentuk semivariogram dinyatakan dengan matriks di bawah ini: [ 𝛾(0) 𝛾(𝑠2− 𝑠1) ⋮ 𝛾(𝑠𝑛 − 𝑠1) 1 𝛾(𝑠1− 𝑠2) 𝛾(0) ⋮ 𝛾(𝑠𝑛− 𝑠2) 1 ⋯ ⋯ ⋱ ⋯ ⋯ 𝛾(𝑠1− 𝑠𝑛) 𝛾(𝑠2− 𝑠𝑛) ⋮ 𝛾(0) 1 1 1 ⋮ 1 0][ 𝜆1 𝜆2 ⋮ 𝜆𝑛 −𝑚] = [ 𝛾(𝑠0− 𝑠1) 𝛾(𝑠0− 𝑠2) ⋮ 𝛾(𝑠0− 𝑠𝑛) 1 ] (2.10)
Misalkan Г disebut semivariogram dan dapat dinyatakan sebagai berikut:
Г = [ 𝛾(0) 𝛾(𝑠2− 𝑠1) ⋮ 𝛾(𝑠𝑛− 𝑠1) 𝛾(𝑠1− 𝑠2) 𝛾(0) ⋮ 𝛾(𝑠𝑛− 𝑠2) ⋯ ⋯ ⋱ … 𝛾(𝑠1− 𝑠𝑛) 𝛾(𝑠2− 𝑠𝑛) ⋮ 𝛾(0) ]
Matriks semivariogram merupakan matriks semi definit negatif
Dengan menyelesaikan sistem persamaan (2.9) atau (2.10) dapat dihitung nilai 𝜆1, 𝜆2, … , 𝜆𝑛. Sehingga nilai taksiran di titik lain yang tidak tersampel dapat dihitung. Pada pembahasan selanjutnya akan dijelaskan cara mencari variansi dari residual taksiran.
19
2.6.4 Penghitungan Variansi Kriging
Variansi dari taksiran Kriging adalah variansi minimum dari residual taksiran. Jika terdapat lebih dari satu model semivariogram atau kovariogram yang valid, variansi dari residual berguna dalam menentukan model semivariogram atau kovariogram manakah yang memberikan hasil taksiran yang terbaik.
Langkah-langkah untuk mencari variansi dari taksiran Kriging dijelaskan sebagai berikut :
1. Kalikan setiap persamaan pada sistem persamaan Kriging dengan λi λ𝑖(∑𝑛𝑗=1λ𝑗𝐶𝑖𝑗+ 𝑚) = λ𝑖𝐶𝑖0 ∀𝑖 = 1,2, … , 𝑛 2. Jumlahkan setiap persamaan diatas sehingga menjadi :
∑ λ𝑖 𝑛 𝑖=1 ∑ λ𝑗𝐶𝑖𝑗 𝑛 𝑗=1 + ∑ λ𝑖 𝑚 𝑛 𝑖=1 = ∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 ∑ ∑ λ𝑖λ𝑗𝐶𝑖𝑗 𝑛 𝑗=1 𝑛 𝑖=1 = ∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 − ∑ λ𝑖 𝑚 𝑛 𝑖=1
Karena∑𝑛𝑖=1𝜆𝑖 = 1, maka persamaannya menjadi :
∑ ∑ λ𝑖λ𝑗𝐶𝑖𝑗 = ∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 − 𝑚 𝑛 𝑗=1 𝑛 𝑖=1
Subtitusikan persamaaan diatas dengan persamaan 𝜎̂𝑅2 = 𝜎̂2+ ∑ ∑ λ𝑖λ𝑗𝐶𝑖𝑗 𝑛 𝑗=1 𝑛 𝑖=1 − 2 ∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 𝜎̂𝑅2 = 𝜎̂2+ (∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 − 𝑚) − 2 ∑ λ𝑖𝐶𝑖0 𝑛 𝑖=1 𝜎̂𝑅2 = 𝜎̂2− (∑ λ 𝑖𝐶𝑖0 𝑛 𝑖=1 + 𝑚)
20 𝜎̂𝑅2 = 𝜎̂2− (∑ λ𝑖𝐶𝑖0
𝑛
𝑖=1
+ 𝑚)
Sehingga diperoleh variansi dari residual taksiran Kriging dalam bentuk kovariogram, yaitu : 𝜎̂𝑅2 = 𝜎̂2− (∑ λ 𝑖𝐶𝑖0 𝑛 𝑖=1 + 𝑚)
Sedangkan variansi dari residual taksiran Kriging dalam bentuk semivariogram adalah :
𝜎̂𝑅2 = ∑ λ𝑖𝛾𝑖 𝑛
𝑖=1
2.7 Median Polish Kriging
Dalam statistik dikenal ukuran pemusatan data yang meliputi mean (rata-rata), median, dan modus. Median segugus data yang telah diurutkan dari yang terkecil sampai terbesar ataupun dari yang terbesar sampai terkecil adalah pengamatan yang tepat di tengah-tengah bila banyaknya mengamatan ganjil, dapat ditulis dengan rumus 𝑀𝑒 =𝑥𝑛+1
2 , atau rata-rata kedua pengamatan yang di tengah bila banyaknya pengamatan genap, dapat ditulis dengan rumus 𝑀𝑒 =1
2(𝑥𝑛2 + 𝑥𝑛
2+1
) [21]. Konsep dasar median polish sama halnya dalam mencari nilai median dalam ukuran pemusatan.
Dalam mengestimasi data spasial yang mengandung pencilan dihasilkan hasil yang kurang baik. Pencilan (outlier) adalah data pengamatan yang nilainya jauh dari data lainnya (sangat besar atau sangat kecil) [1]. Pencilan (outlier) ini terjadi karena kesalahan pencatatan, kalibrasi yang tidak tepat, dan kemungkinan lainnya.
Misalkan himpunan variabel acak {𝑍(𝑠), 𝑠 ∈ 𝐷} memenuhi [7]: 𝑍(𝑠) = 𝜇(𝑠) + 𝑅(𝑠), 𝑠 ∈ 𝐷
21 Dengan 𝜇(𝑠) = 𝐸(𝑍(𝑠)) merupakan rata-rata (mean) dan 𝑅(𝑠) merupakan residual dari proses ordinary kriging. Rata-rata (mean) tidak diketahui, asumsikan 𝜇(𝑠) terurai secara alami menjadi komponen terarah,
𝜇(𝑠) = 𝑎 + 𝑐(𝑥) + 𝑟(𝑦), 𝑠 = (𝑖, 𝑗)′ ∈ 𝐷
Metode median polish membutuhkan suatu grid untuk membentuk matriks dimana elemen dari matriks tersebut merupakan nilai median dalam baris dan kolom. Jika {𝑠𝑖 , 𝑖 = 1, … , 𝑛} pada grid {(𝑥𝑙, 𝑦𝑘)′, 𝑘 = 1, … , 𝑝 ; 𝑙 = 1, … , 𝑞}, maka 𝑠𝑖 = (𝑥𝑙, 𝑦𝑘)′ dapat ditulis,
𝜇(𝑠𝑖) = 𝑎 + 𝑟𝑘+ 𝑐𝑙
di mana 𝑎 merupakan hasil keseluruhan, 𝑟𝑘 merupakan hasil baris ke-k, dan 𝑐𝑙merupakan hasil kolom ke-l.
Metode median polish kriging digunakan untuk menilai data berpencilan berdasarkan pendekatan median dalam bentuk tabel dua arah [12, 15]. Interpolasi digunakan untuk mengestimasi komponen rata-rata di titik tersampel dan titik prediksi target. Untuk melakukan interpolasi pada tabel dua arah dibutuhkan grid secara horizontal dan vertikal. Dengan asumsi tepat satu pengamatan pada setiap simpul grid, estimator OLS (Ordinary Least Squares) digunakan, yaitu
𝑎̂ = 𝑧𝑝+1,𝑞+1 (∞) ,
𝑟̂𝑘= 𝑧𝑘,𝑞+1 (∞) , 𝑘 = 1, … , 𝑝,
𝑐̂𝑙 = 𝑧𝑝+1,𝑙 (∞)
, 𝑙 = 1, … , 𝑞,
Maka, estimator OLS untuk 𝜇(𝑠𝑖) adalah
22 Untuk 𝑠 = (𝑥, 𝑦)′ wilayahnya dibatasi oleh garis yang bergabung dengan empat simpul, yaitu (𝑥𝑙, 𝑦𝑘)′, (𝑥𝑙+1, 𝑦𝑘)′, (𝑥𝑙, 𝑦𝑘+1)′, (𝑥𝑙+1, 𝑦𝑘+1)′ dimana 𝑥𝑙< 𝑥𝑙+1 dan 𝑦𝑘 < 𝑦𝑘+1 maka diperoleh interpolasi median polish sebagai berikut:
𝜇̂ (𝑠) = 𝑎̂ + 𝑟̂𝑘+ ( 𝑦 − 𝑦𝑘
𝑦𝑘+1− 𝑦𝑘) (𝑟̂𝑘+1− 𝑟̂𝑘) + 𝑐̂𝑙+ (
𝑥 − 𝑥𝑙
𝑥𝑙+1− 𝑥𝑙) (𝑐̂𝑙+1− 𝑐̂𝑙), 𝑘 = 1, … , 𝑝 − 1, 𝑙 = 1, … , 𝑞 − 1.
Estimasi median polish kriging mencakup estimasi rata-rata median polish ditambahestimasiresidual dari proses median polish. Model median polish kriging yaitu [7]:
𝑍̂(𝑠𝑖) = 𝑎̂ + 𝑟̂𝑘+ 𝑐̂𝑙+ 𝑅̂(𝑠𝑖)
𝑍̂(𝑠𝑖) = 𝜇̂(𝑠𝑖) + 𝑅̂(𝑠𝑖) (2.12) Dengan menjadikan matriks 𝑝 × 𝑞 dengan nilai pengamatan tersampel sebagai dasarnya. Kemudian bentuk matriks baru dengan dimensi (𝑝 + 1) × (𝑞 + 1) dimana 𝑟̂𝑘 merupakan hasil dari baris bagian pertama untuk kolom selanjutnya, 𝑐̂𝑙 merupakan hasil dari kolom bagian pertama untuk baris selanjutnya, 𝑎̂ merupakan hasil keseluruhan pada (𝑝 + 1) × (𝑞 + 1), dan 𝑅̂(𝑠𝑖) merupakan nilai residual. Untuk residual grid yang tidak tersampel dapat menggunakan residual yang diperoleh dari persamaan ordinary kriging, yaitu [14]:
𝑅̂(𝑠𝑖) = ∑ 𝜆𝑖𝑅(𝑠𝑖) , 𝑠𝑖 ∈ ℝ2 𝑛
23
BAB III
METODE PENELITIAN
3.1 Sumber Data
Data yang digunakan pada penelitian ini adalah data sekunder yang bersumber dari Badan Pengelola Lingkungan Hidup Daerah (BPLHD) Provinsi DKI Jakarta. Data tersebut merupakan data air tanah yang diambil dari satu sampel sumur air tanah dangkal di setiap kelurahan yang ada di Provinsi DKI Jakarta pada tahun 2015. Lokasi titik sampel terdapat di lima wilayah DKI Jakarta dengan rincian sebagai berikut pada setiap wilayah:
1. Kotamadya Jakarta Utara sebanyak 17 titik sampel sumur air tanah, 2. Kotamadya Jakarta Pusat sebanyak 37 titik sampel sumur air tanah, 3. Kotamadya Jakarta Selatan sebanyak 36 titik sampel sumur air tanah, 4. Kotamadya Jakarta Timur sebanyak 25 titik sampel sumur air tanah, dan 5. Kotamadya Jakarta Barat sebanyak 33 titik sampel sumur air tanah.
Data ini terdiri dari data titik koordinat posisi lokasi pengambilan sampel sumur air tanah dangkal (X dan Y), dan data fluorida air tanah (Z).
3.2 Metode Pengolahan Data
Adapun tahapan yang dilakukan dalam mengelola data sekunder sampel air tanah ini. Pengolahan data dilakukan menggunakan metode Ordinary Kriging, dan sebagai berikut ini adalah tahapan-tahapannya:
1. Buat statistik deskriptif dengan tujuan untuk mendapatkan informasi tentang nilai pemusatan berupa rata-rata, variansi, nilai maksimal dan nilai minimal pada data fluorida air tanah, serta gambaran kadar air pada setiap wilayah
24 2. Pengujian asumsi kestasioneran orde dua dengan memplotkan data berdasarkan koordinatnya. Plotting dilakukan sebanyak tiga kali, yaitu dengan memplotkan data fluorida air tanah terhadap absis (X) lokasi sampel, lalu memplotkan data fluorida air tanah terhadap ordinat (Y) lokasi sampel, kemudian memplotkan data fluorida air tanah dengan koordinat lokasi sampel dalam bentuk tiga dimensi. Kemudian menghitung dan menganalis uji Cox-Stuart untuk bukti yang lebih valid sebagai uji kecenderungannya. Jika tidak terdapat kecenderungan (stasioner) maka asumsi metode Ordinary Kriging terpenuhi. Adapun langkah pengujian Cox-Stuart [14, 19] sebagai berikut:
a. Buat data bentuk berpasang-pasangan yaitu (𝑋1, 𝑋1+𝑐), … , (𝑋𝑛, 𝑋𝑛+𝑐)dengan nilai 𝑐 =𝑛
2 untuk n suatu bilangan genap dan 𝑐 = (𝑛+1)
2 untuk n suatu bilangan ganjil. Untuk n bilangan ganjil, harus ada data yang disingkirkan yaitu data tengah atau data ke-c.
b. Setiap pasangan data (𝑋1, 𝑋1+𝑐) untuk 𝑋𝑖 lebih besar dari pada 𝑋𝑖+𝑐 diberi tanda positif (+) dan untuk 𝑋𝑖 lebih kecil dari pada 𝑋𝑖+𝑐 diberi tanda negative (-). Jika 𝑋𝑖 sama dengan 𝑋𝑖+𝑐, maka pasangan data tersebut disingkirkan.
c. Hitung tanda positif (+) dan negatif (-), lalu ambil jumlah tanda yang terkecil.
d. Hitung 𝑃(𝑋 ≤ 𝑇) dengan 𝑛 = 𝑐 dan 𝑝 = 0,5 berdasarkan distribusi peluang binomial.
dengan hipotesis sebagai berikut:
𝐻𝑜: Tidak ada kecenderungan (Trend) dalam data 𝐻1 : Ada kecenderungan dalam data
dan penarikan kesimpulan sebagai berikut: Jika (𝑋 ≤ 𝑇) <𝛼
2 , maka 𝐻0 ditolak dan jika 𝑃(𝑋 ≤ 𝑇) > 𝛼
2 , maka 𝐻0 diterima.
25
Gambar 3.1 Contoh Boxplot Berpencilan
3. Analisa Keberadaan Pencilan
Secara visual pengujian keberadaan pencilan atau outlier pada data dapat menggunakan uji boxplot. Jika suatu data jauh dari data lainnya maka data tersebut dikatakan data pencilan. Contoh plot data berpencilan akan ditampilkan pada Gambar 3.1 berikut ini:
Untuk menguji keberadaan pencilan juga dapat menggunakan uji Z score [10]. Adapun rumus Z score sebagai berikut:
𝑍𝑖 = 𝑋𝑖−𝜇 𝜎 > 𝜃,
dengan 𝜇 merupakan nilai rata-rata (mean), 𝜎merupakan nilai standar deviasi, 𝜃merupakan nilai Z tabel untuk tingkat signifikansi tertentu.
Jika 𝑍𝑖 > 𝜃, maka X dideteksi sebagai pencilan. Untuk tingkah signifikansi 5% maka nilai 𝜃 ≈ 2.
4. Lakukan perhitungan semivariogram eksperimental yaitu 𝛾(ℎ) = 1
2𝑁(ℎ)∑ (𝑍(𝑠𝑖) − 𝑍(𝑠𝑖+ ℎ)) 2 𝑁(ℎ)
𝑖=1 . Dari semivariogram tersebut didapatkan nilai range, sill, dan nugget effect yang nantinya akan digunakan untuk menghitung nilai semivariogram teoritisnya.
5. Bentuk model semivariogram yang sesuai dengan data dilakukan dengan mencoba beberapa model semivariogram teoritisnya, yaitu model Spherical, Exponential, dan Gaussian
26 6. Uji validasi silang dan pemilihan model terbaik.
Validasi silang dilakukan untuk menguji apakah model semivariogram sudah cocok dengan data. Jika model semivariogram tersebut menggambarkan korelasi yang kuat antara 𝑍̂(𝑠0) dan 𝑍(𝑠0), maka nilai taksiran 𝑍̂(𝑠0) akan mendekati nilai sebenarnya 𝑍(𝑠0). Selisih kedua nilai tersebut dikenal juga dengan residual.
Prinsip dasar dalam validasi silang adalah melakukan penaksiran nilai variabel teregional 𝑍̂(𝑠𝑖) berdasarkan nilai variabel teregional 𝑍(𝑠1), … , 𝑍(𝑠𝑖−1), dimana 𝑖 = 2, … , 𝑛, dan 𝑛 adalah jumlah sampel. Berdasarkan prinsip dasar uji validasi silang, penaksiran 𝑍̂(𝑠2) dilakukan berdasarkan nilai variabel teregional 𝑍(𝑠1) yang sudah diketahui. Setelah itu, dibandingkan nilai 𝑍(𝑠2) dengan nilai taksiran 𝑍̂(𝑠2). Selisih antara kedua nilai tersebut disebut residual. Residual diasumsikan berdistribusi normal. Demikian selanjutnya hingga diketahui taksiran variabel teregional 𝑍̂(𝑠𝑛).
Validasi silang dilakukan dengan statistik uji 𝑄1. Statistic uji 𝑄1 digunakan untuk menentukan model variogram yang valid. Berikut rumus 𝑄1 yang menyatakan rata-rata dari residual terbaku 𝑄1 =
1 𝑛−1∑ 𝜀𝑘 𝑛 𝑘=2 dimana 𝜀𝑘 = 𝑒𝑘 𝜎 . Dengan 𝑛 adalah jumlah sampel. Pemilihan model terbaik dapat terpenuhi dengan melihat |𝑄1| yang terkecil.
Berikut langkah-langkah validasi silang terhadap model semivariogram:
a. Misalkan 𝑍(𝑠𝑖) adalah nilai dari variabel teregional 𝑍 di lokasi 𝑠𝑖, dan 𝑠𝑖 merupakan lokasi yang berupa koordinat (𝑋𝑖, 𝑌𝑖) dimana 𝑖 = 1,2, … , 𝑛. Hitung nilai taksiran 𝑍̂(𝑠2) dengan menggunakan Ordinary Kriging menggunakan nilai 𝑍(𝑠1). Sehingga 𝑍̂(𝑠2) dapat dinyatakan sebagai berikut
𝑍̂(𝑠2) = 𝜆1𝑍(𝑠1) Berdasarkan sistem persamaan Ordinary Kriging
[𝛾(𝑠1− 𝑠1) 1 1 𝛾(𝑠1− 𝑠1)] [ 𝜆1 𝜇] = [ 𝛾(𝑠1− 𝑠1) 1 ]
27 b. Bandingkan hasil taksiran 𝑍̂(𝑠2) dengan nilai sebenarnya 𝑍(𝑠2). Kemudian hitung
selisih antar dua nilai tersebut atau biasa disebut residual. 𝑒2 = 𝑍(𝑠2) − 𝑍̂(𝑠2)
c. Lakukan standarisasi terhadap residual yang telah diperoleh pada langkah sebelumnya. Residual ini disebut residual terbaku.
𝜀2 = 𝑒2 𝜎2
d. Ulangi langkah-langkah di atas untuk 𝑍̂(𝑠𝑘) lainnya sampai diperoleh nilai taksiran 𝑍̂(𝑠𝑛) dengan menggunakan nilai 𝑍(𝑠1), … , 𝑍(𝑠𝑛−1). Dimana 𝑘 = 2, … , 𝑛. Secara umum residual dapat ditulis sebagai berikut:
𝑒𝑘= 𝑍(𝑠𝑘) − 𝑍̂(𝑠𝑘) ; 𝑘 = 2, … , 𝑛 Dan residual terbaku dapat ditulis sebagai berikut:
𝜀𝑘= 𝑒𝑘
𝜎𝑘 ; 𝑘 = 2, … , 𝑛 e. Hitung rata-rata keseluruhan residual terbaku (𝑄1), yaitu:
𝑄1 = 1
𝑛 − 1∑ 𝜀𝑘 𝑛
𝑘=2
7. Lakukan uji hipotesis
𝐻0 : Model semivariogram valid 𝐻1 : Model semivariogram tidak valid Dengan keputusan, jika |𝑄1| ≥ 2
√𝑛−1 pada tingkat kepercayaan 95% maka 𝐻0 ditolak dan sebaliknya.Pemilihan model terbaik dapat terpenuhi dengan memilih nilai 𝑄1 yang terkecil.
8. Estimasi menggunakan Median Polish Kriging
Dari model yang terpilih, hitung rata-rata dari median polish dan residual median polish seperti yang dijelaskan pada Bab II. Langkah-langkah menghitung median polish sebagai berikut [15] :
28 1. Buatlah grid pada wilayah persebaran titik sampel. Kemudian hitung median pada grid yang berisi beberapa titik sampel 𝑍(𝑠𝑘𝑙), 𝑘 = 1, … , 𝑝 , 𝑙 = 1, … , 𝑞 tersebut untuk mewakili satu titik tersampel 𝑍(𝑠𝑖). Median untuk jumlah data ganjil yaitu 𝑀𝑒 = 𝑥(𝑛+1
2 )
dan median untuk jumlah data genap yaitu 𝑀𝑒 = 1 2(𝑥(𝑛 2) + 𝑥(𝑛 2+1) ).
2. Buatlah matriks dengan dimensi (𝑝 + 1) × (𝑞 + 1) dimana isi dari matriks 𝑝 × 𝑞 merupakan data sampel 𝑠𝑘𝑙, baris dan kolom selanjutnya diisi nol mengikuti asumsi nilai awal,
𝑠𝑘,𝑙(0) = {𝑠𝑘,𝑙, 𝑘 = 1, … , 𝑝 ; 𝑙 = 1, … , 𝑞 0, lainnya 3. Lakukan iterasi, Untuk 𝑖 = 1, 3, 5, … 𝑠𝑘𝑙(𝑖)= 𝑠𝑘𝑙(𝑖−1)− 𝑚𝑒𝑑{𝑠𝑘𝑙(𝑖−1); 𝑙 = 1, … , 𝑞} 𝑗𝑖𝑘𝑎 𝑘 = 1, … , 𝑝 + 1; 𝑙 = 1, … , 𝑞 𝑠𝑘,𝑞+1(𝑖) = 𝑠𝑘,𝑞+1(𝑖−1) + 𝑚𝑒𝑑{𝑠𝑘𝑙(𝑖−1); 𝑙 = 1, … , 𝑞} 𝑗𝑖𝑘𝑎 𝑘 = 1, … , 𝑝 + 1 dan untuk 𝑖 = 2, 4, 6, … 𝑠𝑘𝑙(𝑖)= 𝑠𝑘𝑙(𝑖−1)− 𝑚𝑒𝑑{𝑠𝑘𝑙(𝑖−1); 𝑘 = 1, … , 𝑝} 𝑗𝑖𝑘𝑎 𝑘 = 1, … , 𝑝; 𝑙 = 1, … , 𝑞 + 1 𝑠𝑝+1,𝑙(𝑖) = 𝑠𝑝+1,𝑙(𝑖−1)+ 𝑚𝑒𝑑{𝑠𝑘𝑙(𝑖−1); 𝑘 = 1, … , 𝑝} 𝑗𝑖𝑘𝑎 𝑙 = 1, … , 𝑞 + 1 dimana 𝑚𝑒𝑑{∙} merupakan median dari nilai pengamatan.
Iterasi ke-1, mengurangkan median baris dari tiap-tiap baris dan tambahkan median baris pada kolom 𝑞 + 1. Kemudian kurangi median kolom dari tiap-tiap kolom, tambahkan median kolom pada 𝑝 + 1 baris dan hitung median baris. Iterasi ke-2, mengurangkan median baris dari tiap-tiap baris dan tambahkan median baris pada kolom 𝑞 + 1 Kemudian kurangi median kolom dari tiap-tiap
29 kolom, tambahkan median kolom pada 𝑝 + 1 baris dan hitung median baris. Proses iterasi dilakukan terus-menerus sampai nilai median kolom dan median baris mendekati konvergen.
4. Proses iterasi dihentikan dengan matriks identitas pada matriks yang diperoleh sebelumnya.
Kemudian jumlahkan rata-rata dan residual dari median polish tersebut. Setelah itu interpolasi menggunakan data yang terbaru. Pengolahan data spasial ini menggunakan metode Median Polish Kriging yang dilakukan dengan bantuan beberapa program statistik seperti Microsoft Office Excel 2013, Software R 3.4.1, dan yang lainnya.
3.3 Alur Penelitian
30
Gambar 3.2 Alur Penelitian
Prediksi data dengan Median PolishKriging
Selesai
Mulai
Meng-input Koordinat Lokasi Setiap Titik (𝑋𝑖, 𝑌𝑖) atau 𝑠𝑖, dengan 𝑖 =
1,2, … ,148, serta Nilai Variabel
Teregional 𝑍 pada Setiap Titik 𝑍(𝑠𝑖)
Membuat statistik deskriptif pada data
Apakah Asumsi Data Stasioner Orde Dua
Terpenuhi?
Menggunakan Metode
Ordinary Kriging
Menghitung nilai semivariogram eksperimental untuk mendapatkan nilai nugget, sill, dan range
Membentuk Model Semivariogram Teoritis Spherical, Eksponensial, dan Gaussian
Tidak
Ya
Uji Validasi Silang
31
BAB IV
HASIL DAN PEMBAHASAN
4.1 Statistika Deskriptif
Statistika deskriptif digunakan untuk mengetahui secara ringkas informasi mengenai suatu data, sepertinilai minimum, nilai maksimum, rata – rata, variansi, dan standar deviasi. Statistik deskriptif data kandungan fluorida air tanah di DKI Jakarta disajikan pada Tabel 4.1 di bawah ini. Adapun data tersebut dilampirkan pada Lampiran I dan peta persebaran data dilampirkan pada Lampiran V.
Tabel 4.1 Statistika Deskriptif Kandungan Fluorida Air Tanah
Minimum Maksimum Rata-rata Variansi Std. Deviasi
0,01 0,95 0,23453 0,03514 0,18746
Dari Tabel 4.1 di atas dapat diketahui bahwa nilai minimum indeks kandungan fluoridaair tanah sebesar 0,01 yaitu terdapat pada wilayah Kelurahan Lenteng Agung. Sementara itu, nilai maksimum untuk indeks kandungan fluoridaair tanah yaitu sebesar 0,95 terdapat di wilayah Kelurahan Sumur Batu. Dari keseluruhan nilai indeks kandungan fluorida air tanah, diperoleh rata-rata sebesar 0,23453. Variansi dari nilai indeks kandungan fluorida air tanah sebesar 0,03514059 dan simpangan baku dari nilai indeks kandungan fluorida air tanah sebesar 0,18746.
Berdasarkan Tabel 2.1 pada Bab II, diperoleh klasifikasi dan persentase kandungan fluorida air tanah di DKI Jakarta. Hasil klasifikasi disajikan pada Tabel 4.2 di bawah ini:
Tabel 4.2 Klasifikasi Kadar Fluorida Air Tanah
Klasifikasi Kadar Fluorida Jumlah Kelurahan Persentase (%)
Rendah 134 90,54
Sedang 14 9,46
Tidak Baik 0 0
32
Gambar 4.1 Plot X Terhadap Fluorida dan Y Terhadap Fluorida
Berdasarkan Tabel 4.2 di atas dapat diketahui bahwa jumlah kelurahan untuk kadar fluorida rendah sebanyak 134 kelurahan dengan persentase 90,54%, sedangkan jumlah kelurahan untuk kadar fluorida sedang sebanyak 14 kelurahan dengan persentase 9,46%. Untuk kadar fluorida tidak baik (di atas 1,5 mg/L) mempunyai persentase 0%. Hal ini berarti bahwa air tanah di DKI Jakarta masih tergolong aman dan layak konsumsi.
4.2 Uji Stasioneritas
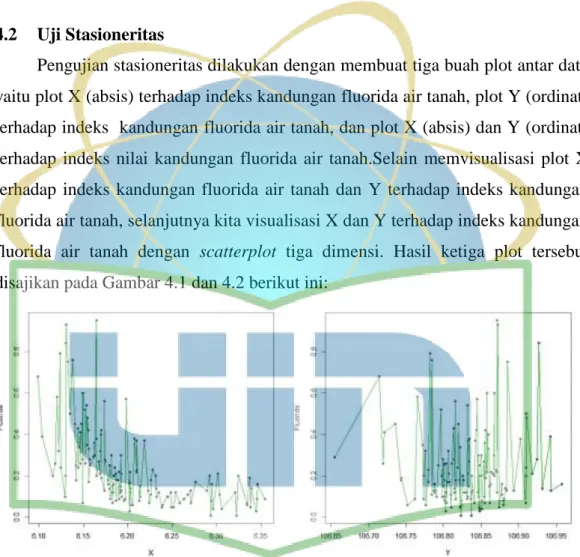
Pengujian stasioneritas dilakukan dengan membuat tiga buah plot antar data yaitu plot X (absis) terhadap indeks kandungan fluorida air tanah, plot Y (ordinat) terhadap indeks kandungan fluorida air tanah, dan plot X (absis) dan Y (ordinat) terhadap indeks nilai kandungan fluorida air tanah.Selain memvisualisasi plot X terhadap indeks kandungan fluorida air tanah dan Y terhadap indeks kandungan fluorida air tanah, selanjutnya kita visualisasi X dan Y terhadap indeks kandungan fluorida air tanah dengan scatterplot tiga dimensi. Hasil ketiga plot tersebut disajikan pada Gambar 4.1 dan 4.2 berikut ini:
Gambar 4.1 di atas menunjukkan plot titik koordinat X terhadap indeks kandungan fluorida air tanah dan plot titik koordinat Y terhadap indeks kandungan fluorida air tanah. Pada gambar tersebut dapat dilihat bahwa plot antara titik koordinat X terhadap indeks kandungan fluorida air tanah tidak mengalami kecenderungan (trend), begitu pula pada titik koordinat Y terhadap indeks kandungan fluorida air tanah tidak mengalami kecenderungan (trend).
33
Gambar 4.2 Scatterplot Tiga Dimensi X dan Y terhadap Indeks Kandungan Fluorida Air Tanah
Gambar 4.2 di atas menunjukkan scatterplot tiga dimensi X dan Y terhadap indeks kandungan fluoridaair tanahPada gambar tersebut dapat dilihat bahwa tidak terdapat kecenderungan (trend) atau membentuk pola tertentu. Dari ketiga plot di atas dapat ditarik kesimpulan bahwa data nilai kandungan fluorida air tanah ini memenuhi asumsi stasioner orde 2.Untuk uji yang lebih valid apakah ada trend atau tidak dapat menggunakan uji Cox-Stuart. Hasil dari pengujian tersebut disajikan pada Tabel 4.3 di bawah ini,
Tabel 4.3 Pasangan Hasil Pengamatan Uji Cox-Stuart Pasangan Data Pasangan Hasil Pengamatan Tanda Pasangan Data Pasangan Hasil Pengamatan Tanda (1; 75) (0,2 ; 0,12) + (38;112) (0,09 ; 0,19) - (2;76) (0,38 ; 0,14) + (39;113) (0,1 ; 0,22) - (3;77) (0,48 ; 0,1) + (40;114) (0,12 ; 0,22) - (4;78) (0,93 ; 0,12) + (41;115) (0,17 ; 0,23) - (5;79) (0,75 ; 0,07) + (42;116) (0,33 ; 0,1) + (6;80) (0,6 ; 0,2) + (43;117) (0,3 ; 0,08) + (7;81) (0,58 ; 0,11) + (44;118) (0,2 ; 0,15) + (8;82) (0,76 ; 0,06) + (45;119) (0,22 ; 0,13) + (9;83) (0,79 ; 0,13) + (46;120) (0,95 ; 0,13) +
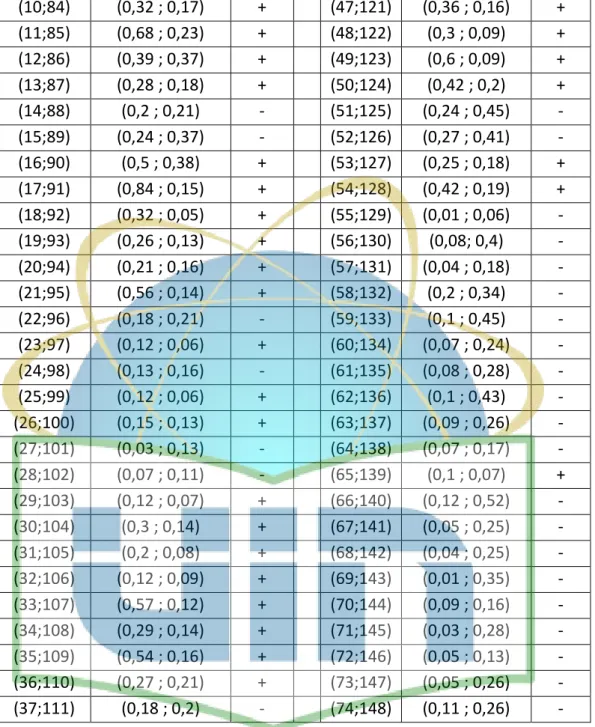
34 (10;84) (0,32 ; 0,17) + (47;121) (0,36 ; 0,16) + (11;85) (0,68 ; 0,23) + (48;122) (0,3 ; 0,09) + (12;86) (0,39 ; 0,37) + (49;123) (0,6 ; 0,09) + (13;87) (0,28 ; 0,18) + (50;124) (0,42 ; 0,2) + (14;88) (0,2 ; 0,21) - (51;125) (0,24 ; 0,45) - (15;89) (0,24 ; 0,37) - (52;126) (0,27 ; 0,41) - (16;90) (0,5 ; 0,38) + (53;127) (0,25 ; 0,18) + (17;91) (0,84 ; 0,15) + (54;128) (0,42 ; 0,19) + (18;92) (0,32 ; 0,05) + (55;129) (0,01 ; 0,06) - (19;93) (0,26 ; 0,13) + (56;130) (0,08; 0,4) - (20;94) (0,21 ; 0,16) + (57;131) (0,04 ; 0,18) - (21;95) (0,56 ; 0,14) + (58;132) (0,2 ; 0,34) - (22;96) (0,18 ; 0,21) - (59;133) (0,1 ; 0,45) - (23;97) (0,12 ; 0,06) + (60;134) (0,07 ; 0,24) - (24;98) (0,13 ; 0,16) - (61;135) (0,08 ; 0,28) - (25;99) (0,12 ; 0,06) + (62;136) (0,1 ; 0,43) - (26;100) (0,15 ; 0,13) + (63;137) (0,09 ; 0,26) - (27;101) (0,03 ; 0,13) - (64;138) (0,07 ; 0,17) - (28;102) (0,07 ; 0,11) - (65;139) (0,1 ; 0,07) + (29;103) (0,12 ; 0,07) + (66;140) (0,12 ; 0,52) - (30;104) (0,3 ; 0,14) + (67;141) (0,05 ; 0,25) - (31;105) (0,2 ; 0,08) + (68;142) (0,04 ; 0,25) - (32;106) (0,12 ; 0,09) + (69;143) (0,01 ; 0,35) - (33;107) (0,57 ; 0,12) + (70;144) (0,09 ; 0,16) - (34;108) (0,29 ; 0,14) + (71;145) (0,03 ; 0,28) - (35;109) (0,54 ; 0,16) + (72;146) (0,05 ; 0,13) - (36;110) (0,27 ; 0,21) + (73;147) (0,05 ; 0,26) - (37;111) (0,18 ; 0,2) - (74;148) (0,11 ; 0,26) -
Tabel 4.3 di atas merupakan tabel berpasangan dari uji Cox-Stuart. Dari tabel tersebut didapatkan 74 pasangan data. Hasil tanda menunjukkan T+ sebanyak 42 dan T- sebanyak 32. Dari uji tanda tersebut, kita ambil T dengan tanda minus (T-) karena jumlahnya lebih kecil dari T+. Setelah itu hitung 𝑃(𝑋 ≤ 𝑇) dengan 𝑛 = 𝐶, 𝑝 = 0,5 berdasarkan distribusi peluang binomial. Berdasarkan distribusi peluang binomial untuk 𝑛 = 74 dan 𝑝 = 0,5 diperoleh
35
Gambar 4.3 Box Plot Kandungan Fluorida Air Tanah 𝑃(𝑋 ≤ 32) = ∑ 𝑏(𝑥; 74, 0,5) 32 𝑥=0 = 𝑃(𝑟 = 0) + 𝑃(𝑟 = 1) + 𝑃(𝑟 = 2) + 𝑃(𝑟 = 3) + 𝑃(𝑟 = 4) + 𝑃(𝑟 = 5) + 𝑃(𝑟 = 6) + 𝑃(𝑟 = 7) + 𝑃(𝑟 = 8) + 𝑃(𝑟 = 9) + 𝑃(𝑟 = 10) + 𝑃(𝑟 = 11) + 𝑃(𝑟 = 12) + 𝑃(𝑟 = 13) + 𝑃(𝑟 = 14) + 𝑃(𝑟 = 15) + 𝑃(𝑟 = 16) + 𝑃(𝑟 = 17) + 𝑃(𝑟 = 18) + 𝑃(𝑟 = 19) + 𝑃(𝑟 = 20) + 𝑃(𝑟 = 21) + 𝑃(𝑟 = 22) + 𝑃(𝑟 = 23) + 𝑃(𝑟 = 24) + 𝑃(𝑟 = 25) + 𝑃(𝑟 = 26) + 𝑃(𝑟 = 27) + 𝑃(𝑟 = 28) + 𝑃(𝑟 = 29) + 𝑃(𝑟 = 30) + 𝑃(𝑟 = 31) + 𝑃(𝑟 = 32) = 0,0000000 + ⋯ + 0,0000001 + 0,0000004 + 0,0000012 + 0.0000038 + 0.0000113 + 0.0000312 + 0.0000802 + 0.0001932 + 0.0004367 + 0.0009280 + 0.0018560 + 0.0034979 + 0.0062184 + 0.0104381 + 0.0165569 + 0.0248354 + 0.0352503 + 0.0473675 = 0,1477075
Selanjutnya berdasarkan uji hipotesis, diperoleh keputusan 𝑃(𝑋 ≤ 32) = 0,1477075 > 0,025, maka H0 diterima, sehingga dapat disimpulkan bahwa tidak ada kecenderungan(trend) dalam data.
4.3 Uji Box-Plot
Jika suatu data jauh dari data yang lain, maka data tersebut mengandung pencilan (outlier). Hasil box plot indeks kandunganfluoridadisajikan pada Gambar 4.3 berikut ini: