DERET
FOURIER
PENDAHULUAN
Dalam bab ini akan dibahas fungsi-fungsi periodik yang dinyatakan dalam bentuk deret tak hingga
Fungsi periodik sering muncul dalam permasalahan getaran mekanik, arus listrik bolak balik, gelombang bunyi, gelombang elektromagnet, hantaran panas, dsb.
Uraian deret fungsi periodik seperti itu disebut DERET FOURIER
Ditemukan oleh seorang matematikawan berkebangsaan Perancis bernama JOSEPH FOURIER
FAKTA TENTANG DERET FOURIER
Fakta tentang deret Fourier dalam kehidupan sehari-hari :
Gelombang suara yang masuk ke dalam telinga manusia merupakan gelombang sinus.
FAKTA TENTANG DERET FOURIER
Alat ECG (Electronic Cardio Graphic)
FUNGSI PERIODIK
Definisi 1:
Sebuah fungsi dikatakan periodik dengan periode
� jika untuk setiap berlaku + � = , dimana
� konstanta positif.
Nilai � positif terkecil dinamakan periode . Jika
Konstanta pada selang dasar dapat diplih
sembarang, bisa 0 atau negatif. Namun = − �
sering dipilih untuk memberikan selang dasar yang
Contoh 1:
Fungsi f = sin mempunyai periode �, �,
�, … karena sin + � , sin + � , sin +
� sama dengan sin .
� merupakan periode terkecil sehingga disebut juga periode sin .
Periode fungsi sin atau cos dimana adalah bilangan bulat positif, adalah �/ .
DERET FOURIER
Definisi 2:
Misalkan adalah sebuah fungsi periodik yang didefinisikan pada selang dasar −�, � dan di luar selang dasar didefinisikan + � = , dengan periode fungsi � = � . Maka fungsi dapat diuraikan dalam deret Fourier yang bersesuaian sebagai berikut :
(1)
1 0 ) sin cos ( 2 ) ( n n n L x n b L x n a a x , �, dan � disebut koefisien-koefisien Fourier dengan:
dengan = , , , , …
L
L
n dx
L x n x
f L
a 1 ( )cos
L L
n dx
L x n x
f L
Definisi 2 digunakan jika fungsi dengan periode � = � memiliki selang dasar simetris terhadap = −�, � .
Definisi 3:
Jika adalah sebuah fungsi periodik dengan periode � yang terdefinisi pada selang dasar
c ≤ ≤ + � atau c ≤ ≤ + �, yaitu + � = . Maka dapat diuraikan dalam deret Fourier sebagai berikut :
1 0 ) sin cos ( 2 ) ( n n n L x n b L x n a a xUntuk koefisieen Fourier, karena untuk
= → � ���
� = sehingga
menjadi
Atau dapat juga dihitung dengan
Ini akan memberikan hasil yang sama karena adalah fungsi periodik.
Sedangkan
� = periode, � = periode = �
c L
c n dx L x n x f L a 2 cos ) ( 1
L c c n dx L x n x f L b 2 sin ) ( 1
L L dx x f La0 1 ( )
c L
c dx x f L a 2
0 ( )
CATATAN PENTING !!!!!!!!!!
Pada dasarnya Definisi 2 dan Defenisi 3 bermakna sama.
Definisi 2 hanya berlaku khusus untuk selang dasar simetris −� ≤ ≤ � .
Namun Definisi 3 berlaku umum, baik untuk selang dasar simetris −� ≤ ≤ � maupun yang tidak simetris c ≤ ≤ + � atau c ≤ ≤ + � .
Contoh 2
:
Diketahui sebuah fungsi = , − < <
, < <
a. Gambarkan grafik diatas
b. Tentukan koefisien Fourier dan c. Uraikan deret Fourier
Jawab :
Dari fungsi yang diberikan dapat diketahui
bahwa periodenya adalah � = , sehingga � = .
Selang dasar − < < .
Maka dapat disimpulkan bahwa selang dasar yang diberikan simetris.
Sehingga dapat dikerjakan dengan Definisi 2 maupun dengan Definisi 3.
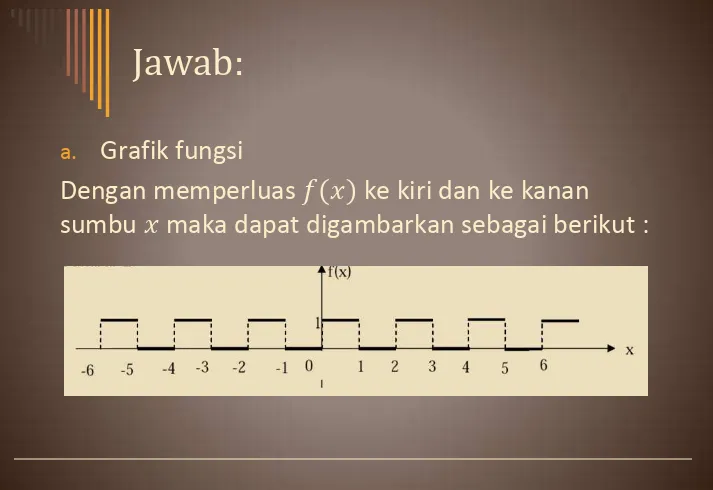
Dengan memperluas ke kiri dan ke kanan
sumbu maka dapat digambarkan sebagai berikut :
a. Grafik fungsi
� �
-5 5 10
-10
3 6
b. Koefisien Fourier
Dengan Defenisi 3
Selang dasar − < < . Menggunakan Defenisi 3, maka selang dasar c ≤ ≤ + �. Dengan demikian
= − dan � = � = . = . Sehingga batas pengintegralan dimulai dari:
Sedangkan untuk = , yaitu dapat
dihitung langsung dari (*) sehingga didapat :
0
0 nπ sin nπ 5 5 3 5 x π n sin nπ 5 5 3 (*) dx 5 x π n cos 5 3 a 5 0 5 0 n 3 dx 5 3 dx 0 cos 5 3 a 5 0 5 0
1 cos nπ
c. Uraian deret Fourier
d. Rumus deret Fourier
= + � sin� + sin � + sin � + ⋯
1
0 ( cos sin )
2 )
(
n
n n
L x n b
L x n a
a x
f
= + � sin� + sin � + sin � + ⋯
= + � − sin − �
∞
Dengan menggunakan Defenisi 2, karena
Sedangkan
1 cos nπ
Kesimpulan
Contoh 3
:
Diketahui sebuah fungsi = , −� < <
, < < �
a. Gambarkan grafik diatas
b. Tentukan koefisien Fourier dan c. Uraikan deret Fourier
a. Grafik fungsi
c. Uraian deret Fourier
d. Rumus deret Fouriernya
= − � − sin − �
∞
Contoh 4
:
Diketahui sebuah fungsi = , < <
, < <
a. Gambarkan grafik diatas
b. Tentukan koefisien Fourier dan c. Uraikan deret Fourier
Jawab:
a. Grafik fungsi
Dengan memperluas ke kiri dan ke kanan
[image:34.720.7.720.27.517.2]Sedangkan
d. Rumus deret Fourier
= + � − sin − �
∞
Contoh 5
:
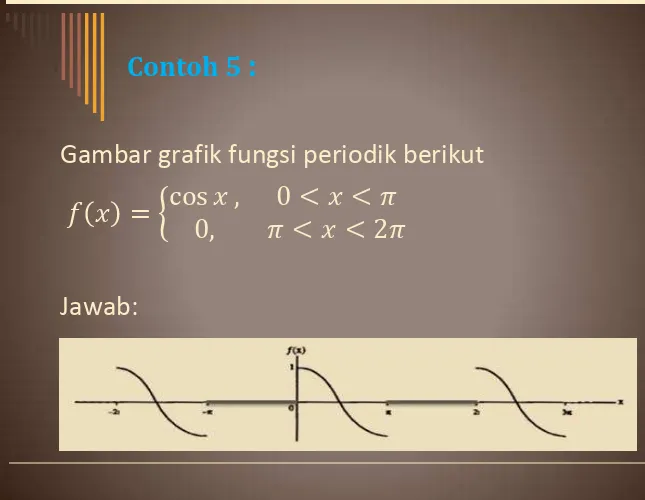
Gambar grafik fungsi periodik berikut
= cos ,, � < < � < < �
MARI BERLATIH MANDIRI
A. Gambarkan grafik fungsi-fungsi dibawah ini:
1. = sin , < < �
, � < < �
2. = , < < �
B. Diketahui sebuah fungsi-fungsi dibawah ini:
a. Gambarkan grafik diatas
b. Tentukan koefisien Fourier dan c. Uraikan deret Fourier
d. Tuliskan rumus deret Fourier untuk diatas
1. = , < < � Jawab ©:
= = �2 + ∞�= �2 cos − �� sin
2. = , − < <
, < <
SYARAT DIRICHLET
Tidak semua fungsi dapat dinyatakan dalam deret Fourier. Syarat sebuah fungsi dapat dinyatakan dalam deret Fourier ditentukan oleh Syarat DIRICHLET berikut :
periodik dengan periode �
terdefinisi dan bernilai tunggal
FUNGSI GANJIL DAN GENAP
Pada deret Fourier untuk fungsi periodik
tertentu mempunyai koefisien Fourier yang sederhana, yaitu 0. Hal ini tentu
mempermudah penguraian menjadi deret Fourier.
Hal ini terjadi pada fungsi-fungsi yang
Definisi 4:
Sebuah fungsi dikatakan
fungsi ganjil jika berlaku − = −
fungsi genap jika berlaku − =
Untuk setiap dalam daerah definisi .
Contoh 6 : Fungsi genap
, , , …
− + , cos , + −�
Contoh 7 : Fungsi ganjil
,
,
,
, …
− +
sin , tan
Sifat-sifat :
Grafik fungsi genap, simetris terhadap sumbu
Grafik fungsi ganjil, simetris terhadap titik pusat
Hasil kali dua fungsi genap adalah fungsi genap
Hasil kali dua fungsi ganjil adalah fungsi genap
Contoh 8 :
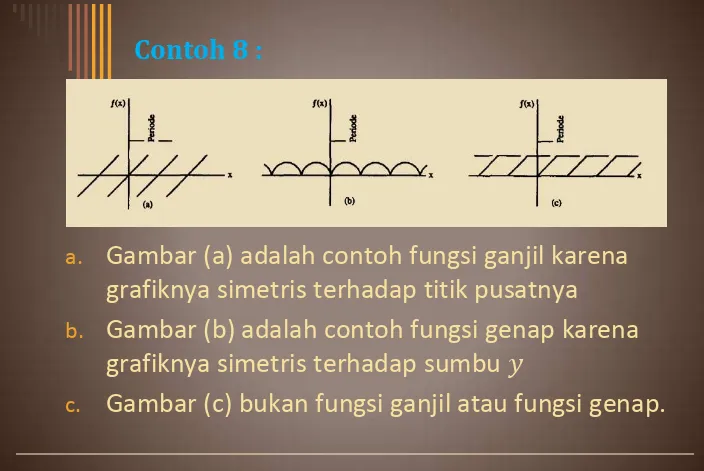
a. Gambar (a) adalah contoh fungsi ganjil karena
grafiknya simetris terhadap titik pusatnya
b. Gambar (b) adalah contoh fungsi genap karena
grafiknya simetris terhadap sumbu
[image:47.720.5.709.32.503.2] Dalam deret Fourier yang berkaitan dengan suatu fungsi ganjil, hanya memuat
suku-suku sinus saja. Sehingga
= dan � =
Maka untuk fungsi ganjil, deret Fourier dapat langsung disajikan kedalam:
Dalam deret Fourier yang berkaitan dengan suatu fungsi genap, hanya memuat
suku-suku cosinus saja. Sehingga � = .
Maka untuk fungsi genap, deret Fourier dapat langsung disajikan kedalam:
L L L dx x f L dx x f L a 00 ( )
2 ) ( 1
L L L n dx L x n x f L dx L x n x f L a 0 cos ) ( 2 cos ) (1
0
n
Contoh 8 :
Tentukan apakah fungsi berikut tergolong
fungsi ganjil, fungsi genap, atau bukan fungsi ganjil dan fungsi genap :
1. = , − ≤ ≤
2. = cos , < < �
, � < < �
3. = − , − < <
, < <
4. = , < <
, < <
5. = , ≤ ≤ �
Jawab:
1. = adalah fungsi ganjil.
Karena − = − . Dari grafik terlihat bahwa simetri terhadap titik pusat.
Untuk lebih jelas lihat gambar berikut :
2. tidak fungsi genap dan tidak fungsi ganjil. Karena tidak memenuhi − = − atau
− = .
3. adalah fungsi ganjil.
Karena memenuhi − = .
4. tidak fungsi genap dan tidak fungsi ganjil. Karena tidak memenuhi − = − atau
− = .
5. tidak fungsi genap dan fungsi ganjil
Karena tidak memenuhi − = − atau
− = .
6. adalah fungsi genap
Karena untuk setiap di daerah defenisinya, berlaku − = .
Dari gambar terlihat bahwa grafik simetris terhadap sumbu .
UJI LATIH MANDIRI
Perderetkan fungsi-fungsi berikut dalam deret
Fourier yang bersesuain dengan menggunakan sifat-sifat fungsi genap atau ganjil jika memungkinkan :
1. = , −� ≤ ≤ �
jawab:
= = � + − � cos
∞
2. = , −� ≤ ≤ �
3. = , − < <
, < <
4. = 8, < <
−8, < <
5. = − , − < <
Deret Fourier Sinus atau Cosinus
Separuh Jangkauan
Adalah suatu deret dimana yang disajikan hanya suku-suku sinus atau suku-suku-suku-suku cosinus.
Untuk separuh jangkauan deret sinus
Untuk separuh jangkauan deret cosinus
n L
n dx L x n x f L b a 0 sin ). ( 2 ; 0
n L