TESIS - SS14 2501 SS14 2501
ESTIMATOR CAMPURAN KERNEL DAN SPLINE
TRUNCATED LINIER MULTIVARIABEL DALAM
REGRESI NONPARAMETRIK
(Studi Kasus : Model Rata-Rata Lama Sekolah di Provinsi Jawa
Tengah)
ALI AKBAR SANJAYA ILHAM PURNOMO NRP. 1314201701
DOSEN PEMBIMBING :
Prof. Dr. Drs. I Nyoman Budiantara, M.Si Dr. Bambang Widjanarko Otok, M.Si.
PROGRAM MAGISTER JURUSAN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT TEKNOLOGI SEPULUH NOPEMBER
TESIS - SS14 2501 SS14 2501
MIXED ESTIMATOR OF KERNEL AND
MULTIVARIABEL LINIER SPLINE TRUNCATED IN
NONPARAMETRIC REGRESSION
(Case Study : Mean Years of Scholling Model in Central Java
Province)
ALI AKBAR SANJAYA ILHAM PURNOMO NRP. 1314201701
SUPERVISOR
Prof. Dr. Drs. I Nyoman Budiantara, M.Si. Dr. Bambang Widjanarko Otok, M.Si.
MASTER PROGRAM
DEPARTMENT OF STATISTICS
FACULTY OF MATHEMATICS AND NATURAL SCIENCE INSTITUTE OF TECHNOLOGY SEPULUH NOPEMBER SURABAYA
vii
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT iii
KATA PENGANTAR v
DAFTAR ISI vii
DAFTAR TABEL ix
DAFTAR GAMBAR x
BAB 1. PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 8
1.3 Tujuan Penelitian 8
1.4 Manfaat Penelitian 8
1.5 Batasan Permasalahan 9
BAB 2. TINJAUAN PUSTAKA 11
2.1 Pemodelan Regresi Parametrik dan Nonparametrik 11
2.2 Regresi Nonparametrik Spline Truncated 12
2.3 Regresi Nonparametrik Kernel 13
2.4. Estimator Campuran Spline dan Kernel 15
2.5 Teorema Dasar Terkait dengan Aljabar Matriks 19
2.6 Tinjauan Non Statistika 19
BAB 3. METODE PENELITIAN 23
3.13.1 Sumber Data 23
3.23.2 Variabel Penelitian 23
3.33.3 Definisi Operasional Variabel Penelitian 23
3.43.4 Tahapan Penelitian 26
BAB 4. HASIL DAN PEMBAHASAN 31
4.1 Bentuk Model Regresi Campuran Kernel dan Spline Truncated
Multivariabel
31
4.2 Estimasi Kurva Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel
viii
Halaman
4.3 Aplikasi pada Model Rata-rata Lama Sekolah di Provinsi Jawa
Tengah
39
4.3.1 Analisis Dekriptif 40
4.3.2 Model Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel
44
4.3.2.1 Pemilihan Titik Knot dan Bandwidth
Optimal dengan Satu Titik Knot
44
4.3.2.2 Pemilihan Titik Knot dan Bandwitdth
Optimal dengan Dua Titik Knot
45
4.3.2.3 Pemilihan Titik Knot dan Bandwitdth
Optimal dengan Tiga Titik Knot
47
4.3.3 Penaksiran Parameter Model Regresi Campuran
Kernel dan Spline Truncated Linier Multivariabel
49
BAB 5 KESIMPULAN DAN SARAN 53
5.1 Kesimpulan 53
5.2 Saran 55
DAFTAR PUSTAKA 57
LAMPIRAN 63
ix
DAFTAR TABEL
Tabel Judul Halaman
Tabel 3.1. Konversi Tahun Pendidikan Tertinggi yang ditamatkan 24
Tabel 4.1 Statistik Deskriptif Variabel Respon dan Variabel Prediktor 40
Tabel 4.2 Nilai GCV dengan Satu Titik Knot 45
Tabel 4.3 Nilai GCV dengan Dua Titik Knot 46
Tabel 4.4 Nilai GCV dengan Tiga Titik Knot 47-48
Tabel 4.5 Perbandingan Nilai GCV Minimum 49
x
DAFTAR GAMBAR
Gambar Judul Halaman
Gambar 2.1 Spline truncated dengan tiga titik knots 13
Gambar 2.2 Visualisasi fungsi kernel dengan berbagai besaran
bandwidth (Guidoum, 2015; data dari Olver et al., 2010)
15
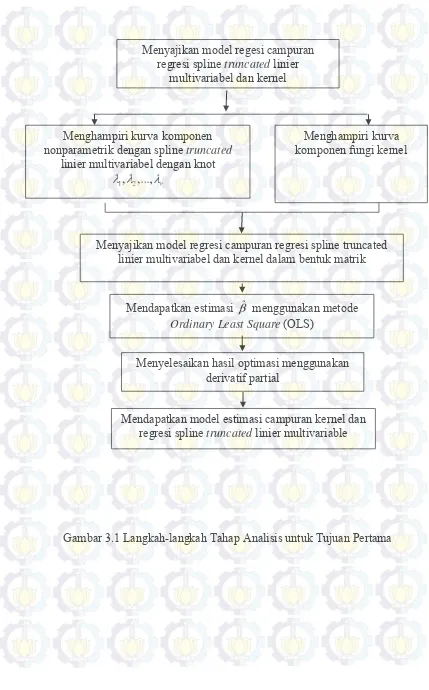
Gambar 3.1 Langkah-langkah Tahapan Analisis untuk Tujuan Pertama
29
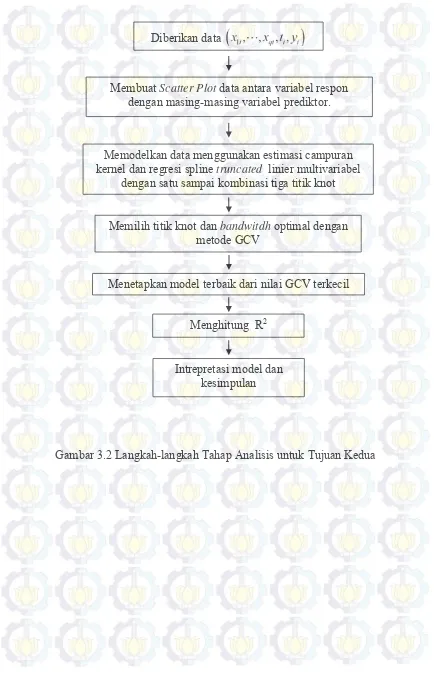
Gambar 3.2 Langkah-langkah Tahapan Analisis untuk Tujuan Kedua
30
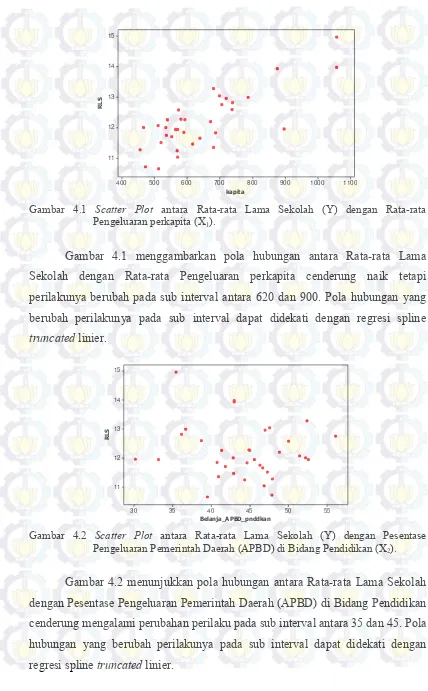
Gambar 4.1 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rata-rata Pengeluaran perkapita (X1).
41
Gambar 4.2 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Pesentase Pengeluaran Pemerintah Daerah (APBD) di Bidang Pendidikan (X2).
41
Gambar 4.3 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rasio Jumlah Murid dengan jumlah Sekolah tingkat SLTA (X3).
42
Gambar 4.4 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rasio Jumlah Murid dengan jumlah Guru tingkat SLTA (X4).
42
Gambar 4.5 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rata-rata Anggota Rumah Tangga (t).
xi
DAFTAR LAMPIRAN
Tabel Judul Halaman
Lampiran 1. Data Regresi Campuran Kernel dan Spline Truncated Linier
Multivariabel 63
Lampiran 2 Program Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel 1 Titik Knot Menggunakan Software R
65
Lampiran 3 Program Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel 2 Titik Knot Menggunakan Software R
69
Lampiran 4 Program Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel 3 Titik Knot Menggunakan Software R
74
Lampiran 5 Output Hasil Program Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel 1 Titik Knot Menggunakan
Software R
79
Lampiran 6 Output Hasil Program Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel 2 Titik Knot Menggunakan Software R
81
Lampiran 7 Output Hasil Program Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel 3 Titik Knot Menggunakan
Software R
v
KATA PENGANTAR
Alhamdulillah, puji syukur penulis panjatkan ke kehadirat Allah SWT, atas segala limpahan rahmat dan kemurahan-Nya penulis dapat menyelesaikan tesis dengan judul “Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel Dalam Regresi Nonparametrik (Studi Kasus : Model Rata-rata
Lama Sekolah di Provinsi Jawa Tengah)”.
Penyelesaian Tesis ini tak lepas dari peranan, dukungan dan motivasi berbagai pihak. Oleh karena itu pada kesempatan ini penulis ingin menyampaikan terima kasih yang sedalam-dalamnya secara khusus kepada istriku yang sholehah : Dewi Yanti, beserta tiga cahaya dan penyejuk hati kami: Adam Surya Permana, Adinda Alya Putri dan Dimas Muhammad Ilham, terima kasih atas kasih sayang, doa, perhatian dan semangat yang selalu mencerahkan hati penulis. Ibunda di Solo dan kedua mertua di Buntok yang sangat saya cintai dan hormati. Terima kasih atas segala cinta, pendidikan, doa dan motivasi yang tiada henti. Selanjutnya penulis ingin menyampaikan rasa terimakasih kepada :
1. Bapak Prof. Drs. Nur Iriawan, M.Ikom., Ph.D selaku dosen wali selama penulis menempuh pendidikan pasca sarjana di ITS.
2. Bapak Prof. Dr. Drs. I Nyoman Budiantara, M.Si dan Bapak Dr. Bambang Widjanarko Otok, M.Si. selaku dosen pembimbing atas motivasi dan kesabarannya dalam mengarahkan penulis dalam menyelesaikan tesis ini. 3. Ibu Dr. Vita Ratnasari, M.Si., Bapak Dr. Sutikno, M.Si dan Ibu Dr. Erni Tri
Astuti, M.Math selaku dosen penguji yang telah memberikan banyak saran dan masukan terhadap tesis ini.
4. Bapak Dr. Suhartono, M.Sc, selaku ketua Jurusan Statistika FMIPA ITS, atas segala kemudahan urusan akademis dan fasilitas yang menunjang di Jurusan Statistika ini.
vi
6. Bapak Kepala Badan Pusat Statistik (BPS) RI beserta seluruh jajarannya, atas kesempatan yang diberikan kepada penulis untuk melanjutkan pendidikan. 7. Bapak Kepala BPS Provinsi Kalimantan Tengah, atas ijin dan kesempatan
yang diberikan kepada penulis untuk melanjutkan studi.
8. Rekan-rekan senasib seperjuangan (Postgraduate BPS angkatan ke-8), atas kekompakan, kerjasama dan kenangan suka duka selama menyelesaikan studi. Masuk bareng, keluar bareng.
9. Penghuni MABES, Mas Duto, Mas Henry, Uda Rory and Mas Aan, atas kekeluargaan yang dijalin selama kita di Surabaya.
10.Penghuni Classic, Mas Muryanto, Mas arip and Daeng Zablin.
11.Penghuni Mabes Cewek, Eunike, Widi, Santi, Yanti, Yani, Dian n Mpih. Share tugasnya jangan malam banget, sudah ngantuk nich..
12.Bu bendahara Afni, Maul, Anita juga Vivin.
13.Mas Fatih, selamat atas kelahiran putri pertamanya menjelang sidang tesis. 14.Rekan – rekan seperjuangan Tesis Regresi Nonparametrik, Rory, Rismal dan
Sulis , atas ketulusan, motivasi dan kesiapan membantu penulis.
15.Dik Irwan dan adik-adik S1, atas bantuan dan diskusinya selama penyusunan tesis ini.
16.Rekan-rekan Angkatan 9, atas dukungan selama Seminar proposal dan Seminar hasil.
17.Semua pihak yang telah membantu selama penulis menyelesaikan studi, yang tidak dapat penulis sampaikan satu persatu.
Semoga tesis ini dapat bermanfaat dan dapat menambah wawasan keilmuan. Penulis menyadari bahwa tesis ini masih jauh dari sempurna. Saran dan kritik yang membangun dari semua pihak, sangat penulis harapkan untuk perbaikan.
Surabaya, Januari 2016
i
ESTIMATOR CAMPURAN KERNEL DAN SPLINE
TRUNCATED LINIER MULTIVARIABEL DALAM REGRESI
NONPARAMETRIK
(Studi Kasus : Model Rata-Rata Lama Sekolah di Provinsi Jawa Tengah) Nama Mahasiswa : Ali Akbar Sanjaya Ilham Purnomo
NRP : 1314201701
Pembimbing 1 : Prof. Dr. Drs. I Nyoman Budiantara, M.Si Pembimbing 2 : Dr. Bambang Widjanarko Otok, M.Si
ABSTRAK
Hubungan variabel respon dengan beberapa variabel prediktor pada regresi nonparametrik tidak selalu menggunakan satu jenis pendekatan seperti spline, kernel, atau deret fourier. Dalam model regresi memungkinkan variabel respon mengikuti kurva regresi nonparametrik yang berbeda antara satu variabel prediktor dengan variabel prediktor lainnya. Pada data berpasangan (x1i,..xpi,ti,yi)
yang hubungan antar variabel prediktor x1i,..xpi, ti, dan variabel respon yi
mengikuti model regresi nonparametrik additif:
1
Komponen prediktor x1i,..xqi, dihampiri dengan fungsi Spline truncated linier
sedangkan komponen prediktor ti dihampiri dengan fungsi kernel. Tujuan
penelitian ini adalah mencari bentuk estimator campuran kernel dan spline
truncated linier multivariabel untuk mengestimasi kurva regresi nonparametrik. Penurunan estimator model dengan menggunakan metode Ordinary Least Square (OLS). Hasil estimator yang diperoleh adalah :
1
Estimator campuran kernel dan regresi spline truncated linier multivariabel bergantung pada titik-titik knot dan bandwidth. Estimator campuran kernel dan regresi spline multivariabel terbaik diperoleh dari titik-titik knot dan parameter bandwidth yang optimal. Estimator Campuran Kernel dan regresi Spline truncated multivariabel diaplikasikan pada data Rata-Rata Lama Sekolah di Propinsi Jawa Tengah dengan dua titik knot optimal menghasilkan nilai R2 sebesar 0,909313.
ii
iii
MIXED ESTIMATOR OF KERNEL AND
MULTIVARIABLE LINEAR SPLINE TRUNCATED
IN NONPARAMETRIC REGRESSION
(Case Study : Mean Years of Schooling Model In Central Java Province)
By : Ali Akbar Sanjaya Ilham Purnomo
Student Identity Number : 1314201701
Supervisor : Prof. Dr. Drs. I Nyoman Budiantara, M.Si Co Supervisor : Dr. Bambang Widjanarko Otok, M.Si
ABSTRACT
The relationship of respond variable with some predictor variables is not always using only single approach such as spline, kernel or Fourier series. In the regression model allows the response variable to follow different nonparametric regression curve between the predictor variables and other predictor variables. Data given in pairs ( x1i , .. xqi , ti , yi ) the relationship
between the predictor variables x1i , .. xqi , ti , and the response variable yi
follow additive nonparametric regression model :
1
Predictor component , x1i .. xqi , approached using Spline Functions linear
predictor component while ti approached by the kernel function . This
research was conducted with the purpose of seeking estimator truncated form of linear spline and kernel to estimate the nonparametric regression curve. Estimator models obtained using Ordinary Least Square method ( OLS ) . The Estimator regression curves are :
1
Mixed Estimator Kernel and multivariable Linier Spline Truncated rely heavily on points knots and bandwidth. Mixed Estimator Kernel and multivariable Linier Spline Truncated is the finest in determining optimal point’s knots and bandwidth. Mixed Estimator Kernel and multivariable Linier Spline Truncated application in Mean Years of Schooling Model Central Java Province have R-Square 0,909313.
iv
1
BAB 1
PENDAHULUAN
1.1Latar Belakang
Dalam beberapa masalah terdapat dua atau lebih variabel yang hubungannya tidak dapat dipisahkan, maka hal tersebut biasanya akan diselidiki sifat hubungannya. Analisis Regresi adalah sebuah teknik statistik untuk membuat model dan menyelidiki hubungan antara dua variabel atau lebih. Misalnya Y
adalah variabel respon dan X adalah variabel prediktor, untuk n buah pengamatan, secara umum antara yi dengan xi dihubungkan dengan model regresi berikut :
yi= f (xi) + εi, i = 1, ..., n (1.1)
dimana εi adalah error random dan f (xi) merupakan suatu fungsi f yang tidak
diketahui dan disebut kurva regresi. Jika kurva regresi diketahui bentuknya, maka disebut sebagai regresi parametrik dan apabila model yang diasumsikan ini benar, maka pendekatan regresi parametrik sangat efisien, tetapi jika tidak, menyebabkan interpretasi data yang menyesatkan (Hardle,1990). Apabila tidak ada informasi apapun tentang bentuk kurva f(xi), maka pendekatan yang digunakan adalah
2
estimator linear, efisien, konsisten, BLUE (Best Linear Unbiased Estimator), yang sangat jarang dimiliki oleh pendekatan regresi lain seperti regresi nonparametrik dan regresi semiparametrik. Kelebihan yang dimiliki oleh regresi parametrik inilah yang menyebabkan model regresi parametrik sangat populer dan sangat disukai oleh berbagai kalangan, baik dari golongan Statistika teoritis maupun golongan Statistika aplikasi (Becher, dkk., 2009; Huang & Liu, 2006).
Pendekatan regresi parametrik untuk tujuan pemodelan dan prediksi tidak tepat pada suatu variabel respon dan variabel prediktor yang bentuk pola hubungannya tidak jelas (tidak mengikuti pola tertentu), dan seolah-olah tidak beraturan (Budiantara, 2009). Model Statistika diharapkan sedapat mungkin menggunakan model yang parsimoni (sederhana), tetapi dalam keadaan dimana terdapat kondisi yang mengharuskan pemodelan menggunakan model yang lebih kompleks, maka model parsimoni tidak selayaknya dipaksakan, karena hasil yang diperoleh akan sangat bias dan memiliki error yang sangat besar (Budiantara, 2009). Berbeda dengan regresi parametrik yang cenderung ada unsur pemaksaan dari peneliti dan peneliti ikut menentukan bentuk estimasi dari kurva regresi, dalam regresi nonparametrik tidak terjadi pemaksaan bentuk kurva regresi tersebut. Pendekatan regresi nonparametrik membiarkan data sendiri yang akan mencari bentuk estimasi dari kurva regresinya, tanpa harus dipengaruhi oleh faktor subyektifitas peneliti (Eubank, 1988; Budiantara, 2001). Ini berarti pendekatan model regresi nonparametrik sangat fleksibel dan obyektif.
3
(2009), Martins-Filho dan Yao (2009) serta Qingguo (2010). Penelitian mengenai estimator wavelet antara lain dilakukan oleh Antoniadis, Bigot dan Sapatinas (2001), Amato dan De Canditiis (2001), Rakotomamonjy, Mary dan Canu (2005) serta Taylor (2009). Penelitian untuk estimator deret fourier dilakukan oleh peneliti antara lain Faber, Douglas, Susan dan Stuart (2004), Tripena dan Budiantara (2007), Galtchouk dan Pergamenshchikov (2009) serta Ratnasari, Budiantara, Zain, Ratna dan Mariati (2015)
Kernel merupakan estimator yang pada awalnya banyak digunakan dalam regresi nonparametrik. Kelompok peneliti pertama yang meneliti kernel diawali oleh Nadaraya (1964) dan Watson (1964). Kemudian diikuti penelitian lain dalam perkembangan regresi kernel, seperti Okumura dan Naito (2006) yang meneliti Metode smoothing kernel untuk regresi multinomial. Yao (2007) yang dalam penelitiannya telah menurunkan distribusi asimtotik dari distribusi kernel dengan menggunakan rata-rata terbobot untuk data longitudinal. Ada juga penelitian tentang estimator kernel untk melihat hubungan antara tingkat ketergantungan internet dengan lama-nya penggunaan internet setiap hari di sekolah menengah oleh Kayri dan Zirhlioglu (2009). Peneliti lain, Aljuhani dan Al Turk (2014) yang melakukan penelitian modifikasi estimasi regresi kernel adaptif Nadaraya-Watson.
Spline pertama kali diperkenalkan oleh Whitaker pada tahun 1923 sebagai pendekatan pola data. Spline yang didasarkan pada suatu persoalan optimasi dikembangkan oleh Reinsc pada tahun 1967 (Wahba, 1990). Pendekatan spline mempunyai suatu basis fungsi, yang biasa digunakan adalah spline
4
yang perilakunya berubah-ubah pada sub-sub interval tertentu. Spline mempunyai kemampuan yang sangat baik untuk digeneralisasikan pada pemodelan Statistika yang kompleks dan rumit. Kelebihan lain dari spline truncated pada penelitian Otok (2006) menunjukkan kurva spline truncated lebih baik dari Multivariate Adaptive Regression Spline (MARS) pada fungsi yang melibatkan satu variabel prediktor. Budiantara dkk (2012) Memodelkan Persentase Penduduk Miskin di Indonesia dengan menggunakan Pendekatan Regresi Nonparametrik Spline. Darmawi dan Otok (2014) dalam penelitiannya menyimpulkan nilai MSE pada kurva Spline truncated lebih kecil dibanding dengan regresi linier pada semua fungsi, hal ini berarti bahwa kurva spline truncated lebih baik dibanding dengan regresi linier.
Estimator lain dalam regesi nonparametrik yang juga digunakan adalah polinomial lokal. Beberapa penelitian tentang polinomial lokal dilakukan oleh Welsh dan Yee (2006) yang menurukan sifat bias dan varians asimtotik dari estimator polinomial lokal tersebut dalam regresi nonparametrik dengan variabel respon lebih dari satu. Penelitian dilakukan di New Zealand dengan menggunakan variabel respon tekanan darah systolic dan diastolic untuk mengukur tingkat kegemukan buruh dan body mass index (BMI) sebagai variabel prediktor.
Pendekatan lain adalah wavelet yang juga sering digunakan dalam regresi nonparametrik. Penelitian antara lain dilakukan oleh Antoniadis dkk (2001) yang mengkaji metode wavelet untuk memodelkan observasi dari suatu signal terkontaminasi gangguan yang berdistribusi Gauss dan bersifat aditif. Peneliti lain Rakotomamonjy (2005) yang menunjukkan evektivitas model kernel wavelet pada metode yang mengkonstruksi pada suatu ruang Hilbert untuk regresi nonparametrik ketika titik-titi sampelnya tidak sama lebar.
5
Kemiskinan di Papua menyimpulkan spline truncated lebih baik daripada deret fourier dalam model regresi nonparametrik multivariabel.
Diantara model-model regresi nonparametrik di atas, spline truncated merupakan salah satu model yang mempunyai model interpretasi statistik dan interpretasi visual sangat khusus dan sangat baik (Budiantara dkk, 2012). Estimator spline truncated memiliki fleksibilitas yang tinggi (Eubank, 1988). Spline truncated juga memiliki kemampuan yang sangata baik menangani data yang perilakunya berubah-ubah pada sub-sub nterval tertentu (Eubank, 1988; Budiantara dkk, 2012). Estimator Kernel juga memiliki beberapa kelebihan, diantaranya estimator kernel memiliki kemampuan yang baik untuk memodelkan data yang tidak mempunyai pola tertentu (Hardle, 1990). Estimator Kernel juga memiliki kecepatan kekonvergenan yang relatif lebih cepat dibandingkan dengan kurva regresi nonparamerik yang lain seperti Polinomial Lokal, Deret Fourier maupun Spline (Hardle, 1990).
6
pola data juga dilakukan oleh Sudiarsa, Budiantara, Suhartono dan Purnami (2015) yang melakukan penelitian mengenai Estimator Gabungan Deret Fourier dan Truncated Spline dalam Regresi Nonparametrik Multivariabel. Dalam penelitia itu, estimator diperoleh melalui optimasi Penalized Least Square (PLS).
Pembangunan manusia merupakan perwujudan tujuan jangka panjang dari suatu masyarakat, dan meletakan pembangunan di sekeliling manusia, bukan manusia di sekeliling pembangunan. Penyertaan konsep pembangunan manusia dalam kebijakan pembangunan tidak berarti meninggalkan berbagai strategi pembangunan terdahulu, antara lain mempercepat pertumbuhan ekonomi, mengurangi kemiskinan dan mencegah perusakan lingkungan. Perbedaannya adalah bahwa dari sudut pandang pembangunan manusia, semua tujuan tersebut diatas diletakan dalam kerangka untuk memperluas pilihan-pilihan bagi manusia.
Human Development Report (HDR) global telah mengembangkan dan
menyempurnakan pengukuran statistik dari pembangunan manusia yaitu berupa Indeks Pembangunan Manusia (IPM). Indikator tersebut melihat tiga masalah pokok yang menjadi ukuran yaitu kesehatan melalui angka harapan hidup, pendidikan serta pendapatan melalui paritas daya beli. United Nations Development Programme (UNDP), pada Tahun 2014 melaporkan peringkat Indeks Pembangunan Manusia (IPM) Indonesia berada di posisi 108 dari 187 negara yang laporkan (UNDP Report, 2014). Peringkat Indonesia secara regional masih lebih baik dari Filipina yang berada di peringkat 117 dimana keduanya masuk kelompok Medium Human Development tetapi masih di bawah empat negara ASEAN lainnya. Dimana Singapura di posisi tertinggi di peringkat 9, Brunei Darussalam berada di peringkat 30 yang menempatkan kedua Negara tersebut termasuk kelompok Very High Human Development, kemudian Malaysia berada di peringkat 62, Thailand berada di peringkat 89 termasuk kelompok High
Human Development.
7
kemudian Propinsi Jawa Barat dengan nilai 73,58, Propinsi Jawa Timur dengan nilai 73,54 dan Terakhir Propinsi Banten dengan nilai 71,90.
Rata-rata lama sekolah penduduk usia 15 tahun keatas merupakan salah satu variabel yang digunakan pada penghitungan IPM selain angka harapan hidup, pengeluaran perkapita dan angka melek huruf. Menurut publikasi BPS pada tahun 2013, Provinsi Jawa Tengah memiliki nilai rata-rata lama sekolah penduduk usia 15 tahun keatas yang terendah dibandingkan provinsi lain di Pulau Jawa. Tertinggi ditempati DKI Jakarta dengan rata-rata lama sekolah sebesar 11 tahun, diikuti D.I Yogyakarta sebesar 9,33 tahun, Banten 8,61 tahun, Jawa Barat 8,11 tahun, Jawa Timur 7,53 tahun dan terakhir Jawa Tengah sebesar 7,43 tahun. Perlu kerja keras pemerintah Propinsi Jawa Tengah untuk mengejar ketertinggalannya dari propinsi lain apalagi untuk memenuhi standar rata-rata lama sekolah yang disarankan UNDP sebesar 15 tahun.
Penelitian mengenai lama pendidikan penah sering dilakukan diberbagai Negara. Penelitian di Republik Rakyat Tiongkok pernah dilakukan Connely dan Zhang (2002) mengenai penentuan kelanjutan sekolah penduduk umur 10 hingga 18 tahun. Penelitian tersebut menyimpulkan lokasi tempat tinggal dan jenis kelamin sangat mempengaruhi dalam pendaftaran dan kelulusan sekolah. Perempuan pedesaan cenderung kurang beruntung dalam kelanjutan sekolahnya. Pendidikan orang tua, jumlah saudara (jumlah anggota kelurga), Produk Domestik Regional Bruto (PDRB) dan biaya sekolah juga sangat berpengaruh dalam kelanjutan pendidikan penduduk. Huisman, Rani dan Smits (2010) dalam penelitiannya di 26 negara bagian India mengungkapkan bahwa faktor sosial rumah tangga sangat berpengaruh dalam mengenyam pendidikan. Katersediaan fasilitas sekolah dan guru juga sangat memegang peran penting. Anak-anak perempuan terutama di pedesaan lebih tertinggal dalam partisipasi pendidikan.
8
persentase desa/kelurahan yang memiliki SLTP, persentase desa/kelurahan yang memiliki SLTA, persentase penduduk perkotaan, persentase kecamatan yang memiliki perguruan tinggi, kontribusi sektor non pertanian dalam PDRB dan rata-rata pendapatan perkapita 1 bulan.
1.2Perumusan Masalah
Dengan memperhatikan latar belakang yang telah diuraikan diatas, permasalahan yang dapat dirumuskan adalah :
1. Bagaimana bentuk Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel dalam regresi nonparametrik aditif ?
2. Bagaimana model Rata-Rata Lama Sekolah di Provinsi Jawa Tengah menggunakan Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel dalam regresi nonparametrik aditif.
1.3Tujuan Penelitian
1. Mendapatkan bentuk Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel dalam regresi nonparametrik aditif.
2. Memodelkan Rata-Rata Lama Sekolah penduduk di Provinsi Jawa Tengah menggunakan Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel dalam regresi nonparametrik aditif.
1.4Manfaat Penelitian
Manfaat yang ingin dicapai dari penelitian ini adalah :
1. Mengembangkan wawasan keilmuan dan pengetahuan tentang regresi nonparametrik spline truncated.
2. Mengembangkan wawasan keilmuan dan pengetahuan tentang regresi nonparametrik kernel.
3. Mengembangkan wawasan keilmuan dan pengetahuan tentang Estimator Campuran Kernel dan Spline Truncated Linier Multivariabel dalam regresi nonparametrik aditif.
9
Multivariabel dalam regresi nonparametrik aditif dapat digunakan untuk memprediksi target rata-rata lama sekolah akibat dari perubahan pada masing-masing variabel prediktor yang mempengaruhi.
1.5Batasan Masalah Penelitian
10
11
BAB 2
TINJAUAN PUSTAKA
2.1 Pemodelan Regresi Parametrik dan Nonparametrik
Pemodelan regresi parametrik digunakan apabila kurva regresi data membentuk pola tertentu, seperti linier, kuadratik ataupun kubik. Model regresi parametrik dalam penggunaanya memerlukan informasi dari masa lalu atau sumber informasi lain yang tersedia yang dapat menggambarkan secara detail tentang data tersebut. Model regresi parametrik juga mempunyai asumsi yaitu bentuk kurva regresi harus diketahui (Eubank, 1999). Metode untuk mengestimasi parameter adalah metode Least Square dan Maximum Likelihood (Wahba, 1990). Pada umumnya, variabel respon y dapat dihubungkan dengan k variabel-variabel prediktor. Model tersebut dalam bentuk (Montgomery & Hines, 1972)
0 1 1 2 2 , 1,2,...,
i i i k ki i
y x x x i n (2.1) dimana yi merupakan variabel respon, x x1, ,...,2 xk sebagai variabel prediktor, i
merupakan error random independen berdistribusi normal dengan mean nol dan varians 2 parameter
0, , ,...,1 2 k
tidak diketahui.
Secara umum bentuk regresi parametrik multivariabel dengan k variabel prediktor pada persamaan (2.1) dapat ditulis dalam bentuk matriks sebagai :
yX
, dimana (2.2)Pada umumnya, y adalah sebuah vektor (n x 1) dari observasi-observasi, X adalah sebuah matriks (n x (k+1)) dari variabel-variabel bebas, adalah sebuah vektor ((k+1)x1) dari koefisien-koefisien regresi dan adalah sebuah vektor (nx1) dari error random. Parameter diestimasi dengan metode kuadrat terkecil yang meminimumkan T dimana :
( ) ( ) T yX T yX
12
Dengan menurunkan parsial T terhadap dan menyamakan dengan nol, maka
diperoleh estimator :
1
ˆ ( T ) T
X X X y
(2.3)
2.2 Regresi Nonparametrik Spline Truncated
Pendekatan regresi nonparametrik yang banyak digunakan adalah spline
truncated. Spline truncated merupakan potongan-potongan polinomial yang memiliki sifat tersegmen dan kontinu. Salah satu kelebihan spline truncated
adalah model ini cenderung mencari sendiri estimasi data kemanapun pola data tersebut bergerak. Kelebihan ini terjadi karena dalam spline truncated terdapat titik-titik knot, yaitu titik perpaduan bersama yang menunjukkan terjadinya perubahan pola perilaku data (Eubank, 1999; Budiantara, 2009). Secara umum, fungsi spline truncated dengan derajad m dan titik-titik knot 1, ,...,2 r adalah
suatu fungsi yang dapat ditulis dalam bentuk sebagai berikut :
yi = f(xi) + εi, i= 1, 2, …., n. (2.4)
Error random εi diasumsikan berdistribusi normal independen dengan mean nol
dan variansi 2.
Sebagai salah satu ilustrasi sederhana diberikan Spline linier
truncated dengan tiga knots pada x 1 2 3 diberikan oleh :
1 1 1
3( ) 1 1( 1) 2( 2) 3( 3) f x x x x x
Fungsi Spline f x3( ) disajikan (Budiantara, 2011) dalam bentuk (di gambar 2.1):
13
Gambar 2.1 Simulasi Spline truncated dengan tiga titik knots
Dalam regresi nonparametrik dengan pendekatan spline truncated, hal penting yang berperan dalam mendapatkan estimator spline truncated adalah pemilihan titik knot yang optimal. Salah satu metode yang sering digunakan dalam memilih titik knot optimal adalah Generalized Cross Validation (GCV). Jika dibandingkan dengan metode lain, misalnya Cross Validation (CV) dan metode Unbiased Risk (UBR) ataupun Generalized Maximum Likelihood (GML), GCV secara teoritis memiliki sifat optimal asymtotik. Metode GCV juga memiliki kelebihan tidak memerlukan pengetahuan terhadap variansi populasi 2 serta
metode GCV invarians terhadap transformasi. Metode GCV merupakan pengembangan dari CV (Wahba, 1990). Fungsi GCV untuk pemilihan titik knot optimal dapat ditunjukkan dalam persamaan berikut:
2.3 Regresi Nonparametrik Kernel
14
cepat. Kurva regresi g t( )i yang dihampiri fungsi kernel, estimasi kurva regresi dapat disajikan dalam bentuk :
dengan K merupakan fungsi kernel. Menurut Hardle (1990), fungsi kernel K dapat berupa :
ke-i variabel prediktor dan adalah bandwidth . Pendekatan kernel tergantung pada bandwidth , yang berfungsi untuk mengontrol smoothness dari kurva estimasi. Pemilihan bandwitdh yang tepat merupakan hal yang sangat penting dalam regresi kernel (Hadijati, 2004; Budiantara dan Mulianah, 2007). Bandwidth
yang terlalu besar akan menghasilkan kurva estimasi yang sangat smooth dan menuju ke rata-rata dari variabel respon, sebaliknya bila bandwidth terlalu kecil akan menghasilkan kurva estimasi yang kurang smooth yaitu hasil estimasi akan menuju ke data. Visualisasi fungsi kernel dengan berbagai besaran bandwidth
15
Gambar 2.2. Visualisasi fungsi kernel dengan berbagai besaran bandwidth
(Guidoum, 2015; data dari Olver et al., 2010)
Estimator kurva regresi (2.8) sangat tergantung pada dua hal, yaitu parameter bandwidth dan fungsi kernelnya (Budiantara dkk, 2015), tetapi dari dua hal tersebut ternyata bandwidth lebih signifikan pengaruhnya terhadap estimator kernel dibanding fungsi kernel. Dalam kaitannya pemilihan bandwidth optimal, akan digunakan metode Generalized Cross Validatian (GCV). Jika estimasi model (2.8) dinyatakan dengan gˆ
t D( ) y maka Fungsi Generalized CrossValidatian (GCV) dalam Hong (1999) didefinisikan dengan :
2 2
2 2
1 ( ( )) 1 ( ( ))
( ) 1 1
[ (( ( ))] [(1 ( ))]
n n
GCV t
tr tr
n n
I D y I D y
I D D
(2.9)
Bandwith optimal diperoleh dengan cara meminimunkan fungsi GCV.
2.4 Estimator Campuran Spline dan Kernel
16
berpasangan ( , , )x t yi i i dengan diasumsikan hubungan antar variabel prediktor
,
i i
x t dan variabel respon yi mengikuti model regresi nonparametrik :
( , )
i i i i
y x t , i=1,2,…,n (2.10) Bentuk kurva regresi diasumsikan tidak diketahui dan hanya diasumsikan smooth dalam arti kontinu dan differensiabel. Error random i berdistribusi normal
dalam estimator campuran kurva regresi nonparametrik adalah mendapatkan bentuk estimasi kurva regresi ( , )x ti i yaitu :
, ˆ ,
ˆ ( , )x ti i f ( )xi g tˆ( )i
(2.12)
Parameter merupakan parameter bandwith dan merupakan titik knot. Estimator campuran regresi spline dan kernel bisa didapatkan dengan kurva regresi f x( )i dihampiri dengan fungsi spline truncated derajad m dan titik knot
1 2
( , ,..., )T r
serta kurva regresi g t( )i dihampiri dengan fungsi kernel. Menurut Budiantara dkk (2015), kurva regresi f x( )i yang diberikan persamaan
(2.5) akan diperoleh :
17
dengan demikian model regresi campuran spline dan kernel persamaan (2.10) menjadi : Estimator parameter dapat diperoleh dengan menggunakan metode Ordinary Least Square (OLS) dari persamaan (2.15) diatas yang menghasilkan persamaan :
Untuk mendapatkan estimator dari parameter , dilakukan derivatif parsial dari persamaan (2.16) Q
/ ,
terhadap diperoleh :18
dengan matrik A adalah :
T
1
T
kemudian dari persamaan (2.11) menunjukkan estimator persamaan kernel :
,
ˆ t
g D y
sehingga didapatkan estimator campuran regresi spline linier dan kernel :
dimana matrik B adalah :
,
,
B A D
Estimator campuran regresi Spline dan Kernel ˆ ,
x t, sangatbergantung kepada banyak dan letak titik knot ( , ,..., ) 1 2 r T dan parameter
bandwitdh . Untuk memperoleh estimator campuran regresi Spline dan Kernel yang terbaik perlu dilakukan pemilihan titik knot dan parameter bandwidth yang optimal. Metode yang biasa digunakan adalah Generalized Cross Validation
(GCV). Fungsi GCV yang diberikan oleh Wahba (1990) adalah :
19
2.5Teorema Dasar Terkait dengan Aljabar Matriks
Beberapa konsep dasar yang digunakan dalam proses mendapatkan estimator model regresi nonparametrik kernel dan spline truncated linier multivariabel berikut ini.
Teorema 2.5.1 (Rencher dan Schaalje 2008: 9, 13)
Pada matriks A dan B, maka berlaku sifat – sifat sebagai berikut : a. Jika matriks A simetris, maka AT = A.
b.
A B
T AT BTc.
AB T B AT TTeorema selanjutnya berkaitan dengan penurunan matriks dan vektor. Teorema 2.5.2 (Rencher dan Schaalje 2008: 56)
Pada vektor adanx, dimana a xT x aT ,aT
a a1, ,...,2 ap
memuat konstanta, dengan ini berlaku
T Ta
a x x a
x x
Teorema 2.5.3 (Rencher dan Schaalje 2008: 56)
Apabila vektor x dan merupakan suatu matriks simetri, maka
T
2
x Ax
Ax x
2.6. Rata-rata Lama Sekolah
20
Gansu RRT, memperkirakan faktor yang mentukan lama sekolah dilihat dari capaian gizi anak, yang diukur dari Z skor dan pendapatan rumah tangga memiliki efek positif pada lama sekolah anak. Pendidikan ibu di Propinsi Gangsu juga sangat mempengaruhi tingkat pendidikan anak-anaknya.
Dalam penelitian lain, Setyawan (2011) yang melakukan penelitian tentang permodelan determinan tingkat pendidikan di Pulau Papua. Dimana dalam penelitian tersebut didapatkan beberapa variabel yang berpengaruh secara signifikan, diantaranya adalah angka harapan hidup, rata-rata pengeluaran rumah tangga perbulan, banyaknya anggota rumah tangga, rasio jenis kelamin, persentase ibu berpendidikan SLTA keatas, rasio murid dengan guru, rasio murid dengan sekolah, persentase penduduk perkotaan, persentase penduduk yang tinggal di pesisir dan persentase angaran pendidikan di APBD. Melliana (2013) dalam penelitiannya menyebutkan bahwa rasio murid guru pada tingkat SLTP/MTS memberikan pengaruh terhadap angka IPM di Provinsi Jawa Timur dimana didalamnya terdapat ukuran tingkat pendidikan. Fasilitas pendidikan merupakan aspek yang tidak bisa diabaikan dalam proses pendidikan khususnya dalam proses belajar mengajar. Berdasarkan penelitian sebelumnya tersebut, penelitian ini banyak mengadopsi variabel-variabel yang telah digunakan dalam penelitian-penelitian yang telah disebutkan diatas. Sehinggah dalam penelitian ini menggunakan variabel-variabel prediktor yaitu Rata-rata Pengeluaran Rumah Tangga per Bulan, Rata-rata banyaknya anggota rumah tangga, Rasio jenis kelamin, Rasio murid terhadap guru dan Rasio murid terhadap sekolah. Berikut ini akan diuraikan konsep serta definisi dari variabel-variabel tersebut secara terperinci.
Rata-rata Lama Sekolah
21
tahun yang dicanangkan oleh pemerintah. Artinya untuk melewati target program tersebut maka angka lama sekolah harus sudah mencapai 9 tahun. Rata-rata Pengeluaran Rumah Tangga per Kapita
Rata-rata Pengeluaran Rumah Tangga per kapita adalah biaya yang dikeluarkan untuk konsumsi anggota rumah tangga selama sebulan dibagi dengan banyaknya anggota rumah tangga merupakan gambaran tingkat kesejahteraan yang dinikmati oleh penduduk sebagai dampak semakin membaiknya ekonomi (BPS, 2011). Variabel rata-rata pengeluaran rumah tangga merupakan salah satu variabel yang mempengaruhi rata-rata lama sekolah pada penelitian Setyawan (2011)
Banyaknya Anggota Rumah Tangga
Pada beberapa kalangan masyarakat tertentu, seringkali banyaknya anggota keluarga menjadi suatu bahan pertimbangan ketika harus memutuskan anggota keluarga yang mana yang harus melanjutkan ke suatu jenjang pendidikan yang lebih tinggi. Kesejahteraan yang masih rendah serta banyaknya jumlah anggota keluarga memaksa mereka untuk menentukan pilihan. Sehingga tentu saja ada anggota keluarga yang akhirnya harus dikorbankan untuk tidak mendapatkan pendidikan yang seharusnya layak untuk diikutinya. Variabel ini merupakan bentuk asimilasi dari variabel yang diteliti oleh Connely dan Zhang (2002) yaitu
Family Size atau banyaknya anggota keluarga. Persentase Anggaran Pendidikan dari APBD
Persentase anggaran pendidikan merupakan alokasi anggaran pendidikan dari total Anggaran Pendapatan dan Belanja Daerah (APBD) pada satu tahun anggaran. Variabel persentase anggaran pendidikan dari Total APBD merupakan variabel yang mempengaruhi rata-rata lama sekolah pada penelitian setyawan (2011)
Rasio Murid dengan Sekolah
22
Penelitian Huisman, dkk (2010) menunjukkan peran kecukupan fasilitas sekolah dalam peningkatan pendidikan.
Rasio Murid dengan Guru
23
BAB 3
METODE PENELITIAN
3.1 Sumber Data
Penelitian ini menggunakan data sekunder dari publikasi yang diterbitkan oleh BPS Provinsi Jawa Tengah dan Direktorat Jenderal Perimbangan Keuangan (DJPK) Kementrian Keuangan Republik Indonesia Tahun 2014 dengan unit observasi adalah seluruh Kabupaten/Kota yaitu sebanyak 35 Kabupaten/Kota di Provinsi Jawa Tengah.
3.2 Variabel Penelitian
Berdasar pada latar belakang dan tujuan penelitian, terdapat satu variabel respon dan lima variabel prediktor yang digunakan. Variabel-variabel tersebut adalah sebagai berikut :
Variabel Respon Y : Rata-Rata Lama Sekolah Variabel Prediktor
X1 : Pengeluaran Per kapita per bulan.
X2 : Persentase Anggaran Pendidikan di APBD.
X3 : Rasio jumlah murid dengan jumlah sekolah SLTA. X4 : Rasio jumlah murid dengan jumlah guru SLTA. t : Rata-rata banyaknya anggota rumah tangga.
Variabel respon dan prediktor akan diaplikasikan terhadap regresi nonparametrik campuran dengan pendekatan kernel dan spline linier truncated
multivariabel.
3.3 Definisi Operasional Variabel Penelitian Rata-Rata Lama Sekolah
24
- Partisipasi sekolah
- Jenjang dan jenis pendidikan tertinggi yang pernah/ sedang diduduki. - Ijasah tertinggi yang dimiliki
- Tingkat/ kelas tertingi yang pernah/ sedang diduduki.
Rumus rata-rata lama sekolah untuk yang partisipasi sekolahnya masih bersekolah dan tidak bersekolah lagi namun tidak tamat adalah :
Rata-rata lama sekolah = tahun konversi + kelas tertinggi yang pernah diduduki - 1
Rata-rata lama sekolah untuk yang partisipasi sekolahnya tidak bersekolah dan tidak bersekolah lagi namun sudah tamat adalah :
Rata-rata lama sekolah = tahun konversi + kelas tertinggi yang pernah diduduki - 1
Adapun tahun konversi pendidikan yang ditamatkan disajikan pada tabel berikut ini :
Tabel 3.1. Konversi Tahun Pendidikan Tertinggi yang ditamatkan
No Pendidikan Tertinggi yang ditamatkan Konversi (tahun)
1 Tidak/belum pernah sekolah 0
2 SD dan setara 6
3 SLTP dan setara 9
4 SLTA dan setara 12
5 D-1 13
6 D-2 14
7 D-3 15
8 D-4/ S-1 16
9 S-2 18
10 S-3 21
Sumber: BPS (2011)
Rata-rata Pengeluaran Rumah Tangga per Kapita
25
tangga tersebut. Sehingga tidak salah juga bila besarnya pengeluaran rumah tangga dijadikan sebagai salah satu tolok ukur kesejahteraan rumah tangga tersebut. Semakin besar pengeluarannya maka semakin banyak kebutuhan rumah tangga yang dapat terpenuhi, sehingga bisa dikatakan bahwa rumah tangga tersebut juga semakin sejahtera.
Persentase Anggaran Pendidikan di APBD
Persentase anggaran pendidikan merupakan alokasi anggaran pendidikan dari total Anggaran Pendapatan dan Belanja Daerah (APBD) pada satu tahun anggaran. Persentase anggaran pendidikan dalam APBD seperti tertuang dalam UU No.20 Tahun 2003 tentang sistem Pendidikan Nasional Pasal 49 ayat (1) yang berbunyi, “ Dana Pendidikan selain gaji pendidik dan biaya pendidikan kedinasan dialokasikan minimal 20 % dari Anggaran Pendapatan Belanja Negara (APBN) pada sektor pendidikan dan minimal 20 % dari Anggaran Pendapatan dan Belanja Daerah (APBD). Data bersumber dari Direktorat Jenderal Perimbangan Keuangan (DJPK) Kementrian Keuangan Republik Indonesia.
Rasio Murid dengan Sekolah
Rasio murid terhadap sekolah merupakan suatu ukuran terhadap kecukupan fasilitas fisik untuk melakukan proses belajar dan mengajar. Semakin banyak sekolah-sekolah yang dibangun akan memberikan peluang yang lebih besar kepada penduduk usia sekolah untuk dapat mengenyam bangku pendidikan.
Rumus Rasio t ht h t
h
M M S
S
dengan:
Rasio t h
MS : Jumlah murid/ siswa yang terdaftar di tingkat pendidikan h pada tahun ajaran t.
t h
26
t h
S : Jumlah sekolah yang tersedia di tingkat pendidikan h pada tahun ajaran t.
Rasio Murid dengan Guru
Rasio murid terhadap guru ini merupakan rata-rata jumlah murid/ siswa per guru di tingkat pendidikan tertentu pada ajaran tertentu (BPS, 2011).
Rumus Rasio t ht
M : Jumlah murid/ siswa yang terdaftar di tingkat pendidikan h pada tahun ajaran t.
Rata-Rata Banyaknya Anggota Rumah Tangga
Mengacu pada konsep rumah tangga serta kondisi sosial masyarakat Jawa Tengah yang lebih relevan jika menggunakan konsep rumah tangga, sehingga dalam penelitian ini akan digunakan variabel banyaknya anggota rumah tangga (household size).
Rumus untuk Rata-rata banyaknya anggota rumah tangga adalah : Rart P Rt
dimana :
Rart : Rata-rata banyaknya anggota rumah tangga. P : Jumlah penduduk suatu wilayah
Rt : Jumlah rumah tanga suatu wilayah
3.4. Tahapan Penelitian
27
1. Membuat model regresi nonparametrik. Diberikan respon yi dengan variabel komponen nonparametrik x xi1, ,..., ,i2 x tiq i :
merupakan satu kurva regresi yang didekati dengan fungsi kernel dan error
i
, i =1,2,…,n saling independen.
2. Menyajikan model estimasi campuran regresi spline linier truncated
multivariabel dan kernel pada regresi nonparametrik tersebut dalam bentuk matrik:
y Ζ ( ) D( ) y
3. Mendapatkan estimasi ˆ menggunakan metode Ordinary Least Square
(OLS) dengan menyelesaikan optimasi:
4. Menyelesaikan optimasi (3) dengan menggunakan derivatif partial:
Q
Dengan Q
I D
y Z
T
I D
y Z
5. Menyamakan derivatif partial tersebut dengan 0, yaitu:
Q
= 06. Mendapatkan estimasi campuran regresi spline linier multivariabel dan kernel pada regresi nonparametrik :
28
Tujuan kedua dari penelitian ini adalah mengaplikasikan model estimasi campuran regresi spline truncated linier multivariabel dan kernel pada regresi
nonparametrik terhadap data Rata-Rata Lama Sekolah di Provinsi Jawa Tengah. Untuk menyelesaikan tujuan kedua, dilakukan langkah-langkah sebagai berikut: 1. Membuat Scatter Plot data antara variabel respon dengan masing-masing
variabel prediktor.
2. Memodelkan data menggunakan estimasi campuran kernel dan regresi spline linier truncated multivariabel dengan berbagai knot (satu knot, dua knot dan
tiga knot).
3. Memilih titik knot dan Bandwitdh optimal dengan metode GCV.
4. Menetapkan model terbaik dari nilai GCV terkecil.
5. Menghitung R2 sebagai bagian dari kriteria kebaikan model.
6. Membuat kesimpulan dari model yang terbentuk.
29
Gambar 3.1 Langkah-langkah Tahap Analisis untuk Tujuan Pertama Menyajikan model regesi campuran
regresi spline truncated linier
multivariabel dan kernel
Menghampiri kurva komponen nonparametrik dengan spline truncated
linier multivariabel dengan knot
Menghampiri kurva komponen fungi kernel
Menyajikan model regresi campuran regresi spline truncated linier multivariabel dan kernel dalam bentuk matrik
Mendapatkan estimasi menggunakan metode
Ordinary Least Square(OLS)
Menyelesaikan hasil optimasi menggunakan derivatif partial
30
Gambar 3.2 Langkah-langkah Tahap Analisis untuk Tujuan Kedua Diberikan data
Memilih titik knot dan bandwitdh optimal dengan
metode GCV
Menetapkan model terbaik dari nilai GCV terkecil
Menghitung R2
Intrepretasi model dan kesimpulan
Memodelkan data menggunakan estimasi campuran kernel dan regresi spline truncated linier multivariabel
dengan satu sampai kombinasi tiga titik knot Membuat Scatter Plot data antara variabel respon
31
BAB 4
HASIL DAN PEMBAHASAN
Berdasarkan tujuan penelitian, pada bahasan ini akan dilakukan estimasi kurva regresi campuran kernel dan spline truncated linier multivariabel. Hasil estimasi kemudian akan diterapkan pada Model Rata-Rata Lama Sekolah di Provinsi Jawa Tengah tahun 2014.
4.1 Bentuk Model Regresi Campuran Kernel dan Spline Truncated Multivariabel
Kajian mengenai regresi nonparametrik campuran kernel dan spline
truncated linier multivariabel pada data berpasangan
x1i, , , ,x t yqi i i
dengandiasumsikan hubungan antar variabel prediktor x1i, , ,x tqi i dan variabel respon yi mengikuti model regresi nonparametrik :
1 kontinyu dan differensiabel. Error random i berdistribusi normal dengan
( ) 0i
E dan ( ) 2
i
Var . Kurva regresi
( , )
x
i it
diasumsikan bersifat additif,sehingga dapat ditulis dalam bentuk :
32
Bentuk pola hubungan variabel respon yi dengan masing-masing variabel
prediktor xi diasumsikan berubah-ubah pada sub-sub interval tertentu, sedangkan
bentuk pola hubungan variabel respon yi dengan variabel ti diasumsikan tidak
variabel prediktor yang didekati kurva regresi spline truncated linier dengan jumlah variabel sebanyak q variabel. g t
i merupakan satu variabel prediktordengan kurva regresi kernel.
Komponen kurva regresi spline truncated linier ( )f xi pada persamaan
(4.2) didefinisikan oleh :
33
4.2 Estimasi Kurva Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel
Sejumlah q variabel prediktor, kurva regresinya dihampiri dengan regresi spline truncated linier dengan titik knot λ1, λ2,…λr maka persamaan ditunjukkan dengan model berikut :
sehingga regresi spline truncated linier masing-masing variabel prediktor adalah :
Selanjutnya regresi spline truncated linier multivariabel adalah :
1
1 2
2
Sehingga diperoleh persamaan regresi spline linier q variabel sebagai berikut :
34 dalam bentuk matrik :
35
Model matriks di atas dapat disajikan dalam bentuk Persamaan sebagai berikut:
36
Dari persamaan (4.2), diberikan fungsi Kernel dengan bentuk :
37
Dari persamaan (4.2), model regresi campuran spline linier dan kernel diberikan :
Estimator parameter dapat diperoleh dengan menggunakan metode Ordinary Least Square (OLS) dari persamaan (4.8) yang menghasilkan persamaan :
Z D
y
y y D
yZ
I D
yZ
(4.9) Selanjutnya jumlah kuadrat error dengan menggunakan teorema 2.5.1 bisa didapatkan sebagai berikut :
38
Apabila persamaan (4.11) disamakan dengan nol, maka akan diperoleh persamaan:
T
ˆ
T
0.
Z Z Z I D y
Selanjutnya Persamaan dapat pula ditulis dalam bentuk :
T
ˆ
T
Z Z Z I D y,
sehingga estimator ˆ diberikan oleh:
'
1
'
ˆ
Z Z Z I D y. (4.12)
Persamaan (4.12) dapat diringkas menjadi bentuk persamaan :
Sehingga didapatkan estimator kurva spline truncated linier multivariabel untuk
dengan matrik A adalah :
,
T
1
T
.39
Kemudian dari persamaan (4.7) menunjukkan estimator persamaan kernel :
,
ˆ t D
g y,
sehingga didapatkan estimator campuran regresi spline linier dan kernel :
bandwitdh . Untuk memperoleh estimator campuran Kernel dan regresi Spline
truncated linier multivariabel yang terbaik perlu dilakukan pemilihan titik knot dan parameter bandwith yang optimal. Metode yang biasa digunakan adalah
Generalized Cross Validation (GCV). Fungsi GCV oleh Wahba (1990) adalah :
Titik knot dan parameter bandwith optimal diperoleh dari nilai GCV terkecil.
4.3 Aplikasi pada Model Rata-rata Lama Sekolah di Provinsi Jawa Tengah
40
adalah Rata-rata Pengeluaran Perkapita (X1), Persentase Pengeluaran Pemerintah Daerah (APBD) di Bidang Pendidikan (X2), Rasio jumlah murid dengan jumlah sekolah SLTA (X3), dan Rasio jumlah murid dengan jumlah guru SLTA (X4), Rata-rata banyaknya Anggota Rumah Tangga (t).
4.3.1 Analisis Dekriptif
Sebelum proses permodelan Regresi Campuran Kernel dan Spline
Truncated Multivariabel pada data Rata-rata Lama Sekolah di Provinsi Jawa Tengah, perlu dilihat statistik deskriptif dari data masing-masing variabel seperti ditunjukkan pada Tabel 4.1.
Tabel 4.1 Statistik Deskriptif Variabel Respon dan Variabel Prediktor
Variabel Jumlah Min Max Range Mean Standard Deviasi
(1) (2) (3) (4) (5) (6) (7)
Y 35 10,649 14,950 4,301 12,185 0,917
X1 35 457,200 1058,300 601,000 644,400 148,400
X2 35 30,210 56,130 25,920 44,366 5,783
X3 35 231,500 520,000 288,400 419,400 35,000
X4 35 7,910 15,385 7,475 11,430 35,000
t 35 3,400 4,300 0,900 3,7286 3,729
Statistik deskriptif yang ditampilakan pada Tabel 4.1 digunakan untuk inisiasi titik-titik knot dan bandwidth. Untuk melihat pola hubungan antara variabel respon dengan masing-masing variabel prediktor dapat dilihat dari grafik
41 Pengeluaran perkapita (X1).
Gambar 4.1 menggambarkan pola hubungan antara Rata-rata Lama Sekolah dengan Rata-rata Pengeluaran perkapita cenderung naik tetapi perilakunya berubah pada sub interval antara 620 dan 900. Pola hubungan yang berubah perilakunya pada sub interval dapat didekati dengan regresi spline
truncated linier. Pengeluaran Pemerintah Daerah (APBD) di Bidang Pendidikan (X2).
42
Gambar 4.3 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rasio Jumlah Murid dengan jumlah Sekolah tingkat SLTA (X3).
Gambar 4.3 tampak pola hubungan antara Rata-rata Lama Sekolah dengan Rasio Jumlah Murid dengan jumlah sekolah tingkat cenderung mengalami perubahan perilaku pada sub interval antara 300 dan 370. Pola hubungan yang berubah perilakunya pada sub interval dapat didekati dengan regresi spline
truncated linier.
Gambar 4.4 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rasio Jumlah Murid dengan jumlah Guru tingkat SLTA (X4).
43
4.3 4.2 4.1 4.0 3.9 3.8 3.7 3.6 3.5 3.4 15
14
13
12
11
rata2 art
R
L
S
Gambar 4.5 Scatter Plot antara Rata-rata Lama Sekolah (Y) dengan Rata-rata Anggota Rumah Tangga (t).
Gambar 4.5 menunjukkan hubungan antara Rata-rata Lama Sekolah dengan Rata-rata Anggota Rumah Tangga tidak memiliki suatu pola yang jelas. Pola hubungan yang tidak jelas dapat didekati dengan fungsi kernel.
Berdasar Gambar scatter plot yang mengambarkan pola hubungan antara variabel respon dan prediktor, maka Model Estimasi Campuran Kernel dan Spline
44
pada masing-masing bagian yang mendekati titik knot dan bandwidth optimum. Sehingga setelah pengolahan data akan didapatkan nilai GCV yang terkecil dan
R-Square yang maksimal, titik knot dan bandwidth yang optimal serta nilai parameter dari model terbaik.
4.3.2 Model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel
Pemilihan Model Regresi Campuran Kernel dan Spline Truncated
Multivariabel terbaik diperoleh dari penentuan titik-titik knot dan bandwidth yang optimal. Penentuan titik knot dan dan bandwidth yang optimal didapatkan dari membandingkan nilai GCV beberapa titik knot dan bandwidth, dimulai dari satu titik knot, dua titik knot dan tiga titik knot. Titik knot dan bandwidth yang optimal ditunjukan dari nilai GCV yang terkecil.
4.3.2.1 Pemilihan Titik Knot dan Bandwidth Optimal dengan Satu Titik Knot
Pemilihan titik knot dan bandwidth yang optimal diawali dengan menggunakan satu titik knot pada masing-masing variabel prediktor spline dan
bandwidth secara bersama-sama. Berikut ini adalah model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel dengan satu titik knot.
45
Tabel 4.2 Nilai GCV dengan Satu Titik Knot
No Titik Knot Bandwidth GCV
5 535,8943 33,22 391,5113 8,084172 50,086936 0,2477013
6 682,0207 33,09796 391,5087 8,066426 20,01842 0,2541300 7 857,3226 33,21954 391,4687 8,124781 8,805228 0,2541810 8 682,02 30,56663 391,51 7,932973 212,1253 0,2543010 9 535,7915 31,22744 391,5101 18,28216 35,43942 0,2552030 10 535,6091 32,20571 391,51 15,39507 7,868713 0,2552310
Berdasarkan Tabel 4.2 dapat diketahui bahwa nilai GCV minimum yang diperoleh dengan satu titik knot yaitu sebesar 0,247713, dimana titik knot optimumnya pada masing-masing variabel prediktor yaitu sebagai berikut.
x1 = 535,7364 ; x2 = 33,22 ; x3 = 391,51 ; x4 = 8,084167 ; α= 12,437285
4.3.2.2 Pemilihan Titik Knot dan Bandwitdth Optimal dengan Dua Titik Knot
Setelah dilakukan pendekatan Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel dengan satu titik knot, selanjutnya dilakukan pendekatan dengan dua titik knot. Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel dengan dua titik knot adalah sebagai berikut.
46
Nilai GCV dari pemodelan dengan menggunakan dua titik knot ditunjukkan oleh Tabel 4.3.
Tabel 4.3 Nilai GCV dengan Dua Titik Knot
No x Titik Knot Bandwidth GCV
1 x2 x3 x4 α
1 549,6119 36,1600 279,6111 858,5652 39,8194 391,5058 12,8300 9,9698 15,393779 0,162737
2 549,2031 36,1600 279,5922 858,3215 39,8044 391,5101 12,8300 9,9700 25,07055 0,1626529
3 550,1292 36,1600 279,6147 958,1087 39,8019 391,5175 12,8300 9,9508 19,51373 0,161697
4 549,8865 36,1600 279,6253 958,1533 39,8353 391,5206 12,8300 9,9479 13,931829 0,1616504
5 549,6736 36,1600 279,6132 958,1051 39,7940 391,5099 12,8301 9,9487 19,087489 0,1615691
6 550,0339 36,1600 279,6149 858,5252 39,8562 391,5058 12,8303 9,9700 8,689574 0,1628829
7 550,2694 36,1600 279,6113 858,4142 39,8136 391,5019 12,8306 9,9700 11,705683 0,1629146
8 550,0595 34,1218 279,6169 656,2516 40,5161 391,6025 10,1962 11,6200 27,865185 0,1638126
9 554,5689 34,1457 279,6160 658,6488 40,6404 391,5374 10,2561 11,6200 19,150274 0,1641383
10 555,9803 34,4436 279,6068 658,3198 40,4213 389,2869 10,4800 11,0404 13,32498 0,1643609
Tabel 4.3 memberikan beberapa alternatif nilai knot untuk masing-masing variabel prediktor. Nilai GCV minimum yang diperoleh dengan 2 titik knot yaitu 0,1615691. Titik-titik knot pada tiap variabel prediktor yang menghasilkan nilai GCV minimum yaitu sebagai berikut.
47
Setelah dilakukan pendekatan Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel dengan satu titik knot dan dua knot, selanjutnya dilakukan pendekatan dengan tiga titik knot. Regresi Campuran Kernel dan Spline
Truncated Linier Multivariabel dengan tiga titik knot adalah sebagai berikut:
Berikut ini merupakan nilai GCV yang didapatkan dengan pemodelan menggunakan tiga titik knot.
Tabel 4.4 Nilai GCV dengan Tiga Titik Knot
No x Knot α GCV MSE
1 x2 x3 x4
1 557,4217 34,5300 279,6133 10,4033 0,91 0,8294 657,5933 38,8500 327,6867 11,6500 0,0724 757,7650 43,1700 423,8333 12,8967
2 557,4217 34,5300 279,6133 657,5933 38,8500 327,6867 10,4033 9,1567 0,61 0,8294 0,0733 757,7650 43,1700 423,8333 12,8967
3 557,4217 34,5300 279,6133 10,4033 0,61 0,8294 657,5933 38,8500 327,6867 11,6500 0,0740 757,7650 43,1700 423,8333 12,8967
48
Tabel 4.4 Nilai GCV dengan Tiga Titik Knot (lanjutan)
No x Knot α GCV MSE
1 x2 x3 x4
5 557,4217 34,5300 279,6133 10,4033 657,5933 38,8500 327,6867 11,6500 0,91 0,8294 0,0769 757,7650 43,1700 375,7600 12,8967
6 557,4217 34,5300 279,6133 657,5933 38,8500 327,6867 10,4033 9,1567 0,91 0,8294 0,0719 757,7650 43,1700 423,8333 12,8967
7 557,4217 34,5300 279,6133 657,5933 38,8500 327,6867 10,4033 9,1567 0,61 0,8294 0,0776 757,7650 43,1700 375,7600 12,8967
8 557,42170 34,53000 279,61330 10,40333 657,59330 38,85000 327,68670 11,65000 0,61 0,8294 0,0786 757,76500 43,17000 375,76000 12,89667
9 557,42170 34,53000 279,61330 9,15667 657,59330 38,85000 327,68670 10,40333 0,91 0,8294 0,0796 757,76500 43,17000 423,83330 11,65000
10 557,42170 34,53000 279,61330 10,40333 657,59330 38,85000 327,68670 11,65000 0,91 0,8294 0,0806 757,76500 43,17000 423,83330 12,89667
Tabel 4.4 menunjukkan bahwa nilai GCV minimum setiap kombinasi yang didapatkan apabila menggunakan tiga titik knot sama besar yaitu sebesar 0,8294. Titik-titik knot optimal pada tiap variabel prediktor yang menghasilkan nilai GCV minimum yang sama ditentukan oleh nilai MSE terkecil yaitu nilai MSE 0,0719. Titik-titik knot optimal tersebut diberikan sebagai berikut.
Pada variabel x11 = 557,4217, x12 = 657,5933 dan x13 = 757,765
Pada variabel x21 = 34,5300 , x22 = 38,8500 dan x23 = 43,1700
Pada variabel x31 = 279,6133, x32= 327,6867 dan x33 = 423,8333
Pada variabel x41 = 9,1567, x42 = 10,4033 dan x43 = 12,8967
Bandwidth α = 0,91
49
Tabel 4.5 Perbandingan Nilai GCV Minimum
Model GCV
1 Knot 0,247713
2 Knot 0,1615691
3 Knot 0,8294
Berdasarkan Tabel 4.5 terlihat bahwa model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel yang memiliki GCV minimum yaitu model regresi dengan dua titik knot dengan nilai GCV sebesar 0,1615691. Hal ini menunjukkan bahwa model Regresi Campuran Kernel dan Spline Truncated
Linier Multivariabel terbaik yaitu model regresi dengan dua titik knot sehingga nilai yang akan digunakan pada pemodelan Rata-rata Lama Sekolah di Jawa Tengah adalah nilai titik knot optimal dari GCV dengan dua titik knot.
4.3.3 Penaksiran Parameter Model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel
Model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel terbaik diperoleh dengan menggunakan titik knot yang optimal. Model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel yang terbentuk yaitu:
50
Tabel 4.6 Estimasi Parameter Variabel Nilai Estimasi Parameter
*
Hasil estimasi parameter pada Tabel 4.6 membentuk persamaan model Regresi Campuran Kernel dan Spline Truncated Linier Multivariabel dengan dua titik knot sebagai berikut :
1 1
1 2 2
2 3 3
3 4
11.2983 0,014419 0,0125 549,6736
0,015746 958,1051 0,209579 0,50945 36,1600
0,389786 39,7940 0,022518 0,0357 6132
0,022471 0,97061 1,2
dengan K adalah fungsi kernel Gaussian.