128
PENENTUAN TITIK-TITIK BATAS OPTIMUM STRATA PADA
PENARIKAN CONTOH ACAK BERLAPIS DENGAN
PEMROGRAMAN DINAMIK
(Kasus : Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008)
Mahyudi Program Studi Pendidikan Matematika
FKIP Universitas Muhammadiyah Bengkulu Email: didimahyudi21@gmail.com
Abstract
Optimum stratification is the method of choosing the best boundaries that make strata internally homogeneous, given some sample allocation. In order to make the strata internally homogenous, the strata should be constructed in such a way that the strata variances for the characteristic under study be as small as possible. This could be achieved effectively by having the distribution of the main study variable known and create strata by cutting the range of the distribution at suitable points. The problem of finding Optimum Strata Boundaries (OSB) is considered as the problem of determining Optimum Strata Widths (OSW). The problem is formulated as a Mathematical Programming Problem (MPP), which minimizes the variance of the estimated population parameter under Neyman allocation subject to the restriction that sum of the widths of all the strata is equal to the total range of the distribution. The distributions of the study variable are considered as continuous with standard normal density functions. The formulated MPPs, which turn out to be multistage decision problems, can then be solved using dynamic programming technique proposed by Bühler and Deutler (1975). After the counting process using C++ program received the width of each stratum. From these results the optimal boundary point can be determined for each stratum. For the two strata to get the optimal point on the boundary x1 = 0.002. For the formation of three strata obtained the optimal point on the boundary x1 = -0.546 and x2 = 0.552. For the formation of four strata obtained optimal boundary point is x1 = -0.869, x2 = 0.003 and x3 = 0.878. In forming five strata obtained optimal boundary point x1 = -1.096, x2 = -0.331, x3 = 0.339 and x4 = 1.107. The establishment of a total of six strata obtained the optimal point on the boundary x1 = -1.267, x2 = -0.569, x3 = 0.005, x4 = 0.579 and x5 = 1.281. Keywords : Stratified Random Sampling, Optimum Stratification,
Standard Normal Distribution, Mathematical Programming, Dynamic Programming PENDAHULUAN
Penarikan contoh (sampling) dalam survei adalah suatu proses untuk memilih sebagian anggota dari suatu populasi dengan prosedur tertentu sehingga dapat digunakan untuk menduga parameter populasi secara sah. Untuk mencapai tujuan tersebut diperlukan metode penarikan contoh yang sesuai. Salah satu teknik penarikan contoh adalah penarikan contoh acak berlapis (stratified random
129
sampling). Pada penarikan contoh acak berlapis, perlu diperhatikan peubah yang
digunakan sebagai dasar pembentukan strata. Apabila peubah kualitatif digunakan untuk stratifikasi, pada umumnya pembentukan strata tidak terlalu mengalami masalah, misalnya berdasarkan tingkat pendidikan, pekerjaan dan jenis kelamin. Sebaliknya, jika peubah yang digunakan untuk stratifikasi adalah peubah kuantitatif maka diperlukan teknik tertentu untuk menentukan batas antar strata sesuai dengan kaidah teknik ini.
Pertimbangan dasar yang diperhatikan dalam penentuan batas-batas optimum strata adalah bahwa anggota populasi dalam strata harus sehomogen mungkin dan antar strata seheterogen mungkin, dengan perkataan lain ragam dalam strata harus sekecil mungkin dibandingkan ragam antar strata. Masalah yang timbul adalah penentuan titik optimum batas stratifikasi yang akan membagi populasi menjadi dua atau lebih strata sehingga memenuhi kriteria di atas.
Metode dalam penentuan titik batas optimum strata telah dikemukakan oleh beberapa peneliti. Lavallée dan Hidiroglou (1988) mengusulkan suatu algoritma untuk menentukan batas-batas strata suatu alokasi kuasa untuk contoh yang distrata dari unit-unit contoh yang tidak tentu. Hidiroglou dan Srinath (1993) dalam Khan (2008) menyajikan suatu algoritma yang lebih umum, yaitu dengan memberikan nilai-nilai yang berbeda untuk mengoperasikan parameter-parameter yang menghasilkan alokasi kuasa, alokasi Neyman, atau gabungan dari alokasi-alokasi ini.
Sweet dan Sigman (1995) dalam Khan (2008) dan Rivest (2002) meninjau kembali algoritma Lavallée dan Hidiroglou dan mengusulkan algoritma versi modifikasi yang menggabungkan hubungan berbeda antara stratifikasi dan peubah-peubah yang diteliti. Nicolini (2001) mengusulkan suatu metode yang diberi nama Natural Class Method (NCM), untuk menentang metode Dalenius dan Hodges yang paling banyak digunakan, tetapi kedua metode tersebut tidak terbukti lebih efisien dari yang lain.
Lednicki dan Wieczorkowski (2003) dalam Khan (2008) mengajukan metode stratifikasi menggunakan metode simpleks dari Nelder dan Mead (1965) dalam Khan (2008). Kemudian Kozak (2004) menyajikan algoritma pencarian secara acak yang dimodifikasi sebagai metode stratifikasi optimum. Algoritma
130 Kozak benar-benar lebih cepat dan efisien dibandingkan dengan algoritma Rivest, dan Lednicki dan Wieczorkowski dilihat dari kemampuan mengendalikan nilai yang lebih kecil pada fungsi objektif tetapi hal itu tidak dapat menjamin bahwa algoritma tersebut menunjukkan optimum global.
Mengingat bahwa masalah penentuan batas optimum strata ekuivalen dengan masalah menentukan lebar optimum strata Khan et al. (2002) dalam Khan (2008), mengatakan bahwa masalah lebar optimum strata sebagai masalah pemrograman matematika. Khan et al. (2002) menerapkan prosedurnya untuk menentukan batas optimum strata terhadap populasi yang memiliki sebaran uniform dan segitiga siku-siku. Kemudian Khan et al. (2005) memperluas pendekatan pemrograman dinamik untuk menentukan batas optimum strata terhadap peubah eksponensial. Khan et al. (2008) juga melakukan pendekatan pemrograman dinamik terhadap peubah yang memiliki sebaran normal baku.
Salah satu pemrograman matematika yang dapat digunakan dalam menentukan lebar optimum strata adalah pendekatan pemrograman dinamik Bühler dan Deutler (1975). Formulasi masalah pemrograman matematika dengan meminimumkan ragam dari parameter populasi yang diduga berdasarkan alokasi Neyman dengan batasan bahwa jumlah lebar dari semua strata sama dengan total jarak dari sebaran peubah yang diamati.
Penentuan Batas Optimum Strata Untuk Peubah Kuantitatif
Misalkan 𝑏0, 𝑏1, ⋯ , 𝑏𝐿 adalah batas-batas strata. Strata h mengandung semua unit dengan satu nilai X dalam interval 𝑏−1, 𝑏 untuk = 1, 2, ⋯ , 𝐿 sehingga 𝑏0 = 𝑚𝑖𝑛 𝑋 dan 𝑏𝐿 = 𝑚𝑎𝑥 𝑋 + 1, dengan 𝑚𝑖𝑛 𝑋 dan 𝑚𝑎𝑥 𝑋 masing-masing adalah nilai minimum dan maksimum peubah stratifikasi (Baillargeon 2010).
Misalkan X adalah peubah acak, diskret atau kontinu dengan fungsi kepadatan peluang 𝑓 𝑥 , 𝑎 ≤ 𝑥 ≤ 𝑏. Untuk menduga rataan populasi µ dengan contoh acak distratifikasi, X dipartisi menjadi L strata 𝑎, 𝑥1 , 𝑥1, 𝑥2 , ⋯ , 𝑥𝐿−1, 𝑏 , sehingga
𝑎 = 𝑥0 ≤ 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1≤ 𝑥𝐿 = 𝑏 (1)
Anggap bahwa dari strata h ( h = 1, 2, ..., L ) mengandung Nh unit, sebuah contoh
131 rataan stratifikasi 𝑥 𝑠𝑡 = 𝐿=1𝑊𝑥 adalah dugaan tak bias untuk µ dengan ragam
𝑉 𝑥 𝑠𝑡 = 𝐿 𝑊 =1 𝜎2 𝑊𝑛 − 1 𝑁 (2) Dengan𝑊 = 𝑁𝑁 , 𝑥 = 𝑛1 𝑦𝑗, 𝜎 2= 1 𝑁−1 × 𝑦𝑗 − 𝜇 2 𝑁 𝑗 =1 𝑛 𝑗 =1 dan𝜇 = 1 𝑁 𝑁𝑗 =1𝑦𝑗 (Cochran 1977) .
Apabila fungsi frekuensi 𝑓 𝑥 diketahui, nilai-nilai Wh dan 𝜎 pada persamaan (2) dapat diperoleh dengan
𝑊 = 𝑥𝑥 −1 𝑓 𝑥 𝑑𝑥(3) 𝜎2 = 1 𝑊 𝑥 2𝑓 𝑥 𝑑𝑥 − 𝜇 2 𝑥 𝑥 −1 (4) dengan 𝜇 = 𝑊1 𝑥𝑓 𝑥 𝑑𝑥 𝑥 𝑥 −1 (5)
adalah rataan dan 𝑥−1 , 𝑥 adalah batas-batas dari strata ke- h. Kemudian persamaan (2) dibaca sebagai fungsi dari titik-titik batas strata dan ukuran contoh dengan 𝑉 𝑥 𝑠𝑡 = 𝑉 𝑥 𝑠𝑡 𝑥1, ⋯ , 𝑥𝐿−1 , 𝑛1 , ⋯ , 𝑛𝐿 .
Jika nh ditetapkan, tujuan stratifikasi optimum adalah untuk menentukan
titik-titik batas optimum strata 𝑥1, ⋯ , 𝑥𝐿−1 sehingga 𝑉 𝑥 𝑠𝑡 adalah minimum. Selain itu, jika rasio pengambilan contoh 𝑛𝑁
kecil atau pengambilan contoh
dengan pengembalian, maka masalah pengoptimuman berikut diperoleh, tergantung pada tipe dari alokasi ukuran total contoh 𝑛 = 𝐿 𝑛
=1 pada strata (Cochran 1977). 1. Alokasi proporsional 𝑛 = 𝑛 ∙ 𝑊 Minimumkan 𝐿=1𝑊𝜎2 dengan kendala 𝑎 = 𝑥0 ≤ 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1 ≤ 𝑥𝐿 = 𝑏 (6) 2. Alokasi sama 𝑛 = 𝑛𝐿 Minimumkan 𝐿=1𝑊2𝜎2 dengan kendala 𝑎 = 𝑥0 ≤ 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1 ≤ 𝑥𝐿 = 𝑏 (7) 3. Alokasi Neyman 𝑛 = 𝑛∙𝑊𝜎 𝑊𝜎 𝐿 =1 Minimumkan 𝐿=1𝑊𝜎 dengan kendala 𝑎 = 𝑥0 ≤ 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1 ≤ 𝑥𝐿 = 𝑏 (8) Masalah pada persamaan (6) dan (8) memiliki struktur sebagai berikut :
132 Minimumkan 𝐿=1∅ 𝑥−1, 𝑥
dengan kendala 𝑎 = 𝑥0 ≤ 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1 ≤ 𝑥𝐿 = 𝑏 (9)
Bühler dan Deutler (1975) telah menyarankan suatu metode pengoptimuman rekursif untuk menyelesaikan persamaan (9) menggunakan teknik pemrograman dinamik sebagai berikut.
Misalkan 𝑓(𝑥) merupakan fungsi frekuensi dan 𝑥0 dan 𝑥𝐿 adalah nilai x terkecil dan terbesar. Jika rataan populasi diduga berdasarkan alokasi Neyman, maka masalah penentuan batas-batas strata adalah untuk memotong jarak,
𝑥𝐿 − 𝑥0 = 𝑑 (10)
pada titik-titik tengah 𝑥1 ≤ 𝑥2 ≤, ⋯ , ≤ 𝑥𝐿−1 sehingga 𝐿=1𝑊𝜎 pada persamaan (8) minimum.
Perhatikan bahwa 𝑓(𝑥) memiliki n fungsi bagianlinear atau non linear sebagai berikut : 𝑓 𝑥 = 𝑔1 𝑥 ; 𝑥0= 𝑎0≤ 𝑥 ≤ 𝑎1 𝑔2 𝑥 ; 𝑎1< 𝑥 ≤ 𝑎2 ⋮ 𝑔𝑛 𝑥 ; 𝑎𝑛−1< 𝑥 ≤ 𝑎𝑛 = 𝑥𝐿 (11)
Juga diasumsikan bahwa ada L strata, li jumlah strata yang dibentuk berdasarkan
fungsi kepadatan 𝑔𝑖 𝑥 ; 𝑖 = 1, 2, ⋯ , 𝑛 dan 𝑛𝑖=1𝑙𝑖 = 𝐿.
Jika 𝑓 𝑥 pada persamaan (11) dapat diintegralkan, menggunakan pernyataan persamaan (3), (4) dan (5), 𝑊, 𝜎2dan 𝜇 diperoleh sebagai suatu fungsi dari titik-titik batas 𝑥 dan 𝑥−1. Sehingga fungsi objektif pada persamaan (8) dapat dinyatakan sebagai fungsi dari titik-titik batas pada 𝑥 dan 𝑥−1. Ambil ∅ 𝑥 , 𝑥−1 = 𝑊𝜎, sehingga masalah persamaan (8) dapat diperlakukan sebagai masalah optimasi untuk menentukan 𝑥1, 𝑥2, ⋯ , 𝑥𝐿−1 seperti dinyatakan pada persamaan (9). Ambil 𝑦 = 𝑥 − 𝑥−1 ≥ 0 yang menunjukkan lebar dari strata ke- (1, 2, ⋯ , 𝐿).
Dengan definisi dari 𝑦 di atas, jarak dari sebaran yang diberikan pada persamaan (10) dinyatakan sebagai fungsi dari lebar strata sebagai
𝑦 = 𝐿=1 𝑥 − 𝑥−1 = 𝑥𝐿− 𝑥0 = 𝑑 𝐿
=1 (12)
Stratifikasi ke- k titik 𝑥𝑘; k = 1, 2, ..., L – 1 dinyatakan sebagai: 𝑥𝑘 = 𝑥0 + 𝑦1+ 𝑦2+ ⋯ + 𝑦𝑘 = 𝑥𝑘−1 + 𝑦𝑘 yang merupakan fungsi lebar strata ke- k dan batas strata ke (k – 1).
133 Perhatikan bahwa dengan menambahkan persamaan (12) sebagai batas/ kendala baru, masalah persamaan (9) dapat ditulis kembali sebagai masalah yang ekuivalen dengan penentuan lebar optimum strata sebagai berikut:
Minimumkan 𝐿=1∅ 𝑦, 𝑥−1 , dengan kendala 𝐿=1𝑦 = 𝑑, dan 𝑦 ≥ 0; = 1, 2, ⋯ , 𝐿(13)
Nilai awal 𝑥0 diketahui. Oleh karena itu, syarat pertama ∅1 𝑦1, 𝑥0 pada fungsi objektif persamaan (13) adalah suatu fungsi dari 𝑦1 itu sendiri. Jika 𝑦1 diketahui, titik stratifikasi selanjutnya 𝑥1 = 𝑥0+ 𝑦1akan diketahui dan syarat kedua pada fungsi objektif ∅2 𝑦2, 𝑥1 akan menjadi fungsi dari 𝑦2 itu sendiri.
Fungsi objektif merupakan fungsi 𝑦 itu sendiri, sehingga masalah pemrograman matematika persamaan (13) dinyatakan sebagai:
Minimumkan 𝐿=1𝛷 𝑦 , dengan kendala 𝐿=1𝑦 = 𝑑, dan𝑦 ≥ 0; = 1, 2, ⋯ , 𝐿(14)
Prosedur Solusi Menggunakan Teknik Pemrograman Dinamik
Sebuah model pemrograman dinamik pada dasarnya adalah sebuah persamaan rekursif berdasarkan prinsip optimalisasi Bellman. Persamaan rekursif ini menghubungkan tahapan yang berbeda dalam suatu metode yang menjamin bahwa tiap tahap solusi layak optimal, juga optimal dan layak untuk semua masalah. Perhatikan submasalah berikut dari persamaan (14) untuk k(< 𝐿) strata pertama: Minimumkan 𝑘=1∅ 𝑦 ,dengan kendala 𝑘=1𝑦 = 𝑑𝑘,dan
𝑦 ≥ 0; = 1, 2, ⋯ , 𝑘 (15) dengan 𝑑𝑘 < 𝑑 adalah lebar total yang tersedia untuk bagian dalam k strata atau nilai tertentu pada k langkah. Catatan bahwa 𝑑𝑘 = 𝑑 untuk 𝑘 = 𝐿.
Fungsi transformasi diberikan oleh: 𝑑𝑘 = 𝑦1+ 𝑦2+ ⋯ + 𝑦𝑘, 𝑑𝑘−1= 𝑦1+ 𝑦2+ ⋯ + 𝑦𝑘−1 = 𝑑𝑘 − 𝑦𝑘, 𝑑𝑘−2= 𝑦1𝑦2+ ⋯ + 𝑦𝑘−2 = 𝑑𝑘−1− 𝑦𝑘−1, ⋮ ⋮ 𝑑2 = 𝑦1+ 𝑦2 = 𝑑3− 𝑦3, 𝑑1 = 𝑦1 = 𝑑2− 𝑦2,
134 Ambil 𝛷𝑘 𝑑𝑘 sebagai notasi nilai minimum fungsi objektif dari persamaan (15), yaitu: 𝛷𝑘 𝑑𝑘 = min 𝑘=1∅ 𝑦 𝑘=1𝑦 = 𝑑𝑘, dan 𝑦 ≥ 0; = 1, 2, ⋯ , 𝑘 . Dari definisi 𝛷𝑘 𝑑𝑘 tersebut, masalah pemrograman matematika persamaan (14) ekuivalen untuk menentukan 𝛷𝐿 𝑑 secara rekursif dengan menentukan 𝛷𝑘 𝑑𝑘 untuk 𝑘 = 1, 2, ⋯ , 𝐿 dan 0 ≤ 𝑑𝑘 ≤ 𝑑. 𝛷𝑘 𝑑𝑘 = min ∅𝑘 𝑦𝑘 + 𝑘−1=1∅ 𝑦 𝑘−1=1𝑦 = 𝑑𝑘 − 𝑦𝑘,dan 𝑦 ≥ 0; = 1, 2, ⋯ , 𝑘 − 1 Untuk suatu nilai tetap dari 𝑦𝑘; 0 ≤ 𝑦𝑘 ≤ 𝑑𝑘
𝛷𝑘 𝑑𝑘 = ∅𝑘 𝑦𝑘 + min ∅ 𝑦 𝑘−1 =1 𝑦 = 𝑑𝑘 − 𝑦𝑘, 𝑘−1 =1 𝑦 ≥ 0; = 1, 2, ⋯ , 𝑘 − 1
Menggunakan prinsip pengoptimalan Bellman, diperoleh hubungan berulang dari teknik pemrograman dinamik sebagai berikut:
𝛷𝑘 𝑑𝑘 0 ≤𝑦𝑘≤𝑑𝑘 ∅𝑘 𝑦𝑘 + 𝛷𝑘−1 𝑑𝑘 − 𝑦𝑘 , 𝑘 ≥ 2
𝑚𝑖𝑛 (16)
Untuk langkah pertama, yaitu untuk k = 1: 𝛷1 𝑑1 = ∅1 𝑑1 𝑦1∗ = 𝑑1, (17) dengan 𝑦1∗= 𝑑
1 adalah lebar optimum strata pertama. Hubungan persamaan (16) dan (17) diselesaikan secara rekursif untuk tiap 𝑘 = 1, 2, ⋯ , 𝐿 dan 0 ≤ 𝑑𝑘 ≤ 𝑑 dan 𝛷𝐿 𝑑 diperoleh. Dari 𝛷𝐿 𝑑 , lebar optimum strata ke- L, 𝑦𝐿∗, diperoleh. Dari 𝛷𝐿−1 𝑑 − 𝑦𝐿∗ lebar optimum strata ke- L-1, 𝑦𝐿−1∗ , diperoleh dan begitu seterusnya sampai 𝑦1∗ diperoleh.
Pemrograman Matematika Untuk Sebaran Normal
Misalkan peubah penelitian x memiliki sebaran normal baku dengan fungsi kepadatan peluang diberikan oleh:
𝑓 𝑥 = 1
2𝜋𝑒𝑥𝑝 − 𝑥2
2 ; −∞ < 𝑥 < ∞
Menurut Bühler dan Deutler (1975), dengan menggunakan definisi persamaan (3), (4) dan (5), dapat dilihat bahwa:
𝑊 = 𝑒𝑟𝑓 𝑦 + 𝑥−1 2 −𝑒𝑟𝑓 𝑥−1 2 2 (18) 𝜇 = 2 𝑒𝑥𝑝 −𝑥−1 2 2 –𝑒𝑥𝑝 − 𝑦 +𝑥−1 2 2 𝜋 𝑒𝑟𝑓 𝑦 +𝑥−1 2 −𝑒𝑟𝑓 𝑥−1 2 , dan
135 𝜎2= 2𝜋 𝑥−1𝑒𝑥𝑝 –𝑥−1 2 2 𝑒𝑟𝑓 𝑦+ 𝑥−1 2 − (𝑦+ 𝑥−1) 𝑒𝑥𝑝 − 𝑦+ 𝑥−1 2 2 𝑒𝑟𝑓 𝑦+ 𝑥−1 2 +(𝑦+ 𝑥−1) 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 𝑒𝑟𝑓 𝑥−1 2 + 𝜋 𝑒𝑟𝑓 𝑦+𝑥−1 2 − 𝑒𝑟𝑓 𝑥−1 2 2 − 𝑥−1𝑒𝑥𝑝 –𝑥−1 2 2 𝑒𝑟𝑓 𝑥−1 2 − 2 𝑒𝑥𝑝 –𝑥−12 2 − 𝑥𝑝 − 𝑦+𝑥−12 2 2 ÷ 𝜋 𝑒𝑟𝑓 𝑦+𝑥−1 2 − 𝑒𝑟𝑓 𝑥−1 2 2 (19) dengan 𝑦 = 𝑥 − 𝑥−1, 𝑒𝑟𝑓 𝑥 − 𝑒𝑟𝑓 𝑥−1 = 2 𝜋 × 𝑒𝑥𝑝 −𝑢 2 𝑑𝑢 𝑥 𝑥 −1 dan = 1, 2, ⋯ , 𝐿.
Dengan demikian, dengan menggunakan nilai pada persamaan (18) dan (19), masalah pemrograman matematika persamaan (14) dapat dinyatakan sebagai berikut: Minimumkan 𝑆𝑞𝑟𝑡 1 2 2𝜋 𝑥−1𝑒𝑥𝑝 – 𝑥−12 2 𝐿 =1 𝑒𝑟𝑓 𝑦+𝑥 2 −1 −(𝑦 + 𝑥−1) 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 𝑒𝑟𝑓 𝑦+𝑥 −1 2 −𝑥−1𝑒𝑥𝑝 – 𝑥 −12 2 𝑒𝑟𝑓 𝑥 −1 2 +(𝑦 + 𝑥−1) 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 𝑒𝑟𝑓 𝑥 −1 2 + 𝟏 𝟒 𝑒𝑟𝑓 𝑦+𝑥 −1 2 − 𝑒𝑟𝑓 𝑥 −1 2 2 −𝟐𝝅𝟏 𝑒𝑥𝑝 –𝑥−12 2 − 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 2 dengan kendala 𝐿=1𝑦 = 𝑑, dan 𝑦 ≥ 0; = 1, 2, ⋯ , 𝐿(20)
dengan sqrt adalah square root, exp adalah eksponensial, dan erf adalah error
function.
METODE PENELITIAN Data
Data yang digunakan dalam penelitian ini menggunakan data SUSENAS Propinsi Jawa Timur Tahun 2008 berupa data pengeluaran per kapita penduduk sebanyak 8607 Kepala Rumah Tangga.
Metode Penelitian
Pembentukan strata dengan menggunakan teknik pemrograman dinamik terbagi menjadi beberapa tahapan sebagai berikut.
Tahap 1. Penyusunan model/ fungsi objektif.
Langkah yang dilakukan pada tahap 1 adalah pembentukan fungsi objektif seperti pada persamaan (20) di mana fungsi kendala 𝐿=1𝑦 = 𝑑, dengan 𝑑 = 𝑥𝐿− 𝑥0. Kemudian tentukan fungsi lebar strata ke- ( − 1), yaitu 𝑥−1.
136 Substitusikan nilai 𝑥−1 ini ke dalam fungsi objektif yang telah disusun. Gunakan persamaan (16) dan (17) untuk mendapatkan persamaan rekursifnya.
Tahap 2. Penyelesaian persamaan rekursif.
Langkah-langkah dalam penyelesaian persamaan rekursif adalah sebagai berikut.
1. Mulai dengan 𝑘 = 1. Tetapkan 𝛷 0, 𝑑0 = 0.
2. Hitung 𝛷1 𝑑1 , nilai minimum RHS (right hand side) dari persamaan rekursif yang diperoleh untuk 𝑦1 = 𝑑1, 0 ≤ 𝑦1 ≤ 𝑑1 dan 0 ≤ 𝑑1 ≤ 𝑑.
3. Simpan nilai 𝛷1 𝑑1 dan 𝑦1.
4. Untuk 𝑘 = 2, nyatakan peubah penjelas sebagai 𝑑𝑘−1 = 𝑑𝑘 − 𝑦𝑘. 5. Tetapkan 𝛷𝑘 𝑑𝑘 = 0 jika 𝑦𝑘 > 𝑑𝑘, di mana 0 ≤ 𝑑𝑘 ≤ 𝑑.
6. Hitung 𝛷𝑘 𝑑𝑘 , nilai minimum RHS dari persamaan rekursif yang diperoleh untuk 𝑦𝑘; 0 ≤ 𝑦𝑘 ≤ 𝑑𝑘.
7. Simpan nilai 𝛷𝑘 𝑑𝑘 dan 𝑦𝑘.
8. Untuk 𝑘 ≥ 3, ⋯ , 𝐿 , kembali ke langkah 4.
9. Pada 𝑘 = 𝐿, 𝛷𝐿 𝑑 diperoleh sehingga nilai optimum 𝑦𝐿∗ dari 𝑦𝐿 diperoleh. 10. Pada 𝑘 = 𝐿 − 1, gunakan penghitungan mundur untuk 𝑑𝐿−1 = 𝑑𝐿− 𝑦𝐿, baca
nilai dari 𝛷𝐿−1 𝑑𝐿−1 , sehingga nilai optimum 𝑦𝐿−1∗ dari 𝑦 𝐿−1.
11. Ulangi langkah ke-10 sampai nilai optimum 𝑦1∗ dari 𝑦1 diperoleh dari 𝛷1 𝑑1 . Penyelesaian persamaan rekursif tersebut menggunakan Program C++.
Tahap 3. Penghitungan nilai optimum fungsi objektif.
Sebagai tahapan terakhir adalah menghitung nilai optimum fungsi objektif untuk setiap strata L yaitu 𝐿=1∅ 𝑦 = 𝐿=1𝑊𝜎.
Untuk mengetahui karakteristik antar strata dilakukan pengujian kehomogenan ragam. Metode statistika untuk menguji kehomogenan ragam adalah uji khi-kuadrat yang dikenal dengan uji Bartlett. Hipotesis yang diuji pada uji Bartlett adalah:
H0 : 𝜎12 = 𝜎22 = ⋯ = 𝜎𝑖2
H1 : paling sedikit ada satu pasang 𝜎𝑖2 ≠ 𝜎𝑖2′ , untuk setiap 𝑖 ≠ 𝑖′ , di mana 𝑖 = 1, 2, ⋯ , 𝑘
Uji Bartlett dapat dilakukan untuk ulangan sama atau tidak sama. Uji khi-kuadarat untuk jumlah ulangan tidak sama adalah:
137 𝜒𝑖𝑡𝑢𝑛𝑔2 = 𝑑𝑏𝑖 𝑙𝑛𝑠𝑔𝑎𝑏2 − 𝑑𝑏𝑖 ∙ 𝑙𝑛𝑠𝑖2
1 +3 𝑘 − 1 1 1𝑑𝑏
𝑖 − 1 𝑑𝑏𝑖
(21)
dengan dbi adalah derajat bebas strata ke-i, si2 adalah ragam dari strata ke-i dan s2gab adalah ragam gabungan untuk semua strata.
Dengan kaidah keputusan sebagai berikut:
Apabila 𝜒𝑖𝑡𝑢𝑛𝑔2 > 𝜒𝛼,𝑘−12 , maka H0 ditolak artinya kehomogenan ragam tidak dapat dipenuhi. Dan jika sebaliknya hipotesis kehomogenan ragam diterima.
HASIL DAN PEMBAHASAN
Data Pengeluaran Per Kapita Propinsi Jawa Timur Tahun 2008
Jawa Timur adalah provinsi yang terdiri dari 29 kabupaten dan 9 kota. Secara umum wilayah provinsi Jawa Timur dapat dibagi menjadi dua bagian besar yaitu Jawa Timur daratan dan Pulau Madura. Luas wilayah Jawa Timur daratan hampir mencapai 90 persen dari luas keseluruhan, sedangkan wilayah Madura hanya sekitar 10 persen. Data yang digunakan pada penelitian ini adalah data pengeluaran per kapita penduduk Jawa Timur tahun 2008 dengan jumlah contoh n = 8607 Kepala Rumah Tangga. Data ini diperoleh dari publikasi BPS dari hasil SUSENAS. Dari data tersebut dapat diperoleh informasi bahwa rata-rata pengeluaran per kapita penduduk Jawa Timur adalah Rp337.105,93 dan ragam Rp8.49 x 1010. Pengeluaran minimum adalah sebesar Rp41.349,94 dan pengeluaran maksimum sebesar Rp5.442.241,45.
Setelah dilakukan uji kenormalan Kolmogorov Smirnov terhadap data pengeluaran per kapita tersebut, hasilnya menunjukkan bahwa adanya penyimpangan asumsi tesebut. Karena metode dalam penelitian ini memerlukan asumsi kenormalan, maka data penelitian tersebut harus ditransformasi, dalam hal ini menggunakan transformasi log.
Penentuan Titik-titik Batas Optimum Strata
Untuk data contoh pengeluaran per kapita (nilai setelah diubah menjadi normal standar) dengan n = 8607 diperoleh nilai terkecil dan nilai terbesar masing-masing adalah 𝑥0 = -3.302 dan 𝑥𝐿 = 5.169. Ini menunjukkan bahwa jarak dari distribusi adalah
𝑑 = 𝑥𝐿− 𝑥0 =5.169 – (-3.302) = 8.471
138 Minimumkan 𝑆𝑞𝑟𝑡 1 2 2𝜋 𝑥−1𝑒𝑥𝑝 – 𝑥 −12 2 𝐿 =1 𝑒𝑟𝑓 𝑦+𝑥 2−1 − (𝑦 + 𝑥−1) 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 𝑒𝑟𝑓 𝑦+𝑥 −1 2 −𝑥−1𝑒𝑥𝑝 – 𝑥 −12 2 𝑒𝑟𝑓 𝑥 −1 2 +(𝑦 + 𝑥−1) 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 𝑒𝑟𝑓 𝑥 −1 2 + 𝟏 𝟒 𝑒𝑟𝑓 𝑦+𝑥−1 2 − 𝑒𝑟𝑓 𝑥 −1 2 2 −𝟐𝝅𝟏 𝑒𝑥𝑝 –𝑥−12 2 − 𝑒𝑥𝑝 − 𝑦+𝑥−1 2 2 2 dengan kendala 𝐿=1𝑦 =8.471 dan𝑦 ≥ 0; = 1, 2, ⋯ , 𝐿(22)
Stratifikasi ke- (k-1) diberikan oleh
𝑥𝑘−1 = 𝑥0 + 𝑦1+ 𝑦2+ ⋯ + 𝑦𝑘−1 = −3.302 + 𝑦1+ 𝑦2+ ⋯ + 𝑦𝑘−1
= 𝑑𝑘−1− 3.302 = 𝑑𝑘− 𝑦𝑘 − 3.302
Substitusikan nilai 𝑥𝑘−1 kedalam persamaan (21) dan dengan mengunakan persamaan (16) dan (17), persamaan rekursif untuk menyelesaikan masalah pemrograman matematika persamaan (21) ditentukan sebagai berikut.
Untuk tahap pertama (k = 1):
𝛷1 𝑑1 = 𝑆𝑞𝑟𝑡 1 2 2𝜋 −3.302𝑒𝑥𝑝 – 10.902 2 𝑒𝑟𝑓 𝑑1−3.302 2 − 𝑑1− 3.302 𝑒𝑥𝑝 − 𝑑1− 3.302 2 𝑒𝑟𝑓 𝑑1−3.302 2 3.302𝑒𝑥𝑝 –10.902 2 𝑒𝑟𝑓 3.302 2 + 𝑑1− 3.302 𝑒𝑥𝑝 − 𝑑1− 3.302 2 2 𝑒𝑟𝑓 3.302 2 + 1 4 𝑒𝑟𝑓 𝑑1−3.302 2 − 𝑒𝑟𝑓 3.302 2 2 − 1 2𝜋 𝑒𝑥𝑝 – 10.902 2 − 𝑒𝑥𝑝 − 𝑑1− 3.302 2 2 2 Pada 𝑦1 = 𝑑1 (23) Untuk tahap 𝑘 = 2, 3, ⋯ , 𝐿
139 𝛷𝑘 𝑑𝑘 = min 0≤𝑦𝑘≤𝑑𝑘 𝑆𝑞𝑟𝑡 1 2 2𝜋 𝑑𝑘 − 𝑦𝑘 − 3.302 exp – 𝑑𝑘− 𝑦𝑘 − 3.302 2 2 erf 𝑑𝑘−3.302 2 − 𝑑𝑘 − 3.302 𝑒𝑥𝑝 − 𝑑𝑘−3.302 2 2 𝑒𝑟𝑓 𝑑𝑘−3.302 2 𝑑𝑘 − 𝑦𝑘 − 3.302 exp – 𝑑𝑘−𝑦𝑘−3.302 2 2 erf 𝑑𝑘−𝑦𝑘−3.302 2 𝑑𝑘 − 3.302 𝑒𝑥𝑝 − 𝑑𝑘−3.302 2 2 erf 𝑑𝑘−𝑦𝑘−3.302 2 + 1 4 𝑒𝑟𝑓 𝑑𝑘−3.302 2 − 𝑒𝑟𝑓 𝑑𝑘−𝑦𝑘−3.302 2 2 −2𝜋1 𝑒𝑥𝑝 – 𝑑𝑘−𝑦𝑘−3.302 2 2 − 𝑥𝑝 − 𝑑𝑘−3.302 2 2 2 +𝛷𝑘−1 𝑑𝑘 − 𝑦𝑘 (24) Penyelesaian persamaan rekursif (22) dan (23) menggunakan pemrograman C++ suntuk menentukan lebar strata optimum 𝑦. Tabel 1 menunjukkan hasil dari penyelesaian ini disertai dengan nilai optimum fungsi objektif 𝐿=1∅ 𝑦 = 𝐿=1𝑊𝜎 untuk 𝐿 = 2, 3, 4, 5 𝑑𝑎𝑛 6.
Tabel 1 Titik-titik batas optimum strata dari sebaran normal baku
Jumlah Strata L
Lebar Optimum Strata (𝑦)
Titik-titik Batas Optimum Strata (𝑥 = 𝑥−1+ 𝑦) Nilai Optimum Fungsi Objektif ∅ 𝑦 𝐿 =1 = 𝑊𝜎 𝐿 =1 2 y1=3.303 y2=5.167 x0 = -3.302 x1= 0.002 xL = 5.169 0.599 3 y1=2.756 y2=1.098 y3=4.617 x0 = -3.302 x1=-0.546 x2=0.552 xL = 5.169 0.424 4 y1=2.432 y2=0.873 y3=0.875 y4=4.291 x0 = -3.302 x1=-0.869 x2=0.003 x3=0.878 xL = 5.169 0.328 5 y1=2.206 y2=0.765 y3=0.670 y4=0.767 y5=4.062 x0 = -3.302 x1=-1.096 x2=-0.331 x3=0.339 x4=1.106 xL = 5.169 0.267 6 y1=2.035 y2=0.698 y3=0.574 x0 = -3.302 x1=-1.267 x2=-0.569 x3=0.005 0.225
140 y4=0.574 y5=0.702 y6=3.888 x4=0.579 x5=1.280 xL = 5.169
Pengujian Kehomogenan Ragam
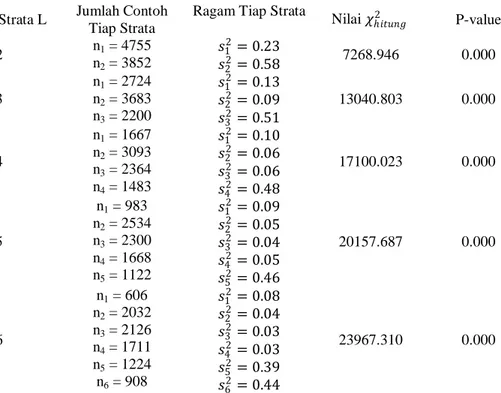
Hasil uji khi-kuadrat untuk setiap strata disajikan pada Tabel 2. Tabel 2 Hasil uji khi-kuadrat untuk setiap jumlah strata
Jumlah Strata L Jumlah Contoh Tiap Strata
Ragam Tiap Strata Nilai 𝜒
𝑖𝑡𝑢𝑛𝑔2 P-value 2 n1 = 4755 n2 = 3852 𝑠12= 0.23 𝑠22= 0.58 7268.946 0.000 3 n1 = 2724 n2 = 3683 n3 = 2200 𝑠12= 0.13 𝑠22= 0.09 𝑠32= 0.51 13040.803 0.000 4 n1 = 1667 n2 = 3093 n3 = 2364 n4 = 1483 𝑠12= 0.10 𝑠22= 0.06 𝑠32= 0.06 𝑠42= 0.48 17100.023 0.000 5 n1 = 983 n2 = 2534 n3 = 2300 n4 = 1668 n5 = 1122 𝑠12= 0.09 𝑠22= 0.05 𝑠32= 0.04 𝑠42= 0.05 𝑠52= 0.46 20157.687 0.000 6 n1 = 606 n2 = 2032 n3 = 2126 n4 = 1711 n5 = 1224 n6 = 908 𝑠12= 0.08 𝑠22= 0.04 𝑠32= 0.03 𝑠42= 0.03 𝑠52= 0.39 𝑠62= 0.44 23967.310 0.000
Dari Tabel 2 terlihat bahwa untuk semua jumlah strata L, menghasilkan nilai khi-kuadrat yang lebih besar daripada nilai khi-kuadrat tabel baik pada taraf nyata 5% maupun pada taraf nyata 1%. Ini berarti bahwa kehomogenan ragam ditolak, yaitu uji menunjukkan perbedaan yang nyata antara ragam-ragam pada setiap jumlah strata L. Hasil ini juga menunjukkan bahwa ada perbedaan keragaman pada masing-masing strata. Hal ini berarti bahwa antar strata lebih bervariasi karakteristiknya (heterogen).
Pembentukan Strata Pengeluaran Per Kapita Jawa Timur Tahun 2008
Lebar strata dan titik-titik batas optimum strata pada Tabel 1 merupakan hasil yang didapatkan dari data yang sudah ditransformasi. Untuk data pengeluaran per kapita Propinsi Jawa Timur Tahun 2008 disajikan pada Tabel 3. Tabel 3 Titik-titik batas optimum strata pengeluaran per kapita Jawa Timur 2008
Jumlah Strata L
Lebar Optimum
Strata (𝑦) Titik-titik Batas Optimum Strata Nilai Ragam Strata 𝑠
141 2 y1 = 35933.33 y2 =5164855. x0 =41349.940 x1 = 277325.3 xL = 5442241. 𝑠12= 339422490 𝑠22=1.281E+11 3 y1 = 0922.869 y2 = 178461.9 y3 = 5061394. x0 =41349.940 x1 = 202272.8 x2 = 380751.9 xL = 5442241. 𝑠12= 880588393 𝑠22=2436769947 𝑠32=1.746E+11 4 y1 = 26525.06 y2 = 109712.0 y3 = 181764.5 y4 = 4982767. x0 = 1349.940 x1 = 167875.6 x2 = 277605.1 x3 = 459449.1 xL = 5442241. 𝑠12= 512400483 𝑠22= 960333991 𝑠32=2599356842 𝑠42=2.159E+11 5 y1 = 06024.82 y2 = 81428.1 y3 = 107872.1 y4 = 187136.5 y5 = 4918068. x0 = 1349.940 x1 = 147398.4 x2 = 228973.7 x3 = 336869.8 x4 = 524125.8 xL = 5442241. 𝑠12= 340941512 𝑠22= 567979981 𝑠32= 953660359 𝑠42=2739191510 𝑠52= 2.492E+11 6 y1 = 92184.35 y2 = 66063.52 y3 =78167.16 y4 = 108808.6 y5 = 191543.5 y6 = 4862690. x0 = 1349.940 x1 = 133543.7 x2 = 199626.4 x3 = 277805.1 x4 = 386780.9 x5 = 579495.9 xL =5442241.452 𝑠12= 253204999 𝑠22= 342296093 𝑠32= 472878135 𝑠42=941057357 𝑠52= 2840506289 𝑠62=2.774E+11
SIMPULAN DAN SARAN Simpulan
Penentuan titik-titik batas optimum strata dapat dianggap sebagai masalah pemrograman matematika dan dapat diselesaikan dengan teknik pemrograman dinamik. Metode ini dapat diterapkan pada data dengan sebaran yang berbeda karena memiliki fungsi objektif yang berbeda pula sesuai dengan sebaran datanya.
Metode ini memberikan hasil berupa lebar masing-masing strata. Oleh karena itu dapat ditentukan titik-titik batas optimum strata dan juga jumlah contoh pada masing-masing strata. Titik-titik batas yang diperoleh menghasilkan ragam di dalam strata sehomogen mungkin dan ragam antar strata seheterogen mungkin. Untuk dua strata diperoleh titik batas optimum pada x1 = 0.002.Untuk pembentukan tiga strata diperoleh titik batas optimum pada x1 = -0.546 dan x2 = 0.552. Untuk pembentukan sebanyak empat strata diperoleh titik batas optimum adalah x1 = -0.869, x2 = 0.003 dan x3 = 0.878. Pada pembentukan sebanyak lima strata diperoleh titik batas optimum x1 = -1.096, x2 = -0.331, x3 = 0.339 dan x4 = 1.107. Sedangkan untuk pembentukan sebanyak enam strata diperoleh titik batas optimum pada x1 = -1.267, x2 = -0.569, x3 = 0.005, x4 = 0.579 dan x5 = 1.281.
142 Metode pemrograman dinamik ini juga memberikan nilai optimum fungsi objektif untuk tiap jumlah strata. Hasilnya menunjukkan bahwa semakin banyak jumlah strata maka nilai optimum fungsi ini akan semakin kecil. Nilai optimum fungsi objektif untuk jumlah strata 2, 3, 4, 5, dan 6 berturut-turut adalah 0.599, 0.424, 0.328, 0.267 dan 0.225.
Saran
Penentuan strata untuk peubah kuantitatif dengan metode pemrograman dinamik dapat menjadi salah satu alternatif dalam menentukan stratifikasi dalam penelitian survei dan dapat dilakukan untuk data dengan sebaran yang lain selain sebaran normal dengan penentuan sebarannya terlebih dahulu.
DAFTAR PUSTAKA
Aoyama H. 1954. A Study of Stratified Random Sampling. Annals of The
Institute of Statistical Mathematics 6:1-36.
Bühler W and Deutler T. 1975. Optimal Stratification and Grouping by Dynamic Programming. Metrika 22:161-175.
BPS [Badan Pusat Statistik] Provinsi Jawa Timur. 2008. Pendataan Potensi Desa
2008 Propinsi Jawa Timur . Jawa timur: Badan pusat Statistik.
Baillargeon S and Rivest LP. 2010. Univariate Stratification of Survey
Populations with The Package Stratification. Paper in Progress.
Cochran WG. 1977. Sampling Techniques, 3rd Edition. New York: John Willey & Sons.
Khan EA, Khan MGM, Ahsan MJ. 2002. Optimum Stratification: A Mathematical Programming Approach. Culcutta Statistical Association Bulletin 52 (special):205-208.
Khan MGM, Najmussehar, Ahsan MJ. 2005. Optimum Stratification for Exponential Study Variable Under Neyman Allocation. Journal of Indian
Society of Agriculture Statistics 59(2):146-150.
Khan MGM, Niraj Nand, Nesar Ahmad. 2008. Determining The Optimum Strata Boundary Points Using Dynamic Programming. Survey Methodology 34: 205-214.
Kish L. 1965. Survey Sampling.New York: John Willey & Sons.
Kozak M. 2004. Optimal Stratification Using Random Search Method in Agricultural Surveys. Statistics in Transition 6(5):797-806.
Lavallée P. 1988. Two-way Optimal Stratification using Dynamic Programming.
Procedings of The Section on Survey Research Methods; Virginia:646-651.
Lavallée P, Hidiroglou M. 1988. On The stratification of Skewed populations.
Survey Methodology 14:33-43.
Levy, Paul S, Stanley L. 1995. Sampling of Populations Methods and
Applications Third Edition.New York: John Willey & Sons.
Nicolini G. 2001. A Method to Define Strata Boundaries. Departmental Working
143 Rivest LP. 2002. A Generalization of Lavallée and Hidiroglou Algorithm for
Stratification in Business Survey. Survey Methodology 28:191-198. Siagian P.2006. Penelitian Operasional: Teori dan Praktek. UI-PRESS.