Analisis energi untuk gerak langkah manusia berjalan
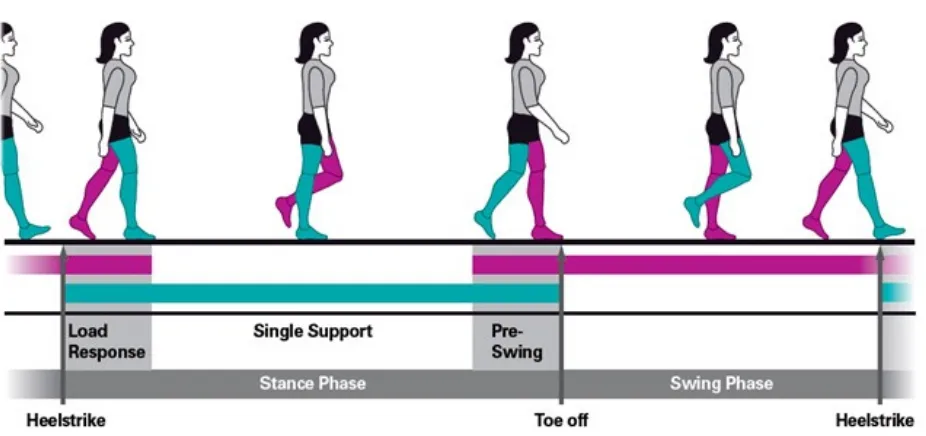
Gerak manusia berjalan atau berlari ditandai dengan lintasan gerak translasi pusat massa orang tersebut. Namun karena tungkai yang bergerak melangkah tidak dapat dianggap sebagi partikel, maka tinjauan geraknya harus memperhitungkan ketegaran tungkai, karenanya model yang lebih tepat digunakan adalah model gerak rotasi tungkai, dengan pinggul yang merupakan tempat beradanya pusat massa tubuh menjadi sumbu rotasi geraknya. Dalam gerak semacam ini, peran tendon sangat penting sebagai komponen penyimpanan energi elastik dan pelepasannya saat diperlukan.
Pada gerak rotasi tungkai saat melangkah terdapat tiga fasa berturutan, Pertama, saat posisi pusat massa tubuh bergerak naik. Kedua, saat tungkai berayun dengan amplitudo sudut θ. Ketiga, saat posisi pusat massa tubuh kembali bergerak turun. Untuk gerak berjalan, pada saat melangkah, selalu ada satu kaki yang bersentuhan dengan tanah, jadi tidak ada saat kaki kedua-duanya melayang ( tidak bersentuhan dengan tanah ); inilah yang membedakan gerak berjalan dan berlari.
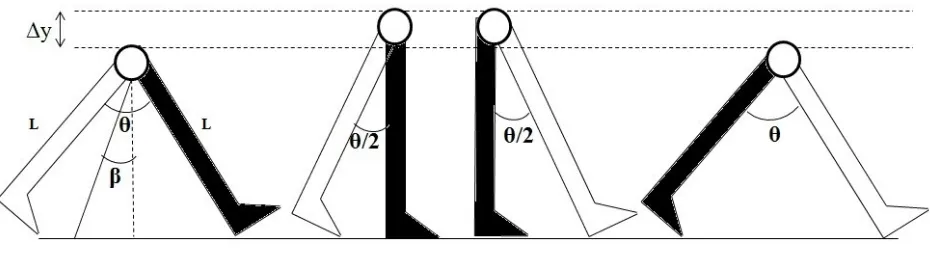
Pada saat terjadi gerak satu langkah sempurna, titik pusat massa tubuh akan berpindah arah mendatar, sejauh x, dengan x = 2L sin (θ/2) , dengan L adalah panjang tungkai, dan θ adalah sudut terbesar antara tungkai depan dengan tungkai belakang ( lihat gambar 2 )
Perhatikan gambar berikut ini
Gambar 2 : Satu Langkah Sempurna
Jika β adalah sudut yang dibentuk tungkai ayun terhadap arah vertikal, maka torsi yang dilakukan otot tungkai tersebut M, dan memenuhi persamaan:
M=Id
Dengan μ menyatakan massa tungkai , g menyatakan percepatan gravitasi , L panjang tungkai dan I menyatakan momen inersia tungkai.
Bila terdapat gangguan dari luar ( misal gaya gesekan/hambatan, dan sebagainya), maka persamaan (1) harus ditulis dalam bentuk :
M=I d
Dengan M luar menyatakan torsi karena adanya pengaruh luar tersebut .
Dari solusi ini terlihat adanya kesesuaian antara gerak tungkai ( osilasi ) dengan apa yang sudah dibahas melalui analisis kinematika terdahulu.
Untuk satu langkah sempurna, tungkai berayun
dari posisi β(0) = - θ
2 hingga ke posisi β (T )= +
θ
2 , dengan perpindahan pusat massa tubuh
sejauh x = 2 L sin ( θ
2 ) dan waktu yang diperlukan untuk kondisi tersebut adalah T.
Jadi T=
2Lsin
(
θ 2)
V , dengan V menyatakan kecepatan rerata gerak pusat massa pada arah mendatar.
Jika persamaan (2) diselesaikan untuk menentukan nilai torsi M, dengan memasukkan
nilai β ( T ) = Selama satu perioda gerak langkah sempurna, dapat didefinisikan daya rerata sebagai
P
R=
W
Dengan demikian diperoleh :
PR =
PPM=mg Δy
1 2T
=
m.g.V
(
1−cos.(
θ 2)
)
sin
(
θ2
)
……….(7)m adalah massa tubuh.
Sehingga daya total tiap langkah adalah :
P = PR + PPM ………..(8)
Dari besaran daya ini dapat ditentukan konsumsi energi yang dikeluarkan tiap kilogram massa tubuh untuk setiap kilometer jarak yang ditempuh sebagai:
KE = P
mV dalam satuan
kJ
kgkm
………( 9.a )atau KE =
0,24P
mV dalam satuan
kkal
kgkm
………..(9.b)dengan P dihitung dari persamaan (7) serta persamaan-persamaan pendukung lainnya
Hasil pengujian terhadap konsumsi energi yang dihitung dari persamaan di atas, akan dicocokkan dengan pernyataan Hukum Margaria5) yang menyatakan bahwa konsumsi energi ini mendekati