BAB II LANDASAN TEORI. Graf adalah kumpulan simpul (nodes) yang dihubungkan satu sama lain

BAB II

LANDASAN TEORI

2.1 Teori Graf

2.1.1 Definisi Graf

Graf adalah kumpulan simpul (nodes) yang dihubungkan satu sama lain melalui sisi/busur (edges) (Zakaria, 2006). Suatu Graf G terdiri dari dua himpunan yaitu himpunan V dan himpunan E.

a. Verteks (simpul) :V = himpunan simpul yang terbatas dan tidak kosong

b. Edge (sisi/busur):E = himpunan busur yang menghubungkan sepasang simpul.

Simpul-simpul pada graf dapat merupakan obyek sembarang seperti kota, atom-atom suatu zat, nama anak, jenis buah, komponen alat elektronik dan sebagainya. Busur dapat menunjukkan hubungan (relasi) sembarang seperti rute penerbangan, jalan raya, sambungan telepon, ikatan kimia, dan lain-lain. Notasi graf: G(V,E) artinya graf G memiliki V simpul dan E busur.

2.1.2 Macam-macam Graf

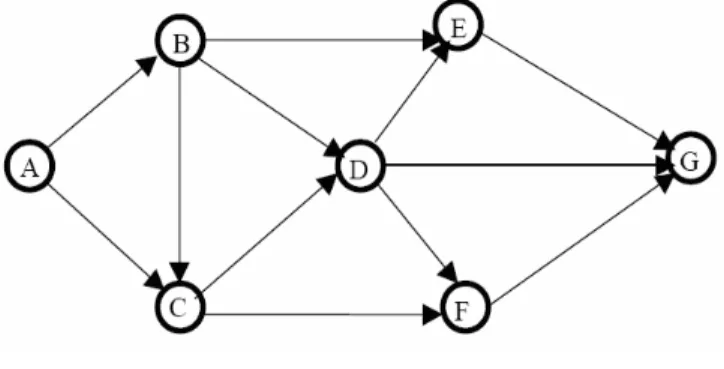
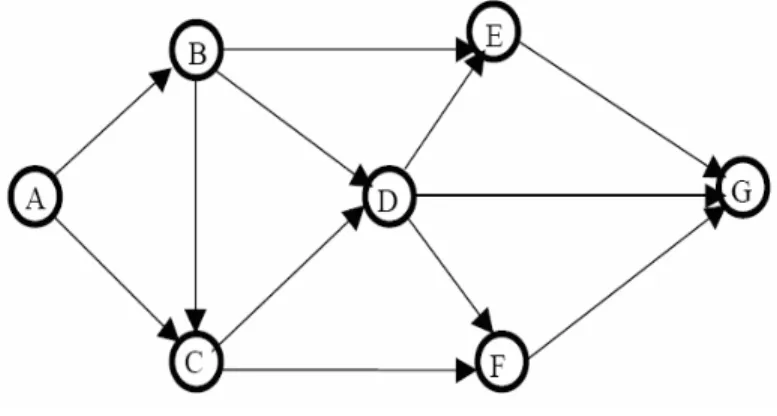
1. Graf berarah dan berbobot : tiap busur mempunyai anak panah dan bobot. Gambar 2.1 menunjukkan graf berarah dan berbobot yang terdiri dari tujuh titik yaitu titik A,B,C,D,E,F,G. Titik menujukkan arah ke titik B dan titik C, titik B menunjukkan arah ke titik D dan titik C, dan seterusnya. Bobot antar titik A dan titik B pun telah di ketahui.

Gambar 2.1 Graf berarah dan berbobot

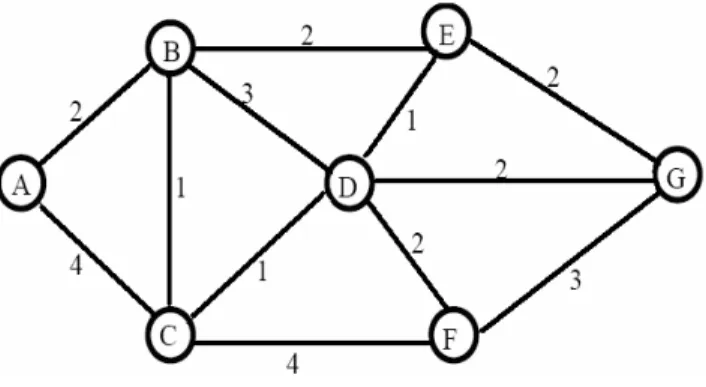
2. Graf tidak berarah dan berbobot : tiap busur tidak mempunyai anak panah tetapi mempunyai bobot. Gambar 2.2 menunjukkan graf tidak berarah dan berbobot. Graf terdiri dari tujuh titik yaitu titik A,B,C,D,E,F,G. Titik A tidak menunjukkan arah ke titik B atau C, namun bobot antara titik A dan titik B telah diketahui. Begitu juga dengan titik yang lain.

Gambar 2.2 Graf tidak berarah dan berbobot

3. Graf berarah dan tidak berbobot: tiap busur mempunyai anak panah yang tidak berbobot. Gambar 2.3 menunjukkan graf berarah dan tidak berbobot.

Gambar 2.3 Graf berarah dan tidak berbobot

4. Graf tidak berarah dan tidak berbobot: tiap busur tidak mempunyai anak panah dan tidak berbobot.

Gambar 2.4 Graf tidak berarah dan tidak berbobot

2.1.2 Representasi Graf

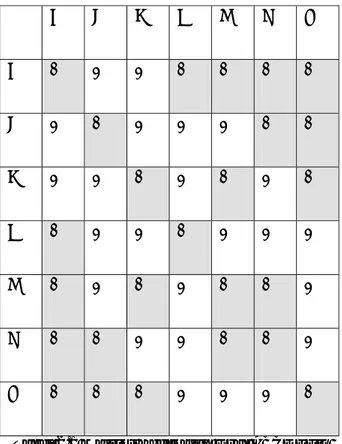
Untuk suatu graf dengan jumlah simpul sebanyak n, maka matriks kedekatan mempunyai ukuran n x n (n baris dan n kolom). Jika antara dua buah simpul terhubung maka elemen matriks bernilai 1, dan sebaliknya bernilai 0 jika tidak terhubung. Tabel matriks kedekatan untuk graf ABCDEFG dapat dilihat pada Tabel 2.1 : A B C D E F G A 0 1 1 0 0 0 0 B 1 0 1 1 1 0 0 C 1 1 0 1 0 1 0 D 0 1 1 0 1 1 1 E 0 1 0 1 0 0 1 F 0 0 1 1 0 0 1 G 0 0 0 1 1 1 0

Tabel 2.1 Matriks Kedekatan Graf ABCDEFG

Pada tabel diatas, elemen matriks kedekatan bernilai 0 untuk diagonal dan elemen yang tidak terhubung dengan simpul lain (elemen matriks bernilai 0 jika simpul tidak terhubung dengan simpul lainnya).

Ruang (memori) yang diperlukan untuk matriks kedekatan adalah : n x n =(N2)

Untuk graf tidak berarah :

- Ruang yang diperlukan = ½ N2 _{– ½ N}

- Derajat simpul i =

∑

= n j j i A 1 ] , [ Untuk graf berarah :

- Derajat luar (out degree) = jumlah dalam 1 baris (matriks) atau banyaknya busur dengan simpul V sebagai kepala.

- Derajat dalam (in degree) = jumlah dalam 1 kolom (matriks) atau banyaknya busur dengan simpul V sebagai ekor.

2. Senarai Kedekatan (Adjacency List)

Pada simpul x dapat dianggap sebagai suatu senarai yang terdiri dari simpul pada graf yang berdekatan dengan x. Representasi senarai kedekatan mempunyai kesamaan fleksibilitas dengan matriks kedekatan, akan tetapi representasi ini lebih tersusun rapi.

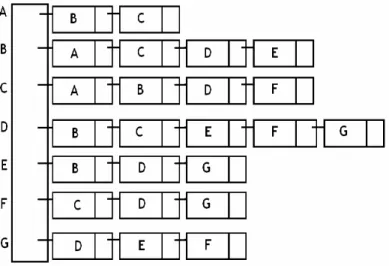
Ruang (memori) yang diperlukan untuk n simpul dan e sisi pada graf tidak berarah = n head node + 2e node list.

Gambar 2.5 Senarai kedekatan graf ABCDEFG

2.2 Permasalahan Optimasi

2.2.1 Penyelesaian Masalah Optimasi

Secara umum, penyelesaian masalah pencarian jalur terpendek dapat dilakukan dengan menggunakan dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional diterapkan dengan perhitungan matematis biasa, sedangkan metode heuristik diterapkan dengan perhitungan kecerdasan buatan.

1. Metode Konvensional

Metode konvensional adalah metode yang menggunakan perhitungan matematis biasa. . Ada beberapa metode konvensional yang biasa digunakan untuk melakukan pencarian jalur terpendek, diantaranya: algoritma Djikstraa, algoritma Floyd-Warshall, dan algoritma Bellman-Ford

2. Metode Heuristik

Metode Heuristik adalah sub bidang dari kecerdasan buatan yang digunakan untuk melakukan pencarian dan optimasi. Ada beberapa algoritma pada metode heuristik yang biasa digunakan dalam permasalahan optimasi, diantaranya algoritma genetika, algoritma semut, logika fuzzy, jaringan syaraf tiruan, pencarian tabu, simulated annealing, dan lain-lain.

2.2.2 Permasalahan Jalur Terpendek (Shortest Path Problem)

Jalur terpendek adalah suatu jaringan pengarahan perjalanan dimana sesorang pengarah jalan ingin menentukan jalur terpendek antara dua kota, berdasarkan beberapa jalur alternatif yang tersedia, dimana titik tujuan hanya satu. Gambar 2.6 menunjukkan suatu graf ABCDEFG yang berarah dan tidak berbobot.

Gambar 2.6 Graf ABCDEFG

Pada gambar diatas, misalkan kita dari kota A ingin menuju Kota G. Untuk menuju kota G, dapat dipilih beberapa jalur yang tersedia :

A Æ B Æ C Æ D Æ E Æ G A Æ B Æ C Æ D Æ F Æ G A Æ B Æ C Æ D Æ G A Æ B Æ C Æ F Æ G A Æ B Æ D Æ E Æ G A Æ B Æ D Æ F Æ G A Æ B Æ D Æ G A Æ B Æ E Æ G A Æ C Æ D Æ E Æ G A Æ C Æ D Æ F Æ G A Æ C Æ D Æ G A Æ C Æ F Æ G

Berdasarkan data diatas, dapat dihitung jalur terpendek dengan mencari jarak antara jalur-jalur tersebut. Apabila jarak antar jalur belum diketahui, jarak dapat dihitung berdasarkan koordinat kota-kota tersebut, kemudian menghitung jalur terpendek yang dapat dilalui.

2.3 Algoritma Semut

Algoritma Semut diadopsi dari perilaku koloni semut yang dikenal sebagai sistem semut (Dorigo, 1996). Secara alamiah koloni semut mampu menemukan rute terpendek dalam perjalanan dari sarang ke tempat-tempat sumber makanan. Koloni semut dapat menemukan rute terpendek antara sarang dan sumber makanan berdasarkan jejak kaki pada lintasan yang telah dilalui. Semakin banyak semut yang melalui suatu lintasan, maka akan semakin jelas bekas jejak kakinya. Hal ini akan menyebabkan lintasan yang dilalui semut dalam jumlah sedikit, semakin lama akan semakin berkurang kepadatan semut yang melewatinya, atau bahkan akan tidak dilewati sama sekali. Sebaliknya lintasan yang dilalui semut dalam jumlah banyak, semakin lama akan semakin bertambah kepadatan semut yang melewatinya, atau bahkan semua semut akan melalui lintasan tersebut.

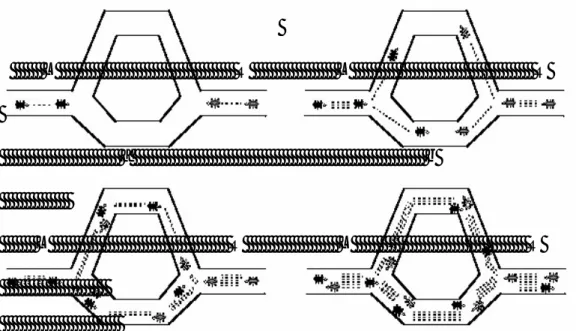
Gambar 2.1 menujukkan perjalanan semut dalam menemukan jalur terpendek dari sarang ke sumber makanan.

L R L R a b L R L R c d Gambar 2.7 Perjalanan semut menemukan sumber makanan.

Gambar 2.7.a di atas menunjukkan ada dua kelompok semut yang akan melakukan perjalanan. Satu kelompok bernama L yaitu kepompok yang berangkat dari arah kiri yang merupakan sarang semut dan kelompok lain yang bernama kelompok R yang berangkat dari kanan yang merupakan sumber makanan. Kedua kelompok semut dari titik berangkat sedang dalam posisi pengambilan keputusan jalan sebelah mana yang akan diambil. Kelompok semut L membagi dua kelompok lagi. Sebagian melalui jalan atas dan sebagian melalui jalan bawah. Hal ini juga berlaku pada kelompok semut R. Gambar 2.7.b dan gambar 2.7.c menunjukkan bahwa kelompok semut berjalan pada kecepatan yang sama dengan meninggalkan feromon atau jejak kaki di jalan yang telah dilalui. Feromon yang ditinggalkan oleh kumpulan semut yang melalui jalan atas telah mengalami banyak penguapan karena semut yang melalui jalan atas berjumlah lebih sedikit dari pada jalan yang di bawah. Hal ini dikarenakan jarak yang ditempuh lebih

panjang daripada jalan bawah. Sedangkan feromon yang berada di jalan bawah, penguapannya cenderung lebih lama. Karena semut yang melalui jalan bawah lebih banyak daripada semut yang melalui jalan atas. Gambar 2.7.d menunjukkan bahwa semut-semut yang lain pada akhirnya memutuskan untuk melewati jalan bawah karena feromon yang ditinggalkan masih banyak. Sedangkan feromon pada jalan atas sudah banyak menguap sehingga semut-semut tidak memilih jalan atas tersebut. Semakin banyak semut yang melalui jalan bawah maka semakin banyak semut yang mengikutinya.

Demikian juga dengan jalan atas, semakin sedikit semut yang melalui jalan atas, maka feromon yang ditinggalkan semakin berkurang bahkan hilang. Dari sinilah kemudian terpilihlah jalur terpendek antara sarang dan sumber makanan.

Dalam algoritma semut, diperlukan beberapa variabel dan langkah-langkah untuk menentukan jalur terpendek, yaitu:

Langkah 1 :

a. Inisialisasi harga parameter-parameter algoritma. Parameter-parameter yang di inisialisasikan adalah :

1. Intensitas jejak semut antar kota dan perubahannya (τij)

2. Banyak kota (n) termasuk koordinat (x,y) atau jarak antar kota (dij)

3. Kota berangkat dan kota tujuan 4. Tetapan siklus-semut (Q)

6. Tetapan pengendali visibilitas (β), nilai β ≥ 0 7. Visibilitas antar kota = 1/dij (ηij)

8. Banyak semut (m)

9. Tetapan penguapan jejak semut (ρ) , nilai ρ harus > 0 dan < 1 untuk mencegah jejak pheromone yang tak terhingga.

10. Jumlah siklus maksimum (NCmax) bersifat tetap selama algoritma

dijalankan, sedangkan τij akan selalu diperbaharui harganya pada setiap

siklus algoritma mulai dari siklus pertama (NC=1) sampai tercapai jumlah siklus maksimum (NC=NCmax) atau sampai terjadi konvergensi.

b. Inisialisasi kota pertama setiap semut.

Setelah inisialisasi τij dilakukan, kemudian m semut ditempatkan pada kota

pertama tertentu secara acak. Langkah 2 :

Pengisian kota pertama ke dalam tabu list. Hasil inisialisasi kota pertama setiap semut dalam langkah 1 harus diisikan sebagai elemen pertama tabu list. Hasil dari langkah ini adalah terisinya elemen pertama tabu list setiap semut dengan indeks kota tertentu, yang berarti bahwa setiap tabuk(1)bisa berisi indeks

kota antara 1 sampai n sebagaimana hasil inisialisasi pada langkah 1. Langkah 3 :

Penyusunan rute kunjungan setiap semut ke setiap kota. Koloni semut yang sudah terdistribusi ke sejumlah atau setiap kota, akan mulai melakukan

perjalanan dari kota pertama masing-masing sebagai kota asal dan salah satu kota-kota lainnya sebagai kota-kota tujuan. Kemudian dari kota-kota kedua masing-masing, koloni semut akan melanjutkan perjalanan dengan memilih salah satu dari kota-kota yang tidak terdapat pada tabuk sebagai kota tujuan selanjutnya. Perjalanan

koloni semut berlangsung terus menerus sampai semua kota satu persatu

dikunjungi atau telah menempati tabuk. Jika s menyatakan indeks urutan

kunjungan, kota asal dinyatakan sebagai tabuk(s) dan kota-kota lainnya

dinyatakan sebagai {N-tabuk}, maka untuk menentukan kota tujuan digunakan

persamaan probabilitas kota untuk dikunjungi sebagai berikut :

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ik' ik' ij ij k ij k p untuk j∈{N-tabuk} ………… (1) dan 0 pk_ij = , untuk j lainnya ……….(2)

dengan i sebagai indeks kota asal dan j sebagai indeks kota tujuan. Langkah 4 :

a. Perhitungan panjang rute setiap semut.

Perhitungan panjang rute tertutup (length closed tour) atau Lk setiap semut

dilakukan setelah satu siklus diselesaikan oleh semua semut. Perhitungan ini dilakukan berdasarkan tabuk masing-masing dengan persamaan berikut :

∑

− = + + = n 1 1 s tabu (s),tabu (s 1) ) 1 ( tabu ), n ( tabu k d k k d k k L ………(3)

dengan dij adalah jarak antara kota i ke kota j yang dihitung berdasarkan

2 j i 2 j i ij (x x ) (y y ) d = − + − ………..(4)

b. Pencarian rute terpendek.

Setelah Lk setiap semut dihitung, akan didapat harga minimal panjang rute

tertutup setiap siklus atau LminNC dan harga minimal panjang rute tertutup secara

keseluruhan adalah atau Lmin.

c. Perhitungan perubahan harga intensitas jejak kaki semut antar kota.

Koloni semut akan meninggalkan jejak-jejak kaki pada lintasan antar kota yang dilaluinya. Adanya penguapan dan perbedaan jumlah semut yang lewat, menyebabkan kemungkinan terjadinya perubahan harga intensitas jejak kaki semut antar kota. Persamaan perubahan ini adalah :

∑

= τ Δ = τ Δ m 1 k k ij ij ……….(5) dengan k ij τ

Δ adalah perubahan harga intensitas jejak kaki semut antar kota setiap semut yang dihitung berdasarkan persamaan

k k ij =_LQ τ

Δ , untuk (i,j) ∈ kota asal dan kota tujuan dalam tabuk ………(6)

0 k ij = τ

Δ , untuk (i,j) lainnya ……….(7)

a. Perhitungan harga intensitas jejak kaki semut antar kota untuk siklus selanjutnya. Harga intensitas jejak kaki semut antar kota pada semua lintasan antar kota ada kemungkinan berubah karena adanya penguapan dan perbedaan jumlah semut yang melewati. Untuk siklus selanjutnya, semut yang akan melewati lintasan tersebut harga intensitasnya telah berubah. Harga intensitas jejak kaki semut antar kota untuk siklus selanjutnya dihitung dengan persamaan :

ij ij ij=ρ⋅τ +Δτ

τ ……….. (8)

b. Atur ulang harga perubahan intensitas jejak kaki semut antar kota.

Untuk siklus selanjutnya perubahan harga intensitas jejak semut antar kota perlu diatur kembali agar memiliki nilai sama dengan nol.

Langkah 6 :

Pengosongan tabu list, dan ulangi langkah 2 jika diperlukan. Tabu list perlu dikosongkan untuk diisi lagi dengan urutan kota yang baru pada siklus selanjutnya, jika jumlah siklus maksimum belum tercapai atau belum terjadi konvergensi. Algoritma diulang lagi dari langkah 2 dengan harga parameter intensitas jejak kaki semut antar kota yang sudah diperbaharui.

Diketahui suatu graph

Dengan jarak antar kota (dij) sebagai berikut:

A B C D E A 0 5 7 3 B 5 0 4 C 7 4 0 5 D 3 0 4 E 5 4 0

Parameter – parameter yang digunakan adalah : Alfa (α) = 1.00

Beta (β) = 1.00 Rho (ρ) = 0.50 Tij awal = 0.01

Maksimum siklus (NCmax) = 2

Tetapan siklus semut (Q) = 1 Banyak semut (m) = 5

Dari jarak kota yang telah diketahui dapat dihitung visibilitas antar kota (ηij) =

1/dij A B C D E

A B C D E A 0 0.2 0.143 0.33 0 B 0.2 0 0.25 0 0 C 0.1 0.25 0 0 0.2 D 0.3 0 0 0 0.25 E 0 0 0.2 0.25 0 Siklus ke -1 : Isi Tabu awal : A B C D E Untuk t=1

Jumlah semut Tiap kota = Kota A = 1 Kota B = 1 Kota C = 1 Kota D = 1 Kota E = 1 Semut ke – 1: - Tabu list = A

- Probabilitas dari kota A ke setiap kota berikutnya dapat dihitung dengan

persamaan

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ' ik ' ik ij ij k ij k

p , untuk j anggota dari tabu.

untuk Σ[tij]α.[ηij]β = (0.01*0) + (0.01*0.2) + (0.01*0.143) + (0.01*0.33)

= 0.00676.

Dengan demikian dapat dihitung probabilitas dari kota A menuju setiap kota =

Kota A = 0.00

Kota C = (0.01)1.00 . (0.143)1.00 / 0.00676 = 0.211 Kota D = (0.01)1.00 . (0.33)1.00 / 0.00676 = 0.492 Kota E = 0.00

- Probabilitas Komulatif = 0.000 0.295 0.507 1.000 1.000

- Bilangan random yang dibangkitkan = 0.699 maka kota yang terpilih adalah kota D

- Tabu List = A D Semut ke – 2 :

- Tabu list = B

- Probabilitas dari kota B ke kota berikutnya dapat dihitung dengan

persamaan

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ik' ik' ij ij k ij k

p , untuk j anggota dari tabu.

untuk Σ[tij]α.[ηij]β = (0.01*0.2) + (0.01*0.25) = 0.0045.

Dengan demikian dapat dihitung probabilitas dari kota B menuju kota =

Kota A = (0.01)1.00 _{. (0.2)}1.00 _{/ 0.0045 = 0.444} Kota B = 0.00 Kota C = (0.01)1.00 _{. (0.25)}1.00 _{/ 0.0045 = 0.556} Kota D = 0.00 Kota E = 0.00 - Probabilitas Komulatif = 0.444 0.444 1.000 1.000 1.000

- Bilangan random yang dibangkitkan = 0.635 maka kota yang terpilih adalah kota C

- Tabu List = B C Semut ke – 3 :

- Probabilitas dari kota C ke kota berikutnya dapat dihitung dengan persamaan

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ' ik ' ik ij ij k ij k

p , untuk j anggota dari tabu.

untuk Σ[tij]α.[ηij]β = (0.01*0.143) + (0.01*0.25) +(0.01*0.2) = 0.005929. Dengan demikian dapat dihitung probabilitas dari kota C menuju kota =

Kota A = (0.01)1.00 . (0.143)1.00 / 0.005929 = 0.241 Kota B = (0.01)1.00 _{. (0.25)}1.00 _{/ 0.005929 = 0.422} Kota C = 0.00 Kota D = 0.00 Kota E = (0.01)1.00 . (0.2)1.00 / 0.005929 = 0.337 - Probabilitas Komulatif = 0.241 0.663 0.663 0.663 1.000

- Bilangan random yang dibangkitkan = 0.368 maka kota yang terpilih adalah kota B

Tabu List = C B Semut ke – 4 :

- Tabu list = D

- Probabilitas dari kota D ke setiap kota berikutnya dapat dihitung dengan

persamaan

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ' ik ' ik ij ij k ij k

p , untuk j anggota dari tabu.

untuk Σ[tij]α.[ηij]β = (0.01*0.3) + (0.01*0) + (0.01*0) + (0.01*0) +

(0.01*0.25) = 0.00583.

Dengan demikian dapat dihitung probabilitas dari kota D menuju kota =

Kota A = (0.01)1.00 . (0.3)1.00 / 0.00583 = 0.514 Kota B = 0.00

Kota C = 0.00 Kota D = 0.00

Kota E = (0.01)1.00 . (0.25)1.00 / 0.00583 = 0.428 - Probabilitas Komulatif = 0.514 0.514 0.514 0.514 0.942

- Bilangan random yang dibangkitkan = 0.3783 maka kota yang terpilih adalah kota A

Tabu List = D A Semut ke – 5 :

- Tabu list = E

- Probabilitas dari kota E ke setiap kota berikutnya dapat dihitung dengan

persamaan

[ ] [ ]

[ ] [ ]

∑

− ∈ β α β α η ⋅ τ η ⋅ τ = } tabu N { ' k ik' ik' ij ij k ij k

p , untuk j anggota dari tabu.

untuk Σ[tij]α.[ηij]β = (0.01*0) + (0.01*0) + (0.01*0.2) + (0.01*0.25) +

(0.01*0) = 0.0045.

Dengan demikian dapat dihitung probabilitas dari kota E menuju kota =

Kota A = 0.00 Kota B = 0.00 Kota C = (0.01)1.00 . (0.2)1.00 / 0.0045 = 0.444 Kota D = (0.01)1.00 . (0.25)1.00 / 0.0045 = 0.556 Kota E = 0.00 - Probabilitas Komulatif = 0.00 0.00 0.444 1.00 1.00

- Bilangan random yang dibangkitkan = 0.1953 maka kota yang terpilih adalah kota C

Tabu List = E C

Perhitungan akan dilanjutkan hingga semut telah menyelesaikan perjalanannya mengunjungi tiap-tiap kota. Hal ini akan berulang hingga sesuai dengan NCmax yang telah ditentukan atau telah mencapai konvergen. Kemudian akan ditentukan jarak terpendek dari semut dari msaing-masing siklus.